Effect of Using Multi-Year Land Use Land Cover and Monthly LAI Inputs on the Calibration of a Distributed Hydrologic Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Model Description
2.3. Data Preparation
2.4. Land Cover Data
2.5. Sensitivity Analysis
2.6. Model Calibration and Validation
2.7. Dynamically Dimensioned Search Algorithm (DDS)
2.8. Model Performance
3. Results
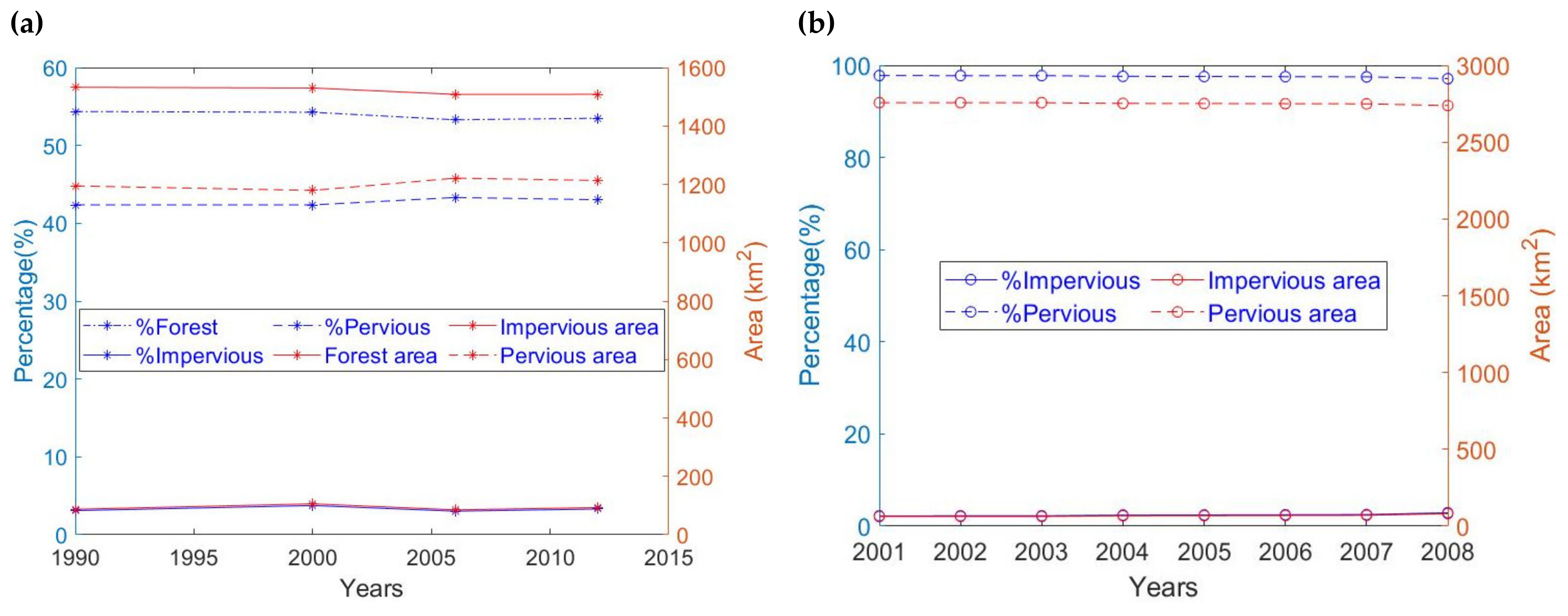
3.1. Land Use Land Cover Variations
3.2. Sensitivity Analysis
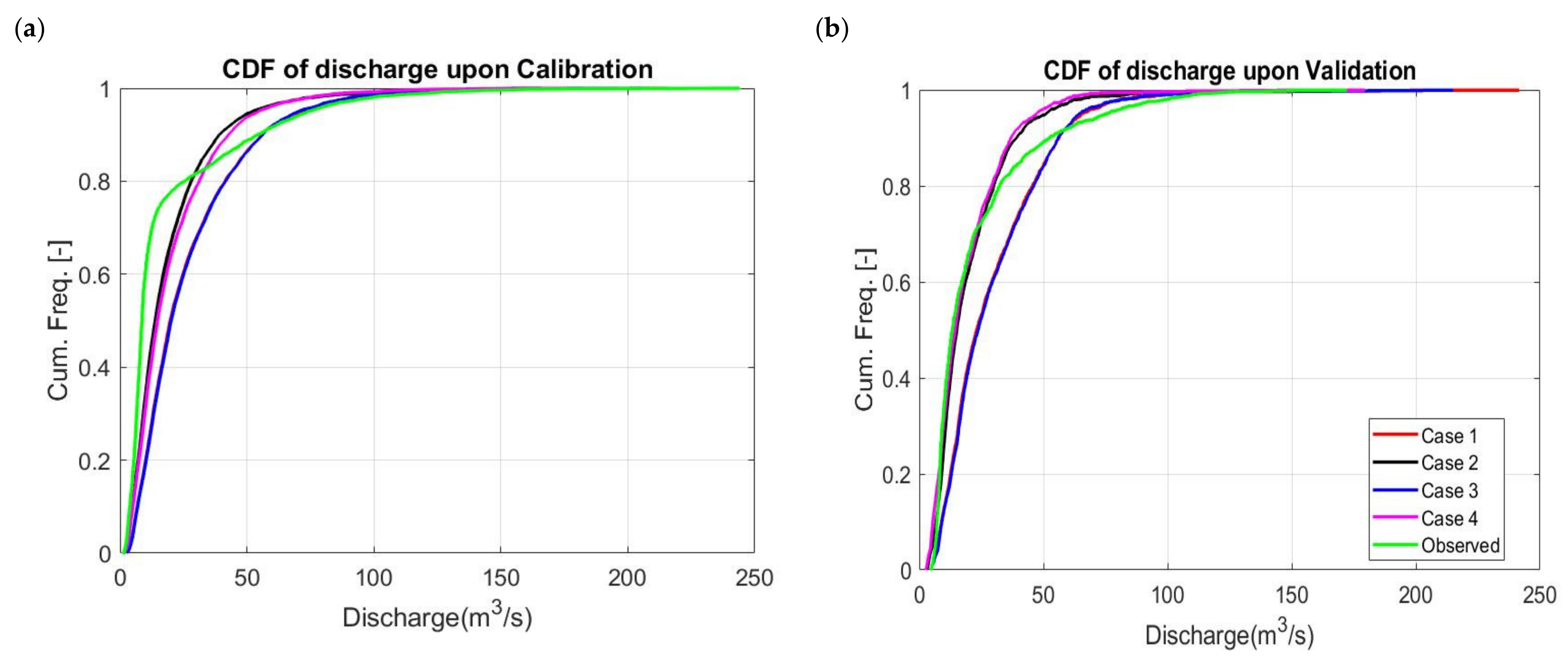
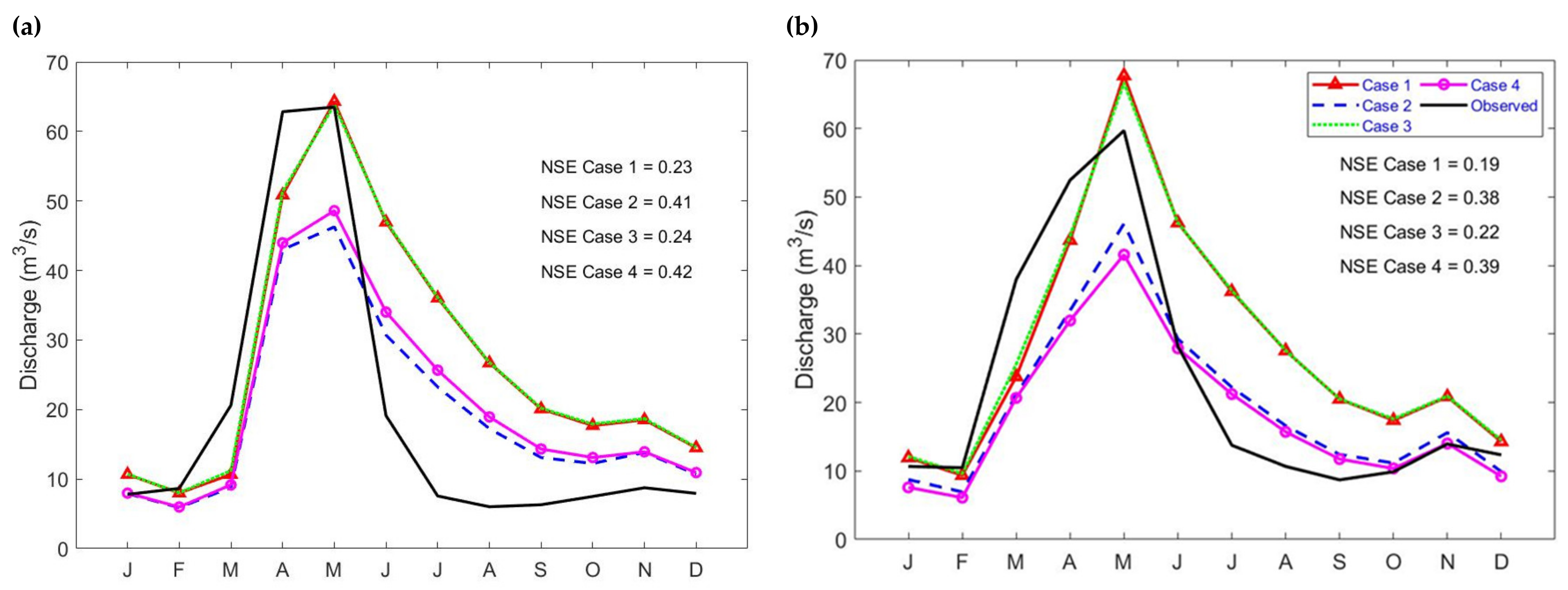
3.3. Model Calibration
3.4. Model Validation
3.5. Hydrological Indices
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
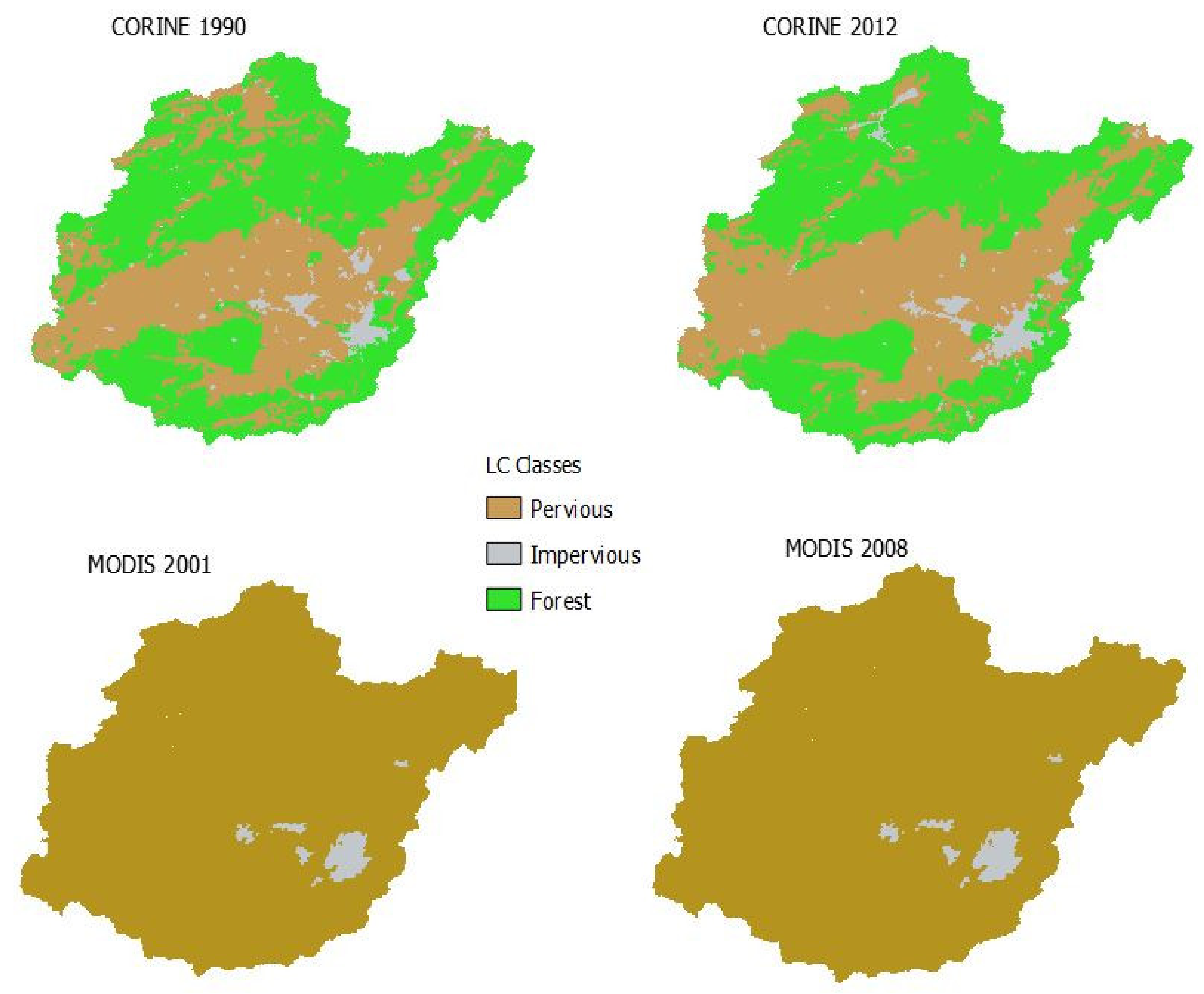
| CORINE Land Cover Classes | Years | |||||||
|---|---|---|---|---|---|---|---|---|
| 1990 | 2000 | 2006 | 2012 | |||||
| %Land Cover | Area km2 | %Land Cover | Area km2 | %Land Cover | Area km2 | %Land Cover | Area km2 | |
| Continuous urban fabric | 0.05 | 1.33 | 0.04 | 1.23 | 0.07 | 1.92 | 0.57 | 16.13 |
| Discontinuous urban fabric | 1.35 | 38.15 | 1.48 | 41.77 | 1.12 | 31.49 | 0.67 | 18.98 |
| Industrial or commercial units | 0.41 | 11.62 | 0.48 | 13.45 | 0.58 | 16.22 | 0.57 | 15.99 |
| Road and rail networks | 0.01 | 0.37 | 0.05 | 1.49 | 0.02 | 0.64 | 0.05 | 1.52 |
| Airports | 0.31 | 8.77 | 0.31 | 8.83 | 0.31 | 8.83 | 0.32 | 9.02 |
| Mineral extraction sites | 0.08 | 2.14 | 0.11 | 3.20 | 0.14 | 3.93 | 0.17 | 4.85 |
| Construction sites | - | - | 0.02 | 0.60 | 0.02 | 0.57 | 0.05 | 1.44 |
| Green urban areas | 0.02 | 0.48 | 0.02 | 0.67 | 0.02 | 0.68 | 0.01 | 0.25 |
| Sport and leisure facilities | 0.22 | 6.15 | 0.21 | 5.83 | 0.18 | 5.14 | 0.21 | 5.89 |
| Non-irrigated arable land | 18.07 | 509.51 | 18.08 | 509.72 | 5.36 | 151.21 | 5.30 | 149.53 |
| Permanently irrigated land | 8.29 | 233.87 | 8.23 | 232.04 | 17.45 | 492.00 | 17.42 | 491.15 |
| Pastures | 2.25 | 63.45 | 2.15 | 60.74 | 4.64 | 130.93 | 4.43 | 125.00 |
| Complex cultivation patterns | 4.19 | 118.15 | 3.97 | 111.93 | 6.25 | 176.34 | 6.26 | 176.63 |
| Land principally occupied by agriculture with significant areas of natural vegetation | 9.56 | 269.55 | 9.39 | 264.73 | 9.60 | 270.74 | 9.61 | 270.95 |
| Broad-leaved forest | 0.78 | 21.88 | 0.82 | 23.07 | 0.51 | 14.37 | 0.48 | 13.45 |
| Coniferous forest | 0.12 | 3.44 | 0.14 | 4.02 | 0.14 | 3.87 | 0.14 | 4.06 |
| Mixed forest | 0.74 | 20.87 | 0.75 | 21.25 | 0.27 | 7.51 | 0.24 | 6.82 |
| Natural grasslands | 25.49 | 718.63 | 25.38 | 715.67 | 31.65 | 892.50 | 32.97 | 929.63 |
| Transitional woodland-shrub | 11.32 | 319.20 | 11.29 | 318.43 | 3.55 | 100.22 | 2.19 | 61.87 |
| Beaches dunes sands | 0.12 | 3.38 | 0.10 | 2.66 | 0.23 | 6.60 | 0.23 | 6.46 |
| Bare rocks | 0.37 | 10.46 | 0.37 | 10.30 | 0.42 | 11.96 | 0.43 | 12.15 |
| Glaciers and perpetual snow | 15.41 | 434.62 | 15.41 | 434.52 | 16.71 | 471.20 | 16.81 | 473.98 |
| Inland marshes | 0.62 | 17.40 | 0.63 | 17.64 | 0.17 | 4.64 | 0.35 | 9.81 |
| Water bodies | 0.04 | 1.10 | 0.40 | 11.17 | 0.41 | 11.45 | 0.33 | 9.42 |
| Parameters | Range | Normalized Sensitivity |
|---|---|---|
| Rotfrcoffore | 0.9–0.999 | 1.00000 |
| pet_aforest | 0.2999–1.3 | 0.48665 |
| pet_apervi | 0.2999–1.3 | 0.14471 |
| Ptflowconst | 0.6462–0.9506 | 0.14227 |
| Infshapef | 1.0–4.0 | 0.09453 |
| ptflowdb | −0.3726–0.1870999 | 0.07084 |
| pet_aimpervi | 0.29999–1.3000 | 0.01222 |
| ptflowclay | 0.0001–0.00289 | 0.01091 |
| rotfrcofimp | 0.9–0.9499 | 0.00945 |
| ptfkssand | 0.006–0.02599 | 0.00339 |
| ptfksconst | −1.2–0.28499 | 0.00841 |
| ptfhigconst | 0.5358–1.1232 | 0.00793 |
| rotfrcofclay | 0.9–0.999 | 0.00339 |
| expslwintflw | 0.05–0.3 | 0.00095 |
| rechargcoef | 0–50.0 | 0.00044 |
| intrecesslp | 0–10.0 | 0.00040 |
| slwintreceks | 1.0–30.0 | 0.00040 |
| pet_bb | 0–1.5 | 0.00039 |
| pet_cc | −2.0–0 | 0.00031 |
| Rotfrcofsand | 0.001–0.09 | 0.00002 |
References
- Jin, X.; Jin, Y.; Yuan, D.; Mao, X. Effects of land-use data resolution on hydrologic modelling, a case study in the upper reach of the Heihe River, Northwest China. Ecol. Modell. 2019, 404, 61–68. [Google Scholar] [CrossRef]
- Moges, E.; Demissie, Y.; Larsen, L.; Yassin, F. Review: Sources of hydrological model uncertainties and advances in their analysis. Water 2021, 13, 28. [Google Scholar] [CrossRef]
- Gan, T.Y.; Biftu, G.F. Effects of model complexity and structure, parameter interactions and data on watershed modeling. In Calibration of Watershed Models; American Geophysical Union: Washington, DC, USA, 2004; pp. 317–329. ISBN 087590355X. [Google Scholar]
- Bulygina, N.; Gupta, H. Estimating the uncertain mathematical structure of a water balance model via Bayesian data assimilation. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Son, K.; Sivapalan, M. Improving model structure and reducing parameter uncertainty in conceptual water balance models through the use of auxiliary data. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Lohani, A.K. Rainfall-Runoff Analysis and Modelling; National Institute of Hydrology: Roorkee, India, 2018. [Google Scholar]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Vrugt, J.A. Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation. Environ. Model. Softw. 2016, 75, 273–316. [Google Scholar] [CrossRef]
- Doherty, J. PEST: Model-Independent Parameter Estimation, User Manual, 5th ed.; Watermark Numerical Computing: Brisbane, Australia, 2010. [Google Scholar]
- Camargos, C.; Julich, S.; Houska, T.; Bach, M.; Breuer, L. Effects of input data content on the uncertainty of simulatingwater resources. Water 2018, 10, 621. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A Review on Hydrological Models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Younghun, J.; Venkatesh, M. Uncertainty Quantification in Flood Inundation Mapping Using Generalized Likelihood Uncertainty Estimate and Sensitivity Analysis. J. Hydrol. Eng. 2012, 17, 507–520. [Google Scholar] [CrossRef]
- Muleta, M.K.; McMillan, J.; Amenu, G.G.; Burian, S.J. Bayesian Approach for Uncertainty Analysis of an Urban Storm Water Model and Its Application to a Heavily Urbanized Watershed. J. Hydrol. Eng. 2013, 18, 1360–1371. [Google Scholar] [CrossRef]
- Rampinelli, C.G.; Knack, I.; Smith, T. Flood Mapping Uncertainty from a Restoration Perspective: A Practical Case Study. Water 2020, 12, 1948. [Google Scholar] [CrossRef]
- Bouslihim, Y.; Rochdi, A.; El Amrani Paaza, N.; Liuzzo, L. Understanding the effects of soil data quality on SWAT model performance and hydrological processes in Tamedroust watershed (Morocco). J. Afr. Earth Sci. 2019, 160, 103616. [Google Scholar] [CrossRef]
- Ficchì, A.; Perrin, C.; Andréassian, V. Impact of temporal resolution of inputs on hydrological model performance: An analysis based on 2400 flood events. J. Hydrol. 2016, 538, 454–470. [Google Scholar] [CrossRef]
- Li, C.Z.; Wang, H.; Liu, J.; Yan, D.H.; Yu, F.L.; Zhang, L. Effect of calibration data series length on performance and optimal parameters of hydrological model. Water Sci. Eng. 2010, 3, 378–393. [Google Scholar] [CrossRef]
- Ilampooranan, I.; Schnoor, J.L.; Basu, N.B. Crops as sensors: Using crop yield data to increase the robustness of hydrologic and biogeochemical models. J. Hydrol. 2020, 125599. [Google Scholar] [CrossRef]
- Orth, R.; Staudinger, M.; Seneviratne, S.I.; Seibert, J.; Zappa, M. Does model performance improve with complexity? A case study with three hydrological models. J. Hydrol. 2015, 523, 147–159. [Google Scholar] [CrossRef]
- Srivastava, A.; Kumari, N.; Maza, M. Hydrological Response to Agricultural Land Use Heterogeneity Using Variable Infiltration Capacity Model. Water Resour. Manag. 2020, 34, 3779–3794. [Google Scholar] [CrossRef]
- Aghsaei, H.; Mobarghaee Dinan, N.; Moridi, A.; Asadolahi, Z.; Delavar, M.; Fohrer, N.; Wagner, P.D. Effects of dynamic land use/land cover change on water resources and sediment yield in the Anzali wetland catchment, Gilan, Iran. Sci. Total Environ. 2020, 712, 136449. [Google Scholar] [CrossRef] [PubMed]
- Setyorini, A.; Khare, D.; Pingale, S.M. Simulating the impact of land use/land cover change and climate variability on watershed hydrology in the Upper Brantas basin, Indonesia. Appl. Geomat. 2017, 9, 191–204. [Google Scholar] [CrossRef]
- Boongaling, C.G.K.; Faustino-Eslava, D.V.; Lansigan, F.P. Modeling land use change impacts on hydrology and the use of landscape metrics as tools for watershed management: The case of an ungauged catchment in the Philippines. Land Use Policy 2018, 72, 116–128. [Google Scholar] [CrossRef]
- Das, P.; Behera, M.D.; Patidar, N.; Sahoo, B.; Tripathi, P.; Behera, P.R.; Srivastava, S.K.; Roy, P.S.; Thakur, P.; Agrawal, S.P.; et al. Impact of LULC change on the runoff, base flow and evapotranspiration dynamics in eastern Indian river basins during 1985–2005 using variable infiltration capacity approach. J. Earth Syst. Sci. 2018, 127, 1–19. [Google Scholar] [CrossRef]
- Tesemma, Z.K.; Wei, Y.; Peel, M.C.; Western, A.W. The effect of year-to-year variability of leaf area index on Variable Infiltration Capacity model performance and simulation of runoff. Adv. Water Resour. 2015, 83, 310–322. [Google Scholar] [CrossRef]
- Chen, Y.; Niu, J.; Kang, S.; Zhang, X. Effects of irrigation on water and energy balances in the Heihe River basin using VIC model under different irrigation scenarios. Sci. Total Environ. 2018, 645, 1183–1193. [Google Scholar] [CrossRef]
- Al-Safi, H.I.J.; Sarukkalige, P.R. The application of conceptual modelling to assess the impacts of future climate change on the hydrological response of the Harvey River catchment. J. Hydro-Environ. Res. 2020, 28, 22–33. [Google Scholar] [CrossRef]
- Bisht, D.S.; Mohite, A.R.; Jena, P.P.; Khatun, A.; Chatterjee, C.; Raghuwanshi, N.S.; Singh, R.; Sahoo, B. Impact of climate change on streamflow regime of a large Indian river basin using a novel monthly hybrid bias correction technique and a conceptual modeling framework. J. Hydrol. 2020, 590, 125448. [Google Scholar] [CrossRef]
- Singh Jasrotia, A.; Baru, D.; Kour, R.; Ahmad, S.; Kour, K. Hydrological modeling to simulate stream flow under changing climate conditions in Jhelum catchment, western Himalaya. J. Hydrol. 2021, 593, 125887. [Google Scholar] [CrossRef]
- Paul, P.K.; Kumari, N.; Panigrahi, N.; Mishra, A.; Singh, R. Implementation of cell-to-cell routing scheme in a large scale conceptual hydrological model. Environ. Model. Softw. 2018, 101, 23–33. [Google Scholar] [CrossRef]
- Uysal, G.; Şorman, A.A.; Şensoy, A. Streamflow Forecasting Using Different Neural Network Models with Satellite Data for a Snow Dominated Region in Turkey. Procedia Eng. 2016, 154, 1185–1192. [Google Scholar] [CrossRef]
- Ertas, C.; Akkol, B.; Coskun, C.; Uysal, G.; Sorman, A.A.; Sensoy, A. Evaluation of Probabilistic Streamflow Forecasts Based on EPS for a Mountainous Basin in Turkey. Procedia Eng. 2016, 154, 490–497. [Google Scholar] [CrossRef]
- Tekeli, A.E.; Akyürek, Z.; Şorman, A.A.; Şensoy, A.; Şorman, A.Ü. Using MODIS snow cover maps in modeling snowmelt runoff process in the eastern part of Turkey. Remote Sens. Environ. 2005, 97, 216–230. [Google Scholar] [CrossRef]
- Dembélé, M.; Hrachowitz, M.; Savenije, H.H.G.; Mariéthoz, G.; Schaefli, B. Improving the Predictive Skill of a Distributed Hydrological Model by Calibration on Spatial Patterns with Multiple Satellite Data Sets. Water Resour. Res. 2020, 56, 1–26. [Google Scholar] [CrossRef]
- Demirel, M.C.; Koch, J.; Mendiguren, G.; Stisen, S. Spatial pattern oriented multicriteria sensitivity analysis of a distributed hydrologic model. Water 2018, 1188. [Google Scholar] [CrossRef]
- Dembélé, M.; Ceperley, N.; Zwart, S.J.; Salvadore, E.; Mariethoz, G.; Schaefli, B. Potential of satellite and reanalysis evaporation datasets for hydrological modelling under various model calibration strategies. Adv. Water Resour. 2020, 143. [Google Scholar] [CrossRef]
- Höllering, S.; Wienhöfer, J.; Ihringer, J.; Samaniego, L.; Zehe, E. Regional analysis of parameter sensitivity for simulation of streamflow and hydrological fingerprints. Hydrol. Earth Syst. Sci. 2018, 22, 203–220. [Google Scholar] [CrossRef]
- Samaniego, L.; Kumar, R.; Attinger, S. Multiscale parameter regionalization of a grid-based hydrologic model at the mesoscale. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Rakovec, O.; Kumar, R.; Mai, J.; Cuntz, M.; Thober, S.; Zink, M.; Attinger, S.; Schäfer, D.; Schrön, M.; Samaniego, L. Multiscale and Multivariate Evaluation of Water Fluxes and States over European River Basins. J. Hydrometeorol. 2016, 17, 287–307. [Google Scholar] [CrossRef]
- Grekousis, G.; Mountrakis, G.; Kavouras, M. An overview of 21 global and 43 regional land-cover mapping products. Int. J. Remote Sens. 2015, 36, 5309–5335. [Google Scholar] [CrossRef]
- Cieślak, I.; Biłozor, A.; Źróbek-Sokolnik, A.; Zagroba, M. The use of geographic databases for analyzing changes in land cover—A case study of the region of warmia and mazury in Poland. ISPRS Int. J. Geo-Inf. 2020, 9, 358. [Google Scholar] [CrossRef]
- An, Y.; Zhao, W.; Zhang, Y. Accuracy assessments of the GLOBCOVER dataset using global statistical inventories and FLUXNET site data. Acta Ecol. Sin. 2012, 32, 314–320. [Google Scholar] [CrossRef]
- Tchuenté, A.T.K.; Roujean, J.L.; de Jong, S.M. Comparison and relative quality assessment of the GLC2000, GLOBCOVER, MODIS and ECOCLIMAP land cover data sets at the African continental scale. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 207–219. [Google Scholar] [CrossRef]
- Box, G.E.P.; Meyer, R.D. An Analysis for Unreplicated Fractional Factorials. Technometrics 1986, 28, 11–18. [Google Scholar] [CrossRef]
- Razavi, S.; Sheikholeslami, R.; Gupta, H.V.; Haghnegahdar, A. VARS-TOOL: A toolbox for comprehensive, efficient, and robust sensitivity and uncertainty analysis. Environ. Model. Softw. 2019, 112, 95–107. [Google Scholar] [CrossRef]
- Clark, M.P.; Kavetski, D.; Fenicia, F. Pursuing the method of multiple working hypotheses for hydrological modeling. Water Resour. Res. 2011, 47, 1–16. [Google Scholar] [CrossRef]
- Rakovec, O.; Hill, M.C.; Clark, M.P.; Weerts, A.H.; Teuling, A.J.; Uijlenhoet, R. Distributed evaluation of local sensitivity analysis (DELSA), with application to hydrologic models. Water Resour. Res. 2014, 50, 409–426. [Google Scholar] [CrossRef]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’ sensitivity analysis of a complex environmental model. Environ. Model. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]
- Chu-Agor, M.L.; Muñoz-Carpena, R.; Kiker, G.; Emanuelsson, A.; Linkov, I. Exploring vulnerability of coastal habitats to sea level rise through global sensitivity and uncertainty analyses. Environ. Model. Softw. 2011, 26, 593–604. [Google Scholar] [CrossRef]
- Tolson, B.A.; Shoemaker, C.A. Dynamically dimensioned search algorithm for computationally efficient watershed model calibration. Water Resour. Res. 2007, 43, 1–16. [Google Scholar] [CrossRef]
- Chu, J.; Peng, Y.; Ding, W.; Li, Y. A Heuristic dynamically dimensioned search with sensitivity information (HDDS-S) and application to river basin management. Water 2015, 7, 2214. [Google Scholar] [CrossRef]
- Jackson, E.K.; Roberts, W.; Nelsen, B.; Williams, G.P.; Nelson, E.J.; Ames, D.P. Introductory overview: Error metrics for hydrologic modelling—A review of common practices and an open source library to facilitate use and adoption. Environ. Model. Softw. 2019, 119, 32–48. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Andréassian, V. A review of efficiency criteria suitable for evaluating low-flow simulations. J. Hydrol. 2012, 420–421, 171–182. [Google Scholar] [CrossRef]
- Kling, H.; Gupta, H. On the development of regionalization relationships for lumped watershed models: The impact of ignoring sub-basin scale variability. J. Hydrol. 2009, 373, 337–351. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash-Sutcliffe and Kling-Gupta efficiency scores. Hydrol. Earth Syst. Sci. Discuss. 2019, 1–7. [Google Scholar] [CrossRef]
- Stagl, J.C.; Hattermann, F.F. Impacts of Climate Change on Riverine Ecosystems: Alterations of Ecologically Relevant Flow Dynamics in the Danube River and Its Major Tributaries. Water 2016, 8, 566. [Google Scholar] [CrossRef]
- Chirachawala, C.; Shrestha, S.; Babel, M.S.; Virdis, S.G.P.; Wichakul, S. Evaluation of global land use/land cover products for hydrologic simulation in the Upper Yom River Basin, Thailand. Sci. Total Environ. 2020, 708, 135148. [Google Scholar] [CrossRef]
- Brown, A.E.; Western, A.W.; McMahon, T.A.; Zhang, L. Impact of forest cover changes on annual streamflow and flow duration curves. J. Hydrol. 2013, 483, 39–50. [Google Scholar] [CrossRef]
- Deckers, D. Predicting Discharge at Ungauged Catchments: Parameter Estimation through the Method of Regionalisation; University of Twente: Enschede, The Netherlands, 2006. [Google Scholar]
- Sahraei, S.; Asadzadeh, M.; Unduche, F. Signature-based multi-modelling and multi-objective calibration of hydrologic models: Application in flood forecasting for Canadian Prairies. J. Hydrol. 2020, 588, 125095. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X.; Zhang, Y.; Liu, C. Incorporating vegetation dynamics noticeably improved performance of hydrological model under vegetation greening. Sci. Total Environ. 2018, 643, 610–622. [Google Scholar] [CrossRef]
- Gao, J.; Sheshukov, A.Y.; Yen, H.; Kastens, J.H.; Peterson, D.L. Impacts of incorporating dominant crop rotation patterns as primary land use change on hydrologic model performance. Agric. Ecosyst. Environ. 2017, 247, 33–42. [Google Scholar] [CrossRef]
- Hardwick, S.R.; Toumi, R.; Pfeifer, M.; Turner, E.C.; Nilus, R.; Ewers, R.M. The relationship between leaf area index and microclimate in tropical forest and oil palm plantation: Forest disturbance drives changes in microclimate. Agric. For. Meteorol. 2015, 201, 187–195. [Google Scholar] [CrossRef]
- Di, N.; Wang, Y.; Clothier, B.; Liu, Y.; Jia, L.; Xi, B.; Shi, H. Modeling soil evaporation and the response of the crop coefficient to leaf area index in mature Populus tomentosa plantations growing under different soil water availabilities. Agric. For. Meteorol. 2019, 264, 125–137. [Google Scholar] [CrossRef]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.; et al. An overview of current applications, challenges, and future trends in distributed process-based models in hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar] [CrossRef]
- Elga, S.; Jan, B.; Okke, B. Hydrological modelling of urbanized catchments: A review and future directions. J. Hydrol. 2015, 529, 62–81. [Google Scholar] [CrossRef]
- Petrucci, G.; Bonhomme, C. The dilemma of spatial representation for urban hydrology semi-distributed modelling: Trade-offs among complexity, calibration and geographical data. J. Hydrol. 2014, 517, 997–1007. [Google Scholar] [CrossRef]
- Sapač, K.; Medved, A.; Rusjan, S.; Bezak, N. Investigation of low- and high-flow characteristics of karst catchments under climate change. Water 2019, 11, 925. [Google Scholar] [CrossRef]
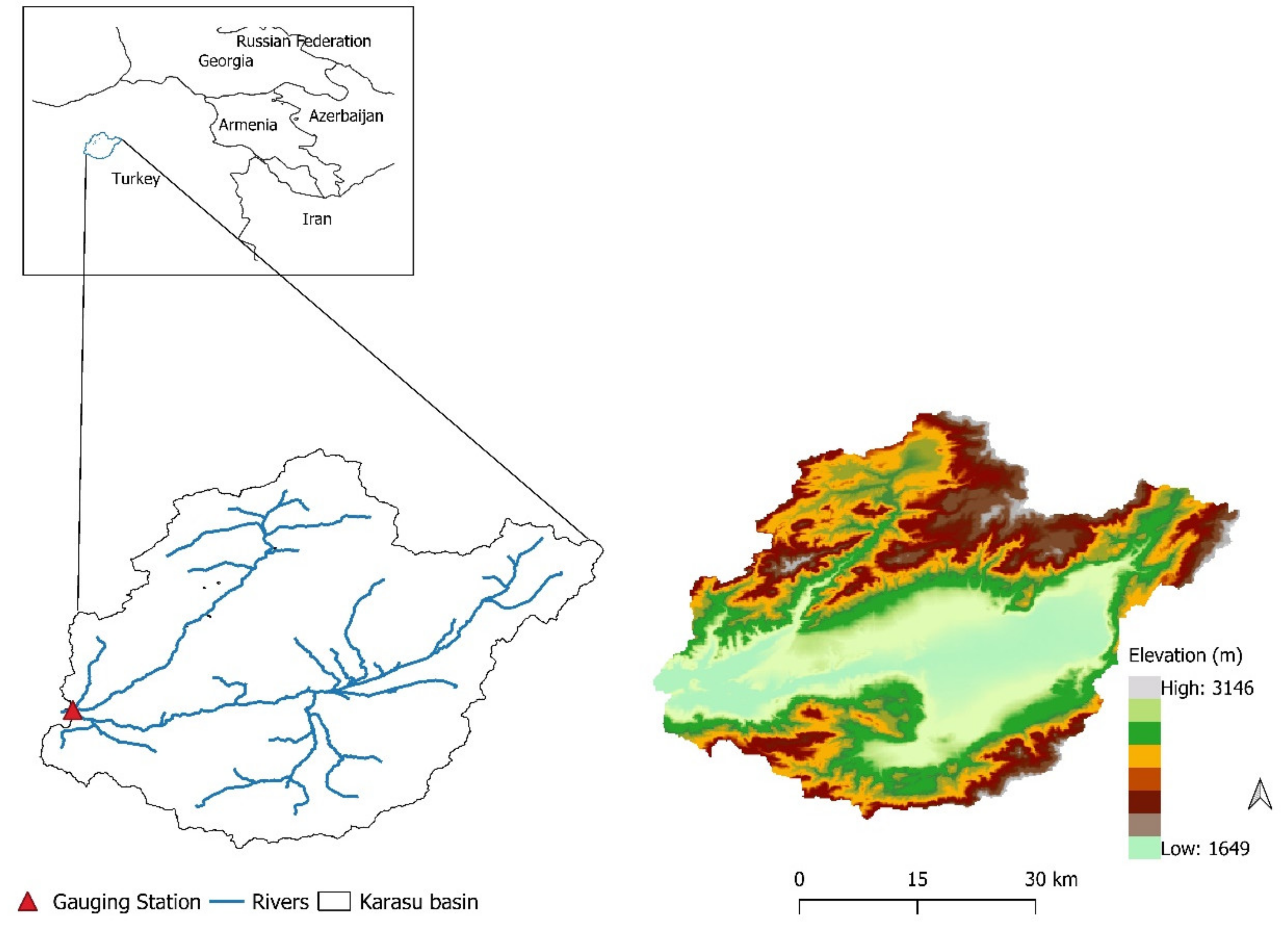

| Variable | Description | Spatial Resolution | Source |
|---|---|---|---|
| Q (daily) | Streamflow | Point | Karasu Aşağı Kağdariç station (#6695500-GRDC ID or #2154-Local ID) |
| P (daily) | Precipitation | 0.25° | E-OBS 20.0e |
| ETref (daily) | Reference evapotranspiration | 0.25° | E-OBS 20.0e |
| Tavg (daily) | Average air temperature | 0.25° | E-OBS 20.0e, MODIS |
| Land cover | Pervious, impervious and forest | 0.001953° | CORINE, MODIS, GlobcoverV2 |
| DEM data | Slope, aspect, flow accumulation and direction | 0.001953° | SRTM |
| Geology class | Two main geological formations | 0.001953° | EUROPEAN SOIL DATABASE |
| Soil class | Soil texture data | 0.001953° | HARMONIZED WORLD SOIL DATABASE |
| Ase | Land Cover Input | PET Correction with LAI |
|---|---|---|
| 1 | 1 year Globcover dataset | No |
| 2 | 1 year Globcover dataset | Yes |
| 3 | MODIS and CORINE datasets | No |
| 4 | MODIS and CORINE datasets | Yes |
| NSE (-) | NSEln | NSEinv | PBIAS (%) | KGE | MAE (m3/s) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cal | Val | Cal | Val | Cal | Val | Cal | Val | Cal | Val | Cal | Val | |
| Case 1 | 0.23 | 0.19 | −0.36 | −0.08 | −0.63 | −0.38 | 43.5 | 29.2 | 0.42 | 0.51 | 15.9 | 15.1 |
| Case 2 | 0.41 | 0.38 | 0.05 | 0.26 | −0.61 | −0.48 | 2.8 | −10.8 | 0.54 | 0.52 | 12 | 10.8 |
| Case 3 | 0.24 | 0.22 | −0.36 | −0.07 | −0.63 | −0.36 | 44.2 | 30.2 | 0.42 | 0.51 | 15.9 | 15 |
| Case 4 | 0.42 | 0.39 | −0.02 | 0.23 | −0.65 | −0.89 | 8.8 | −16.7 | 0.54 | 0.48 | 12.3 | 10.6 |
| Hydrological Indices | Case | Difference (%) |
|---|---|---|
| Annual Discharge | Case 1 | 43.63 |
| Case 2 | 2.89 * | |
| Case 3 | 44.37 | |
| Case 4 | 8.96 | |
| High flows (Q10) | Case 1 | 1.48 * |
| Case 2 | 15.21 | |
| Case 3 | 1.93 | |
| Case 4 | 11.53 | |
| Low flows (Q90) | Case 1 | 2.96 |
| Case 2 | 0.97 * | |
| Case 3 | 3.05 | |
| Case 4 | 1.16 | |
| Wet flows | Case 1 | 91.97 |
| Case 2 | 29.50 * | |
| Case 3 | 92.18 | |
| Case 4 | 40.21 | |
| Dry flows | Case 1 | 2.88 |
| Case 2 | 22.7 | |
| Case 3 | 1.62 * | |
| Case 4 | 21.1 | |
| Base flow | Case 1 | 43.45 |
| Case 2 | 2.78 * | |
| Case 3 | 44.19 | |
| Case 4 | 8.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Busari, I.O.; Demirel, M.C.; Newton, A. Effect of Using Multi-Year Land Use Land Cover and Monthly LAI Inputs on the Calibration of a Distributed Hydrologic Model. Water 2021, 13, 1538. https://doi.org/10.3390/w13111538
Busari IO, Demirel MC, Newton A. Effect of Using Multi-Year Land Use Land Cover and Monthly LAI Inputs on the Calibration of a Distributed Hydrologic Model. Water. 2021; 13(11):1538. https://doi.org/10.3390/w13111538
Chicago/Turabian StyleBusari, Ibrahim Olayode, Mehmet Cüneyd Demirel, and Alice Newton. 2021. "Effect of Using Multi-Year Land Use Land Cover and Monthly LAI Inputs on the Calibration of a Distributed Hydrologic Model" Water 13, no. 11: 1538. https://doi.org/10.3390/w13111538
APA StyleBusari, I. O., Demirel, M. C., & Newton, A. (2021). Effect of Using Multi-Year Land Use Land Cover and Monthly LAI Inputs on the Calibration of a Distributed Hydrologic Model. Water, 13(11), 1538. https://doi.org/10.3390/w13111538








