Analysis of the Spatiotemporal Annual Rainfall Variability in the Wadi Cheliff Basin (Algeria) over the Period 1970 to 2018
Abstract
1. Introduction
2. Methodology
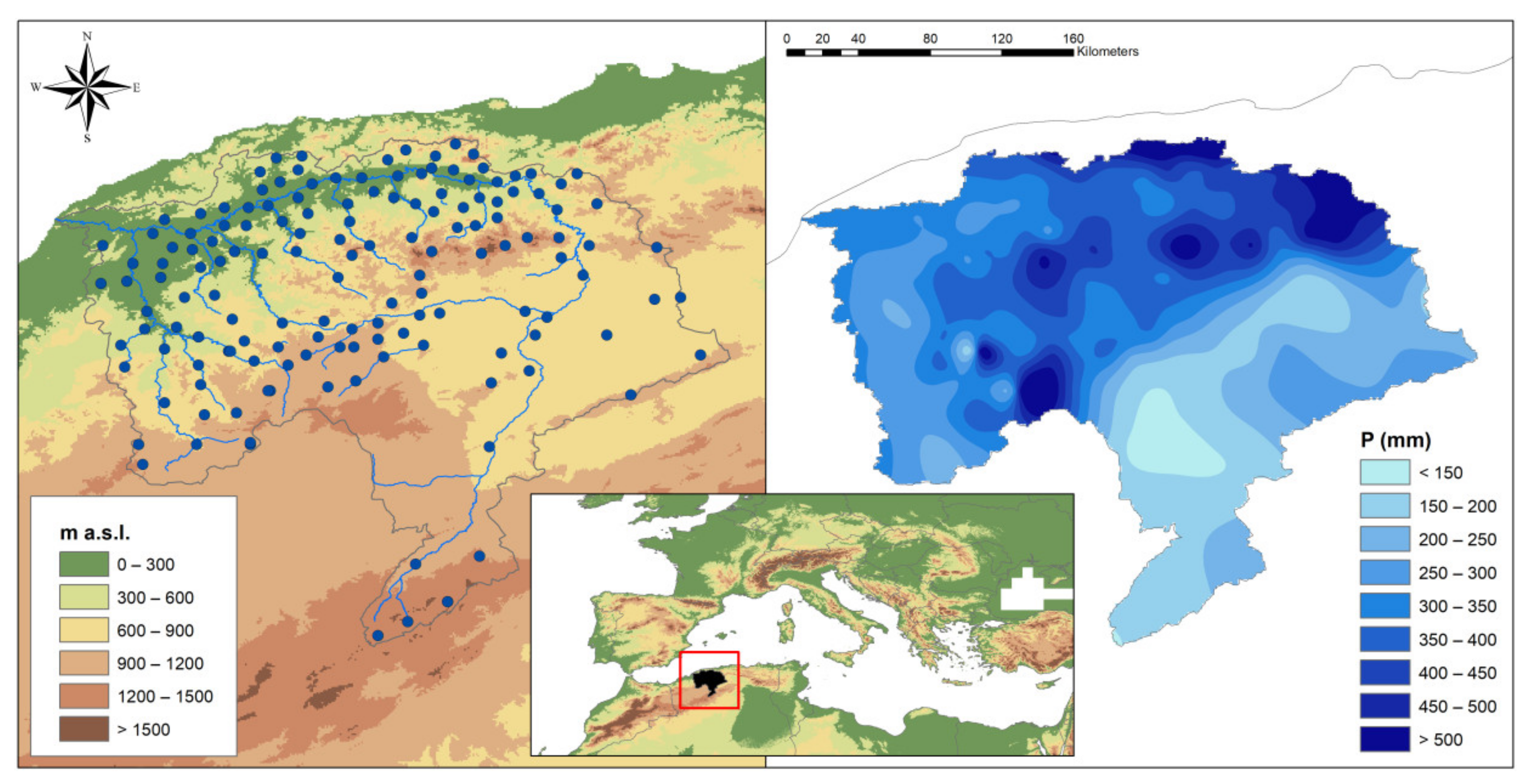
3. Study Area and Data
4. Results and Discussion
5. Conclusions
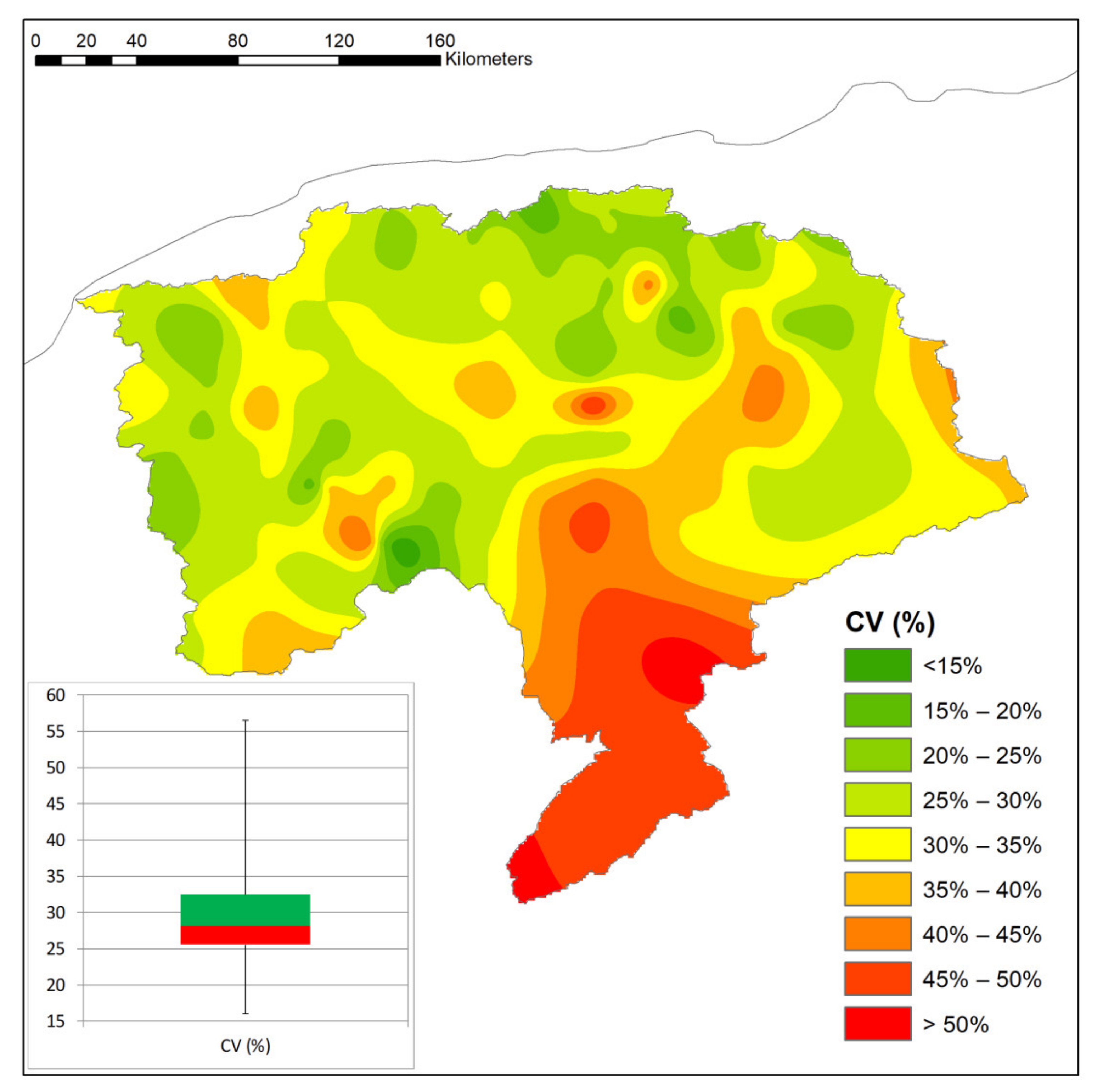
- the CV range between about 16.0% and 56.5%, thus evidencing high variability typical of the Mediterranean basin;
- a spatial gradient in the CV values between the southern and the northern sides of the basin has been identified, with the highest values detected in the mountainous areas of the south side of the region and the northern areas showing the lowest CV values;
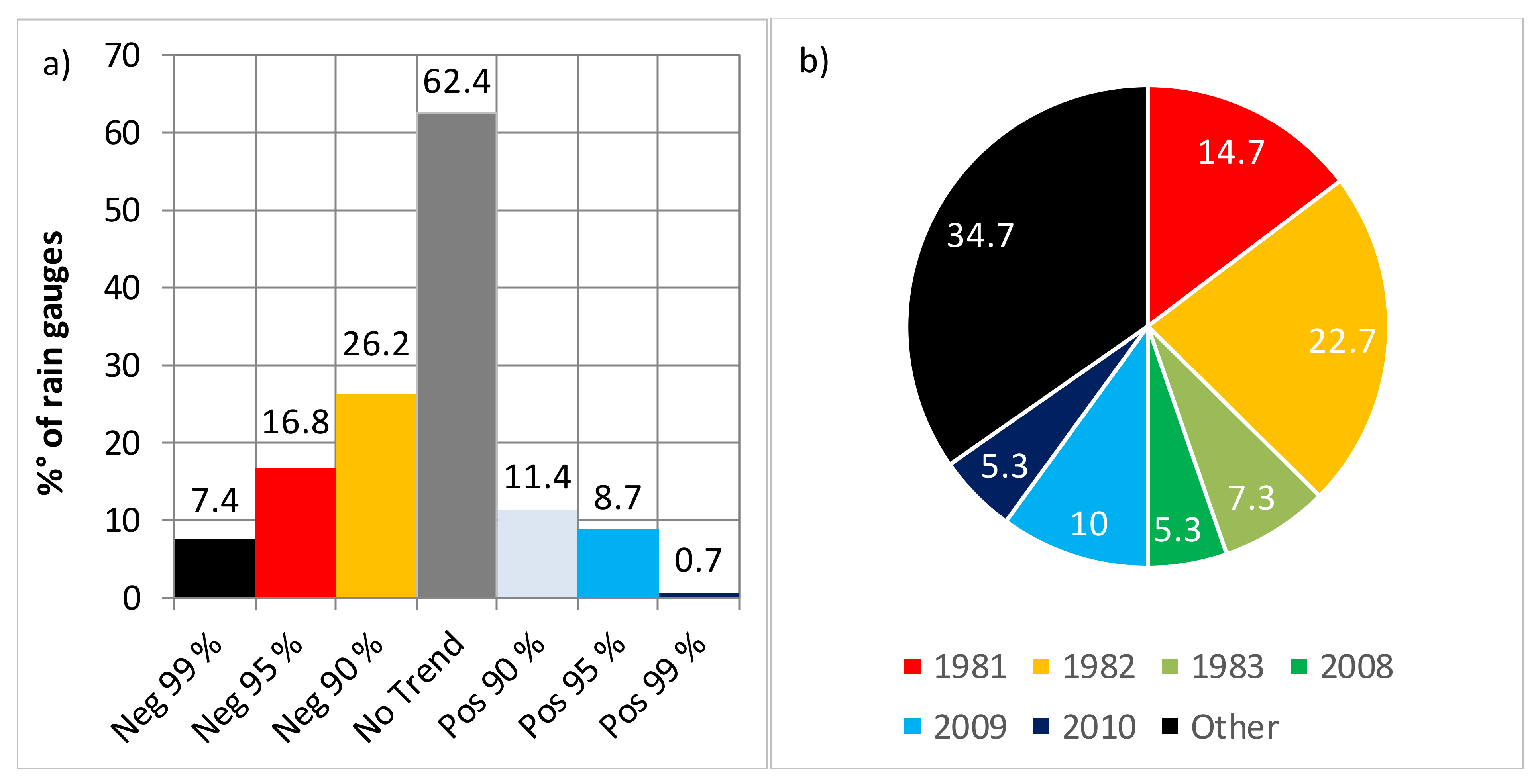
- a general negative trend has been evidenced for the annual rainfall;
- the negative trend mainly involved the northern and the western-central area of the basin while a positive trend has been evidenced in the eastern side of the basin;
- the years 1981, 1982, and 1983 can be considered the most probable change point years for the largest number of stations in the basin.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IPCC. Summary for Policymakers. In Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Caloiero, T.; Caloiero, P.; Frustaci, F. Long-term precipitation trend analysis in Europe and in the Mediterranean basin. Water Environ. J. 2018, 32, 433–445. [Google Scholar] [CrossRef]
- Zittis, G. Observed rainfall trends and precipitation uncertainty in the vicinity of the Mediterranean, Middle East and North Africa. Theor. Appl. Climatol. 2018, 134, 1207–1230. [Google Scholar] [CrossRef]
- Onyutha, C. Identification of sub–trends from hydro–meteorological series. Stoch. Environ. Res. Risk Assess. 2016, 30, 189–205. [Google Scholar] [CrossRef]
- Longobardi, A.; Villani, P. Trend analysis of annual and seasonal rainfall time series in the Mediterranean area. Int. J. Climatol. 2010, 30, 1538–1546. [Google Scholar] [CrossRef]
- Maheras, P.; Tolika, K.; Anagnostopoulou, C.; Vafiadis, M.; Patrikas, I.; Flocas, H. On the relationships between circulation types and changes in rainfall variability in Greece. Int. J. Climatol. 2001, 24, 1695–1712. [Google Scholar] [CrossRef]
- Altin, T.B.; Barak, B. Changes and trends in total yearly precipitation of the Antalya District, Turkey. Procedia Soc. Behav. Sci. 2014, 120, 586–599. [Google Scholar] [CrossRef]
- Shohami, D.; Dayan, U.; Morin, E. Warming and drying of the eastern Mediterranean: Additional evidence from trend analysis. J. Geophys. Res. 2011, 116, D22101. [Google Scholar] [CrossRef]
- Ziv, B.; Saaroni, H.; Pargament, R.; Harpaz, T.; Alpert, P. Trends in rainfall regime over Israel, 1975–2010, and their relationship to large-scale variability. Reg. Environ. Chang. 2014, 14, 1751–1764. [Google Scholar] [CrossRef]
- Donat, M.G.; Peterson, T.C.; Brunet, M.; King, A.D.; Almazroui, M.; Kolli, R.K.; Boucherf, D.; Al-Mulla, A.Y.; Nour, A.Y.; Aly, A.A.; et al. Changes in extreme temperature and precipitation in the Arab Region: Long-term trends and variability related to ENSO and NAO. Int. J. Climatol. 2014, 34, 581–592. [Google Scholar] [CrossRef]
- Meddi, M.; Hubert, P. Impact de la modification du régime pluviométrique sur les ressources en eau du Nord–Ouest de l’Algérie. In Hydrology of the Mediterranean and Semiarid Regions; Servat Najem, E., Leduc, W., Shakeel, E.A., Eds.; IAHS Publ.: Wallingford, UK, 2003; pp. 229–235. [Google Scholar]
- Goubanova, K.; Li, L. Extremes in temperature and precipitation around the Mediterranean basin in an ensemble of future climate scenario simulations. Glob. Planet. Chang. 2007, 57, 27–42. [Google Scholar] [CrossRef]
- Tramblay, Y.; El Adlouni, S.; Servat, E. Trends and variability in extreme precipitation indices over Maghreb countries. Nat. Hazards Earth Syst. Sci. 2013, 13, 3235–3248. [Google Scholar] [CrossRef]
- Elmeddahi, Y.; Issaadi, A.; Mahmoudi, H.; Tahar Abbes, M.; Goossen, M.F.A. Effect of climate change on water resources of the Algerian Middle Cheliff basin. Desalination Water Treat. 2014, 52, 2073–2081. [Google Scholar] [CrossRef]
- Ragab, R.; Prudhomme, C. Climate change and water resources management in arid and semi–arid regions: Prospective and challenges for the 21st Century. Biosyst. Eng. 2002, 81, 3–34. [Google Scholar] [CrossRef]
- Giorgi, F.; Lionello, P. Climate change projections for the Mediterranean region. Glob. Planet. Chang. 2008, 63, 90–104. [Google Scholar] [CrossRef]
- Giorgi, F. Climate change hot-spots. Geophys. Res. Lett. 2006, 33, L08707. [Google Scholar] [CrossRef]
- Longobardi, A.; Boulariah, O. Preliminary long term changes in inter–annual precipitation variability in a Mediterranean region. In Managing Water Resources for a Sustainable Future; Garrote, L., Tsakiris, G., Tsihrintzis, V., Vangelis, H., Tigkas, D., Eds.; EWRA Editorial Office: Athens, Greece, 2019; pp. 461–462. [Google Scholar]
- Conrad, V. The variability of precipitation. Mon. Weather Rev. 1941, 69, 5–11. [Google Scholar] [CrossRef]
- Giorgi, F.; Bi, X. Regional changes in surface climate interannual variability for the 21st century from ensembles of global model simulations. Geophys. Res. Lett. 2005, 32, L13701. [Google Scholar] [CrossRef]
- Pendergrass, A.G.; Knutti, R.; Lehner, F.; Deser, C.; Sanderson, B.M. Precipitation variability increases in a warmer climate. Sci. Rep. 2017, 7, 17966. [Google Scholar] [CrossRef]
- He, C.; Li, T. Does global warming amplify interannual climate variability? Clim. Dyn. 2019, 52, 2667–2684. [Google Scholar] [CrossRef]
- Gajbhiye, S.; Meshram, C.; Mirabbasi, R.; Sharma, S. Trend analysis of rainfall time series for Sindh river basin in India. Theor. Appl. Climatol. 2016, 125, 593–608. [Google Scholar] [CrossRef]
- Chandniha, S.K.; Meshram, S.G.; Adamowski, J.F.; Meshram, C. Trend analysis of precipitation in Jharkhand State, India. Theor. Appl. Climatol. 2017, 130, 261–274. [Google Scholar] [CrossRef]
- He, M.; Gautam, M. Variability and trends in precipitation, temperature and drought indices in the State of California. Hydrology 2016, 3, 14. [Google Scholar] [CrossRef]
- Młyński, D.; Cebulska, M.; Wałęga, A. Trends, Variability, and Seasonality of Maximum Annual Daily Precipitation in the Upper Vistula Basin, Poland. Atmosphere 2018, 9, 313. [Google Scholar] [CrossRef]
- Tian, W.; Liu, X.M.; Wang, K.W.; Bai, P.; Liang, K.; Liu, C.M. Evaluation of six precipitation products in the Mekong River Basin. Atmos. Res. 2021, 255, 105539. [Google Scholar] [CrossRef]
- Qi, B.Y.; Liu, H.H.; Zhao, S.F.; Liu, B.Y. Observed precipitation pattern changes and potential runoff generation capacity from 1961–2016 in the upper reaches of the Hanjiang River Basin, China. Atmos. Res. 2021, 254, 105392. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Hafner Publishing Company: New York, NY, USA, 1962. [Google Scholar]
- Pettitt, A.N. A non–parametric approach to the change point problem. Appl. Stat. 1979, 8, 126–135. [Google Scholar] [CrossRef]
- Insua-Costa, D.; Lemus-Canovas, M.; Miguez-Macho, G.; Llasat, M.C. Climatology and ranking of hazardous precipitation events in the western Mediterranean area. Atmos. Res. 2021, 255, 105521. [Google Scholar] [CrossRef]
- Muthoni, F.K.; Odongo, V.O.; Ochieng, J.; Mugalavai, E.M.; Mourice, S.K.; Hoesche-Zeledon, I.; Mwila, M.; Bekunda, M. Long-term spatial-temporal trends and variability of rainfall over Eastern and Southern Africa. Theor. Appl. Climatol. 2019, 137, 1869–1882. [Google Scholar] [CrossRef]
- Halifa-Martin, A.; Lorente-Plazas, R.; Pravia-Sarabia, E.; Montavez, J.P.; Jimenez-Guerrero, P. Atlantic and Mediterranean influence promoting an abrupt change in winter precipitation over the southern Iberian Peninsula. Atmos. Res. 2021, 253, 105485. [Google Scholar] [CrossRef]
- Del Rio, S.; Herrero, L.; Fraile, R.; Penas, A.P. Spatial distribution of recent rainfall trends in Spain (1961–2006). Int. J. Climatol. 2011, 31, 656–667. [Google Scholar]
- Coscarelli, R.; Gaudio, R.; Caloiero, T. Climatic trends: An investigation for a Calabrian basin (southern Italy). In The Basis of Civilization—Water Science? Rodda, J.C., Ubertini, L., Eds.; IAHS Publ.: Wallingford, UK, 2004; pp. 255–266. [Google Scholar]
- Longobardi, A.; Buttafuoco, G.; Caloiero, T.; Coscarelli, R. Spatial and temporal distribution of precipitation in a Mediterranean area (southern Italy). Environ. Earth Sci. 2016, 7, 189. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E. Application of the innovative trend analysis method for the trend analysis of rainfall anomalies in southern Italy. Water Resour. Manag. 2018, 32, 4971–4983. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Gaudio, R.; Leonardo, G.P. Precipitation trend and concentration in the Sardinia region. Theor. Appl. Climatol. 2019, 137, 297–307. [Google Scholar] [CrossRef]
- Scorzini, A.R.; Leopardi, M. Precipitation and temperature trends over central Italy (Abruzzo Region): 1951–2012. Theor. Appl. Climatol. 2019, 135, 959–977. [Google Scholar] [CrossRef]
- Gentilucci, M.; Barbieri, M.; Lee, H.S.; Zardi, D. Analysis of Rainfall Trends and Extreme Precipitation in the Middle Adriatic Side, Marche Region (Central Italy). Water 2019, 11, 1948. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Mancini, M. Trend detection of annual and seasonal rainfall in Calabria (southern Italy). Int. J. Climatol. 2011, 31, 44–56. [Google Scholar] [CrossRef]
- Lloyd-Hughes, B.; Saunders, M.A. Seasonal prediction of European spring precipitation from El Niño–Southern Oscillation and local sea surfaces temperatures. Int. J. Climatol. 2002, 22, 1–14. [Google Scholar] [CrossRef]
- Conte, M.; Giuffrida, A.; Tedesco, S. The Mediterranean Oscillation. Impact on Precipitation and Hydrology in Italy Climate Water; Publications of the Academy of Finland: Helsinki, Finland, 1989. [Google Scholar]
- Martín-Vide, J.; Lopez-Bustins, J.A. The Western Mediterranean Oscillation and rainfall in the Iberian Peninsula. Int. J. Climatol. 2006, 26, 1455–1475. [Google Scholar] [CrossRef]
- Meddi, M.; Assani, A.A.; Meddi, H. Temporal variability of annual rainfall in the Macta and Tafna catchments, northwestern Algeria. Water Resour. Manag. 2010, 24, 3817–3833. [Google Scholar] [CrossRef]
- Singla, S.; Mahe, G.; Dieulin, C.; Driouech, F.; Milano, M.; El Guelai, F.Z.; Ardoin-Bardin, S. Évolution des relations pluie-débit sur des bassins versants du Maroc. In Global Change: Facing Risks and Threats to Water Resources; Servat, E., Demuth, S., Dezetter, A., Daniell, T., Ferrari, E., Ijjaali, M., Jabrane, R., van Lanen, H.A.J., Huang, Y., Eds.; IAHS Publ.: Wallingford, UK, 2010; pp. 679–687. [Google Scholar]
- Schilling, J.; Freier, K.P.; Hertig, E.; Scheffran, J. Climate change, vulnerability and adaptation in North Africa with focus on Morocco. Agric. Ecosyst. Environ. 2012, 156, 12–26. [Google Scholar] [CrossRef]
- Mariotti, A.; Pan, Y.; Zeng, N.; Alessandri, A. Long–term climate change in the Mediterranean region in the midst of decadal variability. Clim. Dyn. 2015, 44, 1437–1456. [Google Scholar] [CrossRef]
- Sarr, M.A.; Zorome, M.; Seidou, O.; Bryant, C.R.; Gachon, P. Recent trends in selected extreme precipitation indices in Senegal-A changepoint approach. J. Hydrol. 2013, 505, 326–334. [Google Scholar] [CrossRef]
- Tarhule, A.; Tarhule-Lips, R.F.A. Discontinuities in precipitation series in the West African Sahel. Phys. Geogr. 2001, 22, 430–448. [Google Scholar] [CrossRef]
- De Longueville, F.; Hountondji, Y.C.; Kindo, I.; Gemenne, F.; Ozer, P. Long-Term Analysis of Rainfall and Temperature Data in Burkina Faso (1950–2013). Int. J. Climatol. 2016, 36, 4393–4405. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Achite, M.; Caloiero, T.; Wałęga, A.; Krakauer, N.; Hartani, T. Analysis of the Spatiotemporal Annual Rainfall Variability in the Wadi Cheliff Basin (Algeria) over the Period 1970 to 2018. Water 2021, 13, 1477. https://doi.org/10.3390/w13111477
Achite M, Caloiero T, Wałęga A, Krakauer N, Hartani T. Analysis of the Spatiotemporal Annual Rainfall Variability in the Wadi Cheliff Basin (Algeria) over the Period 1970 to 2018. Water. 2021; 13(11):1477. https://doi.org/10.3390/w13111477
Chicago/Turabian StyleAchite, Mohammed, Tommaso Caloiero, Andrzej Wałęga, Nir Krakauer, and Tarek Hartani. 2021. "Analysis of the Spatiotemporal Annual Rainfall Variability in the Wadi Cheliff Basin (Algeria) over the Period 1970 to 2018" Water 13, no. 11: 1477. https://doi.org/10.3390/w13111477
APA StyleAchite, M., Caloiero, T., Wałęga, A., Krakauer, N., & Hartani, T. (2021). Analysis of the Spatiotemporal Annual Rainfall Variability in the Wadi Cheliff Basin (Algeria) over the Period 1970 to 2018. Water, 13(11), 1477. https://doi.org/10.3390/w13111477









