Study on the Horizontal Distribution Law of Flood Water and Sediment Factors under the Effect of Vegetation on a Curved Beach
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design
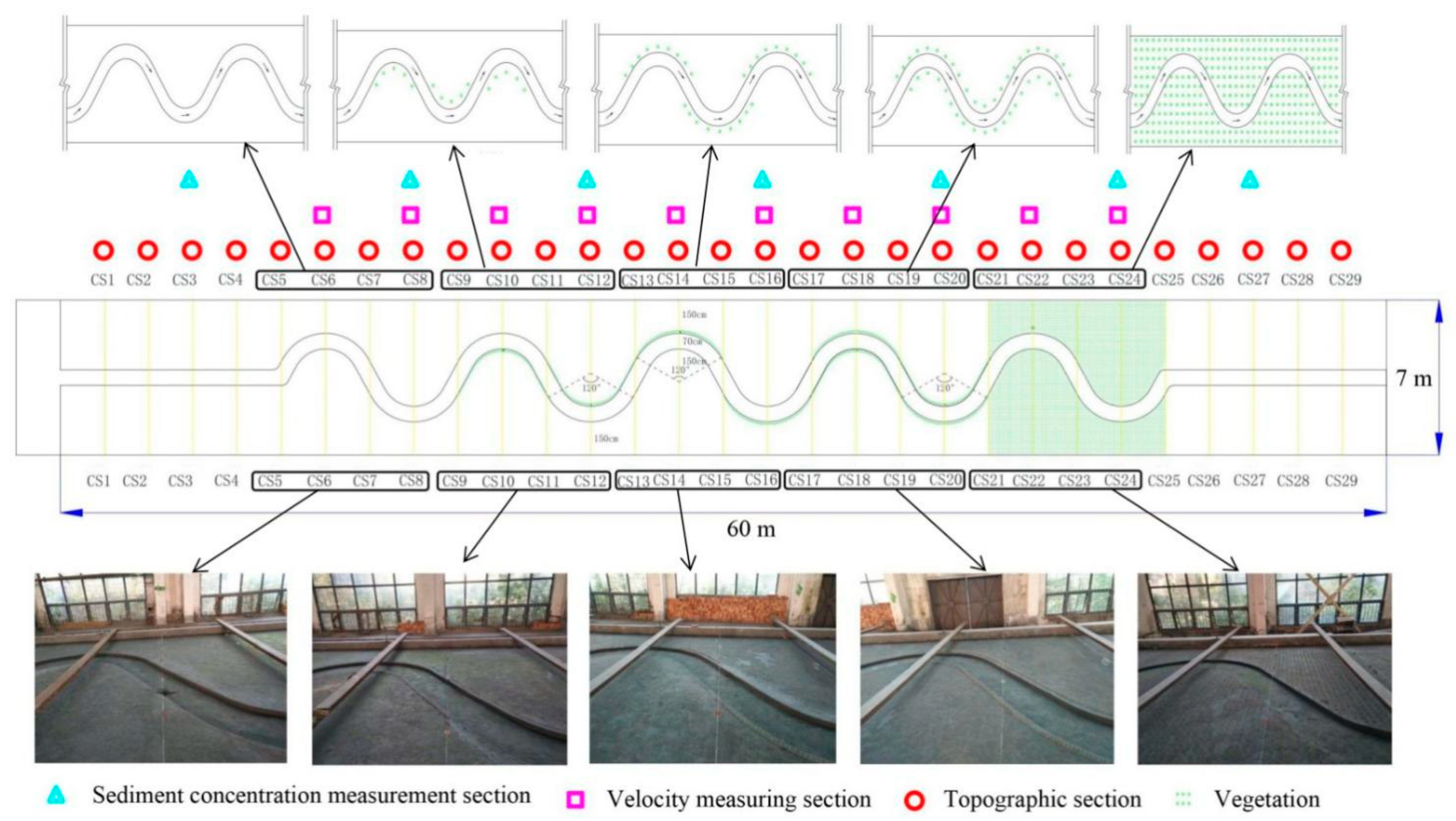
2.1.1. Model Design
2.1.2. Experimental Arrangement
2.2. Transverse Distribution Model of Average Sediment Carrying Capacity
2.3. Theoretical Formula for Transverse Distribution of Water and Sediment
3. Results
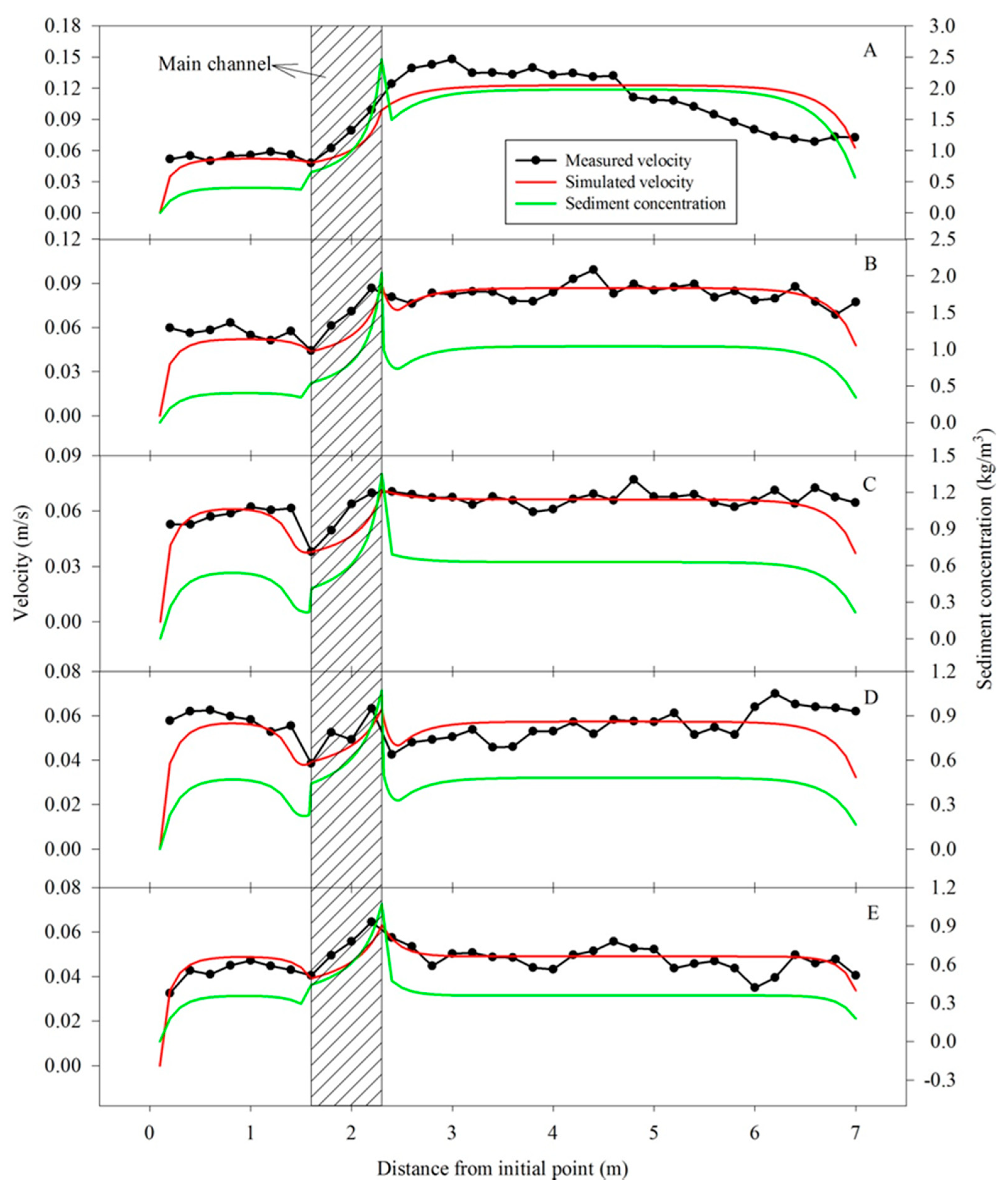
3.1. Transverse Distribution of Floodplain Flood Velocity in Meandering Compound Channels with Beach Vegetation
3.2. Theoretical Calculation of Transverse Distribution of Water and Sediment
3.2.1. Curved Compound Channel without Vegetation in the Beach
3.2.2. Curved Compound Channel with Vegetation on the Convex Bank of the Beach
3.2.3. Curved Compound Channel with Vegetation on the Concave Bank of the Beach
3.2.4. Curved Compound Channel with Vegetation on Both Sides of the Beach
3.2.5. Curved Compound Channel with Full Vegetation on the Beach
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shiono, K.; Tony, L.C.; Spooner, J.; Rameshwaran, P.; Chandler, J.H. The effect of floodplain roughness on flow structures, bedforms and sediment transport rates in meandering channels with overbank flows: Part II. J. Hydraul. Res. 2009, 47, 20–28. [Google Scholar] [CrossRef]
- Huai, W.; Gao, M.; Zeng, Y.; Li, D. Two-dimensional analytical solution for compound channel flows with vegetated floodplains. Appl. Math. Mech. 2009, 30, 1049–1057. [Google Scholar] [CrossRef]
- Ervine, D.A.; Babaeyan-Koopaei, K.; Sellin, R.H.J. Two-dimensional solution for straight and meandering overbank flows. J. Hydraul. Eng. 2000, 126, 653–669. [Google Scholar] [CrossRef]
- Shan, Y.; Liu, C.; Luo, M. Simple analytical model for depth-averaged velocity in meandering compound channels. Appl. Math. Mech. 2015, 36, 707–718. [Google Scholar] [CrossRef]
- Shiono, K.; Knight, D.W. Turbulent open channel flows with variable depth across the channel. J. Fluid Mech. 1991, 222, 617–646. [Google Scholar] [CrossRef]
- Knight, D.W.; Shiono, K. River channel and floodplain hydraulics. Floodplain Process. 1996, 5, 139–181. [Google Scholar]
- Rameshwaran, P.; Shiono, K. Quasi two-dimensional model for straight overbank flows through emergent vegetation on floodplains. J. Hydraul. Res. 2007, 45, 302–315. [Google Scholar] [CrossRef]
- Mehrabani, F.V.; Mohammadi, M.; Ayyoubzadeh, S.A.; Fernandes, J.N.; Rui, M.L.F. Turbulent flow structure in a vegetated non-prismatic compound channel. River Res. Appl. 2020, 36, 1868–1878. [Google Scholar] [CrossRef]
- Pan, Y.; Li, Z.; Yang, K.; Jia, D. Velocity distribution characteristics in meandering compound channels with one-sided vegetated floodplains. J. Hydrol. 2019, 578, 124068. [Google Scholar] [CrossRef]
- Fernandes, J.N.; Leal, J.B.; Cardoso, A.H.; Paquier, A.; Rivière, N. Influence of floodplain and riparian vegetation in the conveyance and structure of turbulent flow in compound channels. E3s Web Conf. 2018, 40, 06035. [Google Scholar] [CrossRef]
- Proust, S.; Peltier, Y.; Fernandes, J.; Leal, J.; Rivière, N. Effect of different inlet flow conditions on turbulence in a straight compound open channel. In Proceedings of the 34th World Congress of the International Association for Hydro-Environment Research and Engineering: 33rd Hydrology and Water Resources Symposium and 10th Conference on Hydraulics in Water Engineering, Brisbane, Australia, 26 July–1 August 2011. [Google Scholar]
- Brito, M.; Fernandes, J.; Leal, J.B. Porous media approach for RANS simulation of compound open-channel flows with submerged vegetated floodplains. Environ. Fluid. Mech. 2016, 16, 1247–1266. [Google Scholar] [CrossRef]
- Tang, X.N.; Knight, D.W. Lateral depth-averaged velocity distributions and bed shear in rectangular compound channels. J. Hydraul. Eng. 2008, 134, 1337–1342. [Google Scholar] [CrossRef]
- Huai, W.; Xu, Z.; Yang, Z.; Zeng, Y. Two dimensional analytical solution for a partially vegetated compound channel flow. Appl. Math. Mech. 2008, 29, 976–982, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Tang, X.N.; Knight, D.W. Lateral distributions of streamwise velocity in compound channels with partially vegetated floodplains. Sci. China Ser. E 2009, 52, 3357–3362. [Google Scholar] [CrossRef]
- Liao, H.; Knight, D.W. Analytic stage-discharge formulas for flow in straight prismatic channels. J. Hydraul. Eng. 2007, 133, 1111–1122. [Google Scholar] [CrossRef]
- Wu, F.C.; Shen, H.W.; Chou, Y.J. Variation of roughness coefficients for unsubmerged and submerged vegetation. J. Hydraul. Eng. 1999, 125, 934–942. [Google Scholar] [CrossRef]
- Stone, B.M.; Hung, T.S. Hydraulic resistance of flow in channels with cylindrical roughness. J. Hydraul. Eng. 2002, 128, 500–506. [Google Scholar] [CrossRef]
- Nepf, H.M. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Kang, H.; Choi, S.U. Turbulence modeling of compound open-channel flows with and without vegetation on the floodplain using the Reynolds stress model. Adv. Water Res. 2006, 29, 1650–1664. [Google Scholar] [CrossRef]
- James, C.S.; Birkhead, A.L.; Jordanova, A.A.; O’Sullivan, J.J. Flow resistance of emergent vegetation. J. Hydraul. Res. 2004, 42, 390–398. [Google Scholar] [CrossRef]
- Liao, H.; Knight, D.W. Analytic stage-discharge formulae for flow in straight trapezoidal open channels. Adv. Water Res. 2007, 30, 2283–2295. [Google Scholar] [CrossRef]
- Tanino, Y.; Nepf, H.M. Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. J. Hydraul. Eng. 2008, 134, 34–41. [Google Scholar] [CrossRef]
- Shiono, K.; Feng, T. Turbulence measurements of dye concentration and effects of secondary flow on distribution in open channel flows. J. Hydraul. Eng. 2003, 129, 373–384. [Google Scholar] [CrossRef]
- Yang, K.; Cao, S.; Knight, D.W. Flow patterns in compound channels with vegetated flood plains. J. Hydraul. Eng. 2007, 133, 148–159. [Google Scholar] [CrossRef]
- Sun, X.; Shiono, K. Flow resistance of one-line emergent vegetation along the floodplain edge of a compound open channel. Adv. Water Res. 2009, 32, 430–438. [Google Scholar] [CrossRef]
- Hu, C.; Ji, Z.; Guo, Q. Flow movement and sediment transport in compound channels. J. Hydraul. Res. 2010, 48, 23–32. [Google Scholar] [CrossRef]
- Quesada-Roán, A.; Ballesteros-Cánovas, J.A.; Granados-Bolaños, S.; Birkel, C.; Stoffel, M. Dendrogeomorphic reconstruction of floods in a dynamic tropical river. Geomorphology 2020, 359, 107133. [Google Scholar] [CrossRef]
- Fischer-Antze, T.; Stoesser, T.; Bates, P.; Olsen, N.R.B. 3D numerical modelling of open-channel flow with submerged vegetation. J. Hydraul. Res. 2001, 39, 303–310. [Google Scholar] [CrossRef]
- Velasco, D.; Bateman, A.; Medina, V. A new integrated, hydro-mechanical model applied to flexible vegetation in riverbeds. J. Hydraul. Res. 2008, 46, 579–597. [Google Scholar] [CrossRef]
- Lambert, M.F.; Sellin, R. Velocity distribution in a large-scale model of a doubly meandering compound river channel. Proc. Inst. Civil. Eng. Water 1996, 118, 10–20. [Google Scholar] [CrossRef]
- Naot, D.; Nezu, I.; Nakagawa, H. Hydrodynamic behavior of partly vegetated open channels. J. Hydraul. Eng. 1996, 122, 625–633. [Google Scholar] [CrossRef]
- Quesada-Román, A.; Villalobos-Chacón, A. Flash flood impacts of Hurricane Otto and hydrometeorological risk mapping in Costa Rica. Geografisk Tidsskrift-Danish. J. Geogr. 2020, 120, 142–155. [Google Scholar]
- Liu, C.; Shan, Y.; Liu, X.; Yang, K.; Liao, H. The effect of floodplain grass on the flow characteristics of meandering compound channels. J. Hydrol. 2016, 542, 1–17. [Google Scholar] [CrossRef]
- Liu, C.; Wright, N.; Liu, X.; Yang, K. An analytical model for lateral depth-averaged velocity distributions along a meander in curved compound channels. Adv. Water Res. 2014, 74, 26–43. [Google Scholar] [CrossRef]
- Darby, S.E. Effect of riparian vegetation on flow resistance and flood potential. J. Hydraul. Eng. 1999, 125, 443–454. [Google Scholar] [CrossRef]
- Helmio, T. Unsteady 1D flow model of compound channel with vegetated floodplains. J. Hydrol. 2002, 269, 89–99. [Google Scholar] [CrossRef]
- Shimizu, Y.; Tsujimoto, T. Numerical analysis of turbulent open-channel flow over a vegetation layer using a k-ε turbulence model. J. Hydrosci. Hydraul. Eng. 1994, 11, 57–67. [Google Scholar]
- Kravchenko, A.G.; Moin, P. Numerical studies of flow over a circular cylinder at Re = 3900. Phys. Fluids 2000, 12, 403. [Google Scholar] [CrossRef]
- Zarrati, A.R.; Tamai, N.; Jin, Y.C. Mathematical modeling of meandering channels with a generalized depth averaged model. J. Hydraul. Eng. 2005, 131, 467–475. [Google Scholar] [CrossRef]
- Liu, C.; Yang, K.; Liu, X.; Huang, E. Analytical Models for Overbank Flows in Meandering Channels with Vegetated Floodplains. J. Sichuan Univ. 2012, 44, 7–12. [Google Scholar]

| Working Condition | Design Flow (m3/h) | Actual Flow | Design Sediment Concentration | Actual Sediment Concentration(kg/m3) | Design Particle Size |
|---|---|---|---|---|---|
| 0 | 100 | 100.2 | no | 0 | no |
| 1 | 100 | 90.7 | no | 0 | no |
| 2 | 100 | 93.1 | small | 5.23 | fine |
| 3 | 100 | 101.3 | large | 35.37 | fine |
| 4 | 100 | 104.8 | middle | 14.39 | fine |
| 5 | 100 | 100.6 | small | 4.84 | coarse |
| 6 | 100 | 101.5 | middle | 14.85 | coarse |
| 7 | 100 | 101.5 | large | 35.30 | coarse |
| Example | Control Equations | Boundary Conditions | Parameters |
|---|---|---|---|
| (1) | ; ; ; | Ud—vertical average downstream velocity; ρ—fluid density; g—acceleration of gravity; H—depth of water; S0—bed slope in downstream direction; f—bed surface friction factor; r—available curvature of bed slope of main trough and beach; y—horizontal coordinate; Γ—secondary flow term; γ—exponent of analytic solution of differential equation; A—unknown constant; K—empirical parameters. | |
| (2) | ; ; ; ; | ||
| (3) | ; ; ; ; | ||
| (4) | ; ; ; ; ; ; ; | ||
| (5) | ; ; ; |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Li, P.; Li, X.; Wang, A.; Wang, Z.; Jian, S. Study on the Horizontal Distribution Law of Flood Water and Sediment Factors under the Effect of Vegetation on a Curved Beach. Water 2021, 13, 1441. https://doi.org/10.3390/w13111441
Zhang M, Li P, Li X, Wang A, Wang Z, Jian S. Study on the Horizontal Distribution Law of Flood Water and Sediment Factors under the Effect of Vegetation on a Curved Beach. Water. 2021; 13(11):1441. https://doi.org/10.3390/w13111441
Chicago/Turabian StyleZhang, Mingwu, Pan Li, Xiaoping Li, Aoxue Wang, Zhenhai Wang, and Shengqi Jian. 2021. "Study on the Horizontal Distribution Law of Flood Water and Sediment Factors under the Effect of Vegetation on a Curved Beach" Water 13, no. 11: 1441. https://doi.org/10.3390/w13111441
APA StyleZhang, M., Li, P., Li, X., Wang, A., Wang, Z., & Jian, S. (2021). Study on the Horizontal Distribution Law of Flood Water and Sediment Factors under the Effect of Vegetation on a Curved Beach. Water, 13(11), 1441. https://doi.org/10.3390/w13111441






