A Method for Estimating the Velocity at Which Anaerobic Metabolism Begins in Swimming Fish
Abstract
:1. Introduction
2. Materials and Methods
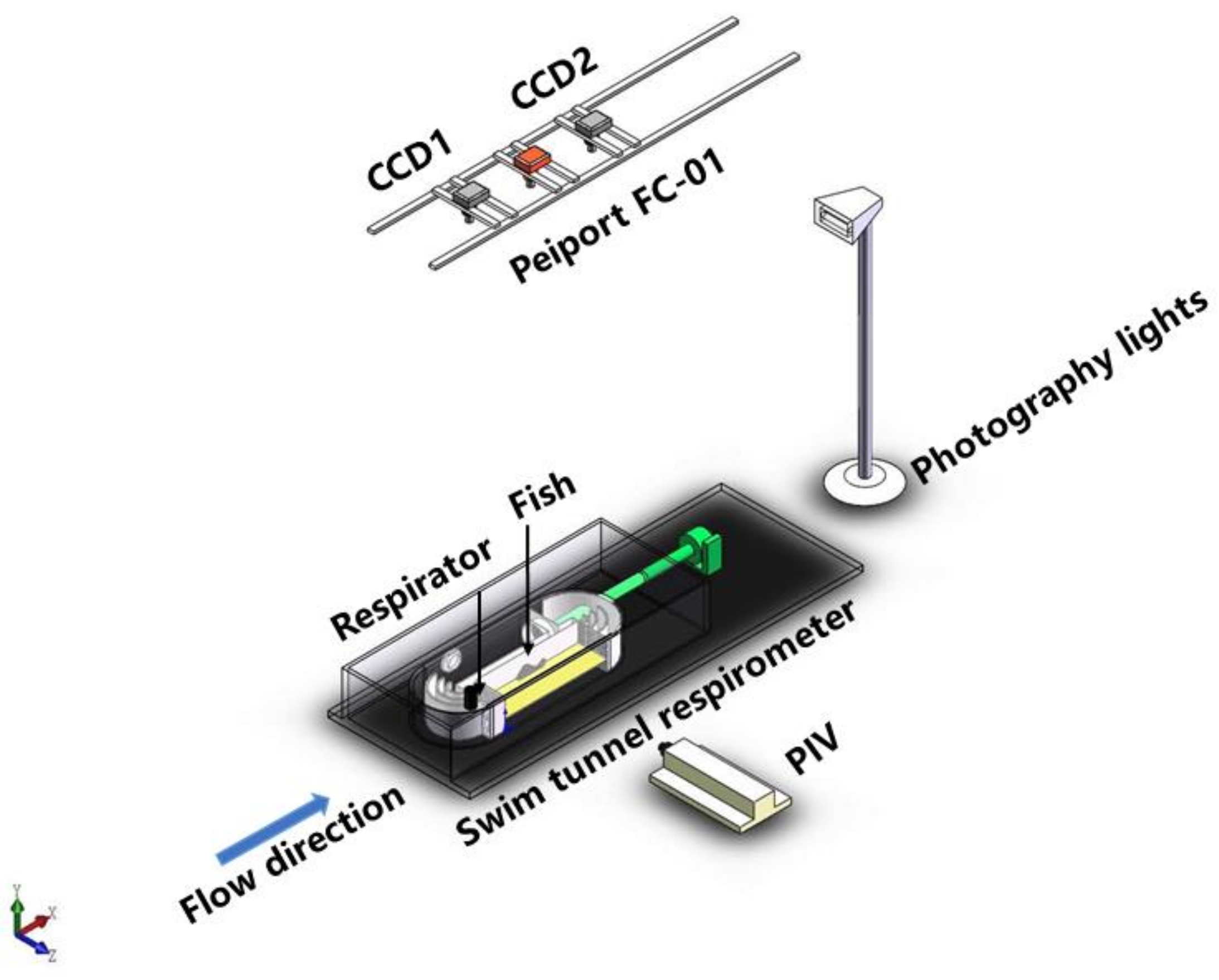
2.1. Respirometer
2.2. Experimental Design
2.3. Morphometric and Statistical Analysis
2.4. Data Analysis
3. Results
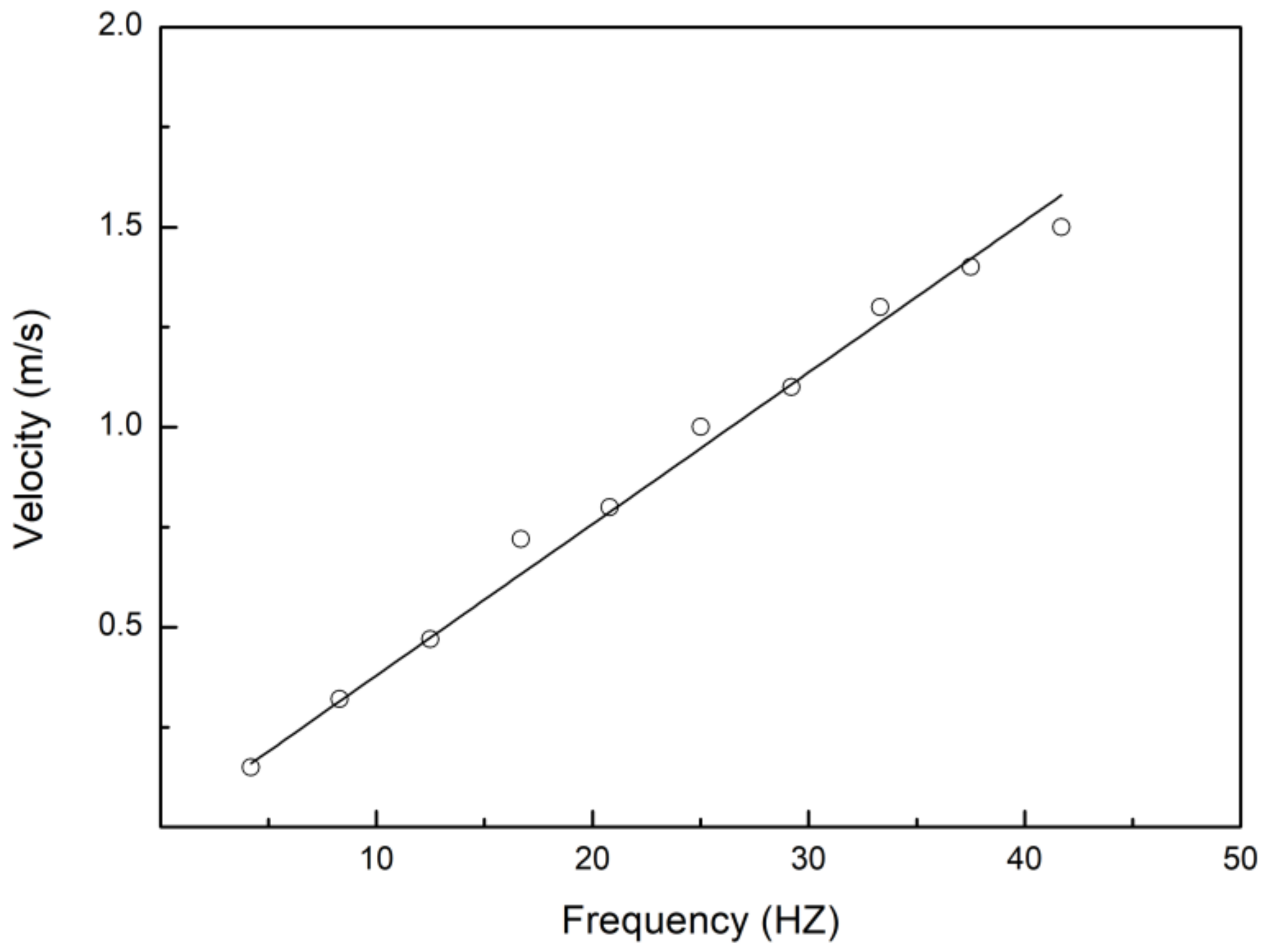
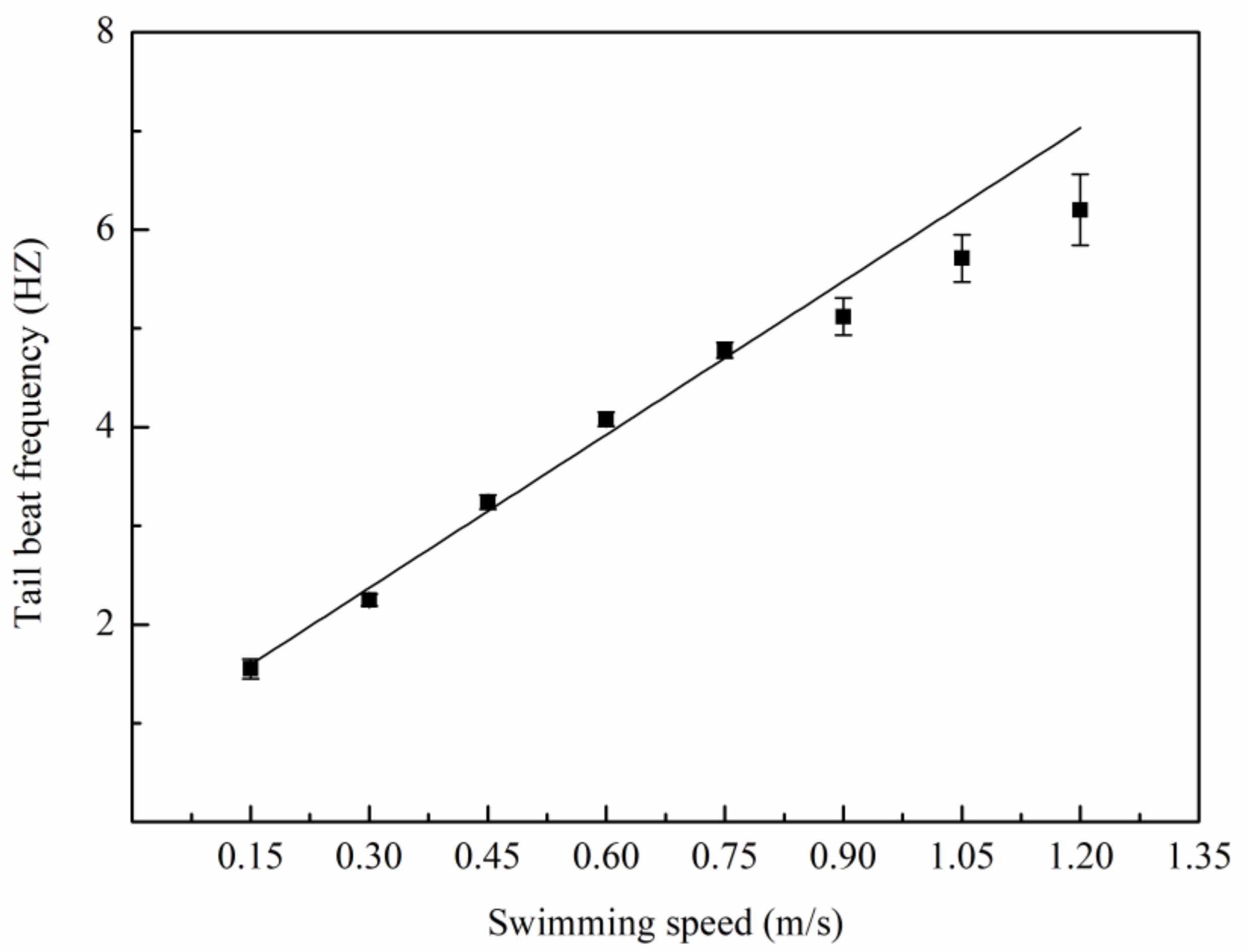
3.1. Swimming Kinematics
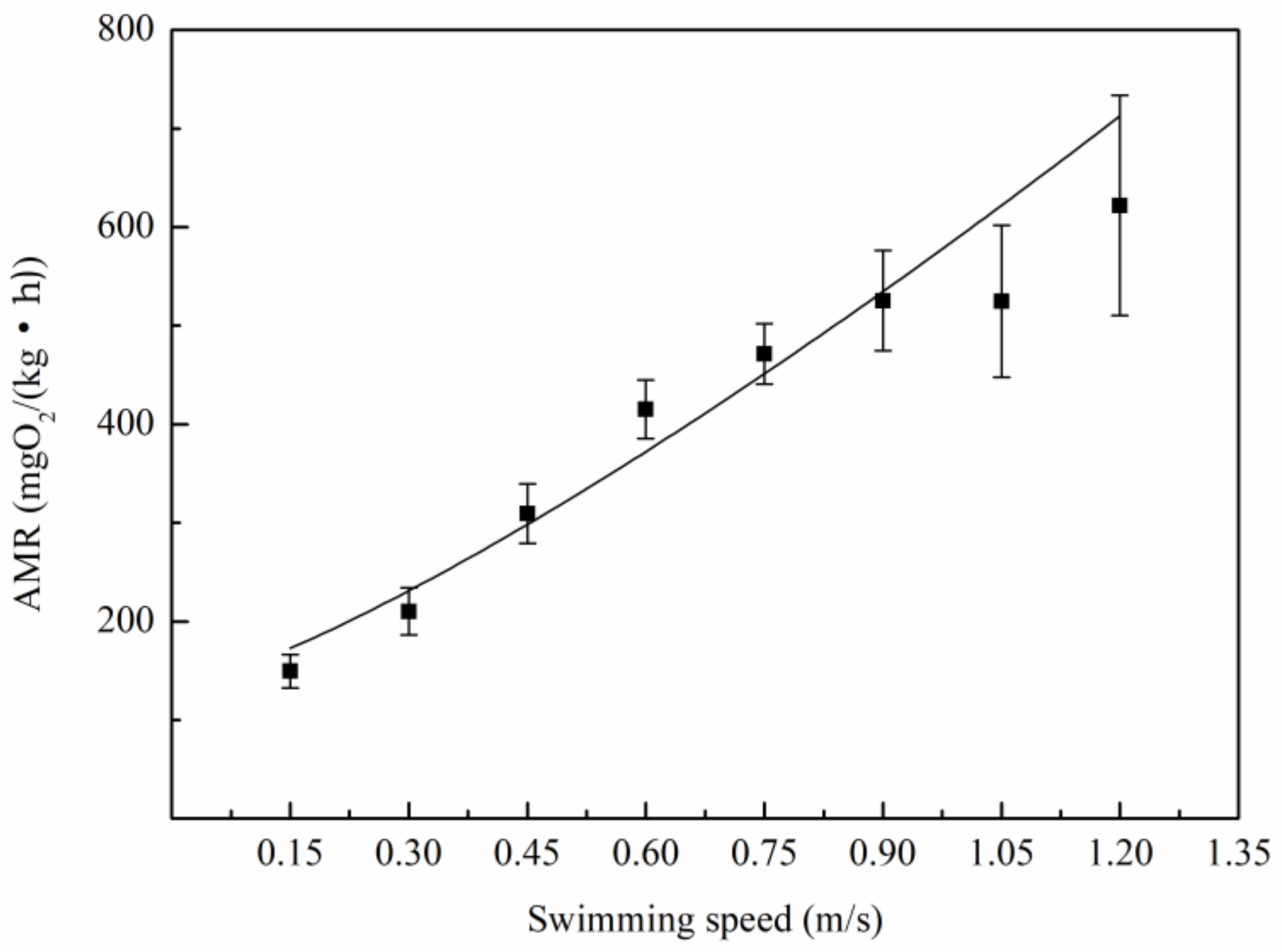
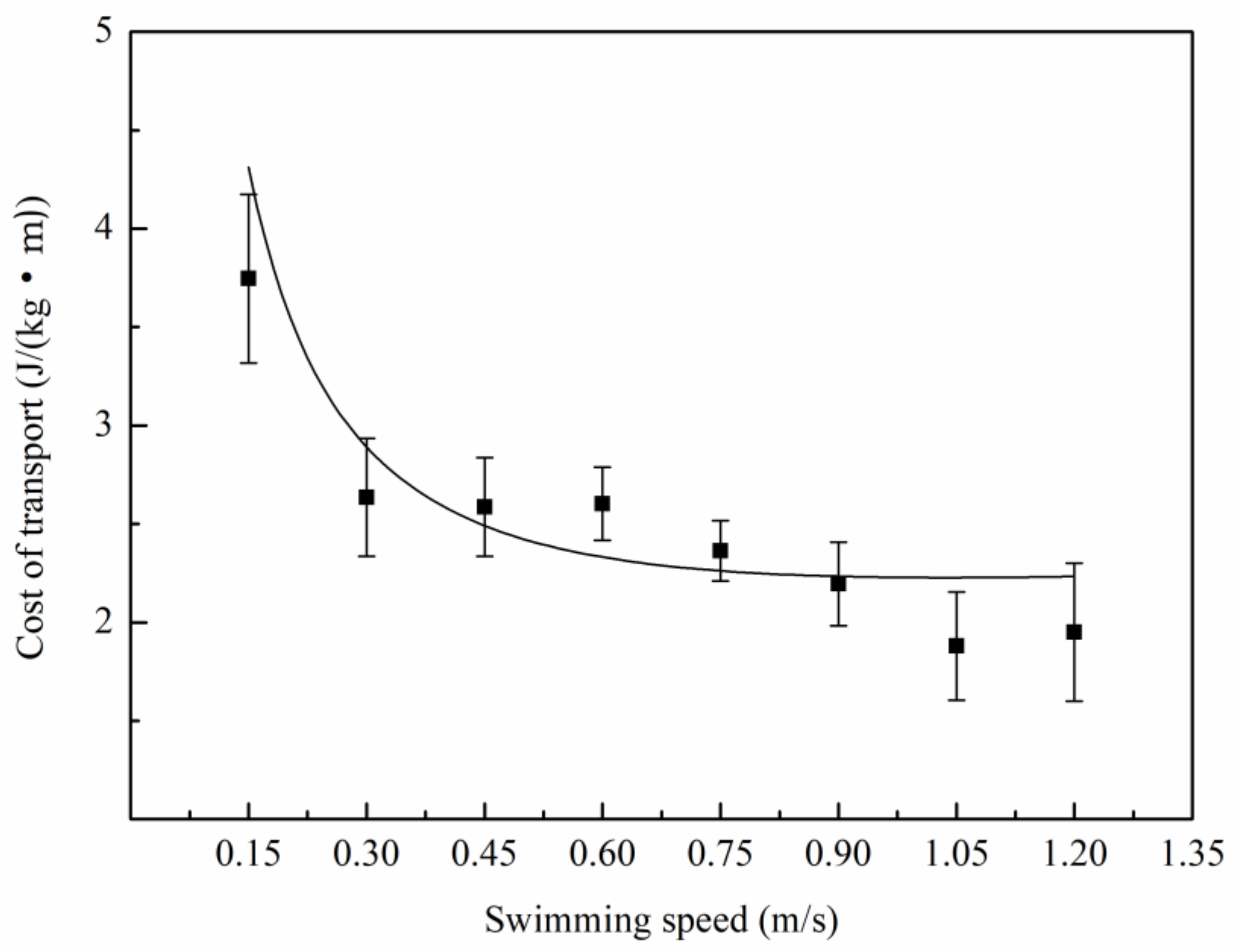
3.2. Relationship Between Oxygen Consumption and Water Velocity
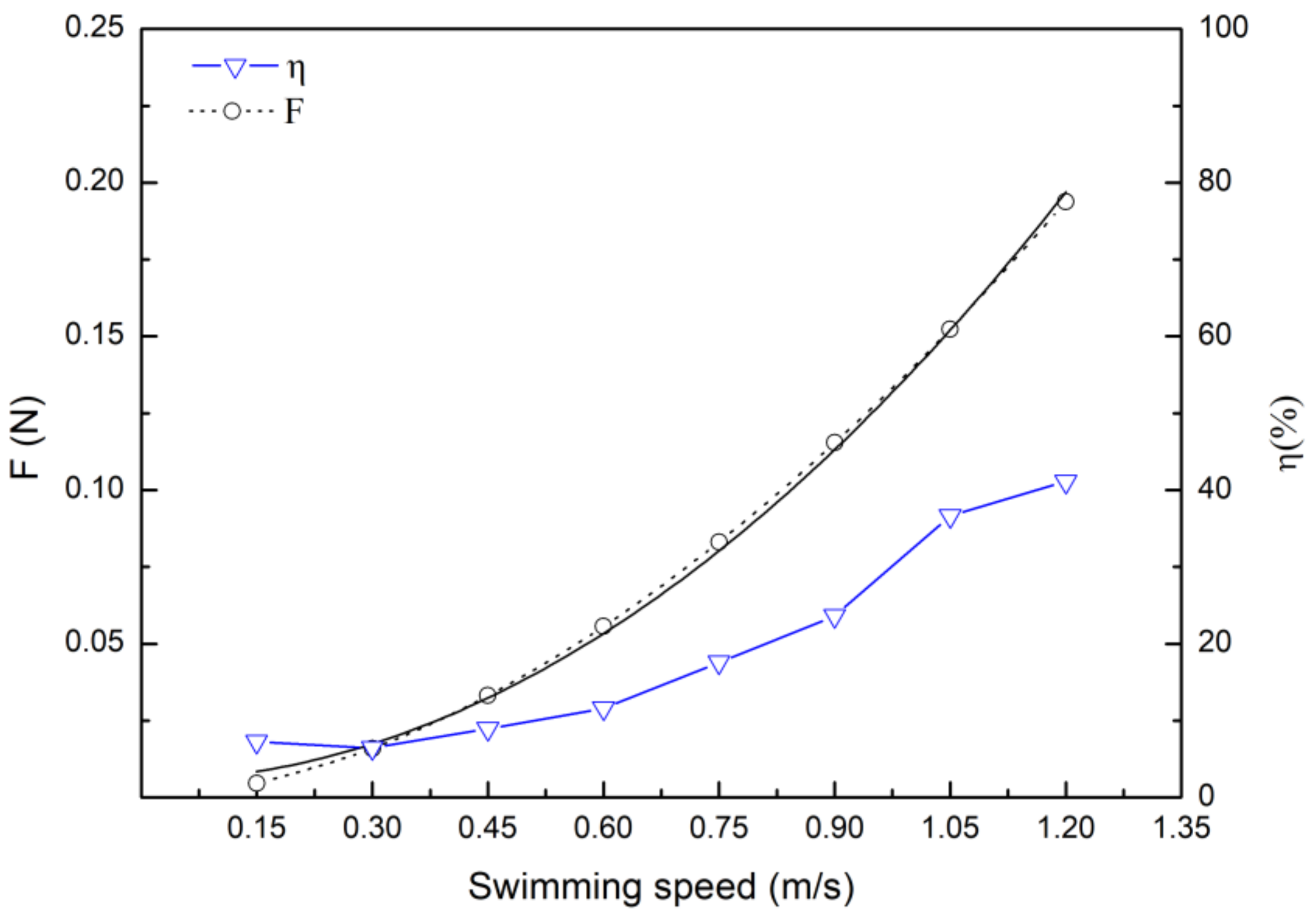
3.3. Drag Calculation Based on Hydrodynamic and Energy Efficiency
4. Discussion
4.1. Swimming Kinematics
4.2. The Relation Between Metabolic Rate and Speed
4.3. Drag Coefficient and Drag Force
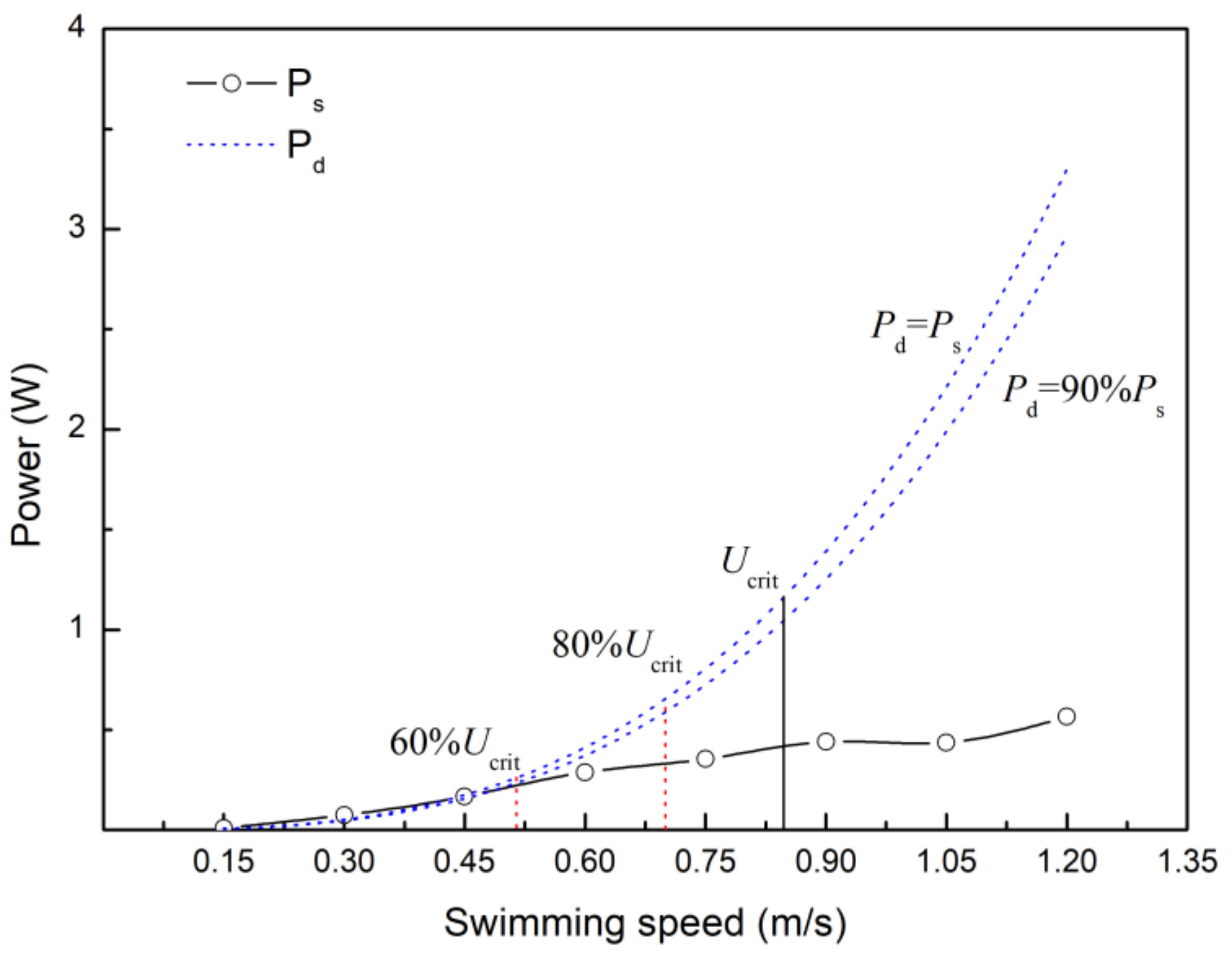
4.4. Estimating the Velocity at which Anaerobic Metabolism Begins
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Mao, X. Review of fishway research in China. Ecol. Eng. 2018, 115, 91–95. [Google Scholar] [CrossRef]
- Cooke, S.J.; Cech, J.J.; Glassman, D.M.; Simard, J.; Louttit, S.; Lennox, R.J.; Cruz-Font, L.; O’Connor, C.M. Water resource development and sturgeon (Acipenseridae): State of the science and research gaps related to fish passage, entrainment, impingement and behavioural guidance. Rev. Fish Biol. Fish. 2020, 30, 219–244. [Google Scholar] [CrossRef]
- Fuentes-Perez, J.F.; Silva, A.T.; Tuhtan, J.A.; Garcia-Vega, A.; Carbonell-Baeza, R.; Musall, M.; Kruusmaa, M. 3D modelling of non-uniform and turbulent flow in vertical slot fishways. Environ. Model. Softw. 2018, 99, 156–169. [Google Scholar] [CrossRef]
- Silva, A.T.; Lucas, M.C.; Castro-Santos, T.; Katopodis, C.; Baumgartner, L.J.; Thiem, J.D.; Aarestrup, K.; Pompeu, P.S.; O’Brien, G.C.; Braun, D.C.; et al. The future of fish passage science, engineering, and practice. Fish Fish. 2018, 19, 340–362. [Google Scholar] [CrossRef] [Green Version]
- Grossman, G.; Ratajczak, R.; Farr, M.D.; Wagner, C.M. Why there are fewer fish upstream. Am. Fish. Soc. Symp. 2010, 73, 63–81. [Google Scholar]
- Rodríguez, T.T.; Agudo, J.P.; Mosquera, L.P. Evaluating vertical-slot fishway designs in terms of fish swimming capabilities. Ecol. Eng. 2006, 27, 37–48. [Google Scholar] [CrossRef]
- Wu, S.; Rajaratnam, N.; Katopodis, C. Structure of flow in vertical slot fishway. J. Hydraul. Eng. 1999, 125, 351–360. [Google Scholar] [CrossRef]
- Ballu, A.; Pineau, G.; Calluaud, D.; David, L. Experimental-Based Methodology to Improve the Design of Vertical Slot Fishways. J. Hydraul. Eng. 2019, 145, 04019031.1–04019031.10. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Xuan, G.; Liang, D. Effect of parameters of pool geometry on flow characteristics in low slope vertical slot fishways. J. Hydraul. Res. 2019, 1–13. [Google Scholar] [CrossRef]
- Larinier, M.; Travade, F.; Porcher, J.P. Fishways: Biological bais, design criteria and monitoring. Bull. Fr. Pêche Piscic 2002, 9–20. [Google Scholar] [CrossRef]
- Calles, O.; Greenberg, L. Connectivity is a two-way street-the need for a holistic approach to fish passage problems in regulated rivers. River Res. Appl. 2009, 25, 1268–1286. [Google Scholar] [CrossRef]
- Ovidio, M.; Sonny, D.; Watthez, Q.; Goffaux, D.; Detrait, O.; Orban, P.; Nzau Matondo, B.; Renardy, S.; Dierckx, A.; Benitez, J.-P. Evaluation of the performance of successive multispecies improved fishways to reconnect a rehabilitated river. Wetl. Ecol. Manag. 2020. [Google Scholar] [CrossRef]
- Santos, H.D.E.; Viana, E.; Pompeu, P.S.; Martinez, C.B.J.N.I. Optimal swim speeds by respirometer: An analysis of three neotropical species. Neotrop. Ichthyol. 2012, 10, 805–811. [Google Scholar] [CrossRef]
- Plaut, I. Critical swimming speed: Its ecological relevance. Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 2001, 131, 41–50. [Google Scholar] [CrossRef]
- Brett, J.R. The Respiratory Metabolism and Swimming Performance of Young Sockeye Salmon. J. Fish. Res. Board Can. 1964, 21. [Google Scholar] [CrossRef]
- Peake, S. An Evaluation of the Use of Critical Swimming Speed for Determination of Culvert Water Velocity Criteria for Smallmouth Bass. Trans. Am. Fish. Soc. 2004, 133. [Google Scholar] [CrossRef]
- Cai, L.; Taupier, R.; Johnson, D.; Tu, Z.; Liu, G.; Huang, Y. Swimming Capability and Swimming Behavior of Juvenile Acipenser schrenckii. J. Exp. Zool. Part A Ecol. Genet. Physiol. 2013, 319A, 149–155. [Google Scholar] [CrossRef] [PubMed]
- Pedley, T.J.; Hill, S.J. Large-amplitude undulatory fish swimming: Fluid mechanics coupled to internal mechanics. J. Exp. Biol. 1999, 202, 3431–3438. [Google Scholar] [CrossRef] [PubMed]
- Haefner, J.W.; Bowen, M.D. Physical-based model of fish movement in fish extraction facilities. Ecol. Model. 2002, 152, 227–245. [Google Scholar] [CrossRef]
- Gu, K.-H.; Chang, K.-H.; Chang, T.-J. Numerical Investigation on Three-Dimensional Fishway Hydrodynamics and Fish Passage Energetics. J. Taiwan Agric. Eng. 2007, 54, 64–84. [Google Scholar]
- Khan, L.A. A three-dimensional computational fluid dynamics (CFD) model analysis of free surface hydrodynamics and fish passage energetics in a vertical-slot fishway. N. Am. J. Fish. Manag. 2006, 26, 255–267. [Google Scholar] [CrossRef]
- Standen, E.M.; Hinch, S.G.; Healey, M.C.; Farrell, A.P. Energetic costs of migration through the Fraser River Canyon, British Columbia, in adult pink (Oncorhynchus gorbuscha) and sockeye (Oncorhynchus nerka) salmon as assessed by EMG telemetry. Can. J. Fish. Aquat. Sci. 2002, 59, 1809–1818. [Google Scholar] [CrossRef]
- Wolfgang, M.J.; Grosenbaugh, M.A. Near-body flow dynamics in swimming fish. J. Exp. Biol. 1999, 17, 202. [Google Scholar]
- Pettersson, L.B.; BroÈnmark, C. Energetic Consequences of an Inducible Morphological Defence in Crucian Carp. Oecologia 1999, 121, 12–18. [Google Scholar] [CrossRef]
- Thiem, J.D.; Dawson, J.W.; Hatin, D.; Danylchuk, A.J.; Dumont, P.; Gleiss, A.C.; Wilson, R.P.; Cooke, S.J. Swimming activity and energetic costs of adult lake sturgeon during fishway passage. J. Exp. Biol. 2016, 219, 2534–2544. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vogel, S. Life in Moving Fluids; Priceton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Mckinley, R.S.; Power, G. Measurement of activity and oxygen consumption for adult lake sturgeon (Acipenser fulvescens) in the wild using radio-transmitted EMG signals. In Wildlife Telemetry: Remote Monitoring Tracking of Animals; Priede, I.M., Swift, S.M., Eds.; Ellis Horwood Ltd.: Pulborough, UK, 1992; pp. 456–465. [Google Scholar]
- Zhu, Y.-P.; Cao, Z.-D.; Fu, S.-J. Aerobic and anaerobic metabolism in response to different swimming speed of juvenile darkbarbel catfish (pelteobagrus vachelli richardson). Acta Hydrobiol. Sin. 2010, 34, 905–912. [Google Scholar] [CrossRef]
- Lee, C.G.; Farrell, A.P.; Lotto, A.; Hinch, S.G.; Healey, M.C. Excess post-exercise oxygen consumption in adult sockeye (Oncorhynchus nerka) and coho (O-kisutch) salmon following critical speed swimming. J. Exp. Biol. 2003, 206, 3253–3260. [Google Scholar] [CrossRef] [Green Version]
- Zobott, H.; Budwig, R.; Caudill, C.C.; Keefer, M.L.; Basham, W. Pacific Lamprey drag force modeling to optimize fishway design. J. Ecohydraul. 2020, 6, 69–81. [Google Scholar] [CrossRef]
- Tarrade, L.; Pineau, G.; Calluaud, D.; Texier, A.; David, L.; Larinier, M. Detailed experimental study of hydrodynamic turbulent flows generated in vertical slot fishways. Environ. Fluid Mech. 2011, 11, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Tu, Z.; Li, L.; Yuan, X.; Huang, Y.; Johnson, D. Aerobic Swimming Performance of Juvenile Largemouth Bronze Gudgeon (Coreius guichenoti) in the Yangtze River. J. Exp. Zool. Part. A Ecol. Genet. Physiol. 2012, 317A, 294–302. [Google Scholar] [CrossRef] [PubMed]
- Webb, P.W. The swimming energetics of trout. I. Thrust and power output at cruising speeds. J. Exp. Biol. 1971, 55. [Google Scholar] [CrossRef]
- Xi, Y.; Zhi-Ying, T.; Jing-Cheng, H.; Xue-Xiang, W.; Xiao-Tao, S.; Guo-Yongand, L. Effects of flow rate on swimming behavior and energy consumption of schizothorax chongi. Acta Hydrobiol. Sin. 2012, 36, 270–275. [Google Scholar] [CrossRef]
- Claireaux, G.; Couturier, C.; Groison, A.-L. Effect of temperature on maximum swimming speed and cost of transport in juvenile European sea bass (Dicentrarchus labrax). J. Exp. Biol. 2006, 209, 3420–3428. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kancharala, A.K.; Philen, M.K. Enhanced hydrodynamic performance of flexible fins using macro fiber composite actuators. Smart Mater. Struct. 2014, 23, 115012. [Google Scholar] [CrossRef]
- Heimerl, S.; Hagmeyer, M.; Echteler, C.J.H. Numerical flow simulation of pool-type fishways: New ways with well-known tools. Hydrobiologia 2008, 609, 189–196. [Google Scholar] [CrossRef]
- Heimerl, S.; Hagmeyer, M.; Kohler, B. Explaining flow structure in a pool-type fishway. Int. J. Hydropower Dams 2006, 13, 74–81. [Google Scholar]
- Sims, D.W. The effect of body size on the standard metabolic rate of the lesser spotted dogfish. J. Fish Biol. 1996, 48, 542–544. [Google Scholar] [CrossRef]
- Claireaux, G.; Lagardère, J.P. Influence of temperature, oxygen and salinity on the metabolism of the European sea bass. J. Sea Res. 1999, 42, 157–168. [Google Scholar] [CrossRef]
- Caputo, F.; Oliveira, M.F.M.d.; Denadai, B.S.; Greco, C.C. Fatores intrínsecos do custo energético da locomoção durante a natação. Rev. Bras. Med. Esporte 2006, 12, 399–404. [Google Scholar] [CrossRef]
- Kern, P.; Cramp, R.L.; Gordos, M.A.; Watson, J.R.; Franklin, C.E. Measuring U-crit and endurance: Equipment choice influences estimates of fish swimming performance. J. Fish Biol. 2018, 92, 237–247. [Google Scholar] [CrossRef]
- Li, S.; Han, L.; Wabg, Z.; Su, G.; Di, G. Study on swimming sbility of crucian carp in Songhua River. Hydro Sci. Cold Zone Eng. 2021, 4, 33–37. [Google Scholar]
- Dickson, K.A.; Donley, J.M.; Sepulveda, C.; Bhoopat, L. Effects of temperature on sustained swimming performance and swimming kinematics of the chub mackerel Scomber japonicus. J. Exp. Biol. 2002, 205 Pt 7, 969–980. [Google Scholar] [CrossRef]
- Steinhausen, M.F.; Steffensen, J.F.; Andersen, N.G. Tail beat frequency as a predictor of swimming speed and oxygen consumption of saithe (Pollachius virens) and whiting (Merlangius merlangus) during forced swimming. Mar. Biol. 2005, 148, 197–204. [Google Scholar] [CrossRef]
- Ohlberger, J.; Staaks, G.; Holker, F. Swimming efficiency and the influence of morphology on swimming costs in fishes. J. Comp. Physiol. B Biochem. Syst. Environ. Physiol. 2006, 176, 17–25. [Google Scholar] [CrossRef] [PubMed]
- Macy, W.K.; Durbin, A.G.; Durbin, E.G. Metabolic rate in relation to temperature and swimming speed, and the cost of filter feeding in Atlantic menhaden, Brevoortia tyrannus. Fish. Bull. 1999, 97, 282–293. [Google Scholar]
- Sepulveda, C.A.; Graham, J.B.; Bernal, D. Aerobic metabolic rates of swimming juvenile mako sharks, Isurus oxyrinchus. Mar. Biol. 2007, 152, 1087–1094. [Google Scholar] [CrossRef]
- Videler, J.J. Fish Swimming; Springer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Beamish, F. Swimming capacity. Fish Physiol. Biochem. 1978, 7. [Google Scholar] [CrossRef]
- Videler, J.J. Energetic consequences of the interactions between animals and water. In Proceedings of the 10th Conference of the European Society for Comparative Physiology and Biochemistry; Thieme: New York, NY, USA, 1989. [Google Scholar]
- Burgetz, I.J.; Rojas-Vargas, A.; Hinch, S.G.; Randall, D.J. Initial recruitment of anaerobic metabolism during sub-maximal swimming in rainbow trout (Oncorhynchus mykiss). J. Exp. Biol. 1998, 201 Pt 19, 2711–2721. [Google Scholar] [CrossRef]
- Hou, Y.; Yang, Z.; An, R.; Cai, L.; Chen, X.; Zhao, X.; Zou, X. Water flow and substrate preferences of Schizothorax wangchiachii (Fang, 1936). Ecol. Eng. 2019, 138, 1–7. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, X.; Zhao, M.; Tong, H. Hydraulics; China Electric Power Press: Beijing, China, 2009; pp. 133–137. [Google Scholar]

| Number of Samples | 0.15 (m/s) | 0.30 (m/s) | 0.45 (m/s) | 0.60 (m/s) | 0.75 (m/s) | 0.90 (m/s) | 1.05 (m/s) | 1.20 (m/s) |
|---|---|---|---|---|---|---|---|---|
| n | 31 | 31 | 31 | 31 | 25 | 14 | 7 | 2 |
| Drag Coefficients | 0.15 m/s | 0.30 m/s | 0.45 m/s | 0.60 m/s | 0.75 m/s | 0.90 m/s | 1.05 m/s | 1.20 m/s |
|---|---|---|---|---|---|---|---|---|
| Cd | 0.0149 | 0.0130 | 0.0120 | 0.0113 | 0.0108 | 0.0104 | 0.0101 | 0.0098 |
| Calibration | Cd = 0.126–0.140 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, F.; Wang, X.; Li, Y.; Hou, Y.; Zou, Q.; Shen, D. A Method for Estimating the Velocity at Which Anaerobic Metabolism Begins in Swimming Fish. Water 2021, 13, 1430. https://doi.org/10.3390/w13101430
He F, Wang X, Li Y, Hou Y, Zou Q, Shen D. A Method for Estimating the Velocity at Which Anaerobic Metabolism Begins in Swimming Fish. Water. 2021; 13(10):1430. https://doi.org/10.3390/w13101430
Chicago/Turabian StyleHe, Feifei, Xiaogang Wang, Yun Li, Yiqun Hou, Qiubao Zou, and Dengle Shen. 2021. "A Method for Estimating the Velocity at Which Anaerobic Metabolism Begins in Swimming Fish" Water 13, no. 10: 1430. https://doi.org/10.3390/w13101430






