Stepped Spillway Slope Effect on Air Entrainment and Inception Point Location
Abstract
1. Introduction
2. Materials and Methods
2.1. Mesh Gridance
2.2. Boundary Conditions
2.2.1. Inlet Boundary
2.2.2. Outlet Boundary
2.3. Walls
2.4. Volume of Fluid
2.5. Turbulence Model
3. Results and Discussions
3.1. The Commencement of the Skimming Flow Regime
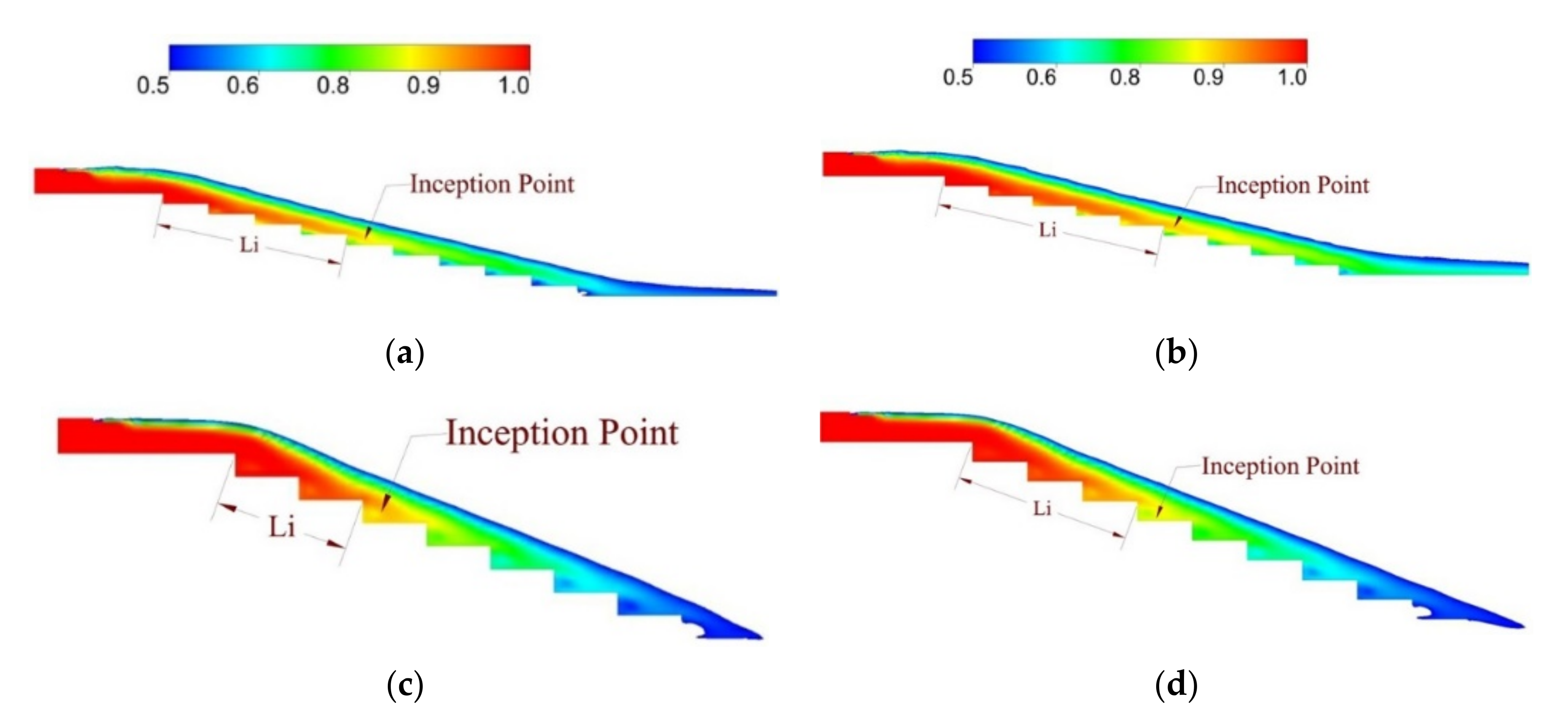
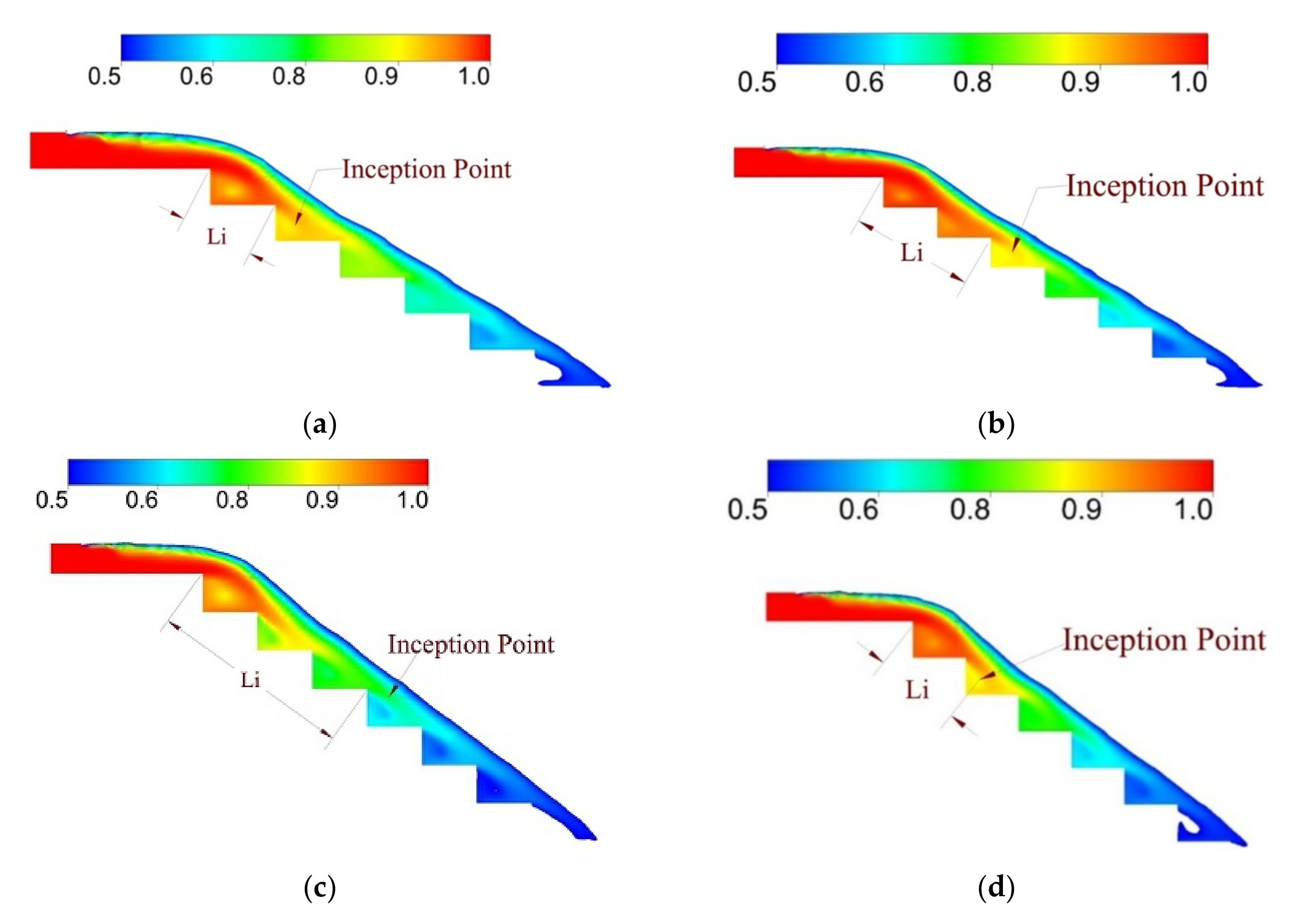
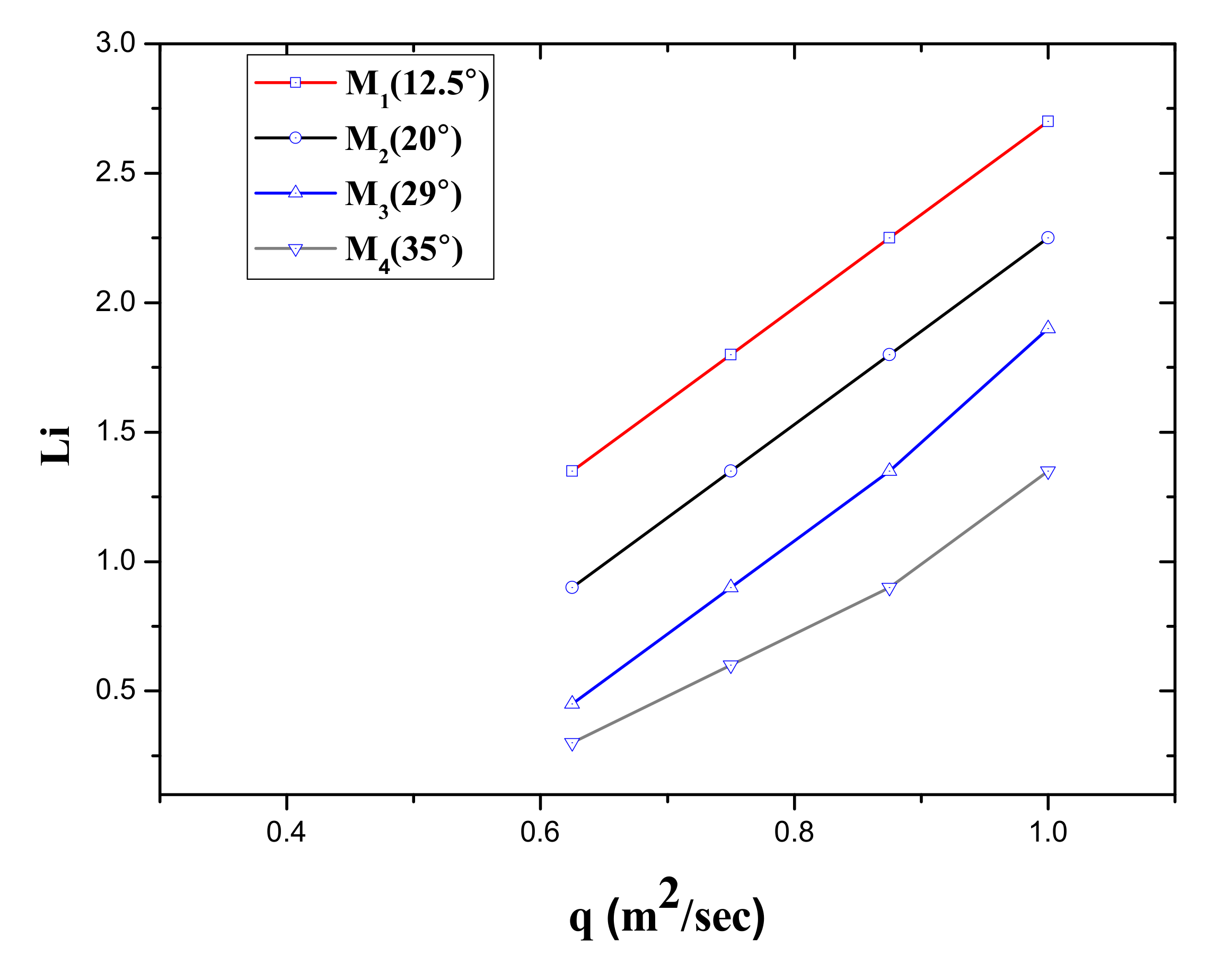
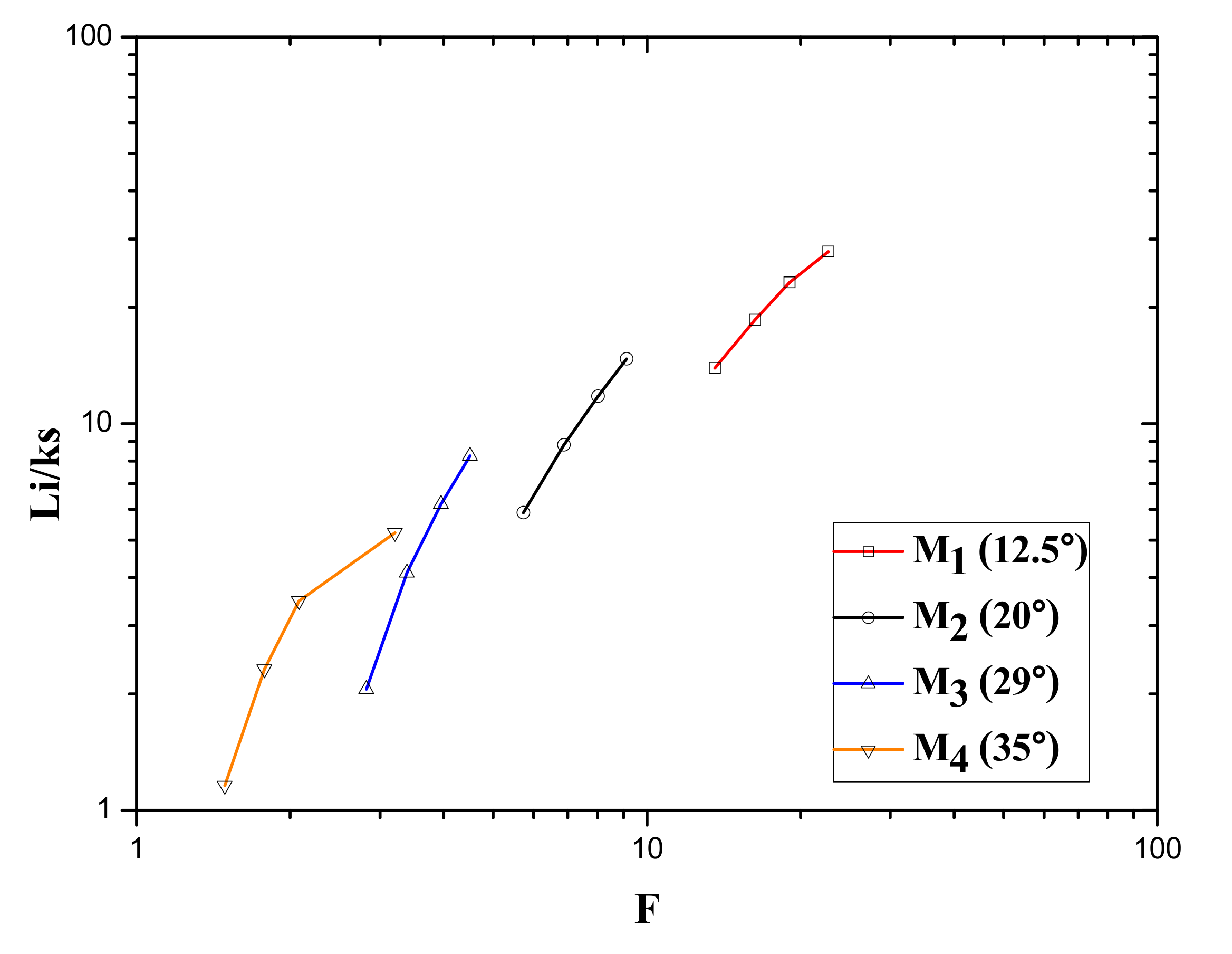
3.2. Effect of Channel Slope on Inception Point Location
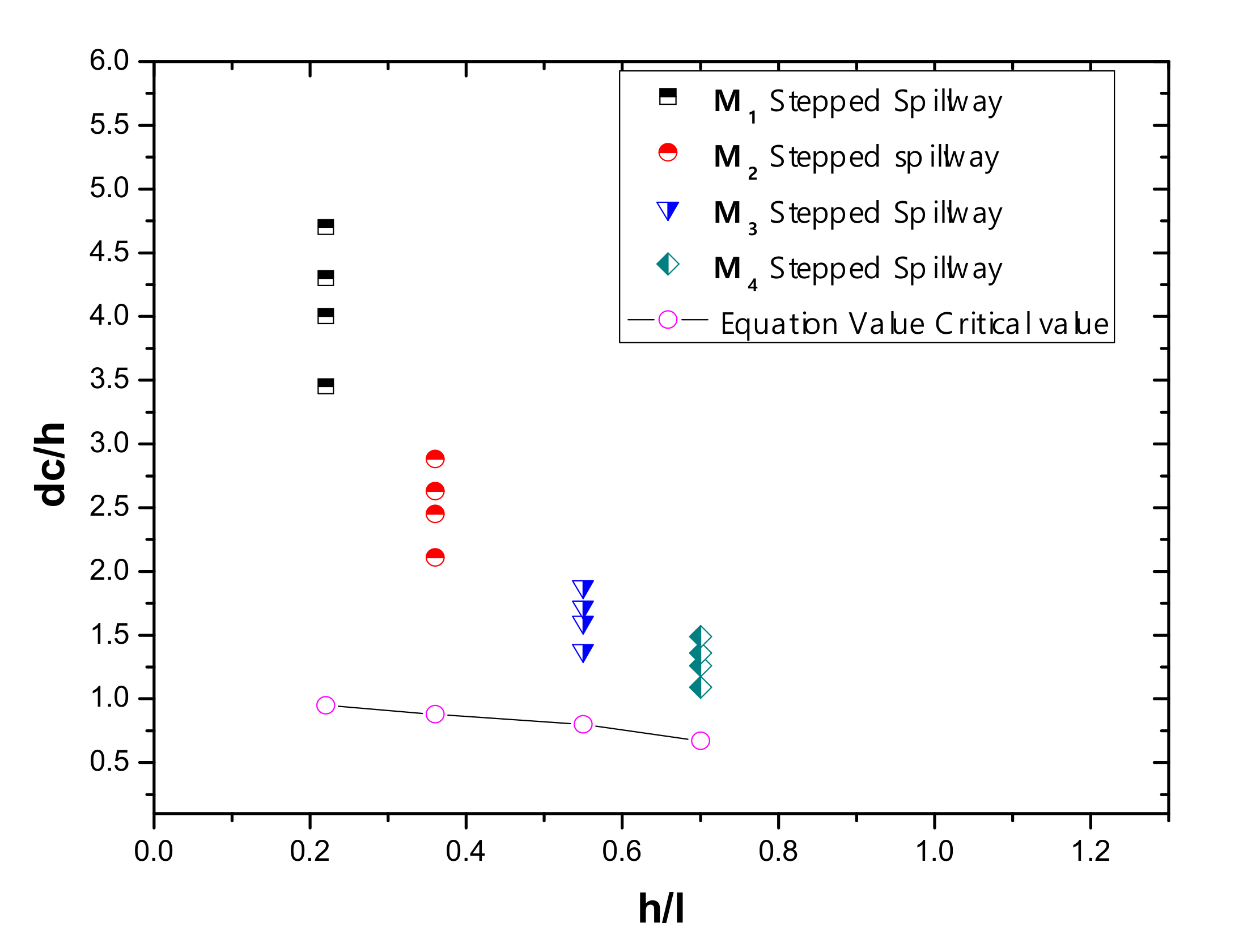
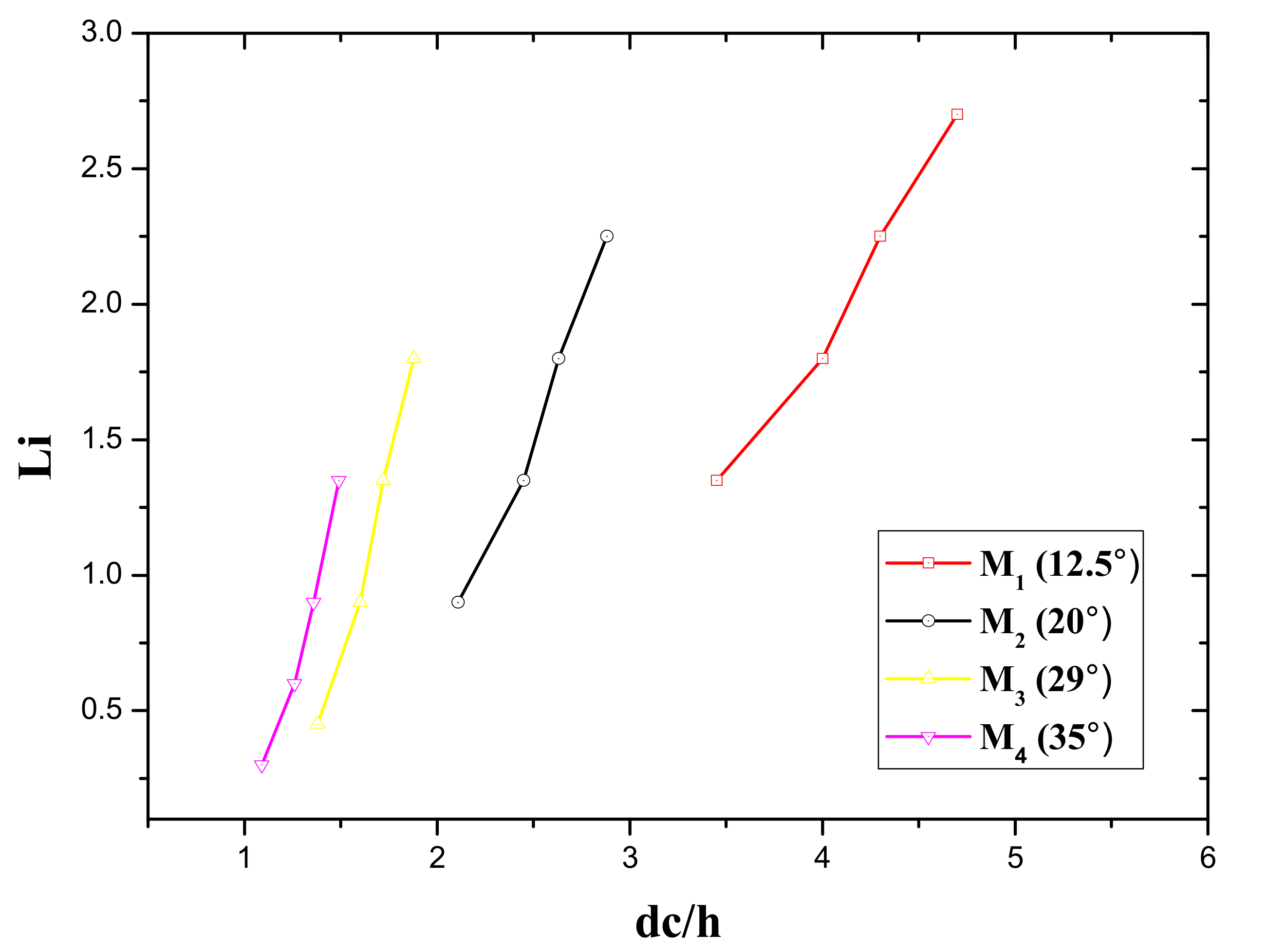
3.3. Variation of Inception Length with Critical Depth
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| model constant (4.04) | |
| model constant () | |
| B | width of the step (m) |
| 1.9 (model constant) | |
| 1.44 (model constant) | |
| coefficient of uniformity | |
| F | Froude surface roughness |
| generation of k due to buoyancy (kg/(ms3)) | |
| generation of k due to fluid Shear (kg/ms3) | |
| g | gravitational acceleration (m/sec2) |
| h | step height (m) |
| hp | height of Pool (m) |
| k | turbulent kinetic energy (m2/s2) |
| ks | roughness height, ks = hcosθ (m) |
| l | step length (m) |
| lp | length of Pool (m) |
| Li | distance of inception point location from spillway crest (m) |
| normalized distance from spillway crest to Inception Point | |
| M1-M4 | number of stepped spillway model |
| N | number of steps |
| S | modulus of mean rate of tensor |
| source term of kinetic energy () | |
| source term of dissipation rate () | |
| mean rate of deformation | |
| P | pressure in (N/m2) |
| Q | unit discharge (m2/s) |
| R | radius of the edge (m) |
| W | width of the step |
| effect of compressibility on turbulence (kg/ms3) | |
| turbulent prandtl number | |
| turbulent prandtl number | |
| velocity in direction (m/s) | |
| velocity in direction (m/s) | |
| volume fraction of air (%) | |
| volume fraction of water (%) | |
| turbulent dissipation rate (m2/s3) | |
| θ | spillway slope (°) |
| molecular dynamic viscosity (kg/ms) | |
| turbulent dynamic viscosity (kg/ms) | |
| cell density (kg/m3) | |
| density of air (kg/m3) | |
| density of water (kg/m3) | |
| t | time in (sec) |
| channel slope (°) | |
| kinematic viscosity (m2/s) | |
| dc | critical depth |
| Relative critical depth | |
| 1.0 (model constant) | |
| 1.2(model constant) |
References
- Chanson, H. Commercial Search Engines, International Databases or Traditional Libraries. J. Hyd. Res. 2005, 43, 85–87. [Google Scholar]
- Amador, A.; Sánchez-Juny, M.; Dolz, J. Hydraulic design of stepped spillways in HCR dams. Water Eng. 2006, 13, 289–302. [Google Scholar]
- Takahashi, M.; Gonzalez, C.A.; Chanson, H. Self-aeration and turbulence in a stepped channel. Int. J. Multiph. Flow 2006, 32, 1370–1385. [Google Scholar] [CrossRef]
- Chamani, M.R. Air inception in skimming flow regime over stepped spillways. In Hydraulics of Stepped Spillways; Minor, H., Ed.; Balkema: Zurich, Switzerland, 2000; pp. 61–67. [Google Scholar]
- Boes, R.M.; Hager, W.H. Two phase flow characteristics of stepped spillway. J. Hyd. Eng. 2003, 129, 661–670. [Google Scholar] [CrossRef]
- Rasmussen, R.E.H. Some experiments on cavitation erosion in water mixed with air. Int. Symp. Cavitation Hydrodyn. 1956, 20, 1–25. [Google Scholar]
- Wilhelms, S.C.; Gulliver, J.S. Bubbles and waves description of self-aerated spillway flow. J. Hydraul. Res. 2005, 43, 522–531. [Google Scholar] [CrossRef]
- Pfister, M.; Hager, W.H.; Minor, H.E. Bottom Aeration of Stepped Spillways. J. Hydraul. Eng. 2006, 132, 850–853. [Google Scholar]
- Amador, A.; Sánchez-Juny, M.; Dolz, J. Characterization of the Nonaerated Flow Region in a Stepped Spillway by PIV. J. Fluids Eng. 2006, 128, 1266–1273. [Google Scholar] [CrossRef]
- Bradley, J.N. Studies of Flow Characteristics, Discharge and Pressures Relative to Submerged Dams; US Department of the Interior, Bureau of Reclamation: Denver, CO, USA, 1945.
- Chanson, H.; Toombes, L. Hydraulics of Stepped Chutes: The Transition Flow. J. Hydraul. Res. 2004, 42, 43–54. [Google Scholar] [CrossRef]
- Matos, J.; Pinheiro, A.N.; Frizell, K.H.; Quintela, A.C. On the Role of Stepped Overlays to Increase Spillway Capacity of Embankment Dams; ICOLD European Symposium (NNCOLD): Geiranger, Norway, 2001; pp. 473–483. [Google Scholar]
- Chanson, H.; Toombes, L. Experimental investigations of air entrainment in transition and skimming flows down a stepped chute. Can. J. Civ. Eng 2002, 29, 145–156. [Google Scholar] [CrossRef]
- Matos, J. Hydraulic design of stepped spillways over RCC dams. In The International Workshop on Hydraulics of Stepped Spillways; Balkema Publication: Zurich, Switzerland, 2000; pp. 187–194. [Google Scholar]
- Christodoulou, G.C. Design of stepped spillways for optimal energy dissipation. Hydropower Dams 1999, 5, 90–93. [Google Scholar]
- Sorensen, R.M. Stepped spillway hydraulic model investigation. J. Hydraul. Eng. 1985, 111, 1461–1472. [Google Scholar] [CrossRef]
- Ohtsu, I.; Yasuda, Y. Characteristics of flow conditions on stepped channels. In Proceedings of the 27th IAHR Congress, San Francisco, CA, USA, 10–15 August 1997; pp. 583–588. [Google Scholar]
- James, C.S.; Matos, J.; Ohtsu, I.; Yasuda, Y.; Takahashi, M.; Tatewar, S.P.; Ingle, R.N.; Porey, P.D.; Chamani, M.R.; Rajaratnam, N. Onset of Skimming Flow on Stepped Spillways. J. Hydraul. Eng. 2001, 127, 519–525. [Google Scholar] [CrossRef]
- Petreka, J.A. The effect of entrained air on cavitation pitting. In Proceedings of the Minnesota International Hydraulics, Minneapolis, MN, USA, 1–4 September 1953; pp. 507–518. [Google Scholar]
- McLean, F.G.; Hansen, K.D. Roller compacted concrete for embankment overtopping protection. In Geotechnial Practice for Dam Rehabilitation; ASCE: New York, NY, USA, 1993. [Google Scholar]
- Chanson, H. The Hydraulics of Stepped Chutes and Spillways; Balkema: Lisse, The Netherlands, 2001; p. 418. [Google Scholar]
- Carosi, G.; Chanson, H. Turbulence characteristics in skimming flows on stepped spillways. Can. J. Civ. Eng. 2008, 35, 865–880. [Google Scholar] [CrossRef]
- Wood, I.R.; Ackers, P.; Loveless, J. General method of critical point prediction on spillways. J. Hyd. Eng. 1983, 109, 308–312. [Google Scholar] [CrossRef]
- Causon, D.M.; Mingham, C.G.; Ingram, D.M. Advances in calculation methods for supercritical flow in spillway channels. J. Hydraul. Eng. 1999, 125, 1039–1050. [Google Scholar] [CrossRef]
- Tufim, A. Solution for spillway flow by finite difference method. J. Hydraul. Res. 2010, 39, 241–247. [Google Scholar] [CrossRef]
- Meireles, I.; Matos, J. Skimming flow in the non-aerated region of stepped spillways over embankment dams. J. Hydr. Eng 2009, 135, 685–689. [Google Scholar] [CrossRef]
- Ahadian, J.; Aghamajidi, R. Investigation of Geometric Effect of Steps on energy dissipation on Stepped Spillway. Appl. Math. Eng. Manag. Technol. 2014, 2, 495–503. [Google Scholar]
- Bombardelli, F.A.; Meireles, I.; Matos, J. Laboratory measurements and multi-block numerical simulations of the mean flow and turbulence in the non-aerated skimming flow region of steep stepped spillways. Environ. Fluid Mech. 2010, 11, 263–288. [Google Scholar] [CrossRef]
- Qian, Z.D.; Hu, X.Q.; Huai, W.X.; Amador, A. Numerical simulation and analysis of water flow over stepped spillways. Sci. China Ser. E Technol. Sci. 2009, 52, 1958–1965. [Google Scholar] [CrossRef]
- Wei, W.L.; Lv, B.; Liu, Y.L.; Yang, X.F. Numerical Simulation of Flow on Stepped Spillway Combined with Wide Tailing Piers and Stilling Basin. Appl. Mech. Mater. 2012, 170, 2047–2050. [Google Scholar] [CrossRef]
- Dong, Z.Y. Numerical simulation of skimming flow over mild stepped channel. J. Hydrodyn. 2006, 18, 367–371. [Google Scholar] [CrossRef]
- Chen, Q.; Dai, G.; Liu, H. Numerical simulation of overflow in stepped spillway. J. Hydraul. Eng 2002, 33, 20–26. [Google Scholar]
- Morovati, K.; Eghbalzadeh, A.; Soori, S. Numerical Study of Energy Dissipation of Pooled Stepped Spillways. Civ. Eng. J. 2016, 2, 208–220. [Google Scholar] [CrossRef]
- Morovati, K.; Eghbalzadeh, A. Study of inception point, void fraction and pressure over pooled stepped spillways using Flow-3D. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 982–998. [Google Scholar] [CrossRef]
- Chen, Q.; Dai, G.; Liu, H. Volume of Fluid Model for Turbulence Numerical Simulation of Stepped Spillway Overflow. J. Hydraul. Eng. 2002, 128, 683–688. [Google Scholar] [CrossRef]
- Wan, W.; Raza, A.; Chen, X. Effect of Height and Geometry of Stepped Spillway on Inception Point Location. Appl. Sci. 2019, 9, 2091. [Google Scholar] [CrossRef]
- Rajaratnam, N. Skimming flow in stepped spillways. J. Hydraul. Eng. 1990, 116, 587–591. [Google Scholar] [CrossRef]
- Wan, W.; Liu, B.; Raza, A. Numerical Prediction and Risk Analysis of Hydraluic Cavitation Damage in a High-Speed-Flow. Shock Vib. 2018, 1817307. [Google Scholar]
- Craft, T.J.; Launder, B.E.; Suga, K. Development and application of a cubic eddy-viscosity model of turbulence. Int. J. Heat Fluid Flow 1996, 17, 108–111. [Google Scholar] [CrossRef]
- Cheng, X.; Chen, Y.; Luo, L. Numerical simulation of air-water two-phase flow over stepped spillways. Sci. China Ser. E Technol. Sci 2006, 49, 674–684. [Google Scholar] [CrossRef]
- Tabbara, M.; Chatila, J.; Awwad, R. Computational simulation of flow over stepped spillways. J. Comp. Struct 2005, 83, 2215–2224. [Google Scholar] [CrossRef]
- Bai, Z.L.; Zhang, J.M. Comparison of Different Turbulence Models for Numerical Simulation of Pressure Distribution in V-Shaped Stepped Spillway. Math. Probl. Eng. 2017, 2017, 3537026. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Joudi, A.R.; Ghahramanzadeh, A.; Ghaderi, A. Investigation of flow pressure distribution over a stepped spillway. Adv. Appl. Fluid Mech. 2016, 19, 811–828. [Google Scholar] [CrossRef]
- Abbasi, S.; Kamanbedast, A.A. Investigation of Effect of Changes in Dimension and Hydraulic of Stepped Spillways for Maximization Energy Dissipation. World Appl. Sci. J. 2012, 18, 261–267. [Google Scholar]
- Roushangar, K.; Akhgar, S.; Salmasi, F.; Shiri, J. Neural networks- and neuro-fuzzy-based determination of influential parameters on energy dissipation over stepped spillways under nappe flow regime. J. Hydr. Eng 2017, 23, 57–62. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A New k-ε Eddy Viscosity Model for High Reynolds-Number Turbulent Flows-Model Development and Validation. Comput. Fluids 1994, 24, 227–238. [Google Scholar] [CrossRef]

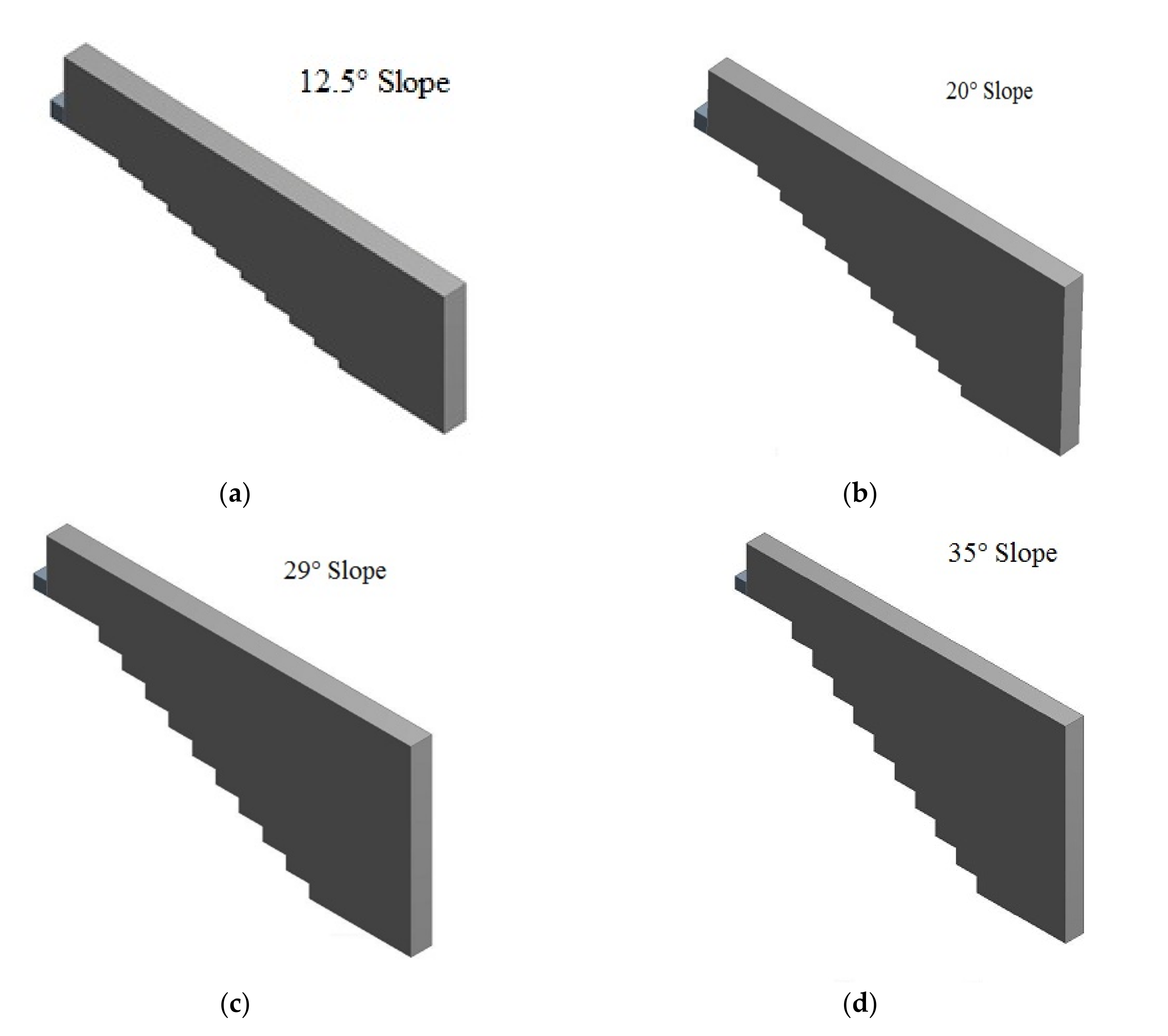


| Model | Step Height (h) | Step Length (m) | Slope |
|---|---|---|---|
| M1 | 0.1 | 0.45 | 12.5° |
| M2 | 0.163 | 0.45 | 19° |
| M3 | 0.25 | 0.45 | 29° |
| M4 | 0.315 | 0.45 | 35° |
| Unit Discharge q (m2/s) | Channel Slope ° | Step Height (m) | Froude Number F | Inception Point Length Li | Surface Roughness ks | Li/ks |
|---|---|---|---|---|---|---|
| 0.625 | 12.5° | 0.1 | 13.58 | 1.35 | 0.097 | 13.91 |
| 0.75 | 12.5° | 0.1 | 16.3 | 1.8 | 0.097 | 18.55 |
| 0.875 | 12.5° | 0.1 | 19.02 | 2.25 | 0.097 | 23.19 |
| 1 | 12.5° | 0.1 | 22.69 | 2.7 | 0.097 | 27.83 |
| 0.625 | 20° | 0.163 | 5.73 | 0.9 | 0.153 | 5.88 |
| 0.75 | 20° | 0.163 | 6.88 | 1.35 | 0.153 | 8.82 |
| 0.875 | 20° | 0.163 | 8.02 | 1.8 | 0.153 | 11.76 |
| 1 | 20° | 0.163 | 9.12 | 2.25 | 0.153 | 14.7 |
| 0.625 | 29° | 0.25 | 2.82 | 0.45 | 0.218 | 2.06 |
| 0.75 | 29° | 0.25 | 3.39 | 0.9 | 0.218 | 4.12 |
| 0.875 | 29° | 0.25 | 3.95 | 1.35 | 0.218 | 6.19 |
| 1 | 29° | 0.25 | 4.5 | 1.8 | 0.218 | 8.25 |
| 0.625 | 35° | 0.315 | 1.49 | 0.3 | 0.258 | 1.16 |
| 0.75 | 35° | 0.315 | 1.78 | 0.6 | 0.258 | 2.32 |
| 0.875 | 35° | 0.315 | 2.08 | 0.9 | 0.258 | 3.48 |
| 1 | 35° | 0.25 | 3.21 | 1.35 | 0.258 | 5.23 |
| Critical Depth dc | Channel Slope ° | Step Height | Surface Roughness ks | dc/h | ks/h |
|---|---|---|---|---|---|
| 0.345 | 12.5° | 0.1 | 0.097 | 3.45 | 0.97 |
| 0.4 | 12.5° | 0.1 | 0.097 | 4 | 0.97 |
| 0.43 | 12.5° | 0.1 | 0.097 | 4.3 | 0.97 |
| 0.47 | 12.5 | 0.1 | 0.097 | 4.7 | 0.97 |
| 0.345 | 20° | 0.163 | 0.153 | 2.11 | 0.938 |
| 0.4 | 20° | 0.163 | 0.153 | 2.45 | 0.938 |
| 0.43 | 20° | 0.163 | 0.153 | 2.63 | 0.938 |
| 0.47 | 20° | 0.163 | 0.153 | 2.88 | 0.938 |
| 0.345 | 29° | 0.25 | 0.218 | 1.38 | 0.872 |
| 0.4 | 29° | 0.25 | 0.218 | 1.6 | 0.872 |
| 0.43 | 29° | 0.25 | 0.218 | 1.72 | 0.872 |
| 0.47 | 29° | 0.25 | 0.218 | 1.88 | 0.872 |
| 0.345 | 35° | 0.315 | 0.258 | 1.09 | 0.819 |
| 0.4 | 35° | 0.315 | 0.258 | 1.26 | 0.819 |
| 0.43 | 35° | 0.315 | 0.258 | 1.36 | 0.819 |
| 0.47 | 35° | 0.315 | 0.258 | 1.49 | 0.819 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raza, A.; Wan, W.; Mehmood, K. Stepped Spillway Slope Effect on Air Entrainment and Inception Point Location. Water 2021, 13, 1428. https://doi.org/10.3390/w13101428
Raza A, Wan W, Mehmood K. Stepped Spillway Slope Effect on Air Entrainment and Inception Point Location. Water. 2021; 13(10):1428. https://doi.org/10.3390/w13101428
Chicago/Turabian StyleRaza, Awais, Wuyi Wan, and Kashif Mehmood. 2021. "Stepped Spillway Slope Effect on Air Entrainment and Inception Point Location" Water 13, no. 10: 1428. https://doi.org/10.3390/w13101428
APA StyleRaza, A., Wan, W., & Mehmood, K. (2021). Stepped Spillway Slope Effect on Air Entrainment and Inception Point Location. Water, 13(10), 1428. https://doi.org/10.3390/w13101428






