Application of a New Improved Weighting Method, ESO Method Combined with Fuzzy Synthetic Method, in Water Quality Evaluation of Chagan Lake
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Method and Improvement
2.2.1. Fuzzy Synthetic Evaluation Method
- Determination of the evaluation indicator, A = {DO, F, CODCR, CODEMN, TP, TN}
- Determination of the standard value of each grade of the evaluation indicator, V = {v1, v2, …, vm}.
- Determination of the distribution function and calculation of the membership degree to construct the fuzzy matrix R [22].
- 4.
- Calculation of the weight vector of all indicators, W = {w1, w2, …, wn}.
- 5.
- In the fuzzy operation, matrix multiplication is used to calculate the weight W and membership R matrices, and the fuzzy synthetic operation result B is obtained.
- 6.
- Comprehensive evaluation. The results of the fuzzy operation are calculated and evaluated according to the principle of weighted average comprehensive evaluation in this study, which regards the water quality grade as a continuous relative position, and values {1, 2, 3, 4, 5} represent water quality grades {I, II, III, IV, V}, and these values are the Z-rank of each water quality grade. The relative position BT, which expresses the grade of water quality by rational numbers rather than integers, of the water quality grade of the indicator can then be obtained by weighting the Z-rank of each water quality grade for each indicator [23]. Additionally, compared to the maximum membership principle, this principle can preserve as much information in the assessment coefficients as possible [24].where BT is relative water quality grade for a sample, bj is the weighted membership degree of the sample to the j-grade water quality, and β is the weighted coefficient with a value of 2.
2.2.2. ESO Method
- Step 1—Entropy weight calculation
- 1
- Calculation of the original matrix, Q = (qij)(m×n), I = 1, 2, …, m; j = 1, 2, …, n.For the “bigger the better” indicator:For the “smaller the better” indicator:
- 2
- The original matrix is normalized to obtain the matrix Cn = (cnij)(m×n)
- 3
- As the logarithm will appear in the entropy calculation, matrix Cn must be modified to prevent its zero element from being unable to be calculated. The revision is as follows:
- 4
- Entropy calculation:
- 5
- Determination of entropy weight:where m is the number of samples, n is the number of indicators, qij is the scale value of indicator j in sample i that expresses the degree of discreteness of an index, xij is the measured value of indicator j in sample i, xmin,j is the minimum value in the measured value of evaluation indicator j, xmax,j is the maximum value in the measured value of evaluation indicator j, cnij is the normalized scale value of indicator j in sample i, c’ij is the normalized scale value of indicator j in revised sample i, Ej is the information entropy of evaluation indicator j, and Wj is the weight value of evaluation indicator j.
- Step 2—Weight correction based on the single-factor evaluation results
- 1
- Determination of the amendment data. The amendment data refers to the basic data used to modify the entropy weight, which can reflect the user’s attitude towards the influencing factors of the parameters. This study thinks that the pollution degree of each parameter is an important factor affecting its weight, so the single-factor evaluation results are used as amendment data. The choice of the amendment data can be determined according to the actual demand and, therefore, it is subjective. However, the ESO method is objective after determining the amendment data. If users agree with the amendment rule of this study, they also could take the single factor assessment results as amendment data, then the subjectivity disappears.
- 2
- Calculation of the amendment entropy weight according to the single-factor evaluation results using the amendment rule. The amendment data can be selected to the requirement. As grade III is used to indicate whether the water quality is qualified or not, the weights of sample indices better than grade III will be reduced, while those of sample indices inferior to grade III will increase, taking grade III water as the reference point in the algorithm proposed in this study. This work is to avoid ignorance to indicators with high pollution to cause an unreasonable result. The formula is as follows.where Wnj is the amendment weight of indicator j, Wj is the entropy weight of indicator j, m is the amendment value according to the single-factor evaluation results, n is the number of samples corresponding to different amendment values, and N is the number of samples.
- 3
- The amendment entropy weight calculated by formula (11) was normalized, then, amendment weight Wn’j based on the result of single-factor evaluation was obtained.where Wnj is the amendment weight of indicator j, W’j is the normalized amendment weight of indicator j (amendment entropy weight).
- Step 3—OSE weight calculation
- 1
- Calculation of the degree by which each indicator exceeds the standard in each sample.For the “bigger the better” indicator:For the “smaller the better” indicator:
- 2
- Determination of the weight value W″ij:where kij is the degree by which sample i exceeds the standard of indicator j, vjt represents the standard value of the t-grade water quality in indicator j, xij is the measured value of indicator j in sample i, and W″ij represents the weight value of indicator j in sample i.
- Step 4—The arithmetic average method was used to calculate the combined weights. The weights obtained here are called ESO weights, as we used the ESO method in this study [17].where Wcij is the combination weight (ESO weight) of the amendment entropy and over-standard weights, W′j is the normalized amendment weight of indicator j, and W″ij is the over-standard weight of indicator j in sample i.
3. Results and Discussion
3.1. Entropy Weight and Amendment Entropy Weight
3.2. Over-Standard and ESO Weights
3.3. Fuzzy Synthetic Evaluation Results
3.4. Applicability of the ESO Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, Z.; Hu, L.; Cheng, H.; Qi, D. Application of Pollution Index Method Based on Dynamic Combination Weight to Water Quality Evaluation. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Guilin, China, 20–22 April 2018. [Google Scholar]
- Lu, R.S.; Lo, S.L.; Hu, J.Y. Analysis of reservoir water quality using fuzzy synthetic evaluation. Stoch. Environ. Res. Risk Assess. 1999, 13, 327–336. [Google Scholar] [CrossRef]
- Rahmati, O.; Samani, A.N.; Mahdavi, M.; Pourghasemi, H.R.; Zeinivand, H. Groundwater potential mapping at Kurdistan region of Iran using analytic hierarchy process and GIS. Arab. J. Geosci. 2014, 8, 7059–7071. [Google Scholar] [CrossRef]
- Lee, S. Determination of Priority Weights under Multiattribute Decision-Making Situations: AHP versus Fuzzy AHP. J. Constr. Eng. Manag. 2015, 141, 05014015. [Google Scholar] [CrossRef]
- Delgado, A.; Romero, I. Environmental conflict analysis using an integrated grey clustering and entropy-weight method: A case study of a mining project in Peru. Environ. Model. Softw. 2016, 77, 108–121. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.-C.; Li, L.-P.; Lin, P.; Xu, Z.-H.; Gao, C.-L. Attribute recognition model for risk assessment of water inrush. Bull. Int. Assoc. Eng. Geol. 2017, 78, 1057–1071. [Google Scholar] [CrossRef]
- Gorgij, A.D.; Kisi, O.; Moghaddam, A.A.; Taghipour, A. Groundwater quality ranking for drinking purposes, using the entropy method and the spatial autocorrelation index. Environ. Earth Sci. 2017, 76, 9. [Google Scholar] [CrossRef]
- Ma, F.; Li, C.; Wang, X.; Yang, Z.; Sun, C.; Liang, P. A Bayesian method for comprehensive water quality evaluation of the Danjiangkou Reservoir water source area, for the middle route of the South-to-North Water Diversion Project in China. Front. Earth Sci. 2013, 8, 242–250. [Google Scholar] [CrossRef]
- Liu, J.G.J.; Jiang, J. Application of different fuzzy assessment methods of water quality assessment in Dianchi Lake. Environ. Pollut. Control. 2010, 32, 20–25. [Google Scholar]
- Liu, K.; Lin, B. Research on influencing factors of environmental pollution in China: A spatial econometric analysis. J. Clean. Prod. 2019, 206, 356–364. [Google Scholar] [CrossRef]
- Qian, B.; Zhu, Y.X.; Wang, Y.X.; Yan, F. Can Entropy Weight Method Correctly Reflect the Distinction of Water Quality Indices? Water Resour. Manag. 2020, 34, 3667–3674. [Google Scholar]
- Zhi-Hong, Z.; Yi, Y.; Jing-Nan, S. Entropy method for determination of weight of evaluating indicators in fuzzy synthetic evaluation for water quality assessment. J. Environ. Sci. 2006, 18, 1020–1023. [Google Scholar]
- Pan, Z.; Wu, K.; Huang, Q. An Improved Method to Determine the Weight on Fuzzy Evaluation of the Water Environmental Quality. Biography 2008, 1, 2. [Google Scholar]
- Yang, J.Y.; Zhang, L.L. Fuzzy Comprehensive Evaluation Method on Water Environmental Quality based on Entropy Weight with Consideration of Toxicology of Evaluation Factors. In Progress in Environmental Science and Engineering; Li, H., Xu, Q.J., Zhang, D., Eds.; Trans Tech Publications Ltd.: Durnten, Switzerland, 2012; pp. 2383–2388. [Google Scholar]
- Yan, F.; Yi, F.H.; Chen, L. Improved Entropy Weighting Model in Water Quality Evaluation. Water Resour. Manag. 2019, 33, 2049–2056. [Google Scholar]
- Wang, X.T.; Yang, W.M.; Xu, Z.H.; Hu, J.; Xue, Y.G.; Lin, P. A Normal Cloud Model-Based Method for Water Quality Assessment of Springs and Its Application in Jinan. Sustainability 2019, 11, 2248. [Google Scholar] [CrossRef] [Green Version]
- Jun, P.; Li, M.; Zhen, Z. The Method of Quadratic Combination Weighting Fuzzy Comprehensive Evaluation applied in Water Quality Assessment. In Proceedings of the International Conference on Material and Environmental Engineering, Jiujiang, China, 21–23 March 2014; Zhang, Y., Ed.; Atlantis Press: Paris, France, 2014; pp. 127–130. [Google Scholar]
- Yan, W.; Li, J.; Bai, X. Comprehensive assessment and visualized monitoring of urban drinking water quality. Chemom. Intell. Lab. Syst. 2016, 155, 26–35. [Google Scholar] [CrossRef]
- Wu, X.; Hu, F. Analysis of ecological carrying capacity using a fuzzy comprehensive evaluation method. Ecol. Indic. 2020, 113, 13. [Google Scholar] [CrossRef]
- Liu, X.M.; Zhang, G.X.; Sun, G.Z.; Wu, Y.; Chen, Y.Q. Assessment of Lake Water Quality and Eutrophication Risk in an Agricultural Irrigation Area: A Case Study of the Chagan Lake in Northeast China. Water 2019, 11, 2380. [Google Scholar] [CrossRef] [Green Version]
- He, Y.J.; Wang, D.; Wang, G.L. Fuzzy Comprehensive Evaluation on North-China Groundwater Quality. In Progress in Environmental Science and Engineering; Pts 1-42013; Xu, Q.J., Ju, Y.H., Ge, H.H., Eds.; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2013; pp. 2729–2733. [Google Scholar]
- Chai, Y.; Xiao, C.; Li, M.; Liang, X. Hydrogeochemical Characteristics and Groundwater Quality Evaluation Based on Multivariate Statistical Analysis. Water 2020, 12, 2792. [Google Scholar] [CrossRef]
- Dong, J.; Li, X.; Fang, Y.; Zheng, X. Evaluation and Rediction of Groundwater Quality Based on Improved Fuzzy Synthesis-Exponential Smoothing. Period. Ocean Univ. China 2020, 50, 126–135. [Google Scholar]
- Liu, L.; Zhou, J.; An, X.; Zhang, Y.; Yang, L. Using fuzzy theory and information entropy for water quality assessment in Three Gorges region, China. Expert Syst. Appl. 2010, 37, 2517–2521. [Google Scholar] [CrossRef]
- Baodong, F. Fuzzy, comprehensive evaluation model for groundwater quality. China Rural Water Hydropower 1998, 9, 29–32. [Google Scholar]
- Vranešević, M.; Belić, S.; Kolaković, S.; Kadović, R.; Bezdan, A. Estimating Suitability of Localities for Biotechnical Measures on Drainage System Application in Vojvodina. Irrig. Drain. 2016, 66, 129–140. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, J.; Zou, Q. Comprehensive Analysis of Coordination Relationship between Water Resources Environment and High-Quality Economic Development in Urban Agglomeration in the Middle Reaches of Yangtze River. Water 2020, 12, 1301. [Google Scholar] [CrossRef]
- Kan, B.; Fu, Q.; Song, Z. Application of fuzzy matter-element model based on the multiple superscale to evaluating water quality in wetland. J. Safety Environ. 2009, 9, 97–99. [Google Scholar]
- Wang, Y.; Sheng, D.; Wang, N.; Ma, H.; Wu, J.; Xu, F. Variable Fuzzy Set Theory to Assess Water Quality of the Meiliang Bay in Taihu Lake Basin. Water Resour. Manag. 2014, 28, 867–880. [Google Scholar] [CrossRef]
- Zhang, L.; Li, W.-J.; Lai, W. Application Research on Improved BP Neural Network for Water Quality Comprehensive Evaluation. In Proceedings of the International Conference on Graphic and Image Processing, Hong Kong, China, 26–27 October 2013; Zhu, Z., Ed.; SPIE—International Society for Optics and Photonics: Bellingham, WA, USA, 2013. [Google Scholar]
- Wu, C.; Ren, Y.; Zhang, B.; Zhang, B. Evaluation of Water Quality of Neijiang in Zhenjiang Based on Fuzzy Mathematics. In Proceedings of the International Conference on Intelligent Computation and Industrial Application (ICIA2011), Hong Kong, China, 18–19 June 2011. [Google Scholar]
- Zhang, Y.B.; Si, X.L. Quality Assessment of Surface Water Environment Based on Improved Grey Correlation Method. Yellow River 2017, 39, 109–111, 127. [Google Scholar]
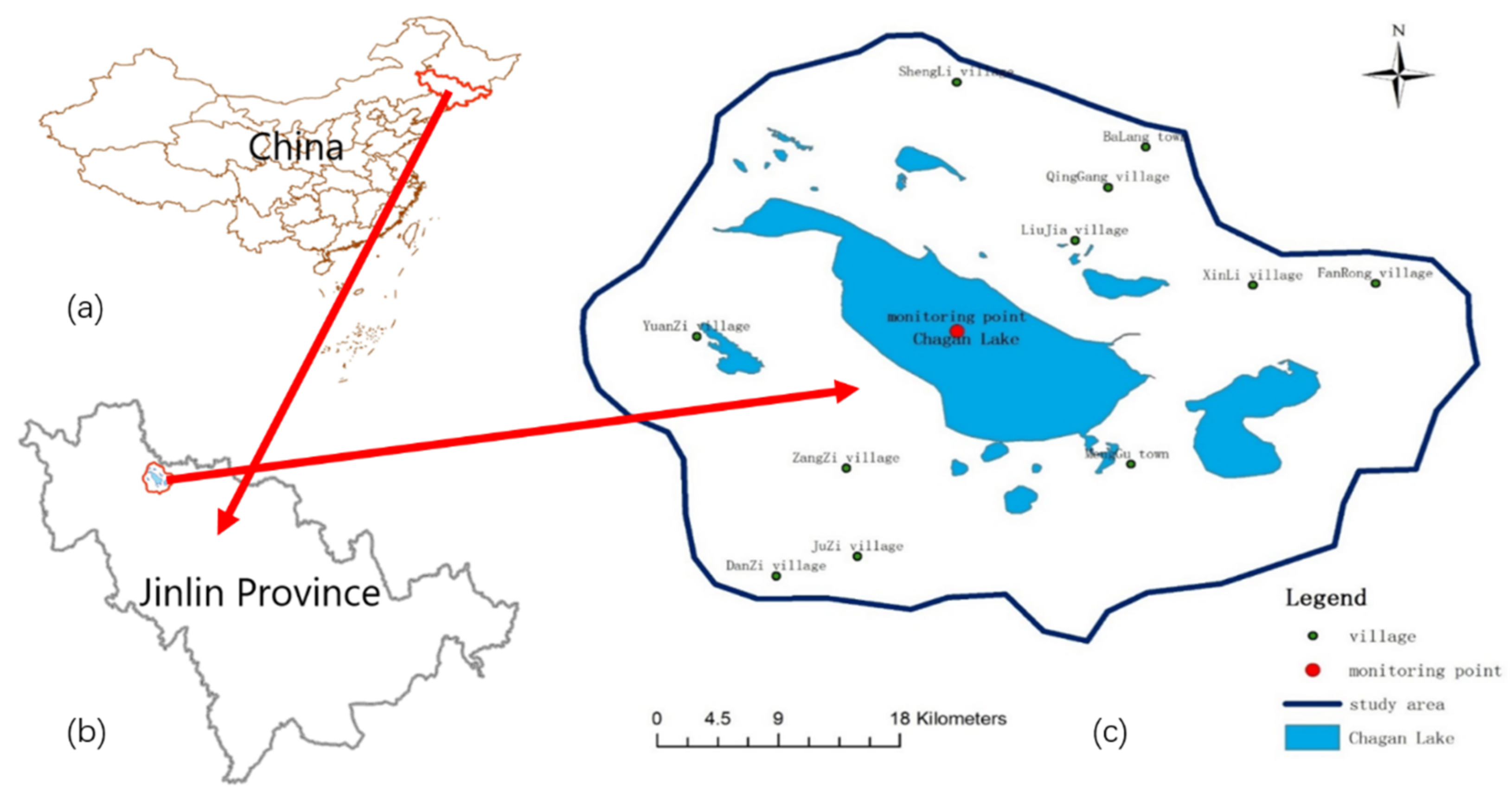
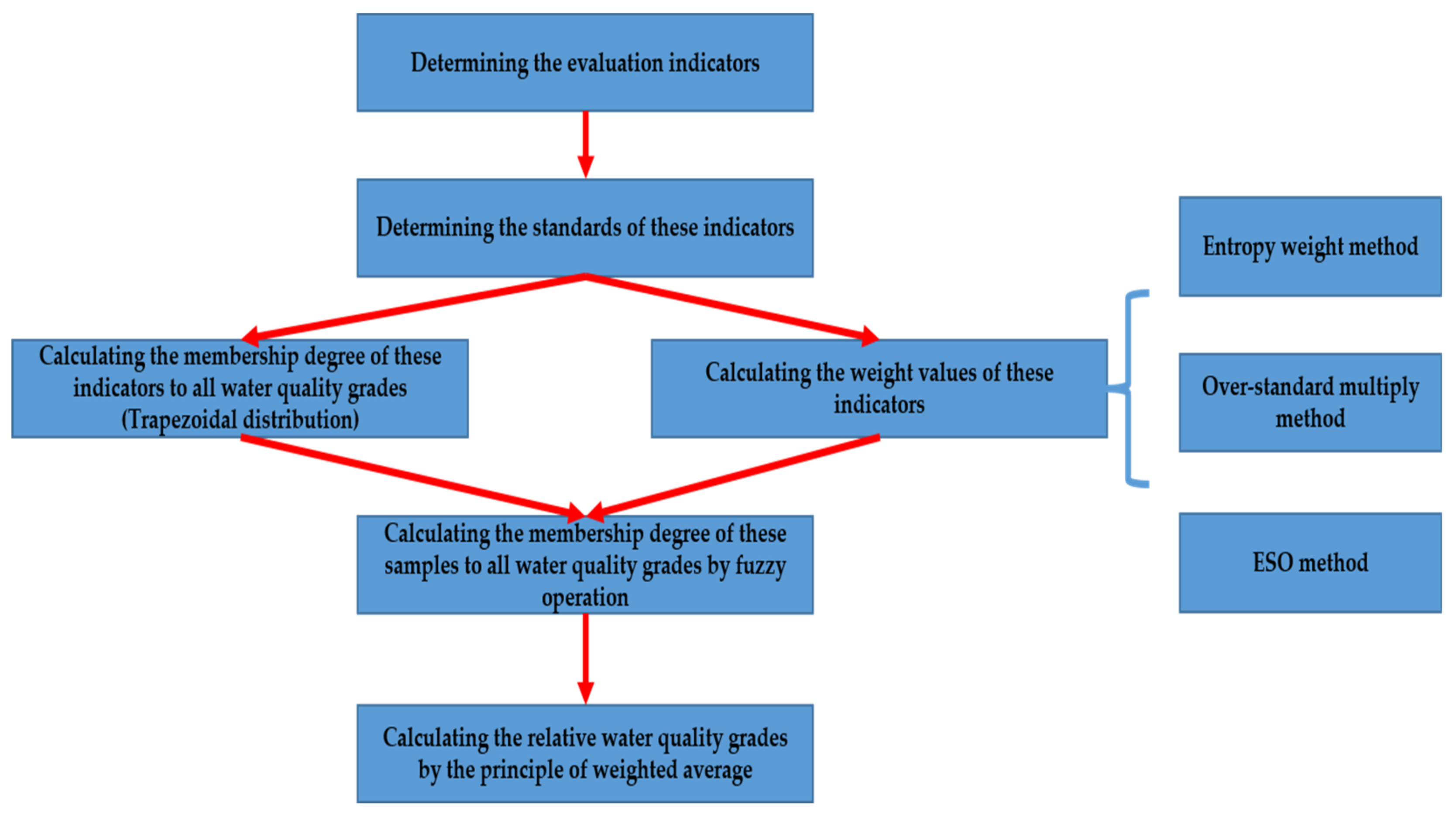
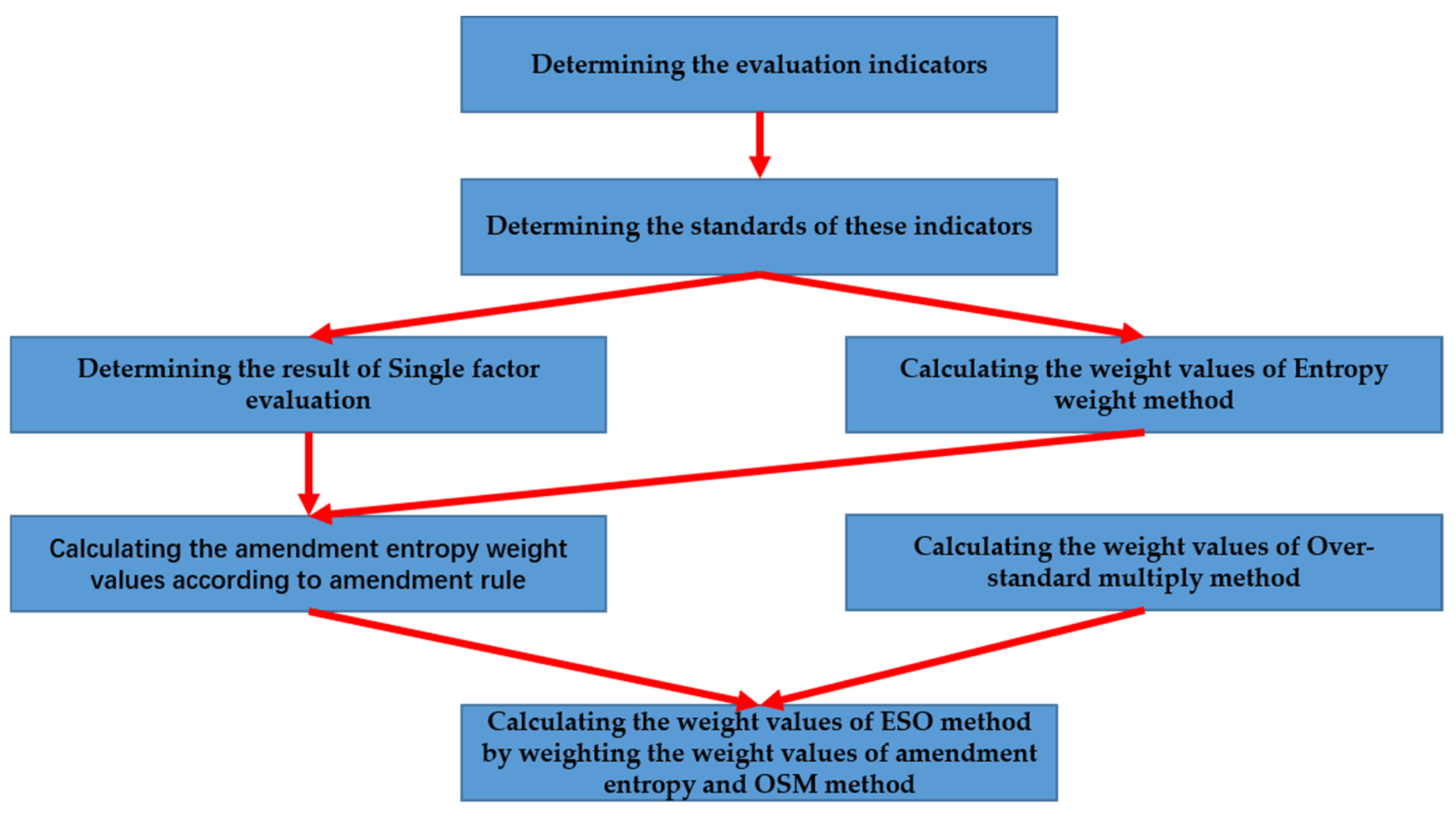
| Grade | I | II | III | IV | V | Inferior V |
|---|---|---|---|---|---|---|
| m | 0 | 0 | 1 | 2 | 3 | 4 |
| Year | DO | F | NH3-N | CODCr | CODMN | BOD5 | TP | TN |
|---|---|---|---|---|---|---|---|---|
| 2007 | I | IV | III | IV | IV | III | V | IV |
| 2008 | I | IV | III | IV | IV | III | V | IV |
| 2009 | I | Inferior V | III | V | IV | III | IV | IV |
| 2010 | I | IV | III | V | IV | III | V | IV |
| 2011 | I | IV | II | V | IV | III | III | IV |
| 2012 | I | IV | II | V | IV | III | III | IV |
| 2013 | I | IV | II | V | IV | III | III | IV |
| 2014 | I | IV | II | V | IV | IV | III | IV |
| 2015 | II | Inferior V | II | V | IV | III | IV | IV |
| 2016 | II | Inferior V | II | V | IV | IV | III | V |
| DO | F | NH3-N | CODCr | CODMn | BOD5 | TP | TN | |
|---|---|---|---|---|---|---|---|---|
| Entropy weight | 0.114 | 0.105 | 0.096 | 0.122 | 0.110 | 0.140 | 0.207 | 0.105 |
| Amendment entropy Weight | 0.000 | 0.168 | 0.024 | 0.208 | 0.135 | 0.103 | 0.228 | 0.135 |
| Variance (10−4) | 3.18 | 2.94 | 2.68 | 3.54 | 3.04 | 4.25 | 5.97 | 2.82 |
| Year | DO | F | NH3-N | CODCr | CODMn | BOD5 | TP | TN |
|---|---|---|---|---|---|---|---|---|
| 2007 | 0.069 | 0.122 | 0.092 | 0.154 | 0.133 | 0.079 | 0.195 | 0.155 |
| 2008 | 0.07 | 0.139 | 0.066 | 0.158 | 0.118 | 0.079 | 0.183 | 0.182 |
| 2009 | 0.061 | 0.162 | 0.063 | 0.193 | 0.113 | 0.085 | 0.165 | 0.158 |
| 2010 | 0.071 | 0.115 | 0.071 | 0.176 | 0.130 | 0.080 | 0.202 | 0.156 |
| 2011 | 0.077 | 0.168 | 0.069 | 0.201 | 0.158 | 0.067 | 0.095 | 0.164 |
| 2012 | 0.075 | 0.167 | 0.049 | 0.220 | 0.168 | 0.097 | 0.071 | 0.153 |
| 2013 | 0.082 | 0.155 | 0.065 | 0.203 | 0.158 | 0.104 | 0.076 | 0.155 |
| 2014 | 0.078 | 0.185 | 0.059 | 0.203 | 0.140 | 0.120 | 0.059 | 0.156 |
| 2015 | 0.085 | 0.194 | 0.054 | 0.179 | 0.116 | 0.084 | 0.139 | 0.150 |
| 2016 | 0.080 | 0.166 | 0.061 | 0.169 | 0.133 | 0.097 | 0.082 | 0.212 |
| Year | DO | F | NH3-N | CODCr | CODMn | BOD5 | TP | TN |
|---|---|---|---|---|---|---|---|---|
| 2007 | 0.035 | 0.145 | 0.058 | 0.181 | 0.134 | 0.091 | 0.212 | 0.145 |
| 2008 | 0.038 | 0.153 | 0.045 | 0.183 | 0.126 | 0.091 | 0.205 | 0.159 |
| 2009 | 0.030 | 0.165 | 0.043 | 0.201 | 0.124 | 0.094 | 0.196 | 0.146 |
| 2010 | 0.035 | 0.141 | 0.047 | 0.192 | 0.132 | 0.091 | 0.215 | 0.146 |
| 2011 | 0.039 | 0.168 | 0.047 | 0.204 | 0.146 | 0.085 | 0.161 | 0.150 |
| 2012 | 0.037 | 0.167 | 0.036 | 0.214 | 0.152 | 0.100 | 0.149 | 0.144 |
| 2013 | 0.041 | 0.161 | 0.045 | 0.206 | 0.147 | 0.104 | 0.152 | 0.145 |
| 2014 | 0.039 | 0.176 | 0.041 | 0.205 | 0.137 | 0.111 | 0.143 | 0.146 |
| 2015 | 0.042 | 0.181 | 0.039 | 0.194 | 0.125 | 0.094 | 0.183 | 0.142 |
| 2016 | 0.040 | 0.167 | 0.042 | 0.188 | 0.134 | 0.100 | 0.155 | 0.174 |
| Year | Single-Factor Evaluation Method | Over-Standard Method | Entropy Method | Amendment Entropy Method | ESO Method |
|---|---|---|---|---|---|
| 2007 | V | 3.344 | 2.988 | 3.512 | 3.438 |
| 2008 | V | 3.802 | 3.535 | 3.867 | 3.847 |
| 2009 | Inferior V | 4.028 | 3.542 | 4.100 | 4.079 |
| 2010 | V | 3.587 | 3.299 | 3.663 | 3.639 |
| 2011 | V | 3.413 | 2.731 | 3.392 | 3.411 |
| 2012 | V | 3.700 | 2.987 | 3.555 | 3.649 |
| 2013 | V | 3.302 | 2.905 | 3.275 | 3.303 |
| 2014 | V | 3.402 | 2.859 | 3.314 | 3.385 |
| 2015 | Inferior V | 4.026 | 3.491 | 4.043 | 4.050 |
| 2016 | Inferior V | 4.021 | 3.281 | 3.735 | 3.895 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Xiao, C.; Chai, Y.; Feng, X.; Liang, X.; Fang, Z. Application of a New Improved Weighting Method, ESO Method Combined with Fuzzy Synthetic Method, in Water Quality Evaluation of Chagan Lake. Water 2021, 13, 1424. https://doi.org/10.3390/w13101424
Zhao W, Xiao C, Chai Y, Feng X, Liang X, Fang Z. Application of a New Improved Weighting Method, ESO Method Combined with Fuzzy Synthetic Method, in Water Quality Evaluation of Chagan Lake. Water. 2021; 13(10):1424. https://doi.org/10.3390/w13101424
Chicago/Turabian StyleZhao, Wenbin, Changlai Xiao, Yunxu Chai, Xiaoya Feng, Xiujuan Liang, and Zhang Fang. 2021. "Application of a New Improved Weighting Method, ESO Method Combined with Fuzzy Synthetic Method, in Water Quality Evaluation of Chagan Lake" Water 13, no. 10: 1424. https://doi.org/10.3390/w13101424
APA StyleZhao, W., Xiao, C., Chai, Y., Feng, X., Liang, X., & Fang, Z. (2021). Application of a New Improved Weighting Method, ESO Method Combined with Fuzzy Synthetic Method, in Water Quality Evaluation of Chagan Lake. Water, 13(10), 1424. https://doi.org/10.3390/w13101424





