1. Introduction
The projected future changes in the land-use, climate, and water cycle lead to an increasing demand for modeling approaches and frameworks for the simulation of hydrological processes at local and regional scale of water resource management. Therefore, a well parameterized and calibrated physically based hydrological model, which is capable of realistically reproducing the behavior of the hydrologic system, is considered particularly important in order to provide decision makers in water resources management with reliable predictions [
1]. Soil hydraulic properties have a major impact on the main hydrological processes in catchment areas [
2,
3]. Therefore, information on these soil properties plays a key role in water balance modeling, and an adequate parameterization of soils is one of the most important tasks in physically based catchment modeling [
4,
5]. Richard’s equation [
6], which describes the water flow in unsaturated soil by combining the Darcy–Buckingham law with the continuity equation, is the dominant concept of soil physics in hydrological textbooks [
7,
8,
9]. It can be considered as the fundamental concept underlying “physically-based” hydrological models [
10]. To solve this equation, information on soil hydraulic properties is required [
11].
Parameters of soil properties are usually measured as point observations at small scales. However, water balance modeling in catchments requires parameter values at larger spatial scales such as grid cells or the entire catchment [
12]. The Richard’s equation is parameterized by either observed soil properties (i.e., measured relations of soil water content and matric potential) or constitutive equations such as the Gardner–Russo model [
13], the Brooks-Corey model [
13], or the Mualem–van Genuchten model [
14,
15]. These empirical models represent a basic hydro-physical characteristic of the soil: the relation between soil water content and matric potential [
16].
Among the empirical models developed to parameterize the water flow in unsaturated soils, the traditional van Genuchten parameterization [
15] has evolved to a de facto standard and is widely used because of its higher degree of fit to observed soil water retention data [
17]. Nevertheless, to practically apply this model, obtaining its unknown empirical fitting parameters based on known experimental data (namely, a measured soil water retention curve) is essential. Moreover, at larger spatial scales, such as those of catchment models, direct measurements are not feasible due to the area coverage and the heterogeneity of the soil properties. Therefore, various methods have been developed to determine the van Genuchten parameters, and subsequently, the soil water retention curves using soil parameters that are easier to measure, such as texture, organic matter content, and bulk density. The term pedotransfer function (PTF) has been introduced to define these functional relationships that transfer available measurable soil properties into missing soil properties (e.g., soil hydraulic and soil chemical characteristics) [
18]. The derivation of a PTF is usually based on a two-step process. First, the selected water retention function (e.g., van Genuchten) is fitted to measured water retention curves. In the second step, the parameter values determined in this process are related to the selected soil properties [
17,
19]. During the last three decades, soil scientists have developed a broad set of PTFs that differ with respect to:
Applied methods (e.g., statistical regression techniques, data mining and exploration techniques);
The underlying database of measured soil moisture retention data used to fit van Genuchten model estimates; and
Required input parameters or predictors (e.g., grain size distribution, bulk density, organic matter content) to derive PTF.
Extensive reviews on this content were given by Pachepsky and Rawls (2004) [
20]; Wösten et al. (2001) [
11]; Vereecken et al. (2010) [
17]; and Patil and Singh (2016) [
21]. Accuracy and uncertainty of PTFs were evaluated by Schaap and Leij (1998) [
22]. They showed that the performance of PTFs may depend strongly on: the data employed for calibration and evaluation, input soil properties, and different applied methods. The databases that have been used to derive PTFs show four remarkable differences:
Parameterization of soil hydraulic properties should be done in such a way that the hydrological processes simulated using a water balance model match the locally observed processes [
24,
25]. From a modeler’s perspective, the inconsistencies in the data bases used for deriving the different PTFs complicate the evaluation of their reliability in a specific case. For instance, Vereecken et al. (1992) [
26] showed that 90% of the variation in predicted moisture supply was attributed to estimation errors in hydraulic properties when using the PTFs developed by Vereecken et al. (1989, 1990) [
27,
28]. In another study, Chirico et al. (2010) [
29] analyzed the effect of PTF prediction uncertainty on soil water balance components at the hillslope scale. They found that simulated evaporation is more affected by the PTF model error than by errors due to uncertainties in model input data. This sensitivity can result in a compensation of structural model errors by soil parameters, if no careful evaluation of the parameterization of soil hydraulic properties or the simulation of depth-dependent soil moisture content is made [
30]. As a result, investigating the model behavior in response to change in the method used to estimate soil hydraulic properties, such as using different types of PTFs, is of major relevance to modelers. However, selection of PTF is usually not guided by its effect on the runoff behavior of the catchment model.
Therefore, the aim of this paper is to evaluate the impact of PTF selection on subsequent changes in the hydrological model behavior. We hypothesize that the PTF-specific soil water retention and hydraulic conductivity curves distinctly affect the water balance and runoff characteristics of the hydrological model, and the resulting differences may be related to the respective soil hydraulic properties of the study area as well as to the methodology to derive the PTF. To test the hypothesis (i) we adapted the soil parameterization in a calibrated and validated hydrological model by varying the underlying PTFs and determined the effects on the soil hydraulic properties of the catchment; and (ii) we analyzed the resulting changes in the model behavior with respect to the catchment outlet, as well as the spatial and temporal variation of the total flow and the flow components.
4. Discussion
The selection of the PTF to estimate the soil hydraulic properties which are included in a hydrological model is often done without taking the runoff characteristics of the catchment into consideration. Therefore, it is of particular interest to the modeling community to have a quantitative description of the change in model behavior caused by the choice of PTF, in order to make decisions that are more informed. We hypothesized that the water balance and runoff behavior of a catchment are distinctly affected by the characteristics of the PTFs that primarily represent the water retention and hydraulic conductivity curves. Thus, we considered the soil parameterization of different PTFs in a hydrological catchment model to quantify the changes in soil hydraulic properties of the Glonn catchment as well as to analyze the resulting shifts in its water balance components and runoff characteristics.
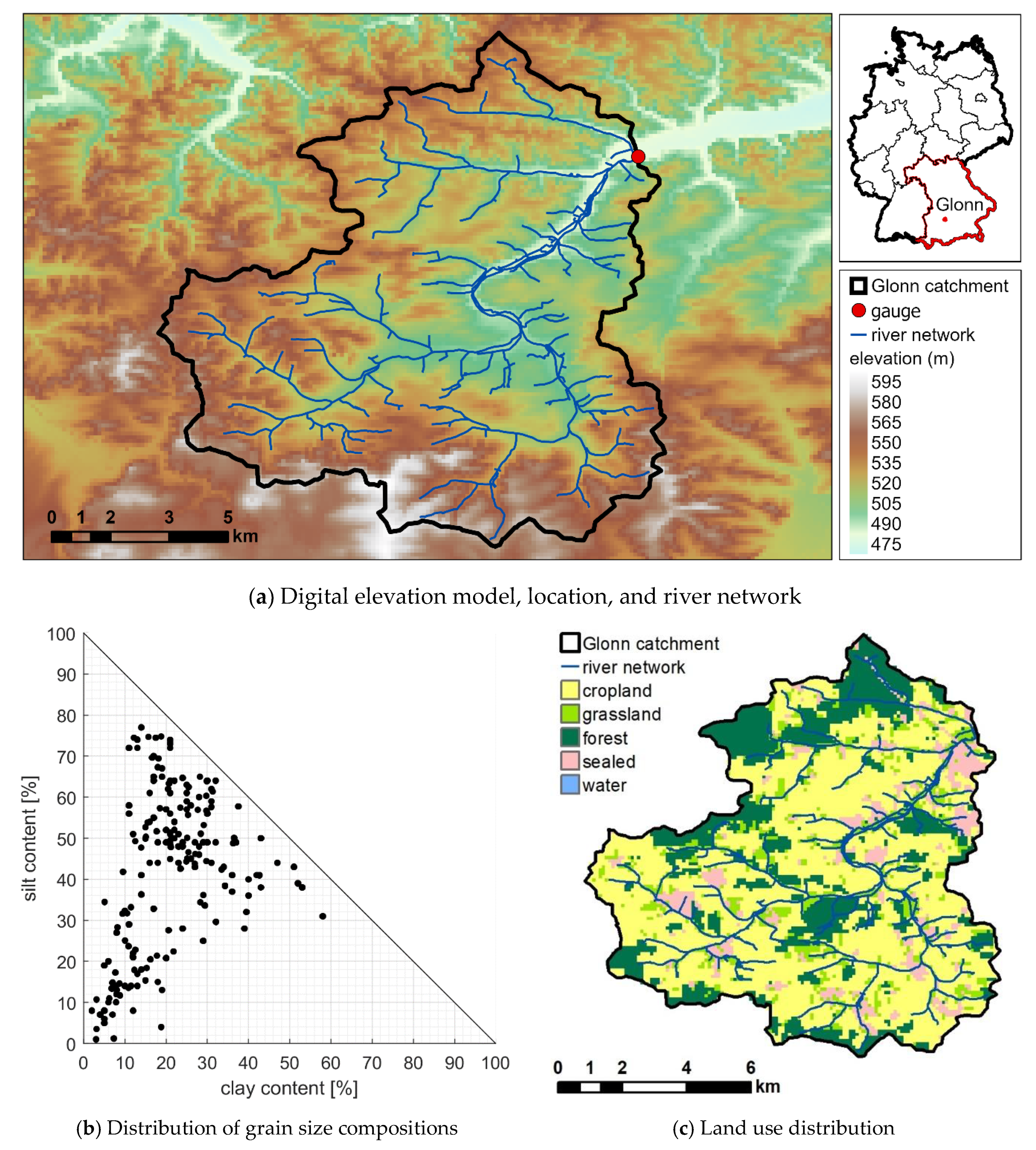
As shown in
Figure 1b, the Glonn catchment covers a wide range of different soil texture classes. It is therefore well suited for studying the influence of PTFs on soil hydraulic properties as well as the resulting runoff behavior. This high diversity allowed holding a more profound analysis of the spatial and temporal variability of different runoff characteristics depending on the choice of the respective PTF. The good representation of the runoff behavior by WaSiM-ETH suggests the general suitability of this hydrological model for the intended investigation. Moreover, the implementation of a layered soil structure made it possible to consider the underlying soil properties in detail.
The baseline scenario and the 10 other scenarios (
Table 3) were chosen in such a way that the influence of modified van-Genuchten parameters or saturated hydraulic conductivities could be separately explored. Since the calibration was only performed for the baseline scenario, the differences in the runoff behavior amongst scenarios can be directly attributed to the modified soil parameters. Nevertheless, this approach cannot provide a definitive assessment of the suitability of the PTFs to represent the runoff behavior in the catchment. This evaluation would require the calibration of all scenarios using the same calibration strategy. However, due to the resulting over-imposition of the runoff behavior by the calibration parameters, the direct analysis of the particular influence of the changed soil properties would no longer be possible. Therefore, the calibration of the scenarios was not performed. Nevertheless, the parameters of the calibrated baseline scenario are within the parameter space of the other scenarios, and thus their hydrographs scatter around the measured runoff.
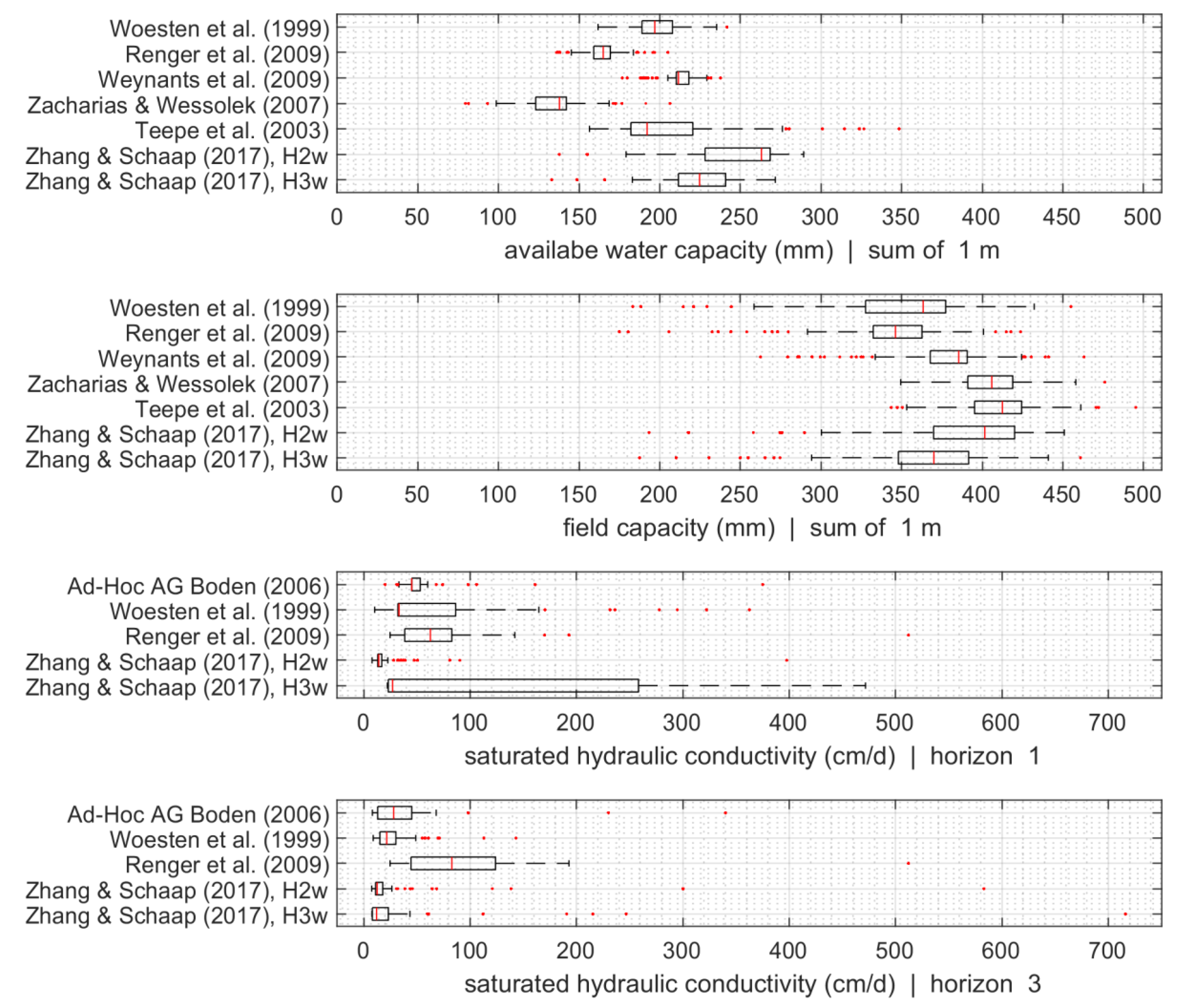
The considered PTFs resulted in a wide range of different shapes for the water retention and saturated hydraulic conductivity curves. The shape of the water retention curve is mainly associated with the parameters n and α which are included in the soil parameterization in WaSiM-ETH (
Table 1). The parameters are related to the process of saturation and desaturation of the soil [
52]. The hydraulic parameters AWC, FC, and K
sat determined for a quantitative comparison of the curves showed significant differences in their spatial distribution (
Figure 2). These differences become particularly evident when comparing the individual scenarios with the baseline scenario. This issue is important because spatial variability of soil hydraulic properties is regarded as a significant factor to water distribution in the catchment [
53].
The quality and quantity of the changes in the soil hydraulic properties induced by different PTFs are remarkably affected by their underlying databases, predictors, and methods used to develop the predictive equations. For example, apart from the soil texture classes, there is a significant effect on estimates of soil hydraulic properties, when both OM and BD variables and when only one of them are inputs to the equations (PTFs) [
54]. Consequently, the impact of land use and geographic attributes on soil BD and OM [
55] leads to a different description of the same soil in the PTFs (i.e., different input values into the equation) and this may account for the observed variation in soil hydraulic properties [
11,
43]. As a result, the spatial distribution of the differences that we observed between AWC and K
sat simulated by the scenarios and those of the baseline scenario could be attributed to the land use distribution as well as the proximity to watercourses (
Figure 1 and
Figure 3). AWC depends to a large extent on the bulk density and the silt content. Hence, PTFs that do not include BD typically result in lower AWC values in soils with lower bulk densities, such as those found in the upper soil horizons of forest soils in a study by [
56,
57]. They also identified the BD and soil texture as major factors explaining spatial variance in AWC for a study area in China.
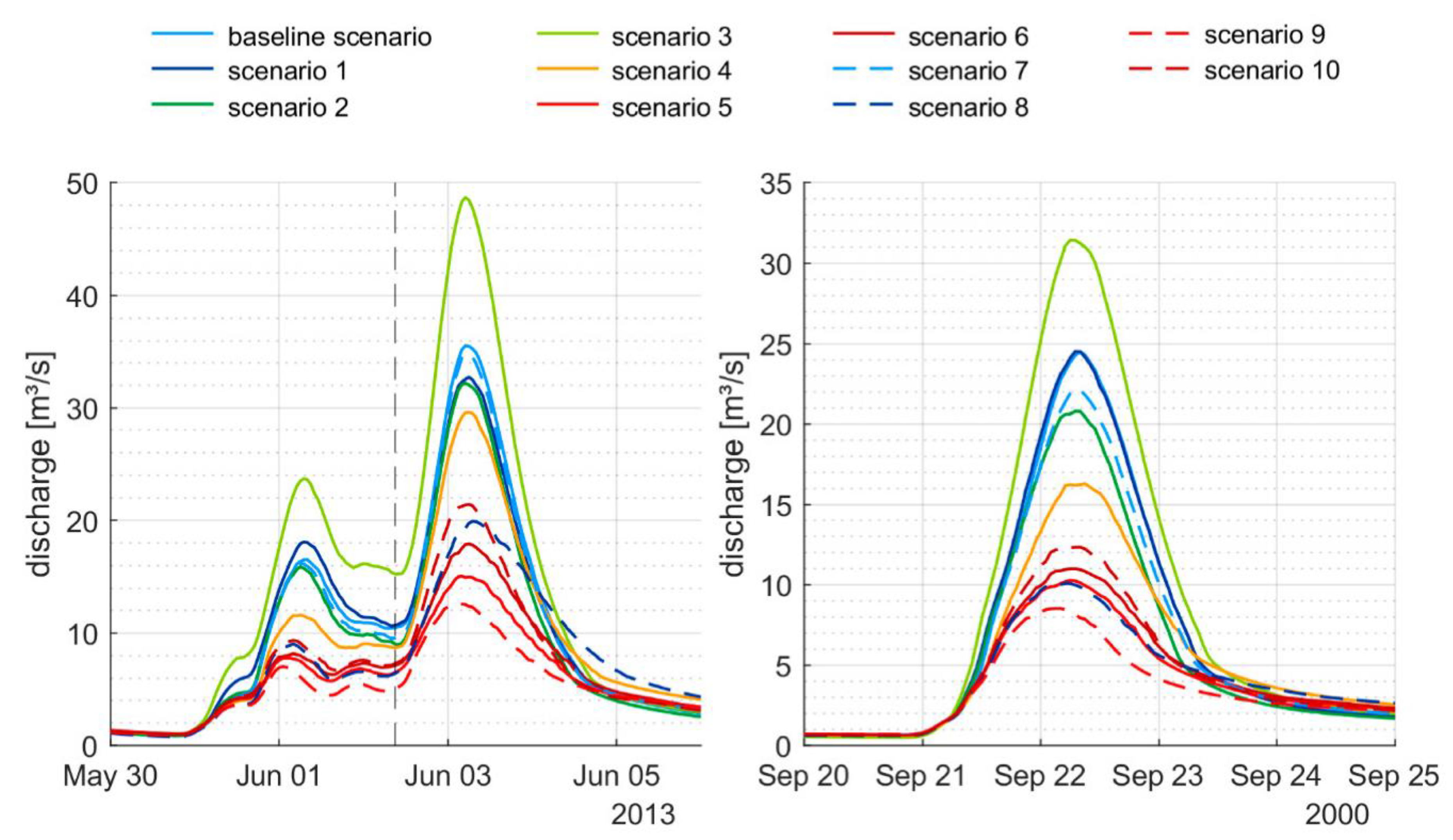
The qualitative and quantitative analysis of the discharge hydrographs (
Figure 4 and
Table 5) as well as the respective signature indices analysis (
Table 6) showed distinct differences in the runoff behavior of the catchment through investigated PTFs. The variation of the peak discharge differences between the scenarios and the baseline scenario is caused by the respective pre-event conditions, including the initial soil moisture, and consequently the available soil water storage volume, as well as infiltration capacity.
The differences in model behavior due to soil parameterizations through different PTFs were already analyzed in a study by [
58] using a 1D hydrological model. They showed that even when the very same soil was considered in the entire parameterization scheme, and simulated transpiration and soil moisture were consistent with observations, yet the runoff processes or total water balance could be estimated incorrectly. Based on a multi-criteria evaluation, they found that only one of 24 investigated parameterizations resulted in a realistic behavioral model. The complexity of this evaluation is increased by focusing on a closed hydrological catchment, as it was considered in this study. Here, in comparison to above-mentioned 1D model (i.e., only one cell), adjusting the soil hydraulic properties in our catchment model by various PTFs affects the neighboring cells in the spatial domain as well.
In addition, the runoff behavior in the model is influenced by the choice of the calibration parameters. As a result, an insufficient parameterization of the soil can be at least partially compensated by an appropriate adjustment of the model calibration. However, even after calibration, a model may still represent an unrealistic water distribution across the landscape [
59]. Therefore, in addition to get the right answer, for example by comparing runoff hydrographs at the catchment outlet, it is also required to analyze whether we are getting the “right answers for the right reasons” [
60].
Ultimately, depending on the soil and topographic characteristics, we tracked the spatial distributions of the changes in the main hydrological processes (
Table 7 and
Table 8,
Figure 5).
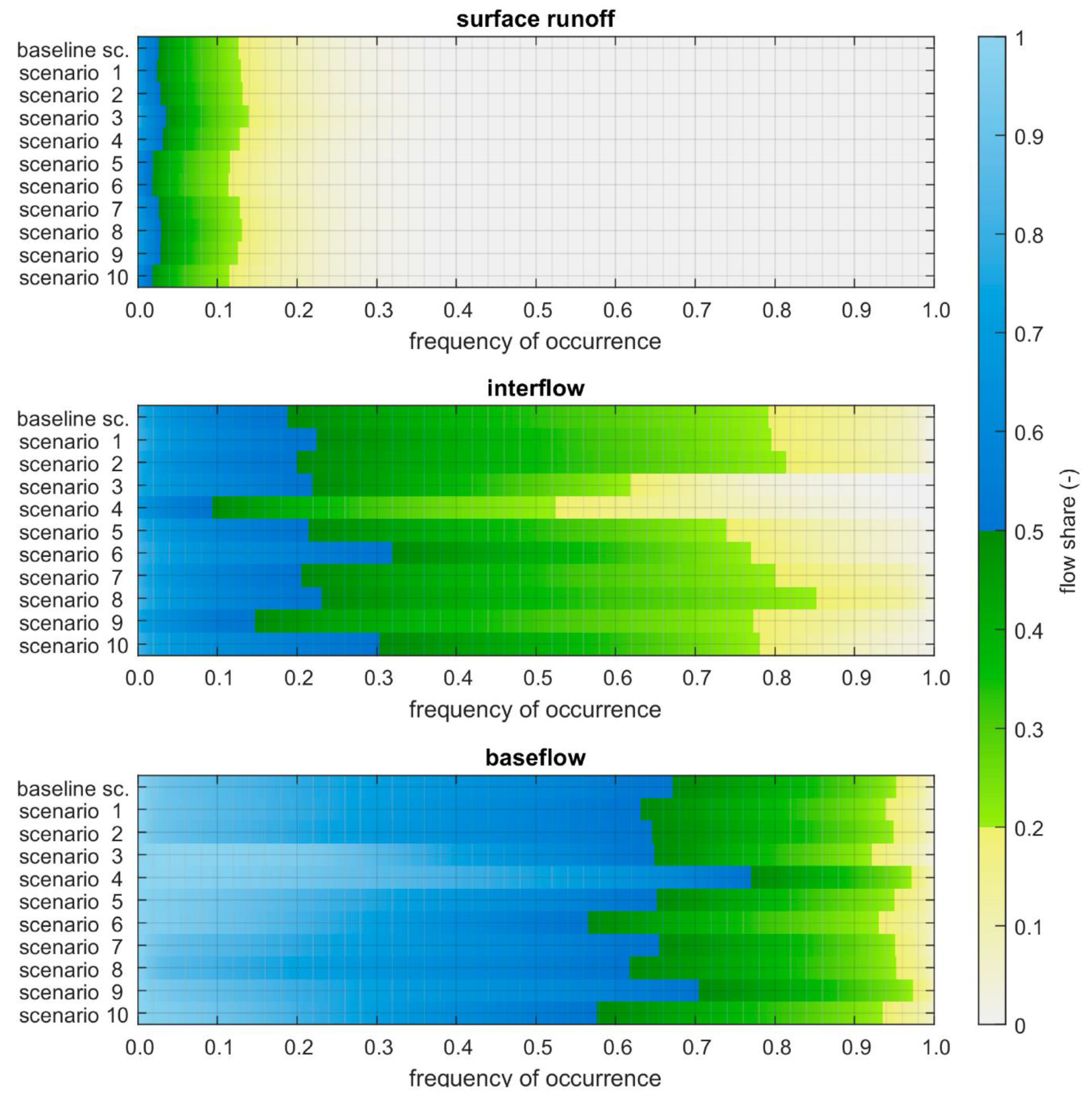
Our results led to a similar conclusion where remarkable differences amongst water balance components of the individual scenarios against the calibrated case were obtained. Furthermore, analysis of frequency of occurrence of runoff components (
Figure 5) displayed a pronounced contrast amongst scenarios. This indicates that the dominance of surface runoff, interflow, and baseflow within the catchment and during time periods can be shifted depending on how the soil hydraulic properties are parameterized. In addition to temporal patterns of runoff components, we examined the spatial patterns of runoff and evapotranspiration in the catchment (
Table 8). The outcome was relevant to the previous mentioned argument, where spatial patterns were also quite distinguishable amongst different scenarios. The quantified influence of various PTFs on temporal and spatial patterns of water budget components provided the same evidence to the fact that spatial variability in soil hydraulic characteristics and model errors initiated from application of different PTF cases, may introduce their own uncertainty to model simulation. This is consistent with what has been found by [
61]. They compared the performance of two different soil hydraulic parameterization techniques in terms of outputs of catchment water balance simulated by the model HydroGeoSphere, and underlined the potential flaws of choosing different parameterizations in spatially distributed modeling.
Finally, it may be concluded that the information contained in streamflow data is not sufficient to derive physically reasonable soil parameter values only via calibration. This indicates that the resulted uncertainty most likely comes from different descriptions of soil water characteristics (i.e., PTF cases). On this account, deriving the “spatial distribution of variability” from different scenarios, our methodology revealed that choosing a specific PTF may significantly influence the spatial distribution of soil hydraulic properties (e.g., K
sat and AWC) and also the way water is being distributed across the landscape prior to the catchment outlet. As a result, owing to the fact that the spatial variability of K
sat and AWC affects the temporal response of the catchment to precipitation and runoff concentration, one can consider that selection of a particular PTF makes evident changes in the distribution among groundwater infiltration, runoff and evapotranspiration in the catchment [
53,
62].
It is important to highlight the fact that most of the PTFs yet show limitations considering the effects of soil inhomogeneity due to structure or macropores, and widely available soil datasets (e.g., FAO Harmonized World Soil Database) may fail to reflect actual field conditions. This warrants further evaluation of PTFs using extensive observed data and particular inclusion the effects of soil structure and macropores [
39,
63]. Moreover, since soil hydrological parameters vary significantly even within a small area, most of the PTFs are usually applicable with acceptable accuracy only in the regions where those functions were developed [
64]. This study showed that the uncertainly forced by selection of PTFs are mainly represented in the spatial distribution of runoff components which are not distinctly addressed by hydrological model calibration against observed discharge time series at the catchment outlet. This recommends that emphasis should be made to soil parameterization oriented towards a “plausible hydrological behavior in terms of spatial patterns of runoff components” during catchment modeling.
According to our knowledge, no comprehensive work was dedicated to carefully analyze the impact of different PTF selection on spatial distribution of internal hydrological processes in the catchment, which underlines the novelty of this research. Indeed, at this stage of understanding, the question of “which PTFs are performing the best?” still remains to be addressed. Since answering this question is beyond the topic of this paper, we therefore believe that future research is clearly required to quantify and qualify the spatial difference in distribution of internal hydrological processes introduced by various PTFs. In other words, application of PTFs in hydrological models without evaluating the spatial patterns of soil moisture, evapotranspiration, and runoff processes produced by different PTFs may ultimately lead to implausible results and possibly to incorrect decisions in water management. This entails investigation of additional information, which usually has to be elaborately collected, for instance, by mapping the dominant runoff generation processes in the area, or retrieving the spatial patterns of evapotranspiration and soil moisture using remote sensing methods, and evaluation at a scale commensurate with hydrological model [
51,
65].