Applications of Two-Dimensional Spatial Routing Procedure for Estimating Dispersion Coefficients in Open Channel Flows
Abstract
1. Introduction
2. Material and Methods
2.1. Estimation of Dispersion Coefficients
2.1.1. Velocity-Based Method
2.1.2. Concentration-Based Method
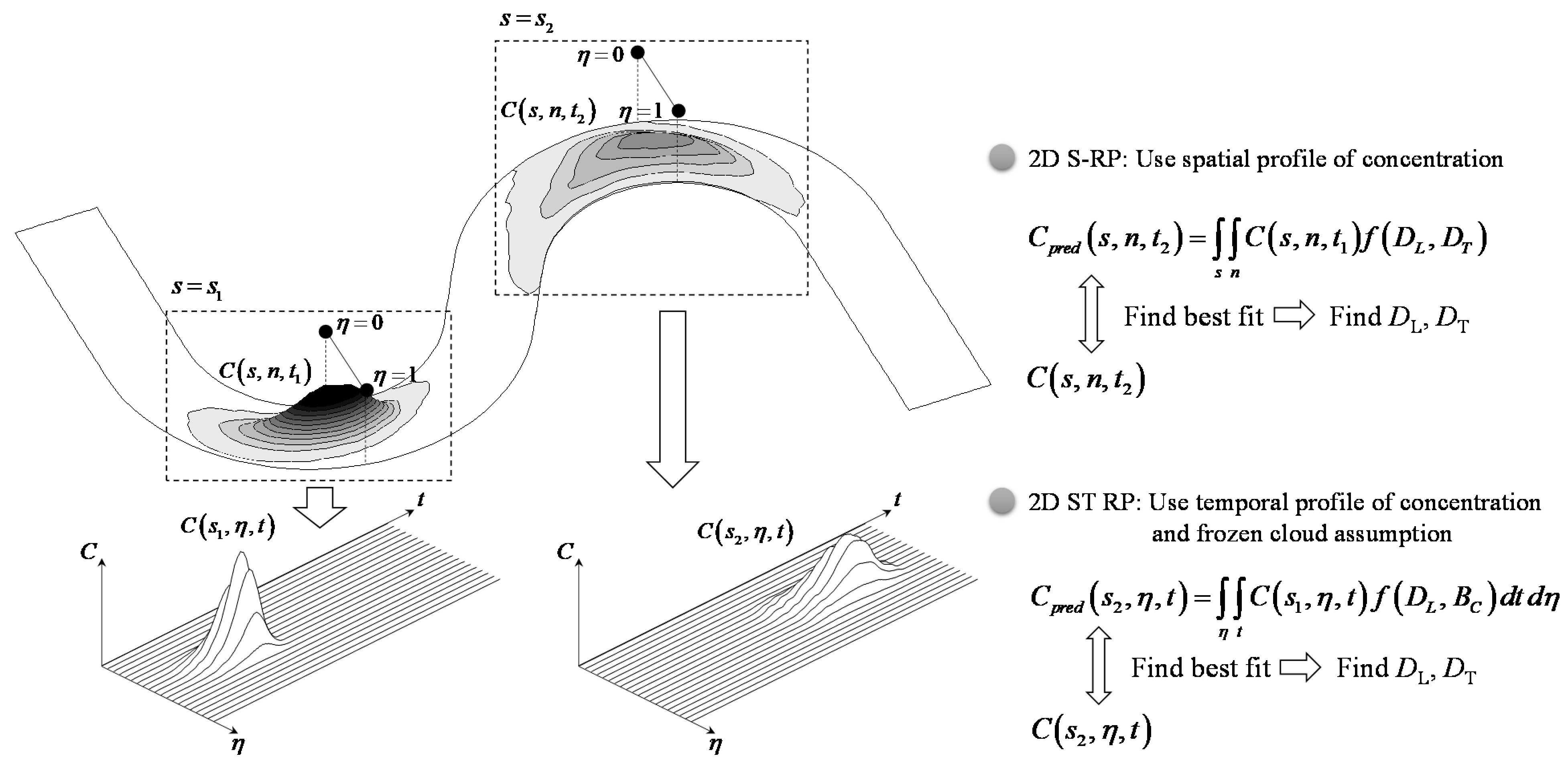
Routing Procedure Using Concentration-Time Curves
Routing Procedure Using Spatial Distributions of Concentration
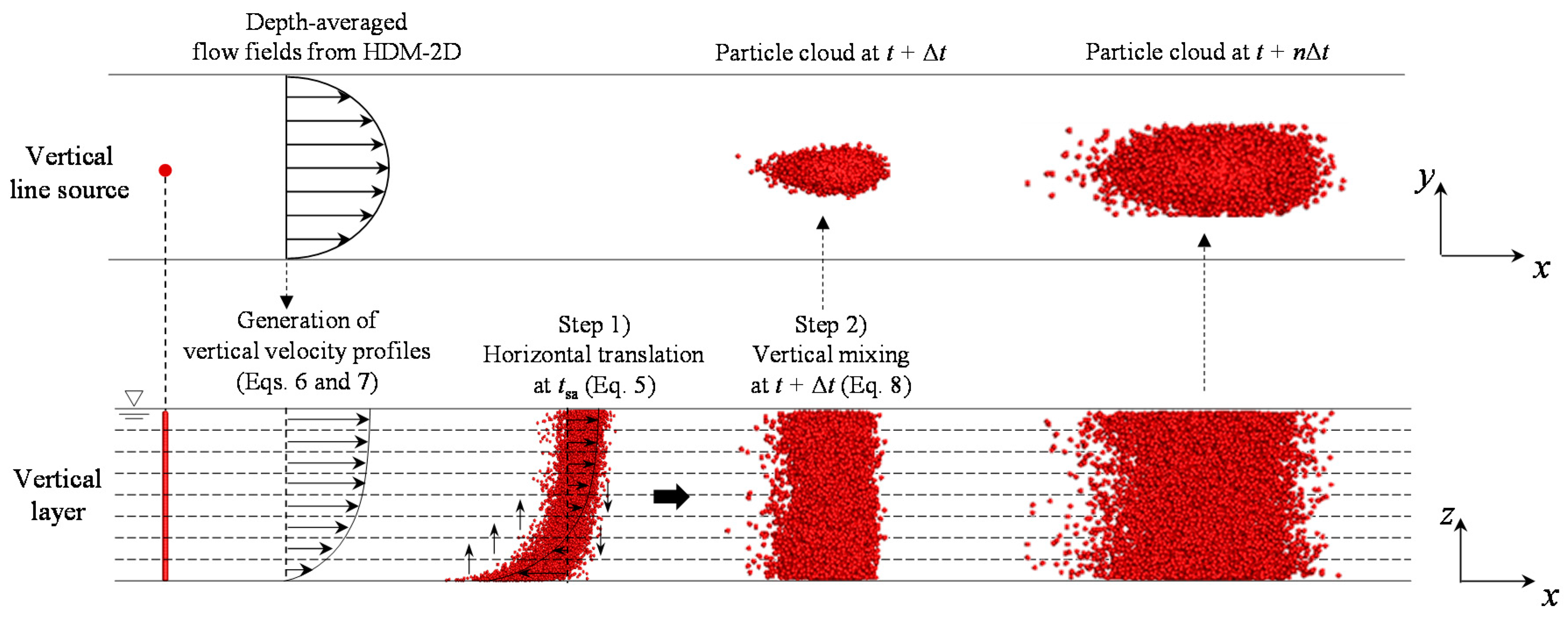
2.2. Model Descriptions
2.3. Generation of Concentration Fields for Estimating Routing Procedures
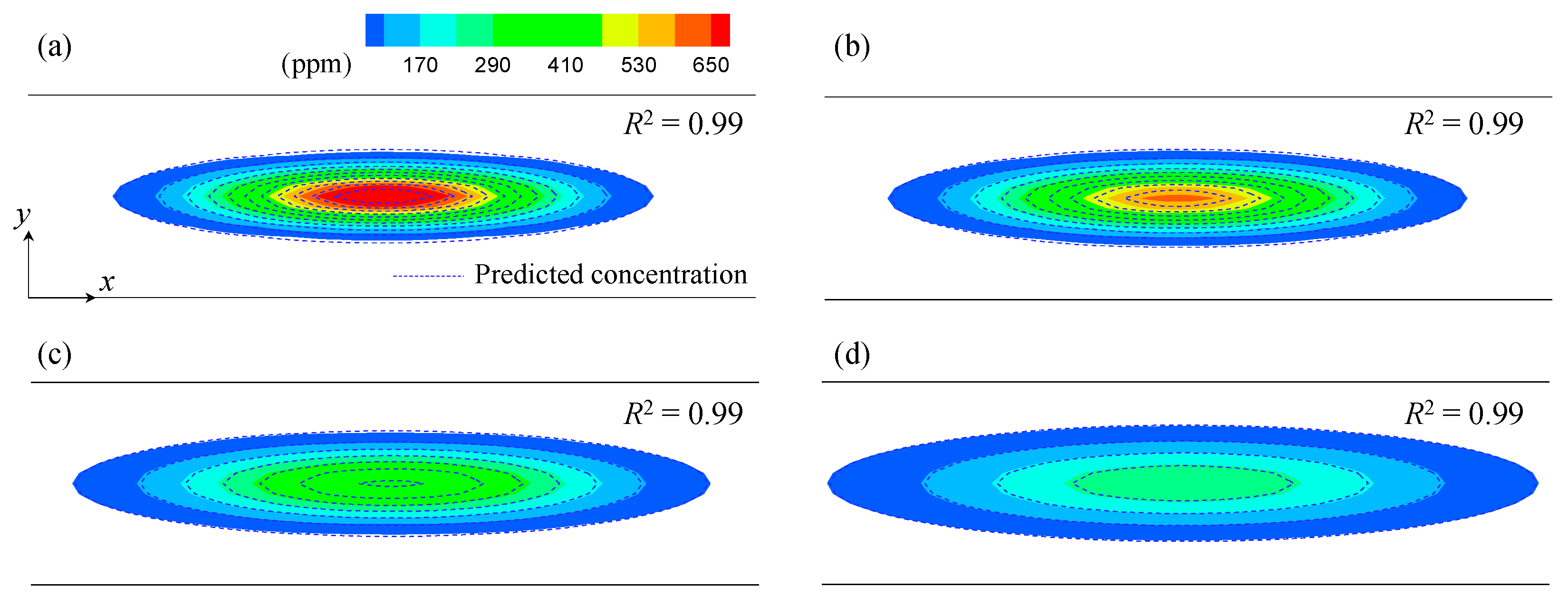
2.3.1. Idealized Concentration Fields to Evaluate the Frozen Cloud Assumption
2.3.2. Generation of Concentration Fields in M2 Channel Using the PDM-2D Simulation Results
3. Results
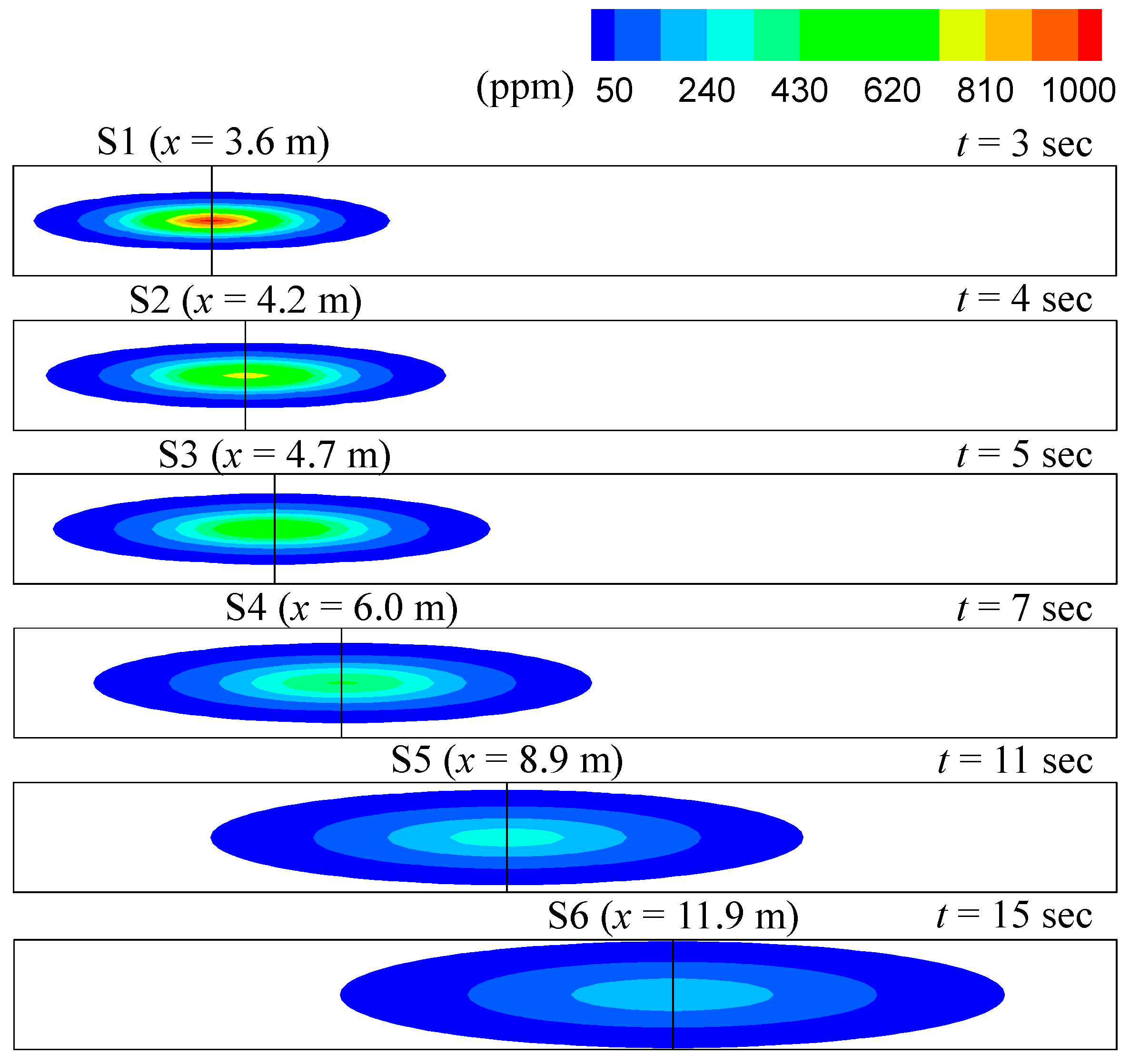
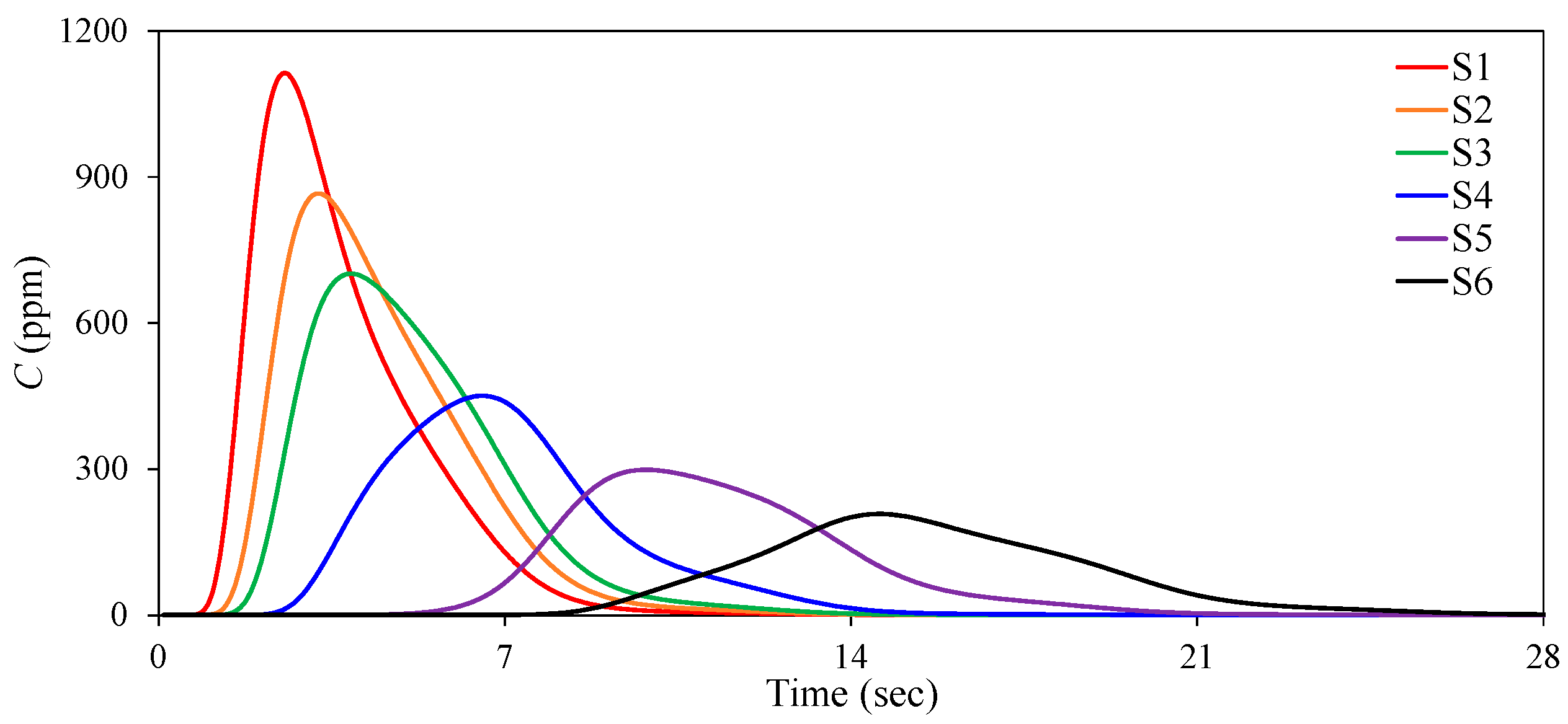
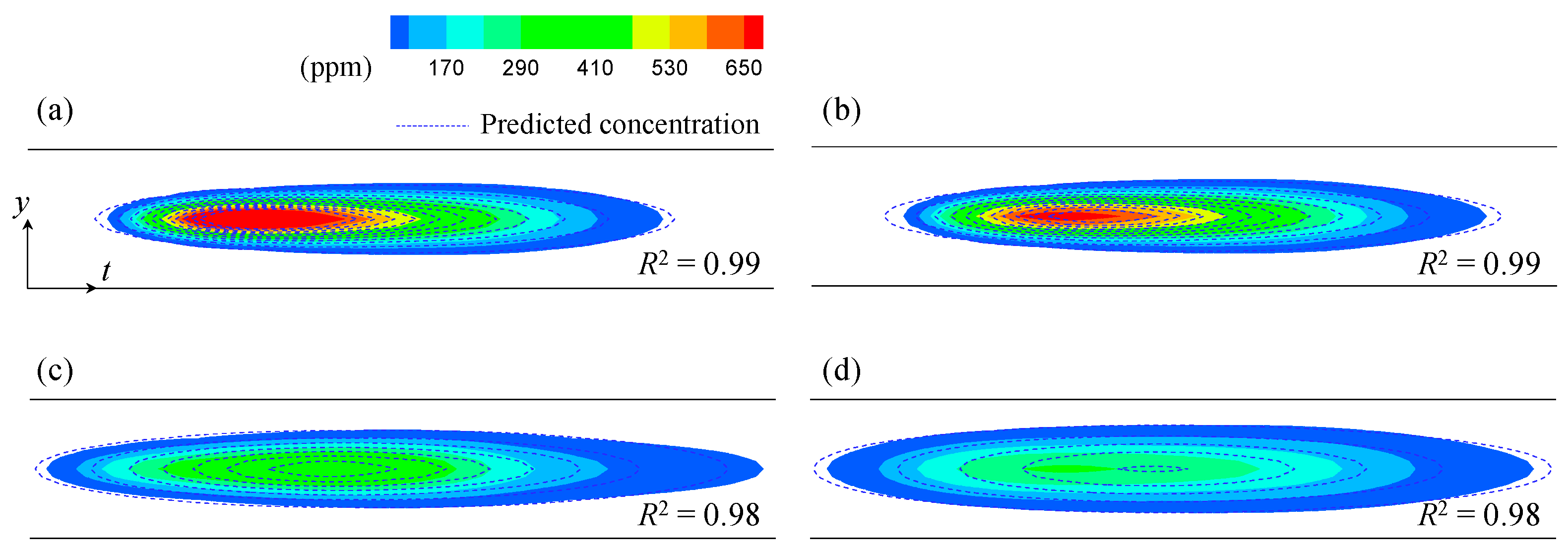
3.1. Evaluations of the Frozen Cloud Assumption
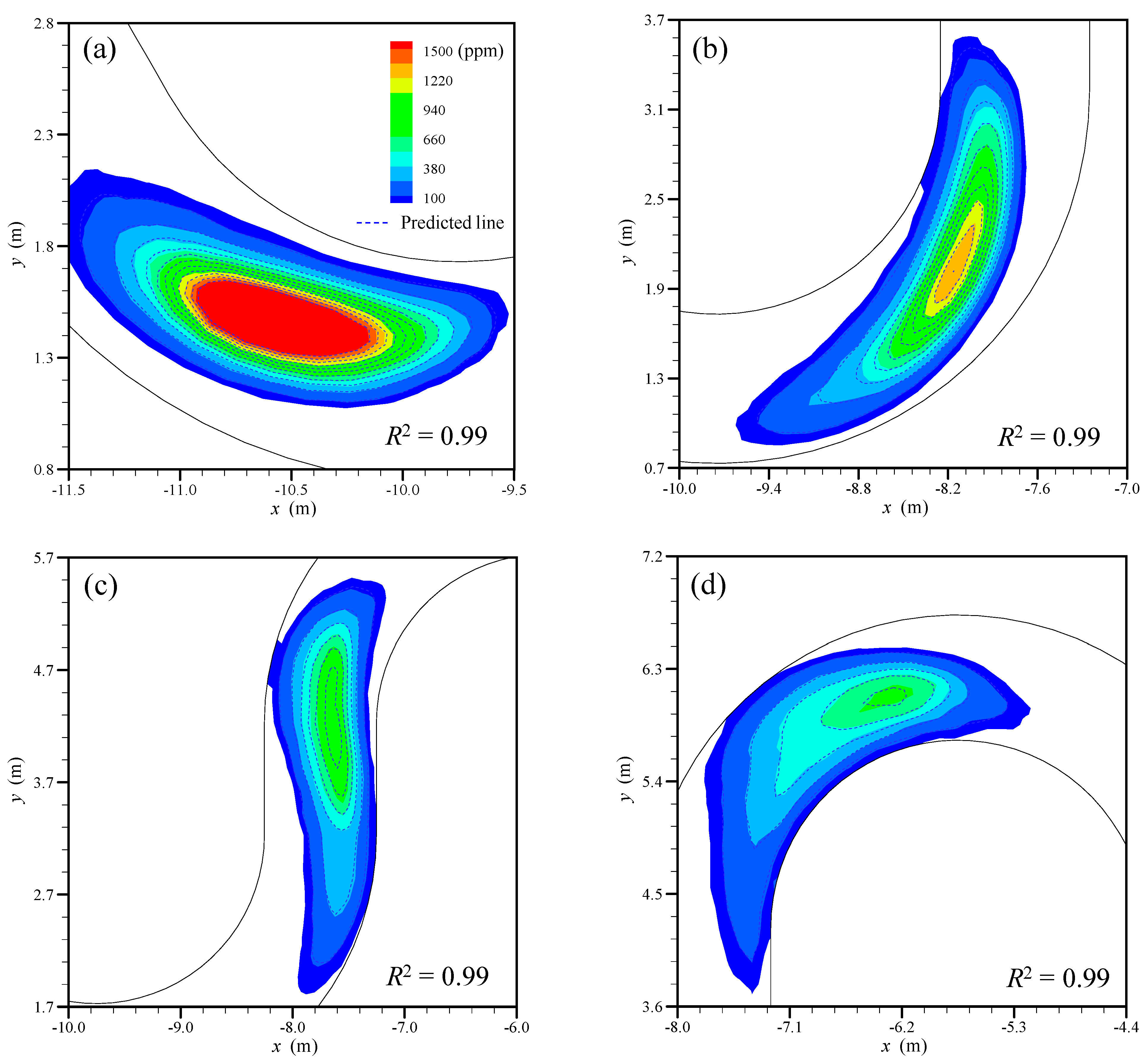
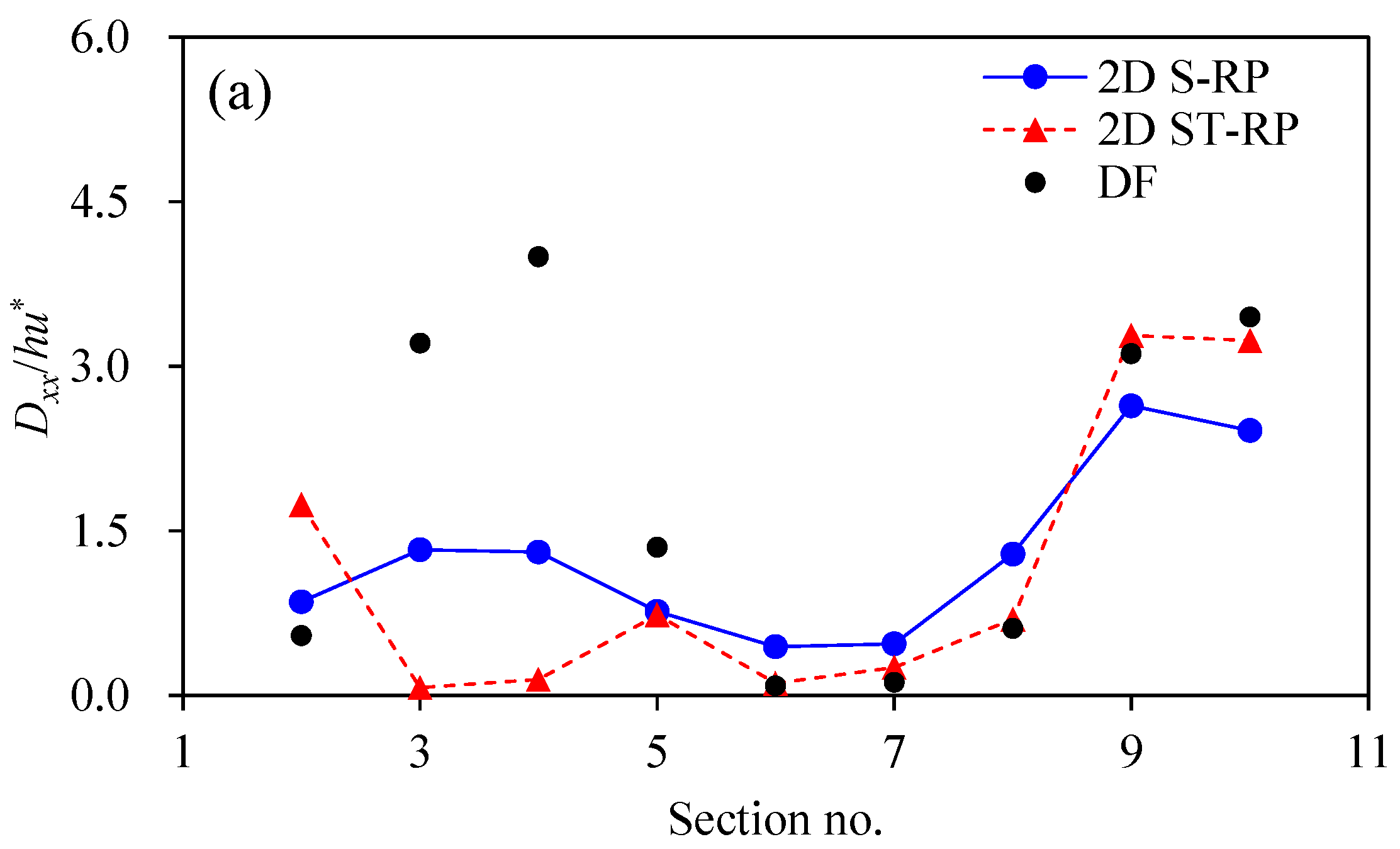
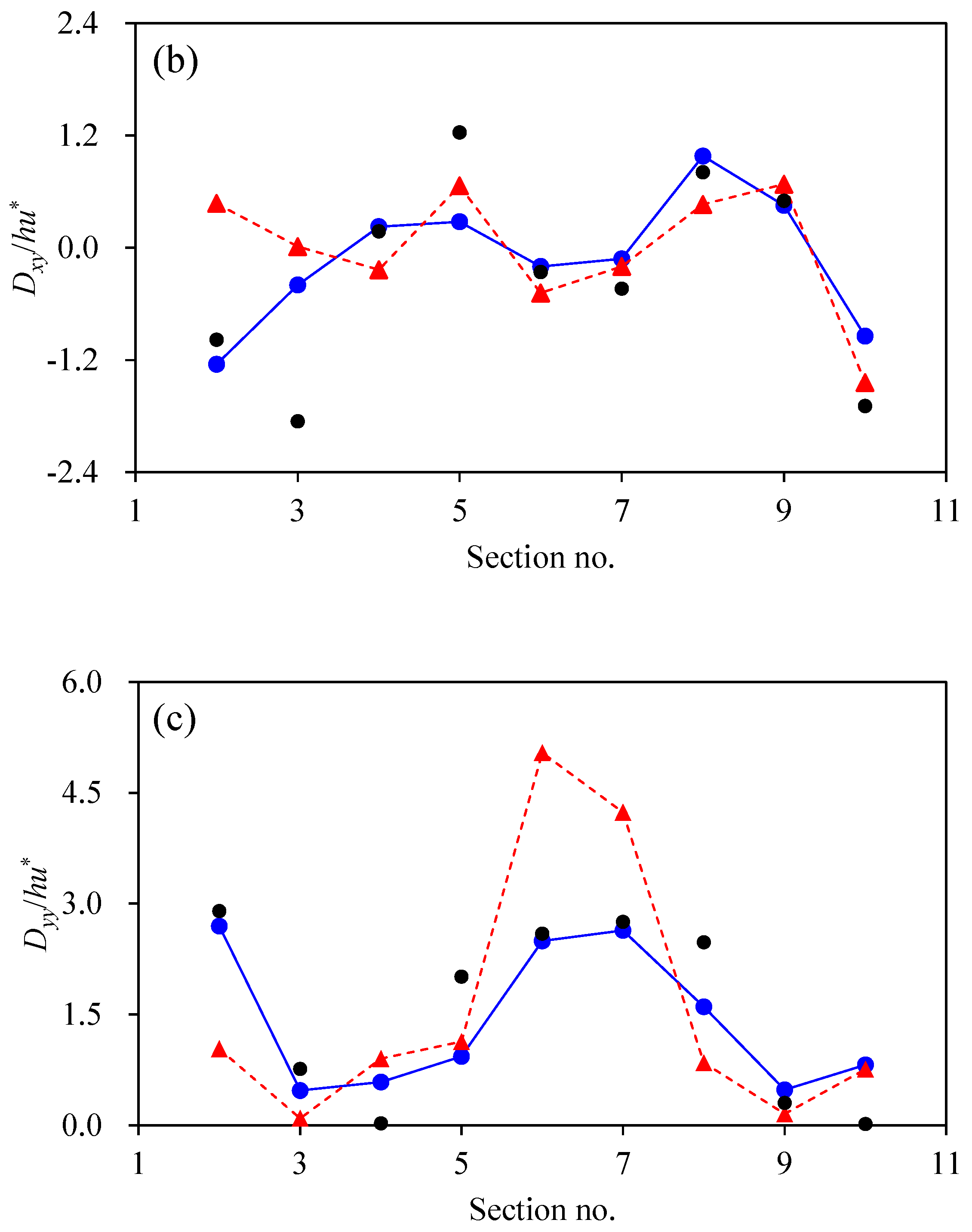
3.2. Estimations of the Dispersion Coefficients in Meandering Channel
4. Discussions
4.1. Validity of the Frozen Cloud Assumption
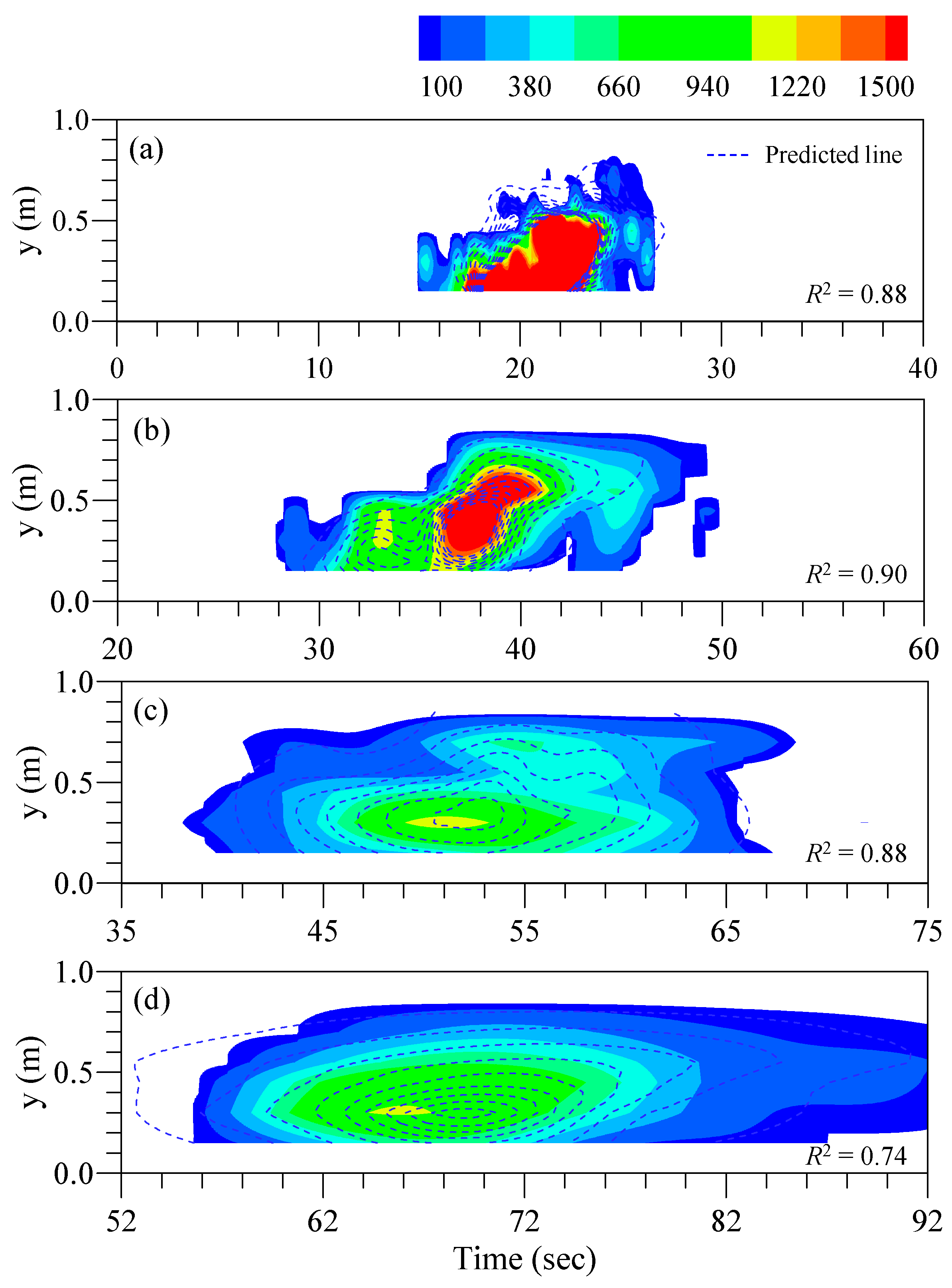
4.2. Applicability to Non-Fickian Mixing
5. Conclusions
- For a solute mixing problem under the unsteady flow condition, the 2D S-RP provides quite accurate estimation results of dispersion coefficients when the mixing shows the Fickian dispersion.
- The temporal concentration curves present the non-Fickian mixing due to the unsteady flow condition even though the solute cloud shows the Fickian dispersion. Thus, the dispersion coefficients by the 2D ST-RP using the temporal data contain errors due to violation of the frozen cloud assumption.
- Both the dispersion coefficients calculated by the 2D ST-RP and the 2D S-RP showed errors against to the results using the velocity-based method for the solute mixing in the initial period where the non-Fickian mixing occurs. These discrepancies showed that the two routing methods were derived based on the Fickian dispersion model.
- The results obtained using the 2D S-RP in the meandering channel more accurately exhibited the spatial variability along the meander cycle of dispersion coefficients compared to the 2D ST-RP.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fischer, H.B.; List, J.E.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters, 2nd ed.; Academic Press: San Diego, CA, USA, 1979; pp. 80–147. [Google Scholar]
- Shen, C.; Niu, J.; Anderson, E.J.; Phanikumar, M.S. Estimating longitudinal dispersion in rivers using Acoustic Doppler Current Profilers. Adv. Water Resour. 2010, 33, 615–623. [Google Scholar] [CrossRef]
- Kim, D. Assessment of longitudinal dispersion coefficients using Acoustic Doppler Current Profilers in large river. J. Hydro-Environ. Res. 2012, 6, 29–39. [Google Scholar] [CrossRef]
- Lee, M.E.; Seo, I.W. Spatially variable dispersion coefficients in meandering channels. J. Hydraul. Eng. 2013, 139, 141–153. [Google Scholar] [CrossRef]
- Park, I.; Seo, I.W.; Shin, J.; Song, C.G. Experimental and numerical investigations of spatially-varying dispersion tensors based on vertical velocity profile and depth-averaged flow field. Adv. Water Resour. 2020, 142, 103606. [Google Scholar] [CrossRef]
- Jung, S.H.; Seo, I.W.; Kim, Y.D.; Park, I. Feasibility of velocity-based method for transverse mixing coefficients in river mixing analysis. J. Hydraul. Eng. 2019, 145, 04019040. [Google Scholar] [CrossRef]
- Shin, J.; Seo, I.W.; Baek, D. Longitudinal and transverse dispersion coefficients of 2D contaminant transport model for mixing analysis in open channels. J. Hydrol. 2020, 583, 124302. [Google Scholar] [CrossRef]
- Boxall, J.B.; Guymer, I. Analysis and prediction of transverse mixing coefficients in natural channels. J. Hydraul. Eng. 2003, 129, 129–139. [Google Scholar] [CrossRef]
- Seo, I.W.; Park, S.W. Effects of velocity structures on tracer mixing in a meandering channel. J. Korean Soc. Civil Eng. 2009, 29, 35–45. (In Korean) [Google Scholar]
- Yotsukura, N.; Sayre, W.W. Transverse mixing in natural channels. Water Resour. Res. 1976, 12, 695–704. [Google Scholar] [CrossRef]
- Holley, F.M.; Nerat, G. Field calibration of stream-tube dispersion model. J. Hydraul. Eng. 1983, 109, 1455–1470. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, D.Z. Transverse mixing in an unregulated North River. J. Hydraul. Eng. 2011, 137, 1426–1440. [Google Scholar] [CrossRef]
- Baek, K.O. Flowchart on choosing optimal method of observing transverse dispersion coefficient for solute transport in open channel flow. Sustainability 2018, 10, 1332. [Google Scholar] [CrossRef]
- Sayre, W.W.; Chang, F.M. A Laboratory Investigation of Open Channel Dispersion Processes for Dissolved, Suspended, and Floating Dispersants; USGS Professional Papers No. 433-E; United States Government Printing Office: Washington, DC, USA, 1968; pp. 59–61. [Google Scholar]
- Holley, E.R.; Siemons, J.; Abraham, G. Some aspects of analyzing transverse diffusion in rivers. J. Hydraul. Res. 1972, 10, 27–57. [Google Scholar] [CrossRef]
- Beltaos, S. Transverse mixing tests in natural streams. J. Hydraul. Div. 1980, 106, 1607–1625. [Google Scholar] [CrossRef]
- Baek, K.O.; Seo, I.W. Routing procedures for observed dispersion coefficients in two-dimensional river mixing. Adv. Water Resour. 2010, 33, 1551–1559. [Google Scholar] [CrossRef]
- Fischer, H.B. Dispersion predictions in natural streams. J. Sanit. Eng. Div. 1968, 94, 927–944. [Google Scholar] [CrossRef]
- Singh, S.K.; Beck, M.B. Dispersion coefficient of streams from tracer experiment data. J. Hydraul. Eng. 2003, 129, 539–546. [Google Scholar] [CrossRef]
- Baek, D.; Seo, I.W.; Kim, J.S.; Nelson, J.M. UAV-based measurements of spatio-temporal concentrqation distributions of fluorescent tracers in open channel flows. Adv. Water Resour. 2019, 127, 76–88. [Google Scholar] [CrossRef]
- Legleiter, C.J.; McDonald, R.R.; Nelson, J.M.; Kinzel, P.J.; Perroy, R.L.; Baek, D.; Seo, I.W. Remote sension of tracer dye concentrations to support dispersion studies in river channels. J. Ecohydraul. 2019, 4, 131–146. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Manley, P.V.; Erwin, S.O.; Bulliner, E.A. An experimental evaluation of the feasibility of inferring concentrations of a visible tracer dye from remotely sensed data in turbid rivers. Sensors 2020, 12, 57. [Google Scholar] [CrossRef]
- Taylor, G.I. The dispersion of matter in turbulent flow through a pipe. Proc. R. Soc. Lond. A: Math. Phys. Eng. Sci. 1954, 223, 446–468. [Google Scholar]
- Piasecki, M.; Katopodes, N.D. Identification of stream dispersion coefficients by adjoint sensitivity method. J. Hydraul. Eng. 1999, 125, 714–724. [Google Scholar] [CrossRef]
- Lee, M.E.; Seo, I.W. Analysis of pollutant transport in the Han River with tidal current using a 2D finite element model. J. Hydro-Environ. Res. 2007, 1, 30–42. [Google Scholar] [CrossRef]
- Lee, M.E.; Seo, I.W. 2D finite element pollutant transport model for accidental mass release in rivers. KSCE J. Civil Eng. 2010, 14, 77–86. [Google Scholar] [CrossRef]
- Alavian, V. Dispersion tensor in rotating flows. J. Hydraul. Eng. 1986, 112, 771–777. [Google Scholar] [CrossRef]
- Seo, I.W.; Choi, H.J.; Kim, Y.D.; Han, E.J. Analysis of two-dimensional mixing in natural streams based on transient tracer tests. J. Hydraul. Eng. 2016, 142, 04016020. [Google Scholar] [CrossRef]
- Fischer, H.B. Methods for Predicting Dispersion Coefficients in Natural Streams, with Applications to Lower Reaches of the Green and Duwamish Rivers Washington (No. 582-A); US Government Printing Office: Washington, DC, USA, 1968; pp. 6–13. [Google Scholar]
- Baek, K.O.; Seo, I.W.; Jung, S.J. Evaluation of transverse dispersion coefficient in meandering channel from transient tracer tests. J. Hydraul. Eng. 2006, 132, 1021–1032. [Google Scholar] [CrossRef]
- Seo, I.W.; Baek, K.O.; Jeon, T.M. Analysis of transverse mixing in natural streams under slug tests. J. Hydraul. Res. 2006, 44, 350–362. [Google Scholar] [CrossRef]
- Park, I.; Seo, I.W. Modeling non-Fickian pollutant mixing in open channel flows using two-dimensional particle dispersion model. Adv. Water Resour. 2018, 111, 105–120. [Google Scholar] [CrossRef]
- Rozovskii, I.L. Flow of Water in Bends of Open Channels; Academy of Science of Ukrainian SSR: Moscow, Russia, 1957. [Google Scholar]
- Jackson, P.S. On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 1981, 111, 15–25. [Google Scholar] [CrossRef]
- Odgaard, A.J. Meander flow model. I: Development. J. Hydraul. Eng. 1986, 112, 1117–1136. [Google Scholar] [CrossRef]
- Seo, I.W.; Song, C.G. Numerical Simulation of Laminar Flow past a Circular Cylinder with Slip Conditions. Inter. J. Numer. Methods Fluids 2012, 68, 1538–1560. [Google Scholar] [CrossRef]
- Song, C.G.; Seo, I.W.; Kim, Y.D. Analysis of secondary current effect in the modeling of shallow flow in open channels. Adv. Water Resour. 2012, 41, 29–48. [Google Scholar] [CrossRef]
- Seo, I.W.; Kim, Y.D.; Song, C.G. Validation of Depth-Averaged Flow Model Using Flat-Bottomed Benchmark Problems. Sci. World J. 2014, 2014, 197539. [Google Scholar] [CrossRef] [PubMed]
- Seo, I.W.; Kim, Y.D.; Song, C.G. Analysis of Flow Characteristics around Islands due to Semi-Diurnal Currents in the Han River, Korea. KSCE J. Civil Eng. 2015, 19, 1905–1915. [Google Scholar] [CrossRef]
- Elder, J.W. The dispersion of marked fluid in turbulent shear flow. J. Fluid Mech. 1959, 5, 544–560. [Google Scholar] [CrossRef]
- Rutherford, J.C. River Mixing; John Wiley and Sons: London, UK, 1994; pp. 62–63. [Google Scholar]
- Chatwin, P.C. On the interpretation of some longitudinal dispersion experiments. J. Fluid Mech. 1971, 48, 689–702. [Google Scholar] [CrossRef]
- Valentine, E.M.; Wood, I.R. Longitudinal dispersion with dead zones. J. Hydraul. Div. 1977, 103, 975–990. [Google Scholar] [CrossRef]
- Boxall, J.B.; Guymer, I. Longitudinal mixing in meandering channels: New experimental data set and verification of a predictive technique. Water Resour. 2007, 11, 341–354. [Google Scholar] [CrossRef]
- Chatwin, P.C. Presentation of longitudinal dispersion data. J. Hydraul. Div. 1980, 106, 71–83. [Google Scholar] [CrossRef]
- Denton, R.A. Analytical asymptotic solutions for longitudinal dispersion with dead zones. J. Hydraul. Res. 1990, 28, 309–329. [Google Scholar] [CrossRef]
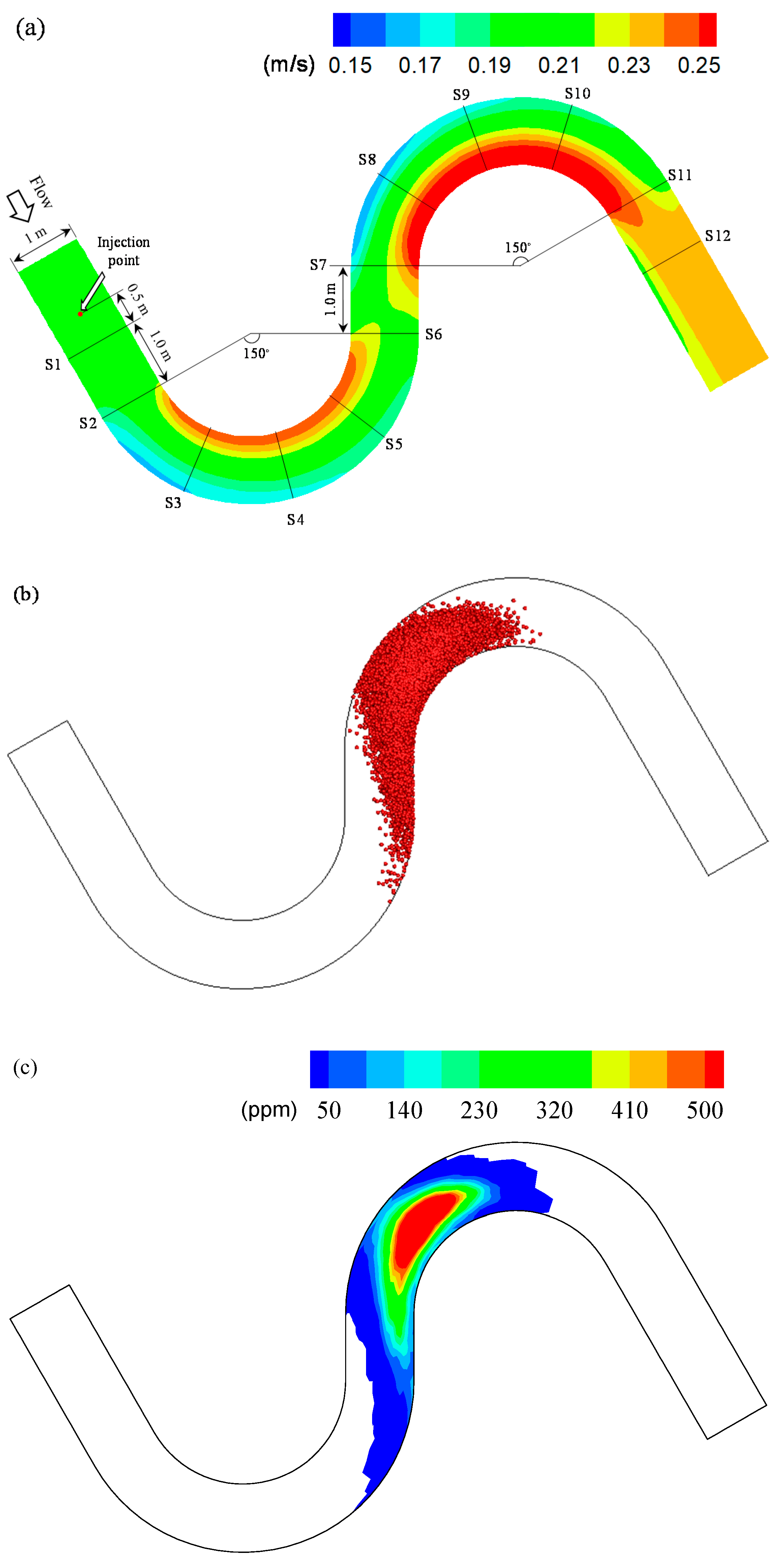
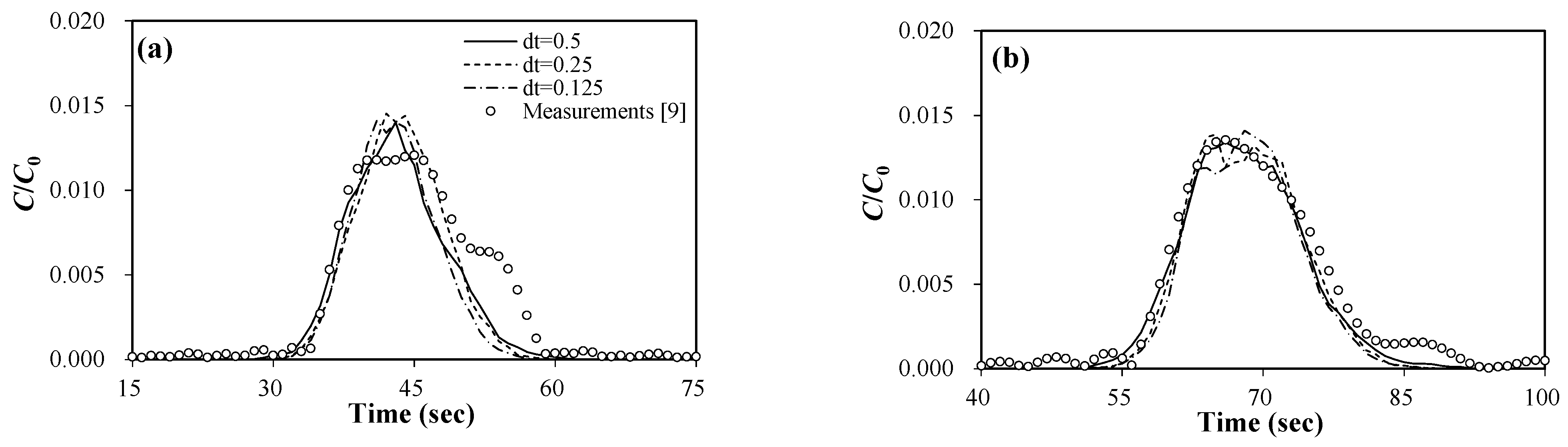
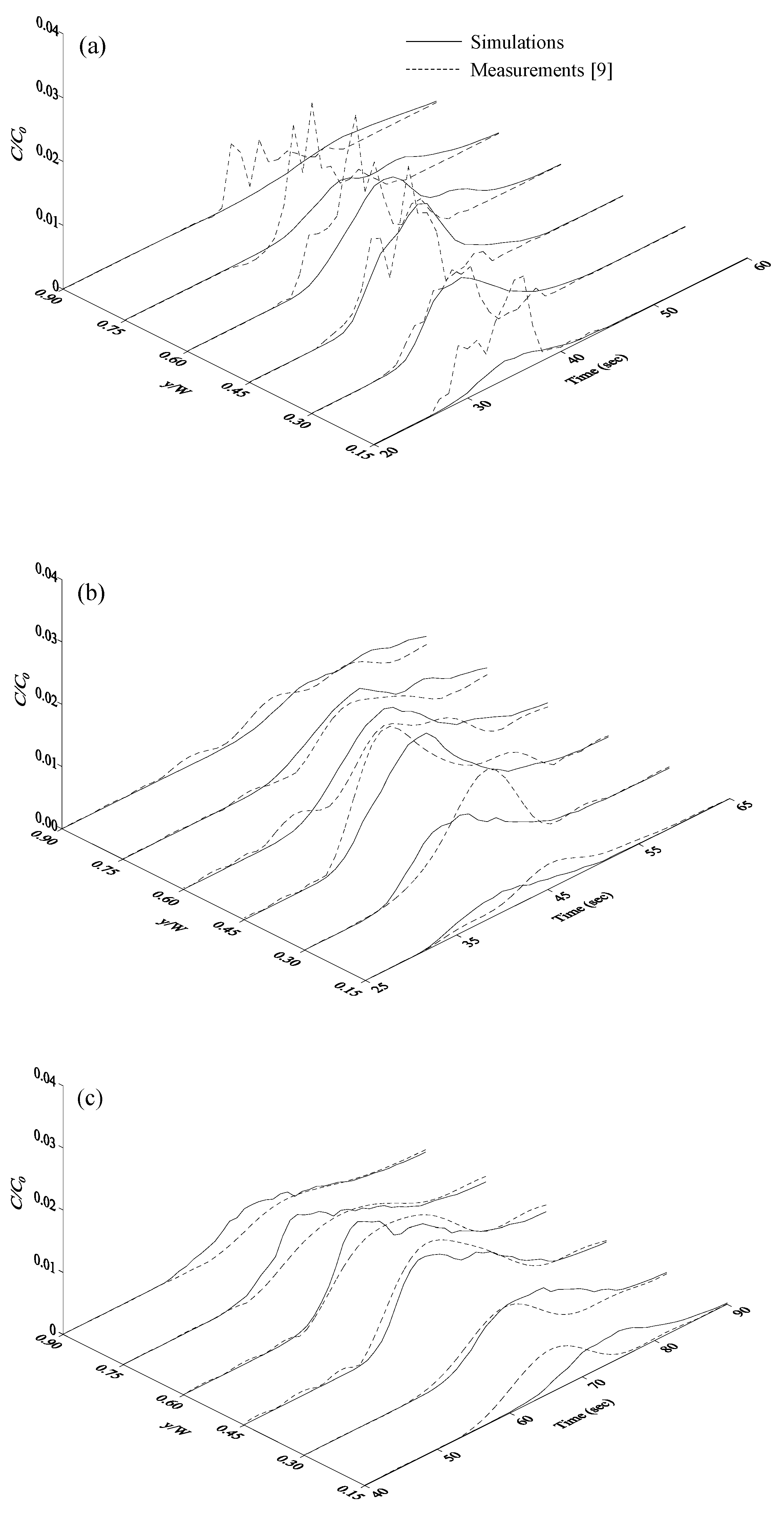
| Q (m3/s) | h (m) | U (m/s) | (m/s) | (ppm) | Δt (s) | L | No. of Particles |
|---|---|---|---|---|---|---|---|
| 0.06 | 0.4 | 0.15 | 0.0078 | 100,000 | 0.5 | 300 | 30,000 |
| Section No. | y/W | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Exp. | Sim. | Exp. | Sim. | Exp. | Sim. | Exp. | Sim. | ||
| S5 | 0.30 | 0.013 | 0.011 | 35.3 | 36.0 | 34.9 | 36.1 | 0.72 | 0.63 |
| 0.45 | 0.022 | 0.021 | 37.1 | 38.0 | 36.6 | 38.3 | 0.43 | 0.59 | |
| 0.70 | 0.030 | 0.006 | 39.8 | 41.0 | 40.5 | 43.8 | 0.92 | 0.36 | |
| S6 | 0.30 | 0.014 | 0.009 | 44.8 | 42.0 | 44.4 | 42.5 | 0.29 | 0.62 |
| 0.45 | 0.020 | 0.015 | 40.5 | 45.0 | 43.9 | 45.3 | 0.60 | 0.68 | |
| 0.70 | 0.008 | 0.011 | 50.1 | 51.0 | 50.7 | 52.1 | 0.16 | 0.54 | |
| S9 | 0.30 | 0.008 | 0.008 | 67.5 | 0.44 | 68.1 | 71.6 | 0.44 | 0.41 |
| 0.45 | 0.015 | 0.013 | 65.3 | 0.56 | 68.2 | 69.3 | 0.56 | 0.62 | |
| 0.70 | 0.008 | 0.013 | 69.3 | 0.62 | 72.0 | 68.5 | 0.62 | 0.58 | |
| Routing Span | ||||||
|---|---|---|---|---|---|---|
| 2D ST-RP | 2D S-RP | Analytic Solution | 2D ST-RP | 2D S-RP | Analytic Solution | |
| S1-S2 | 0.135 | 0.163 | 0.163 | 0.0048 | 0.0041 | 0.0041 |
| S1-S3 | 0.166 | 0.163 | 0.0047 | 0.0041 | ||
| S1-S4 | 0.178 | 0.163 | 0.0051 | 0.0041 | ||
| S1-S5 | 0.136 | 0.163 | 0.0033 | 0.0041 | ||
| S1-S6 | 0.165 | 0.163 | 0.0027 | 0.0041 | ||
| Avg. | 0.156 | 0.163 | 0.0041 | 0.0041 | ||
| S2-S3 | 0.153 | 0.163 | 0.0042 | 0.0041 | ||
| S2-S4 | 0.196 | 0.163 | 0.0057 | 0.0041 | ||
| S2-S5 | 0.141 | 0.163 | 0.0050 | 0.0041 | ||
| S2-S6 | 0.173 | 0.163 | 0.0051 | 0.0041 | ||
| Avg. | 0.166 | 0.163 | 0.0050 | 0.0041 | ||
| S3-S4 | 0.195 | 0.163 | 0.0058 | 0.0041 | ||
| S3-S5 | 0.134 | 0.163 | 0.0050 | 0.0041 | ||
| S3-S6 | 0.170 | 0.163 | 0.0050 | 0.0041 | ||
| Avg. | 0.166 | 0.163 | 0.0053 | 0.0041 | ||
| S4-S5 | 0.144 | 0.163 | 0.0038 | 0.163 | ||
| S4-S6 | 0.092 | 0.163 | 0.0042 | 0.0041 | ||
| Avg. | 0.118 | 0.163 | 0.0040 | 0.0041 | ||
| S5-S6 | 0.208 | 0.163 | 0.0044 | 0.0041 | ||
| Section No. | ||||
|---|---|---|---|---|
| 2D ST-RP | 2D S-RP | 2D ST-RP | 2D S-RP | |
| 2 | 0.89 | 3.33 | 2.19 | 0.22 |
| 3 | 0.08 | 1.49 | 0.11 | 0.31 |
| 4 | 0.09 | 1.37 | 1.09 | 0.52 |
| 5 | 1.81 | 1.14 | 0.27 | 0.56 |
| 6 | 5.95 | 2.52 | 0.09 | 0.43 |
| 7 | 4.73 | 2.64 | 0.27 | 0.47 |
| 8 | 1.38 | 2.44 | 0.34 | 0.46 |
| 9 | 3.80 | 2.73 | 0.02 | 0.39 |
| 10 | 4.33 | 2.85 | 0.11 | 0.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, J.; Rhee, D.; Park, I. Applications of Two-Dimensional Spatial Routing Procedure for Estimating Dispersion Coefficients in Open Channel Flows. Water 2021, 13, 1394. https://doi.org/10.3390/w13101394
Shin J, Rhee D, Park I. Applications of Two-Dimensional Spatial Routing Procedure for Estimating Dispersion Coefficients in Open Channel Flows. Water. 2021; 13(10):1394. https://doi.org/10.3390/w13101394
Chicago/Turabian StyleShin, Jaehyun, Dongsop Rhee, and Inhwan Park. 2021. "Applications of Two-Dimensional Spatial Routing Procedure for Estimating Dispersion Coefficients in Open Channel Flows" Water 13, no. 10: 1394. https://doi.org/10.3390/w13101394
APA StyleShin, J., Rhee, D., & Park, I. (2021). Applications of Two-Dimensional Spatial Routing Procedure for Estimating Dispersion Coefficients in Open Channel Flows. Water, 13(10), 1394. https://doi.org/10.3390/w13101394






