Transmissivity Estimates by Specific Capacity Data of Some Fractured Italian Carbonate Aquifers
Abstract
:1. Introduction
- Q—discharge of pumping well (L3/T);
- sw—steady-state drawdown (L).
2. Materials and Methods
2.1. Hydrogeological Setup and Well Characteristics
2.2. Analytical Methods for Pumping Test Analysis
- s—drawdown (L);
- Q—pumping discharge (L3/T);
- T—transmissivity (L2/T);
- W(u)—Theis well function, (dimensionless);
- t—time from the beginning of pumping (T);
- S—storage coefficient (dimensionless);
- r—radial distance from the pumping well (L).
2.3. Empirical Relationships between Specific Capacity and Transmissivity
3. Results
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Richard, S.K.; Chesnaux, R.; Rouleau, A.; Coupe, R.H. Estimating the reliability of aquifer transmissivity values obtained from specific capacity tests: Examples from the Saguenay-Lac-Saint-Jean aquifers, Canada. Hydrol. Sci. J. 2016, 61, 173–185. [Google Scholar] [CrossRef]
- Mace, R.E. Determination of transmissivity from specific capacity tests in a karst aquifer. Groundwater 1997, 35, 738–742. [Google Scholar] [CrossRef]
- Mace, R.E. Estimating Transmissivity Using Specific-Capacity Data (Vol. 1). Bureau of Economic Geology, University of Texas at Austin, USA, 2001. Available online: https://www.researchgate.net/profile/Robert-Mace-2/publication/275832466_Estimating_transmissivity_using_specific-capacity_data/links/5547e45a0cf2b0cf7ace9684/Estimating-transmissivity-using-specific-capacity-data.pdf (accessed on 25 March 2021).
- Razack, M.; Huntley, D. Assessing transmissivity from specific capacity in a large and heterogeneous alluvial aquifer. Ground Water 1991, 29, 856–861. [Google Scholar] [CrossRef]
- Huntley, D.; Nommensen, R.; Steffey, D. The use of specific capacity to assess transmissivity in fractured-rock aquifers. Ground Water 1992, 30, 396–402. [Google Scholar] [CrossRef]
- El-Naqa, A. Estimation of transmissivity from specific capacity data in fractured carbonate rock aquifer, central Jordan. Environ. Geol. 1994, 23, 73–80. [Google Scholar] [CrossRef]
- Fabbri, P. Transmissivity in the geothermal Euganean Basin; a geostatistical analysis. Ground Water 1997, 35, 881–887. [Google Scholar] [CrossRef]
- Jalludin, M.; Razack, M. Assessment of hydraulic properties of sedimentary and volcanic aquifer systems under arid conditions in the Republic of Djibouti (Horn of Africa). Hydrogeol. J. 2004, 12, 159–170. [Google Scholar] [CrossRef]
- Hamm, S.Y.; Cheong, J.Y.; Jang, S.; Jung, C.Y.; Kim, B.S. Relationship between transmissivity and specific capacity in the volcanic aquifers of Jeju Island, Korea. J. Hydrol. 2005, 310, 111–121. [Google Scholar] [CrossRef]
- Al Farrah, N.; Van Camp, M.; Walraevens, K. Deducing transmissivity from specific capacity in the heterogeneous upper aquifer system of Jifarah Plain, NWLibya. J. Afr. Earth Sci. 2013, 85, 12–21. [Google Scholar] [CrossRef]
- Srivastav, S.K.; Lubczynski, M.W.; Biyani, A.K. Upscaling of transmissivity, derived from specific capacity: A hydrogeomorphological approach applied to the Doon Valley aquifer system in India. Hydrogeol. J. 2007, 15, 1251–1264. [Google Scholar] [CrossRef]
- Hsu, S.M.; Chou, P.Y. Applicability of method to estimate transmissivity based on yield-drawdown analysis in mountainous fractured-rock aquifers: A case study in Taiwan. Eng. Geol. 2019, 262, 105315. [Google Scholar] [CrossRef]
- Piscopo, V.; Formica, F.; Lana, L.; Lotti, F.; Pianese, L.; Trifuoggi, M. Relationship Between Aquifer Pumping Response and Quality of Water Extracted from Wells in an Active Hydrothermal System: The Case of the Island of Ischia (Southern Italy). Water 2020, 12, 2576. [Google Scholar] [CrossRef]
- Logan, J. Estimating transmissibility from routine production tests of water wells. Hydrogeol. J. 1964, 2, 35–37. [Google Scholar] [CrossRef]
- Ad Yalkar, P.G.; Mani, V.V.S. An attempt at estimating the transmissibilities of Trappean aquifers from specific capacity values. Hydrogeol. J. 1972, 17, 237–241. [Google Scholar] [CrossRef]
- Verbovšek, T. Estimation of transmissivity and hydraulic conductivity from specific capacity and specific capacity index in dolomite aquifers. J. Hydrol. Eng. 2008, 13, 817–823. [Google Scholar] [CrossRef]
- Motti, A.; Natali, N. La Storia Degli Open Data Geotematici del Servizio Geologico della Regione Umbria e la Definizione Della Rappresentatività Geologica. Technical Report Regione Umbria (Italy), Servizio Geologico. Available online: https://www.researchgate.net/publication/329339254_La_storia_degli_open_data_geotematici_del_Servizio_Geologico_della_Regione_Umbria_e_la_definizione_della_rappresentativita_geologica (accessed on 20 March 2021). (In Italian).
- Colacicchi, R.; Pialli, G. Dati a conferma di una lacuna dovuta ad emersione nel Giurese di Monte Cucco (Appennino Umbro). Boll. Soc. Geol. Ital. 1967, 86, 179–192. (In Italian) [Google Scholar]
- Barchi, M.; Lavecchia, G. Structural style of the Umbrie-Marches fold belt: Buckle folding or thrust ramping? In Proceedings of the 73° Congresso Nazionale della Società Geologica d’Italia, Roma, Italy, 29 September–4 October 1986. (In Italian). [Google Scholar]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979; p. 604. [Google Scholar]
- Boscherini, A.; Checcucci, R.; Natale, G.; Natali, N. Carta Idrogeologica della Regione Umbria (scala 1:100.000). Giornale di Geologia Applicata 2005, 2, 399–404. (In Italian) [Google Scholar] [CrossRef]
- Civita, M. Idrogeologia Applicata e Ambientale; Casa Editrice Ambrosiana: Milano, Italy, 2005; p. 800. (In Italian) [Google Scholar]
- Valigi, D.; Mastrorillo, L.; Barchi, M.R.; Cardellini, C.; Checcucci, R.; Di Matteo, L.; Frondini, F.; Mirabella, F.; Viaroli, S.; Vispi, I. Springs discharge variations induced by strong earthquakes: The Mw 6.5 Norcia event (Italy, 30 October 2016). Rend. Online Soc. Geol. Ital. 2019, 47, 141–146. [Google Scholar] [CrossRef]
- Di Matteo, L.; Dragoni, W.; Azzaro, S.; Pauselli, C.; Porreca, M.; Bellina, G.; Cardaci, W. Effects of earthquakes on the discharge of groundwater systems: The case of the 2016 seismic sequence in the Central Apennines, Italy. J. Hydrol. 2020, 583, 124509. [Google Scholar] [CrossRef]
- Viaroli, S.; Mirabella, F.; Mastrorillo, L.; Angelini, S.; Valigi, D. Fractured carbonate aquifers of Sibillini Mts. (Central Italy). J. Maps 2021, 17, 140–149. [Google Scholar] [CrossRef]
- Cambi, C.; Valigi, D.; Di Matteo, L. Hydrogeological study of data-scarce limestone massifs: The case of Gualdo Tadino and Monte Cucco structures (Central Apennines, Italy). Boll. di Geofis. Teor. ed Appl. 2010, 51, 345–360. [Google Scholar]
- Di Matteo, L.; Valigi, D.; Cambi, C. Climatic characterization and response of water resources to climate change in limestone areas: Considerations on the importance of geological setting. J. Hydrol. Eng. 2013, 18, 773–779. [Google Scholar] [CrossRef] [Green Version]
- Cambi, C.; Dragoni, W. Groundwater, Recharge Variability and Climatic Changes: Considerations Arising from the Modelling of a Spring in the Umbria-Marche Apennines. Hydrogéologie 2000, 4, 11–25. Available online: https://www.researchgate.net/profile/Walter-Dragoni/publication/233511654_Groundwater_yield_climatic_changes_and_recharge_variability_Considerations_out_of_the_modelling_of_a_spring_in_the_Umbria-Marche_Apennines/links/09e4150aa4773a6434000000/Groundwater-yield-climatic-changes-and-recharge-variability-Considerations-out-of-the-modelling-of-a-spring-in-the-Umbria-Marche-Apennines.pdf (accessed on 20 March 2021).
- Di Matteo, L.; Dragoni, W.; Valigi, D. Update on knowledge of water resources of Amelia Mountains (Central Italy). IJEGE 2009, 1, 83–96. [Google Scholar] [CrossRef]
- Mastrorillo, L.; Baldoni, T.; Banzato, F.; Boscherini, A.; Cascone, D.; Checcucci, R.; Petitta, M.; Boni, C. Quantitative hydrogeological analysis of the carbonate domain of the Umbria Region (Central Italy). IJEGE 2009, 1, 137–155. [Google Scholar] [CrossRef]
- Boni, C.; Baldoni, T.; Banzato, F.; Cascone, D.; Petitta, M. Hydrogeological study for identification, characterisation and management of groundwater resources in the Sibillini mountains national park (Central Italy). IJEGE 2010, 2, 21–39. [Google Scholar] [CrossRef]
- Basilici, G. Sedimentary facies in an extensional and deep-lacustrine depositional system: The Pliocene Tiberino Basin, Central Italy. Sediment. Geol. 1997, 109, 73–94. [Google Scholar] [CrossRef]
- Regione Umbria. Piano Ottimale Dell’utilizzazione delle Risorse Idriche Della REGIONE Umbria. Studi sulle Strutture Carbonatiche; Unpublished Technical Report of Assessorato Difesa del Suolo, Ambiente e Infrastrutture; Regione Umbria: Perugia, Italy, 1989. (In Italian) [Google Scholar]
- Dupuit, J. Mouvement de l’eau a travers le terrains permeables. C. R. Hebd. Seances Acad. 1857, 45, 92–96. [Google Scholar]
- Thiem, G. Hydrologische Methoden; Gebhardt: Leipzig, Germany, 1906. [Google Scholar]
- Theis, C.V. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using groundwater storage. Eos 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Cooper, H.H., Jr.; Jacob, C.E. A generalized graphical method for evaluating formation constants and summarizing well-field history. Am. Geophys. Union Trans. 1946, 27, 526–534. [Google Scholar] [CrossRef]
- Meier, P.M.; Carrera, J.; Sánchez-Vila, X. An evaluation of Jacob’s method for the interpretation of pumping tests in heterogeneous formations. Water Resour. Res. 1998, 34, 1011–1025. [Google Scholar] [CrossRef]
- Kruseman, G.P.; De Ridder, N.A. Analysis and Evaluation of Pumping Test Data; Publication 47; The International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1970; 370p. Available online: https://hwbdocuments.env.nm.gov/Los%20Alamos%20National%20Labs/General/31955.pdf (accessed on 28 March 2021).
- Fetter, C.W. Applied Hydrogeology; Waveland Press: Long Groove, IL, USA, 2000; 599p. [Google Scholar]
- Long, J.C.; Remer, J.S.; Wilson, C.R.; Witherspoon, P.A. Porous media equivalents for networks of discontinuous fractures. Water Resour. Res. 1982, 18, 645–658. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.P.; Woessner, W.W.; Hunt, R.J. Applied Groundwater Modeling: Simulation of Flow and Advective Transport; Academic Press Inc.: San Diego, CA, USA, 2015. [Google Scholar]
- Warren, J.E.; Root, P.J. The behavior of naturally fractured reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef] [Green Version]
- Moench, A.F. Double-porosity models for a fissured groundwater reservoir with fracture skin. Water Resour. Res. 1984, 20, 831–846. [Google Scholar] [CrossRef]
- Escobar, F.H.; Saavedra, N.; Escorcia, G.; Polania, J. Pressure and pressure derivative analysis without type-curve matching for triple porosity reservoirs. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Perth, Australia, 18–20 October 2004. [Google Scholar] [CrossRef]
- Lancia, M.; Saroli, M.; Petitta, M. A double scale methodology to investigate flow in karst fractured media via numerical analysis: The Cassino plain case study (central Apennine, Italy). Geofluids 2018, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Bourdet, D.; Whittle, T.; Douglas, A.; Picard, Y. A New Set of Types Curves Simplifies Well Test Analysis. World Oil 1983, 196, 95–106. Available online: https://blasingame.engr.tamu.edu/z_zCourse_Archive/P648_19A/P648_19A_Reading_Portfolio/World_Oil_(Bourdet)_Pressure_Derivative_Type_Curves_(OCR)_(pdf).pdf (accessed on 1 April 2021).
- Renard, P.; Glenz, D.; Mejias, M. Understanding diagnostic plots for well-test interpretation. Hydrogeol. J. 2009, 17, 589–600. [Google Scholar] [CrossRef] [Green Version]
- Ferroud, A.; Rafini, S.; Chesnaux, R. Using flow dimension sequences to interpret non-uniform aquifers with constant-rate pumping-tests: A review. J. Hydrol. 2019, 2, 100003. [Google Scholar] [CrossRef]
- Issaka, M.B.; Ambastha, A.K. A generalized pressure derivative analysis for composite reservoirs. J. Can. Pet. Technol. 1999, 38. [Google Scholar] [CrossRef]
- Jacob, C.E. Drawdown test to determine effective radius of artesian well. Trans. Am. Soc. Civ. Eng. 1947, 112, 1047–1064. [Google Scholar] [CrossRef]
- Eagon, H.B., Jr.; Johe, D.E. Practical solutions for pumping tests in carbonate-rock aquifers. Ground Water 1972, 10, 6–13. [Google Scholar] [CrossRef]
- Wolansky, R.M.; Corral, M.A. Aquifer Tests in West-Central Florida, 1952–1976; Water-Resources Investigations Report 84–4044; US Geological Survey: Orlando, FL, USA, 1984; 133p. Available online: https://pubs.usgs.gov/wri/1984/4044/report.pdf (accessed on 1 April 2021).
- Checcucci, R.; Dragoni, W.; Marchetti, G. Le risorse idriche strategiche in Umbria. Conoscenze e prospettive di utilizzo. Quaderni di Geologia Applicata 1999, 2, 4133–4142. (In Italian) [Google Scholar]
- Rorabaugh, M.I. Graphical and Theoretical Analysis of Step-Drawdown Test of Artesian Well. Proceedings of American Society of Civil Engineers, Minnesota International Hydraulics Convention, Minneapolis, MN, USA, 1–4 September 1953; Volume 79, pp. 1–23. [Google Scholar]
- Halford, K.J.; Weight, W.D.; Schreiber, R.P. Interpretation of transmissivity estimates from single-well pumping aquifer tests. Ground Water 2006, 44, 467–471. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Xiang, Y.; Hu, J.; Li, T.; Cai, C.; Cai, J. Unsteady flow to a partially penetrating pumping well with wellbore storage in a dual-permeability confined aquifer. J. Hydrol. 2020, 591, 125345. [Google Scholar] [CrossRef]
- Boni, C.; Bono, P.; Capelli, G. Schema Idrogeologico dell’Italia Centrale. Mem. Soc. Geol. It. 1986, 35, 991–1012. Available online: https://www.idrogeologiaquantitativa.it/wordpress/wp-content/uploads/2009/11/Pubb_1986_Schema_Italia_Centrale.pdf (accessed on 1 April 2021). (In Italian).
- Cencetti, C.; Dragoni, W.; Nejad Massoum, M. Contributo alle conoscenze delle caratteristiche idrogeologiche del Fiume Nera (Appennino centro-settentrionale). Geol. Appl. Hidrogeol. 1989, 24, 191–210. [Google Scholar]
- Boni, C.; Preziosi, E. Una possibile simulazione numerica dell’acquifero basale di M. Coscerno—M.Aspra (Bacino del F. Nera). In Proceedings of the 3° Convegno Nazionale Giovani Ricercatori in Geologia Applicata, Potenza, Italy, 28–30 October 1993; Available online: https://www.idrogeologiaquantitativa.it/wordpress/wp-content/uploads/2009/11/Pubb_1993_M_Coscerno.pdf (accessed on 1 April 2021). (In Italian).
- Preziosi, E.; Romano, E. From a hydrostructural analysis to the mathematical modelling of regional aquifers (Central Italy). IJEGE 2009, 1, 183–198. [Google Scholar] [CrossRef]
- Olcott, P.G. Ground Water Atlas of the United States: Connecticut. Maine, Massachusetts, New Hampshire, New York, Rhode Island, Vermont: US Geological Survey Hydrologic Investigations Atlas HA–730M, 1995. Available online: https://pubs.usgs.gov/ha/ha730/ch_m/M-carbonate.html (accessed on 7 April 2021).
- Sardinha, J.; Carneiro, J.F.; Zarhloule, Y.; Barkaoui, A.; Correia, A.; Boughriba, M.; Rimi, A.; El Houadi, B. Structural and hydrogeological features of a Lias carbonate aquifer in the Triffa Plain, NE Morocco. J. Afr. Earth Sci. 2012, 73, 24–32. [Google Scholar] [CrossRef]
- Al-Dabbas, M.; Al-Kubaisi, Q.; Hussain, T.A.; Al-Qaraghuli, S. Hydrogeological characteristics of Dammam confined aquifer, West Razzaza Lake, Iraq. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 737, p. 012162. [Google Scholar]
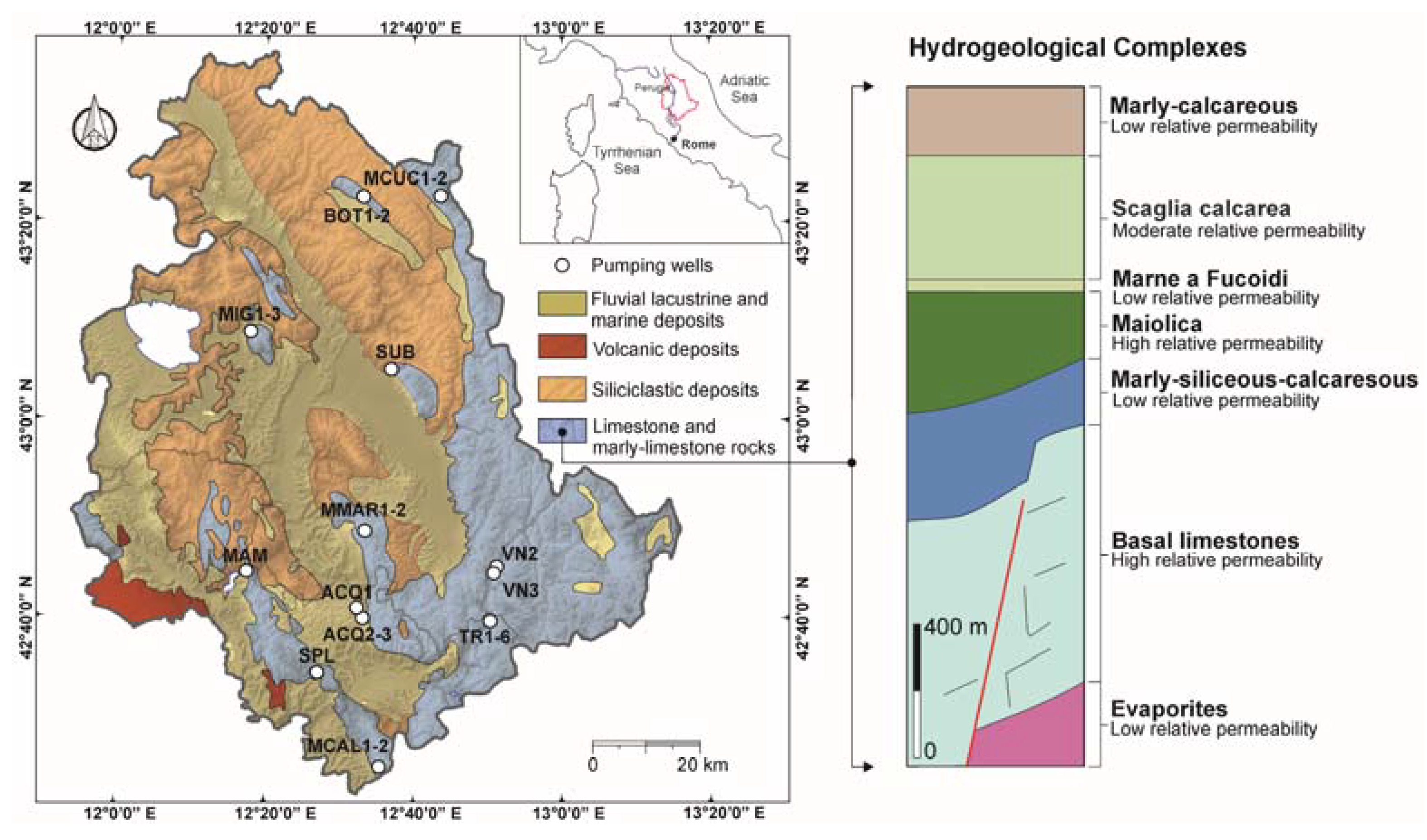
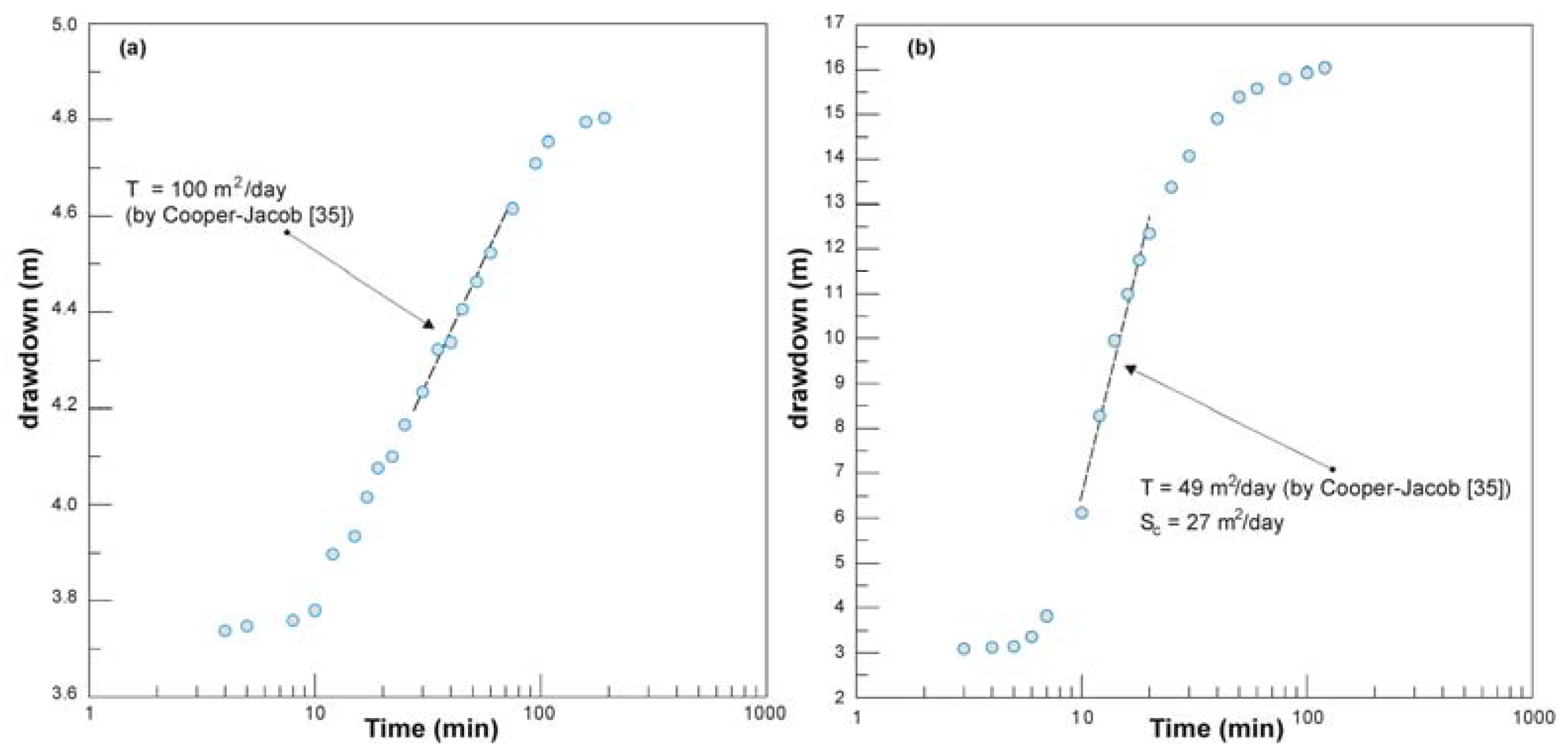
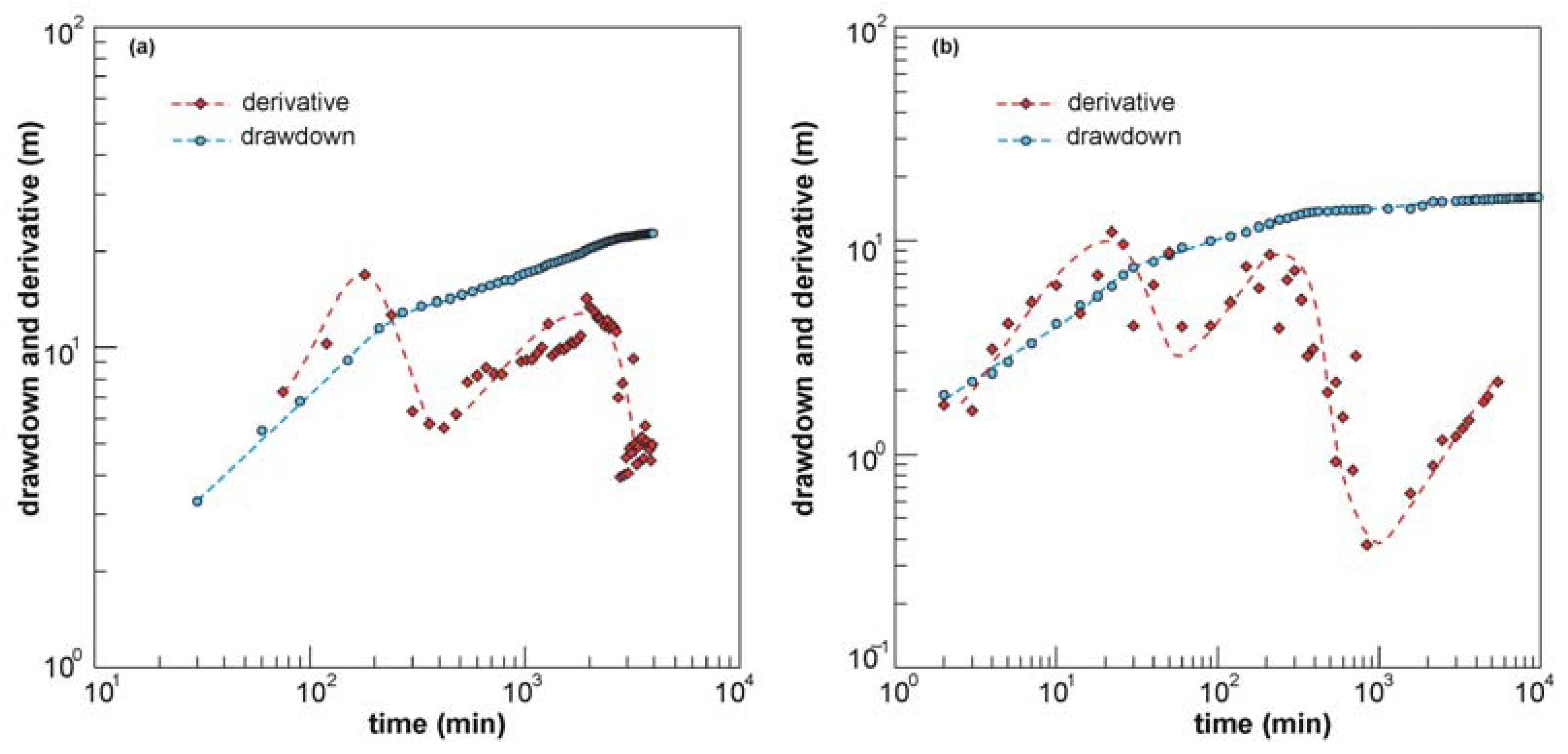
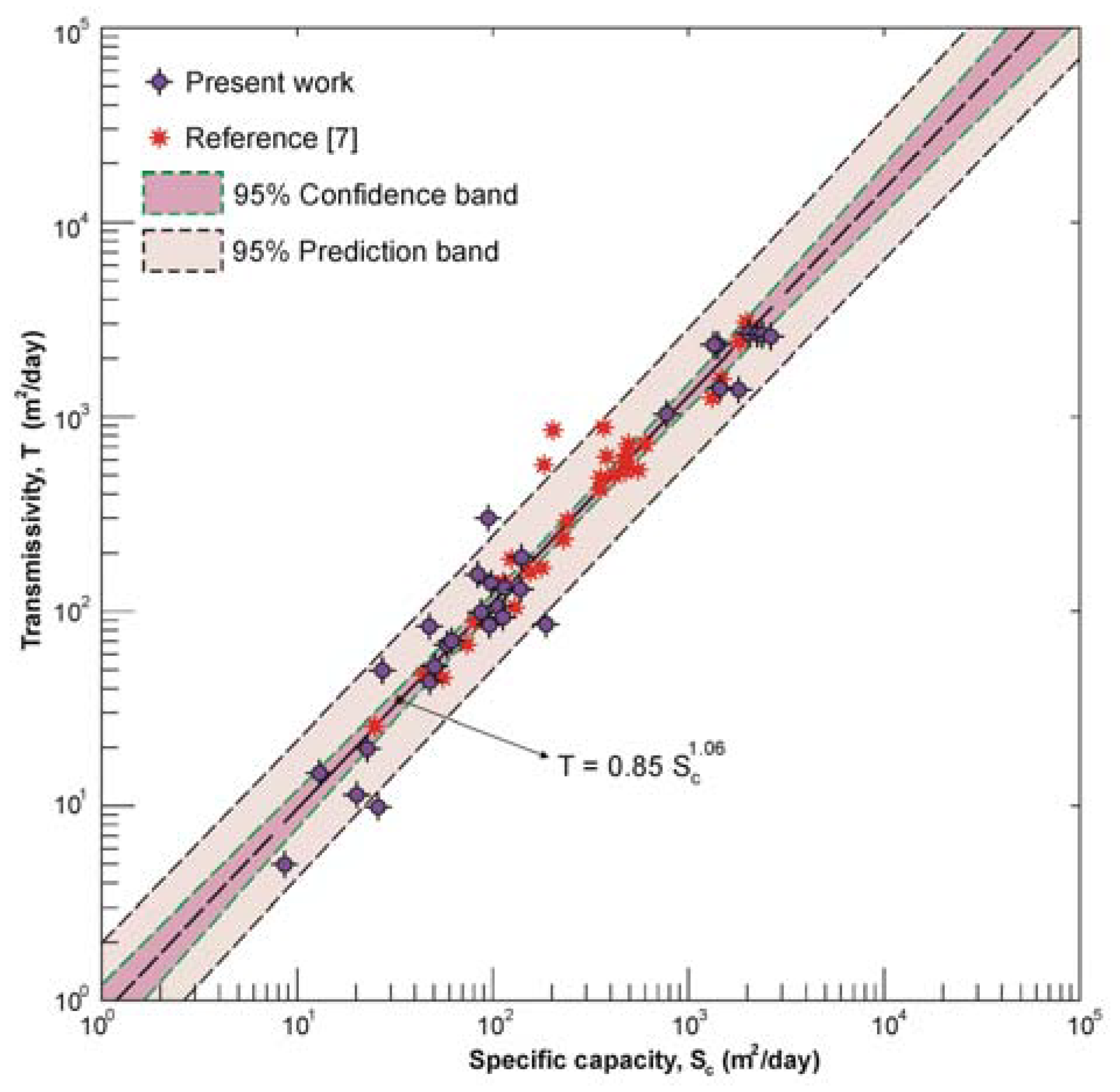
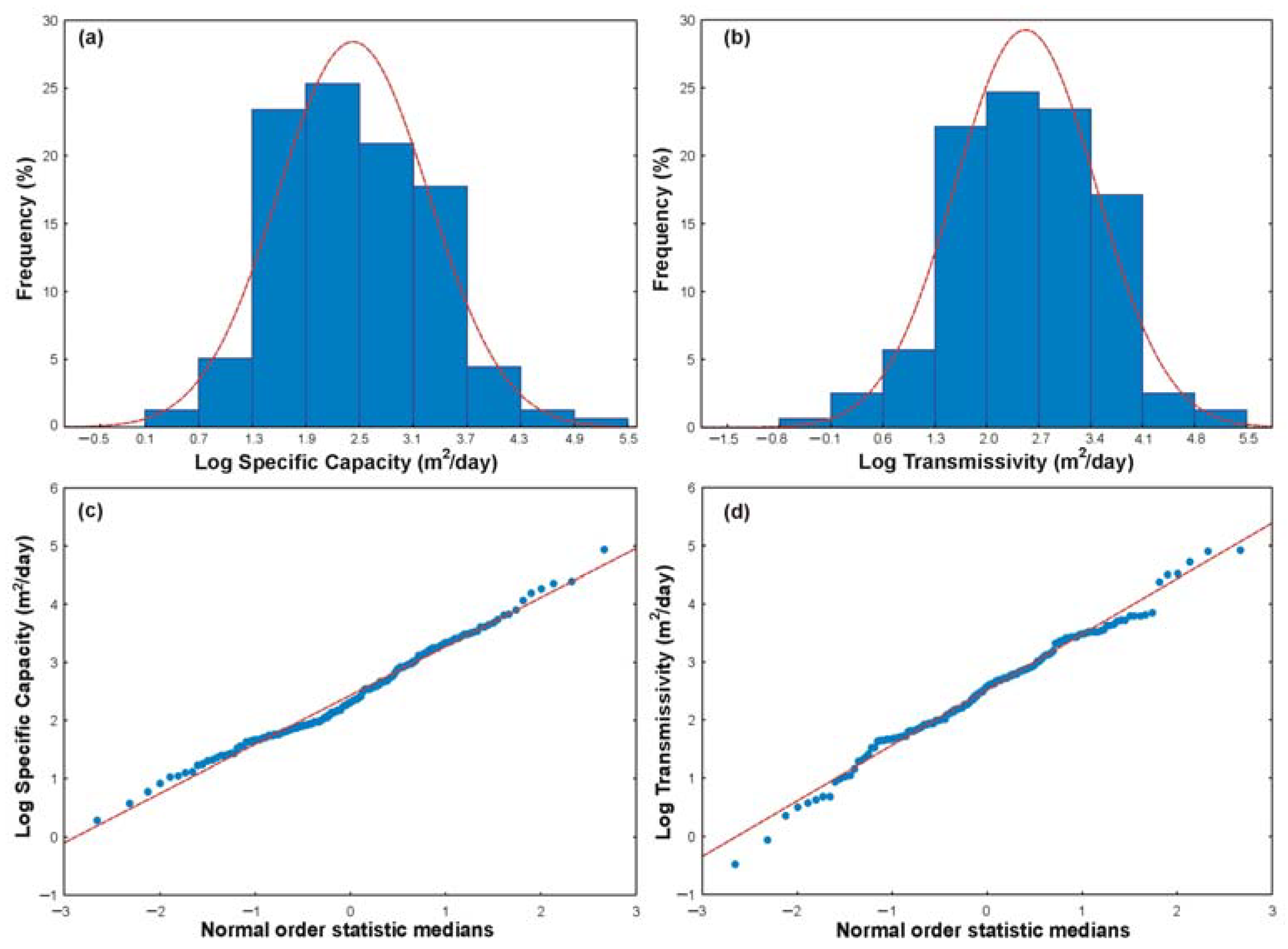
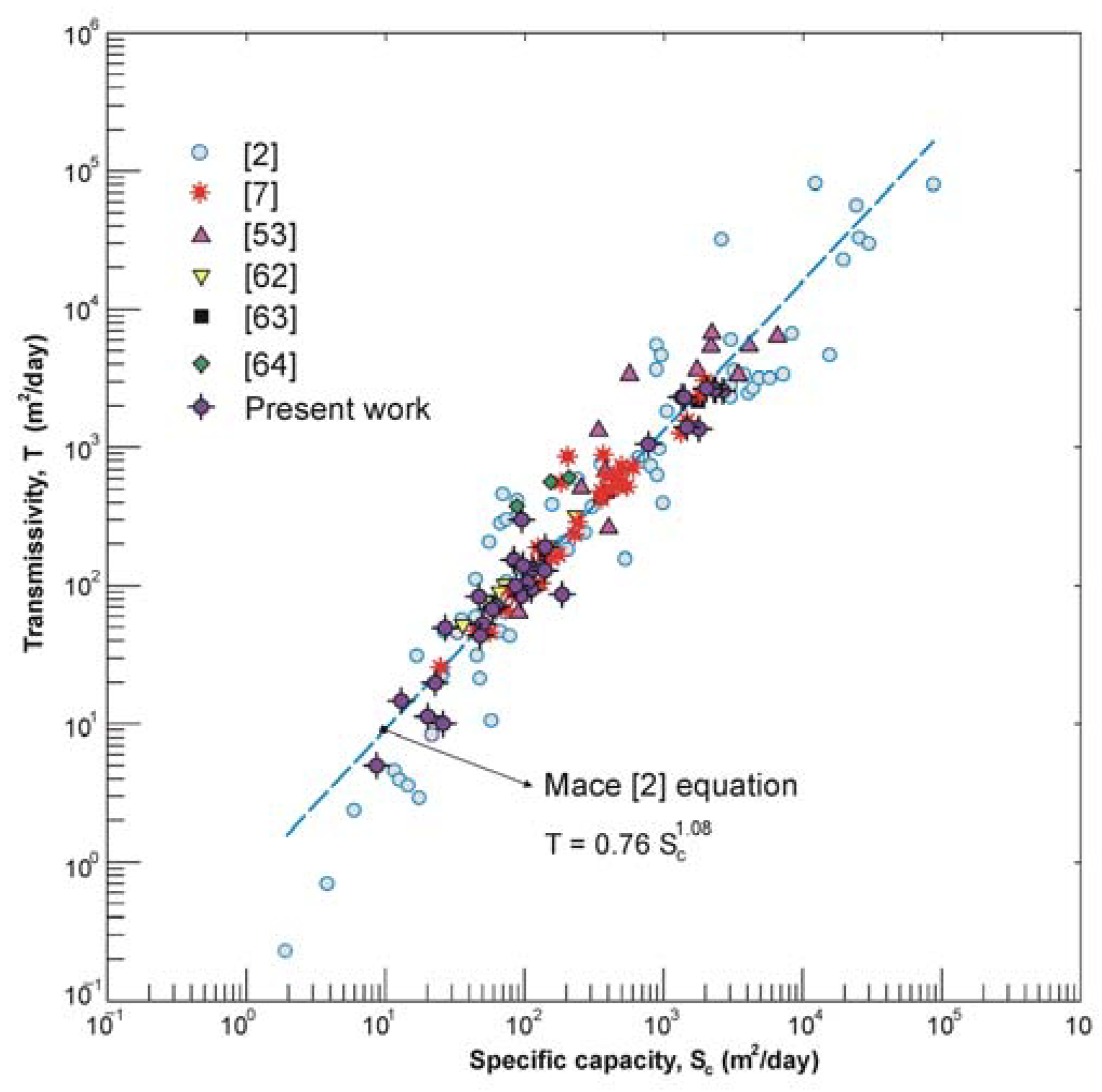
| Name | Well Depth (m) | Hydrogeological Complex | Source |
|---|---|---|---|
| BOT1 | 200 | BL | Umbra Acque Company (ATI2 Umbria) |
| BOT2 | 200 | BL | Umbra Acque Company (ATI2 Umbria) |
| MCUC1 | 250 | MA | Umbria Region |
| MCUC2 | 200 | MA | Umbria Region |
| MIG1 | 85 | MA | Umbra Acque Company (ATI2 Umbria) |
| MIG2 | 102 | MA | Umbra Acque Company (ATI2 Umbria) |
| MIG3 | 109 | MA | Umbra Acque Company (ATI2 Umbria) |
| MIG4 | 105 | BL | Umbra Acque Company (ATI2 Umbria) |
| SUB | 445 | SC-MA | Umbra Acque Company (ATI2 Umbria) |
| MMAR1 | 429 | SC | Umbria Region |
| MMAR2 | 436 | MA | Umbria Region |
| MAM | 240 | MA | Umbra Acque Company (ATI2 Umbria) |
| SPL | 300 | BL | Present work |
| ACQ1 | 45 | TRA | Present work |
| ACQ2 | 60 | TRA | Present work |
| ACQ3 | 48 | TRA | Present work |
| VN2 | 140 | MA | Umbria Region |
| VN3 | 150 | MA | Umbria Region |
| TR1 | 300 | BL | SII (ATI4 Umbria) |
| TR2 | 300 | BL | SII (ATI4 Umbria) |
| TR3 | 300 | MA-CD | SII (ATI4 Umbria) |
| TR4 | 300 | MA | SII (ATI4 Umbria) |
| TR5 | 300 | CD-BL | SII (ATI4 Umbria) |
| TR6 | 300 | CD | SII (ATI4 Umbria) |
| MCAL1 | 280 | BL | Umbria Region |
| MCAL2 | 270 | BL | Umbria Region |
| Author | Setting | Empirical Relationships | n. Data | Range of Application (m2/day) |
|---|---|---|---|---|
| Reference [52] * | Fractured carbonate (Northwestern Ohio aquifer, USA) | T = 3.24 Sc0.81 | - | 10–2000 |
| Reference [53] | Fractured/karstic carbonate (Floridan aquifer, USA) | T = 1.23 Sc1.05 | 14 | 100–100,000 |
| Reference [6] | Fractured carbonate (Amman-Wadi Sir aquifer, Jordan) | T = 1.81 Sc0.917 | 237 | 3–20,000 |
| Reference [2] | Fractured/karstic carbonate (Edwards aquifer, USA) | T = 0.76 Sc1.08 | 71 | 1–100,000 |
| Reference [7] | Fractured carbonate (Euganean basin, North-East Italy) | T = 0.85 Sc1.07 | 45 | 6–2500 |
| Name | PTs Type | Method of PTs Analysis | Sc (m2/day) | T (m2/day) |
|---|---|---|---|---|
| BOT1 | step-drawdown | 2 | 1800 | 1361 |
| BOT2 | step-drawdown | 2 | 1469 | 1400 |
| MCUC1 | step-drawdown | 2 | 86 | 100 |
| MCUC2 | step-drawdown | 2 | 9 | 5 |
| MIG1 | step-drawdown | 2 | 62 | 71 |
| MIG2 | step-drawdown | 2 | 115 | 132 |
| MIG3 | step-drawdown | 2 | 13 | 15 |
| MIG4 | step-drawdown | 2 | 59 | 67 |
| SUB | step-drawdown | 2 | 27 | 49 |
| MMAR1 | step-drawdown | 2 | 26 | 10 |
| MMAR2 | step-drawdown | 2 | 778 | 1050 |
| MAM | step-drawdown | 2 | 186 | 86 |
| SPL | constant-rate | 2 | 50 | 53 |
| ACQ1 | step-drawdown | 2 | 140 | 130 |
| ACQ2 | step-drawdown | 2 | 112 | 94 |
| ACQ3 | step-drawdown | 2 | 47 | 84 |
| VN2 | step-drawdown | 1 | 1350 | 2318 |
| VN2 | step-drawdown | 1 | 1412 | 2317 |
| VN3 | step-drawdown | 1 | 2667 | 2578 |
| VN3 | step-drawdown | 1 | 2373 | 2635 |
| VN3 | step-drawdown | 1 | 2304 | 2635 |
| VN3 | constant-rate | 1 | 2036 | 2693 |
| TR1 | step-drawdown | 2 | 94 | 84 |
| TR1 | constant-rate | 2 | 95 | 300 |
| TR2 | step-drawdown | 2 | 23 | 20 |
| TR2 | step-drawdown | 2 | 20 | 11 |
| TR3 | step-drawdown | 2 | 84 | 154 |
| TR4 | step-drawdown | 2 | 105 | 106 |
| TR5 | constant-rate | 3 | 97 | 140 |
| TR6 | constant-rate | 2 | 141 | 190 |
| MCAL1 | step-drawdown | 2 | 86 | 100 |
| MCAL2 | constant-rate | 4 | 48 | 43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valigi, D.; Cambi, C.; Checcucci, R.; Di Matteo, L. Transmissivity Estimates by Specific Capacity Data of Some Fractured Italian Carbonate Aquifers. Water 2021, 13, 1374. https://doi.org/10.3390/w13101374
Valigi D, Cambi C, Checcucci R, Di Matteo L. Transmissivity Estimates by Specific Capacity Data of Some Fractured Italian Carbonate Aquifers. Water. 2021; 13(10):1374. https://doi.org/10.3390/w13101374
Chicago/Turabian StyleValigi, Daniela, Costanza Cambi, Roberto Checcucci, and Lucio Di Matteo. 2021. "Transmissivity Estimates by Specific Capacity Data of Some Fractured Italian Carbonate Aquifers" Water 13, no. 10: 1374. https://doi.org/10.3390/w13101374
APA StyleValigi, D., Cambi, C., Checcucci, R., & Di Matteo, L. (2021). Transmissivity Estimates by Specific Capacity Data of Some Fractured Italian Carbonate Aquifers. Water, 13(10), 1374. https://doi.org/10.3390/w13101374









