1. Introduction
Achieving the Sustainable Development Goals of the United Nations by 2030, and Goal 6 in particular (sustainable management of water and sanitation for all) will require significant investment in increasing irrigation efficiency (IE) and supporting water reallocation from agriculture to domestic and environmental uses [
1,
2,
3]. Given the importance of ensuring continued food production and economic and social viability for a growing population, focus has been placed on improving infrastructure and on-farm practices to allow the same agricultural production for less water, with water savings transferred to other uses [
4].
However, there is ongoing debate in the literature around the impact of local IE measures on basin-wide flow [
5]. The concern is that water saved at the farm scale may not reduce water consumption at the basin scale, as a portion of water previously extracted would have remained unconsumed and returned to the basin to be reused elsewhere [
6,
7,
8,
9]. For this paper, return flow refers to that water which has been diverted from rivers for irrigation but causes gains in rivers either due to surface drainage (surface return) or groundwater-surface water interaction (ground return). The suggestion is that for a given amount of water diversion from a river to an irrigation scheme, more efficient irrigation generally leads to less return flow to the river [
6,
9,
10,
11].
Any discussion around IE is made challenging by the lack of clarity around what constitutes IE and therefore what savings are possible [
9]. Accounting for water use by irrigation can occur at multiple scales from on-farm to irrigation districts and river basins [
12]. The approach to understanding the role of IE for water savings hinges on the scale of concern [
5,
12]. In this regard, much of the literature around IE has focused on the distinction between classical irrigation efficiency and effective irrigation efficiency and the need to distinguish between recoverable and non-recoverable water within the parcel of water not consumed by crops [
5,
7,
13].
This paper does not enter the debate around the definition of IE. Rather, it examines how best to consider and assess the potential risk of basin wide IE projects in reducing the return flows to rivers. This paper examines the south-eastern Murray–Darling Basin (MDB) in Australia, where concerns have been raised over large government funded water infrastructure projects aimed at reallocating water to the environment, while maintaining irrigation-dependent communities [
14]. Some of the funded projects were on-farm, while others were to improve the efficiency of off-farm delivery networks.
There have been four studies [
15,
16,
17,
18], from here on referred to as I, II, II, IV respectively, which have assessed the impact of IE on return flows at regional to basin scale. These have resulted in a range of assessments of the risk in meeting basin water management objectives from low to very high. Three of these studies (II–IV) have assumed that ground returns will dominate return flows. This study develops one of the four approaches in more detail in order to analyze sensitivities, especially from regional characteristics and type of action under the projects, to the risk of not meeting downstream water objectives. The results are used to illustrate the reasons for the wide-varying assessments. The estimates are also compared to monitoring and other modeling outputs to show that some assessments are over-estimating impact. The results have implications for risks assessments and water accounting elsewhere; and for applying concepts of recoverable and beneficial water. The next section will describe the context for the study and develop the objectives of this paper in more detail.
2. Study Area
This section briefly describes the hydrology and irrigation history of the MDB; water reform process and history of IE changes; Basin Plan (BP), water recovery and the IE projects; and risks to BP objectives. More comprehensive descriptions of the MDB are available [
19,
20,
21,
22].
2.1. Hydrology and Irrigation History
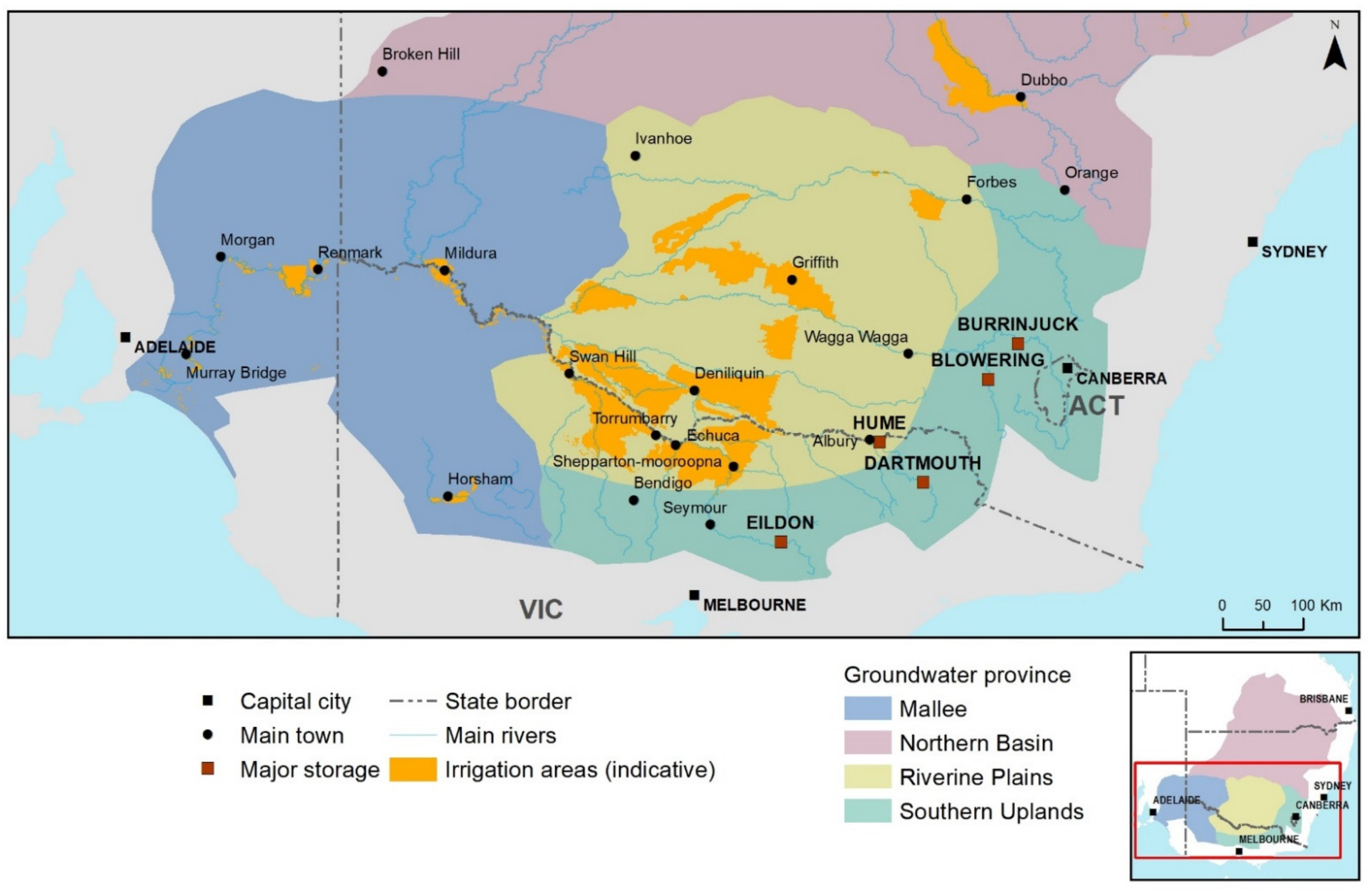
The study region, shown in
Figure 1, consists of the alluvial plains of river valleys in the states of New South Wales (Murrumbidgee, Murray) and Victoria (Murray, Ovens, Kiewa, Goulburn, Broken, Loddon, Campaspe) in south-eastern Australia. These rivers flow into the Murray River, which then flows through South Australia to the Southern Ocean. The Darling River, which drains the northern MDB, joins the Murray River downstream of the study region. The winter-dominated rainfall decreases from the headwaters of these rivers in the Great Dividing Range to the semi-arid downstream boundary of the study area. The hydrology is characterized by large annual variability and low run-off, relative to major rivers globally. The study area and downstream regions support a wide range of complex and dynamic ecosystems, including river red gum forests, floodplain forests, and the Coorong and Lower Lakes at the end of the system [
20].
A long history of irrigation development has resulted in a high degree of regulation and large water storages. The total volume of major water storages is now about 13,900 Gl or 92% of the historical annual streamflow, with the main storages located on the Murray, Goulburn and Murrumbidgee (
Figure 1). The main irrigated crops are dairy (pastures), rice, cereals, fruit, nuts, grapes and more recently cotton/maize. The irrigation areas (shown in
Figure 1) are mainly supplied by surface water from these storages travelling through streams and channels. By 2000, the annual use of surface water across the MDB approximated the estimated natural mean annual outflow [
23].
Groundwater is also used, representing approximately 11% of the diverted water. The main groundwater resource is the confined alluvial sand and gravel aquifers (Calivil, Renmark Formations) of the Goulburn Sedimentary Plain (Victoria), Lower Murray and Lower Murrumbidgee (New South Wales). Groundwater is also pumped from the shallow Shepparton Formation, which consists of fragmented sand aquifers within a lower permeability alluvial formation. Together, these form the major alluvial systems shown in
Figure 1, which underlie the study region [
24]. The major sources of recharge to these aquifers include river leakage and flooding, which create areas of fresher groundwater in the otherwise brackish to saline regional groundwater [
25,
26]. Irrigation with surface water has led to the development of groundwater mounds, causing land salinization and waterlogging. The objectives of extraction from the shallow aquifer are for water table control; and where possible, for an opportunistic groundwater resource. Waterlogging and salinity have been declining since 2000 and extraction is mainly as a respource.
2.2. Water Reform Process and Irrigation Efficiency Developments
As irrigation areas developed, underlying water tables rose, leading to waterlogging and land salinity. Water table control measures, such as groundwater pumping, and surface and sub-surface drainage were increasingly required to control these problems. The higher water tables and water table control measures meant increasing brackish and saline return flows from irrigation areas to streams and potentially much more into the future. By the 1980s, concerns of longer periods of high salinity (>1000 mg/L) of river water in the South Australia portion of the Murray River [
27] and associated risk to water supplies led to the 1988 Salinity and Drainage Strategy. Under this strategy, southern Basin states and federal government agreed to use engineering schemes to divert saline inflows away from rivers and encourage more efficient irrigation water use.
Modifications to the flow regimes of the major tributaries led to major environmental degradation during the 1980s. Despite the use of IE for salinity purposes, diversions of surface water increased to allow further agricultural development. A cap on surface water diversions was agreed in 1995 (and finalized in 1997) to help prevent further degradation. An accounting process was developed, based on river modeling, to ensure integrity of the cap. Agreement was reached in 2003 to return 500 Gl/y of water to the environment. This was monitored through a clearly defined water allocation system with entitlements (or rights) to take water. These actions aligned with the national water reforms that were being developed during this time [
28]. The adoption of nationally agreed water reform packages in 1994 and 2004 facilitated the expansion of water markets across connected valleys and eventually state borders in the Murray–Darling Basin. This enabled water users to sell or buy water in response to the price of water and commodities, while maintaining the cap on diversions.
Drier climatic conditions began in 1997, culminating in the Millennium Drought, 2001–2009. Water trade is credited with helping the irrigation industry through the Millennium Drought by providing greater flexibility with water entitlements to address reduced water availability. This enabled farmers with lower water production to forego totally their production and instead receive payment for selling their water allocation to those farmers with higher value production, enabling them to continue. The combination of the cap, water trade and drought conditions encouraged continued uptake of IE projects during the period 1995 to 2009, despite capping of diversions. Changes in the irrigation water use and return flows in the southern riverine plains were evident by 2009 [
22].
Such changes led to concerns that issues unaccounted for in the entitlement system may affect water availability. In particular, several studies were undertaken to quantify risks resulting from IE changes on surface water flow (e.g., [
29,
30], I, II). These studies found that the impacts were less significant than other catchment changes such as climate change. In particular, II assessed the risk of IE on return flows as low. Monitoring showed that surface water returns and salt loads reduced from the period 1995 to 2009 ([
27,
31], III). On the basis of assessments such as I and II, government agencies in the MDB concluded there was little need for further work in assessing IE impacts as part of water planning, unless further conflicting information arose.
2.3. Basin Plan, Water Recovery and the IE Projects
The federal government established the Commonwealth Water Act in 2007, which set up the Murray–Darling Basin Authority (MDBA) and rules for the Basin Plan (BP). The BP was released in 2012 and was intended to take full effect by 2019 [
32,
33]. The BP replaced the initial cap with the establishment of a ‘sustainable diversion limit’ (SDL) on the volume of the MDB’s water resources (both surface water and groundwater) allocated for consumptive uses. At the same time, in order to rehabilitate environmental values, the environment was given the ability to hold water entitlements, a right to water that can be called from storage to meet environmental needs [
34]. To “bridge the gap” between the existing cap (Baseline Diversion Limit or BDL) and the new lower surface water SDLs, the federal government created a program to recover an additional 2750 Gl of entitlements from the consumptive pool. (This goal has been reduced by 607 Gl/y byundertaking offset works that give the equivalent outcome as the recovery of entitlements). This program provided funds to purchase water entitlements from willing sellers, and to obtain water savings from infrastructure modernization and irrigation efficiency improvements. This paper focusses on the various on-farm and off-farm infrastructure modernization and irrigation efficiency projects to recover water (lumped here as IE projects). The IE projects considered here started in 2007 and are now largely complete. The participants agreed to transfer a portion of water savings to the Commonwealth in the form of legal water rights in return for funding IE projects. The rest of the water savings generated by the infrastructure upgrades can be retained by the program participant. The IE projects are designed to deliver neutral or positive socio-economic outcomes for the MDB and its residents. The federal government has recently decided that there would be no further water buybacks; and any further recovery of entitlements would occur through a similar program, with an emphasis on off-farm IE projects [
35].
Box 1 shows examples of IE projects.
Table 1 shows the volumes of savings from the IE projects relative to environmental targets for the main river valleys relevant to this paper. These river valleys represent about 90% of the total savings of the IE projects. Further details of individual projects can be found in III. The aggregate gap between the BDL and SDL for these valleys is 1582 Gl/year, which represents about 21% of the aggregate BDL. The aggregate water entitlements to be recovered for the environment from IE projects is 672 Gl/y. The main differences between the IE projects and the broader IE changes occurring across the study area are that (a) these incur government funding, (b) about two-thirds of the savings is used to recover water entitlements for the environment, rather than go to further agricultural production, and (c) about three-quarters are from off-farm projects, which may not have occurred outside of such a funding program. While irrigators were willing to fund on-farm projects, and hence were likely to continue in absence of such a funding program, major off-farm projects required coordination and/or funding from government and irrigation companies.
Box 1. Examples of off-farm and on-farm irrigation efficiency projects.
Examples of off-farm projects are:
Channel rationalization, automation and remediation, service point replacement and rationalization
Decommissioning of irrigation systems
Infrastructure upgrade
Part land retirement
Metering improvements
Piping water rather than channel delivery | Examples of actions of on-farm projects are:
Drainage reuse
Laser grading
Improving gravity channel surface irrigation
Installing or improving pipe and riser
Installing or improving sprinkler
Installing or improving micro or drip irrigation
Automation, irrigation scheduling, soil moisture monitoring
Piping, plastic lined or upgraded channel
Improving pipes |
2.4. Impact of IE Projects on Return Flows
Concerns have been raised in relation to the reduction in return flows from the IE projects [
37,
38,
39,
40,
41,
42]. The lack of consideration of these impacts within water accounting could risk meeting environmental objectives. For example, the authors of one study ‘estimate that AUD 3.5 billion have been spent on irrigation water infrastructure upgrades for water recovery that have generated no apparent public good and have failed to help achieve the key objects of the Water Act 2007’ [
38]. These concerns have been raised in various submissions to reviews and on national radio and television.
In response to these concerns, the MDBA conducted an independent assessment (III), which found that the program would lead to a best-estimate reduction in return flows by 16% of the water recovered under this program. A later published study, IV, found a mid-point estimate of 84% of the recovered water. This last result would mean a high risk of not meeting water management objectives. This appeared to be in contradiction with the earlier government findings, based on the assessments (I, II). Together, the assessments (I–IV) captured the full range of possible impacts, with implications for the Basin Plan from being insignificant to requiring the BP to be paused.
There are undoubtedly deficiencies in knowledge that lead to large predictive uncertainties. When this happens, the issue needs to be framed within a risk management framework to ensure BP objectives are met, despite these deficiencies in knowledge. However, in this case, knowledge does exist to explain some of the discrepancy between studies.
The discrepancy between the analyses of III and IV has already been attributed to the difference in assumptions about the groundwater connectivity between irrigation areas and streams, rather than the differences in approach (IV, [
43]). IV assumed that any change in seepage to groundwater from irrigation areas led to an equivalent change in return ground return flows, while III used prior groundwater modeling outputs to estimate the degree to which these changes were attenuated. Both assumptions were justified on the basis of mass balance principles, but changes to components of the water balance other than return flows, e.g., evaporation and groundwater storage have been shown to be important [
43]. The difference between these and the earlier studies have not yet been resolved.
Since these studies have been conducted, the original IE program is largely complete, and some final reports and audits are now available. Some monitoring data would now be available to assess any changes in seepage to shallow groundwater under the irrigation areas and on salt loads to streams. Given the decision made by the federal government about future water recovery [
35], it would appear timely to provide an updated assessment that incorporates this further information.
This paper further develops the approach of III to enable a more direct comparison of the different approaches. The study adds to the earlier approach by including an uncertainty and risk assessment. The comparative study and methodological description should be useful for irrigation areas elsewhere.
The commentary in this paper is constrained to the hydrological impacts on return flows and their management. It does not delve into issues such as the choice between water buybacks and water infrastructure upgrades in recovering water for the environment or the implications for the price of water or for other sources of water. The assessments of these issues have a strong social and economic component.
The study is constrained to the southern riverine plain, where approximately 90% of the IE projects occur. Only a minor component of the IE program has occurred in the northern MDB. Hence, issues that may be more important in the history of water management in the northern MDB than in the southern MDB, are only briefly discussed here, if at all.
Many of the terms to do with IE are value-laden or potentially misinterpreted. For example, water use efficiency and water savings are terms that have varying definitions and can lead to long discussion. In this paper, we will refer to projects and the proposed savings as IE projects and savings, irrespective of whether these are truly more efficient, and the savings are true savings. Where a value is given to, say, water use efficiency, the term is defined in that context.
3. Methods
This section, in conjunction with the
Appendix A, describes the:
Modeling approach to link IE projects to changes in return flows;
Underlying theory for the estimation of the reduction in return flows;
Data sets used to parameterize the model;
Approach to determination of predictive uncertainty;
Datasets used to test predictions; and
Risk management framework for the issue.
3.1. Modeling Approach
Any IE project will change the water balance, e.g., upgrading channel lining will change the channel leakage component of the water balance. This change in one component then causes a hydrological response, where the changes in the various other mean annual water balance components will eventually balance. One of these changes will be reduced return flows, which can be expressed as a fraction of the original change in water balance. Proposed water savings will be used to estimate the original changes in water balance. It is implicitly assumed that irrigation areas are initially in a dynamic hydrological quasi-equilibrium, reacting to variations in climate and irrigation applications, but with groundwater, possibly evolving more slowly.
The analysis of the impacts of the IE program on return flows consists of the following steps:
Dividing the program into IE projects within independent irrigation areas;
Dividing IE projects within each irrigation areas into off-farm and on-farm projects;
Estimating the changes to water balance components as implied by each IE project using relevant studies in reports and papers;
Aggregating the changes in water balance components for each network, divided into on-farm and off-farm projects;
Using a water balance analysis to estimate the response of return flows to the change in water balance; and
Aggregating the impacts on return flows according to irrigation regions and across the southern riverine plains as a whole.
3.2. Theory
The theory underlying steps (3–5) is described in the
Appendix A, with the final equations described in this section. We then describe how it has been applied to the south-eastern MDB and how predictive uncertainty is determined. A glossary of notation is found in
Table A1 in the
Appendix A.
The water balance for the irrigation area prior to the IE projects is described in Equations (A1)–(A6) in the
Appendix A.
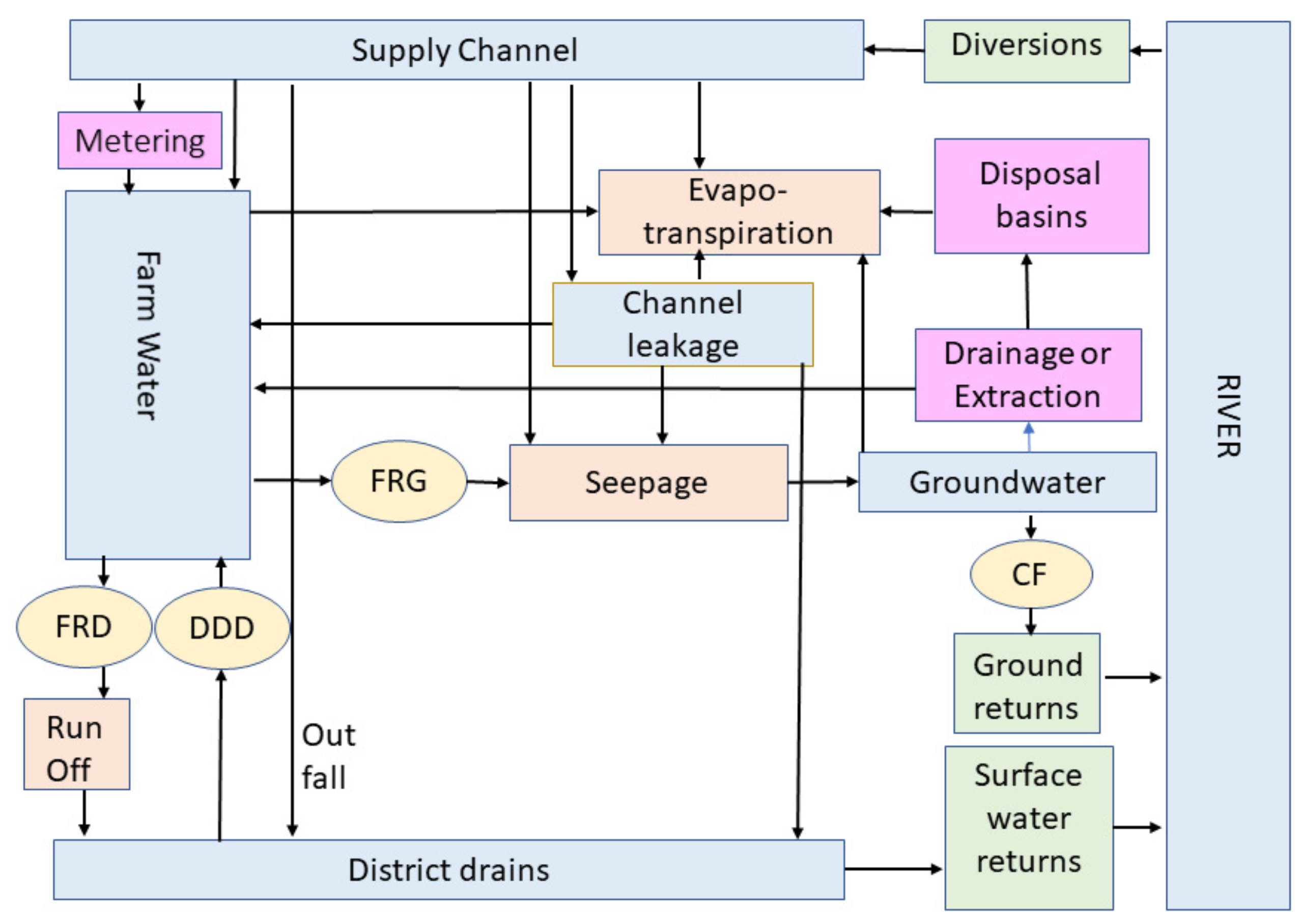
Figure 2 shows a flow diagram of the irrigation water balance. It also shows the four parameters that are used for the calculations: (1) FRD, the fraction of water applied becoming farm run-off to district drains; (2) DDD, the fraction of district drainage water that is diverted for irrigation; (3) FRG, the fraction of water applied becoming farm recharge to groundwater; and (4) CF, the fraction of seepage to groundwater that returns to rivers within 50 years. While not included explicitly in the modeling, disposal basins are discussed later.
The theory for the impact of off-farm projects is described in Equations (A7)–(A17) in the
Appendix A.
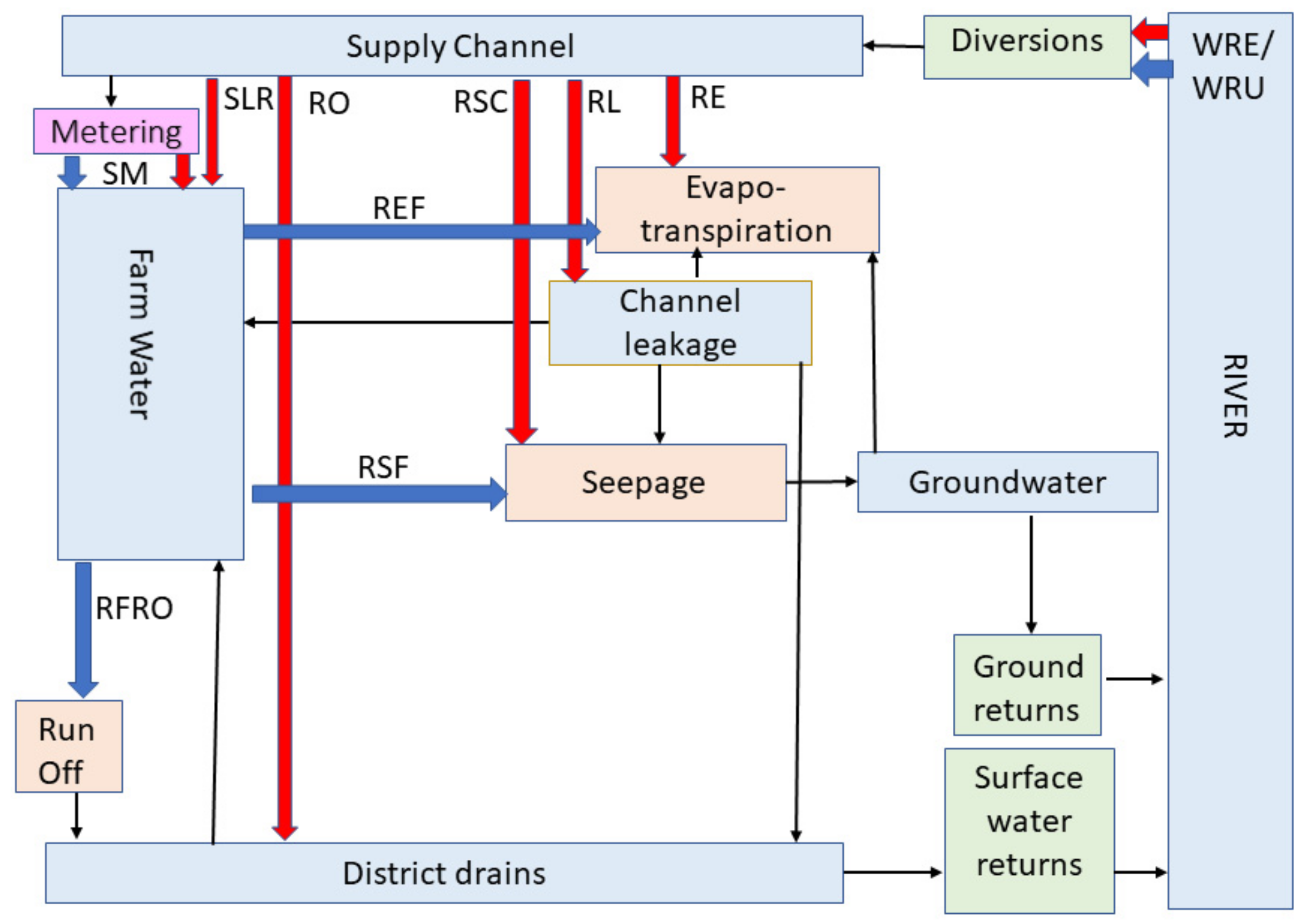
Figure 3 shows the flow diagram of the perturbation to that water balance caused by these changes. The actions are represented by specific changes in water balance, as shown by the red arrows. Specifically, these are SLR, the savings from land retirement; RO, the reduction of outfall; RSC, the reductions in channel seepage; RL, reductions in channel leakage; RE, the reductions in evaporation from channel surface; SM, the savings due to a due to improvements in metering and RWE/RWU are the transfer of entitlements for the environment and urban water supply. The key equations for calculating the reductions in surface return flows, RSRFOFF, and ground return flows, RGRFOFF, due to off-farm projects are given respectively by:
where
PRDD, PRF and PRS are the proportion of channel leakage that respectively moves to district drains, farms and seepage; and WRF is the proposed savings that go to the proponent. Equations (1) and (2) are linear in the water balance components associated with the proposed savings. The reductions in return flows can be estimated using a spreadsheet.
The modeling of impacts of on-farm projects on return flows are described in Equations (A18)–(A22),
Appendix A. The blue arrows in
Figure 3 shows the water balance actions associated with on-farm actions: (1) REF, the reduction in evaporation from irrigated land; (2) RSF, the reduction in seepage from irrigated land; (3) RFRO, the reduction in run-off from irrigated land; and (4) SM, the savings due to improved metering. SM is the same as for off-farm projects, but in some cases, is included in on-farm projects and where so, is denoted by SMF. The main relevant Equations are:
where:
3.3. Datasets
The IE program was divided into 7 regions, based on networks, hydrogeology and surface water:
Murrumbidgee: the irrigation systems that overlie the Lower Murrumbidgee Alluvium, including the Murrumbidgee Irrigation Area (MIA), Coleambally Irrigation Area (CIA) and several smaller irrigation areas. The largest action in this valley occurred to the west with the decommissioning of the whole Nimmie-Carrie district.
NSW Murray: irrigation systems that overlie the Lower Murray. Irrigation areas include Berriquin, Deniliquin and Wakool. The region is divided into two areas (a) upstream and (b) downstream of a hydrological constriction of the Murray River at the Barmah Choke.
Victorian Murray: Irrigation areas include Shepparton and Kerang. This area was divided into two areas (a) upstream and (b) downstream of the Barmah Choke. Most of this area overlies the Goulburn Sedimentary Plain. A small percentage of the program is in the western Murray Basin, but was not separated.
Each of the (a) Goulburn, (b) Loddon, (c) Campaspe and (d) Broken river valleys were considered separately. Most of the irrigation systems overlie the Goulburn Sedimentary Plain. The Goulburn and Broken areas are upstream of the Barmah Choke, while the Loddon and Campaspe systems are downstream.
Only a brief description of the data used will be given here. Many of the details are available in III. The Murray–Darling Basin Authority (MDBA) and the Australian Government Department of Agriculture and Water Resources (DAWR) provided project data on water recovery and allocation of water saving between environment, irrigation and urban use.
To implement the theory described earlier, the water savings needed to be partitioned into reduction in evaporation; seepage; leakage (or theft) and escape; and savings from metering and land retirement. The reduction in leakage (or theft) needs to be partitioned into reduction in evaporation and seepage from leakage, reduction in farm use of leakage and input of leakage into district drains. Escape refers to the net amount of water returning to the river at the system level and therefore becomes surface return flow. DAWR provided data on the sources of water saving for major projects in NSW. The estimates were obtained by examining water loss reports related to key irrigation networks. The reports included analysis of ‘hotspots’, irrigation modernization plans, applications for funding and additional reports from grant recipients. The information in these reports was not generally in a format that could be used, directly or consistently, for estimating the sources of water saving. Judgement had to be applied to reach the final estimates for different projects.
Data was also gathered from project review or final reports [
43], III, audit reports and technical assessment reports [
44,
45,
46,
47,
48], both published and unpublished, for some of the projects, especially in Victoria. To complete the assessment, many assumptions had to be made for assessing the magnitude of the overall impacts. They are not for providing accurate results at individual project level.
There is also a need to parameterize the variables: DDD, FRD, FRG and CF. The value of 0.95 was given to the variable DDD (fraction of district drainage water being diverted for irrigation) for Victorian projects on the basis of analyzing the surface water data [III]. The same variable was given a value of zero in NSW as the escape term in the data provided by DAWR is the net amount of water returning to the river at the irrigation system level. While a value of 0.1 was given to the value of FRD (fraction of water applied becoming farm runoff to district drains) for Victorian systems from previous analysis [
43], a value 0.03 was used in NSW. Reasons for the latter included (1) NSW has legislation preventing farm irrigation run-off and (2) the value of DDD is set to zero for NSW, meaning that FRD is the net escape after drainage re-use at irrigation system level. As the theory has not formally included a term on drainage diversion to disposal basins, this component is incorporated into the value for FRD to account for the net irrigation runoff at system level. CF was derived using previously available groundwater modeling outputs [
42].
3.4. Uncertainty Analysis
Given the nature of a preliminary risk assessment, it is necessary to provide an analysis of predictive uncertainty. The main equations describing the uncertainty analysis are shown in Equations (A23)–(A26),
Appendix A. The analysis is simplified by the main equations being linear in the water balance components associated with actions. Additionally, it will be seen that the estimate of the return flows is often dominated by one term and therefore can be expected to be sensitive to any errors in this term. Where there is a very dominant term, the predictive uncertainty in RRF is given by:
where η = ΔQ
P/Q
P, and ε = ΔA
P/A
P, the subscript P denotes the value of j which dominates the estimation of RRF, A
P is the main coefficient and Q
P is the principal water balance component. The dominant terms for the reduction in the different return flows are:
Off-farm ground return: seepage from channels directly and indirectly from channel leakage;
Off-farm surface return: outfalls and leakage from channels to drains;
On-farm ground return: farm seepage; and
On-farm surface return: farm run-off and farm seepage.
While fluxes, such as seepage and leakage are notoriously spatially heterogeneous, the relative uncertainty in the fluxes at a regional scale will be more constrained. The relative uncertainty, η, in the principal flux, QP is estimated regionally than for specific projects. At the regional scale, losses from channels or surface discharge from irrigation areas will generally be well-determined from studies of delivery efficiency and flow measurements, while that for farms less so. A value of 30% is applied to η for off-farm projects and 50% for on-farm projects.
The linear coefficients Aj are dependent on the four parameters DDD, FRD, CF and FRG. The relative uncertainty in the linear coefficients (ε) can be therefore estimated from the uncertainty in each of the four parameters:
The terms DDD and FRD are handled differently for NSW and Victoria and are constrained by measurements of surface flows from irrigation areas. For Victoria, (1-DDD) is allowed to range between 0.025 and 0.1. FRD is held constant at 0.1 as return flows are not sensitive to this term. Conversely for NSW, FRD is allowed to range between 0.0 and 0.06, while DDD is held constant at 0.0.
The range for CF has been previously found to be 0.05–0.25 for the Lower Murrumbidgee; 0.15–0.40 for the Lower Murray and 0.15–0.45 for the Goulburn Sedimentary Basin [
39]. This range was used in the uncertainty analysis.
FRG is held constant at 0.1, as return flows are not sensitive to this term.
3.5. Comparison with Other Modeling Studies
The results from this study are compared with results using the best interpretation of the modeling approaches of I, II and IV. An interpretation of their approaches has been necessary as the study regions had not coincided with the current study region or impacts were not specifically reported. The details are described below.
The modeling of I had analyzed reductions of irrigation return flows by 50% and 75%, rather than any specific IE program. Irrigation returns were assumed to be 10% of the diversions. The results have been replicated by using, values of BDL for different river valleys as estimates of diversion.
The modeling of II had analyzed reductions of irrigation returns by 50% and 75% rather than by any specific IE program. They reasoned that there is little room for any further reductions in seepage, and only considered groundwater returns. These were estimated using groundwater inputs from [
23]. For the region, the analogous models are used [
49,
50].
The modeling of IV uses values for F obtained from the international literature, assuming good connectivity between seepage or run-off and streams. The value of F between 0.2 and 0.5 can be multiplied by total proposed savings for each region.
3.6. Comparison with Monitoring and Existing Groundwater Modeling Outputs
Modeling outputs from papers (I–IV) can be compared to some groundwater modeling outputs and environmental monitoring. This should help guide whether certain models are consistent with measurements and groundwater knowledge.
The estimation of the return flows is difficult. The large temporal variability of flow means that long time periods are required. The high salinity of groundwater provides a tracer of groundwater inflows to streams and hence can be used to estimate volumes, often coupled with modeling. The western part of the riverine plains is saline, and discharges into streams there. Outputs from salinity analysis for that part of the riverine plains [
51] will be used to estimate groundwater inflow to streams.
It is difficult to extrapolate these estimates across the whole region as groundwater is not saline across the whole region, nor are all streams gaining. As lower water tables can lead to increased losses from losing streams, reduced seepage from IE projects could affect these areas. Groundwater models can provide information on the groundwater discharge to streams, groundwater recharge from streams and the impacts of irrigation recharge. The last provides an upper limit for any reduction in return flows from reduced seepage, while the first can be compared to salinity monitoring. In particular, modeling outputs for the southern riverine plains [
49] and Lower Murrumbidgee [
50] groundwater models will be used for this purpose.
Reduced seepage should affect water tables under irrigation areas. Most of the irrigation areas have been monitoring shallow water tables for some time because of their importance for salinity and waterlogging. It should therefore be feasible to monitor the effects of reduced seepage over the historical record. For this paper, the shallow water table monitoring under the Shepparton Irrigation Area is used [
52]. The levels are monitored annually in August across approximately 1000 bores.
3.7. Risk Management Framework
MDBA uses an adaptive management framework for the Basin Plan. This includes the assessment of risk for prioritizing activities for further work and incorporation as part of Basin Plan activities. The risk from IE projects had been assessed in 2008–2010 as low. In part, this was based on impact assessments (I, II), together with prior river modeling to assess risks to various water supply and environmental water objectives. This resulted in a low risk being posed to environmental assets and all groups of water entitlement holders but three. NSW concluded that ‘No further assessment is necessary for reduced irrigation return flows unless compelling evidence can be produced that this will significantly reduce water availability’.
Additionally, MDB governments assessed that:
Residual risk was low, as impacts were considered to be manageable through water releases as necessary;
Third party impacts to groundwater entitlements by reduced seepage were also considered to be manageable through existing rules in the groundwater plans; and
There are clear salinity benefits to reducing return flows.
Previously, MDBA had considered that in the absence of river modeling to assess impact on management objectives that a reduction of return flows by more than 100 Gl/y was a low risk. Others [
53] adapted this so that the 100–400 Gl/y range was considered to be a moderate risk.
In this paper, we review these considerations with the new results. As a precautionary approach, consistent with the risk management framework, we aim to provide an upper limit to predictions.
4. Results
Table 2 shows the savings from the IE projects according to regions and to off-farm and on-farm projects. It also shows the percentage of savings attributed to changes in different components of the water balance. Most of water savings is caused by actions that directly reduce water applied to agricultural land: land retirement (24%), savings from improved water metering (23%) and reductions in leakage from channel to farm (4%); and most of the reduction of inputs to regional drains (16%).
The water savings are estimated to reduce evaporation by only a 7%. The reduction in evaporation will not reduce return flows, while the reductions in return flows from reductions in water for irrigation will be approximately 5% of those savings.
The reduction in seepage (26%) and the residual component of reduced input to regional drains will reduce return flows more. The ratio of the water savings that is caused by reduced seepage is higher for on-farm projects (~56%) than for off-farm projects (~15%).
The most notable difference across regions is land retirement with little in Victoria (13%) and much higher in the Murrumbidgee (46%). The latter is due to the decommissioning of a whole irrigation district, namely the Nimmie-Carrie.
The impacts on return flows are presented in
Table 3. The total reduction in return flows is estimated to be between 30 and 205 Gl/y, with a best estimate of 106 Gl/y. The reduction is therefore between 3 and 20% of the proposed savings, with a best estimate of 10%. This best estimate also represents 16% of the recovered environmental entitlements.
The large range of possible reduction in return flow means that, in the absence of river modeling, the impact is considered to be low (<100 Gl/y) to medium (100–400 Gl/y). As expected, most (~78%) of the reduction occurs via a groundwater pathway. This high dependence on a groundwater pathway occurs in all regions despite large differences in groundwater connectivity. This is due to the large fraction of water that is diverted back to irrigated agriculture, rather than return to the main rivers.
The ratio of reduction in return flows to total savings is significantly greater for on-farm projects (21%) than for off-farm projects (6%). This can be largely attributed to the higher fraction of the savings that come from reduced seepage, rather than those actions that directly lead to less water for irrigation.
The ratio of reductions in return flows to the total savings is greater in NSW Murray (18%) and lower in the Murrumbidgee (4%). The lower value in the Murrumbidgee can be attributed to the low connectivity factor and the large land retirement. The NSW Murray has a higher percentage of savings caused by seepage reduction and a mid-range connectivity factor.
There is a net reduction of water going to farms by approximately 30% of the total savings. While the fraction of the total savings intended to be returned to irrigated agriculture is nominated in the project proposal, this is more than compensated by land retirement, improved metering and reduction of water being recycled to farms. There will be much variation between agricultural enterprises with some enterprises obtaining more water entitlements than before, while others will have less or none. This will be modified by trade and other developments that occur outside of this government funded IE program. The reduction in mean farm water entitlements from irrigation as a ratio of savings is much greater for off-farm projects (~45%) than for on-farm projects (~−10%).
Table 4 shows a comparison of the range of methodologies (I–IV) as applied to the study region, noting that those for I and II are for a 50–75% reduction in return flows, rather than for a specific IE program. The results show that the upper limit of estimates for approach III is towards the lower limit for IV, while those for II are almost an order of magnitude less than those for I.
Table 5 shows various groundwater fluxes as estimated by regional groundwater models. The column of most interest is the last column as this estimates the maximum reduction in ground return flows. Not surprisingly, the methodology of II provides the closest value to this, as the methodology uses these estimates as a starting point. The methodology of III provides estimates, where the lower end of the range overlaps with these estimates, while the methodologies of I and IV provide numbers much larger than the estimated groundwater impacts. It should be noted that surface water returns are not included in these estimates. The other columns show that groundwater-surface water interaction is dominated by stream losses to groundwater in this region. Not only will lower water tables reduce groundwater discharge to streams, but they will also lead to increased leakage from streams.
The first column can be compared directly to salt monitoring in streams. Monitoring of salt loads from the riverine plains [
49] show that the highest salt loads are from the western portion of the study area. The measured groundwater contribution on Riverine Plains was estimated in 2006 to be 210,000 tonnes/y (Tables 2–10) [
51]. The volume of groundwater inflows that this salt load represents depends on the groundwater salinity. The groundwater in the west of this region is notoriously saline (3000–>14,000 mg/L) [
52]. The inflows represent ~11–55 Gl/y groundwater inflow for the Torrumbarry to Swan Hill reach of the Murray River and Edward-Wakool region. This is comparable to the numbers in
Table 5. This lends support for the lower numbers being generated by the groundwater modeling.
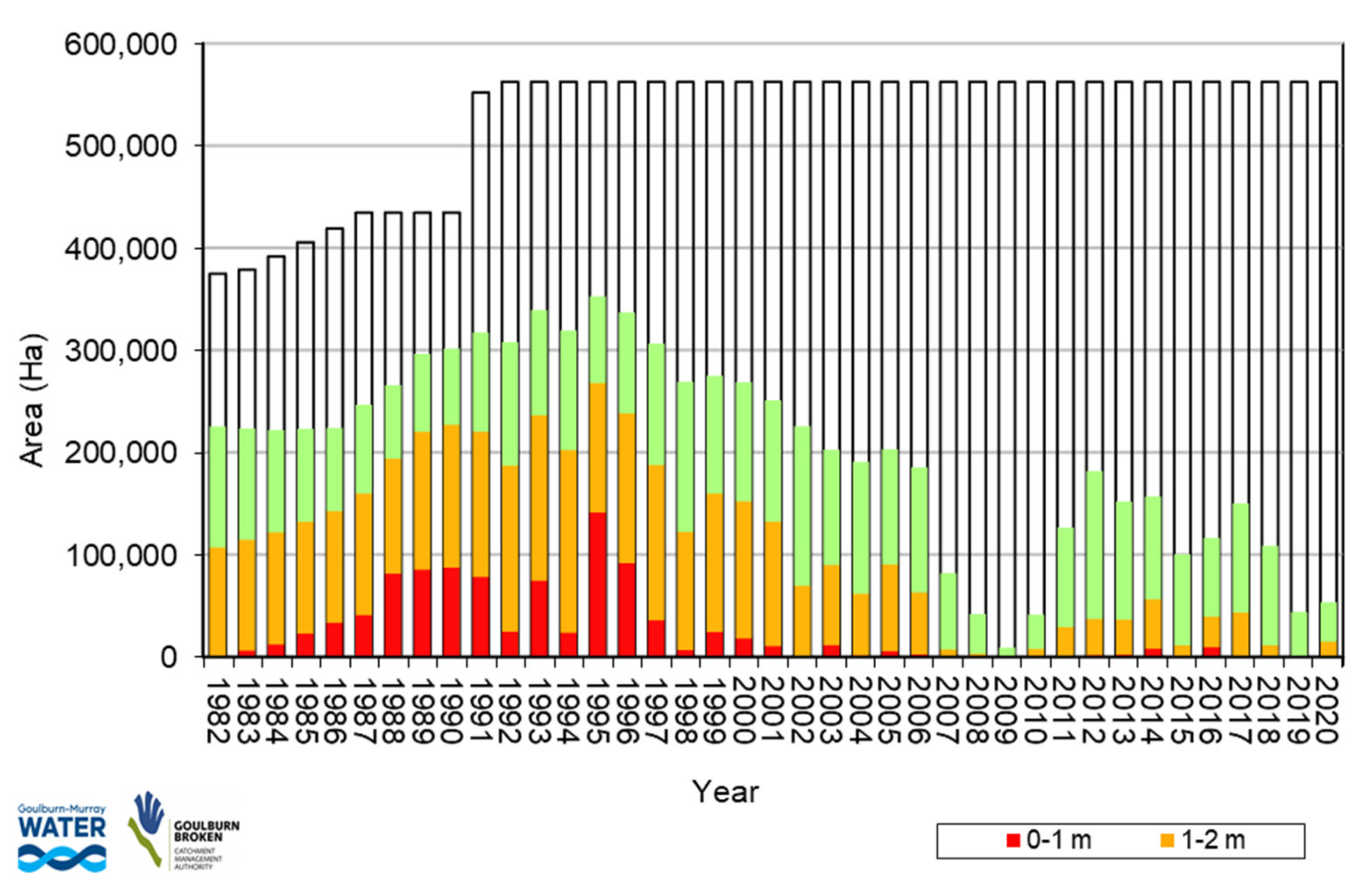
Figure 4 shows the history of shallow water tables under the Shepparton Irrigation Area in Victoria for the period 1982–2020. Rising water tables are apparent before 1995, falling water tables from 1995 to 2007, and water tables remaining low since then. The water tables are primarily responding to rainfall. Not only is recharge higher during wetter periods, but water allocations are higher, groundwater extraction and water trade out of the area are lower, all of which would lead to higher water tables. The introduction of the Basin Plan with lower water allocations and the IE projects from 2011 should be leading to lower water tables, but a more detailed analysis would be required to ascertain this. The large proportion of shallow water tables up to 1995 shows why land salinization and waterlogging has been a concern. It is expected that shallow water tables may return after years of higher rainfall.
5. Discussion
Like many regions of the world, policy makers in the MDB are grappling with how best to return water to the environment whilst also maintaining a viable irrigation industry. The current approach has been a government funded IE program, investing in a range of both on-farm and off-farm efficiency measures. The analysis undertaken, using the approach of III, indicates that the impact of reduced return flows due to the IE program is to up to 20% of total savings or 30% of the water entitlements recovered for the environment. The impact on return flows was greater for on-farm projects (33% recovered water) than for off-farm projects (10%), with most of the impact on return flows via a groundwater pathway. The risk management framework requires confidence in the upper limit for impacts, as this defines whether any management is being conservative.
5.1. Confidence of Estimates
There are several underlying assumptions to the described approach. The uncertainty associated with these assumptions can be divided into the following categories:
5.1.1. Uncertainty with Respect to Implementation and Impact on Proposed Savings
The proposed actions are assumed to have been implemented and do result in the proposed savings. In assessing the implications of this assumption, three issues need to be considered. The first is that the transfer of entitlements occur irrespective of whether proposed savings are real with any residual risk being borne by the proponent. Secondly, the impact on return flows is negatively correlated with the success of implementation, i.e., no implementation means no reduction in return flows, while over-success means greater reductions of return flows. Thirdly, the IE program is not occurring in isolation, but is occurring against the background of other IE projects, and other processes that reduce seepage.
Implementation of IE program is largely complete, although on-ground auditing of the program is yet to be completed. Off-farm actions are often coordinated by government and private administrative entities that have stricter compliance and reporting conditions. Completion reports show whether works have been achieved and the measured change in conveyance efficiency. Available reports indicate that delivery (or conveyance) efficiency has improved; and water use has been reduced [
44,
45,
46,
47,
48,
54].
Reporting of the effectiveness of on-farm projects is less transparent. It is possible that due to the drought and market outlook that not all on-farm IE projects have occurred. If so, the reduction in return flows will be under-estimated. It is generally in the interest of the irrigator to implement IE projects, as is occurring for more general IE projects. On-farm water use efficiency has been improving for more than 40 years and there has been a background trend of improving efficiency. Four percent of irrigation land is made more efficient every year. Thus, in terms of return flows, the reduction will occur anyway, but perhaps later.
Water productivity (irrigation receipts per Ml of water) of participating farmers is reported [
55] to have increased by 25%, as did water demand; with water trade sufficient to explain additional water use. As shown in
Figure 4, it is difficult to separate any impacts from more general IE activities from the IE program alone.
Considered together, the full implementation of proposed on-ground works will be more likely for off-farm projects than on-farm projects, but on-farm IE projects would be expected to be occurring in irrigation areas, as it has historically done. As a precautionary approach, we would expect the reduction in return flow to occur, as per the assumption.
5.1.2. Uncertainties with Respect to Parameters and Inputs
This study has conducted an analysis of predictive uncertainty caused by uncertainties in the input data (water balance components) and parameters used in the analysis. This provides a conservative value for the impact; namely 20% of total savings for all projects, 13% for off-farm projects and 37% for on-farm projects. The analysis is using regional averages for many of these parameters, while there may be high spatial variability of these parameters. The analysis identifies the key inputs and parameters, to which return flows are most sensitive, namely seepage inputs and CF. An upper limit for CF has been estimated [
43]. The low values of the parameters, FRD, FRG, DDD (Victoria), and CF all contribute to a lower estimate of return flows.
5.1.3. Structural Uncertainties Associated with Unmodeled Processes
No model represents all processes. Structural uncertainty refers to non-representation or poor representation of processes. A water balance approach is a classical approach to estimating response to water savings action and is considered a robust approach. Two forms of structural uncertainty are considered here: (1) non-inclusion of some processes relevant to irrigation water balance; and (2) anthropogenic or economic responses to IE projects.
Some irrigation processes have not been included as they represent a minor component of the water balance of main irrigation areas; or would lead to conservative estimates of return flows. For example, some groundwater that is returned to the land surface by sub-surface or surface drainage or groundwater pumping. Often, this water is brackish to saline. Where it is sufficiently fresh, water may be used for irrigation directly or ‘shandied’ with river water in supply channels and then used for agriculture. Where it is more saline, it is diverted to salt disposal basins. None of these processes are currently included in the modeling, which would have led to lower return flows.
The hydrological parameters in irrigation areas have been assumed to be not changing. This is seen in the application of a constant CF and FRD. We would expect that as groundwater systems change, CF may change and surface run-off in these flat areas may reduce. The latter could impact on return flows, but much of this has occurred already. Falling water tables are expected to increase CF, by reducing groundwater discharge to the land surface and to drains, where water is recycled or diverted.
The regional groundwater models used to determine CF may not well represent the local flow systems. The semi-confining Lower Shepparton Formation is a throttle for recharge to the lower aquifer. This may mean that the estimate of CF is initially too high and approaches the modeled value as water tables fall.
IE projects may lead to responses by irrigators that impact on return flows. The theory here strictly only considers the direct actions associated with savings. There are at least two important responses that may occur. The first is that volumes of pumping and drainage to avoid salinity and waterlogging and due to lower groundwater availability, may be reduced as seepage is decreased. Some irrigation areas are even discussing using managed aquifer recharge schemes to augment water supply once pumping for salinity control is no longer needed. Reduction in discharge by pumping and drainage has the opposite response to reduced seepage and will offset some of the return flows from the savings.
Secondly, the modernization of irrigation infrastructure may lead to changed irrigation footprint, whether this is to take advantage of the new infrastructure or the water recovery leads to a change in demand. Any such changes need to be considered within broader changes in irrigation, such as trade, changes in extraction under the cap and efficiency improvements. Any local increase in development will increase return flows in that area.
5.1.4. Sensitivity Factors for Return Flows
The results have shown three different factors influencing the impact on return flows as a proportion of total proposed savings. The first is the importance of the groundwater pathway relative to surface flows. This is consistent with previous studies [
31] and highlights the change in hydrology before 2000. The second is the groundwater connection between irrigation areas and the major rivers. Regional variations have been found to be due to a combination of the proportion of on-farm projects and the connectivity factor, CF. The third is the importance of on-farm projects relative to off-farm projects. Off-farm projects have less proportional impact on return flows than on-farm projects. This is not only due to its water savings actions leading to less reduction in seepage, but off-farm projects include land retirement and better metering, which both lead to less water for irrigation. The latter would be similar in hydrological impacts to water buybacks.
5.1.5. Comparison with Field Monitoring and Groundwater Modeling
The direct measurement or estimation of return flows is complex. For example, in the South Australian portion of the MDB, this is done to refine salinity strategies [
56], but not done more widely. Existing groundwater modeling and salinity monitoring analyses support the view that 200 Gl/y is a conservative estimate of the reduction of return flow from the IE program. More than this, they support the view that all processes that lead to a reduction in seepage can only lead to a reduction in return flows of less than 200 Gl/y. The groundwater monitoring in the Shepparton irrigation area shows that the IE program is only one of several processes (rainfall, water allocation, water trade, groundwater extraction) that leads to reduced seepage and ultimately reduced return flows. Any management of the risk from return flows need to consider all of these processes.
The monitoring indicates that the approach III may be overestimating the reduction in return flows. Any over-estimation of the reduction in return flows could be due to range of different factors, including an overestimation of the seepage component of the savings in approach III, underestimation of groundwater irrigation in groundwater models; and poor representation of local groundwater flow processes in the groundwater models [
43]. The latter two would imply that CF between seepage and streams may be less than that derived from the model.
5.2. Comparison with Previous Studies
All of the studies that are relevant to this topic (I–IV) are best described as desk-top preliminary risk assessments, aimed at determining the degree of risk associated with the issue and hence whether further work is warranted. This study is built upon III and while there are differences and additions, the results here are not surprisingly similar to those from that study. This approach allows direct comparison with the other studies.
IV estimates a parameter F, defined as the ratio of change in return flows to proposed total savings, from documented studies from around the world. F is estimated to between 0.2 and 0.5. Comparisons with
Table 4 and
Table 5 shows that the lower limit from that study coincides with the upper limit of this study and hence, there is an underlying bias.
In deriving the estimates, IV has assumed that CF equals one and has chosen the value of F on this basis. Our study has determined F for various regions and for types of savings. Had CF been assumed to be one, as in IV, our study would have produced F values averaging 0.19 for off-farm projects and 0.53 for on-farm projects. This implies that most of the bias is due to assumptions about CF. It also means indirectly that the estimates in our study are broadly consistent with the range of seepage estimates from documented international studies.
The value of CF is based on mass balance principles. A value of one was assumed for IV, which implies that changes to other groundwater balance components are negligible. However, changes to other components such as evaporation from shallow water tables and groundwater storage can be significant [
43]. Many of the irrigation areas in the study region were subject to waterlogging and salinity and drops in water table, as seen in the water table monitoring, e.g., [
53]. This would mean that reduced seepage may lead to a reduction in evaporation from shallow water tables, and this implies that CF is less than one.
The estimates of II appear to be lower than that of III. Both approaches rely on the same groundwater models, which indicate a maximum reduction in return flows. Some of the estimate in III is due to surface return flows; but is insufficient to explain the difference. The groundwater models do not represent local flow systems well and it is likely that seepage changes do not equate to recharge changes in the model, implying CF may be effectively lower.
The estimates from I are about an order of magnitude higher than the estimates from II and higher and three times greater than the total groundwater-surface water exchange. This coarse estimation approach is similar to other earlier studies and perhaps times, when surface returns were more significant. II considered the estimates from I of irrigation returns for the NSW Murray as ‘unrealistic’ and ’should be disregarded’. They are within the range of IV, noting that they reflect reduction of all irrigation recharge, not just that reduction due to the government funded IE program.
When these results are compared to the monitoring, it is evident that the estimates of I are too high; only the low end of estimates by IV are feasible but even then, are likely to be too high; the estimates by III appear to be higher than the groundwater modeling results, which themselves are consistent with salt loads monitoring, while those of II are consistent with both the monitoring and modeling. This means that connectivity is highly likely to be towards the low range of estimates, rather than close to one. The potentially high estimates of III, means that it is possible that more of the seepage is contributing to evaporation or sub-surface drainage from shallow water tables than is currently assumed in the groundwater models. More than this, the results suggest that there is a limit to the cumulative reduction in ground return flows from irrigation areas that is possibly comparable to the estimates from III.
5.3. Risk Assessment and Management
A previous risk assessment in 2008–2010 by government agencies highlighted several issues discussed below.
What has changed since the earlier assessment? The BP has been developed since the risk assessment, and new management objectives have been defined. During the relatively dry period in the last two decades, the importance of lower flows is increasingly recognized for conveyance, water quality, and environmental condition. Low flows will be more sensitive to reduced return flows than medium to high river flows, which are relevant for many of the prior environmental objectives. Despite their importance, low flows are difficult to measure and model. Mean annual impacts of reductions in return flows of less than 100 Gl/y would be difficult to detect, within the large temporal variability of flows in the southern MDB as this represents less than 1% of the mean annual surface flow. This also means that adaptively managing low flows by changing the water or land management policy in irrigation areas as levers would be difficult. Additionally, the long time periods for changes in groundwater pressures to move to streams means that by the time observations are made, it is too late to undo changes in irrigation areas that have caused a problem.
An alternative strategy for maintaining low flows is through releases of water from storage or changed surface water management. Such releases of water will affect the SDL and may require more water to be recovered. The volumes involved depend on the management chosen. The water can be released as needed; but requires sufficient water in storage for drier periods. Reduced low flows during dry periods can occur for reasons other than reduced seepage, e.g., reduced runoff [
57] or reduced dryland recharge.
Adaptive groundwater management: The underlying groundwater systems, particularly the unconfined systems provide some opportunity to use groundwater management policy to adapt to the cumulative changes in seepage. The groundwater systems are currently being managed adaptively to avoid water logging and salinity and to protect groundwater users [
58]. For the last thirty years, reducing salinity and waterlogging has been the goal for regional plans. However, many of the shallow groundwater systems underlying irrigation areas are saline and have low transmissivity and such an adaptive strategy for managing groundwater systems is not always possible. The deeper groundwater resources in the semi-confined aquifers under all areas also currently have adaptive measures that can constrain groundwater allocation on the basis of falling pressures. This means that third party impacts on groundwater resources from IE are built into current groundwater plans. While this is still a negative impact, it is one that has been incorporated into the water management plans associated with the BP. Any reduction in groundwater extraction will also offset some of the reductions in return flows, thus reducing them further.
Salinity benefits: Saline inflows to the rivers of the MDB has been managed for over twenty years through three successive basin salinity strategies. The active diversion of return flows to salt disposal basins, together with IE improvements have been successful for meeting the Basin salinity target at a major water offtake for Adelaide water supply by 2010. The target of 800 μS/cm for 95% of the time has continued to be met since then. In parallel, the salt loads from the southern riverine plains have been reduced [
27]. Because of the success of the salinity strategies, trials are being conducted to reduce the pumping (and hence costs) of salt interception schemes in western Murray Basin, used to divert very saline groundwater from the river. Any further reductions in return flows, especially in the western part of the study area may allow pumping costs to be further reduced.
There is a trade-off between the benefits of reduced return flows for salinity control and the costs associated with reduced stream flows, especially low flows. To the west of the region, groundwater inflows are saline, while to the east they are either fresh to brackish or negative. This means that the salinity benefits relative to costs of streamflow depletion increases to the west of the region.
Overall risk: In the absence of river modeling, the results indicate a low to moderate risk for stream depletion, with the main risk being due to low flows. However, the analysis shows that all factors that may reduce seepage and return flows should be considered within the risk management framework. To properly manage the impact of return flows on stream flows, there is a need to provide better models for low flows and their relation to nearby regional groundwater systems. Despite these uncertainties, it is clear that prior assessments of high to very high risk of stream depletion are not realistic. Additionally, the reduction of return flows will benefit stream salinity.
Reduced recharge will also reduce land salinity and water logging; but may lead to a negative a third-party impact on underlying groundwater resources.
5.4. Transferrability of Approach
The four prior assessments of IE impacts on stream depletion show four different approaches to the issue. Two of the approaches occurred before the BP, and before there was any specific program to reallocate entitlements to the environment. The approach in III (and in this paper) is the only one that deals with how seepage depends on IE and regional characteristics, and therefore is able to better represent spatial risk. Approach IV uses studies from around the world to estimate changes in seepage. While this produces a similar range of F, its efficacy for a given situation depends on ability to match the field situation.
The approach developed in III and further developed in this paper can be used in any area, where an irrigation water balance can be constructed. The approach:
Is consistent with the concept of recovered and unrecovered water by focusing on elements that becomes seepage or run-off as a proportion of the proposed water savings;
Does provide a structure for organizing input data for projects to account for return flows;
Shows the applicability of a sensitivity parameter, CF, within water accounting and how it may be estimated;
Provides water accounting within a risk framework, and as such, provides prioritization for funding and a process to improve the analyses, as required. Any accounting needs to not deal with mean annual volumes but the variability of flows, especially low flows; and
Can have more details incorporated should the risk be deemed sufficiently high and more data be collected. The modeling could integrate off-farm and on-farm projects within networks. To better capture behavioral responses to external conditions and reduced seepage and to support policy-making, multi-agent modeling could be used. Additionally, higher resolution spatial variability of properties could be incorporated.
The results in this study have been heavily influenced by historical changes in irrigation practices that have led to most surface water returns being diverted away from the river. This has meant that many local groundwater flows that are intercepted by regional drains would also be diverted. This means that the major component of return flows to major streams is through regional groundwater. This history has led to lower impacts on return flows and greater sensitivity to factors such as the groundwater connectivity between irrigation areas and streams.
The dominance of ground return flows can be problematic for water accounting. For example, the times scales for groundwater pressure transmission are larger than surface water processes. Some of the concepts of recoverable water become more difficult when water seeps into water of a particular salinity; and causes pressure changes that may mobilize water of a different salinity. Where irrigation occurs on brackish to saline groundwater, there is little potential to keep recycling water from streams to irrigation areas. While there is some scope for upstream water to dilute saline inflows, there is a limit when there are existing water quality issues. Water accounting may therefore need to address salt mobilization and changes in salt balances for parts of the hydrological cycle.
6. Conclusions
This paper analyzes the impact of irrigation efficiency projects on return flows to major rivers in the southern-eastern Murray–Darling Basin in Australia. In particular, the projects of most interest are part of a basin-wide irrigation infrastructure modernization and water efficiency program (IE program) that uses savings from this program to reallocate about 700 Gl/y of water entitlements for the environment, while maintaining neutral to positive socio-economic outcomes for regional communities. Changes in irrigation prior to the program had led to a large reduction in surface water returns, meaning that any further major reduction of return flows would need to occur through groundwater return flows. Previous studies had ranked the risk from IE projects on surface flow from low to very high.
This paper develops one of the modeling approaches further and found that the IE program will lead to reduced return flows of up to 20% of the total proposed savings. The reduction in the change in seepage to the proposed savings ranged from 19% of savings from off-farm IE projects to 53% for on-farm projects. The main sensitivities were the connectivity between irrigation areas and major tributaries and the degree to which savings occurred by seepage. The latter was heavily influenced by the proportion of on-farm and off-farm projects, where on-farm projects led to larger proportionate reductions in seepage relative to savings. The lower reduction from off-farm projects were mostly due to water savings from land retirement, and or made possible due to better metering.
These results were compared with three other studies of IE improvements on return flows. Two of the studies resulted in much higher reduction in return flows as a proportion of changed seepage and run-off, while one was lower than or comparable to the detailed example in this paper. Stream salinity monitoring and groundwater modeling outputs support the lower values.
The water tables are regularly measured under most irrigation areas in the study areas. This monitoring shows the impacts of reduced seepage over the last fifteen years from lower rainfall, lower surface water allocations, water trade and irrigation efficiency projects. The management of return flows will mean managing all these drivers, rather than just IE. The reduced seepage has allowed the reduction of groundwater pumping to protect agricultural land from salinity and waterlogging, and this offsets some of the predicted reductions in return flows.
Salinity strategies over the last thirty years have used IE and engineering options to reduce saline inflows to meet the Basin salinity target for the Murray River by 2010. Further reductions in saline return flows should further reduce in-river salinity mitigation costs, which need to be weighed against the costs of reduced surface flow.
The approach used in this paper may be useful for other irrigation areas in the provision of water accounting in a risk framework.
Author Contributions
Conceptualization, A.C.H. and Q.J.W.; Formal Analysis, G.R.W.; Investigation, G.R.W. and Q.J.W.; Methodology, G.R.W., A.C.H. and Q.J.W.; Validation, G.R.W. and Q.J.W.; Writing—Original Draft, G.R.W., A.C.H. and Q.J.W.; Writing—Review and Editing, A.C.H., Q.J.W. and R.R. All authors have read and agreed to the published version of the manuscript.
Funding
This paper builds on work [
27], which was funded by the Murray–Darling Basin Authority. AH was funded through an ARC DECRA award (DE180100550).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data has either been referenced or reported in manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The funders of the original project collated some of the data and contextural information, but otherwise had no role in the design of the study; analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A. Water Balance Equations and Uncertainty
We consider the five water balances relating to the delivery channel, district drains, water imported to irrigated land, irrigated land itself and the groundwater. Each independent area is fed by diversions of water from the river into a delivery channel. The water balance of this channel is given by:
where DR is the diversion volume for irrigation that comes from the river; E is the evaporation from the channel water surface; SC is the seepage under the channel bed and lower channel banks, O is the outfall (unscheduled flow through outfall flow or flow escape structures); L is the leakage through structures or holes or cracks in channel banks; FWS is the water delivered to farms, which is supplemented by a volume M to allow for bias and deficiencies in off-farm metering.
The losses of water through bank leakage leads to other hydraulic fluxes, the balance of which is described by:
where ETL is the evapotranspiration in channel reserve areas, FL the water used by nearby farmers, SL the downward seepage, and DDL the component of leakage that finds its way to the district drains.
Not all the outfall from an irrigation area becomes surface return flow, as some is diverted for irrigation, while some is added from other inputs. The water balance of the district drainage channels is given by:
where SRF is the surface return flow; DDD is the fraction of district drainage diverted for irrigation; FRO is farm runoff to district drains; and DDG is the groundwater inflow to the district drain.
The total water imported to irrigated land is given by:
where FG is the volume of water pumped from groundwater diverted for farm water supply. The first three terms in RHS of Equation (A4) respectively represent the water supplied by the channel plus the supplement to account for metering and the water diverted from the district drainage channel. The water balance for irrigated land is given by:
where TF is the transpiration from irrigated land, EF is the evaporative loss from irrigated land, SF is the seepage rate under irrigated agriculture and MF is the supplementary water applied to account for bias and deficiencies in on-farm metering. M and MF are the same process, but M is for off-farm projects, while MF is for on-farm projects. The groundwater balance is given by:
where S is the groundwater storage, t time and GRF is the groundwater return flow.
Appendix A.1. Changed Surface Water Balance Due to off-Farm and on-Farm IE Projects
If an irrigation system undergoes a hydraulic stress, caused by IE projects, the water balance will change accordingly. The total recovered water from these measures (TWR) can be partitioned into that recovered by off-farm (WROFF) and on-farm (WRON) actions:
Some water gained by these measures is for the environment and urban water supplies. The entitlements for the water are transferred by legal agreement. The difference between TWR and the water recovered for the environment and urban supply is the intended recovery of water for irrigated agriculture (WRF), i.e.,
where WRE and WRU are the water recovered for environment and urban water supply. The recovery of water for the environment and urban water supplies leads to a reduction in diversion for irrigation given by the sum of WRE and WRU.
The next step is to define the terms WROFF and WRON in terms of changes in water balance. For example, the different off-farm water use projects can be partitioned into water balance components, as given by:
where the prefix R before a variable means a reduction in the value of that variable and a prefix S indicates a saving of water from that variable and SLR are the savings from irrigation land retirement. It is useful to consider the reduction in water balance components as a fraction of the recovered water. Hence, Equation (A8) becomes:
where the prefix P represents the proportion of the variable with respect to the recovered water.
Similarly, the on-farm measures can be partitioned into changes in the water balance components for the new volume of imported water:
TWR, RWOFF and WRON therefore reflect the magnitude of the hydraulic stress applied to the irrigation system as the total IE project or partitioned into off-farm or on-farm projects. The values assigned to these are described in the next section.
The response of the irrigation surface water system to these stresses is quantified by considering the change in water balance components in Equations (A1)–(A6) due to these stresses. We assume that, apart from groundwater returns the hydrological system returns quickly to equilibrium. We will also assume that changes in FG and DDG are zero; and discuss the implications of these assumptions later. The total change in surface and ground return flows is the sum of these components for off- and on- farm measures.
Appendix A.2. Off-Farm Projects
To assess reduction in water supply to farms, we need to allow for the water savings from land retirement. i.e.,
This is consistent with Equations (A1) and (A10b). The reduction in the total water imported to agricultural land is given by (using Equations (A4) and (A12):
We shall assume that the reduction in the leakage components can be approximated by:
where RL
j represent the components RDDL, RFL, RSL and ETL, and PR
j is a proportionality constant for that j component.
The reduction in the surface return flows due to off-farm actions is given by Equation (A3):
where RFROOFF is the reduction in the runoff from irrigated land from off-farm actions, and can be equated to the runoff that would have occurred using water that is no longer applied, i.e.,
where FRD is the fraction of water applied becoming farm runoff to district drains.
Equations (A12), (A14) and (A15) can be used in a spreadsheet to calculate the reduction in surface water flow from off-farm measures.
The reduction in groundwater return flow due to off-farm projects is given by:
where CF is the connectivity between seepage and return flows [
39]; RSFOFF is the reduction in seepage from irrigated land from off-farm projects, and can be equated to the seepage that would have occurred from the irrigation water that is no longer applied, i.e.,
FRG is the fraction of water applied becoming farm recharge to groundwater. The approximation of change in groundwater return flow using a connectivity factor has been previously discussed [
43] and provides estimates for CF for the major groundwater systems.
Equations (A12), (A16) and (A17) can be used in a spreadsheet to calculate the ground return flow from off-farm measures. The equations can be rearranged to be a linear combination of the water saving components and the transfer of entitlements to the environment and urban water supplies. The coefficients are functions of the four parameters FRD, FRG, CF and DDD. This linearity will be used in the uncertainty analysis below.
The linearity also implies that these equations could be rearranged by considering WROFF as a stressor and dividing the equations by WROFF to express all changes in fluxes as ratios of WROFF. This implies that the return flows are linear in WROFF, provided the proportion of flows remain the same.
Appendix A.3. On-Farm Projects
The farm water balance (Equation (A5)) for the currently applied water can be adapted using Equation (A10a) to give:
The left-hand side of Equation (A18) is the difference between the reduction in the water applied to irrigated land and the reduction in transpiration from irrigated agriculture. The right-hand side therefore provides the effective recovery of water for additional irrigated agriculture (ERWF). This is different from WRON due to the change in the recycled runoff.
Equation (A3) for the surface water balance can be adapted to give:
where RFROON is the reduction in runoff from irrigated land due to on-farm measures. This term can be divided into the reduction of runoff from current water minus the additional runoff from the extra recovered water:
Equations (A18)–(A20) can be used in a spreadsheet to calculate the reduction in surface return flow due to on-farm measures.
The reduction in ground return flow is given by:
where RSFON is the reduction in farm seepage from the on-farm measures. This can be divided into the reduction in seepage from the water currently applied minus the additional seepage from the extra irrigation water from recovered water, i.e.,
Equations (A18), (A21) and (A22) can be used in a spreadsheet to calculate the reduction in ground return flow.
As with the off-farm projects, the equations can be expressed as a linear combination of the various components of the water savings or as a ratio of the stressor WRON.
Uncertainty Analyses
Linearity: The Equations (A16), (A17), (A21) and (A22) can be rearranged so that changes in surface and ground returns for both on-farm and off-farm projects are linear in the water components of the water savings and the water recovered for the environment and urban water supplies. We assume that the water savings and water recovered will have little uncertainty as water recovered is through transfer of water entitlements. Within this section, we consider parametric errors due to (1) estimation of the water components of the savings and (2) errors in the parameters DDD, FRD, FRG and CF, which affects the linear coefficients. The prediction error of return flows is given by:
where RRF, A
j and Q
j are the estimated values for the change in surface or groundwater return flow, linear coefficients and water balance inputs for the jth component of the water savings and δ represents the difference from the true value. As shall be seen, the estimate of the return flows is often dominated by one term and therefore be expected to be sensitive to any errors in this term. Where this term is very dominant, Equation (A23) approaches:
where η = ΔQ
P/Q
P, and ε = ΔA
P/A
P and the subscript P denotes the value of j which dominates the estimation of RRF. More generally, where one term is dominant, we can use the approximation:
where the terms ε and η are now modified to reflect a more general relative error than just the dominant term. The test that is applied to determine whether one term is dominant is L1 > 0.7, where:
Table A1.
Glossary of symbols, definitions and equations in the
Appendix A, where first used.
Table A1.
Glossary of symbols, definitions and equations in the
Appendix A, where first used.
| DR | Mean annual diversion of water from river for irrigation | Gl | A1 |
| E | Mean annual evaporation from irrigation channel | Gl | A1 |
| SC | Mean annual seepage from irrigation channel | Gl | A1 |
| O | Mean annual outfall from irrigation channel | Gl | A1 |
| L | Leakage from irrigation channel | Gl | A1 |
| FWS | Water supplied for irrigated agriculture from irrigation channel | Gl | A1 |
| M | Supplementary delivery of water for irrigated agriculture to allow for metering errors | Gl | A1 |
| ETL | Mean annual volume of evapotranspiration from channel leakage | Gl | A2 |
| FL | Mean annual volume delivered to nearby irrigated agriculture from channel leakage | Gl | A2 |
| SL | Mean annual volume of seepage from channel leakage | Gl | A2 |
| DDL | Mean annual volume of leakage input to district drains | Gl | A2 |
| SRF | Mean annual return of irrigation water to rivers by surface flow | Gl | A3 |
| DDD | Fraction of district drainage water diverted for irrigation | 1 | A3 |
| FRO | Mean annual volume of runoff from farms | Gl | A3 |
| DDG | Mean annual groundwater input to drains | Gl | A3 |
| TFW | Mean annual volume of water imported to irrigation land | Gl | A4 |
| FG | Mean annual volume of pumped groundwater that is diverted for irrigated agriculture | Gl | A4 |
| TF | Mean annual transpiration from irrigated agriculture | Gl | A5 |
| EF | Mean annual evaporation from irrigated land | Gl | A5 |
| MF | Mean annual volume of supplementary water delivered within farm to allow for poor metering | Gl | A5 |
| SF | Mean annual volume of seepage below irrigated agriculture | Gl | A5 |
| S | Groundwater storage | Gl | A6 |
| GRF | Mean annual return of irrigation water to river by groundwater | Gl | A6 |
| TWR | Mean annual volume of total water recovered from water measures | Gl | A7a |
| WROFF | Mean annual volume of water recovered from off-farm measures | Gl | A7a |
| WRON | Mean annual volume recovered from on-farm measure | Gl | A7a |
| WRF | Mean annual volume of the proposed water savings recovered for farms | Hl | A7b |
| WRE | Mean annual volume of water recovered for the environment | Gl | A7b |
| WRU | Mean annual volume of water recovered for urban water supply | Gl | A7b |
| Prefix R | Reduction in the variable | | |
| Prefix S | Savings from the variable | | |
| SLR | Savings from land retirement | Gl | A8 |
| Prefix P | The ratio of component of variable to total variable | 1 | A9 |
| RSRFOFF | The reduction in surface return flow due to off-farm measures | Gl | A14 |
| RFROOFF | The reduction in runoff from irrigated land due to on-farm measures | Gl | A15 |
| | RGRFOFF, RSFOFF, RSRFON, RFROON, RGRFON, RSFON defined in similar fashion to that above | Gl | A16–17, A19–22 |
| FRD | Fraction of water applied becoming farm runoff to district drains | 1 | A15 |
| CF | Fraction of seepage to groundwater that returns to rivers within 50 years | Gl | A16 |
| FRG | Fraction of water applied becoming farm recharge to groundwater | 1 | A17 |
| ERWF | Effective recovery of water for irrigated agriculture from on-farm measures | Gl | A18 |
| Prefix δ | Uncertainty in variable | | A23 |
| Aj | Coefficients (e.g., DDD, CF, FRD, FRG) | 1 | A23 |
| Qj | Mean annual Fluxes (e.g., ET, S, L…) | Gl | A23 |
References
- Garrick, D.; De Stefano, L.; Yu, W.; Jorgensen, I.; O’Donnell, E.; Turley, L.; Aguilar-Barajas, I.; Dai, X.; Leão, R.D.S.; Punjabi, B.; et al. Rural water for thirsty cities: A systematic review of water reallocation from rural to urban regions. Environ. Res. Lett. 2019, 14, 043003. [Google Scholar] [CrossRef]
- Garrick, D.E.; Hall, J.W.; Dobson, A.; Damania, R.; Grafton, R.Q.; Hope, R.; Hepburn, C.; Bark, R.; Boltz, F.; De Stefano, L.; et al. Valuing water for sustainable development. Science 2017, 358, 1003–1005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Richter, B.D.; Abell, D.; Bacha, E.; Brauman, K.; Calos, S.; Cohn, A.; Disla, C.; O’Brien, S.F.; Hodges, D.; Kaiser, S.; et al. Tapped out: How can cities secure their water future? Hydrol. Res. 2013, 15, 335–363. [Google Scholar] [CrossRef] [Green Version]
- O’Donnell, E.L.; Garrick, D.E.; Horne, A.C. Reallocation through irrigation modernization: The ‘once-in-a-hundred-year’ opportunity of the North-South Pipeline, Australia. Water Secur. 2019, 6, 100028. [Google Scholar] [CrossRef]
- Lankford, B. Fictions, fractions, factorials and fractures; on the framing of irrigation efficiency. Agric. Water Manag. 2012, 108, 27–38. [Google Scholar] [CrossRef]
- Grafton, R.Q.; Williams, J.; Perry, C.J.; Molle, F.; Ringler, C.; Steduto, P.; Udall, B.; Wheeler, S.A.; Wang, Y.; Garrick, D.; et al. The paradox of irrigation efficiency. Science 2018, 361, 748–750. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perry, C.J. Does Improved Irrigation Technology Save Water? A Review of the Evidence. Discussion Paper on Irrigation and Sustainable Water Resources Management in the Near East and North Africa. Food and Agriculture Organisation of the United Nations,2017. Available online: http://www.fao.org/3/i7090en/I7090EN.pdf (accessed on 3 May 2021).
- Molden, D.; Oweis, T.; Steduto, P.; Bindbaraban, P.; Hanjra, M.A.; Kijne, J. Improving agricultural water productivity: Between optimism and caution. Agric. Water Manag. 2010, 97, 528–535. [Google Scholar] [CrossRef]
- Perry, C. Efficient irrigation; inefficient communication; flawed recommendations. Irrig. Drain. 2007, 56, 367–378. [Google Scholar] [CrossRef]
- Linstead, C. The Contribution of Improvements in Irrigation Efficiency to Environmental Flows. Front. Environ. Sci. 2018, 6, 6. [Google Scholar] [CrossRef]
- A Scott, C.; Vicuna, S.; Gutiérrez, I.B.; Meza, F.J.; Ortega, C.V. Irrigation efficiency and water-policy implications for river basin resilience. Hydrol. Earth Syst. Sci. 2014, 18, 1339–1348. [Google Scholar] [CrossRef] [Green Version]
- Lankford, B.; Closas, A.; Dalton, J.; Gunn, E.L.; Hess, T.; Knox, J.W.; van der Kooij, S.; Lautze, J.; Molden, D.; Orr, S.; et al. A scale-based framework to understand the promises, pitfalls and paradoxes of irrigation efficiency to meet major water challenges. Glob. Environ. Chang. 2020, 65, 102182. [Google Scholar] [CrossRef]
- Perry, C. Accounting for water use: Terminology and implications for saving water and increasing production. Agric. Water Manag. 2011, 98, 1840–1846. [Google Scholar] [CrossRef]
- Grafton, R.Q.; Williams, J.G. Paddling blind: Why we urgently need a water audit. The Conversation, 26 August 2019. Available online: https://theconversation.com/paddling-blind-why-we-urgently-need-a-water-audit-122118 (accessed on 3 May 2021).
- SKM. Murray Darling Basin Risk Assessment—Murray Region. Technical Assessment. Report to MDBC, unpublished, 2009.
- NSW Office of Water. Assessment of risk to NSW Murray-Darling Basin shared water resources—2008, NSW Office of Water, Sydney, 2010. Available online: http://www.water.nsw.gov.au/__data/assets/pdf_file/0007/548971/risk_assessment_mdb_shared_water_resources.pdf (accessed on 3 May 2021).
- Wang, Q.J.; Walker, G.; Horne, A. Potential Impacts of Groundwater Sustainable Diversion Limits and Irrigation Efficiency Projects on River Flow Volume under the Murray-Darling Basin Plan: An Independent Review. Report written for the MDBA, University of Melbourne, 2018, 73p. Available online: https://www.mdba.gov.au/sites/default/files/pubs/Impacts-groundwater-and-efficiency-programs-on-flows-October-2018.pdf (accessed on 3 May 2021).
- Williams, J.; Grafton, R.Q. Missing in action: Possible effects of water recovery on stream and river flows in the Murray–Darling Basin, Australia. Australas. J. Water Resour. 2019, 23, 78–87. [Google Scholar] [CrossRef] [Green Version]
- Hart, B.T.; Davidson, D. Case Study 1—The Murray-Darling Basin Plan, Chapter 13. In Decision-Making in Water Resource Policy and Management: An Australian Perspective; Hart, B., Doolan, J., Eds.; Academic Press; Elsevier: London, UK, 2017. [Google Scholar] [CrossRef]
- Hart, B.; Bond, N.; Byron, N.; Pollino, C.; Stewardson, M. Chapter 1, Introduction to the Murray-Darling Basin System, Australia. In Murray-Darling Basin: Its Future Management from Catchment to the Coast; Hart, B.T., Bond, N., Byron, N., Pollino, C., Stewardson, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Stewardson, M.J.; Walker, G.; Coleman, M.; Hart, B. Hydrology of the Murray-Darling Basin. Chapter 3. In Murray-Darling River System: Its Future Management from Catchment to the Coast; Hart, B., Bond, N., Byron, N., Pollino, C., Stewardson, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Rendell, R.; Toulmin, M.; Fitzpatrick, C.; Lyle, C.; Cummins, T.; Harriss, D.; Smith, M.; Holland, G.; Willis, A.; Lacy, J.; et al. Water use efficiency in irrigated agriculture: An Australian Perspective. Australian Water Partnership, Canberra, 2020. Available online: https://waterpartnership.org.au/wp-content/uploads/2020/05/Water-Use-Efficiency-in-Irrigated-Agriculture-web.pdf (accessed on 4 May 2021).
- CSIRO. Water availability in the Murray-Darling Basin. Summary of a report to the Australian Government from the CSIRO Murray-Darling Basin Sustainable Yields Project. CSIRO, Australia, 2008, 12p. Available online: https://publications.csiro.au/publications/#publication/PIprocite:e9be58a8-b6af-47a7-b6e6-a6fbcf281cd9 (accessed on 4 May 2021).
- Walker, G.; Barnett, S.; Richardson, S. Developing a coordinated groundwater management plan for the interstate Murray-Darling Basin. Chapter 8. In Sustainable Groundwater Management: A Comparative Analysis of French and Australian Policies and Implications to Other Countries; Global Issues in Water Policy 24; Jean-Daniel Rinaudo, J.-D., Holley, C., Barnett, S., Montginoul, M., Eds.; Springer Nature: Cham, Switzerland, 2020; pp. 143–161. [Google Scholar] [CrossRef]
- Braaten, R.; Gates, G. Groundwater-surface water interaction in inland New South Wales: A scoping study. Water Sci. Technol. 2003, 48, 215–224. [Google Scholar] [CrossRef] [PubMed]
- Parsons, S.; Evans, R.; Hoban, M. Surface–groundwater connectivity assessment. A report to the Australian Government from the CSIRO Murray-Darling Basin Sustainable Yields Project. CSIRO, Australia, 2008. Available online: https://publications.csiro.au/rpr/download?pid=procite:6df0b2aa-a7af-44ff-8a38-eacde04b9e69&dsid=DS1 (accessed on 4 May 2021).
- Hart, B.; Walker, G.; Katupitiya, A.; Doolan, J. Salinity Management in the Murray–Darling Basin, Australia. Water 2020, 12, 1829. [Google Scholar] [CrossRef]
- Tisdell, J.; Ward, J.; Grudzinski, A. the development of water reform in Australia. Cooperative research Centre or Catchment Hydrology, Technical Report 02/5, 2002. Available online: https://ewater.org.au/archive/crcch/archive/pubs/pdfs/technical200205.pdf (accessed on 4 May 2021).
- Earth Tech Engineering. Preliminary Review of Selected Factors That May Change Future Flow Patterns in the River Murray System, unpublished report to the Murray-Darling Basin Commission, 2003. Available online: https://www.mdba.gov.au/sites/default/files/archived/mdbc-governance-reports/2168-review_of_selected_factors_may_change_flow_in_river_murray.pdf (accessed on 4 May 2021).
- Van Dijk, A.; Evans, W.R.; Hairsine, P.; Khan, S.; Nathan, R.; Paydar, Z.; Viney, N.; Zhang, L. Risks to the Shared Water Resources of the Murray-Darling Basin. MDBC Publication No. 22/06, Murray-Darling Basin Commission, Canberra, Australia, 2003. Available online: https://www.mdba.gov.au/sites/default/files/archived/mdbc-RTSWR-reports/227_CSIRO_Part_2_shared_water_resources.pdf (accessed on 4 May 2021).
- URS. Final Report: Murray-Darling Basin return flows investigation. Canberra: Report to the Murray-Darling Basin Authority. Unpublished work, 2010.
- MDBA. Guide to the Murray-Darling Basin Plan; Murray-Darling Basin Authority: Canberra, Australia, 2010. Available online: https://www.mdba.gov.au/publications/archived-information/basin-plan-archives/guide-proposed-basin-plan (accessed on 3 May 2021).
- Australian Government. Basin Plan. Murray-Darling Basin Authority. 2012. Available online: https://www.mdba.gov.au/basin-plan/plan-murray-darling-basin (accessed on 3 May 2021).
- Horne, A.C.; O’Donnell, E.L.; Tharme, R.E. Chapter 17—Mechanisms to Allocate Environmental Water. In Water for the Environment; Academic Press: London, UK, 2017. [Google Scholar]
- DAWE. Murray-Darling Communities Investment Package. Department of Agriculture, Water and the Environment, Australian Government, Canberra, ACT. 2020. Available online: https://www.agriculture.gov.au/water/mdb/water-investment-package (accessed on 3 May 2021).
- MDBA. Transition Period Water Take Report 2018–19, Murray‒Darling Basin Authority Canberra. 2020. CC BY 4.0. Available online: https://www.mdba.gov.au/sites/default/files/pubs/transition-period-water-take-report-2018-19-full-report_0.pdf (accessed on 3 May 2021).
- Grafton, R.Q.; Williams, J. Myths about Water Savings and Subsidies for Capital-Intensive Irrigation Technologies: Policy Implications for Australia.: Submission made on 21 March 2017 to the House of Representatives Standing Committee on Agriculture and Water Resources Inquiry into Water Use Efficiency in Australian Agriculture. Available online: https://www.pc.gov.au/__data/assets/pdf_file/0004/222538/subdr093-water-reform-attachment2.pdf (accessed on 3 May 2021).
- Grafton, R.Q.; Williams, J. Failures to Deliver on the Key Objectives of the Water Act 2007. Submission to the South Australian Murray-Darling Basin Royal Commission. 2018. Available online: https://www.environment.sa.gov.au/files/sharedassets/public/river_murray/royal-commission/submissions/profs_quentin-grafton-john-williams-act-mdb-rc-gen.pdf (accessed on 3 May 2021).
- MDBRC. Murray-Darling Basin Royal Commission Report. Murray-Darling Basin Royal Commission, Government of South Australia. 2019. Available online: https://apo.org.au/sites/default/files/resource-files/2019-01/apo-nid217606.pdf (accessed on 3 May 2021).
- Wentworth Group of Concerned Scientists. Review of water reform in the Murray-Darling Basin. Canberra, Australia. 2017. Available online: https://wentworthgroup.org/wp-content/uploads/2017/12/Wentworth-Group-Review-of-water-reform-in-MDB-Nov-2017.pdf (accessed on 3 May 2021).
- Wentworth Group of Concerned Scientists. Assessment of river flows in the Murray-Darling Basin: Observed versus expected flows under the Basin Plan 2012-2019, Sydney. 2020. Available online: https://wentworthgroup.org/wp-content/uploads/2020/08/MDB-flows.pdf (accessed on 3 May 2021).
- ATSE. ATSE submission to the Standing Committee on Agriculture and Water Resources Inquiry into Water Use Efficiency in Australian Agriculture. 2017. Available online: https://www.atse.org.au/wp-content/uploads/2019/02/water-use-efficiency-australian-agriculture.pdf (accessed on 3 May 2021).
- Walker, G.; Wang, Q.J.; Horne, A.C.; Evans, R.; Richardson, S. Estimating groundwater-river connectivity factor for quantifying changes in irrigation return flows in the Murray–Darling Basin. Australas. J. Water Resour. 2020, 24, 121–138. [Google Scholar] [CrossRef]
- DSE. Water Savings Protocol Technical Manual for the Quantification of Water Savings in Irrigation Water Distribution Systems. 2012. Available online: https://www.water.vic.gov.au/__data/assets/pdf_file/0017/413063/Audit-of-Irrigation-Modernisation-Water-Recovery-2017-18.pdf (accessed on 4 May 2021).
- RMCG. Background Report to Support the Farm Works Guidelines. Goulburn Murray Integrated Farm Modernisation Program. Unpublished Report, 2009.
- TNCL. Trangie Nevertire Co-operative Ltd. (TNCL) Final Project Report under Round One of the Private Irrigation Infrastructure Operators Program in NSW, 2016. Available online: https://www.agriculture.gov.au/sites/default/files/sitecollectiondocuments/water/trangie-nevertire-final-project-report.pdf (accessed on 4 May 2021).
- Cardno. Audit Report: Audit of Irrigation Modernisation Water Recovery 2016/17 Irrigation Season. 2017. Available online: https://www.water.vic.gov.au/__data/assets/pdf_file/0017/413063/Audit-of-Irrigation-Modernisation-Water-Recovery-2017-18.pdf (accessed on 4 May 2021).
- NIBM. PIIOP Modernisation Project—Final Report prepared for Narromine Irrigation Board of Management. 2017. Available online: https://www.agriculture.gov.au/sites/default/files/sitecollectiondocuments/water/narromine-project-report.pdf (accessed on 4 May 2021).
- CSIRO. Groundwater Modelling Report—Southern Riverine Plain. CSIRO: Water for a Healthy Country National Research Flagship. Australia: CSIRO. 2010. Available online: https://publications.csiro.au/publications/publication/PIcsiro:EP114053 (accessed on 4 May 2021).
- CSIRO. Groundwater Modelling Report—Lower Murrumbidgee. CSIRO: Water for a Healthy Country National Research Flagship. Australia: CSIRO. 2010. Available online: https://publications.csiro.au/publications/publication/PIcsiro:EP114046 (accessed on 4 May 2021).
- RPS. Assessing the salinity impacts on changes to irrigation on the Riverine Plains—Phase 3 and 4 Report. Report for MDBA (2013), 69pp, RPS. Echucha, Victoria. Available online: https://www.mdba.gov.au/sites/default/files/pubs/ISAF%20-%20Phase%203_4_reports_Final.pdf (accessed on 4 May 2021).
- Goulburn-Murray Water. Shepparton Irrigation Area Water Table Contours August 2020. Available online: https://www.gbcma.vic.gov.au/downloads/WatertableMaps/Watertable_Contours_Flyer_Nov20.pdf (accessed on 4 May 2021).
- Walker, G.R.; Wang, Q.J.; Horne, A.; Evans, R.; Richardson, S. Potential cumulative impacts on river flow volume from increased groundwater extraction under the Murray-Darling Basin Plan. Australas. J. Water Resour. 2020, 24, 105–120. [Google Scholar] [CrossRef]
- Sustainable Soils Management. Tenandra Scheme Modernisation Project Final Report, 2017. Available online: https://www.agriculture.gov.au/sites/default/files/sitecollectiondocuments/water/tenandra-final-project-report.pdf#:~:text=Final%20Report%20%E2%80%93%20Tenandra%20Scheme%20Modernisation%20Project%2011,ML%20of%20water%20entitlements%20to%20the%20Australian%20Government (accessed on 4 May 2021).
- Hughes, N.; Donoghoe, M.; Whittle, L. Farm Level Effects of On-Farm Irrigation Infrastructure Programs in the Southern Murray–Darling Basin. Aust. Econ. Rev. 2020, 53, 494–516. [Google Scholar] [CrossRef]
- Yan, W.; Li, C.; Woods, J. Loxton–Bookpurnong Numerical Groundwater Model 2011 Volume 1: Report and Figures, DFW Technical Report 2011/22, Government of South Australia, through Department for Water, Adelaide. Available online: https://www.waterconnect.sa.gov.au/Content/Publications/DEW/DFW_TR_2011_22_Vol_1.pdf (accessed on 4 May 2021).
- Saft, M.; Peel, M.C.; Western, A.W.; Zhang, L. Predicting shifts in rainfall-runoff partitioning during multiyear drought: Roles of dry period and catchment characteristics. Water Resour. Res. 2016, 52, 9290–9305. [Google Scholar] [CrossRef]
- Goulburn-Murray Water. Shepparton Irrigation Region Groundwater Management Area Local Management Plan June 2015. Available online: https://www.g-mwater.com.au/downloads/gmw/Groundwater/Shepparton_Irrigation_Region_WSPA/29022016_-_3786511-v25-SHEPPARTON_IRRIGATION_REGION_GROUNDWATER_LOCAL_MANAGEMENT_PLAN.pdf (accessed on 4 May 2021).
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).