A Multi-Objective Decision Making System (MDMS) for a Small Agricultural Watershed Based on Meta-Heuristic Optimization Coupling Simulation
Abstract
:1. Introduction
2. Materials and Methods
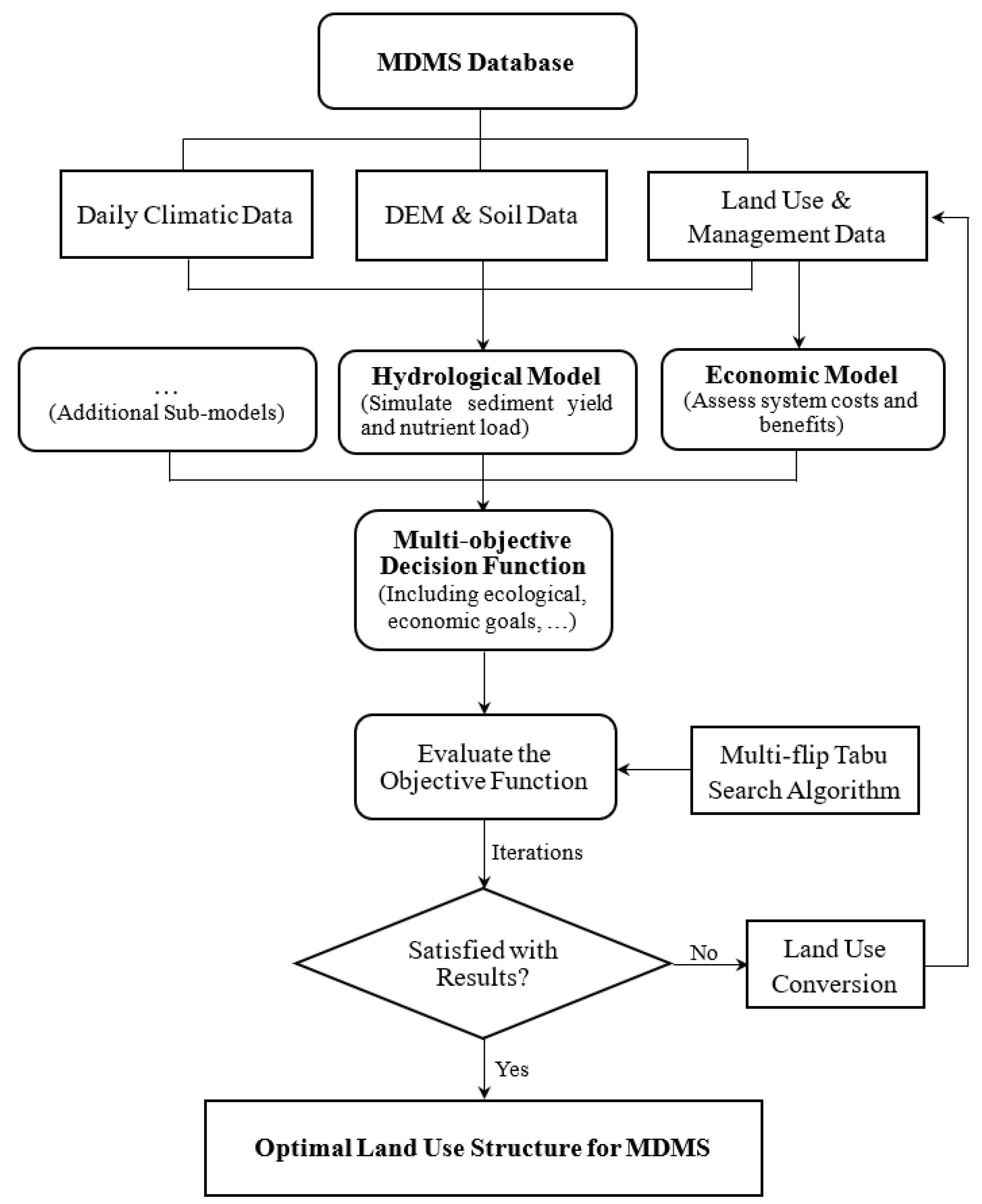
2.1. Description of MDMS
2.2. Study Area and Data
2.3. Methods
2.3.1. Coupling Simulation Models
- (1)
- AnnAGNPS model
- (2)
- EBE model
2.3.2. Multi-Objective Decision Function
- (1)
- Environmental impact assessment function
- (2)
- Economic benefit evaluation function
- (3)
- Total objective function
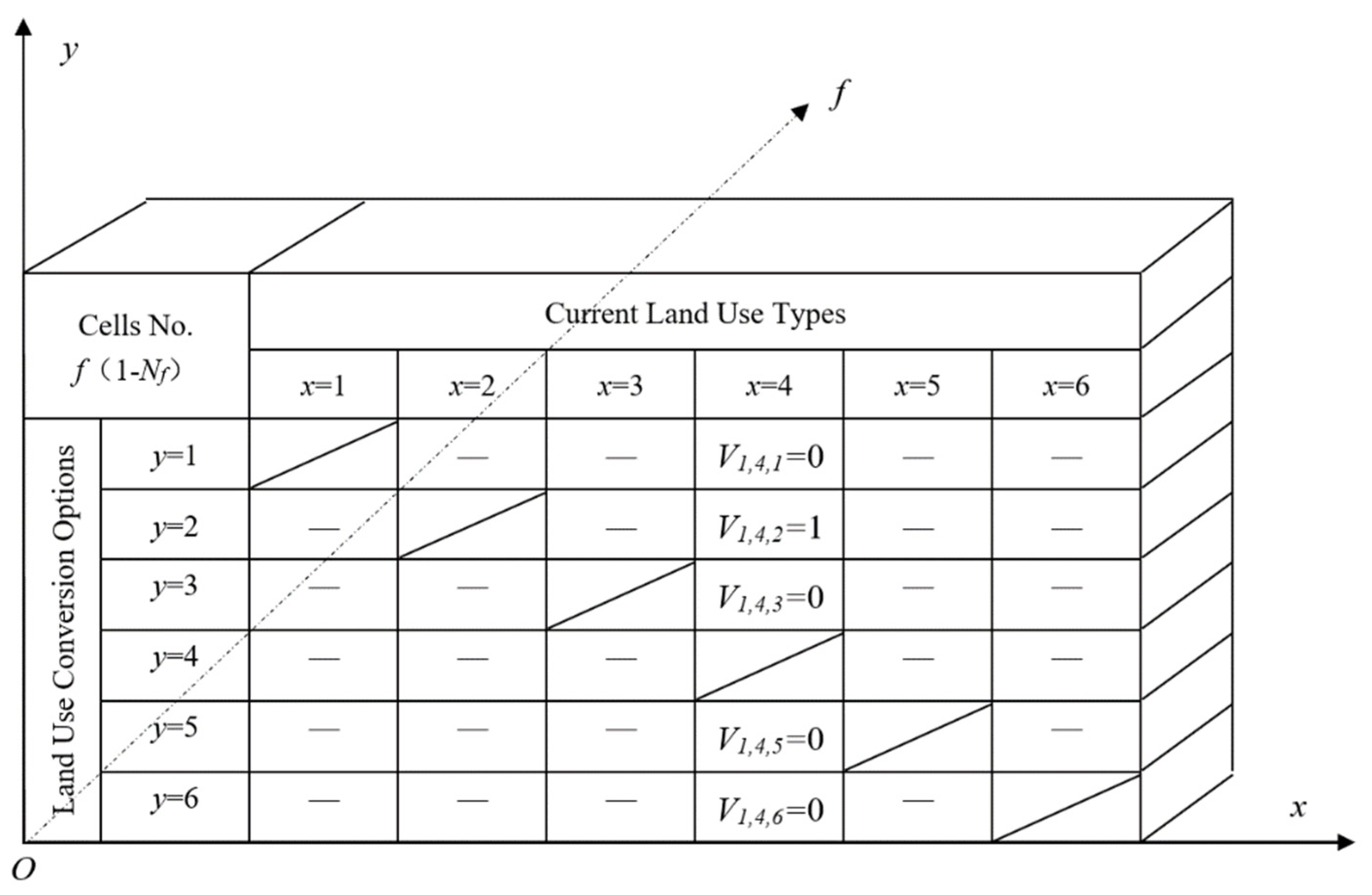
2.3.3. Improved Meta-Heuristic Search Algorithm
- (1)
- Selection of the initial solution: current land use structure. This step is the initialization running of integrated model system. Set all land change variables Vf,x,y to 0, initialize the tabu list, and run the integrated model to obtain the objective function value for the base line scenario;
- (2)
- Way to explore the solution domain: randomly start to explore the solution domain with multiple structures, diversified movement modes such as “select move”(Equation (7)), “cancel move” (Equation (8)) and “switch move” (Equation (9)) were adopted.
- (3)
- Length of the candidate list: 30;
- (4)
- Number of iterations: 600;
- (5)
- Optimal solution of the candidate set and the global optimal solution, etc.
3. Results
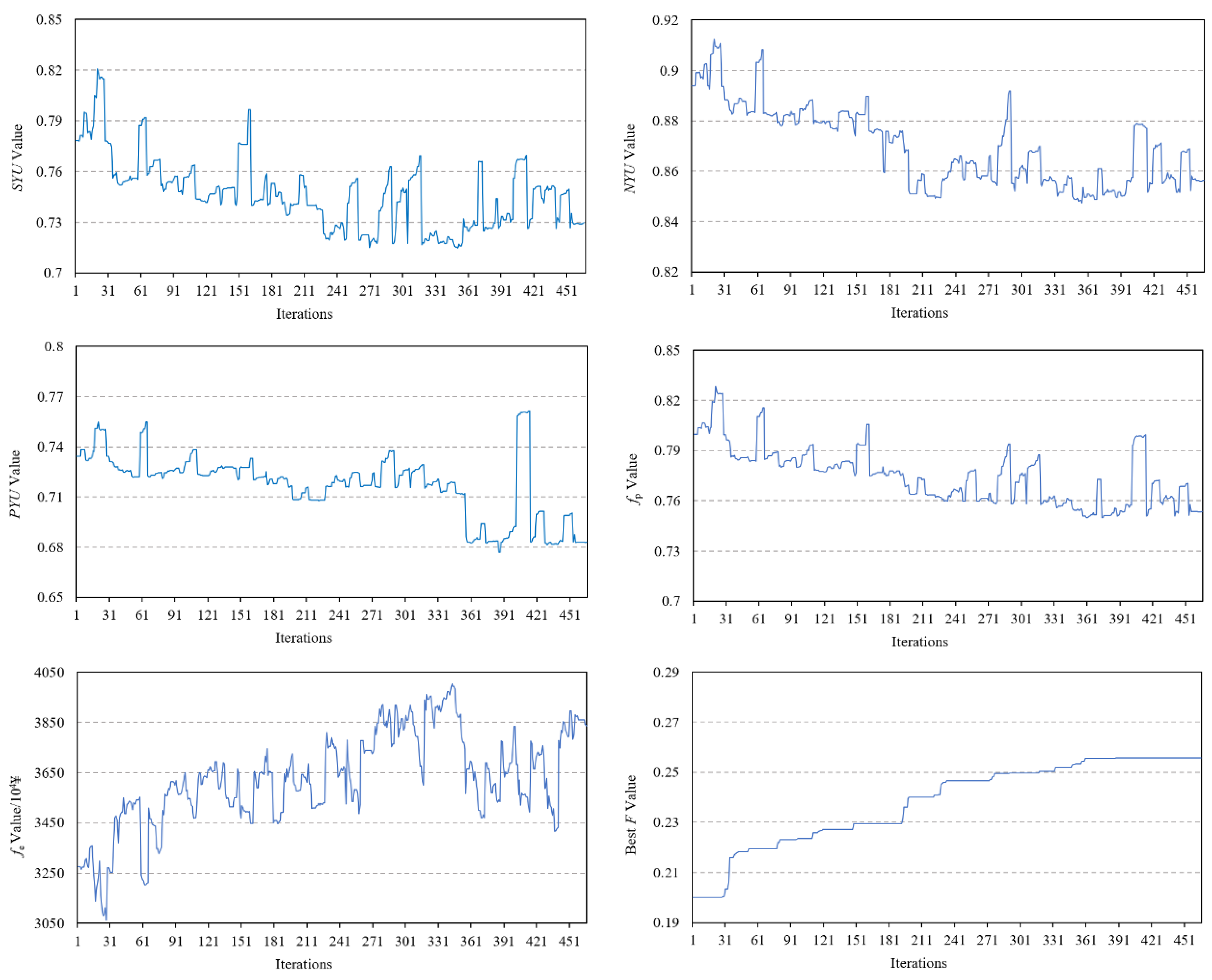
3.1. Objective Function Value and Iterations
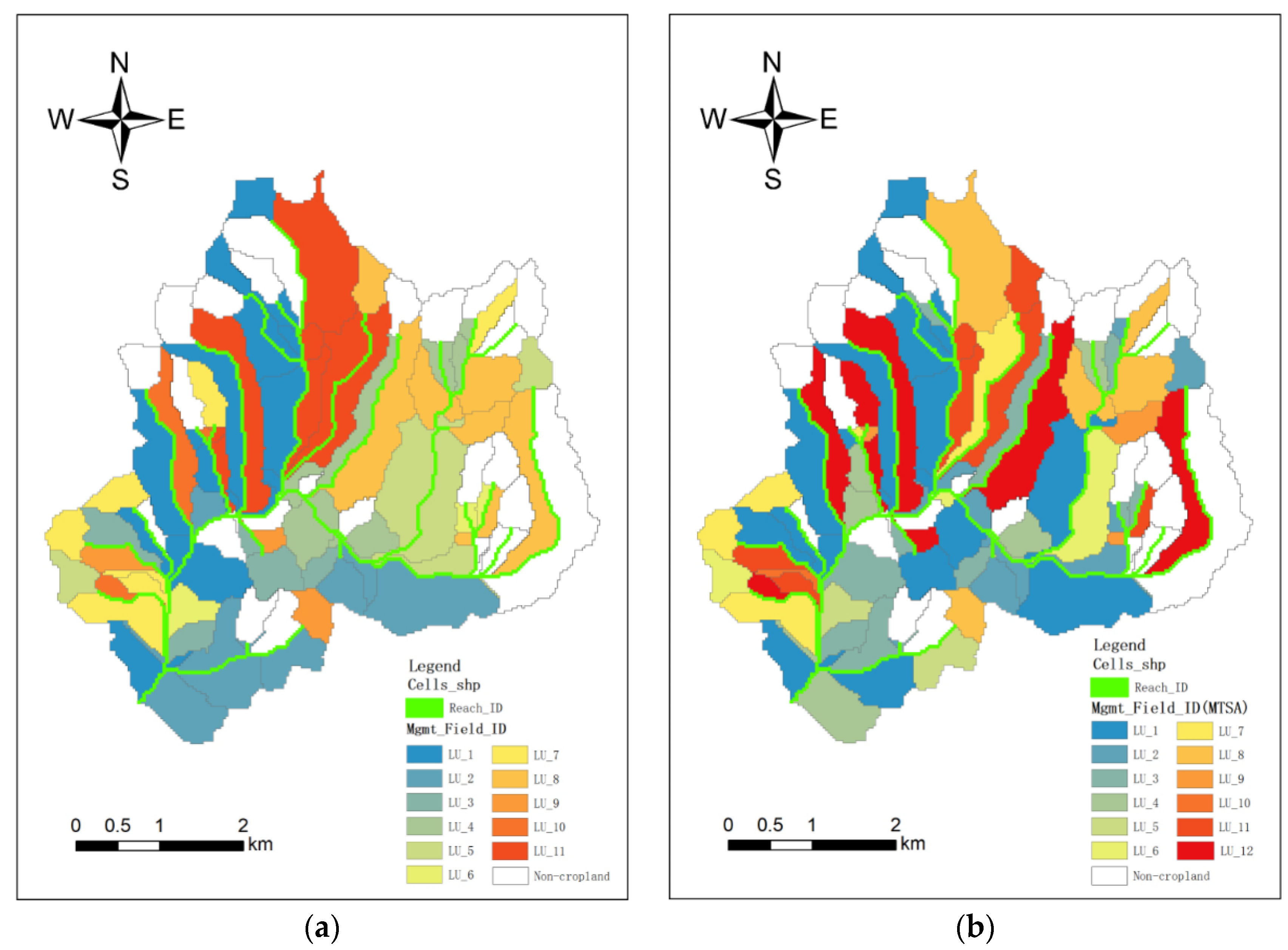
3.2. Variation of Land Use Area after Optimization
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Postel, S.L.; Daily, G.C.; Ehrlich, P.R. Human Appropriation of Renewable Fresh Water. Science 1996, 271, 785–788. [Google Scholar] [CrossRef]
- Dorf, R.C. Chapter 1—Sustainability, Economics, and the Environment. In Technology, Humans, and Society; Academic Press: San Diego, CA, USA, 2001; pp. 1–37. [Google Scholar] [CrossRef]
- Gleick, P.H. Global Freshwater Resources: Soft-Path Solutions for the 21st Century. Science 2003, 302, 1524–1528. [Google Scholar] [CrossRef] [Green Version]
- Foley, J.A.; DeFries, R.; Asner, G.P.; Barford, C.; Bonan, G.; Carpenter, S.R.; Chapin, F.S.; Coe, M.T.; Daily, G.C.; Gibbs, H.K.; et al. Global Consequences of Land Use. Science 2005, 309, 570–574. [Google Scholar] [CrossRef] [Green Version]
- Vörösmarty, C.J.; McIntyre, P.B.; Gessner, M.O.; Dudgeon, D.; Prusevich, A.; Green, P.; Glidden, S.; Bunn, S.E.; Sullivan, C.A.; Liermann, C.R.; et al. Global threats to human water security and river biodiversity. Nature 2010, 467, 555–561. [Google Scholar] [CrossRef]
- Hazell, P.B.R.; Wood, S. Drivers of Change in Global Agriculture. Philos. Trans. R. Soc. B Biol. Sci. 2007, 363, 495–515. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karki, R.; Tagert, M.L.M.; Paz, J.O.; Bingner, R.L. Application of AnnAGNPS to model an agricultural watershed in East-Central Mississippi for the evaluation of an on-farm water storage (OFWS) system. Agric. Water Manag. 2017, 192, 103–114. [Google Scholar] [CrossRef]
- Li, Y.; Tang, C.; Huang, Z.; Hussain, Z.; Are, K.S.; Abegunrin, T.P.; Qin, Z.; Guo, H. Increase in farm size significantly accelerated stream channel erosion and associated nutrient losses from an intensive agricultural watershed. Agric. Ecosyst. Environ. 2020, 295, 106900. [Google Scholar] [CrossRef]
- Thornton, J.A.; Rast, W.; Holland, M.M.; Jolankai, G.; Ryding, S.-O. Assessment and Control of Nonpoint Source Pollution of Aquatic Ecosystems: A Practical Approach, 1st ed.; Informa Healthcare: New York, NY, USA, 1999; pp. 296–299. [Google Scholar]
- A Martínez-Casasnovas, J.; Sánchez-Bosch, I. Impact assessment of changes in land use/conservation practices on soil erosion in the Penedès–Anoia vineyard region (NE Spain). Soil Tillage Res. 2000, 57, 101–106. [Google Scholar] [CrossRef]
- Ouyang, W.; Jiao, W.; Li, X.; Giubilato, E.; Critto, A. Long-term agricultural non-point source pollution loading dynamics and correlation with outlet sediment geochemistry. J. Hydrol. 2016, 540, 379–385. [Google Scholar] [CrossRef]
- Alilou, H.; Rahmati, O.; Singh, V.P.; Choubin, B.; Pradhan, B.; Keesstra, S.; Ghiasi, S.S.; Sadeghi, S.H. Evaluation of watershed health using Fuzzy-ANP approach considering geo-environmental and topo-hydrological criteria. J. Environ. Manag. 2019, 232, 22–36. [Google Scholar] [CrossRef] [PubMed]
- Karan, S.K.; Ghosh, S.; Samadder, S.R. Identification of spatially distributed hotspots for soil loss and erosion potential in mining areas of Upper Damodar Basin—India. Catena 2019, 182, 104144. [Google Scholar] [CrossRef]
- Baginska, B.; Milne-Home, W.; Cornish, P. Modelling nutrient transport in Currency Creek, NSW with AnnAGNPS and PEST. Environ. Model. Softw. 2003, 18, 801–808. [Google Scholar] [CrossRef]
- Anctil, F.; Filion, M.; Tournebize, J. A neural network experiment on the simulation of daily nitrate-nitrogen and suspended sediment fluxes from a small agricultural catchment. Ecol. Model. 2009, 220, 879–887. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Mehaffey, M.H.; Lopez, R.D.; Bingner, R.L.; Bruins, R.; Erickson, C.; Jackson, M.A. AnnAGNPS Model Application for Nitrogen Loading Assessment for the Future Midwest Landscape Study. Water 2011, 3, 196–216. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Chen, Z.; Wu, Y.; Zhu, Y.; Li, P. Advances on Agricultural Non-point Source Pollution and the Control in Regions around Hungtse Lake. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2016, 40, 1–8. (In Chinese) [Google Scholar]
- Gudino-Elizondo, N.; Biggs, T.W.; Bingner, R.L.; Langendoen, E.J.; Kretzschmar, T.; Taguas, E.V.; Taniguchi-Quan, K.T.; Liden, D.; Yuan, Y. Modelling Runoff and Sediment Loads in a Developing Coastal Watershed of the US-Mexico Border. Water 2019, 11, 1024. [Google Scholar] [CrossRef] [Green Version]
- Pulighe, G.; Bonati, G.; Colangeli, M.; Traverso, L.; Lupia, F.; Altobelli, F.; Marta, A.D.; Napoli, M. Predicting Streamflow and Nutrient Loadings in a Semi-Arid Mediterranean Watershed with Ephemeral Streams Using the SWAT Model. Agronomy 2019, 10, 2. [Google Scholar] [CrossRef] [Green Version]
- Hua, W.; Huaiyu, Y.; Fengnian, Z.; Bao, L.; Wei, Z.; Yeye, Y. Dynamics of nutrient export from the Yangtze River to the East China sea. Estuarine Coast. Shelf Sci. 2019, 229, 106415. [Google Scholar] [CrossRef]
- Yan, R.; Li, L.; Gao, J. Framework for quantifying rural NPS pollution of a humid lowland catchment in Taihu Basin, Eastern China. Sci. Total. Environ. 2019, 688, 983–993. [Google Scholar] [CrossRef]
- Jin, S.; Niu, K.; Han, D. The Path of Agricultural Green Development and Its Orientation in the 14th Five-Year Plan Period. Reform 2020, 2, 30–39. (In Chinese) [Google Scholar]
- Ministry of Water Resources. China River Sediment Bulletin 2018. Available online: http://www.mwr.gov.cn/sj/tjgb/zghlnsgb/201906/t20190618-1342326.html (accessed on 25 June 2020).
- Changjiang Water Resources Commission. Notice on Soil and Water Conservation in the Yangtze River Basin in 2018. Available online: http://www.cjw.gov.cn/zwzc/bmgb/2018gb/ (accessed on 26 June 2020).
- Yang, G.; Yu, X.; Li, H.; Zhu, J. The Course, Experience and Prospect of Integrated Watersheds Management. J. Lake Sci. 2004, 16, 1–10. (In Chinese) [Google Scholar]
- Yang, G. Water Issues in the Yangtze River and Its formation Causes and Controlling Strategies. Resour. Environ. Yangtze Basin 2012, 21, 821–830. (In Chinese) [Google Scholar]
- Yang, G.; Yu, X.; Li, H.; Gao, J. Introduction to Integrated Watershed Management; Science Press: Beijing, China, 2013. [Google Scholar]
- Chen, Y.; Wang, Y.; Li, L.; Yu, X. Research on Integrated Management Strategy of Chinese River Basin; Science Press: Beijing, China, 2016. [Google Scholar]
- Yin, W.; Hu, D.; Fan, P. Analysis and Countermeasure of Existing Problems in River Basin Water Environmental Management in China. Pollut. Control Technol. 2017, 30, 80–83. (In Chinese) [Google Scholar]
- Liu, J.; Dietz, T.; Carpenter, S.R.; Alberti, M.; Folke, C.; Moran, E.; Pell, A.N.; Deadman, P.; Kratz, T.; Lubchenco, J.; et al. Complexity of Coupled Human and Natural Systems. Science 2007, 317, 1513–1516. [Google Scholar] [CrossRef] [Green Version]
- Palmer, M.A. Beyond infrastructure. Nat. Cell Biol. 2010, 467, 534–535. [Google Scholar] [CrossRef]
- Cheng, G.; Li, X. Integrated research methods in watershed science. Sci. China Earth Sci. 2015, 58, 1159–1168. [Google Scholar] [CrossRef]
- Zou, R.; Guo, H.; Chen, B. A Multiobjective Approach for Integrated Environmental Economic Planning Under Uncertainty. Civ. Eng. Environ. Syst. 2000, 17, 267–291. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, H.; Chen, B.; Zhang, B. An Inexact Multi-objective Economic-environmental Planning Model for Hemoluo Region, Xinjiang. J. Basic Sci. Eng. 2001, 9, 33–42. (In Chinese) [Google Scholar]
- Li, X.; Cheng, G.; Lin, H.; Cai, X.; Fang, M.; Ge, Y.; Hu, X.; Chen, M.; Li, W. Watershed System Model: The Essentials to Model Complex Human-Nature System at the River Basin Scale. J. Geophys. Res. Atmos. 2018, 123, 3019–3034. [Google Scholar] [CrossRef]
- Bulkley, J.W. Integrated Watershed Management: Past, Present, and Future. J. Contemp. Wat. Res. Edu. 1995, 100, 3–15. [Google Scholar]
- Ballweber, J.A. Prospects for Comprehensive, Integrated Watershed Management under Exiting Law. Water Resour. Update 1995, 100, 19–27. [Google Scholar]
- Wang, L.; Meng, W.; Guo, H.; Zhang, Z.; Liu, Y.; Fan, Y. An Interval Fuzzy Multiobjective Watershed Management Model for the Lake Qionghai Watershed, China. Water Resour. Manag. 2006, 20, 701–721. [Google Scholar] [CrossRef]
- Ballweber, J.A. A Critique of Watershed Management Efforts in the Lower Mississippi Alluvial Plain. JAWRA J. Am. Water Resour. Assoc. 1999, 35, 643–654. [Google Scholar] [CrossRef]
- Qi, H.; Altinakar, M.S. Integrated Watershed Management with Multiobjective Land-Use Optimizations under Uncertainty. J. Irrig. Drain. Eng. 2013, 139, 239–245. [Google Scholar] [CrossRef]
- Cobourn, J.; Lewis, S.R. Integrated watershed management and floodplain protection on the carson river in the western usa. Int. J. Environ. Impacts: Manag. Mitig. Recover. 2018, 1, 221–231. [Google Scholar] [CrossRef]
- Brombal, D.; Niu, Y.; Pizzol, L.; Moriggi, A.; Wang, J.; Critto, A.; Jiang, X.; Liu, B.; Marcomini, A. A participatory sustainability assessment for integrated watershed management in urban China. Environ. Sci. Policy 2018, 85, 54–63. [Google Scholar] [CrossRef]
- Gessesse, T.A.; Khamzina, A.; Gebresamuel, G.; Amelung, W. Terrestrial carbon stocks following 15 years of integrated watershed management intervention in semi-arid Ethiopia. Catena 2020, 190, 104543. [Google Scholar] [CrossRef]
- Lee, K.S.; Chung, E.-S.; Chung, E.-S. Development of integrated watershed management schemes for an intensively urbanized region in Korea. HydroResearch 2007, 1, 95–109. [Google Scholar] [CrossRef]
- Ye, Q.; Li, Y.; Zhuo, L.; Zhang, W.; Xiong, W.; Wang, C.; Wang, P. Optimal Allocation of Physical Water Resources Integrated with Virtual Water Trade in Water Scarce Regions: A Case Study for Beijing, China. Water Res. 2018, 129, 264–276. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, Z.; Song, R.; Han, R.; Xu, B.; Luo, Y. Multi-objective Optimization Model of Water Resource Allocation for Mainstream Channel Segment of Yellow River Basin. J. Yangtze River Sci. Res. I 2017, 34, 18–22. (In Chinese) [Google Scholar]
- Alamanos, A.; Latinopoulos, D.; Loukas, A.; Mylopoulos, N. Comparing Two Hydro-Economic Approaches for Multi-Objective Agricultural Water Resources Planning. Water Resour. Manag. 2020, 34, 4511–4526. [Google Scholar] [CrossRef]
- Behmel, S.; Damour, M.; Ludwig, R.; Rodríguez, M. Participative approach to elicit water quality monitoring needs from stakeholder groups—An application of integrated watershed management. J. Environ. Manag. 2018, 218, 540–554. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.; Wang, F.; Ji, L.; Yu, J. Agricultural Production Structure Adjustment Based on A Multi-objective Control in the Tiaoxi Watershed. J. Zhejiang Univ. (Agric. Life Sci.) 2019, 45, 66–74. (In Chinese) [Google Scholar]
- Alamdari, N.; Sample, D.J. A Multiobjective Simulation-Optimization Tool for Assisting in Urban Watershed Restoration Planning. J. Clean. Prod. 2019, 213, 251–261. [Google Scholar] [CrossRef]
- Alamanos, A.; Mylopoulos, N.; Loukas, A.; Gaitanaros, D. An Integrated Multicriteria Analysis Tool for Evaluating Water Resource Management Strategies. Water 2018, 10, 1795. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Brown, D.G.; Moore, M.R.; Currie, W.S. Optimizing Spatial Land Management to Balance Water Quality and Economic Returns in a Lake Erie Watershed. Ecol. Econ. 2018, 145, 104–114. [Google Scholar] [CrossRef]
- Cai, Y.; Rong, Q.; Yang, Z.; Yue, W.; Tan, Q. An Export Coefficient Based Inexact Fuzzy Bi-level Multi-objective Programming Model for the Management of Agricultural Nonpoint Source Pollution under Uncertainty. J. Hydrol. 2018, 557, 713–725. [Google Scholar] [CrossRef]
- Geng, R.; Yin, P.; Sharpley, A.N. A Coupled Model System to Optimize the Best Management Practices for Nonpoint Source Pollution Control. J. Clean. Prod. 2019, 220, 581–592. [Google Scholar] [CrossRef]
- Qi, H.; Altinakar, M.S. A conceptual framework of agricultural land use planning with BMP for integrated watershed management. J. Environ. Manag. 2011, 92, 149–155. [Google Scholar] [CrossRef]
- Liu, G.; Chen, L.; Wang, W.; Sun, C.; Shen, Z. A water quality management methodology for optimizing best management practices considering changes in long-term efficiency. Sci. Total. Environ. 2020, 725, 138091. [Google Scholar] [CrossRef]
- Alamanos, A.; Rolston, A.; Papaioannou, G. Development of a Decision Support System for Sustainable Environmental Management and Stakeholder Engagement. Hydrology 2021, 8, 40. [Google Scholar] [CrossRef]
- Park, C.H.; Joo, J.G.; Kim, J.H. Integrated washland optimization model for flood mitigation using multi-objective genetic algorithm. HydroResearch 2012, 6, 119–126. [Google Scholar] [CrossRef]
- Yoo, D.G.; Kim, J.H. Meta-heuristic algorithms as tools for hydrological science. Geosci. Lett. 2014, 1, 4. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.J.; Anzab, N.R.; Asl-Rousta, B.; Kim, J.H. Multi-Objective Optimization-Simulation for Reliability-Based Inter-Basin Water Allocation. Water Resour. Manag. 2017, 31, 3445–3464. [Google Scholar] [CrossRef]
- Young, R.A.; Onstead, C.A.; Bosch, D.D.; Anderson, W.P. AGNPS: A Nonpoint-Source Pollution Model for Evaluating Agricultural Watersheds. J. Soil Water Conserv. 1989, 44, 168–173. [Google Scholar]
- Bingner, R.L.; Theurer, F.D.; Yuan, Y.P.; Taguas, E.V. AnnAGNPS Technical Processes Documentation, Version 5.5; USDA-ARS: Washington, DC, USA, 2018; pp. 1–8. [Google Scholar]
- Yuan, Y.; Locke, M.; Bingner, R. Annualized Agricultural Non-Point Source model application for Mississippi Delta Beasley Lake watershed conservation practices assessment. J. Soil Water Conserv. 2008, 63, 542–551. [Google Scholar] [CrossRef] [Green Version]
- Chahor, Y.; Casalí, J.; Giménez, R.; Bingner, R.; Campo, M.; Goñi, M. Evaluation of the AnnAGNPS model for predicting runoff and sediment yield in a small Mediterranean agricultural watershed in Navarre (Spain). Agric. Water Manag. 2014, 134, 24–37. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, Y.; Ni, J.; Xie, D. Best management practices for agricultural non-point source pollution in a small watershed based on the AnnAGNPS model. Soil Use Manag. 2019, 36, 45–57. [Google Scholar] [CrossRef]
- Abdelwahab, O.; Ricci, G.; De Girolamo, A.; Gentile, F. Modelling soil erosion in a Mediterranean watershed: Comparison between SWAT and AnnAGNPS models. Environ. Res. 2018, 166, 363–376. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, J.; Zhuang, J.; Wang, X.; Zhang, S. Parameters sensitivity and applicability evaluation of AnnAGNPS model in small watershed of Yangtze River Delta. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2020, 45, 1–13. (In Chinese) [Google Scholar]
- Liu, Y.; Wang, R.; Guo, T.; Engel, B.A.; Flanagan, D.C.; Lee, J.G.; Li, S.; Pijanowski, B.C.; Collingsworth, P.D.; Wallace, C.W. Evaluating efficiencies and cost-effectiveness of best management practices in improving agricultural water quality using integrated SWAT and cost evaluation tool. J. Hydrol. 2019, 577, 123965. [Google Scholar] [CrossRef]
- Ghebremichael, L.T.; Veith, T.L.; Hamlett, J.M. Integrated watershed- and farm-scale modeling framework for targeting critical source areas while maintaining farm economic viability. J. Environ. Manag. 2013, 114, 381–394. [Google Scholar] [CrossRef] [PubMed]
- Getahun, E.; Keefer, L. Integrated modeling system for evaluating water quality benefits of agricultural watershed management practices: Case study in the Midwest. Sustain. Water Qual. Ecol. 2016, 8, 14–29. [Google Scholar] [CrossRef]
- Kraff, D.; Steinman, A.D. Integrated watershed management in Michigan: Challenges and proposed solutions. J. Great Lakes Res. 2018, 44, 197–207. [Google Scholar] [CrossRef]
- Hong, B.; Limburg, K.E.; Hall, M.H.; Mountrakis, G.; Groffman, P.M.; Hyde, K.; Luo, L.; Kelly, V.R.; Myers, S.J. An integrated monitoring/modeling framework for assessing human–nature interactions in urbanizing watersheds: Wappinger and Onondaga Creek watersheds, New York, USA. Environ. Model. Softw. 2012, 32, 1–15. [Google Scholar] [CrossRef]
- Teka, K.; Haftu, M.; Ostwald, M.; Cederberg, C. Can integrated watershed management reduce soil erosion and improve livelihoods? A study from northern Ethiopia. Int. Soil Water Conserv. Res. 2020, 8, 266–276. [Google Scholar] [CrossRef]
- Zadeh, L. Optimality and non-scalar-valued performance criteria. IEEE Trans. Autom. Control. 1963, 8, 59–60. [Google Scholar] [CrossRef]
- Srivastava, P.; Hamlett, J.M.; Robillard, P.D.; Day, R.L. Watershed optimization of best management practices using AnnAGNPS and a genetic algorithm. Water Resour. Res. 2002, 38, 3-1. [Google Scholar] [CrossRef] [Green Version]
- Altinakar, M.S.; Qi, H.; Altınakar, M.S. Numerical-Simulation Based Multiobjective Optimization of Agricultural Land-Use with Uncertainty. World Environ. Water Resour. Congr. 2008 2008, 1–10. [Google Scholar] [CrossRef]
- Cong, W.; Sun, X.; Guo, H.; Shan, R. Comparison of the SWAT and InVEST models to determine hydrological ecosystem service spatial patterns, priorities and trade-offs in a complex basin. Ecol. Indic. 2020, 112, 106089. [Google Scholar] [CrossRef]
- Qi, H.; Altinakar, M.S.; Altınakar, M.S. Vegetation Buffer Strips Design Using an Optimization Approach for Non-Point Source Pollutant Control of an Agricultural Watershed. Water Resour. Manag. 2010, 25, 565–578. [Google Scholar] [CrossRef]
- “Jenny” Zhen, X.-Y.; Yu, S.L.; Lin, J.-Y. Optimal Location and Sizing of Stormwater Basins at Watershed Scale. J. Water Resour. Plan. Manag. 2004, 130, 339–347. [Google Scholar] [CrossRef]
- Li, H.; Lin, J.; Zhang, J.; Zhang, X.; Zhang, L.; Wang, Z. Spatial Variability of Soil Organic Carbon and Total Nitrogen Based on Small Watershed Scale. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2008, 32, 38–42. (In Chinese) [Google Scholar]

| No. | Model | Input Data Required | Data Source |
|---|---|---|---|
| 1 | AnnAGNPS | Topographic feature data | Nanjing Planning and Natural Resources Bureau |
| 2 | Land use data | Tillage Protection Station of Gaochun district, Nanjing | |
| 3 | Soil basic data | Nanjing Planning and Natural Resources Bureau | |
| 4 | Laboratory analysis | ||
| 5 | Soil hydrology grouping | Laboratory analysis | |
| 6 | Meteorological data | Meteorological Bureau of Gaochun District, Nanjing | |
| 7 | Agricultural management data | Tillage Protection Station of Gaochun District, Nanjing | |
| 8 | EBE | Cost and benefit of agricultural land use | Data from Gaochun district yearbooks and Jiangsu Provincial Price Bureau |
| Types of Agricultural Land Use | Cost (¥104/ha) | Production Benefit (¥104/ha) | ||
|---|---|---|---|---|
| paddy field | LU_1 | rice (summer), wheat (winter) | 2.18 | 3.92 |
| LU_2 | rice (summer), rape (winter) | 2.06 | 3.98 | |
| LU_3 | rice (summer), corn (spring) | 1.95 | 4.70 | |
| LU_4 | soybean (summer), wheat (winter) | 1.46 | 2.55 | |
| LU_5 | soybean (summer), rape (winter) | 1.33 | 2.60 | |
| LU_6 | soybean (summer), corn (spring) | 1.22 | 3.32 | |
| dry land | LU_7 | corn (autumn), wheat (winter) | 1.79 | 2.88 |
| LU_8 | corn (autumn), rape (winter) | 1.67 | 2.93 | |
| LU_9 | soybean (summer), wheat (winter) | 1.52 | 2.16 | |
| LU_10 | soybean (summer), rape (winter) | 1.39 | 2.21 | |
| LU_11 | sweet potato (spring), rape (winter) | 2.93 | 5.01 | |
| LU_12 | sweet potato (spring), wheat (winter) | 3.05 | 4.96 | |
| Objective Function Value | SYU | NYU | PYU | fp | fe (¥104) | F |
|---|---|---|---|---|---|---|
| Initial value | 0.7781 | 0.894 | 0.7345 | 0.7998 | 3275.38 | 0.2003 |
| Optimal value | 0.7261 | 0.8516 | 0.6829 | 0.7508 | 3775.78 | 0.2555 |
| Variation (%) | −6.68 | −4.74 | −7.03 | −6.13 | 15.28 | 27.56 |
| Types of Agricultural Land Use | Initial Area (ha) | Optimal Area (ha) | Rate (%) | Ratio (%) | ||
|---|---|---|---|---|---|---|
| paddy field | LU_1 | rice (summer), wheat (winter) | 395.46 | 618.12 | 56.30 | 52.85 |
| LU_2 | rice (summer), rape (winter) | 297.18 | 115.20 | −61.24 | 9.85 | |
| LU_3 | rice (summer), corn (spring) | 92.88 | 176.40 | 89.92 | 15.08 | |
| LU_4 | soybean (summer), wheat (winter) | 143.82 | 122.76 | −14.64 | 10.50 | |
| LU_5 | soybean (summer), rape (winter) | 202.77 | 53.46 | −73.64 | 4.57 | |
| LU_6 | soybean (summer), corn (spring) | 37.53 | 83.70 | 123.02 | 7.16 | |
| dry land | LU_7 | corn (autumn), wheat (winter) | 146.70 | 139.59 | −4.85 | 16.28 |
| LU_8 | corn (autumn), rape (winter) | 279.63 | 219.15 | −21.63 | 25.56 | |
| LU_9 | soybean (summer), wheat (winter) | 53.55 | 28.17 | −47.39 | 3.29 | |
| LU_10 | soybean (summer), rape (winter) | 53.82 | 6.12 | −88.63 | 0.71 | |
| LU_11 | sweet potato (spring), rape (winter) | 323.73 | 152.19 | −52.99 | 17.75 | |
| LU_12 | sweet potato (spring), wheat (winter) | 0 | 312.21 | - | 36.41 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Zhang, J.; Meng, M.; Chen, P.; Liu, X.; Liu, G.; Gu, Z. A Multi-Objective Decision Making System (MDMS) for a Small Agricultural Watershed Based on Meta-Heuristic Optimization Coupling Simulation. Water 2021, 13, 1338. https://doi.org/10.3390/w13101338
Zhang S, Zhang J, Meng M, Chen P, Liu X, Liu G, Gu Z. A Multi-Objective Decision Making System (MDMS) for a Small Agricultural Watershed Based on Meta-Heuristic Optimization Coupling Simulation. Water. 2021; 13(10):1338. https://doi.org/10.3390/w13101338
Chicago/Turabian StyleZhang, Shuifeng, Jinchi Zhang, Miaojing Meng, Peixian Chen, Xin Liu, Guoliang Liu, and Zheyan Gu. 2021. "A Multi-Objective Decision Making System (MDMS) for a Small Agricultural Watershed Based on Meta-Heuristic Optimization Coupling Simulation" Water 13, no. 10: 1338. https://doi.org/10.3390/w13101338





