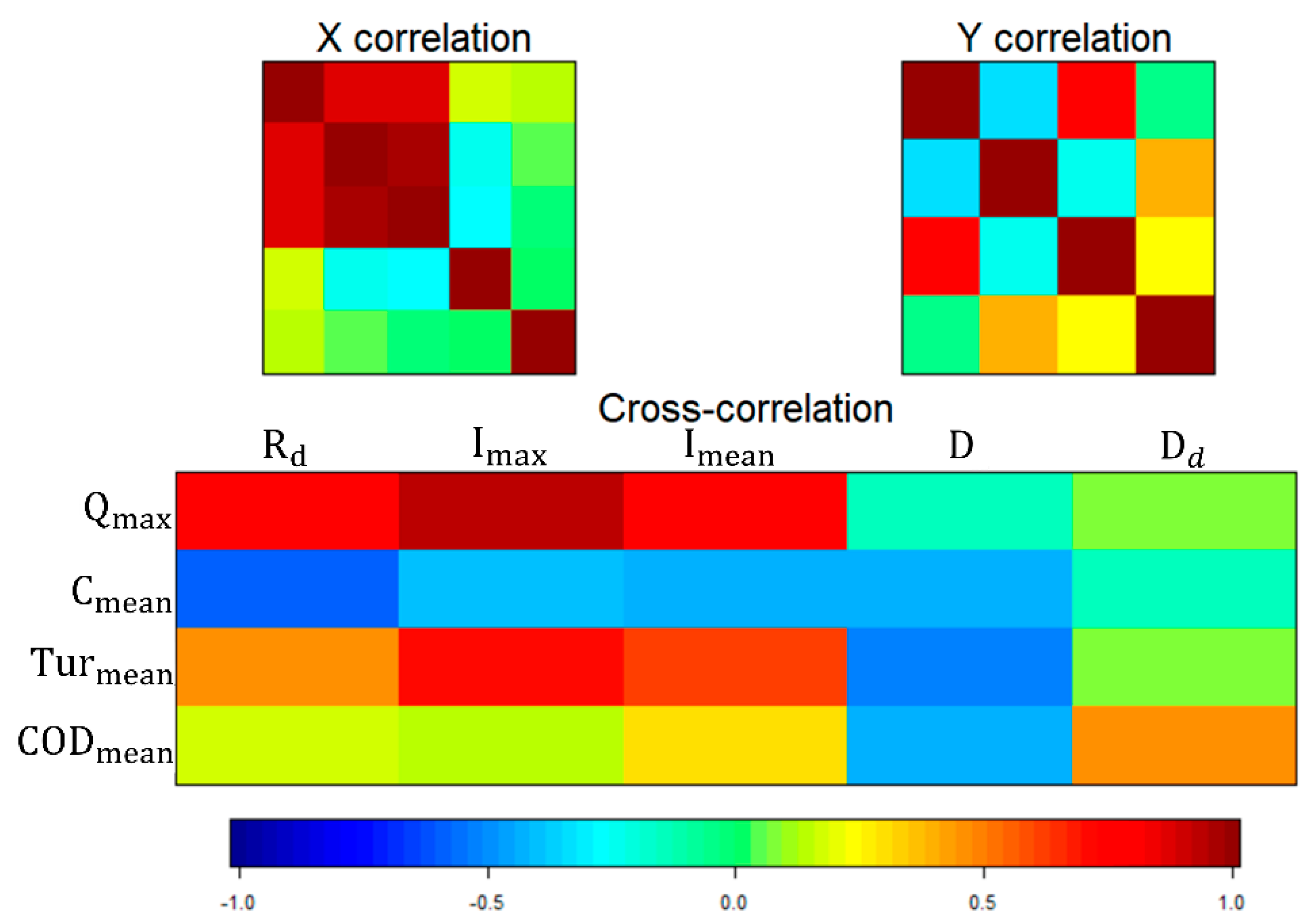
The correlation graph for the El Vado (
Figure 6) and Multifamiliares (
Figure A4) CSOs shows that the average intensity of rain (I
mean), has an influence on the maximum discharge flow (Q
max), for this correlations a
p value less than 0.05 was obtained (
Table A3 and
Table A4). It is considered a significant correlation. Furthermore, in the El Vado CSO the maximum intensity of precipitation (I
max) is related to the maximum flow Q
max (
p value < 0.05). This same relationship is obtained in the Multifamiliares CSO, but with
p value of 0.10. Sandoval et al. [
14], in their research on the main CSO in Berlin, found that the maximum and average intensity of precipitation is related to the volume of water discharged, as well as the maximum flow and the average discharge flow. At CSO El Vado, a significant relationship was also found between total precipitation R
d and maximum flow Q
max.
In the El Vado and Multifamiliares CSOs, the I
max and I
mean respectively also seem to influence the values of the average turbidity (Tur
mean) (
Figure 6 and
Figure A4). In the same way, these correlations obtained a
p value less than 0.05. According to Murillo [
57], turbidity helps determine the amount of suspended material, where the higher the intensity of rain is, the greater the drag of suspended solids will be. Likewise, Sandoval et al. [
14] found a relationship between I
max and I
mean with the value of total suspended solids.
For the Multifamiliares CSO (
Figure A4), it was also found that the Tur
mean is related to the duration of the dry period prior to a rainfall event (D
d) with a statistical significance related to a
p value less than 0.05. In this CSO, it was also found that the COD
mean is related to the average intensity of precipitation (I
mean) with a
p value of 0.12. D
d and I
mean, which can influence the amount of drag material due to the runoff and resuspension of material deposited in the drainage ducts that cause higher pollution loads [
2,
14,
20].
The results of the correlational analysis between the rainfall and CSO parameters for the Multifamiliares CSO showed a similar pattern to the results obtained for the El Vado CSO, mainly between the parameters Imax, Imean, Qmax and Turmean.
3.4.1. Canonical Correlation Analysis
The Canonical Correlation Analysis was carried out only for the El Vado CSO. For the Multifamiliares and Coliseo, it was not possible to perform a CCA due to the insufficient number of available trials (six trials or less) [
43].
From the CCA, only two canonical variables L(1) and L(3) were found to be statistically significant (
p value ≈ 0). For both canonical variables, the correlation is close to one. This means that two canonical correlations would be sufficient to measure the association between the rainfall and CSO variables [
41].
Table 3a shows the canonical loadings (ρ) obtained between L(1) and L(3) and the rainfall characteristics (independent variables). On the other hand,
Table 3b shows the canonical loadings obtained between the canonical variables L(1) and L(3) and the characteristics of the CSO (response variables).
Regarding the CCA presented for the El Vado CSO, in
Table 3a,b, the values of ρ greater than 0.4–0.5 between L(1) and L(3) and the characteristics of rainfall and CSO indicate the possible influence of rainfall on the CSO variables, an aspect consistent with the results found by Sandoval et al. [
14]. From the analysis of L(1), the maximum intensity of rainfall (I
max), the average intensity (I
mean) and the total rainfall depth (R
d) seem to have influence on the variables Q
max and Tur
mean. These relationships agree with those obtained from the analysis of the correlation matrices. From the analysis of L(3), it was determined that the duration of the rain (D) and the total rainfall depth (R
d) (to a lesser degree) are related to the mean turbidity values (Tur
mean).
3.4.2. Partial Least Squares Regression (PLSR)
Next, we describe the construction of the PLSR model for the pollutant Turmean at the El Vado CSO. In the same way, the PLSR prediction models were determined for the other dependent variables, Cmean, CODmean, and Qmax, for all CSOs.
Figure A6 shows the root mean squared error of Prediction (RMSEP) for the variable Tur
mean as a function of the number of components used in the construction of the model.
Table 4 shows the percentage of variability explained by each of the components of the model. Considering the reduction of the RMSEP and the levels of variability explained, two components were determined for the construction of the PLS model to predict Tur
mean for the El Vado CSO (
Figure A7).
After performing the PLSR for all the dependent variables, fit equations were obtained that can estimate the output CSO characteristics (COD
mean, C
mean, Tur
mean, Q
max) based on the input rainfall characteristics (R
d, I
max, I
mean, D and D
d). The structure of the PLSR is reported in Equation (1).
the regression coefficients (C
1, C
2, C
3, C
4, C
5 and C
6) of the PLSR models for the prediction of the CSO variables in the El Vado CSO are presented in
Table 5. The results of the PLSR for the Multifamiliares and Coliseo CSOs are presented in
Table A5 and
Table A6, respectively.
The determination coefficient
for the prediction of the CSO parameters in the El Vado CSO ranged from 0.60 to 0.81 (
Table 5); for the Multifamiliares CSO, this value was between 0.91 and 0.37 (
Table A5) and for the Coliseo CSO, it was in the range of 0.84 and 0.18 (
Table A6). On average, the El Vado CSO presents the highest values of
, this means that in this CSO, the equations had a better fit.
The lowest
values were recorded in the determination of
for the Multifamiliares and Coliseo CSOs (0.37 and 0.18, respectively). These last CSOs have a contribution area approximately three times smaller than the El Vado CSO area. On the other hand, the
value obtained for the prediction of
in the El Vado CSO was 0.71 (
Table 5). This result suggests that the equations obtained for the
would be better fitted to a larger basin.
In the Coliseo CSO, the values of
showed the widest range of variability. This may be because a smaller number of tests were performed on this combined sewer overflow compared to the other two CSOs, which may have affected the fit of the prediction equations. Thus, in the El Vado CSO nine CSO events were registered with a total of 161 samples, while in the Multifamiliares CSO six events were registered with 124 samples, finally in the Coliseo CSO three CSO events were registered with 46 samples (
Table A2).
The average of the
values for the prediction of the variables
and
in the three CSOs presents a smaller range of variation than in the other two variables. This suggests that the
and
possibly contain less uncertainty or that their predictions are less sensitive to the uncertainty of the rain. Sandoval et al. [
14] found a similar result for these same variables.
For the prediction of
in the Coliseo CSO, a low determination coefficient (
) was obtained. The value of
measures the goodness of fit-of-the-model to a set of data [
58], in this case, the equation obtained for
in the Coliseo CSO does not have a good fit, so it is considered a low precision model.
The PLSR results are also displayed through a triplot that represents the cases, the response variables (CSO:
,
,
,
) and the predictor variables (Rainfall:
,
,
,
,
) measures for the same cases.
Figure 7 shows the triplot for the El Vado CSO, while the triplots for the Multifamiliares and Coliseo CSOs are shown in
Figure A8 and
Figure A9, respectively.
The triplots of the El Vado and Multifamiliares CSO (
Figure 7 and
Figure A8, respectively) showed similar relationships between the variables of rainfall and CSO. These results are consistent with the relationships that were determined through the correlation analysis and CCA. In these two CSOs, a correlation was determined between the independent variables
and
with dependent variable
. A relationship of the average intensity (
) with the average Turbidity (
) was also observed, as well as a positive relationship between
and the
. Similarly, a negative relationship between the total rainfall depth (
) and mean conductivity (
) was observed.
The triplot obtained for the Coliseo CSO (
Figure A9) differs from the triplots made for the El Vado (
Figure 7) and Multifamiliares (
Figure A8) CSOs. As mentioned above, this may be due to the small sample size used in the Coliseo CSO analysis.
The relationships found determine the influence of rainfall parameters on the behavior and dynamics of pollutants during CSO events. These relationships can be used in the construction of integrated ecological models for the evaluation and complete analysis of the city’s sanitation systems, their impact on the receiving bodies and their restoration.