Abstract
Recently, a continuous reinforcement learning model called fuzzy SARSA (state, action, reward, state, action) learning (FSL) was proposed for irrigation canals. The main problem related to FSL is its convergence and generalization in environments with many variables such as large irrigation canals and situations beyond training. Furthermore, due to its architecture, FSL may require high computation demands during its learning process. To deal with these issues, this work proposes a computationally lighter generalizing learned Q-function (GLQ) model, which benefits from the FSL-learned Q-function, to provide operators with a faster and simpler mechanism to obtain operational instructions. The proposed approach is tested for different water requests in the East Aghili Canal, located in the southwest of Iran. Several performance indicators are used for evaluating the GLQ model results, showing convergence in all the investigated cases and the ability to estimate operational instructions (actions) in situations beyond training, delivering water with high accuracy regarding several performance indicators. Hence, the use of the GLQ model is recommended for determining the operational patterns in irrigation canals.
1. Introduction
The operation of hydraulics of irrigation canals is complex because they are large-scale systems with significant delays [1]. Likewise, complexity appears in their scheduling due to factors such as cropping pattern, irrigation quota, irrigation duration, the numerous water requests and the short time available between water requests and deliveries [2]. Therefore, there is a strong need for methods that can handle these issues to improve water delivery.
Water delivery methods can be rotational, on-demand, and on-request. For the rotational method, water delivery parameters (timing and volume) are fixed during the growing season, and farmers have little flexibility regarding the reception of water. In the on-demand method, water delivery parameters are more flexible, requiring a fully automatic control system and large capacity canals. Therefore, it involves higher costs than the rest of water delivery methods [3]. The flexibility and cost halfway approach is the on-request method, where water delivery parameters are variable according to an agreement between farmers and canal managers, and the canal capacity is low as in the rotational method. In this way, each farmer receives water based on the agreed flow rate, duration, and frequency.
In this article, we focus on the on-request method, where the canal’s authority collects water requests, checks them with the water allocated to each farmer, decides the amount of water to be delivered, and extracts the corresponding operations using canal operators’ experiences. Finally, an operator moves along the canal from upstream to downstream and regulates the structures to deliver water to the farmers. The operational instructions (hereafter actions), i.e., the timing and the extent of the adjustments in canal structures to be performed by the operator, are complicated, and delivery accuracy depends significantly on their precision [4].
In large irrigation canals, there are many structures involved in water requests, and daily extraction of the actions to precisely deliver water becomes complicated during a season. However, supplying water based on the on-request method is quite practical, provided that the actions are extracted accurately [5]. In general, this type of decision-making problem is common for all water delivery methods, and several optimization approaches have been proposed to deal with this issue.
A typical regulation method in this context is that of proportional–integral (PI) controllers, whose coefficients can be optimized to minimize undesired mutual interactions and maximize performance, as conducted by the authors of [6], who use linear matrix inequalities (LMIs) to this end. A different approach is employed by the authors of [7], who used simulated annealing (SA) for scheduling water delivery in irrigation canals based on the rotational method.
Ramesh et al. [8] used particle swarm optimization (PSO) to schedule water delivery based on the on-demand method. This optimization method was also followed by the authors of [9] to schedule water delivery in irrigation canals, with two canals in China as a case study. The results showed the robustness, efficiency, real applicability, and quick response of the model in finding the optimum water schedule.
Furthermore, advanced model-based optimization based methods such as model predictive control (MPC) have been reported to be useful for the management of water systems [10]. For example, MPC was used to extract the actions and optimize the operator’s route in the human-in-the-loop control scheme presented in [11]. MPC was also used by the authors of [12] to develop an in-line storage strategy so as to improve the operation of main canals. The results revealed that the model can establish water level within the considered dead band regarding the maximum and average deviation of water depth from the target. Again, MPC was used by [13] to deal with predictable and unpredictable water demands in irrigation canals, showing good performance in both cases. Recently, reinforcement learning (RL), which has been used successfully in many fields [14], has also been proposed to generate actions. In particular, the authors of [15] used fuzzy SARSA (state, action, reward, state, action) learning (FSL) to extract actions in on-request irrigation canals, outperforming the traditional manual operation.
In the current research, the FSL model developed by the authors of [15] for learning actions is complemented by using a generalizing learned Q-function (GLQ). The generalization means that FSL can only extract actions directly for a limited number of water requests (inputs) in a learning process. To this end, it maps fuzzy inputs to the discrete actions generating a Q-function, i.e., the actions matrix of a zero-order Takagi–Sogeno–Kang (TSK) fuzzy system. In this paper, we focus on generalizing FSL by providing its learned Q-function to the GLQ so as to estimate actions for a wider range of situations, which may differ from those that are used for learning. In addition, we also consider the issue of FSL convergence, which means that FSL must find a response with a fair reward and an acceptable operational performance. Since the results of the FSL model are valid only if it converges to an eligible value, this topic has been studied in other fields, e.g., robot control [14], although these results are difficult to transpose to the coupled dynamics of irrigation canals. Indeed, the learning process may diverge. For this reason, this property is explored in this work as well. Finally, as will be seen, the proposed approach is much lighter in terms of computation burden because the SARSA learning process can be avoided during real-time operations. Hence, the resulting control method can be easily provided to the canal operators, who can run the method on handheld devices so that they can enjoy the benefits of the learning without actually performing the SARSA process.
To assess the proposed method, we performed tests on a nonlinear simulated version of a real canal, the East Aghili Canal in Iran, which was implemented in irrigation conveyance system simulation (ICSS) [16]. The GLQ model was developed in MATLAB 2013a to estimate the corresponding actions of any states in the East Aghili Canal using the QAC-function (Q-function of the Aghili Canal). Water delivery and water depth performance indicators were used for evaluating the results. The recorded data of the East Aghili Canal were used as a case study.
The rest of the article is structured as follows: First, the canal selected for this case study and its specifications are introduced. Then, the FSL model and its components are presented in two subsections describing the architecture of the FSL and the simulation model. After that, the generalization and convergence properties of FSL are presented and investigated. Simulation results are presented after the introduction of the corresponding water delivery and depth performance indicators. Finally, some conclusions are put forward in the last section.
2. Materials and Methods
2.1. Studied Canal
The Gotvand irrigation network of Khuzestan province (southwest Iran) is shown in Figure 1. It has two main canals, namely the Gotvand Main Canal (G.M.C) and the Aghili Main Canal (A.M.C). The A.M.C has two sub-main canals, including the east Aghili and west Aghili canals.
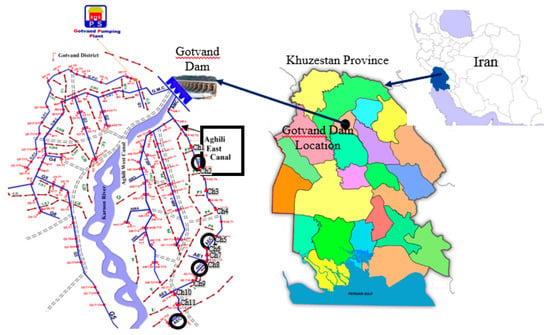
Figure 1.
Layout of the East Aghili Canal on the Gotvand irrigation network.
The canal profile, a block plan, and a block profile are illustrated in Figure 2. A reach is defined as the distance between two successive structures, and a block is defined as the distance between two successive check structures. The East Aghili Canal has 32 reaches, 11 check structures (Ch1–Ch11), 21 turnouts (TO1–TO21), and 11 blocks (B1–B11). Water enters each block from the inlet of the block, which is the outlet of the upstream block, and exits from the outlet of the block, which is the inlet of the next block. For example, the outflow from block B5 is the inflow to B6, the outflow from B6 is the inflow to B7, etc.
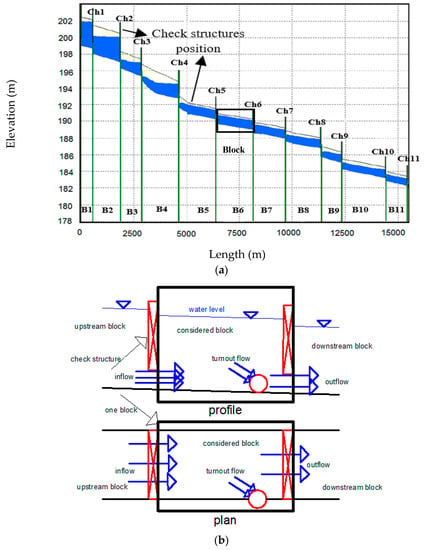
Figure 2.
The East Aghili Canal layout: (a) canal profile; (b) profile and plan of a block (B6).
The specifications of the East Aghili Canal are listed in Table 1. The check structures and turnouts are rectangular sluice gates. The canal length, Manning’s roughness coefficient, and trapezoidal cross-section side slopes are 16.215 km, 0.017, and 1:1, respectively. The base width of the canal is 1.5 m at the lengths of 0–9.5 km and is 1 m at the lengths of 9.5–16.2 km. The bed slope of the canal varies between 0.0001 and 0.0004 along the canal.

Table 1.
Specifications of the East Aghili Canal.
The turnouts are rectangular gates adjusted by an operator to deliver water to the farmers. Flow passing through a turnout to the farm depends only on its gate opening if water depth establishes precisely at the target depth (normal). A check structure regulates water depth to its target value by adjusting the gate opening. Precisely establishing water depth at target depth is a complicated task in practice due to water depth fluctuations; therefore, a dead band is defined. The dead band is a margin around target depth within which water depth must be established. A dead band of ± 10% was used in this study based on previous studies [17]. Therefore, check structures are adjusted to control water depth within the dead band, and turnouts are adjusted to deliver water accurately. For this purpose, optimized instructions for gate adjustments are needed.
2.2. Water Distribution System as an RL Problem
The foundational idea of RL is learning from interaction. A water distribution system has one or more learning agents (controllers) that interact with their environment (irrigation canal) to achieve a goal (handling water requests to precisely deliver water). To this end, agents sense aspects of the environment (canal state) and choose actions while considering the environmental uncertainty. In this problem, a good policy allows the learning agent to improve its operational capabilities to deliver water to the farmers fairly and timely. This policy can be obtained from a Q-function, which specifies the long-term desirability of states.
2.3. Architecture of FSL
FSL is an advanced RL method to learn appropriate actions from specific states (inputs), memorize them, and finally generalize the learning policy to a wide range of states. Figure 3 shows a simplified diagram of the FSL system and its learning method.
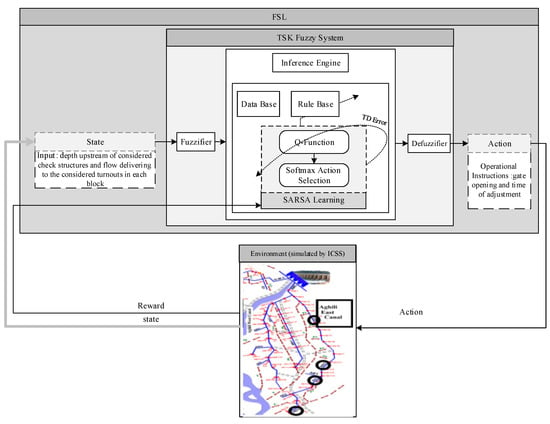
Figure 3.
A simplified diagram of the system and the learning method.
The architecture of FSL utilizes a fuzzy inference system (FIS) as a comprehensive function approximator to obtain an approximate model for the state–action value function in continuous state space and to generate continuous actions [18]. The FIS, as a main unit of any fuzzy system, consists of:
- (i)
- A fuzzifier which converts crisp inputs into fuzzy values using the membership functions (MF). The resulting fuzzy sets may have pre-specified linguistic values for each axis of the feature space. In particular, an MF indicates the collection of possible values that a feature may have, with its Y-axis indicating its degree ∊ [0, 1] and the X-axis containing the variable range [19].
- (ii)
- An inference engine that applies the inference operations based on “IF…THEN” fuzzy rules contained on a rule base. The first step to construct the rules is to find a suitable partition of the feature space into fuzzy subspaces using “OR” and “AND” operators (antecedent part). Then, the consequent part of each is chosen according to a reasoning mechanism [20].
- (iii)
- A defuzzifier to convert the fuzzy value into a crisp value.
The FIS model of original FSL is an n-input one-output zero-order TSK fuzzy system [18] with R rules. In this FIS model, the antecedent part defines fuzzy subspaces as states and the consequent part determines the discrete candidate action set and its values referred to as Q-function. Consider rule Ri in this TSK fuzzy system as follows:
where s = x1 × … × xn represents the vector of n-dimensional input state, Li = Li1 × … × Lin is the fuzzy set of rule i, m is the number of candidate actions for the i-th rule, aij is the j-th candidate action (1 ≤ j ≤ m) of the i-th rule, and the weight qij is the value of action j in rule i. The Q-function
is learned by applying the SARSA process. The number of candidate actions is m in each fuzzy rule; therefore, the dimension of Q-function is 2n × m.
Ri: If x1 is Li1 and ... and xn is Lin, then (αi1 with value Qi1) or … or (αim with value Qim)
In each step t of this process, the following sequence occurs: observe state st, apply action at, and receive reward rt+1, observe next state st+1, and apply next action at+1. The name “SARSA” is taken from this sequence (st, at, rt+1, st+1, at+1).
When FSL is running, a -function is created first. The vector of state s, including target depths upstream of the check structures and requested water by farmers, is mapped to the antecedent part of the TSK fuzzy system. The normalized firing strength of i-th rule () is obtained by fuzzy logic operator intersection, which gives the product of the input membership degrees of the rule . The probability of selecting action (operational instruction) in the rule is calculated using the softmax action selection method which is defined by
where is the value of the candidate action in rule , is a temperature parameter, and subscript shows the iteration number. As can be seen, the softmax method calculates the selection probability of each action using the parameters of and the defined temperature, which influences the learning speed. The initial temperature in this research was 30, and was determined by a trial and error. At the beginning of the learning, all values in the Q-function are zero; therefore, they had the same chance to be selected. During the learning, the Q-function value of the actions that receive a higher reward is increasing. Considering the selected parameters, the selection probability of all candidate actions in each rule is calculated, and the action with a higher chance is selected to be exerted.
During the learning process, the temperature decreases, and the value consequently increases according to the softmax action selection method. In iterations except iteration 1, the action with higher probability is chosen according to Equation (3), where denotes the index of the selected candidate action in rule i. The final action () in each step k is calculated using
The temperature decreases during the learning as
When the temperature is high, the actions are selected with the same probability. At lower temperatures, the actions with higher values are more likely to be chosen. FSL converges as the temperature reaches a lower threshold, which was set as 0.001 in this work.
The -function is updated using the approximate function
where is learning rate, is reward (described in the next section), and is a discount factor that indicates the relevance of the last action in the learning process, which was set as 0.009 by trial and error. It approximates the worthiness of the selected candidate actions based on the assigned reward. In this equation, the expression in the parentheses is called temporal difference error (TD error). The learning rate () is decreased using
It should be noted that FSL does not learn anything if . The initial value of the learning rate was set as 0.9 by trial and error. Here, one iteration is completed. The model running is continued in each iteration until the iterations, which were set as 1200 using a trial and error process, are terminated (t = 1200).
2.4. Simulating the Canal for FSL
The ICSS hydrodynamic model was used for simulating the East Aghili Canal. The open-source ICSS model written in the FORTRAN programming language by the authors of [16] was evaluated by the Canadian Society for Civil Engineering Task Committee on River Models, which verified the steady and unsteady flow calculations of ICSS using high-quality laboratory data (e.g., 0.29% and 0.68% errors obtained for maximum water depth at the upstream and the downstream ends of the flume, respectively). The obtained hydrograph had no error and predicted the flow accurately, as shown in Shahverdi [21], where field data of the canal were gathered to calibrate the flow coefficients of check and turnout gates and Manning’s roughness coefficient, resulting in 0.7, 0.6, and 0.017, respectively.
ICSS was placed within the FSL code of MATLAB 2013a. For this purpose, the original code of the ICSS was converted to a digital library link (DLL) file by a FORTRAN program termed ICSS DLL. This file was called in the FSL MATLAB m-file environment.
The ICSS interacts with FSL. The inputs to the ICSS DLL are the actions selected in each iteration, and its outputs are the simulated water depths upstream of the check structures, delivered flow to the turnouts, and flow passing under the check structures. The time interval () was 0.01 h, and the total simulation time was 24 h. Briefly, ICSS DLL reads the actions from the previous iteration, simulates the canal condition based on the actions, and finally gives the mentioned outputs for the reward calculation using reward function. A reward () is assigned to the selected and applied action with the ICSS DLL using
where is the sum of the differences between requested and delivered water flow in the turnouts; is the simulated depth upstream of the check structure in each time step; and is the target depth upstream of the check structure, which is equal to the normal depth in each reach. According to the reward function, if water depth is inside the dead band and by applying the selected action, then maximum reward () becomes 10000, which corresponds to the best action. Otherwise, a punishment is given to the selected action. As can be seen, a penalty (negative reward) with a linear function is assigned if water depth exceeds the dead band; otherwise, a reward (positive value) is assigned.
2.5. The FIS Structure in Water Delivery Problems
In the context of water delivery and distribution systems, the generalization and convergence specifications of FSL mean that FSL can learn appropriate actions for a few states (water requests) and can estimate actions of any states. Thus, in this research, a zero-order TSK fuzzy system was created and learned using the SARSA algorithm for all blocks of the canal.
The state s has two main elements, including the target depth upstream of the check structure (Yt) and delivered water to the turnouts (TO). Therefore, the dimension n of the state is related to the number of turnouts existing in the considered block and one target depth upstream of the check structure. Each element of s (xl, 1 ≤ l ≤ n) is determined based on its minimum and maximum values according to the canal data. The defined TSK fuzzy system associated with block 1 is shown in Figure 4. Since the first block has three turnouts and one check structure, the input state of its fuzzy system has four variables. The second block has two turnouts and one check structure, and therefore its associated fuzzy system has three input variables as the input state. Here, two MFs were defined for each dimension of the input space, and the fuzzy subspaces were created using the “AND” operator. The minimum and maximum values of each variable in FIS were defined based on the corresponding desired values, which were obtained using hydraulic and geometry parameters of the canal. The action includes gate openings (GO), and their time of adjustment (TA) is the appropriate action and is the FIS output. The output of the first and second FIS has seven and five elements, respectively.
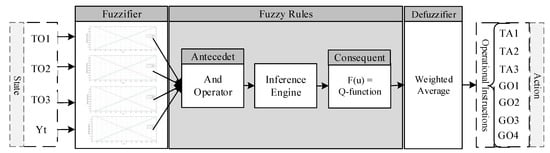
Figure 4.
The defined Takagi–Sogeno–Kang (TSK) fuzzy system associated with block 1.
Since the MFs for each input dimension are equal to 2, the total number of rules become 2n considering grid partitioning. For example, in Figure 4, the state input for the first block had 4 variables (n = 4), and its fuzzy system had 16 rules.
The output of this FIS is a vector with seven elements. The candidate values of each element were computed according to some specified boundaries. The proposed values for both GO1 and GO2 range between 1 cm and 22 cm. The range of candidate values ranges from 1 cm to 17 for GO3 and from 1 cm to 42 cm for Yt. The candidate actions of TA1, TA2, and TA3 range from 0.01 h to 0.41 h. The number of candidate actions for each element of the output is three in this research. Thus, there are 2187 (m = 37) candidate actions in each fuzzy rule; therefore, the dimension of Q-function for the system output is 16×2187 (2n × m). The weight Qij is the value of the candidate action vector j (actionij = (GO1, GO2, GO3, GO4, TA1, TA2, TA3)ij) in rule i. The most relevant parameters and their values used in this research are as Table 2.

Table 2.
The most relevant parameters and their values.
2.6. Generalizing Learned Q-Function (GLQ) Model
In the GLQ model, the QAC-function is included within the inference engine of fuzzy system instead of the SARSA process, and a greedy action selection method is used rather than the softmax one defined as
where is the state, is the fixed selected candidate action, and the denotes the action that maximizes . The greedy action selection method estimates the best action for any input using QAC-function, provided that Q is the highest. These estimated actions can be applied to the real canal structure manually by an operator.
The components of the GLQ model, developed in MATLAB 2013a, are a TSK fuzzy system, a greedy action selection method, the ICSS DLL model to test the system, and the reward function (Equation (8)). The consequent part of the TSK fuzzy system includes QAC-function. The GLQ model maps any input to the antecedent part of the TSK fuzzy system, calculates the corresponding actions based on the greedy action selection method, and the actions are displayed. Finally, an operator utilizes the canal to operate the structures using calculated operational instructions. The developed GLQ model architecture is shown in Figure 5.
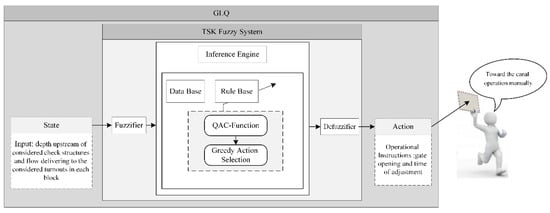
Figure 5.
The developed generalizing learned Q-function (GLQ) model architecture.
The comparison between Figure 5 and Figure 3 illustrates the main differences between the FSL and GLQ models:
- FSL uses SARSA to learn a Q-function, which is used by the GLQ to estimate actions from any input. Therefore, strictly speaking, the GLQ does not include the SARSA learning process.
- The action selection methods are different: FSL uses softmax, and the GLQ is based on a greedy selection mechanism.
- FSL uses feedbacks from the environment to learn and provide better responses; however, there is neither feedback interaction nor learning in the GLQ. In particular, FSL uses the ICSS model to simulate the canal and computes the reward and performance indicators. As for the GLQ, water depth and flows can be measured in the real canal to compute the reward and performance indicators.
- FSL requires a high-performance computer system to learn the Q-function, whereas the GLQ model can be installed on the mobile phone of the operator to be used anywhere. Therefore, a computer can be used for learning operational instructions of different canals to reduce costs. In fact, FSL learns online, and the GLQ is used offline. However, FSL may be used to generate manual instructions that operators can use, it requires expertise, and a high-performance computer is necessary.
- SARSA can keep learning, whereas QAC-function in the GLQ can be updated anytime. For this purpose, the learning process by SARSA must be continued from where the learning is terminated. The result is an updated QAC-function that can be replaced with the existing QAC-function in the GLQ, which is an advantage. For example, operators could perform their work with their handheld QAC-function and then provide the collected data to a server so as to upgrade their QAC-functions.
2.7. Investigating the Procedure of the Convergence and Generalization
As earlier mentioned, a water delivery programming in irrigation canals is complicated due to the numerous and varied requests for water, the number of structures, the unsteady canal flow conditions, and the short time between water requests and water delivery. It is difficult for the canal manager to find the best actions for any water requests in a short time. In this section, we study the properties of convergence and generalization for the proposed scheme.
To learn the consequent part of the TSK fuzzy system and generate corresponding Q-function, i.e., the QAC-function for the studied canal, some limited number of states were considered. The states were the delivered flows to the turnouts in season 2011, named s1, s2, and s3, that correspond to maximum flow, average flow, and minimum flow, respectively. For all three states, FSL learned the corresponding actions, and the QAC-function was created. It must be noted that there was only one QAC-function in which the arrays were updated in each iteration of the learning process. If FSL reaches the maximum possible reward in all states, i.e., or at least a reward more than 8500, during the learning process, its convergence is attained for the practical use of the method. Otherwise, the FSL divergences and their answers are not certified.
To investigate the generalization property of FSL, four different water requests from the East Aghili Canal data, which differ with those used for learning QAC-function, were randomly selected and named Request 1–Request 4. Then, corresponding actions for them were estimated using the developed GLQ model, and corresponding rewards and relative error, i.e., ||, were calculated. If the relative error is less than 15% or the assigned reward is higher than 8500, the generalization of FSL is both possible and accurate. Therefore, actions of unlimited water requests by users can be estimated using the GLQ model quickly.
2.8. Performance Indicators
In this research, water delivery performances for each turnout located in the East Aghili Canal were determined using the measure of performance relative to adequacy (MPA) and the measure of performance relative to efficiency (MPE) as suggested by the authors of [22]. The MPA is a spatial and temporal average of the ratio between the delivered and required flow, i.e.,
If the MPA is 1, water is delivered sufficiently, otherwise, turnouts can suffer from water shortage depending on the value of the MPA.
The MPE is a spatial and temporal average of the ratio of required to delivered flow defined as
where is the number of turnouts, is delivered discharge, is requested discharge, is the simulation time step, is total simulation time, and is the number of time steps of the simulation period and is defined as . If the MPE is 1, water is delivered efficiently, otherwise, efficiency decreases.
The performance standards according to the authors of [22] are given in Table 3.

Table 3.
Performance standards by Molden and Gates [22].
For water depth control evaluation, two indicators given by the authors of [23] were used, namely the maximum absolute error (MAE) demonstrated in Equation (12) and the integral of absolute magnitude of error (IAE) demonstrated in Equation (13).
where is the required target depth upstream of the check structure, and is the water level in each time step.
3. Results and Discussion
FSL tries to find the best actions for water requests in the East Aghili Canal. The FSL convergence processes for state s1 are shown in Figure 6 for different blocks. These figures show rewards and their related moving averages with a period of five iterations for all blocks.
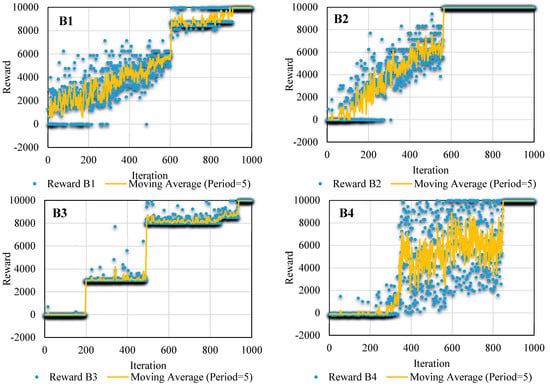
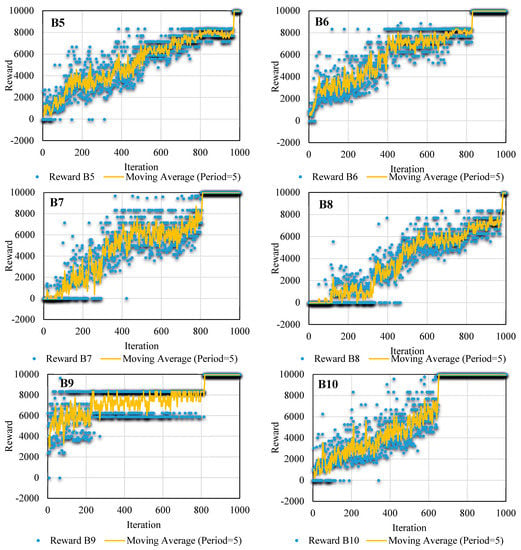
Figure 6.
The fuzzy SARSA (state, action, reward, state, action) learning (FSL) convergence to the desired reward in different blocks.
As shown, various operations were selected, and different rewards were assigned to the selected operations. The reward could be either positive or negative. According to the reward function, it is positive if water depth variations are within the dead band of ± 10%, and it is negative if water depth leaves the dead band. During the learning, the rewards are gradually increased and finally converged to a constant reward. The minimum reward during the learning was 9951, obtained in block 1 (B1) using the learning process, meaning that water depth variations were within the dead band; therefore, water was delivered to the turnouts with high accuracy. The maximum and minimum number of the FSL iterations obtained were 548 and 970, corresponding to B2 and B8, respectively. The same results were obtained for state s2 and state s3.
It should be noted that the reward value is calculated using Equation (8) depending on depth deviation from its target and flow deviation from the requested flow. The depth and flows are controlled using the corresponding turnout or check structure.
As shown in Figure 6, FSL converged with high accuracy in all blocks and extracted actions; therefore, the FSL convergence was certified. Note that the minimum value of the acceptable reward was 8537.
The greedy action selection method used in the GLQ model estimated corresponding operational instruction for water requests using the QAC-function. The assigned rewards for each operational instruction were estimated using the GLQ model, and the corresponding relative errors are presented in Table 4 for all blocks. The rewards ranges were between 9897 and 8537, respectively. Additionally, the relative errors were between 1% and 15%, respectively.

Table 4.
Assigned rewards of water requests and corresponding relative errors.
A noteworthy point here is the time of extracting actions by FSL in comparison to the GLQ. According to the authors of [4], the learning time of daily actions is 0.95 h in the East Aghili Canal. Since there are about 120 irrigation days per irrigation season in this canal, 114 h (4.75 days) are required by FSL to learn the corresponding actions. Using the proposed method, the QAC-function of this article was learned after 3.8 h from only 4 days of water requests. Therefore, a sensible reduction in the learning time and generalizability are the two main advantages of the GLQ when compared to standard FSL.
The following rules are a piece of fuzzy rule base learned in the FSL process for the first block of the East Aghili Canal:
R6: If TO1 is low and TO2 is high and TO3 is low and Yt is high, then action is [1 cm, 22 cm, 1 cm, 1 cm, 0.41 h, 0.21 h, 0.01 h].
R7: If TO1 is low and TO2 is high and TO3 is high and Yt is low, then action is [1 cm, 22 cm, 17 cm, 41 cm 0.21 h, 0.01 h, 0.01 h].
R8: If TO1 is low and TO2 is high and TO3 is high and Yt is high, then action is [1 cm, 22 cm, 17 cm, 1 cm, 0.41 h, 0.01 h, 0.01 h].
For example, the first rule (R6) expresses a situation in which low water is requested in the first turnout, high water is requested in the second turnout, low water is requested in the third turnout, and high target depth is observed upstream of the check structure. Thus, the action instruction should reduce the amount of gate opening in the first and third gates to 1 cm at the time of 0.41 h and 0.01 h, respectively. Additionally, it should increase the second gate to 22 cm at the time of 0.21 h while fixing the gate opening related to Yt at an opening of 1cm.
The water delivery performance indicator, MPA, is illustrated in Figure 7 in all blocks for investigated water requests (Request 1–Request 4). As shown, the minimum and maximum values of the MPA indicator are 0.93 and 1, respectively. The desired value of the MPA indicator is 1. In the worst condition, the MPA value is 0.93; however, it falls in the range of 0.9 to 1.0 regarding the criteria presented in [22]. Therefore, “good” performance is shown, and the water is delivered adequately. Furthermore, the corresponding reward for the MPA indicator of 0.93 is 8537, showing that FSL is generalizable.
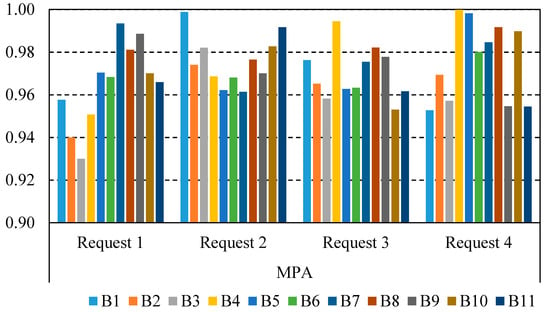
Figure 7.
The MPA performance indicator in the East Aghili Canal.
The water delivery performance indicator, MPE, is illustrated in Figure 8 in all blocks for investigated water requests (Request 1–Request 4). As shown, the minimum and maximum values of the MPE indicator are 0.95 and 0.99, respectively. The desired value of the MPE indicator is 1. The least value of the MPA indicator is 0.95; however, it falls in the range of 0.9-1.0 regarding the criteria presented in [22]. Therefore, “good” performance is shown and water is delivered efficiently. Furthermore, the corresponding reward for the MPA indicator of 0.95 is 9750.
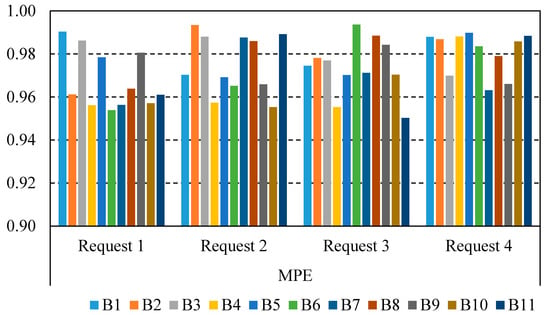
Figure 8.
The MPE performance indicator in the East Aghili Canal.
The performance indicators of MAE and IAE in the East Aghili Canal are illustrated in Figure 9 and Figure 10, respectively. As shown, the maximum values of the water depth indicators, i.e., MAE and IAE, are 10% and 8.8%, respectively. Furthermore, the minimum values of the MAE and IAE are 1.47% and 1.07%, respectively. The lower these indicators, the better the performance. Moreover, performance results show improvements with respect to other methods, e.g., the maximum deviations from the defined ±10% dead-band is 10%, much below the 42% reported in [17].
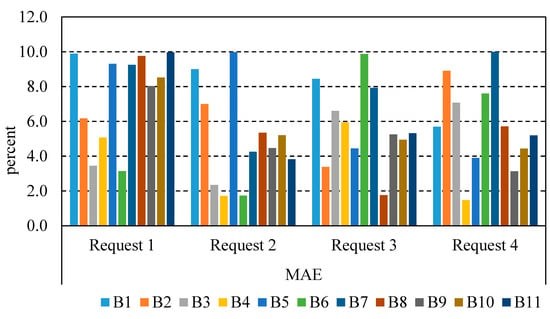
Figure 9.
The maximum absolute error (MAE) performance indicator in the East Aghili Canal.
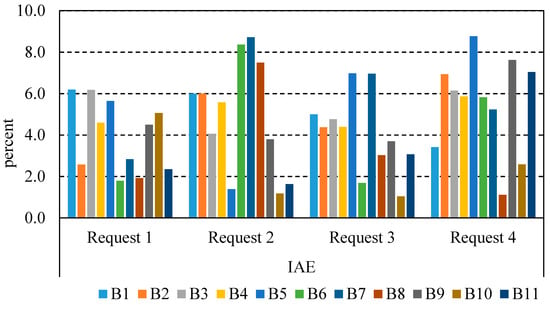
Figure 10.
The absolute magnitude of error (IAE) performance indicator in the East Aghili Canal.
Therefore, the water level does not leave the dead band, and performance is acceptable. Water delivery to the turnouts was accurate, and water depths fluctuations were low.
In addition, the investigated water depth and delivery indicators for the canal are illustrated in Figure 11. As shown, a “good” performance is obtained according to the performance criteria presented in [22]. Overall, all the above values and corresponding figures show that FSL can be generalized using the GLQ model.
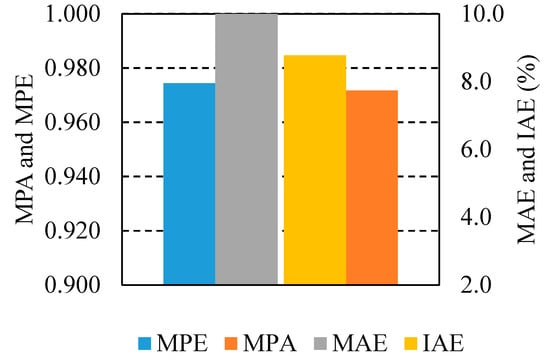
Figure 11.
The performance indicators in the East Aghili Canal.
According to the rewards, corresponding relative errors, and performance indicator values, it can be concluded that the FSL generalization is possible in irrigation canals, i.e., it is possible to train the system with typical situations, so a good performance can be expected in practice. Moreover, the system can learn new things in the future.
4. Conclusions
A light GLQ function for the real-time of irrigation canals based on FSL was proposed. Additionally, the convergence and generalization of the FSL model were explored in a simulated irrigation canal. The former is necessary to confirm the generalization results of the FSL model. If the learned results of the consequent part of a zero-order TSK fuzzy system, i.e., Q-function, can estimate accurately actions for a wide range of water requests, then FSL can be considered as a generalizable tool for irrigation canals. For this purpose, the GLQ (generalizing learned Q-function) model was developed in MATLAB 2013a.
The GLQ model developed in the current research benefits from both a TSK fuzzy system and the SARSA process. The antecedent part of the TKS fuzzy system was defined using water requests made by farmers. The consequent part is an unknown function found using the SARSA process. In the SARSA process, an action is selected and employed to the corresponding structure. The worthiness of the employed action is assessed using a reward, and this continues until the best action is found. The fully hydrodynamic ICSS model was used for simulating the canal and providing water depths, flows, and the adjustment of the canal’s structure.
Three states, which include water requests by farmers, were used for learning the consequent part of the fuzzy system in the East Aghili Canal, i.e., the QAC-function, and finding appropriate actions. In each state, the model was run for each block separately, the assigned rewards were followed, and finally, the QAE-function was generated. The convergence analysis showed that FSL can converge to a constant reward that corresponds to a relative error of less than 15%. The reward shows the accuracy of water delivery since the delivered flow deviation from the desired one (requests by farmers) is used in the reward calculation. As a consequence, reward convergence holds, and generalization is possible.
Actions were extracted using the QAE-function for states that differ from those used for learning. Water delivery performance indicators, including MPA and MPE, used for evaluating the GLQ results, were 0.96, which is very close to their desired values, i.e., 1. MAE and IAE were less than 10% and 6.2%, respectively. Considering the results, the FSL convergence accuracy was certified, and its consideration for real applications is therefore recommended.
Author Contributions
Conceptualization, K.S., F.A.-H. and J.M.M.; methodology, K.S., F.A.-H.; software, K.S. and F.A.-H.; validation, K.S. and F.A.-H.; formal analysis, K.S., F.A.-H., J.M.M. and X.T.; resources, K.S. and F.A.-H. and X.T.; writing—original draft preparation, K.S., F.A.-H. and X.T.; writing—review and editing, K.S., J.M.M. and X.T.; visualization, K.S., J.M.M. and X.T.; supervision, J.M.M. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support from the Spanish Ministry of Economy is gratefully acknowledged (project C3PO, with ref. DPI2017-86918-R).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Figueiredo, J.; Botto, M.A. Automatic Control Strategies Implemented on a water canal prototype. IFAC Proc. Vol. 2005, 38, 22–27. [Google Scholar] [CrossRef]
- Liu, F.; Feyen, J.; Malaterre, P.-O.; Baume, J.-P.; Kosuth, P. Development and Evaluation of Canal Automation Algorithm CLIS. J. Irrig. Drain. Eng. 1998, 124, 40–46. [Google Scholar] [CrossRef]
- Mathur, Y.; Sharma, G.; Pawde, A. Optimal Operation Scheduling of Irrigation Canals Using Genetic Algorithm. Int. J. Recent Trends Eng. 2009, 1, 11–15. [Google Scholar]
- Omidzade, F.; Ghodousi, H.; Shahverdi, K. Comparing Fuzzy SARSA Learning and Ant Colony Optimization Algorithms in Water Delivery Scheduling under Water Shortage Conditions. J. Irrig. Drain. Eng. 2020, 146, 04020028. [Google Scholar] [CrossRef]
- Burt, C. The irrigation Sector shift from construction to modernization: What is required for success? Irrig. Drain. 2013, 62, 247–254. [Google Scholar] [CrossRef]
- Arauz, T.; Maestre, J.; Tian, X.; Guan, G. Design of PI Controllers for Irrigation Canals Based on Linear Matrix Inequalities. Water 2020, 12, 855. [Google Scholar] [CrossRef]
- Monem, M.J.; Nouri, M.A. Application of PSO method for optimal water delivery in irrigation networks. Iran. J. Irrig. Drain. 2010, 4, 73–82. [Google Scholar]
- Ramesh, B.R.; Venugopal, K.; Karunakaran, K. Zero-One Programming Model for Daily Operation Scheduling of Irrigation Canal. J. Agric. Sci. 2009, 1, 13. [Google Scholar] [CrossRef][Green Version]
- Liu, Y.; Yang, T.; Zhao, R.; Li, Y.-B.; Zhao, W.; Ma, X. Irrigation Canal System Delivery Scheduling Based on a Particle Swarm Optimization Algorithm. Water 2018, 10, 1281. [Google Scholar] [CrossRef]
- Van Overloop, P.-J. Model Predictive Control on Open Water Systems; IOS Press: Delft, The Netherlands, 2006. [Google Scholar]
- Van Overloop, P.; Maestre, J.M.; Sadowska, A.D.; Camacho, E.; De Schutter, B. Human-in-the-Loop Model Predictive Control of an Irrigation Canal [Applications of Control]. IEEE Control. Syst. 2015, 35, 19–29. [Google Scholar] [CrossRef]
- Hashemy, S.M.; Monem, M.J.; Maestre, J.M.; Van Overloop, P.-J. Application of an In-Line Storage Strategy to Improve the Operational Performance of Main Irrigation Canals Using Model Predictive Control. J. Irrig. Drain. Eng. 2013, 139, 635–644. [Google Scholar] [CrossRef]
- Shahdany, S.H.; Taghvaeian, S.; Maestre, J.; Firoozfar, A. Developing a centralized automatic control system to increase flexibility of water delivery within predictable and unpredictable irrigation water demands. Comput. Electron. Agric. 2019, 163, 104862. [Google Scholar] [CrossRef]
- Derhami, V.; Majd, V.J.; Ahmadabadi, M.N. Fuzzy Sarsa Learning and the proof of existence of its stationary points. Asian J. Control. 2008, 10, 535–549. [Google Scholar] [CrossRef]
- Shahverdi, K.; Monem, M.J.; Nili, M. Fuzzy Sarsa Learning of Operational Instructions to Schedule Water Distribution and Delivery. Irrig. Drain. 2016, 65, 276–284. [Google Scholar] [CrossRef]
- Manz, D.H.; Schaalje, M. Development and application of the irrigation conveyance system simulation model. In International Seminar on the Application of the Irrigation Mathematical Modeling for the Improvement of Irrigation Canal Operation; CEMAGREF: Montpelier, France, 1992. [Google Scholar]
- Savari, H.; Monem, M.J.; Shahverdi, K. Comparing the Performance of FSL and Traditional Operation Methods for On-Request Water Delivery in the Aghili Network, Iran. J. Irrig. Drain. Eng. 2016, 142, 04016055. [Google Scholar] [CrossRef]
- Derhami, V.; Majd, V.J.; Ahmadabadi, M.N. Exploration and exploitation balance management in fuzzy reinforcement learning. Fuzzy Sets Syst. 2010, 161, 578–595. [Google Scholar] [CrossRef]
- Sugeno, M.; Takagi, T. Multi-dimensional fuzzy reasoning. Fuzzy Sets Syst. 1983, 9, 313–325. [Google Scholar] [CrossRef]
- Harandi, F.A.; Derhami, V. A reinforcement learning algorithm for adjusting antecedent parameters and weights of fuzzy rules in a fuzzy classifier. J. Intell. Fuzzy Syst. 2016, 30, 2339–2347. [Google Scholar] [CrossRef]
- Shahverdi, K. Development of on-request Operation System for Irrigation Networks Using Reinforcement Learning Algorithm (Case Study: East Aghili Calnal). In Water Structures Engineering; Tarbiat Modares University: Tehran, Iran, 2015; p. 130. [Google Scholar]
- Molden, D.J.; Gates, T.K. Performance Measures for Evaluation of Irrigation-Water-Delivery Systems. J. Irrig. Drain. Eng. 1990, 116, 804–823. [Google Scholar] [CrossRef]
- Clemmens, A.J.; Kacerek, T.F.; Grawitz, B.; Schuurmans, W. Test Cases for Canal Control Algorithms. J. Irrig. Drain. Eng. 1998, 124, 23–30. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).