An Overland Flood Model for Geographical Information Systems

Abstract

A variety of flood models and commercial flood simulation software are provided in the literature, with different accuracies and precisions changing from coarse to fine, depending on model structure and detailed descriptions of basin and hydrologic properties. These models generally focus on river processes, taking overland processes as inputs of 1D or 2D hydrodynamic or hydrologic river flow models. Due to the discrete structure of overland flow and unknown-dynamic boundary conditions, such classical approaches are not cable of fast and reliable spatio–temporal estimations for overland flows, and require detailed and well-organized spatial data that cannot be immediately obtained during an emergency. A spatially-distributed Geographical Information Systems (GIS) based flood model is developed in this study to simulate overland floods, using cellular automata principles. GIS raster cells are considered hydrologic homogeneous areas throughout which hydrologic properties remain constant. Hydrodynamic flow principles, conservations of mass, momentum and energy are applied at pixel level to simulate floodwaters. The proposed GIS model is capable of directly manipulating spatio–temporal pixel level data (e.g., topography, precipitation, infiltration, surface roughness etc.) for modeling of rainfall-induced overland floods; therefore, it can provide fast, temporal and spatial flood depth estimations as well as maximum flood depths and times of concentration for all pixels throughout a study area. The model is quite simple and easy to apply via easily creatable GIS input layers, and is thus very convenient for preliminary engineering applications that need quick and fast response. Its main advantage is that it does not need a predefined flood boundary and boundary conditions. This advantage is especially valuable for coastal plains where delineation of a basin is generally too difficult. Floodwaters of Cyclone Nargis/Myanmar were simulated to test the model. Sensitivity analyses were applied to evaluate the effects of the model parameters (i.e., surface roughness and infiltration rates) on simulation results. The study shows that the proposed GIS model can be readily applied for the fast and inexpensive modeling of rainfall caused floods in areas where flood boundaries and boundary conditions cannot be clearly identified.

1. Introduction

Experiences have shown that the only reliable way to prevent flood damage and casualties is to keep people away from floodwaters [1,2]. In order to achieve this purpose, hydrologic and hydraulic deterministic models have been traditionally used as valuable tools providing timely and detailed information on flood characteristics and impacts [3,4,5,6], and promise great value for flood management practices, regarding both rainfall-induced (i.e., pluvial) floods and river-induced (i.e., fluvial) floods. Indeed, during an emergency, the main requirement is generally to forecast flood impacts rather than to predict statistical flood characteristics by stochastic models [7,8,9]. Hydrologic river-induced flood models basically try to elucidate flood behavior by integrating three main hydrologic components, precipitation, infiltration and runoff [10,11,12] via a vast variety of empirical, numeric and statistical approaches [5,8,13,14]. Deterministic river-induced flood models analyze surface processes generally by empirical approaches, black box models or hydrodynamic models. Empirical approaches and black box models are easy to apply and to integrate with the models of the other hydrologic components; they provide single point estimates at the outlet of the considered basin rather than spatial estimates for overland processes [15]. On the contrary, hydrodynamic river-induced flood models account successfully for surface processes [9,16,17,18] provided that there is a continuity in floodplain flows within a well-defined boundary [5,8,13,14]. They have high accuracy and spatial/temporal capabilities in flood modeling but suffer from some difficulties in practice when evaluating rainfall induced overland floods. These difficulties may be summarized as follows: (1) During an extreme flood, a river generally does not flow in its regular bed—the flood extent is a dynamic process—so that boundary conditions cannot be defined properly, (2) The most destructive effects of floods occur generally on low-elevated plain areas; however, rivers do not usually have regular, natural flood courses in such areas but separate into tributaries to form deltas. Most of the population potentially under the threat of threat of flooding live in such areas, where the main economical/agricultural activities take place, (3) Lateral surface flows, varying spatially and temporally, cannot be easily and properly considered in a traditional hydrodynamic model, which uses lumped data at model boundaries, (4) Traditional hydrodynamic models may not be easily applied in emergencies because of the problems related with parameterization, time limitation and lack of trained personnel [4,19,20,21,22,23,24,25,26]. In addition, hydrodynamic river-induced flood models require highly accurate and precise data. Such data may not be available in developing countries such as Myanmar.

A variety of improvements, relying on spatial data and remote sensing technologies that allow detailed description of basin properties and instantaneous measurement of precipitation, have been suggested in the literature to reduce the above drawbacks. For instance, Garrote and Bras (1995) developed a real time flood forecasting model that uses a digital elevation model (DEM) coupled with spatial rainfall data, aggregating surface flows to give a response at the outlet of basin [20]. Liu and De-smedt (2005) introduced a spatially distributed hydrological model that combines a digital elevation model and soil and land use data to forecast flood hydrographs for a specific flow section in a considered river basin [4]. Bates et al. (1998) used satellite images to define dynamic inundation boundaries and to forecast spatially distributed flow properties such as water depth and velocity. However, this approach could only account for seasonal changes in possible flood boundaries [27]. Cobby et al. (2003) used Airborne Scanning Laser Altimetry data for parameterization of two-dimensional hydraulic flood model frictions caused by bathymetric measurements and vegetation heights [16]. Knebla et al. (2005) developed a framework for regional flood modeling, using NEXRAD (The Next Generation Weather Radar), GIS (Geographical Information Systems) and HEC (The Hydrologic Engineering Center River Analysis System) models [7]. In addition to these attempts, some commercial hydrologic simulation models included some spatial data analysis modules that integrate GIS and remote sensing data into the classical hydrodynamic modeling so as to provide detailed descriptions for initial and boundary conditions. There is also various commercial hydrodynamic flood simulation software in the literature for river-induced floods, with different accuracies and precisions changing from coarse to fine, depending on model structure and detailed description of basin and hydrologic properties. Focusing on river processes, these models consider overland processes as inputs of 1D or 2D hydrodynamic or hydrologic river flow models, taking overland flows as static or dynamic model boundary conditions. Due to discrete structure of overland flow and unknown-dynamic boundary conditions, such approaches require detailed and well organized spatial data that cannot be immediately obtained during an emergency, thus hampering fast modeling and reliable spatio–temporal estimations for overland flows.

On the other hand, rainfall-induced (i.e., pluvial) floods require the prior involvement of land processes, contrary to river induced floods (i.e., river overflowing and tsunami surging). They are of discrete structures of overland flow and unknown-dynamic boundary conditions. Some researchers such as Bates & De Roo (2000) and Hunter et al. (2005) developed some Cellular Automata approaches that rely on shallow water equations to facilitate flood inundation modeling processes [21,22]. Chen et al. (2009) developed and tested a GIS-based urban flood inundation model (GUFIM) that consists of a storm–runoff and inundation components [28]. The storm–runoff model therein is based on the Green–Ampt model, and the inundation model uses the output of the storm–runoff model, regarding rainfall characteristics, soil properties, and drainage infrastructure [28]. Yamazaki et al., (2017) showed that MERIT-DEM (Multi Error Removed Improved Terrain- Digital Elevation Model) perform much better for pluvial flood modelling, though it has the same resolution as the SRTM (Shuttle Radar Topography Mission) 3 arc data [29]. Zhu (2010) used the relationship between water volume and water level to model inundated areas for a given water level and for a given peak discharge [19]. Xianhong Meng et al. (2019) developed a semi-physical distributed hydraulic model relying on GIS platforms for urban rainstorm inundations [30]. Tehrany et al. (2017) derived the extent of flood prone areas in China, using the three standalone statistical methods of frequency ratio (FR), logistic regression (LR) and weight of evidence (WoE) and compared the efficiency of them [31]. Yamazaki et al. (2019), developed MERIT-Hydro to provide a global stream network contributing a better flood modeling [32]. All these studies showed that the models of rainfall induced floods suffer from inexistency of regular river course, spatial size of the area under threat, lack of area-wide hydrologic data and limited time to organize spatial data for model simulations. To increase the effectiveness of rainfall induced flood simulations, many improvements on hydrodynamic models are suggested in the literature. For example, Ferraro et al. (2020) proposed a rigorous approach for a priori design of a computational mesh, to approximate an optimal computational mesh, for a time-saving process [33]. Costabile et al. (2019) examined two-dimensional shallow water equations for the hydraulic characterization of the river drainage networks, to determine scaling laws that describe the relations between the water depth threshold and a dimensionless area [34]. Cea and Bladé et al. (2015) decoupled hydrological discretization scheme for solving the shallow water equations in hydrological applications involving surface runoff in rural and urban basins, to simplify code and to lower computational cost per time step [35]. As an alternative approach, GIS flexibility on data manipulation and hydrodynamic model capability in flood modelling may be combined to facilitate modeling procedure and to get reliable spatio–temporal estimations for overland flows.

This study proposes an overland flood model that relies on cellular automata, fast aiming and empirical GIS modeling. It is a practical GIS model on the basic hydraulic principles, taking into account real time hydrologic parameters such as spatial precipitation, land covers, soil properties, elevation etc. to estimate over land flows. The model uses spatial data in an integrated way with a cell-by-cell manipulation algorithm that eliminates problems associated with dynamical flood extent and boundary conditions. It directly uses basic hydrodynamic flow principles at pixel level, to model spatio–temporal flood behavior. It has GIS flexibility in data provision and manipulation, and hydrodynamic model capability in spatio–temporal modeling. The study first introduces the structure of the proposed model, and then models the flood in Myanmar caused by the Cyclone Nargis, the deadliest cyclone on Bengal Bay since 1970. The MODIS (Moderate Resolution Imaging Spectroradiometer) flood water product from the Aqua and Terra satellites was used to evaluate the estimated flood extent. Sensitivity analyses were conducted to test effects of surface roughness and infiltration rate on model results. The advantages and disadvantages of the proposed flood model are discussed at the end of the study. The cellular automata model proposed herein presents a practical solution for simulating rainfall-induced floods in difficult-to-define natural catchments when calibrated hydrologic models are not available, and can be readily used for rainfall induced flood modelling in any GIS environment. Providing dynamical water depth and extent estimations for overland flows (i.e., flow hydrographs and concentration times for all pixels in a study area), the model relies on input GIS layers (e.g., layers of digital elevation and basic hydrologic variables), for which the boundaries are the sides of these raster layers. This should provide a valuable tool for fast, real time, rainfall induced flood simulations, especially in flat areas. Giving pixel level temporal and quantitative information on floodwaters, can be beneficially used in many aspects of disaster management.

2. Materials and Methods

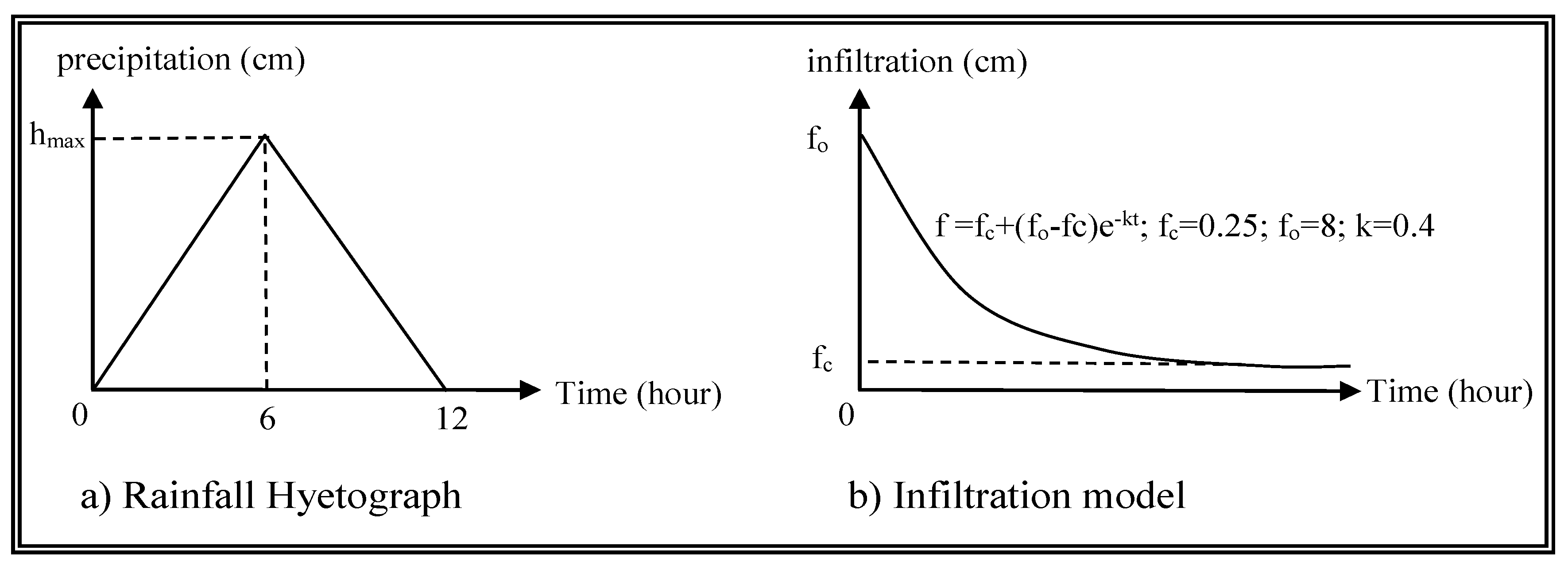
2.1. Background

Regional flood modeling studies in the literature have generally relied on the idea of considering a watershed basin as a combination of small hydrological homogeneous units [9]. Nash (1957) showed that a watershed basin can be represented by a series of identical linear reservoirs [36]. This idea was developed further into the concept of hydrologic homogeneous region by several investigators. Various approaches were developed to define hydrologic homogeneous regions, based on in situ measurements and remote sensing data [6,11,37,38,39,40,41]. However, these approaches generally need a multitude of statistical parameters and define subjective and broad homogenous areas, so that they cannot be readily applied for dynamic spatio–temporal flood analyses.

GIS provides a practical and beneficial environment for fast and visual evaluation of the spatial and temporal behavior of floodwaters [1,26]. Hydrologic inputs such as rainfall, infiltration and runoff can be readily defined and manipulated in a GIS environment, spatially and temporally [42,43,44,45]. Such a data provision and manipulation capability gives an opportunity to conduct a cell-by-cell analysis for flood modeling via cellular automata approach. Cellular automata basically attempts to define the study area as a lattice of discrete identical cells. It then calculates cell values by deterministic rules, taking the values of neighboring cells into account [46,47,48,49]. Accordingly, GIS raster pixels (or cells) may be considered as hydrologic homogeneous units where hydrologic properties do not change significantly, and basic hydrodynamic flow principals can be applied for them.

Ahmad and Simonovic (2004) refer to several models that use the cellular automata concept for modeling surface waters [50]. For instance, Miller et al. (1993) used this concept to calculate monthly flows at the mouths of the world’s major rivers by an atmospheric general circulation model [51]. Sausen et al. (1994) proposed a model for simulating continental monthly runoff, using a liner advection scheme based on a function of the terrain slope [52]. Naden (1992) incorporated spatial variability into a unit hydrograph type flood estimation procedure, using a network width function indicating the number of subsequent channels at successive distances away from basin outlet [53]. Regarding the rainfall-caused floods, Ozga-Zielinska et al. (2002) developed a cellular automata model that uses the number of potential contributing cells for calculating surface runoff in an individual cell within a cell grid [8]. This model relies on elevation and static flow directions (i.e., flow accumulation function) [8]. Flow accumulation function in its traditional form does not provide a dynamic approach that takes into account changing flood depth and extent [8]. Ahmad and Simonovic (2004) made a valuable attempt to model surface flows on a cell-by-cell basis. They simulated flood propagation by coupling a system dynamics (SD) approach and GIS. In their study, the water balance is provided based on rainfall rate, evaporation rate and inflow/outflow water excesses; excess water is defined as the difference between the volume of floodwater in a cell and cell’s storage capacity which is determined regarding sinks in the study area; to provide flow exchange between cells, calculated excess waters are distributed to four neighbor cells in descending order of slope differences [50]. Ahmad and Simonovic’s (2004) model has some practical limitations. Since flow exchanges between grid cells are calculated based on proportionality in the amounts of excessive waters in considered pixel and neighboring pixels, the model does not account for temporal exchanges between cells (it assumes that all of the excessive water in a cell is transferred within a considered time step). The other limitation is the definition of “storage capacity” hampering mass conservation at pixel level, as it does not distinguish topographic sinks and sinks due to possible outliers in the digital elevation model. In addition, the use of sinks for estimation of the storage capacity lacks infiltration rate. Because model exchanges data between SD and GIS, this model also has problems with data importing [50]. The literature also provides some fast-processing GIS approaches relying on Hierarchical Filling and Spilling [54,55,56,57]. They neglect the dynamic of flow process but are capable of identifying water depths at the end of a rainfall event, with low computational costs.

To address above given limitations, this paper presents a cellular automata model for rainfall induced (i.e., pluvial) floods, integrating basic hydrodynamic flow principals into GIS raster cells. It allows flood modeling when model boundaries and boundary conditions cannot be clearly defined (e.g., for deltas, coastal plains or other flat areas).

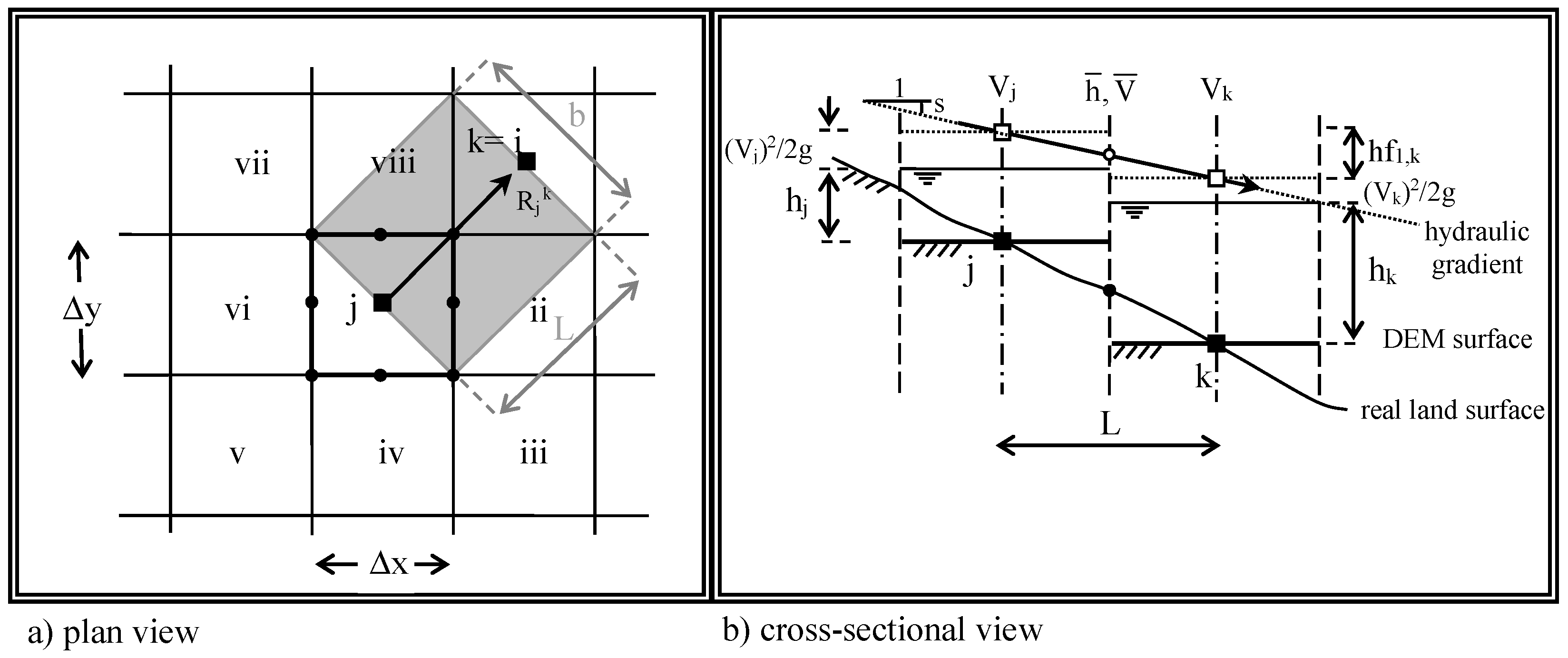
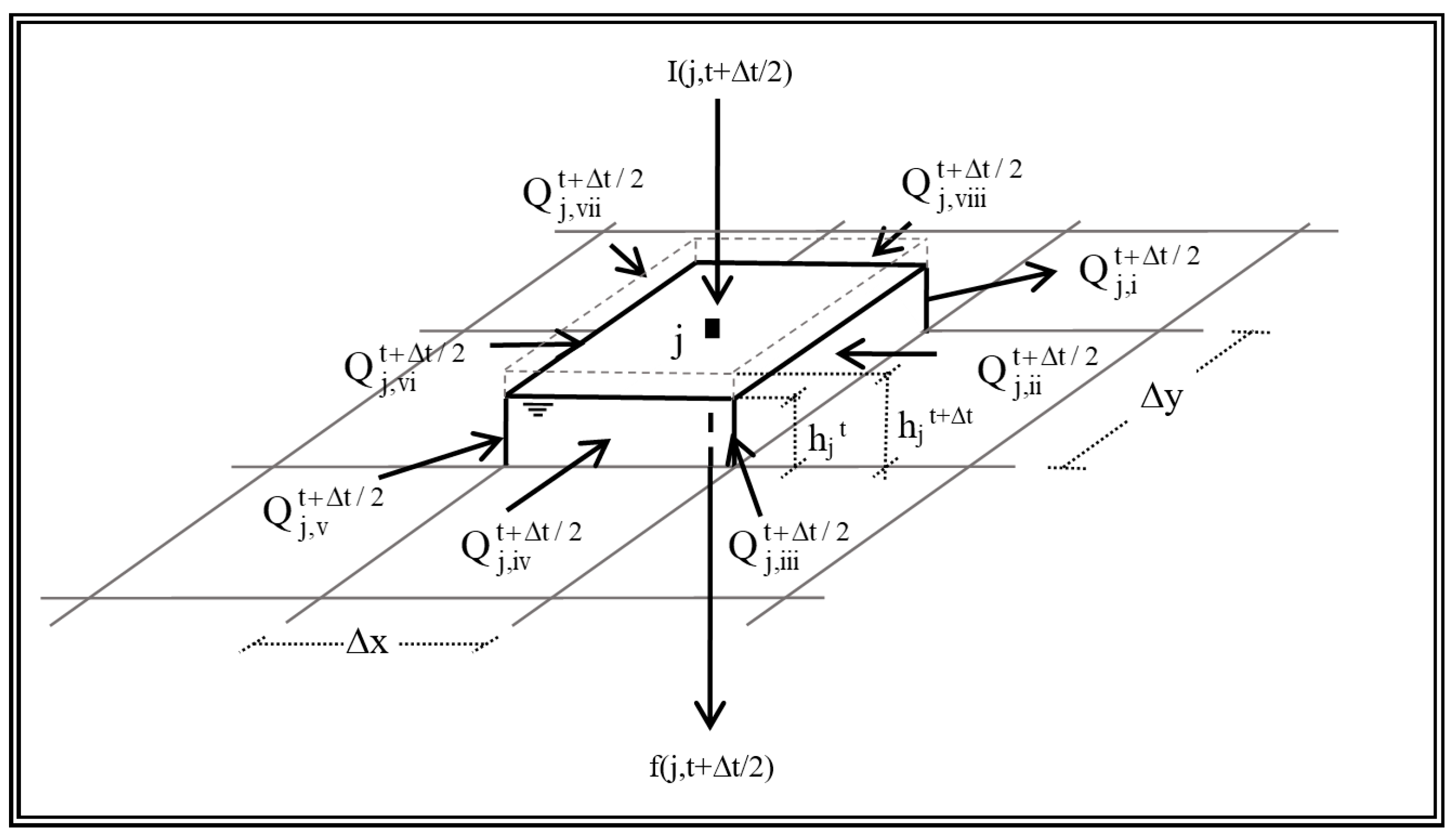
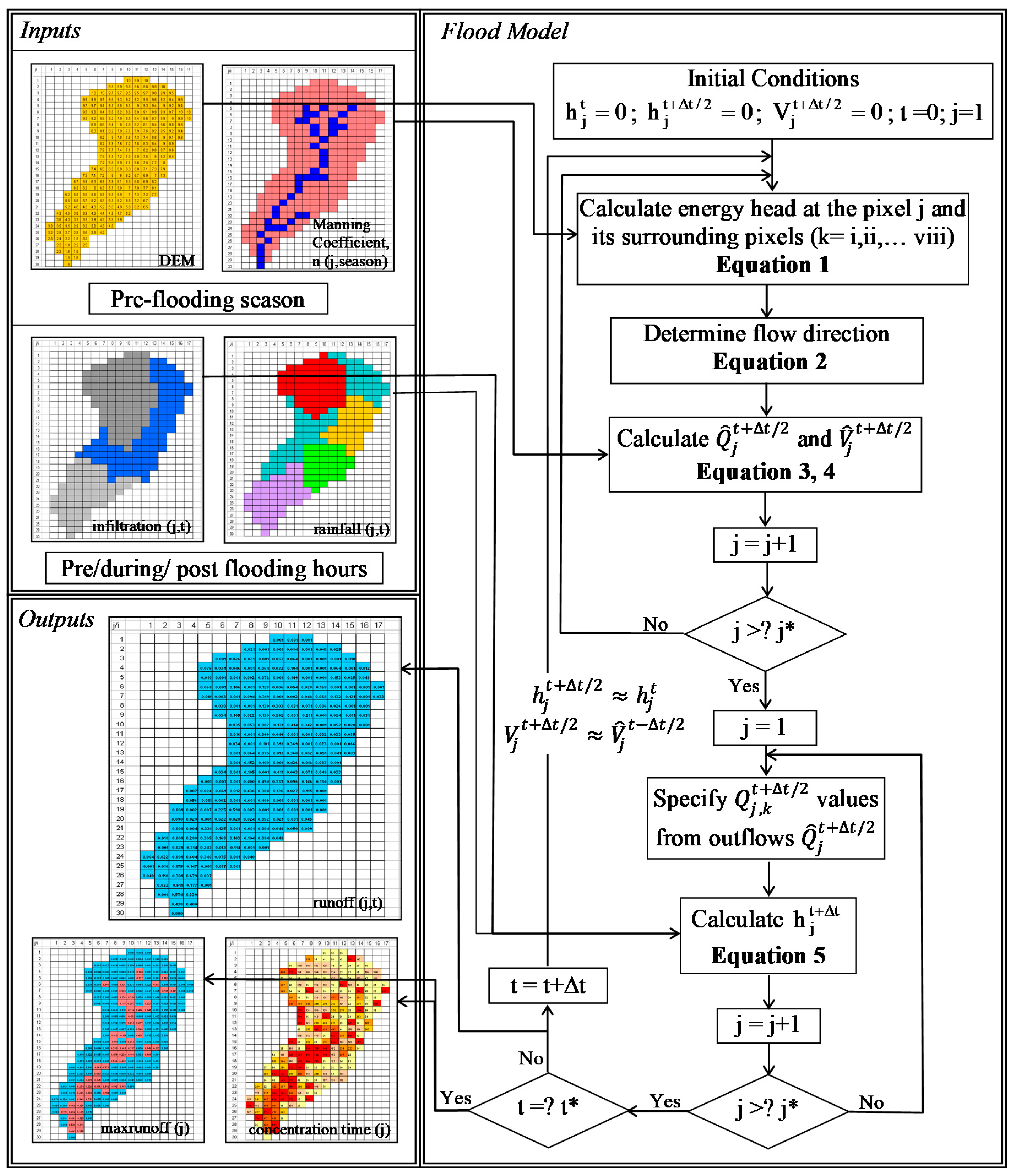
2.2. Model Structure

Hydrodynamic models use simplified forms of Navier–Stokes equations to simulate flood characteristics in predefined one or multi-dimensional meshes [23,24,58,59]. Since Navier–Stokes equations do not have a closed-form solution except for very simplified cases, they cannot be directly used in a cellular automata model contrary to the energy and continuity equations.

Figure 1 shows computation details of the cell-by-cell processing proposed herein. For a small enough pixel j, as in this figure, the hydrologic characteristics, such as land cover, soil type, land slope, etc., can be regarded as uniform [60]. O’Callaghan and Mark (1984) showed how drainage networks can be extracted by digital elevation data [61]. Using O’Callaghan and Mark’s principal that flood waters in a pixel can flow to one of eight surrounding pixels (i.e., toward i, ii, …, viii), the flow direction can be determined by means of the maximum hydraulic gradient. For a small time interval Δt, the outflow discharge of the considered pixel j can be regarded as steady (i.e., not changing by time). Therefore, the Bernoulli equation can be used to calculate the maximum hydraulic gradient associated with the flow direction, assuming that floodwaters are incompressible and inviscid [15,23,24]. For time intervals 0–Δt, Δt–2Δt, 2Δt–3Δt, the Bernoulli equation between the pixel j and its surrounding pixels (i.e., k = i, ii, …, viii) can be expressed by equation (1) (see Figure 1). Using a semi-implicit scheme that solves the Bernoulli Equation in fractional times and the Continuity Equation in non-fractional times, we can define the maximum hydraulic gradient ${\widehat{s}}_j^{t+\mathsf{\Delta }t/2}$ by Equation (2). Note that since the Bernoulli Equation assumes a steady flow, a full implicit scheme that uses same time equations does not account for the next time variables.

$$\begin{array}{c}\stackrel{E_j^{t+\mathsf{\Delta }t/2}}{\overbrace{z_j+h_j^{t+\mathsf{\Delta }t/2}+\frac{1}{2g}{\left(V_j^{t+\mathsf{\Delta }t/2}\right)}^2}}=\stackrel{E_k^{t+\mathsf{\Delta }t/2}}{\overbrace{z_k+h_k^{t+\mathsf{\Delta }t/2}+\frac{1}{2g}{\left(V_k^{t+\mathsf{\Delta }t/2}\right)}^2}}+h{f}_{j,k}^{t+\mathsf{\Delta }t/2};\\ h{f}_{j,k}^{t+\mathsf{\Delta }t/2}=s_{j,k}^{t+\mathsf{\Delta }t/2}·L_{j,k}\end{array}$$

(1)

$${\widehat{s}}_j^{t+\mathsf{\Delta }t/2}=max·{\left[\frac{\left(E_j^{t+\mathsf{\Delta }t/2}-E_k^{t+\mathsf{\Delta }t/2}\right)}{L_{j,k}}\right]}_{k=i}^{viii}$$

(2)

where:

z_j is the elevation of the pixel j;

$h_j^{t+\mathsf{\Delta }t/2}$ and $V_j^{t+\mathsf{\Delta }t/2}$ are, respectively, the water depth and runoff velocity in the pixel j. They may be assumed to be zero for t = 0;

$h{f}_{j,k}^{t+\mathsf{\Delta }t/2}$ and $s_{j,k}^{t+\mathsf{\Delta }t/2}$ are, respectively, the energy loss and hydraulic gradient for a considered direction, pixel and time interval;

$E_j^{t+\mathsf{\Delta }t/2}$ and $E_k^{t+\mathsf{\Delta }t/2}$ are the energy heads for the pixel j and k.

L_j,k is the distance between considered pixel j and surrounding pixels k.

Following the flow direction and using the flow velocity calculated by the Manning Equation (3), the outflow ${\widehat{Q}}_j^{t+\mathsf{\Delta }t/2}$ from pixel j can be calculated by Equation (4). Note that the outflow of the pixel j is the inflow to the pixel ${\widehat{k}}_j$ (i.e., the pixel in the direction of maximum hydraulic gradient for the pixel j).

$${\widehat{V}}_j^{t+\mathsf{\Delta }t/2}=\frac{1}{{\overline{n}}_j}{\left({\widehat{R}}_j^{t+\mathsf{\Delta }t/2}\right)}^{2/3}{\left({\widehat{s}}_j^{t+\mathsf{\Delta }t/2}\right)}^{1/2}$$

(3)

$${\widehat{Q}}_j^{t+\mathsf{\Delta }t/2}={\widehat{b}}_j^{t+\mathsf{\Delta }t/2}·{\widehat{h}}_j^{t+\mathsf{\Delta }t/2}·{\widehat{V}}_j^{t+\mathsf{\Delta }t/2}$$

(4)

where:

${\widehat{V}}_j^{t+\mathsf{\Delta }t/2}$ and ${\widehat{Q}}_j^{t+\mathsf{\Delta }t/2}$ are the flow velocity and flow rate leaving pixel j in the direction of the maximum hydraulic gradient;

${\overline{n}}_j$ is a mean value of the Manning coefficient for pixels j and ${\widehat{k}}_j$;

${\widehat{R}}_j^{t+\mathsf{\Delta }t/2}$ is the hydraulic radius which can be assumed equal to the water depth ${\widehat{h}}_j^{t+\mathsf{\Delta }t/2}$ between pixels j and ${\widehat{k}}_j$. For a small pixel size and time interval, ${\widehat{h}}_j^{t+\mathsf{\Delta }t/2}$ can be approximated as ${\widehat{h}}_j^{t+\mathsf{\Delta }t/2}=(h_j^t+{\widehat{h}}_j^t)/2$ regarding a uniform hydraulic gradient throughout the flow direction;

$h_j^t$ and ${\widehat{h}}_j^t$ are the water depths in the pixel j and ${\widehat{k}}_j$, respectively.

${\widehat{b}}_j^{t+\mathsf{\Delta }t/2}$ is a hypothetical channel width in the flow direction, and equal to $\sqrt{\mathsf{\Delta }{x}^2+\mathsf{\Delta }{y}^2}$ for the flow directions toward the pixels iii, v and vii. It is equal to $\mathsf{\Delta }x$ for the flow directions toward the pixels iv and viii and to $\mathsf{\Delta }y$ for thee= flow directions toward the pixels ii and vi.

Manning’s equation is valid for fully turbulent flows [9,23]. Reynold’s number can be used to determine the presence or absence of turbulent flow conditions, and then the Darcy–Weisbach equation can be exercised to calculate flow velocities for transitional and laminar flows. However, since floodwaters can be considered fully turbulent, in practice, there is no need to employ these calculations, except when detailed examination of overland flow is required [9,15].

Once the outflows/inflows of all pixels have been calculated by Equation (4), flood depths can be calculated using continuity Equation (5). Figure 2 shows outflows from/inflows to pixel j for a time interval Δt. Using these components, the continuity equation may be written at the end of a time interval Δt as follows:

$$h_j^{t+\mathsf{\Delta }t}=h_j^t+\mathsf{\Delta }t·\left[I\left(j,t+\mathsf{\Delta }t/2\right)-f\left(j,t+\mathsf{\Delta }t/2\right)\right]+\frac{\mathsf{\Delta }t}{\mathsf{\Delta }x·\mathsf{\Delta }y}{\displaystyle \sum }_{k=i}^{viii}{Q}_{j,k}^{t+\mathsf{\Delta }t/2}$$

(5)

where:

$I\left(j,t+\mathsf{\Delta }t/2\right)$ and $f\left(j,t+\mathsf{\Delta }t/2\right)$ are, respectively, the precipitation (inflow) and infiltration (outflow) rates for the time interval t to t + Δt.

$Q_{j,k}^{t+\mathsf{\Delta }t/2}$ refers to the surface flows. For the outflow (i.e., for the direction of the maximum hydraulic gradient), $Q_{j,k}^{t+\mathsf{\Delta }t/2}$ is calculated by Equation (4); for the inflows, $Q_{j,k}^{t+\mathsf{\Delta }t/2}$ is calculated as outflows of contributing neighbors of pixel j.

In order to solve the Bernoulli Equation and Continuity Equation in subsequent fractional times, and therefore to provide a full time simulation, it may be assumed that $h_j^{t+\mathsf{\Delta }t/2}\approx h_j^t$ and $V_j^{t+\mathsf{\Delta }t/2}\approx {\widehat{V}}_j^{t-\mathsf{\Delta }t/2}$, for small Δt values. Since net water outflow is calculated at fractional times (see Equation (4)), the assumption of $h_j^{t+\mathsf{\Delta }t/2}\approx h_j^t$ may only result in a time shift on calculations, which is ignorable for small Δt values. Similarly, since water depth changes are calculated at non-fractional times (see Equation (5)), the assumption of $V_j^{t+\mathsf{\Delta }t/2}\approx {\widehat{V}}_j^{t-\mathsf{\Delta }t/2}$ may only result in underestimates in depths for large Δt values, however, this is to be compensated at the next half time step when velocities are calculated via Equation (5). The numerical stability of the computations is provided here by the Courant Condition [9].

Repeating the procedure defined above for subsequent time steps (i.e., t = Δt, 2Δt, 3Δt, …, t*), the flow chart in Figure 3 shows the algorithm for the simulation of rainfall-induced floods. In the Figure, symbols j* and t* refer, respectively, to the total number of pixels and total simulation time. Accordingly, for a region enclosing the boundary of the basin feeding a study area, the Digital Elevation Model, Manning Coefficients, Infiltration Parameters/Model and spatio–temporal rainfall observations/simulations are arranged into GIS layers, during pre/intra/post flooding times. These GIS layers are the inputs of the Overland Flood Model. Note that the GIS layers should enclose all the pixels feeding the study area; other pixels may be excluded by pre-post GIS analyses. During simulations, pixels corresponding to natural wet areas, such as the sea or lakes, and the first and last pixel columns/rows have to be distinguished in the model from the rest of the pixels. The maximum flood depth in these pixels may be adjusted to a constant value (e.g., zero) in order to exclude computations there. Such a numerical approximation prevents redundant numerical calculations on wet areas and outflowing waters, while ignoring the impacts of inflowing waters outside of study area. A GIS clipping function can successfully handle the exclusion of this impact (i.e., the pixels with out-of-basin contributions), once the model gives results. As a first step of the model simulation, initial conditions such as initial overland water depth, flow velocity, infiltration rates are defined into the model for all the pixels. Then, outflows are calculated for each pixel by using Equations (1)–(4) via the methodology defined above. Inflows are determined regarding the outflows of surrounding pixels. Once inflows and outflow of the pixels are obtained, flood depths are calculated for all pixels by Equation (5). This procedure is repeated until a required simulation time, j*. The algorithm in Figure 3 produces flood depth grids at each time interval and maximum flood depth/time of concentration grids at the end of the simulation. Strictly speaking, the model automatically calculates the times of concentrations for each pixel, finding the times of maximum depth observed at each pixel, and creating a times of concentration image at the end of simulation. The modeling procedure given here can be easily loaded into a commercial GIS program as a GIS function.

3. Application

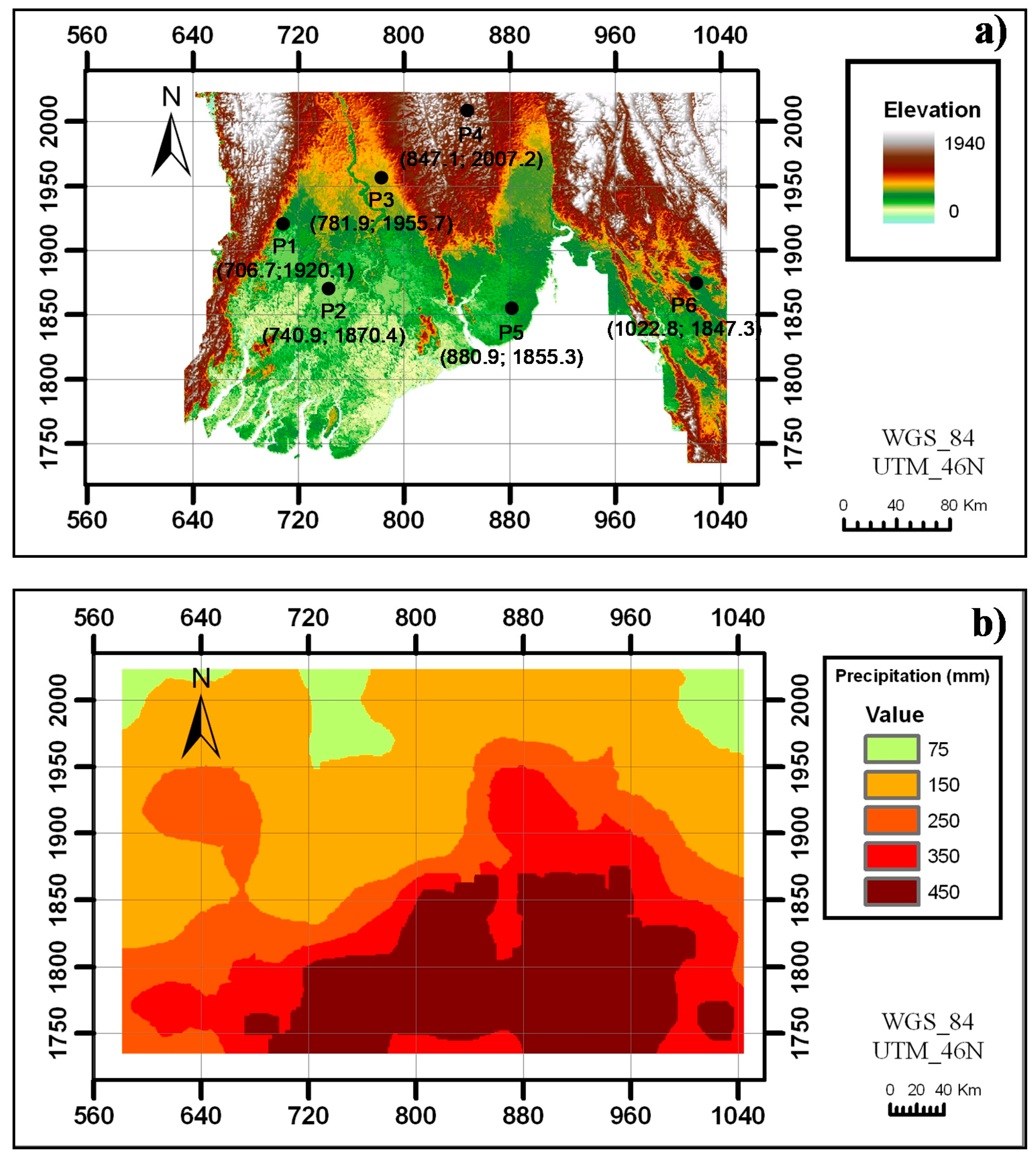
3.1. Study Area and Data

The Cyclone Nargis landed on the Myanmar coast on 2 May 2008. It is considered the deadliest cyclone with 138,000 of fatalities in Bengal Bay since 1970. Flood waters caused by Nargis spread over Myanmar’s coastal area largely consisting of the Ayeyarwady River delta. The combination of the almost flat surface of this region and intensive rainfall of Nargis made Myanmar a proper testbed for the proposed cellular automata model. In this specific case, traditional GIS functions designed to delineate watershed basins (such as “flow accumulation” and “flow direction”) could not be applied effectively due to the almost flat surface of the area. Without a delineated watershed basin and extracted stream network, none of the hydrodynamic flood models could be applied.

The SRTM 3 arc-second (90 m resolution) data provided by CGIAR-CSI (Consultative Group for International Agricultural Research - Consortium for Spatial Information) was used to create a DEM of the region (Figure 4a). A hydraulically corrected DEM is created by filling sinks and removing peaks, to provide a continuous drainage network before modeling. A GIS pit removal function is used for this purpose. Cumulative rainfall data from Tropical Rainfall Measuring Mission (TRMM) for 27 April–4 May was used to define input precipitation (Figure 4b). Due to the unavailability of ground-based hydrologic data in Mynamar, the input hyetograph was approximated by TRMM image data and the forward speed of the cyclone.

The shape of hyetograph in Figure 5a was assumed to be of a triangle type for the entire study area. The peak value of the hyetograph h_max was determined by equalizing the area of hyetograph to the pixel value of the cumulative rainfall in the TRMM image, and the duration was determined considering the total time of precipitation. Regarding simplicity in modeling [62], the Horton Model was used to model infiltration. Infiltration parameters were selected based on the ranges specified by Horton (1933) (Figure 5b) [63]. The Manning coefficient was assumed as 0.035. This value was provided for flood plains–pasture type land cover by Chow et al. (1988) and approximately corresponds to the land cover in Ayeyarwady delta [9]. The model’s sensitivity to infiltration rate and manning coefficient are investigated in Section 3.3.

The model results were verified with flood extent data from a MODIS image (250 m resolution) that was taken by Aqua and Terra satellites on 5 May 2008 (Figure 6). The MODIS image is a pre-processed image that represents all four days of the cyclone. It was the only image for the time of Cyclone Nargis, showing flood covered areas. Since the simulation results contain quantitative data, they should be converted into categorical data to compare with data from MODIS image. Therefore, the calculated maximum flood depth grid was classified into categorical data (i.e., “flood” and “no flood”) by using 5 cm, 2 cm and 1 cm threshold values, and then the obtained qualitative grids were compared with data from MODIS image by measuring the extent of their spatial overlaps.

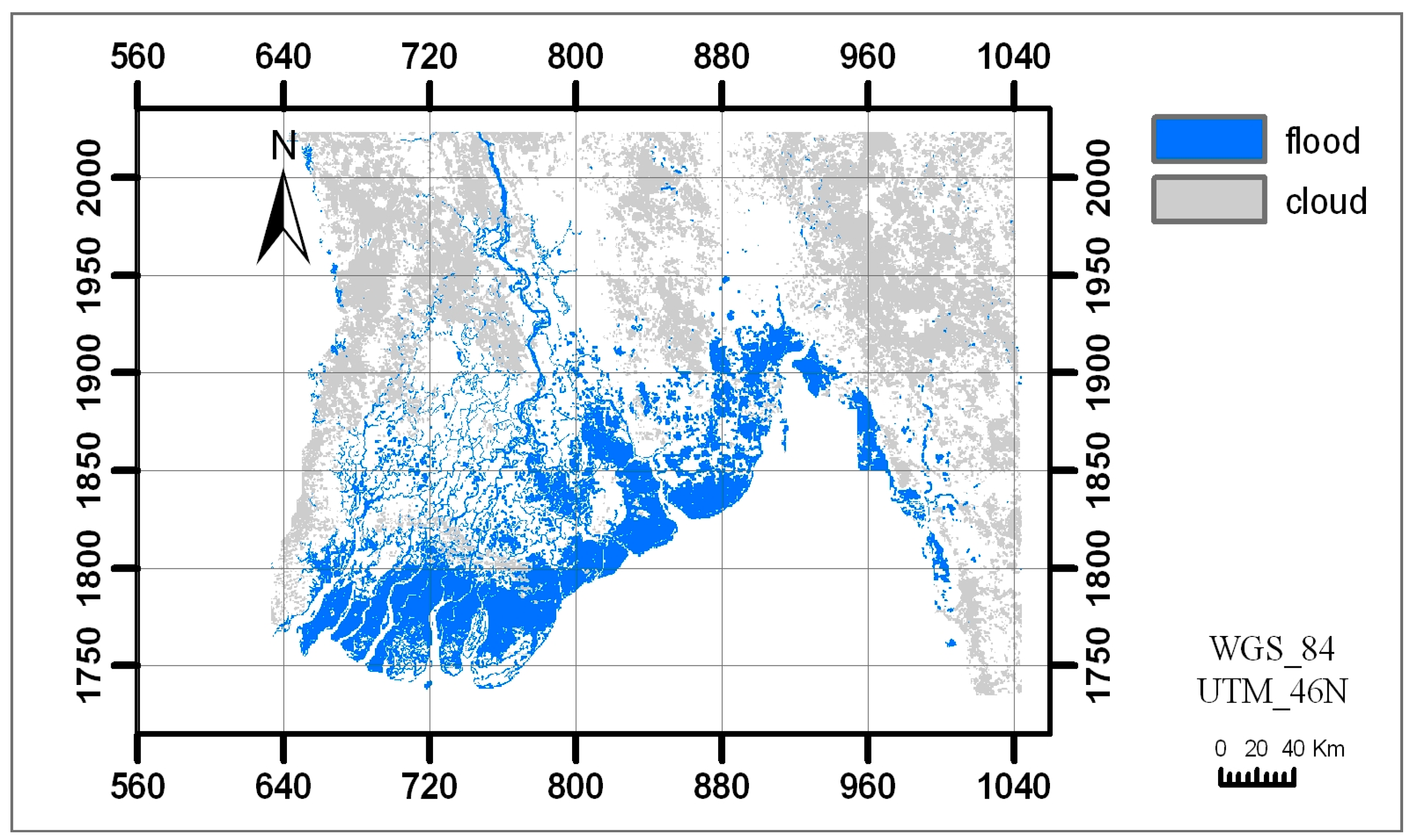
3.2. Flood Simulation for Cyclone Nargis

Following the flow chart in Figure 3, the simulations were coded in the Visual Basic (VB) environment. Prior to the analyses, input TRMM and DEM data were converted into the ASCII format to provide inputs for hydrodynamic analyses. To increase the speed of calculations, the precipitation outside of the study area, which can be neglected, and associated flow contributions were not taken into consideration. In addition, base flows and ground water contribution were ignored as they are negligible compared to the magnitude of the flood. A sixty-hour simulation was conducted to calculate temporal GIS grids on flood depth changes. Maximum flood depths and concentration times were determined by analyzing these output GIS grids. Temporal changes in flood depths were exemplified on six randomly selected locations (Figure 4a).

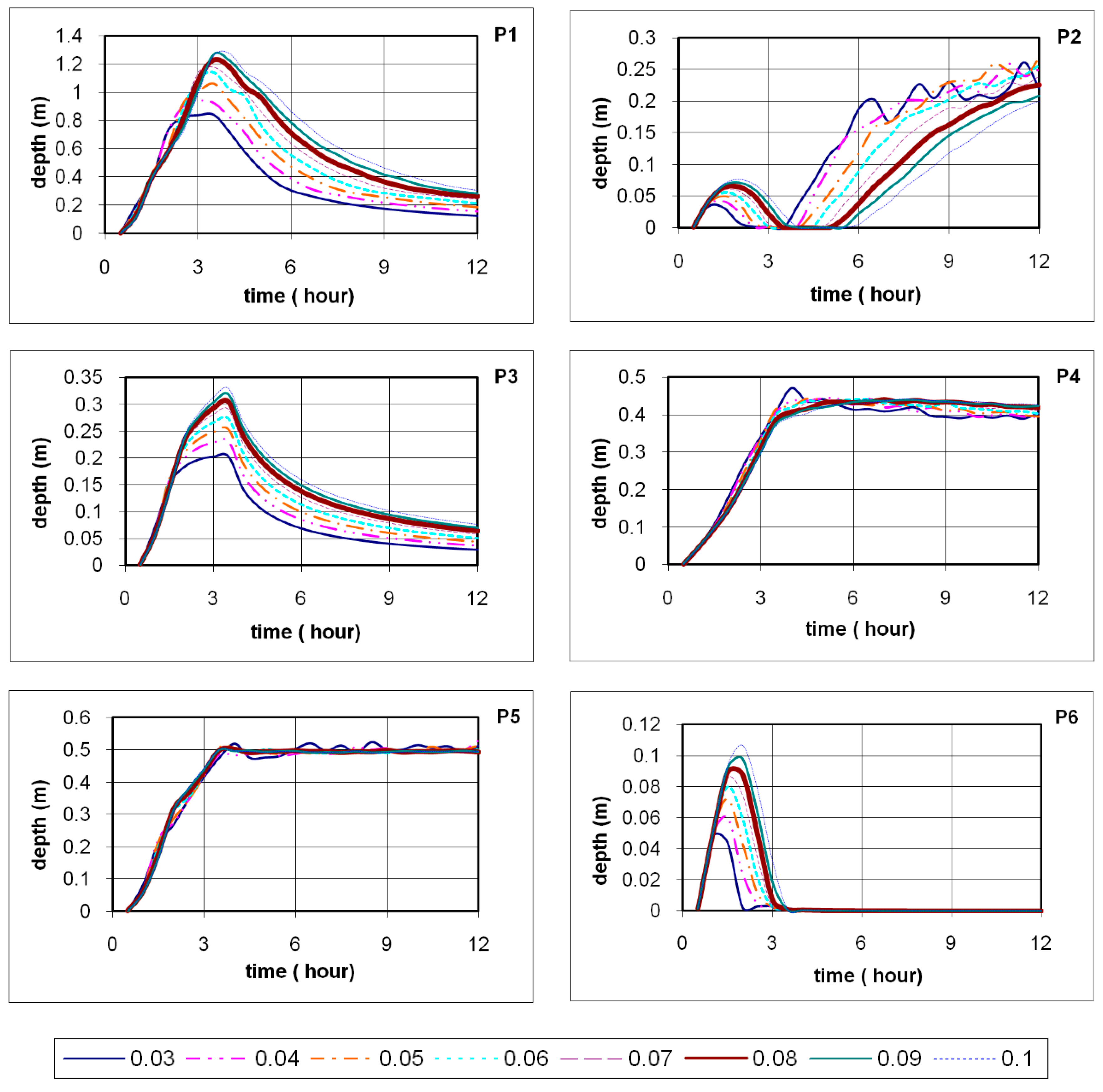
3.3. Sensitivity Analyses

Sensitivity analyses were conducted to determine the effects of the Manning coefficient and infiltration rate on flood depths. A three-hour uniform rainfall hyetograph was assumed for the study area to discard the effect of spatial and temporal rainfall changes on model results. Twelve-hour simulations were conducted to analyze the sensitivity of the proposed flood model to the Manning coefficient and infiltration rate.

To evaluate the role of the Manning coefficient in the modeling process, the infiltration rate was assumed to be zero and the Manning coefficient was changed systematically within the range 0.03–0.1. The limits of this range refer, respectively, to the clean–straight stream channels and dense tree regions [9]. To evaluate the role of the infiltration rate in the modeling process, the Manning coefficient was assumed constant and equal to 0.035 throughout the study area while infiltration indices were changed systematically within the range of 0 to 9 cm/hour. An infiltration index, contrary to an infiltration model, ignores initial abstraction [64,65]; however, it was used here to provide a homogeneous impact on calculations and better reveal the effects of different infiltration rates.

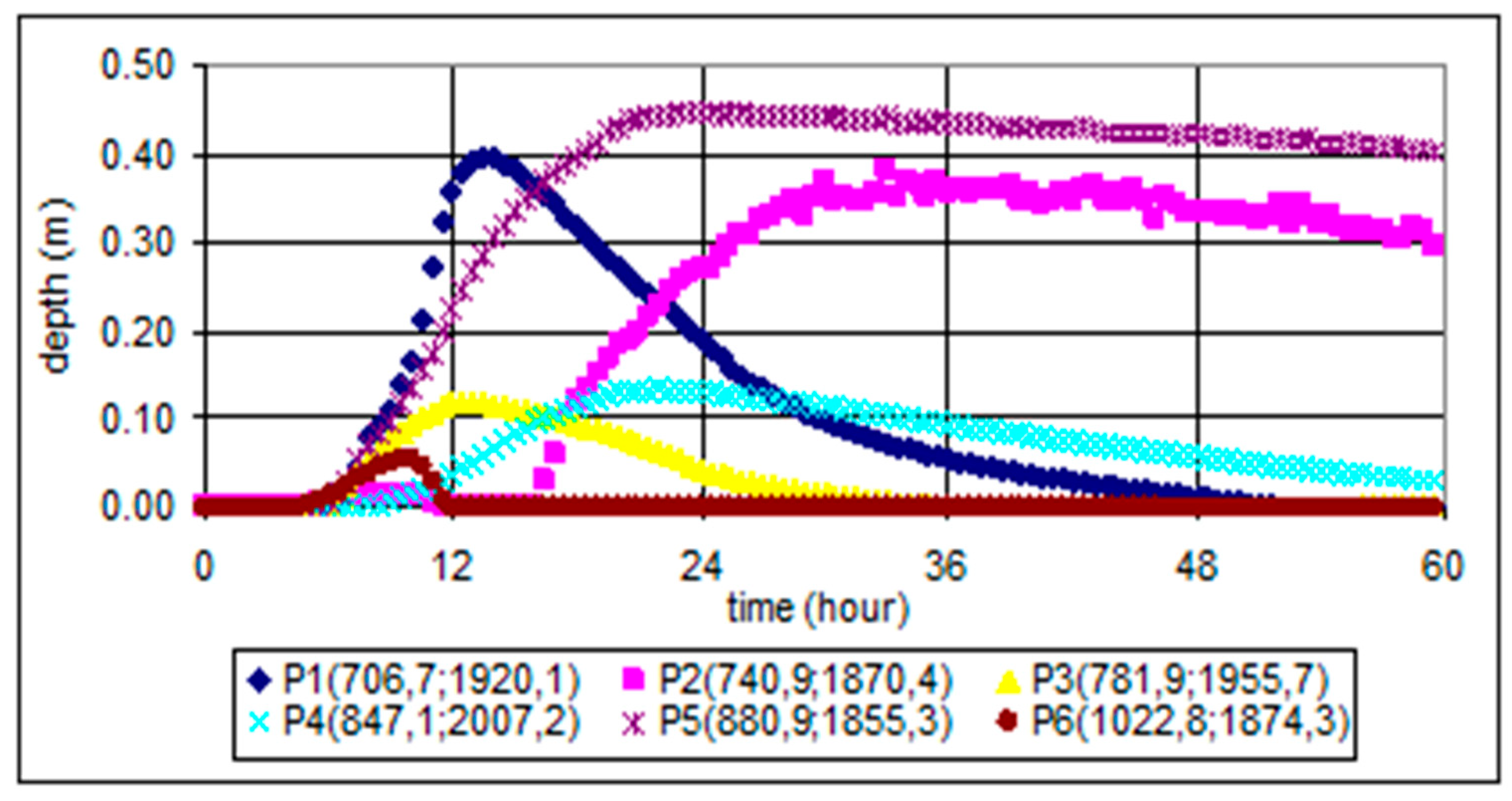
4. Results

GIS grids depicting flood depths for the 0th, 12th, 24th, 36th, 48th, 60th hours (Figure 7) and GIS grids depicting maximum flood depth and concentration time (Figure 8) were obtained as flood simulation results.

Figure 7 shows that, for the 12th hour, when the rainfall stopped, the surface runoff pattern coincided with the precipitation pattern (Figure 4b). For the next hours, after the rainfall stopped, surface runoff depended mainly on gravitational forces. Accordingly, floodwaters accumulated on narrow valleys and plain areas enclosing the intersections of river tributaries. Low slope areas at low elevations drain late, therefore flood waters accumulate there, contrary to high slope areas at high elevations which drain fast. Main drainage paths and low-lying flat areas have higher maximum flood depths. Concentration times are generally high through these regions due to the contributions from upstream (Figure 8).

The flood extent derived from the MODIS image (Figure 6) was used to verify the calculated maximum flood extension (Figure 8a), reclassified according to selected thresholds. The comparison between the flood extents of the MODIS image and the maximum flood depths is given in

Table 1. Overlapping ratios of the flood extents of Modis image and the proposed model.

	Threshold Depths Used to Obtain the Flood Extent Images (cm)
	5	2	1
Percentage, %	57	71	77

. This comparison revealed that overlapping ratios change with selected threshold values from 57% for a 5 cm threshold to 77% for a 1 cm threshold. Visual analysis of both datasets (see Figure 6 and Figure 8a) shows a good agreement on cloud-free areas.

Simulated flood depths (Figure 7) were used to explore temporal behavior of the flood depths in the selected pixels (Figure 4a, Figure 7a and Figure 8a). These pixels were selected so as to represent different topographic hydrologic properties of the study area, distributed evenly along the land surface.

Figure 9 shows flood depth curves obtained for these pixels. Note that the changes of water depth can be used to evaluate the outflow hydrographs. The analysis of Figure 9 reveals how a pixel’s geomorphologic location affects the flood depth curves. Pixels one and three (Figure 4a, Figure 7a and Figure 8a) are located at the intersection of the coastal plain and a mountainous area. Flood depths in these pixels increase rapidly due to the effect of the runoff from mountains and then decrease slowly due to the sudden change in the slope that becomes milder. Pixel two is located in the middle of the coastal plain and at slightly higher elevation than surrounding pixels. For this pixel, Figure 9 shows an initial gentle depth rise and fall for the time interval 0–12 h and a sudden increase after the 15th hour. Pixel four is located in a plateau region upon the mountain; therefore, there is no sharp increment in the flood depth curve. Pixel five is located on a region close to the coastline where floodwaters accumulate; the maximum flood depth in this pixel is significantly higher compared to the other pixels. Pixel six is located outside the main drainage area; the flood depth curve rapidly recesses due to the lack of the contribution from the upper areas. It should be noted that spatio–temporal images of instant flow rates may also be created to facilitate visual interpretation of the flood’s impact on pixels, if needed. To be able to focus on pixel based temporal and volumetric changes, pixel-based hydrographs (i.e., Figure 9) were used here.

Figure 10 shows the results of the sensitivity analysis regarding the Manning coefficient for the selected pixels. Flood depths in pixel P1 and P3 increase with increasing the Manning coefficient. For the pixel P1 and P3, the Manning coefficient has no significant effect on the concentration time, but it affects the duration of recession. During the rainfall, the effect of different manning coefficients on flood depths in pixel P2 are similar to those in P1 and P3; however, for subsequent hours, it reverses due to the upper basin contributions reaching pixel P2. This proves that a decrease in the surface roughness on the main flow path and an increase in the surface roughness on the upper basins can lead to potential flood mitigation. Flood depth changes in P4 and P5 reveal similar behavior. Because of the effect of ponding in these pixels, calculated flood depths show no show no noticeable sensitivity to the Manning coefficient. P6 is not in the main flood path, and it is not subject to a significant flood depth due to drainage. The concentration time is short and the slope of the recession curve is high. For this pixel, high Manning coefficient results in high flood depths and delayed recession.

Figure 11 shows the results of the sensitivity analysis regarding infiltration rate, for the selected pixels. For most of the six locations, the infiltration rate has a more evident effect on the flood depth and recession time than the Manning coefficient. For pixel P6, which is geographically not subject to significant flood impact, this effect is slightly different. The location of P6 does not allow it to receive significant flood contributions from upper areas, therefore, infiltration rate considerably affects the travel time and the shape of the flood depth curves. The flood depth in pixel P2 increases after the 6th hour due to water contributions from upper areas. The location of P2 allows rainwater to drain easily. However, water contributions from upper areas that are significantly high for low infiltration rates increase the flood depth in this pixel.

5. Discussion

5.1. Model

The proposed cellular automata model relies on the Bernoulli and Continuity equations. The following assumptions are needed to use them in the model: (1) incompressible fluid; (2) inviscid flow; (3) steady flow; (4) flow along streamline. Floodwaters moving on a small pixel can be considered incompressible and inviscid, and may be assumed as steady for a small time interval compared to the duration of precipitation. The assumption of steady flow may not be true for large time intervals and spatial resolution (i.e., pixel size). This can cause numerical errors for pixels with high slope that produce high flow velocity. The assumption of flow along the streamline can be approximately provided since flood waters in a given pixel can flow in only eight directions (see Figure 1a). The most beneficial aspect of the proposed model is its capability to integrate spatio–temporal data and hydrodynamic flow principles by using a GIS environment. The proposed model can be used at different stages of disaster management. Its grid structure allows the use of different infiltration, precipitation and abstraction models. Seasonal changes in runoff characteristics can also be evaluated at pixel level by using variable Manning coefficients.

The main advantages of the model include:

• Its helpfulness for rainfall-induced flood analysis of plain areas where the most of the population generally lives, and a watershed basin cannot be easily delineated.
• There is no need to use a predefined flood extent, and thus it is very beneficial to cope with defining dynamic flood boundaries.
• Its use of hydrodynamic principles.
• The pixel level consideration of basin topography, land cover and soil properties.
• The possibility of integrating different rainfall and infiltration models.
• The consideration of pixel-level changes in rainfall and infiltration.
• The fast pre-modelling procedure due to the cellular automata processing.
• The temporal flood depth estimations at pixel level.
• The temporal flood extent estimations.
• The maximum flood depth and concentration time estimations at pixel level.
• Its practical application for disaster managers before, during and after disaster.

The disadvantages are:

• Unlike classical hydrodynamic models, the proposed model cannot provide good estimations for floods within well-defined river courses due to the simplification of hydrodynamic principles.
• The assumption of flow along the streamline excludes backwater effects and causes biases in calculated flow paths, for large spatial resolution; however, they can be negligible for small spatial resolutions and time intervals. The Courant Condition of the numerical stability [9] is applied in this study when spatial resolutions and time intervals are determined. Deviations from the flow path will be small for small pixels and automatically corrected along subsequent time steps due to the energy and mass conservation within pixels.
• Since the Manning equation relies on the assumption of fully turbulent flow, the model cannot accurately estimate low flood depths. Though laminar flow principles still can be included in this model, only high flood depths are the main concern for emergency managers.
• The speed of the cellular automata processing highly depends on the spatial resolution and time interval selected.
• The constant values assigned for natural wet areas to exclude them from analyses may cause underestimated flood depths in the pixels adjacent to small artificial ponds and narrow river tributary–sea intersections. For pixels located at the boundaries of the computational domain (i.e., first and last row and column), this assignment may cause either overestimation or underestimation depending on the direction of the maximum hydraulic gradient in these pixels. The potential solution to this problem is elimination of results obtained for these pixels.
• Upstream inflows or failure of engineering structures cannot be simulated by the proposed model. Full hydrodynamic models such as HEC (Hydraulic Engineering Center), SWMM (Storm Water Management Model) or MIKE series can provide good estimations for such simulations, especially when catchments and boundary conditions can be well defined. One solution for problems with upstream flows may be keeping study area large to include all the pixels in a considered basin and exclude results obtained for other pixels. This can be implemented readily by a GIS clipping function.
• The model may not easily simulate the impact of some engineering structures on the flow dynamics (e.g., obstructions from the bridge piers, flow regulation from dams and weirs, etc.).

5.2. Myanmar Flooding from Cyclone Nargis

The results of analysis show that Myanmar’s coast is remarkable vulnerable to flooding (See Figure 7, Figure 8 and Figure 9). High flood depths were observed on narrow flow sections, plain areas and conjunction points of river tributaries as well as along intersections between low slope coastal areas and high slope mountains. Mountainous areas with high slopes drain fast and are subject to low flood depths and short concentration time. The maximum flood depth highly correlates with the concentration time. Maximum flood depth along the coastline is approximately half a meter without considering localized flood impacts. In the coastal region, the recession of floodwaters begins a few days after the cyclone landfall. The maximum flood depth obtained from the model is in good agreement with the flood extent data from MODIS image for low thresholds (Table 1). The following shortcomings of MODIS based flood extent data and model simulations could affect the data in Table 1:

• MODIS data lack ground truth control and validation.
• The MODIS image contains large cloud cover.
• MODIS data most likely include combined effect of storm surges and floods.
• The infiltration rate and Manning coefficient used in simulations may not represent the entire study area, and this could cause over/underestimations for some pixels.

In the case of available high-resolution flood extent images, the local behavior of the model results would be better evaluated, producing a detailed picture of the aftermath of the disaster.

5.3. Sensitivity Analyses

Sensitivity analyses have shown that the Manning coefficient and infiltration rate affect flood depth estimations. Different values for the Manning coefficient may result in the increment or decrement of flood depths, depending on pixel location. Infiltration always attenuates floodwaters. Its effect on the shape of flow hydrographs is more noticeable than those of the Manning coefficient. This means that proper the estimation of infiltration parameters may be more important than those of the Manning coefficient, for flood managers. Therefore, area-wide pixel-based estimations on infiltration parameters would result in higher accuracy of model results. Note that it is not practically possible to change infiltration rates in nature, but the Manning coefficient may be changed by applying appropriate land management or erosion control measures [15,23].

6. Conclusions

The spatially-distributed GIS based flood model proposed in this study presents a practical solution for simulating overland flows, integrating spatial data and hydrodynamic flow principles. It needs no delineated watershed basin, no predefined flood extent. Using hydrodynamic principles, the model provides temporal flood depth estimations at pixel level. Unlike classical hydrodynamic river models, the proposed model provides good estimations for overland flows, outside of river courses. There are also hydrodynamic models specifically developed for simulating rainfall-induced floods. They need more pre-modeling efforts and mostly require detailed knowledge of the study area in a well-defined boundary, which is generally not available during a disaster for a disaster area. The model assumes a fully turbulent flow which is the case during floods, however, laminar flow principles still can be included in the model. The speed of the cellular automata processing highly depends on the spatial resolution and time interval selected. The case study of Nargis shows that the model provides good depth estimations on plain areas, conjunctions of river tributaries, low slope coastal areas and high slope mountains. According to the proposed model, the coastline of Myanmar on the occasion of Nargis was subject to flood depths up to 0.5 m. The maximum flood depths were in a good agreement with the MODIS image. The recession of floodwaters begins a few days after the cyclone landfall.

It is concluded in the study that overland rainfall induced flood flows can be well defined by the spatially-distributed GIS model proposed in this study, simply using GIS layers in terms of topography, and basic hydrologic parameters. The model’s simple hydrodynamic structure, capability in integrated spatial and temporal data analyses and practicality in pre-post disaster management should make it attractive for hydrologists, coastal engineers, disaster managers and decision makers. The model can also be used for erosion control studies as well as for flood risk/insurance management in coastal areas where a high concentration of population and infrastructure are associated with higher exposure and vulnerability. From a disaster management perspective, the main advantage of the model is its power to conduct real time simulations that can be used in estimation of affected populations and areas to allocate resources for disaster mitigation and relief efforts.