Abstract
This study was conducted at Laman Sayur, Malaysia Agro Exposition Park Serdang (MAEPS), to investigate the hydraulic performance of a small-scale drip irrigation system. The modelling was carried out using EPANET software to understand how the drip irrigation system is operated. Model results show that the errors are small, i.e., 2.2% and 3.0% for pressures, and 1.7% for discharge in lateral pipe 1 and lateral pipe 2. The root mean square error (RMSE) and the mean bias error (MBE) for discharge were recorded at 0.04 L/h and 0.03 L/h for lateral pipe 1 and 0.04 L/h and 0.02 L/h for lateral pipe 2. RMSE and MBE for pressure were recorded at 0.61 m and 0.68 m for lateral pipe 1, and 0.79 m and 0.68 m for lateral pipe 2, respectively. These results show that the model yields good performance. For hydraulic performance, the field measurement was conducted with four operating pressures: P1 (15.3), P2 (20.4), P3 (25.5), and P4 (28.6) meters. The hydraulic parameters evaluated were the coefficient of uniformity (CU), the emission uniformity (EU), the coefficient of variation (CV), and the emitter flow variation (EFV). The operating pressure during the measurement is constant according to the specified pressure. The results show that CU, CV, and EU are in the excellent classification, and values of CU and EU have more than 95% efficiency. The value for CV is below 0.03, which is excellent. The EFV is 10% when operating at 25.5 m and 15.3 m and is considered desirable. On the other hand, for the 28.6 m and 15.3 m operating pressures, the EFV parameters were recorded at 13.6% and 10.29%, respectively, and are classified acceptable. This study concluded that the operating pressures, P2 (20.4 m) and P3 (25.5 m), were performed under excellent classification for all hydraulic parameters evaluated. Based on the outputs from the model, it is inferred that the existing drip irrigation system at Laman Sayur MAEPS is operated in an over-powered state. With the current pump power consumption, the irrigation system could be operated at a minimum of four times the capacity of the existing irrigation system. To reduce the power consumption, it is suggested that the system is operated at a lower pumping power. This would minimize the operating costs especially for the development of a new drip irrigation system that has the same capacity as the drip irrigation system that is currently being operated at Laman Sayur, MAEPS Serdang.
1. Introduction
Studies have found that the drip irrigation method is the best method as compared to other irrigation methods because the drip irrigation method provides high uniformity. Drip irrigation systems typically use 30 to 50% less water than the other irrigation systems as they provide only the water needed by plants [1]. The operation of drip irrigation systems uses low flow rates and pressure and enables farmers to irrigate at lower cost by using smaller pumps, and smaller, lightweight pipes [2]. The drip irrigation system is the most effective method in terms of water use and labor. As they are complex, drip irrigation systems should be designed, installed, and maintained properly [3]. The root system of most vegetables is located on the top layer of the soil and requires regular irrigation. Thus, drip irrigation is the most efficient and economical method for irrigation in vegetable production.
Drip irrigation has the greatest potential for efficient water and fertilizer usage. To minimize irrigation and fertilization costs, drip irrigation is important to maximize nutrient intake while using a minimum amount of water and fertilizer. The lateral drip irrigation system comprises a pressurized pipeline with an inline or an online emitter. The proper hydraulic design of lateral drip systems usually requires precise assessment of the total head loss represented by friction loss along the pipe and the emitter, and the local loss due to the emitter’s connection [4]. Local losses should be considered in any drip irrigation because the installation of large numbers of emitters along lateral pipes will affect the overall loss. Reliable methods to estimate local losses either based on kinetic load [5,6,7] or equivalent length [8,9,10] have been reported in the literature. The relationships were developed based on empirical data. Currently, Baiamonte [11] derives a relationship between the equivalent length and the minor losses coefficient. The important design variables influencing minor losses, i.e., the emitter flow rate, the inside pipe diameter, and the emitter spacing are illustrated. The procedure is analytical; it does not consider empirical equivalent length formulas that do not necessarily cover the entire range of conditions in the real-world contexts in which the formulas will be applied.
The losses in the emitter are due to the connection between the lateral pipe and the emitter [12]. The determination of the total head loss in a drip irrigation system is very important to ensure the system operates with sufficient pressure. The average operating pressure head for emitter, distribution of uniformity, and head loss between lateral and manifold will arise as a result of the optimal economic impact [10]. The determination of head loss can be done in the field by placing the pressure gauge at the desired pipe point. This determination is important to ensure adequate head to carry out the irrigation activity. The modelling of drip irrigation systems is a good way to facilitate the determination of the required head to ensure the irrigation system can distribute water uniformly to the plant. This irrigation system modelling helps farmers to determine the head required to carry out the operational procedure of the system. Modelling is one of the ways to identify weaknesses in a drip irrigation system. With the model, the simulation to illustrate the actual condition of the overall drip irrigation system can be easily investigated. This actual condition of the system is needed to ensure that the systems can be operated in the best possible condition. Software packages such as Irrilab [11], which is based on explicit relationship, are useful for optimal designing of rectangular micro-irrigation units in uniform slopes. Alternatively, the older EPANET software [13] that has been widely used as the computational engine for most water distribution system models is still promising. The uniformity of water distribution is one of the important parameters in determining the efficiency of the design of drip irrigation systems. Clogging for a long period of time has been the major obstacle in the development of drip irrigation. Emitter clogging can reduce the uniformity of the irrigation system, especially when fertilizer (fertigation) is applied. Therefore, proper assessment to select an appropriate emitter is necessary to prevent clogging [14]. Drip irrigation can increase yields and save water by about 50% as compared to other irrigation techniques [15]. This can make the investment in a drip irrigation system economically viable, compensating for the high capital cost for drip equipment [16]. Slope is one of the factors that affects the uniformity of water distribution. Baiamonte [17] reported that the coefficient of variation (CV) decreases with increasing slope, showing a minimum CV value, CV min, equal to 2%, over which CV, as for best manifold position (BMP) = 0.5, increases with slope.
Kumar and Singh [18], and Tyson and Cutis [19], stated that the drip irrigation system depends on the physical and hydraulic properties of the drip tubing. The most important feature is the uniform distribution of water in the design, management, and use of the system. The selection of water pressure is the main factor to be considered in the drip irrigation design during the irrigation process [19]. The efficiency of the drip irrigation system depends on the uniformity of the water distribution which can be evaluated by measuring the flow rate in each emitter [18]. The uniformity of water distribution also depends on the design, the distance between the emitters, the emitter material, and the manufacturing processes. The performance of drip irrigation systems also depends on the emission uniformity (EU) throughout the system. It measures the uniformity of emissions discharged from all emitters. Other parameters considered are the co-efficient of variation (CV), and the uniformity co-efficient (CU) [20].
Operating pressure is considered very important in the design of drip irrigation systems. Failure to provide proper operating pressure will result in the reduction of performance which in turn contributes to system failure [21]. In addition, non-static operating pressure can cause problems such as broken pressure regulators, broken lines, and mounted emitter [19]. This study aims to develop a numerical model of an existing drip irrigation system that is operating at Laman Sayur, MAEPS greenhouse, to compare the results from the fieldwork with the results obtained from the numerical model, and to evaluate the hydraulic performance of the existing drip irrigation system based on the American Society of Agricultural Engineering (ASAE) standard.
2. Materials and Methods
2.1. Study Area
This study was conducted at Laman Sayur located within the territory of Malaysia Agro Exposition Park Serdang (MAEPS) as shown in Figure 1. MAEPS is known as one of the largest exhibition parks and showgrounds in Asia, and was established to serve as the center for agro-based events and activities in Malaysia. The exhibition park is located on a 130 hectare property belonging to the Malaysian Research and Development Institute (MARDI). For this study, the assessment of the hydraulic performance of a drip irrigation system was conducted in a small-scale greenhouse plantation, where domestic water is the source of water used in the system.
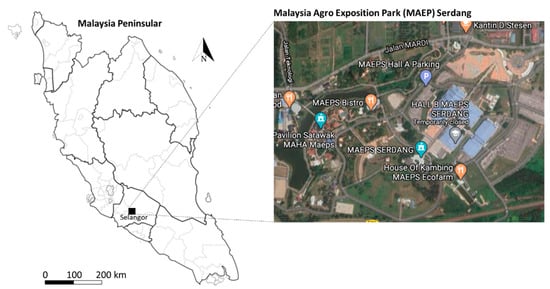
Figure 1.
Study area. Inset represents the location of study area. The map was captured using Google Maps [22].
2.2. Data Collection
Data collection for this drip irrigation system includes measuring the geometry and dimensions of the drip irrigation system components. The hydraulic parameters including emitter flow discharges and pressure head were also collected. The measured parameters are used to validate the outputs obtained from the numerical model developed.
2.3. Drip Irrigation System Layout
The drip irrigation system at Laman Sayur, MAEPS, uses a basic irrigation system. The identification of drip irrigation system components including the pipe size, pipe length, pipe diameter, and pipe components was carried out. This is very important in order to prepare the system layout in the numerical model. Every single component is required to be included in the model so that the numerical model can replicate the real existing system. It is noted that the existing system is then verified by an EPANET numerical model.
The system has two tanks, two fertilizer tanks, one pump, one filter, 20 valves, two different pipe sizes, and 400 emitters connected to lateral pipes for the whole system. A water tank of 300-gallon capacity is used to store water. An electric motor of 1 horsepower (hp) with a centrifugal pump is used for pumping water from the tank, connecting with a filter. The system utilizes only one pump that operates for the entire system and is sufficient for the small-scale plantation. The system is equipped with two manifold pipes (PVC pipe) of 28 mm diameter fitted separately and separated by valves. Each manifold pipe is connected to two lateral pipes (LDPE pipe) with a diameter of 20 mm with 17.5 mm inner diameter, and each lateral pipe is 31 m long. The distance between the emitters along the lateral pipe is 60 cm mounted on each left and right plant pot. A total of 100 emitters were installed along the lateral pipes and a total of 400 emitters with 460 mm length were installed in this drip irrigation system. The drip irrigation system is laid on a horizontal bed. Each crop (plant pot) is equipped with one emitter. The overall system is illustrated in Figure 2.
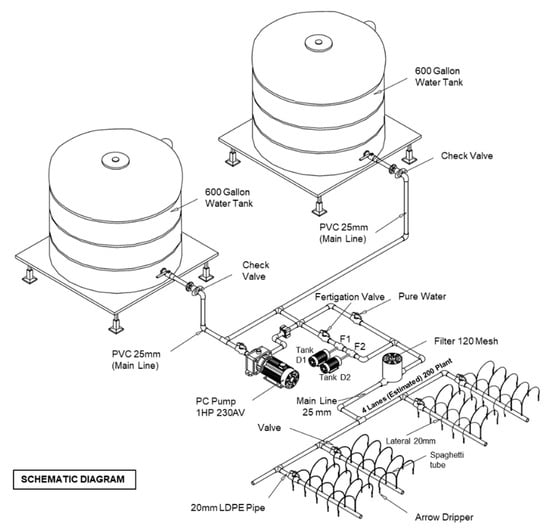
Figure 2.
Overall drip irrigation system components.
2.4. Measurement of Hydraulic Parameters of the Irrigation System
The measurement of hydraulic parameters includes the flow discharge and pressure from the emitter on each lateral pipe distributed along lateral pipe 1 and lateral pipe 2. Ten location points at each lateral pipe were selected to record pressure readings and measure the discharge. Figure 2 shows the simplified illustration diagram of measuring locations, denoted by the integers in the planter box. The selection of location points was arbitrary, and each point location was different for each lateral pipe. The discharge of emitters was measured using a volumetric method. Measuring tools such as a graduated measuring cylinder, a catch can, and a stopwatch were used. The discharge measurement lasted for two min at each point location. The collected water in the catch can for each emitter was measured using a measuring cylinder. Next, the volume of water was divided by time to obtain the discharge (q) in liters per second (L/s). Flowrate measurements of each emitter were performed with various operating pressures of 15.3, 20.4, 25.5, and 28.6 m.
The experiment was conducted in a one plot design with two lateral pipes. The field layout of the drip irrigation system is presented in Figure 3.
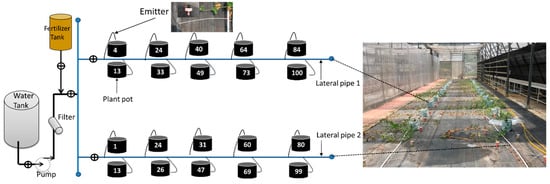
Figure 3.
Emitter locations for the measurement of pressure and flow rate. The numbers in the planter pot indicate the plant pot numbers where the measurements were done. Photos in the diagram show the spaghetti emitter used in the existing system. Each lateral pipe has 100 emitters.
2.5. Hydraulic Performance Evaluation
Hydraulic performance is calculated to obtain the actual performance of an irrigation system. To determine the efficiency of the existing drip irrigation system, the emission uniformity (EU), emitter flow variation (EFV), coefficient of uniformity (CU), and coefficient of variation (CV) are determined in accordance with the American Society of Agricultural Engineering (ASAE) [20]. Table 1 shows the coefficient parameters used to measure the hydraulic performance of the drip irrigation system. EU, CU, and EFV coefficient parameters adopt a percentage value to indicate drip irrigation performances. A higher percentage indicates good performance while a lower percentage means poor performance or unacceptable. For the CV, a range value of 0.05–0.15 was used. If the value is less than 0.05, the performance is excellent. If the value is greater than 0.15, it is classified as unacceptable performance.

Table 1.
The coefficients involved in the calculation of hydraulic performance include coefficient of uniformity (CU), emission uniformity (EU), coefficient of variation (CV), and emitter flow variation (EFV) [20].
2.6. Numerical Modelling and Model Performance
Rossman [13] developed EPANET to investigate the hydraulic behavior within pressurized pipe networks. In this study, the widely known EPANET software has been applied. Besides EPANET, there are other software programs that can be used such as hydrauliCAD [23], AFT Fathom [24], InfoWorks [25], WaterCAD [26], WaterGEMS [27], AquaFlow [28], DIDAS [29], DOMIS [30], HydroCalc [31], IRRICAD [32], IrriPro [33], IrriExpress [34], and IrriLab [35]. The Irrilab software package [11], for example, was developed based on simple explicit analytical solutions, and thus does not require many trial and error attempts and time-consuming iterations. IrriLab software is based on the basic hydraulic equations from the manifold to the end of both the downhill and the uphill sides of the laterals, and provides the minimum pressure required, minimizing the energy consumption. These software packages are useful to simulate water distribution systems in pressurized pipelines. However, each software has its own advantages. Software selection does not necessarily lead to a single software but depends on the needs of the study to be performed.
In this study, EPANET software is preferable due to its simplicity, and the fact that the software is open source and free to download. The EPANET model was originally developed by the United States Environmental Protection Agency. EPANET is a computer program that performs extended period simulation of hydraulic and water quality behavior within pressurized pipe networks. EPANET is designed as a research tool to enhance our understanding of the movement and distribution of water in distribution systems. A network consists of pipes, nodes (pipe junctions), pumps, valves, and storage tanks or reservoirs. EPANET tracks the flow of water in each pipe, the pressure at each node, and the height of the water in each tank throughout the network during various simulation periods.
The total head involved in EPANET is divided into two types, namely head loss due to friction along the lateral pipe, and minor loss due to the installation of the emitter. In this study the head loss is calculated using the Darcy–Weisbach formula as expressed in Equation (1) [7].
Hf is friction loss of the pipe (m), L is pipe length (m), D is the pipe’s internal diameter (m), V is the velocity in pipe (m/s), g is the acceleration due to gravity (9.81 (m/s2)) and f is the friction coefficient (-). The friction coefficient, f is determined by f = 0.302/(Re) 0.25 for 2000 < Re < 36,000 [5]. The minor loss can be determined in a general form as given in Equation (2) [7].
hLminor is the head loss due to fitting and insertion of emitter, k is the head loss coefficient, v is the velocity in pipe (m/s), and g is acceleration due to gravity (9.81 (m/s2)). The k coefficient due to insertion of emitter can be expressed as [7]
where, Di is internal diameter of the pipe (m), and Dg is the internal diameter due to the emitter (m).
k = 0.056 × [(Dg/Di)17.83 − 1]
Figure 4 shows dimensions for calculating the k coefficient value using Equation (3).
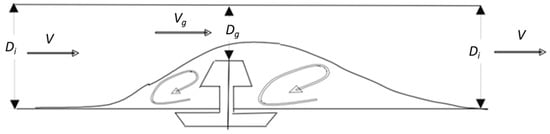
Figure 4.
Parameters involved in calculating minor loss for online type emitters [7].
For the drip irrigation system, the layout was prepared in the model to represent the existing drip irrigation system in the greenhouse. To validate the model, a comparison result between model and measurement was carried out. The statistical error indexes (e.g., RMSE, MBE, and MAPE) were calculated to determine the performance of the model. Table 2 shows the equations and associated descriptions of the statistical error index applied in this study.

Table 2.
Statistical error index.
3. Results and Discussion
The field measurement was carried out to preliminarily identify the existing layout of the drip irrigation system including the pipe sizes, pipe lengths, pipe diameters, and pipe components. Hydraulic measurements involving discharge and pressure measurements were then carried out to assess the hydraulic performance of the existing drip irrigation system. Results from the measurements are presented in Section 3.1. Next, modelling work was performed to gain insight into how the existing drip irrigation system operates. Results obtained from the measurements were compared with the model outputs and are presented in Section 3.2 and Section 3.3.
3.1. Hydraulic Performance of an Existing Drip Irrigation System
The overall hydraulic performance of the drip irrigation system with different operating pressures is shown in Table 3. Four different operating pressures, i.e., 15.3, 20.4, 25.5, and 28.6 m were applied in this study. For all operating pressures, the coefficient uniformity (CU), the coefficient of variation (CV) the emission uniformity (EU), and the emitter flow variation (EFV) parameters were assessed.

Table 3.
Coefficient values and classification of hydraulic parameters of the existing drip irrigation system.
Based on Table 3, results show that the existing drip irrigation system performs well, operating at all operating pressures. Hydraulic parameters such as CU and EU indicate that the existing system operates in an excellent fashion when both parameters are under excellent classification. According to [39,40], high coefficients of uniformity of at least 85% and emission uniformity greater than 90% indicate a well-designed drip irrigation system.
The coefficient of variation (CV) shows an excellent level of flow variation with the marginal values between 0.02 and 0.03. The results of emitter flow variation (EFV) are greater than 10% when operated at pressures 15.3 m and 28.6 m and are considered acceptable, while at 20.4 m and 25.5 m pressure operations, the emitter flow variation is 10%, considered as desirable. This result indicates that the higher and lower pressures are affected by the variation of discharge in each emitter. This finding is similar to the study conducted by [20], who found that the CU, CV, and EU are classified as excellent but the EFV is classified as inacceptable. The EFV result obtained by [41] could be due to the type of emitter used. In their study, non-pressure compensating emitters were applied. The pressure compensating emitter, the one that is applied in the existing drip irrigation system, will give approximately the same flow rate for a specified operating pressure range. In contrast, the non-pressure compensating emitter requires a constant operating pressure to obtain uniform water distribution. Overall, according to the ASAE standard, the coefficient values of the uniformity parameters obtained in this study were found to be within the excellent range. The existing drip irrigation system is well-designed; however, the question remains as to whether the existing drip irrigation system at Laman Sayur, MAEPS Serdang, is under- or over-operated.
3.2. Comparing Model Results and Measurement: Pressure and Discharge in Lateral Pipes 1 and 2
Figure 5 shows the results comparison between model and measurement for discharge and pressure in lateral pipe 1 and lateral pipe 2. The discharge data collected from ten emitters in lateral pipe 1 show that the measurement is similar to the discharge output from the model. The emitter installed in the system is a pressure compensated type; therefore, the flow rate is set at 2 L/h for operating pressure ranges from 15.3 m to 40.8 m in the model. The measured discharges at all ten emitters show that the reading is approximately 2.00 L/h, where the maximum reading is 2.07 L/h at emitters 4, 13, and 24, and the lowest reading is 1.95 L/h, observed at the lateral end, i.e., emitter 100. The measured pressure reading at the beginning of the manifold was 26.03 m. In lateral pipe 1, the measured pressure at the emitter 4 was 24.46 m. In comparison, the model pressure is 25.54 m, slightly higher than the measured value. Both the measured and model pressure readings at the emitters show a further decrease, indicating that losses have occurred in the pipe. The calculated head loss, hf, considering both friction and minor losses for lateral pipe 1 shows an increasing loss, starting lower, hf = 0.49 m at the lateral front and higher, hf = 4.63 m at the lateral end. The measured pressure of the last emitter, i.e., point 100 is 21.77 m, slightly higher than the model’s pressure which is 21.40 m.
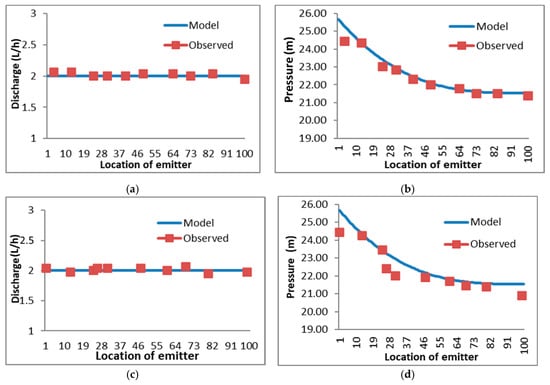
Figure 5.
Comparison between measured and modelled discharges and pressures at emitters in lateral pipe 1 and lateral pipe 2. (a) Discharge at emitters on lateral pipe 1; (b) Pressure at emitters on lateral pipe 1; (c) Discharge at emitters on lateral pipe 2; (d) Pressure at emitters on lateral pipe 2.
Similar to the results obtained in lateral pipe 1, the discharge data collected from ten emitters along lateral pipe 2 are in agreement with the discharge output from the model. Measured discharges range from 1.95 L/h to 2.07 L/h along lateral pipe 2 (see Figure 5c). Modelled discharge is constant at 2.00 L/h at all emitters as the pressure compensated emitter was used. Pressure drop is observed both during the measurement and in the model. However, the measured pressures are slightly lower than the modelled pressures as can be seen in Figure 5d. The measured pressure at the emitter front is 24.46 m while the model output gives pressure of 25.67 m. The measured pressure at the emitter end is 20.89 m and underpredicts the modelled pressure, which is 21.54 m. The calculated head loss, hf, considering both friction and minor losses for lateral pipe 2 shows an increasing loss, starting lower, hf = 0.13 m at the emitter front and higher, hf = 4.62 m at the emitter end.
3.3. Model Performance
Statistical error indexes are used to determine the performance of the observed data as compared to model outputs. Three error indexes, i.e., the Root Mean Square Error (RMSE), the Mean Bias Error (MBE), and the Mean Absolute Percentage Error (MAPE) were used. In this study, these three performance indicators were calculated using equations provided in Table 2 for each lateral pipe. The computed errors are displayed in Table 4.

Table 4.
Statistical error index for measurement data.
From Table 4, the error index of discharge for lateral pipe 1 is similar to that of the error index for lateral pipe 2. The RMSE recorded an error of 0.04–2 L/h—for both lateral pipe 1 and lateral pipe 2, respectively. The MBE recorded a bias error of 0.03 L/h for lateral pipe 1 and 0.02 L/h for lateral pipe 2. On the other hand, MAPE for the two lateral pipes gives similar results, an absolute percentage error at 1.7%. As can be seen in Figure 6 (lower panels), the R2 pressures for both lateral pipes are 0.99, indicating a perfect fit between measurement and model. This shows that the model yields good performance in term of discharge.
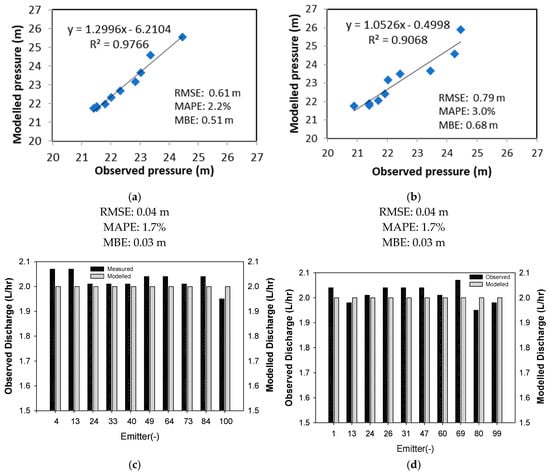
Figure 6.
Modelled and observed pressure (upper) and discharge (lower) on lateral pipe 1 and lateral pipe 2. (a) Pressure on lateral pipe 1; (b) Pressure on lateral pipe 2; (c) Discharge on lateral pipe 1; (d) Discharge on lateral pipe 2.
The error index is also calculated for pressure distribution along the lateral pipes. From Table 4, the RMSE recorded an error of 0.61 m and 0.79 m for lateral pipe 1 and lateral pipe 2, respectively. The MBE gives a mean bias of 0.51 m and 0.68 m for lateral pipe 1 and lateral pipe 2. The MAPE result shows that an absolute error is 2.2% and 3.0% along lateral pipe 1 and lateral pipe 2, respectively. The R2 discharge for lateral pipe 1 is 0.97 while for lateral pipe 2, it is 0.91. This could be due to the condition of the emitters and the lateral pipes. A minor clogging is expected to occur, which leads to inconsistent results between lateral pipes 1 and 2. Although R2 for lateral pipe 2 is slightly lower than that for lateral pipe 1, a good fit between measurement and model is achieved. This shows that the model gives good performance in terms of pressure. According to [42,43], the maximum error between the model and observation results should be less than 10%. In this study, the errors calculated are below 10%, i.e., 2.2% and 3.0% for pressure and 1.7% for discharge in lateral 1 and lateral 2, thus indicating that the model’s performance is good. This indicates that this model replicates the existing drip irrigation system and therefore can be used to improve the performance of any new drip irrigation systems in the future, provided that a similar design layout is applied.
Based on the comparison between lateral pipe 1 and lateral pipe 2, the error for discharge for lateral pipe 1 is similar to that of lateral pipe 2. On the other hand, the error for pressure distribution for lateral pipe 2 is slightly higher than that of lateral pipe 1. The performance of the existing drip irrigation system can be assessed through analytical solutions. Baiamonte [11,17,44] provided a simple analytical solution to estimate the minimum pressure required for a horizontal lateral pipe. This solution could be used to provide a quick estimate of the inlet pressure required for a drip irrigation system.
Assuming that the pressure head tolerance is 0.1 (10%), the minimum inlet pressure required for the existing drip irrigation system at Laman Sayur, MAEPS, is 24.70 m. It is observed that the existing inlet pressure is 28.56 m, higher than the required minimum inlet pressure, thus the existing system is over-operated. The analytical solution also can be used to check the condition of the entire range of pressure used in the drip irrigation system. For lateral pipe 1, the minimum and maximum pressures at emitter are 20.27 m and 24.78 m, respectively. For lateral pipe 2, the minimum and maximum pressures at emitter are 19.96 m and 24.39 m, respectively. The measured pressures at emitters along the lateral pipes 1 and 2 are within the minimum and maximum pressure range.
Numerical modelling helps to determine the right components and specifications to obtain the best design, especially in determining the pump power needed to carry out irrigation operations at an optimum efficiency. Employing the right pump power can save costs while increasing the efficiency of a drip irrigation system.
4. System Curve and Pump Curve
The analysis of this study is extended by developing a system curve. The system curve is developed to determine the pump characteristic that is best suited to a system and its distance to determine the operating point for maximum efficiency. The measured value for head loss along the lateral pipe is about 4.3 m; the minimum pressure to be maintained in the first emitter is 19.3 m so as to maintain the pressure at 15 m in the last emitter at the end of the lateral pipe. The existing system employs an OSIP pump, model ZM 100, with a 0.75 kW power pump. The head range for the pump is between 31 m and 11 m associated with a flow rate ranging from 10 L/min to 90 L/min, respectively.
The pressure applied to this system is within 4.3 m of the head drop along the lateral pipes. The minimum pressure required to ensure a consistent discharge at 2 L/h is 15 m. For the existing drip irrigation system, the pump operates at a pressure of 31 m for a discharge of 13.2 L/m as shown in Figure 7. This indicates that the pressure applied is excessive for the pump used. The ideal capacity for this pump is a flow rate of 52.8 L/min at an operating pressure of 25 m and maintaining a lateral pressure of 15 m (head loss at the system before lateral pipe equals 5.5 m). With this setup (the discharge of 52.8 L and a 25 m operating pressure), the pump can operate at a minimum of four times the capacity of the existing system by setting a minimum pressure of 15 m along the lateral pipes.
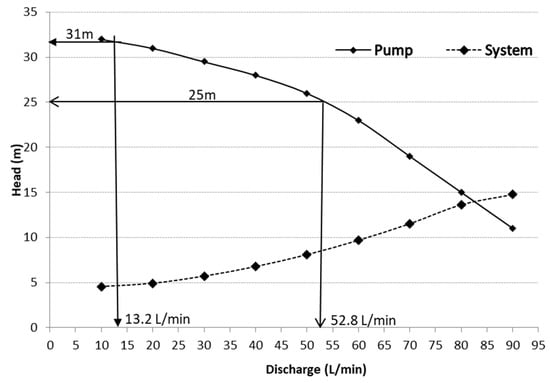
Figure 7.
System curve and pump curve of the existing drip irrigation system.
In this study it was found that the drip irrigation system can effectively operate by providing the required discharge. This irrigation system uses a pressure compensated dripper with the aim of obtaining a uniform discharge for each plant. The use of a pressure compensated dripper requires the control of certain pressure operations to obtain the desired flow rate. For this study, the required operating pressure is between 15.3–40.8 m. With the EPANET software it is easier to determine the right number of plants required for the desired pressure setting. EPANET will visually show each node (fitting, valve, and emitter) including flowrate, pressure, etc. With this information, the number of emitters and plants can be identified more easily. This will ensure that the designed system can operate at high efficiency. Based on the results from the model, it is inferred that the existing drip irrigation system is being operated in over-powered state. With the current pump power being used, the irrigation system could operate at four times the capacity of the existing irrigation system. In order to maintain the operating pressure at 15 m throughout the lateral pipe, a total flowrate of 52.8 L/min is required. A pump with a lower capacity of 0.56 kW can be used. The use of a lower power pump will reduce operating costs.
5. Conclusions
The hydraulic performance and modelling of the pressurized drip irrigation system of a small greenhouse plantation were studied. The ASAE standard was applied to investigate the hydraulic performance of the existing drip irrigation system. Statistical error indexes were used to indicate the performance of the model. The modelling helps to determine the appropriate components and specifications to obtain the best design, especially in determining the pump power needed to carry out irrigation operations at an optimum efficiency. Using the right pump power can save costs while increasing efficiency. An agreement between model and measurement is achieved with a low error index for all error indexes, i.e., RMSE, MAPE, and MBE. The RMSE shows errors of 0.04 L/h, and the mean bias error is between 0.02 L/h and 0.03 L/h for the flow rate distribution. For the pressure distribution, the RMSE ranges between 0.61 and 0.79 m and the mean bias error range is from 0.51 m to 0.68 m. The maximum error between the model and measurement results is less than 10%, thus indicating that the model has good performance and can be used to improve performance of drip irrigation systems in the future.
For hydraulic performance, from the results of different hydraulic parameters such as the emission uniformity (EU), the coefficient of uniformity (CU), and the coefficient of variation (CV), it can be seen that the drip irrigation system at Laman Sayur, MAEP Serdang, performs well and has met the ASAE standards. The emitter flow variation (EFV) is more than 10% for the 28.6 m and 15.3 m operation pressures where it is classified as acceptable, whereas for the 20.4 m and 25.5 m pressure operations the EFV gives a value of 10%, which is considered as desirable. Hydraulic performance studies of drip irrigation systems help in determining the appropriate range of operating pressure, type of emitter, distance between emitter, and discharge of each emitter. If the discharge information for each emitter is known, the timing for irrigation can be determined based on the needs of the crop. In conclusion, the results obtained from this study help in determining the desired irrigation capacity using an appropriate pump. The hydraulic performance of the studied system shows that it is optimized by setting the operating pressure within the range of 15.3 to 40.3 m, as recommended by the emitter manufacturer. The modelling procedures presented in this study can be applied to other irrigation systems such as commercial growers producing small fruit and vegetables with or without plastic mulch.
Author Contributions
E.H.S. conducted the field experiment, data collection, data analysis, and preparation of the initial manuscript; M.S.A.R. edited the manuscript, replotting figures, re-analyzing data and providing the main supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors acknowledge Malaysian Agro Exposition Park Serdang, providing the site for experiment and collecting data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Almajeed, A.; Alabas, M. Evaluation the Hydraulic Performance of Drip Irrigation System with Multi Cases. Glob. J. Res. Eng. 2013, 13, 2249–4596. [Google Scholar]
- Robert, A. Irrigation of vegetable and small fruit crops. In Natural Resource Engineering Specialist; University of Missouri Extension: Columbia, MO, USA, 2005. [Google Scholar]
- Ahmad, M.A.G.; Mangrio, G.A.; Wahab, A. Design Evaluation and Irrigation Scheduling of Drip Irrigation System on Citrus Orchard. Pak. J. Meteorol. 2015, 12, 37–48. [Google Scholar]
- Provenzano, G.; Pumo, D.; Di Dio, P. Simplified Procedure to Evaluate Head Losses in Drip Irrigation Laterals. J. Irrig. Drain. Eng. 2005, 131, 525–532. [Google Scholar] [CrossRef]
- Bagarello, V.; Ferro, V.; Provenzano, G.; Pumo, D. Evaluating pressure losses in drip-irrigation lines. J. Irrig. Drain. Eng. 1997, 123, 1–7. [Google Scholar] [CrossRef]
- Provenzano, G.; Pumo, D. Experimental analysis of local pressure losses for microirrigation laterals. J. Irrig. Drain. Eng. 2004, 130, 318–324. [Google Scholar] [CrossRef]
- Celik, H.K.; Karayel, D.; Lupeanu, M.E.; Rennie, A.E.W.; Akinci, I. Determination of head losses in drip irrigation laterals with cylindrical in-line type emitters through CFD analysis. Bulg. J. Agric. Sci. 2015, 21, 703–710. [Google Scholar]
- Watters, G.Z.; Keller, J. Trickle Irrigation Tubing Hydraulics; ASAE Technical Paper; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1978. [Google Scholar]
- Pitts, D.J.; Ferguson, J.A.; Wright, R.E. Trickle irrigation lateral design by computer analysis. Trans. ASAE 1986, 29, 1320–1324. [Google Scholar] [CrossRef]
- Chamba, D.; Zubelzu, S.; Juana, L. Energy, cost and uniformity in the design of drip irrigation systems. Biosyst. Eng. 2019, 178, 200–218. [Google Scholar] [CrossRef]
- Baiamonte, G. Explicit relationships for optimal designing rectangular microirrigation units on uniform slopes: The IRRILAB software application. Comput. Electron. Agric. 2018, 153, 151–168. [Google Scholar] [CrossRef]
- Juana, L.; Rodr;ı´guez-Sinobas, L.; Losada, A. Determining Minor Head Losses in Drip Irrigation Laterals. I: Methodology. J. Irrig. Drain. Eng. 2002, 128. [Google Scholar] [CrossRef]
- Rossman, L.A. Epanet 2 Users Manual; US EPA: Cincinnati, OH, USA, 2000.
- Zhou, B.; Li, Y.; Song, P.; Zhou, Y.; Yu, Y.; Bralts, V. Anti-clogging evaluation for drip irrigation emitters using reclaimed water. Irrig. Sci. 2017, 35, 181–192. [Google Scholar] [CrossRef]
- Sivanappan, R.K. Prospects of micro-irrigation in India. Irrig. Drain. Syst. 1994, 8, 49–58. [Google Scholar] [CrossRef]
- Dhawan, B. Drip Irrigation: Evaluating Returns. Econ. Political Wkly. 2000, 35, 3775–3780. [Google Scholar]
- Baiamonte, G. Advances in designing drip irrigation laterals. Agric. Water Manag. 2018, 199, 157–174. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, P. Evaluation of Hydraulic Performance of Drip Irrigation System. J. Agric. Eng. 2004, 44, 106–108. [Google Scholar]
- Tyson, T.W.; Curtis, L.M. Evaluating Water Distribution Uniformity in Micro-Irrigation Systems. 2009. Available online: https://studylib.net/doc/18713005/evaluation-water-distribution-uniformity (accessed on 17 July 2020).
- ASAE. Field Evaluation of Micro Irrigation Systems 2003; EP458; American Society of Agricultural Engineers: St. Joseph, MI, USA, 2003; pp. 760–765. [Google Scholar]
- Valipour, M. Sprinkle and Trickle Irrigation System Design Using Tapered Pipes for Pressure Loss Adjusting. J. Agric. Sci. 2012, 4, 125–133. [Google Scholar] [CrossRef][Green Version]
- Google Maps. Available online: https://www.google.com.my/maps (accessed on 6 July 2020).
- hidrauliCAD. Available online: http://hydraulicad.com/ (accessed on 6 July 2020).
- AFTFathom. Available online: https://www.aft.com/products/aft-software-overview (accessed on 6 July 2020).
- Infoworks. Available online: https://www.innovyze.com/en-us/products/infoworks-ws-pro (accessed on 6 July 2020).
- WaterCAD. Available online: https://www.bentley.com/en/products/product-line/hydraulics-and-hydrology-software/watercad (accessed on 6 July 2020).
- WaterGEMS. Available online: https://www.bentley.com/en/products/product-line/hydraulics-and-hydrology-software/watergems (accessed on 6 July 2020).
- AquaFlow. Available online: https://www.toro.com/en/agriculture/grower-connection/design-aides/design-software (accessed on 6 July 2020).
- DIDAS. Available online: https://app.agri.gov.il/didas/ (accessed on 6 July 2020).
- DOMIS. Available online: http://domis.iari.res.in/pages/dripd.php (accessed on 6 July 2020).
- HydroCalc. Available online: http://www.netafim.com/hydrocalc-software-1 (accessed on 6 July 2020).
- IRRICAD. Available online: https://www.irricad.com/ (accessed on 6 July 2020).
- IrriPro. Available online: https://www.irriworks.com/homepage/15-design (accessed on 6 July 2020).
- IrriExpress. Available online: https://www.irriexpress.com/pages/about-us (accessed on 6 July 2020).
- IrriLab. Available online: https://www.facebook.com/irrilab/ (accessed on 6 July 2020).
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)? Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Chakraborty, D.; Elzarka, H. Performance testing of energy models: Are we using the right statistical metrics? J. Build. Perform. Simul. 2017, 11, 433–448. [Google Scholar] [CrossRef]
- Swamidass, P.M. (Ed.) Mean Absolute Percentage Error (MAPE). In Encyclopedia of Production and Manufacturing Management; Springer: Boston, MA, USA, 2000. [Google Scholar]
- Amound, A.I. Significance of Energy Losses Due to Emitter Connections in Trickle Irrigation Lines. J. Agric. Eng. Res. 1995, 60, 1–5. [Google Scholar] [CrossRef]
- Solomon, K.H. Irrigation Uniformity and Yield Theory. Ph.D. Thesis, Department of Agricultural and Irrigation Engineering, Utah State University, Logan, UT, USA, 1983. [Google Scholar]
- Pragna, G.; Kumar, G.M.; Shankar, M.S. Hydraulic Performance Evaluation of Drip System by Developing Relationship between Discharge and Pressure. Int. J. Pure Appl. 2017, 5, 758–765. [Google Scholar] [CrossRef]
- Krutz, G.; Thompson, L.; Claar, P. Design of Agricultural Machinery; John Wiley & Sons: New York, NY, USA, 1984; p. 473. ISBN 047108672. [Google Scholar]
- Sakakibara, N. Finite Element in Fracture Mechanics; University of Texas: Austin, TX, USA, 2008. [Google Scholar]
- Baiamonte, G. Linking the Kinetic Energy Fraction and Equivalent Length Method for Trickle Irrigation Design Under Local Losses. J. Irrig. Drain. Eng. 2020, 146. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).