Abstract
This paper presents a classification using a decision tree algorithm of hydraulic jump over rough beds based on the approach Froude number, Fr1. Specifically, 581 datasets, from literature, were analyzed. Of these, 280 datasets were for natural rough beds and 301 were for artificial rough beds. The said dataset was divided into four classes based on the energy losses. To compare the performance of the decision tree classifier (J48), a multi-layer neural network (NN) was used. The results suggest an improved performance in terms of classification accuracy by the J48 algorithm in comparison to the NN classifier. Furthermore, the classifier model had only four leaves and achieved an accuracy of 91.56%. Furthermore, classification results showed that the first class (A) of hydraulic jump over the rough beds is approximately similar to that for the smooth bed. Moreover, in the next three classes (B, C, and D), upper values of Fr1 decreased with respect to the smooth bed classes. Lastly, in class D, the upper value of Fr1 reduced to 7.45, which indicates that the shear stress (i.e., the energy loss) grows sharply with increasing Fr1. Put simply, bed roughness effectively increases the energy dissipation with an increase in the Fr1.
1. Introduction
The hydraulic jump is a natural phenomenon caused by an abrupt change in the open channel flow regime from a supercritical to a subcritical condition. This phenomenon is used for energy dissipation that reduces the excess kinetic energy of high velocity flow. Stilling basin is an effective energy dissipator for reducing the exit velocity in the downstream of hydraulic structures such as spillways, drops, and sluice gates [1]. The hydraulic jump formed in a stilling basin (with a smooth bed) has been widely investigated by many researchers and their results have been reported. A jump occurred in a horizontal, rectangular, and smooth channel, which is classified based on the incoming Froude number (Fr1). Four different types of jumps are generally defined, which includes weak jump (1.7 < Fr1 ≤ 2.5), transition or oscillating jump (2.5 < Fr1 ≤ 4.5), steady jump (4.5 < Fr1 ≤ 9), and strong or choppy jump (Fr1 > 9) [2].
To prevent scouring and cavitation damages of stilling basin and reducing the construction cost of the structure, it is recommended to stabilize and confine the hydraulic jump inside the stilling basin. A reduction in the length of the stilling basin (i.e., length of hydraulic jump) is achieved by using appurtenances (natural and artificial rough elements) within the stilling basin so that the tail-water depth is somewhat less than the sequent depth of the free jump [3]. Natural rough elements are made up of sediment particles consisting of various levels of roughness [4]. Additionally, in artificial rough elements, devices such as sill, baffle blocks, block ramps, and screens are installed into the stilling basin [5]. Figure 1 shows the sketches of hydraulic jump over the natural and artificial rough bed with related variables. In the figure, y1 is the incoming flow depth, y2 is the tail water depth, Lj is the jump length, ks is natural bed roughness, and t is the size of artificial bed roughness.
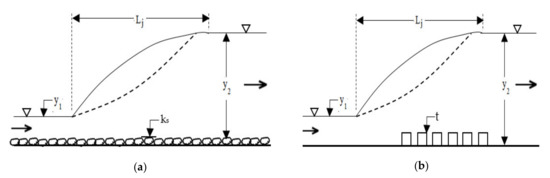
Figure 1.
Sketches of hydraulic jump over the rough bed: (a) natural rough bed and (b) artificial rough bed.
In recent years, several studies have been conducted to evaluate the effect of natural and artificial roughened beds on the characteristics of the hydraulic jump. Ead and Rajaratnam [6] studied the hydraulic jumps on corrugated beds and indicated that the jump length on corrugated beds is one half of its length over smooth beds. In addition, the results showed the attractiveness of corrugated beds for energy dissipation below hydraulic structures. Carollo et al. [7] evaluated the hydraulic jump over the natural rough bed with different diameters of gravels and cobbles. They suggested equations for estimating the relative sequence depth and rolling length. Misra et al. [8] investigated the turbulent flow structure of a weak hydraulic jump using particle image velocimetry measurements. They reported that a thin, curved shear layer oriented parallel to the surface is responsible for most of the turbulence production with the turbulence intensity decaying rapidly away from the toe of the breaker. Chern and Syamsuri [9] studied the effect of the corrugated bed on hydraulic jump characteristics using a smoothed particle hydrodynamics model (SPH). It was found that the sinusoidal bed can dissipate more energy than other beds. Furthermore, the proposed SPH model is capable of simulating the effect of corrugated beds on hydraulic jump characteristics. Dorrell et al. [10] analyzed three-dimensional flow structure and dynamics of hydraulic jumps in stratified, density-driven flows. Field observations suggested a newly identified type of hydraulic jump, which was a stratified low Froude number (<1.5–2) subaqueous hydraulic jump with an enhanced ability to transport sediment downstream of the jump. Dhar et al. [11] investigated the natural hydraulic jumps in thin film flow through channels slightly deviated from the horizontal. They revealed the existence of submerged jump, wavy jump, smooth jump, and no jump conditions as a function of liquid Reynolds number, scaled channel length, and channel inclination.
Generally, modeling studies in hydraulic engineering can help to properly understand the physical phenomena in laboratories. Such models are universally introduced as physically-based and data-driven models [12]. Physically-based models (knowledge-driven models) can, in principle, be applied to almost any kind of hydraulic problem. These models are based on our understanding of the physics of the hydraulic phenomena, which use physical equations to describe the phenomena characteristics. Although physically-based models are more widely applicable, they require large amounts of data and computational resources [13]. In contrast, a data-driven model is based on a limited knowledge of the phenomena and is defined as a model connecting together the different variables of the physical characteristics of a phenomenon. On the other word, these models capture a relationship between input and output variables without the physics being explicitly provided [14]. Since the development of data science and data mining methods in recent years, researchers have been encouraged to involve complex problems. In complex datasets, modelling the data using a proper method can become a real problem. In this condition, non-parametric classification techniques such as neural networks (NNs), decision tree (DT), support vector machines (SVMs), and k- nearest neighbors (k-NN) are extensively being used to overcome the problem [15].
Energy dissipation structures (stilling basin) are designed to confirm the hydraulic jump formation to prevent the expected damage to the structure. Design engineers should be careful about the selection of features to satisfy the stability of the jump. The stilling basins are designed to induce a steady jump. This type of jump serves the best economic conditions for the design of stilling basins. Position of steady jump is the least sensitive type to fluctuations in the tailwater elevation and forms steadily at the same location. In other words, the jump is well balanced and the performance is at its best [1]. Normally, conditions of the tailwater depth and jump type are determined by the upstream supercritical flows’ Froude number, which is the most important criteria for selecting a type of stilling basin. Classification of hydraulic jumps over rough beds can be applied in practice on hydro-technical constructions to estimate the type of hydraulic jump and specifically to evaluate the efficiency of spillways and stilling basins as well as modify the structures components as needed. Additionally, classification results can be applied for the design of spillways and energy dissipation basins for hydro-technical structures.
Keeping in view the effectiveness of data-driven models in various water resource engineering problems, especially on the hydraulic jump [2,16,17,18,19], this study aims to classify the hydraulic jump over rough beds (natural and artificial) based on the Froude numbers using a decision tree and neural network classifiers. The main reason for using decision tree classifiers is that they produce simple, understandable, and practical results (if-then rules) with high accuracy and reliability comparable to other classifiers like a neural network [20,21]. Additionally, low computational costs, easy interpretation of the model produced, and no requirement to user-defined parameters are the other advantages of decision tree classifiers [21]. On the other hand, neural networks are likely the most effective, flexible, and successful machine learning technique used to classify the different applications [22]. Datasets and methods used to classify the hydraulic jump over rough beds were introduced and obtained results are shown and discussed.
2. Materials and Methods
2.1. Datasets Used
The experimental data of the hydraulic jump over both natural and artificial rough beds were collected from existing literature. The summary of used hydraulic jump data (datasets) is provided in Table 1. The total number of data collected was 581 runs, which includes 280 runs on a natural rough bed and 301 runs on artificial rough beds.

Table 1.
Summarized characteristics of the experiments for both natural and artificial rough beds.
Generally, energy loss depends on hydraulic and geometric variables in a hydraulic jump. Specific energy upstream and downstream of the hydraulic jump is calculated by using depths (y1, y2) and mean flow velocities (V1, V2) using the following equations.
where E1, V1, and y1 are the energy, mean velocity, and depth of flow upstream of the hydraulic jump and E2, V2, and y2 are energy, mean velocity of flow, and depth of flow downstream of the hydraulic jump, respectively. Energy loss of a hydraulic jump is calculated using the relative energy dissipation rate equation.
where ΔE is the difference between the energy before and after the hydraulic jump (ΔE = E1−E2). Based on the energy loss variations within the available dataset, hydraulic jump is categorized in four classes based on the Froude number (Table 2). In this study, the Froude number was selected as the variable involved (input data) and classes of hydraulic jump (classes A, B, C, and D) were considered as a variable derived (output data). The classification process was done in three strategies including (1) datasets of natural rough bed, (2) datasets of artificial rough bed, and (3) combination of both datasets of natural and artificial rough bed.
E1 = y1 + V12/2g
E2 = y2 + V22/2g
ΔE/E1 = (E1 − E2)/E1

Table 2.
Classification of the hydraulic jump based on energy losses.
2.2. Classification Algorithms
2.2.1. Decision Tree Algorithm (J48)
The decision tree algorithm is an effective method to perform the hierarchical classification whereas the data set is divided into purer and more homogenous subsets, according to a set of tests used on one or more input parameters at each node of the tree. Decision tree classifiers have a simple figure that effectively classifies the datasets and can be easily stored. Due to their conceptual simplicity and computational performance, decision tree classifiers are used in different tasks [30]. Decision tree classifiers can carry out automatic variable selection and complexity reduction while the tree structure gives easily intelligible and interpretable results regarding the forecasting or generalizability of the classification [20]. The design of the decision tree involves three stages: splitting the nodes, specifying which nodes are the terminal nodes, and allocating class labels to terminal nodes [31]. The allocation of class labels to terminal nodes is based on the weighted vote, where it is assumed that specified classes are more prominent than other classes. A tree consists of a root node (including all of the data), a set of internal nodes (splits), and a set of terminal nodes (leaves). In a decision tree, each node has only one source node and two or more descendent nodes. A given datum is classified by going down the tree and consecutively subdividing it on the basis of the decision structure defined by the tree until a leaf is created [32].
In this study, J48, a decision tree classifier, as a C4.5 well-known algorithm [31,33], is used to classify the hydraulic jump over rough beds. In the decision tree classifier, the training data were divided into smaller subsets that may result in a very large and complex tree. In most cases, fitting a decision tree until all leaves contain data of a single class may over-fit the noise in the training data. If the training data have errors, then over-fitting the tree to the data may result in poor performance for unseen cases. To avoid the problem of over-fitting, the original tree is generally pruned to improve the classification accuracy when datasets outside the training set are used. The decision tree classifier (J48) uses an error-based pruning procedure that uses training data itself for pruning the over-grown tree. More descriptions about the decision tree algorithm are provided in Quinlan [31] and Witten and Frank [33].
2.2.2. Neural Network Classifier (NN)
A neural network (NN) is a biological nervous system, which consists of a large number of interconnected artificial elements divided in layers (input, hidden, output), but working in union to solve a problem. The most important ability of the neural networks is that they can identify the complex non-linear relationships between input-output data, use sequential training procedures, and modify themselves to the data. More details of NN can be found in Hassoun [34]. Multi-layer perceptron neural network is the most used model for classification and is extensively used in various disciples [35,36]. Many previous research studies on the classification tasks have confirmed that NNs perform better than traditional classification methods based on the classification accuracy. Although NNs are used for a wide variety of applications with acceptable efficiency, it is widely reported that NNs are sensitive to many parameters such as the size and quality of the training data set, network topology, over fitting issues, and training parameters [35].
For models training and validation in the present study, K-fold cross-validation was used. Cross-validation involves dividing the data randomly into k parts (i.e., fold, k = 10 in this study) in which the class was represented in almost the same ratio as in the full datasets. Out of the 10 parts, one part was held out in turn and then the learning scheme was trained on the remainder parts. The performance of the trained model is then estimated on the holdout set. Therefore, the learning process is performed a total of 10 times on different training sets. Lastly, 10 errors calculated were averaged to provide a total error computing [33]. The best topology of the NN classifier was selected by a trial-and-error method and the value of various user-defined parameters are provided in Table 3. In this research, open-source WEKA (Waikato Environment for Knowledge Analysis) software was used for both the decision tree and NN classifier (www.cs.waikato.ac.nz/mL/weka/).

Table 3.
Details of user-defined parameters for the best topology of a neural network (NN) classifier in the datasets.
3. Results and Discussion
Classification accuracies obtained by the decision tree algorithm (J48) and NN classifier models with different datasets are provided in Table 4. Results indicate that the J48 algorithm provides accurate classification as well as an NN classifier with all three datasets. In the following, results of the decision tree classifier model were presented because of its ability in producing if-then rules. The structure of these rules gives useful information regarding the classification of the jump.

Table 4.
Classification accuracy by the decision tree (J48) and NN classifiers for different datasets.
In the natural bed, the decision tree classifier model has four leaves and correctly classified about 95% of the data (accuracy = 95.36%). Figure 2a,b provide the decision tree and classification chart of the hydraulic jump in a natural rough bed, respectively. In Figure 2a, the numbers in brackets (e.g., 6/1 for class A) stands for the total number of data (e.g., 6) and the false classifications (e.g., 1) falling in each class, respectively. The first class (A) is related to Fr1 ≤ 2.68. This class is similar to the hydraulic jump over the smooth bed (Fr1 ≤ 2.5). In the second class (B), the Froude number changes from 2.68 to 4.16. An upper value of Fr1 of natural rough bed is less than Fr1 = 4.7 of the smooth bed. In the third class, the upper value of Fr1 was reduced significantly to 7.35 with respect to Fr1 = 9 of the smooth bed.
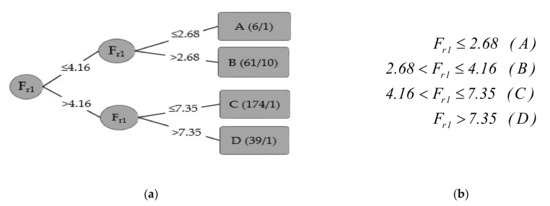
Figure 2.
Decision tree and classification chart of the hydraulic jump in a natural rough bed: (a) Decision tree classifier model (the numbers in brackets (e.g., 6/1 for class A) stands for the total number of data (e.g., 6) and the false classifications (e.g., 1) falling in each class, respectively). (b) Classification chart.
To show the interclass distributions and possible false classifications, the confusion matrix by the decision tree classifier with a dataset using natural rough surfaces is provided in Table 5. Results from Table 5 suggest that the most incorrectly classified cases lie in class C where nine cases were wrongly classified as class B and one case was wrongly classified as class D. Overall, the total correctly classified instances were 267 cases with 13 incorrectly classified cases.

Table 5.
Confusion matrix of the decision tree for a natural rough bed.
In the artificial bed, the decision tree classifier model also has four leaves and correctly classified about 91% of the data (i.e., 91.36%, Table 2). Under this condition, the accuracy of the classifier was reduced due to the different hydraulic and geometry condition in the dataset. The decision tree and classification chart of the hydraulic jump on an artificial rough bed is provided in Figure 3a,b, respectively. In Figure 3a, the numbers in brackets (e.g., 4/1 for class A) stands for the total number of data (e.g., 4) and the false classifications (e.g., 1) falling in each class, respectively. Results indicate that, for class A, the Froude number reached 2.73. In the second class (B), the upper value of Fr1 reached 3.85 (2.73 ≤ Fr1 ≤ 3.85). A comparison of Figure 2 and Figure 3 indicates almost the same value of the Froude number for classes A and B on artificial and natural beds. In the third class (C), the upper value of Fr1 increased from Fr1 = 7.35 on natural beds to 7.80 with artificial rough beds.
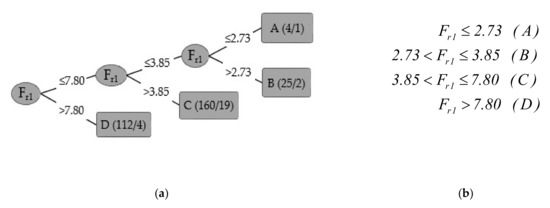
Figure 3.
Decision tree and classification chart of the hydraulic jump in an artificial rough bed: (a) Decision tree classifier model (the numbers in brackets (e.g., 4/1 for class A) stands for the total number of data (e.g., 4) and the false classifications (e.g., 1) falling in each class, respectively), (b) classification chart.
Confusion matrix (Table 6) using a decision tree classifier with this dataset shows interclass distributions and possible false classifications. The false classification cases could result from the fluctuations of downstream water surface of the hydraulic jump especially in high Froude numbers [1] and, consequently, the measurement error of the water surface level. In an artificial rough bed, the hydraulic jump classification process was accurate for A, B, and C classes, but, for the D class, cases beyond the diagonal line (shown in grey in Table 6) had some deviations. The most incorrectly classified cases were in the D class where 18 cases were wrongly classified as class C. Overall, the total correctly classified instances were 275 and 26 cases and were incorrectly classified.

Table 6.
Confusion matrix of the decision tree for an artificial rough bed.
With the full dataset consisting of both natural and artificial beds, a generated decision tree classifier model has four leaves and correctly classified about 92% of the data (i.e., 91.556%, Table 2). Figure 4a,b provide the decision tree and classification chart of the hydraulic jump with a full dataset, respectively. In Figure 4a, the numbers in the brackets (e.g., 11/2 for class A) stands for the total number of data (e.g., 11) and the false classifications (e.g., 2) falling in each class, respectively. In the first class (A), Fr1 is less than 2.73. This class is similar to the hydraulic jump over the smooth bed (Fr1 ≤ 2.5). It means that energy loss of rough bed in Fr1 ≤ 2.73 is similar to a smooth bed. Pagliara et al. [37] concluded that, at a low Froude number (Fr1 ≤ 3), the sequent depth over the rough bed is approximately the same of the Belanger equation, while, for larger Fr1, the data fall below the smooth boundary curve. In the second class (B), the Froude number changes from 2.73 to 3.87. A and B hydraulic jump classes of all rough beds are similar to artificial beds. Simsak [24] reported that, when Fr1 is greater than 3.9 (in rough beds), a constant linear correlation is obtained between the jump-length parameter and incoming Froude number values. Mahtabi and Sattari [19] investigated the sequent depth of the hydraulic jump over a rough bed using the M5 Model Tree and concluded that Fr1 is a basic parameter in development of the model tree in the root with a value of 4.225. It should be noted that hydraulic jump stilling basins are designed to induce a steady jump or a strong jump. The incoming Froude number should be above 4.5 in practice [27]. It seems that the design value in the rough beds may be adjusted to above 4, approximately.
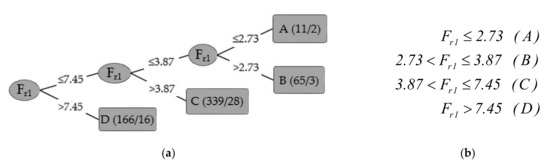
Figure 4.
Decision tree and classification chart of the hydraulic jump with all rough bed: (a) Decision tree classifier model (the numbers in brackets (e.g., 11/2 for class A) stands for the total number of data (e.g., 11) and the false classifications (e.g., 2) falling in each class, respectively). (b) Classification chart.
In the third class (C), the upper value of Fr1 reached 7.45. This value is almost near the upper value of Fr1 in the natural beds. This value is significantly smaller than Fr1 = 9 for the smooth bed. It means that roughness of the bed increases the energy dissipation efficiently. In an earlier study, Evcimen [23] also stated that the energy loss in a hydraulic jump on rough beds is 5–10% larger than that for a free jump on smooth beds. Habib and Nassar [38] found that the apron of 90% staggered roughness length increases the relative energy loss by 17%. In addition, Elnikhely [39] observed that the roughness bed increases the energy loss by about 14% in comparison with the smooth bed. Most researchers have reported that the shear stress on rough beds is independent of the relative roughness. The amount of shear stress coefficient was found to be a function of an incoming Froude number [6,25,40]. The interaction forces between the supercritical flow of the liquid and bed roughness has a significant effect in increasing the shear stress especially at high values of the Froude number. The apparent bed roughness induces more turbulent intensity, which generates more drag force and shear stress, and, consequently, increases the energy loss [41]. In Figure 5, variation of ∆E/E1 versus Fr1 and domain of hydraulic jump classes are shown. The largest number of hydraulic jump data is related to C and D classes of a hydraulic jump. The relative energy loss gets closer to 90% of the specific energy of incoming flow asymptotically. Ayanlar [42] stated that the gain in energy loss for the jumps on a rough bed decreases as the incoming Froude number increases and tends to be constant at a value of 7% when the Froude number is greater than 8. Abbaspour et al. [25] reported that the energy loss on a corrugated bed is 5–19% more than smooth beds, and, for Froude numbers more than 7, the energy loss parameter was about 10%. It seems that the strong or choppy jump over rough beds occurs in Froude numbers above 7 or 8 (approximately in Fr1 > 7.5 or class D).

Figure 5.
Variation of ∆E/E1 versus Fr1 along with the ranges of smooth and rough regimes and hydraulic jump classes (A, B, C, D).
Confusion matrix (Table 7) provides interclass distributions and possible false classifications for the entire dataset. In all rough beds, the hydraulic jump classification process was accurate for class A, but for the B, C, and D classes, cases beyond the diagonal line (shown in grey in Table 7) had some deviations. Incorrectly classified cases with this dataset are: 1 in the A class, 16 in the B class, 18 cases in the C class, and 14 in the D class, which suggests a maximum number of wrongly classified cases lie in class C. Overall, the total correctly classified instances were 532 cases with 49 incorrectly classified cases. Thus, for rough beds, it can be concluded that decision tree algorithms can effectively be used to classify the hydraulic jump with reasonable accuracy. In contrast to other classifiers such as a neural network where each data sample is tested against all classes, thereby decreasing their efficiency, decision tree classifier tests a sample against only certain subsets of classes, and, therefore, removes unnecessary computations [43]. The main advantage of the decision tree classifier is to produce user-friendly rules (if-then rules). Furthermore, no lengthy training is required, as in the case of neural networks, nor is any specific data model assumed, as in the case of statistical classifiers [44]. Other advantages of use of the decision tree classifier are that it implicitly perform a parameter selection as the most important parameter is selected first during the node splitting process.

Table 7.
Confusion matrix of the decision tree for all rough beds.
4. Conclusions
In this study, a decision tree algorithm (J48) and NN classifiers were used to derive if-then rules for classifying the hydraulic jump over the rough bed (natural and artificial). The classification results indicate that two classifiers have produced good classification performance for the overall rough beds. However, the J48 algorithm has produced the best classification performance with accuracy of 91.57% for rough beds. Moreover, the results of the decision tree classifier showed that classification of the hydraulic jump over the rough bed is different from the smooth beds. Specifically, for rough beds, the shear stress is significantly higher (4–15 times, depending on the type of roughness) than that for smooth beds. Additionally, the shear stress grows sharply with the increasing approach Froude number. In other words, the interaction forces between the supercritical flow of the liquid and bed roughness has a significant effect in increasing the shear stress, especially at high values of the Froude number. Consequently, higher shear stress in rough beds leads to higher energy losses in the hydraulic jump when compared to smooth beds. Based on the results of the decision tree classifier model, the first class (A) of the hydraulic jump over the rough beds approximates a smooth bed. In the next three classes (B, C, and D), upper values of Fr1 decrease with respect to the smooth bed classes. Lastly, in class D, the upper value of Fr1 is 7.45, which indicates that the roughness of the bed increases the energy dissipation for the higher Froude number.
Author Contributions
Conceptualization, G.M. and H.M.A. Methodology, G.M., H.M.A., and M.P. Software, G.M., M.P., and B.C. Supervised the investigation, H.M.A. and B.C. Writing—original draft preparation, G.M. All authors contributed to reviewing and editing the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chow, V.T. Open Channel Flow; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Negm, A.M. Optimal roughened length of prismatic stilling basins. In Proceedings of the 5th International Conference on Hydro Science and Engineering Conference, Warsaw, Poland, 18–21 September 2002. [Google Scholar]
- Peterka, A.J. Hydraulic Design of Stilling Basins and Energy Dissipators; USA Bureau of Reclamation: Washington, DC, USA, 1958.
- Rajaratnam, N. Hydraulic jumps on rough beds. Can. Inst. Transp. Eng. 1968, 11, 1–8. [Google Scholar]
- Afzal, N.; Bushra, A.; Seena, A. Analysis of Turbulent Hydraulic Jump over a Transitional Rough Bed of a Rectangular Channel: Universal Relations. J. Eng. Mech. 2011, 137, 835–845. [Google Scholar] [CrossRef]
- Ead, S.; Rajaratnam, N. Hydraulic Jumps on Corrugated Beds. J. Hydraul. Eng. 2002, 128, 656–663. [Google Scholar] [CrossRef]
- Carollo, F.G.; Ferro, V.; Pampalone, V. Hydraulic Jumps on Rough Beds. J. Hydraul. Eng. 2007, 133, 989–999. [Google Scholar] [CrossRef]
- Misra, S.K.; Kirby, J.T.; Brocchini, M.; Veron, F.; Thomas, M.; Kambhamettu, C. The mean and turbulent flow structure of a weak hydraulic jump. Phys. Fluids 2008, 20, 35106. [Google Scholar] [CrossRef]
- Chern, M.J.; Syamsuri, S. Effect of Corrugated Bed on Hydraulic Jump Characteristic Using SPH Method. J. Hydraul. Eng. 2013, 139, 221–232. [Google Scholar] [CrossRef]
- Dorrell, R.M.; Peakall, J.; Sumner, E.; Parsons, D.R.; Darby, S.E.; Wynn, R.; Özsoy, E.; Tezcan, D. Flow dynamics and mixing processes in hydraulic jump arrays: Implications for channel-lobe transition zones. Mar. Geol. 2016, 381, 181–193. [Google Scholar] [CrossRef]
- Dhar, M.; Das, G.; Das, P.K. Planar hydraulic jumps in thin film flow. J. Fluid Mech. 2019, 884, 1–26. [Google Scholar] [CrossRef]
- Kim, M.; Gerba, C.P.; Choi, C.Y. Assessment of physically-based and data-driven models to predict microbial water quality in open channels. J. Environ. Sci. 2010, 22, 851–857. [Google Scholar] [CrossRef]
- Liang, J.; Li, W.; Bradford, S.A.; Simunek, J. Physics-Informed Data-Driven Models to Predict Surface Runoff Water Quantity and Quality in Agricultural Fields. Water 2019, 11, 200. [Google Scholar] [CrossRef]
- Friedl, M.; Brodley, C. Decision tree classification of land cover from remotely sensed data. Remote. Sens. Environ. 1997, 61, 399–409. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines; Prentice Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Abbaspour, A.; Farsadizadeh, D.; Ghorbani, M.A. Estimation of hydraulic jump on corrugated bed using artificial neural networks and genetic programming. Water Sci. Eng. 2013, 6, 189–198. [Google Scholar] [CrossRef]
- Karbasi, M.; Azamathulla, H.M. GEP to predict characteristics of a hydraulic jump over a rough bed. KSCE J. Civ. Eng. 2016, 20, 3006–3011. [Google Scholar] [CrossRef]
- Mahtabi, G.; Mehrkian, R.; Taran, F. New optimized equations with intelligent models for predicting hydraulic jump characteristics over artificial and natural rough beds. Int. J. Opt. Civ. Eng. 2019, 9, 147–158. [Google Scholar]
- Mahtab, G.; Sattari, M.T. Investigation of Hydraulic Jump Characteristics in Rough Beds Using M5 Model Tree. Jordan J. Agric. Sci. 2016, 12, 631–648. [Google Scholar] [CrossRef]
- Pal, M.; Mather, P. An assessment of the effectiveness of decision tree methods for land cover classification. Remote. Sens. Environ. 2003, 86, 554–565. [Google Scholar] [CrossRef]
- Salmasi, F.; Sattari, M.T.; Pal, M. Application of data mining on evaluation of energy dissipation over low gabion-stepped weir. Turk. J. Agric. For. 2016, 36, 95–106. [Google Scholar] [CrossRef]
- Saravanan, K.; Sasithra, S. Review on Classification Based on Artificial Neural Networks. Int. J. Ambient. Syst. Appl. 2014, 2, 11–18. [Google Scholar] [CrossRef]
- Evcimen, T.U. The Effect of Prismatic Roughness Elements on Hydraulic Jump. Master’s Thesis, Middle East Technological University, Ankara, Turkey, 2005. [Google Scholar]
- Sismak, C. Forced Hydraulic Jump on Artificially Roughened Beds. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2006. [Google Scholar]
- Abbaspour, A.; Dalir, A.H.; Farsadizadeh, D.; Sadraddini, A. Effect of sinusoidal corrugated bed on hydraulic jump characteristics. HydroResearch 2009, 3, 109–117. [Google Scholar] [CrossRef]
- Elsebaie, I.H.; Shabayek, S. Formation of Hydraulic Jumps on corrugated Beds. Int. J. Civ. Environ. Eng. 2010, 10, 40–50. [Google Scholar]
- Evcimen, T.U. Effect of Prismatic Roughness on Hydraulic Jump in Trapezoidal Channels. Ph.D. Thesis, Middle East Technical University, Ankara, Turkey, 2012. [Google Scholar]
- Neluwala, N.; Karunanayake, K.; Sandaruwan, K.; Pathirana, K. Characteristics of hydraulic jumps over rough beds—An experimental study. Eng. J. Inst. Eng. Sri Lanka 2013, 46, 1. [Google Scholar] [CrossRef]
- Velioglu, D.; Tolyay, N.D.; Dincer, A.E. A Numerical and experimental study on the characteristics of hydraulic jumps on rough beds. In Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Gupta, G. A self explanatory review of decision tree classifiers. In International Conference on Recent Advances and Innovations in Engineering (ICRAIE-2014), Jaipur, India, 9–11 May 2014; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2014; pp. 1–7. [Google Scholar]
- Quinlan, J.R. C4.5 Programs for Machine Learning. Morgan Kaufmann: Burlington, MA, USA, 1993. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Wadsworth: Belmont, CA, USA, 1984. [Google Scholar]
- Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2005. [Google Scholar]
- Hassoun, M.H. Fundamentals of Artificial Neural Networks; MIT Press: London, UK, 1995. [Google Scholar]
- Yuan, H.; Van Der Wiele, C.F.; Khorram, S. An Automated Artificial Neural Network System for Land Use/Land Cover Classification from Landsat TM Imagery. Remote. Sens. 2009, 1, 243–265. [Google Scholar] [CrossRef]
- Garcia-Salgado, B.P.; Ponomaryov, V.I.; Robles-Gonzalez, M.A.; Robles-Gonzales, M.A. Parallel multilayer perceptron neural network used for hyperspectral image classification. Proc. SPIE 2016, 9897, 98970K. [Google Scholar] [CrossRef]
- Pagliara, S.; Lotti, I.; Palermo, M. Hydraulic jump on rough bed of stream rehabilitation structures. HydroResearch 2008, 2, 29–38. [Google Scholar] [CrossRef]
- Habib, A.; Nassar, M. Characteristics of flow and scour under the effect curved steel roughness elements. Egypt. J. Eng. Sci. Technol. 2016, 16, 6–7. [Google Scholar] [CrossRef]
- Elnikhely, E.A. Effect of Staggered roughness elements on flow characteristics in rectangular channel. Int. J. Res. Eng. Technol. 2014, 23, 359–370. [Google Scholar]
- Izadjoo, F.; Bejestan, M. Corrugated Bed Hydraulic Jump Stilling Basin. J. Appl. Sci. 2007, 7, 1164–1169. [Google Scholar] [CrossRef]
- Akib, S.; Ahmed, A.A.; Imran, H.M.; Mahidin, M.F.; Ahmed, H.S.; Rahman, S. Properties of Hydraulic Jump over Apparent Corrugated Beds. Dam Eng. 2015, 25, 65–77. [Google Scholar]
- Ayanlar, K. Hydraulic Jumps on Corrugated Beds. Master’s Thesis, Middle East Technological University, Ankara, Turkey, 2004. [Google Scholar]
- Safavian, S.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Pal, M.; Mather, P.M. Decision Tree Based Classification of Remotely Sensed Data. In Proceedings of the Asian Conference on Remote Sensing, Singapore, 5–9 November 2001. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).