An Enhanced Approach to the Spatial and Statistical Analysis of Factors Influencing Spring Distribution on a Transboundary Karst Aquifer
Abstract
1. Introduction
2. Proposed Methodology
2.1. Weights of Evidence Technique
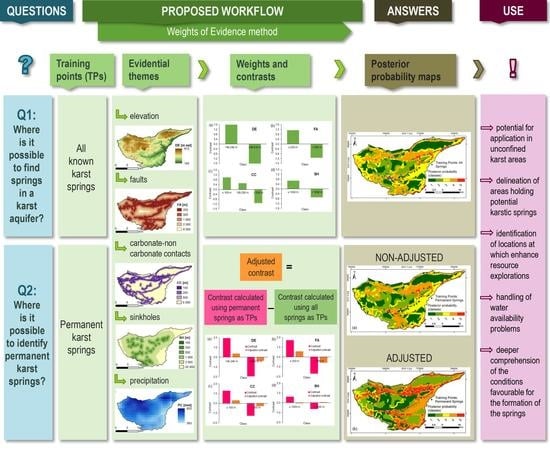
2.2. Workflow for the Application of the WofE Technique for Karst Springs
- I
- Q1—where is it possible to find karst springs?
- II
- Q2—where is it possible to identify the permanent karst springs?
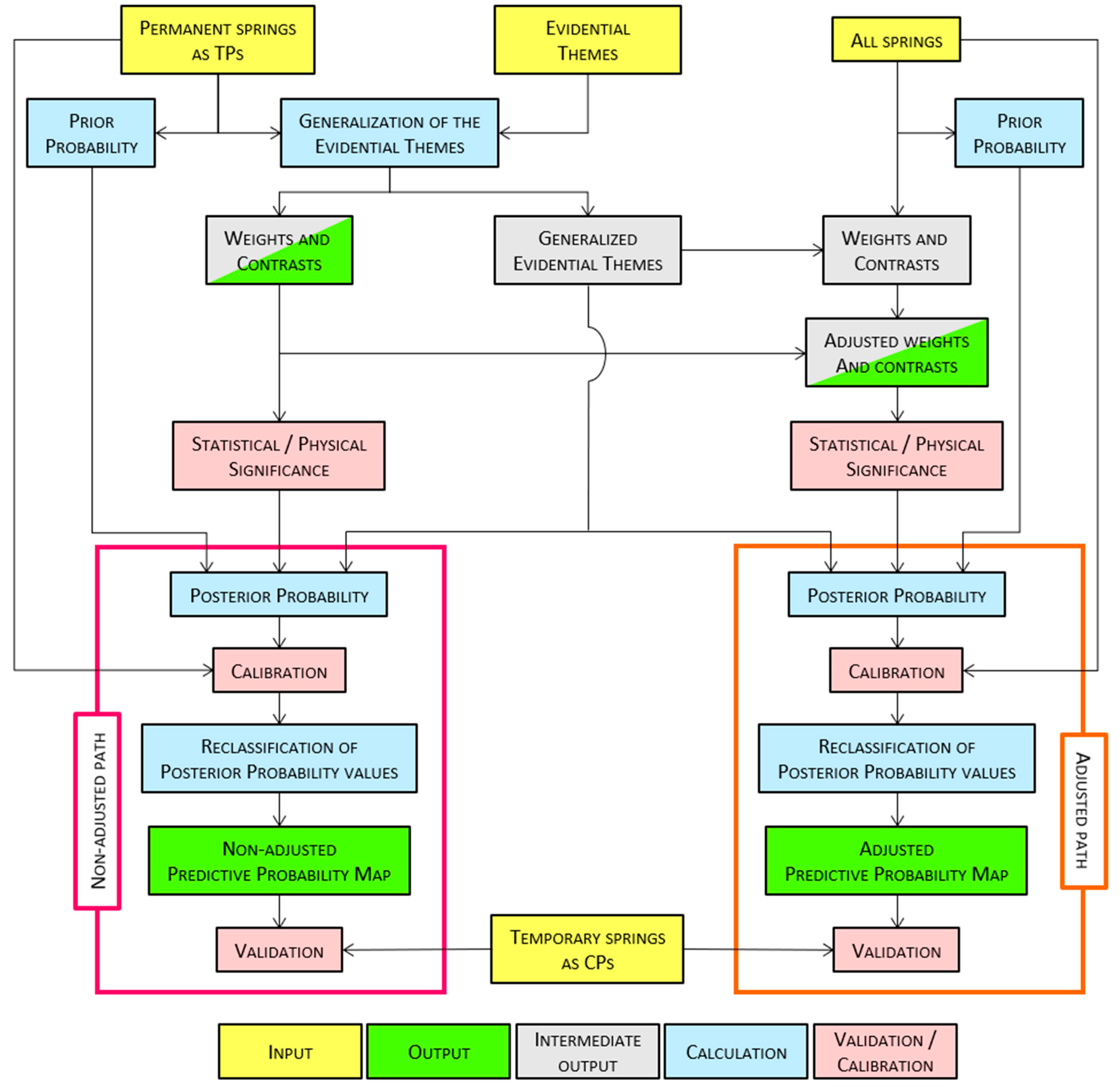
- calculation of the prior probability;
- generalisation of the evidential themes, and evaluation of contrast C, weights W+ and W−;
- evaluation of the statistical and physical significance of the generalised evidential themes; and
- creation of the posterior probability map.
- analysis using the permanent springs as TPs (calculation of the prior probability, generalisation of the evidential themes, evaluation of contrast C, weights W+ and W−, statistical and physical significance, and creation of the posterior probability map);
- analysis using all springs as TPs on the generalised evidential themes (evaluation of contrast C, weights W+ and W−, statistical and physical significance) and calculation of the prior probability;
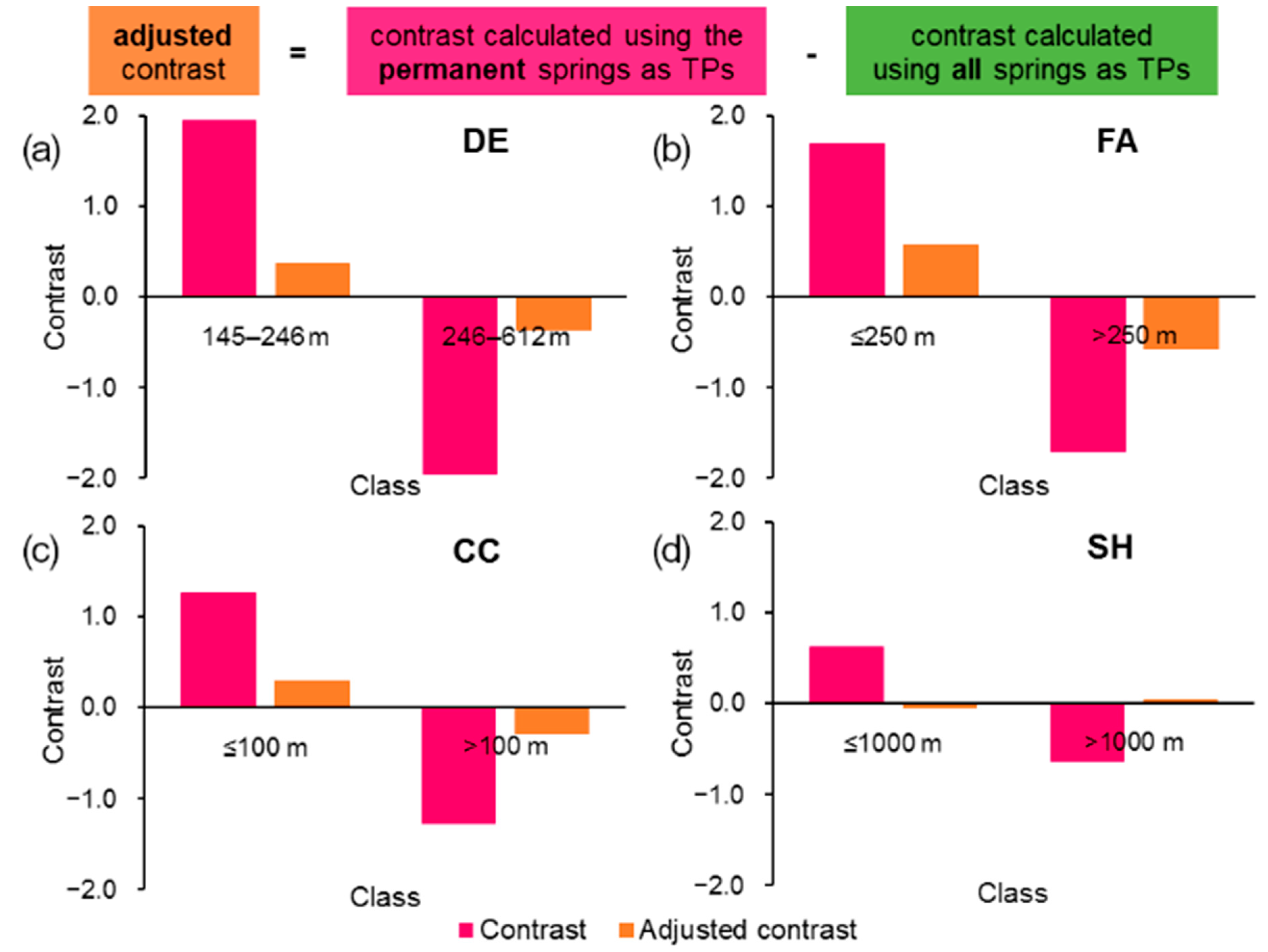
- calculation of the adjusted contrast and weights, by subtracting C, W+ and W− calculated using all springs as TPs (step 2) from C, W+ and W− calculated using the permanent springs as TPs (step 1);
- creation of the adjusted posterior probability map using: (i) the prior probability calculated using all springs and (ii) adjusted weights obtained from step 3;
- reclassification of the posterior probability values in 5 classes, using the geometrical interval classification method; and
- comparison of the adjusted posterior probability map (step 4) with the posterior probability map, obtained using the standard WofE approach (step 1), and their derived reclassified maps, through calibration and validation techniques (Table 1). In this phase, we use the temporary springs, as CPs, for the validation of the adjusted map.
3. Application of the Proposed Workflow
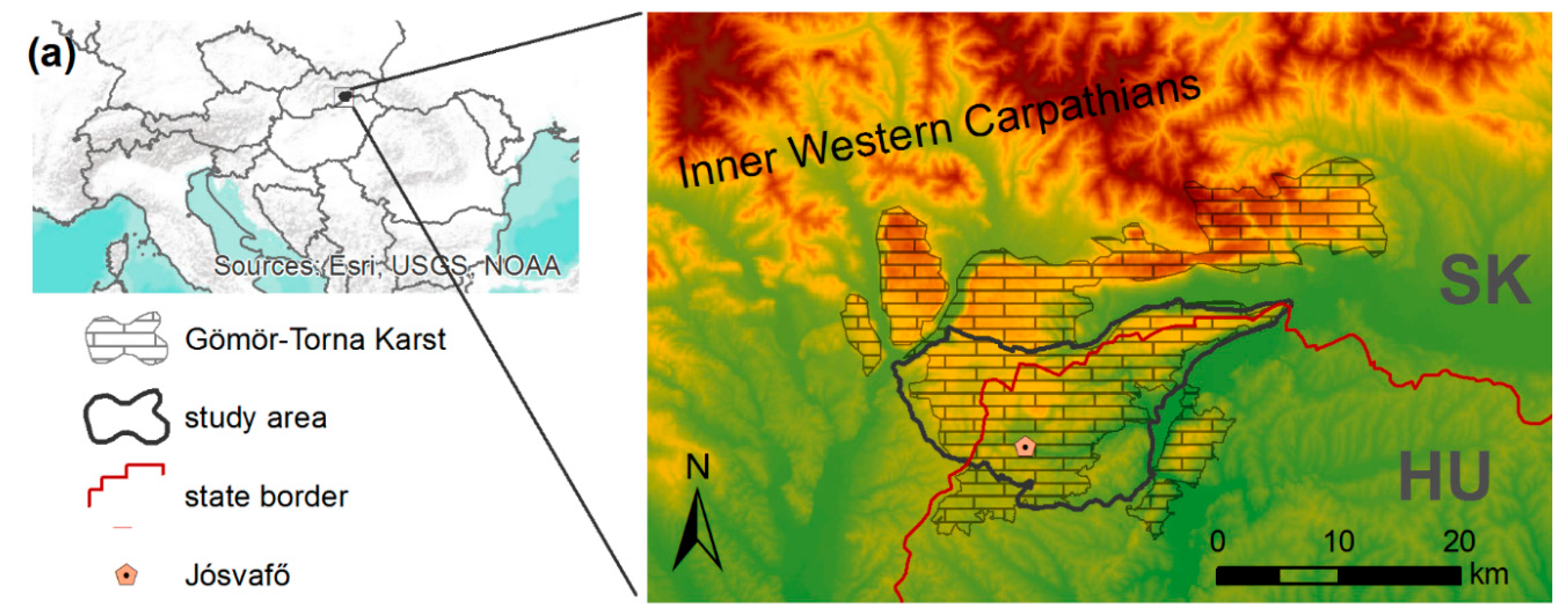
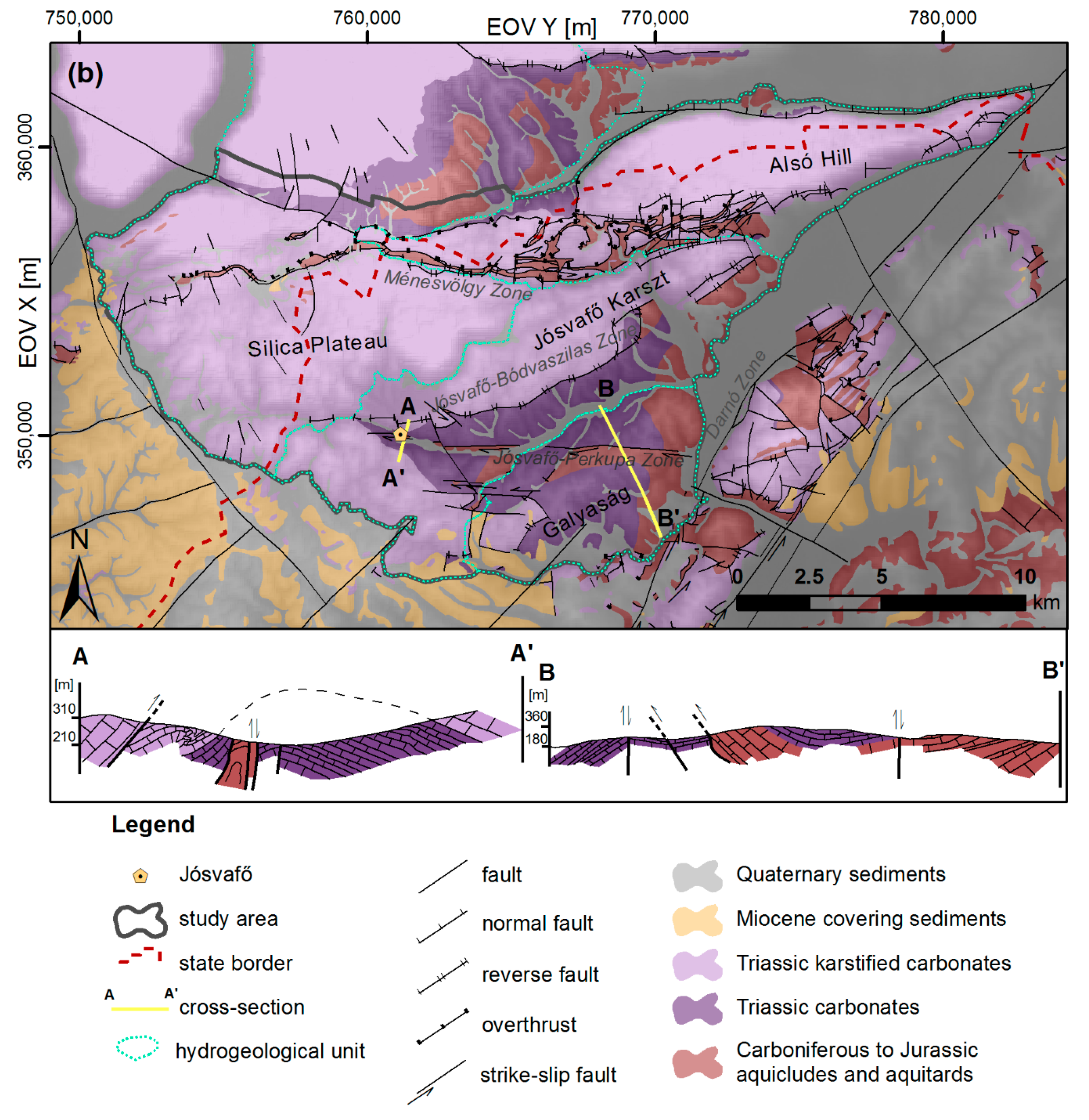
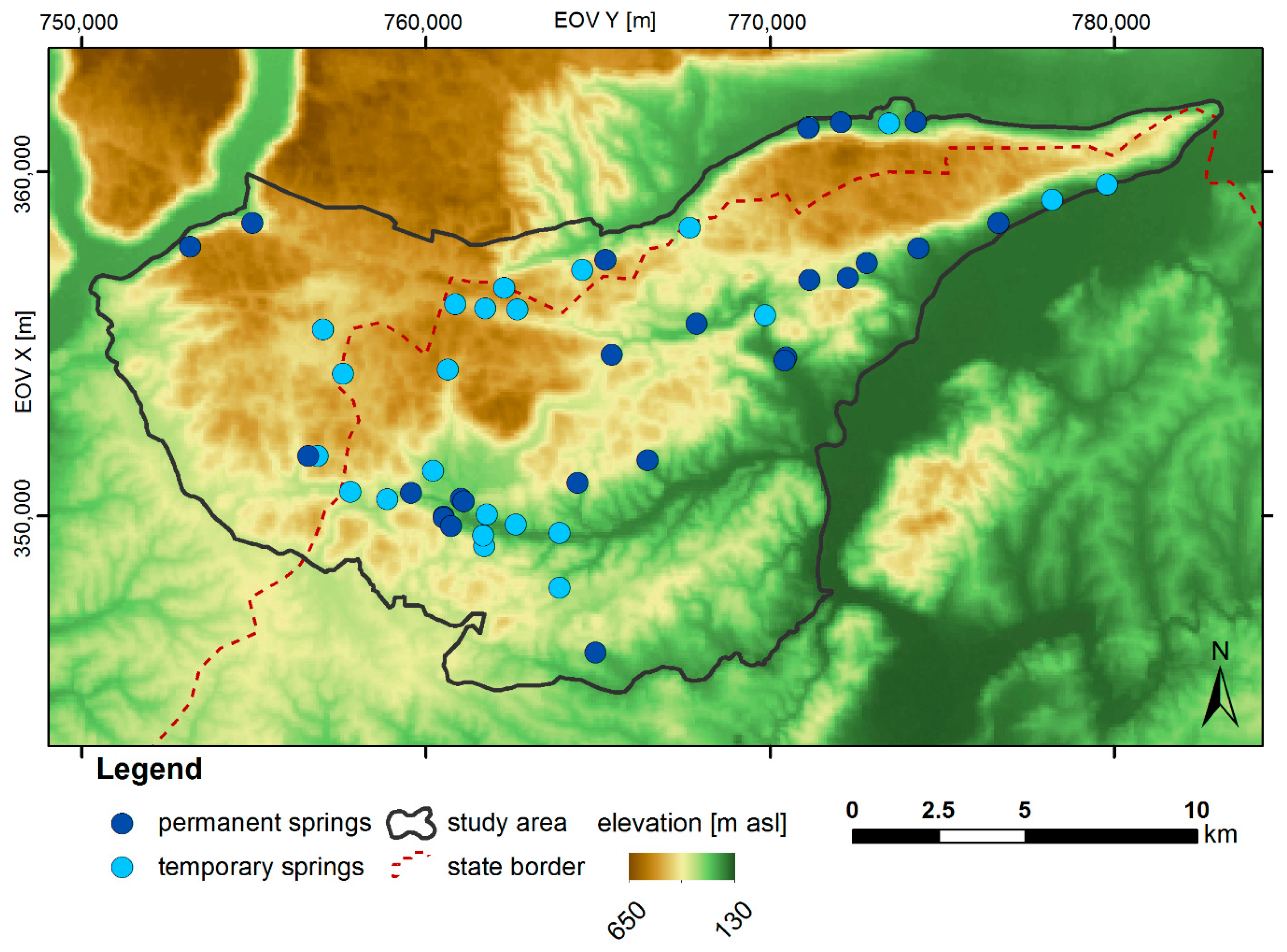
3.1. Geological and Hydrogeological Characterisation of the Study Area
3.2. Evidential Themes
3.3. Response Variables
4. Results
4.1. Location of Springs (Q1)
4.2. Location of Permanent Springs (Q2)
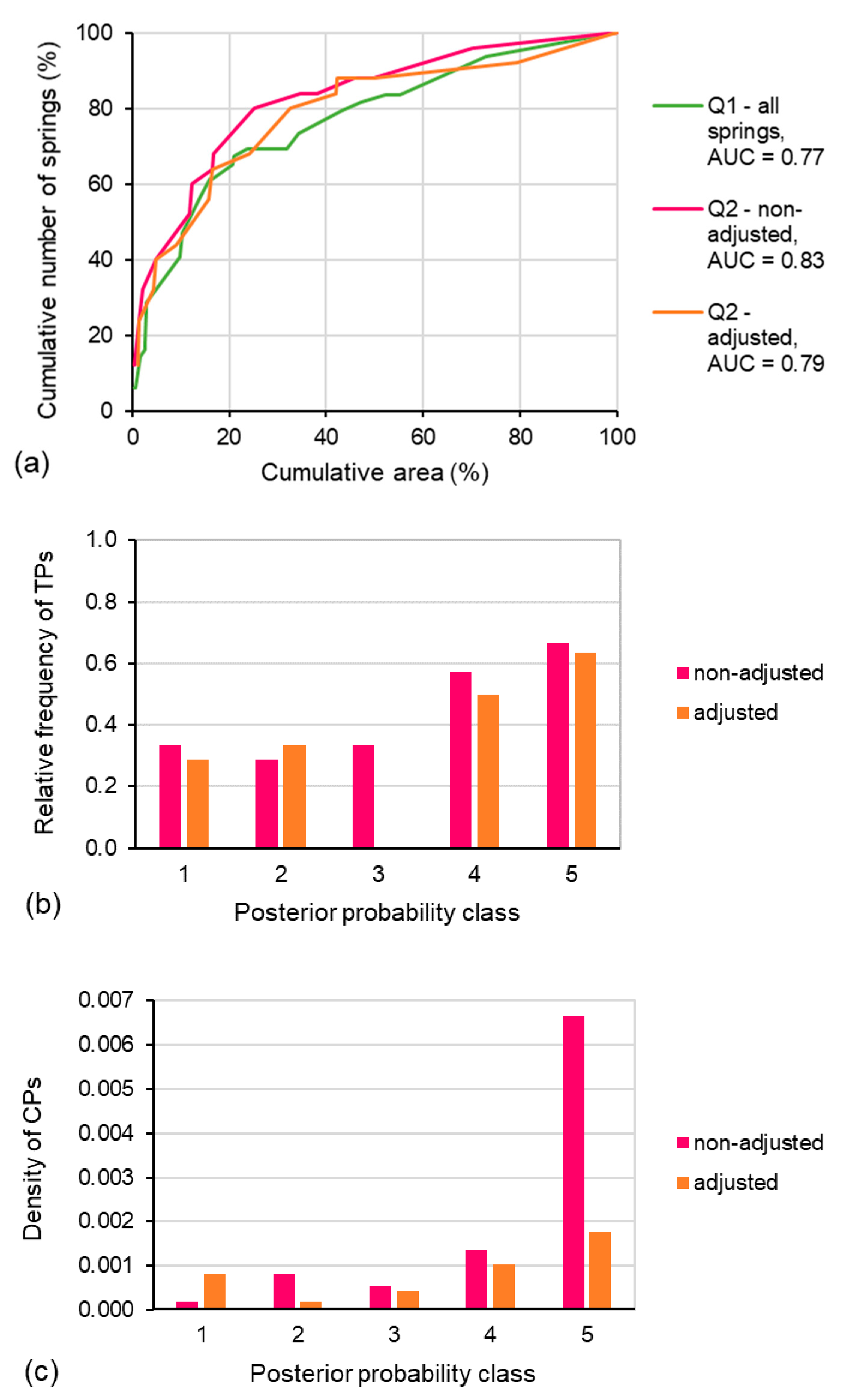
4.3. Validation
5. Discussion
6. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ford, D.; Williams, P.D. Karst Hydrogeology and Geomorphology; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Goldscheider, N.; Drew, D. Methods in Karst Hydrogeology: IAH: International Contributions to Hydrogeology, 26; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Zwahlen, F. Vulnerability and Risk Mapping for the Protection of Carbonate (Karst) Aquifers, Final Report (COST Action 620). European Commission, Directorate-General XII Science; Office for Official Publications of the European Communities: Brussels, Belgium, 2004.
- Gleick, P.H. Climate change, hydrology, and water resources. Rev. Geophys. 1989, 27, 329–344. [Google Scholar] [CrossRef]
- Butscher, C.; Huggenberger, P. Modeling the Temporal Variability of Karst Groundwater Vulnerability, with Implications for Climate Change. Environ. Sci. Technol. 2009, 43, 1665–1669. [Google Scholar] [CrossRef]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; Van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M. Ground water and climate change. Nat. Clim. Chang. 2013, 3, 322–329. [Google Scholar] [CrossRef]
- Green, T.R. Linking climate change and groundwater. In Integrated Groundwater Management; Springer: Cham, Switzerland, 2016; pp. 97–141. [Google Scholar]
- Toth, J. Groundwater discharge: A common generator of diverse geologic and morphologic phenomena. Hydrol. Sci. J. 1971, 16, 7–24. [Google Scholar] [CrossRef]
- Engelen, G.B.; Kloosterman, F.H. Hydrological Systems Analysis: Methods and Applications; Springer Science & Business Media: Berlin, Germany, 2012; Volume 20. [Google Scholar]
- Goldscheider, N. Hydrogeology and Vulnerability of Karst Systems: Examples from the Northern Alps and the Swabian Alb. Ph.D. Thesis, Karlsruhe University, Karlsruhe, Germany, 2002. [Google Scholar]
- Tóth, J. Springs seen and interpreted in the context of groundwater flow-systems. In Proceedings of the GSA Annual Meeting, Portland, OR, USA, 18–21 October 2009. [Google Scholar]
- Kresic, N.; Stevanovic, Z. Groundwater Hydrology of Springs: Engineering, Theory. In Management, and Sustainability; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Iván, V.; Mádl-Szőnyi, J. State of the art of karst vulnerability assessment: Overview, evaluation and outlook. Environ. Earth Sci. 2017, 76, 112. [Google Scholar] [CrossRef]
- Stevanović, Z. Karst Aquifers—Characterization and Engineering; Stevanović, Z., Ed.; Springer International Publishing: Cham, Switzerland, 2015; p. 692. [Google Scholar]
- Bonacci, O.; Terzić, J.; Roje-Bonacci, T.; Frangen, T. An Intermittent Karst River: The Case of the Čikola River (Dinaric Karst, Croatia). Water 2019, 11, 2415. [Google Scholar] [CrossRef]
- Sorichetta, A.; Masetti, M.; Ballabio, C.; Sterlacchini, S. Aquifer nitrate vulnerability assessment using positive and negative weights of evidence methods, Milan, Italy. Comput. Geosci. Uk 2012, 48, 199–210. [Google Scholar] [CrossRef]
- Bonham-Carter, G.F. Geographic Information Systems for Geoscientists-Modeling with GIS. Comput. Methods Geosci. 1994, 13, 398. [Google Scholar]
- Raines, G.L. Evaluation of weights of evidence to predict epithermal-gold deposits in the Great Basin of the Western United States. Nat. Resour. Res. 1999, 8, 257–276. [Google Scholar] [CrossRef]
- Sterlacchini, S.; Ballabio, C.; Blahut, J.; Masetti, M.; Sorichetta, A. Spatial agreement of predicted patterns in landslide susceptibility maps. Geomorphology 2011, 125, 51–61. [Google Scholar] [CrossRef]
- Lee, S.; Kim, Y.-S.; Oh, H.-J. Application of a weights-of-evidence method and GIS to regional groundwater productivity potential mapping. J. Environ. Manag. 2012, 96, 91–105. [Google Scholar] [CrossRef] [PubMed]
- Corsini, A.; Cervi, F.; Ronchetti, F. Weight of evidence and artificial neural networks for potential groundwater spring mapping: An application to the Mt. Modino area (Northern Apennines, Italy). Geomorphology 2009, 111, 79–87. [Google Scholar] [CrossRef]
- Cervi, F.; Blöschl, G.; Corsini, A.; Borgatti, L.; Montanari, A. Perennial springs provide information to predict low flows in mountain basins. Hydrol. Sci. J. 2017, 62, 2469–2481. [Google Scholar] [CrossRef]
- Arthur, J.D.; Wood, H.A.R.; Baker, A.E.; Cichon, J.R.; Raines, G.L. Development and implementation of a Bayesian-based aquifer vulnerability assessment in Florida. Nat. Resour. Res. 2007, 16, 93–107. [Google Scholar] [CrossRef]
- Pollicino, L.C.; Masetti, M.; Stevenazzi, S.; Colombo, L.; Alberti, L. Spatial Statistical Assessment of Groundwater PCE (Tetrachloroethylene) Diffuse Contamination in Urban Areas. Water 2019, 11, 1211. [Google Scholar] [CrossRef]
- Kessler, H. Az aggteleki barlangrendszer hidrográfiája [The hydrology of the Aggtelek Cave System]. Földr. Közl 1938, 66, 1–30. [Google Scholar]
- Jakucs, L. Vízföldtani megfigyelések a Gömöri-karszton [Hydrogeological observations on the Gömör Karst]. Földt. Közl 1951, 81, 442–445. [Google Scholar]
- Izápy, G.; Maucha, L. Az Aggteleki-hegység karszthidrológiai vizsgálata a Jósvafői kutató állomáson. In Karsztvízkutatás Magyarországon Ia. kötet. Felszín alatti vizeink kutatása, feltárása, hasznosítása és védelme. Szemelvények a kutatás és oktatás intézményeinek munkáiból; VITUKI: Budapest, Hungary, 2004. [Google Scholar]
- Gruber, P. A Baradla–Domica-barlangrendszer hidrológiai kutatásának eredményei [Summary of the Hydrologycal Research of the Baradla–Domica Cave System]. Karsztfejlődés [Karst Development] 2016, 21, 187–201. [Google Scholar] [CrossRef]
- Iván, V.; Mádl-Szőnyi, J. Vulnerability assessment and its validation: The Gömör-Torna Karst, Hungary and Slovakia. Geol. Soc. Lond. Spec. Publ. 2017, 466. [Google Scholar] [CrossRef]
- Maucha, L. Az Aggteleki-hegység karszthidrológiai kutatási eredményei és zavartalan hidrológiai adatsorai 1958–1993 [Results and undisturbed data of karst hydrological researches on Aggtelek Hills 1958–1993 (in Hungarian)]. VITUKI Rt. Hidrológiai kiadványa 1998, 414. [Google Scholar]
- Masetti, M.; Poli, S.; Sterlacchini, S.; Beretta, G.P.; Facchi, A. Spatial and statistical assessment of factors influencing nitrate contamination in groundwater. J. Environ. Manag. 2008, 86, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Arthur, J.D.; Baker, A.E.; Cichon, J.R.; Wood, A.R.; Rudin, A. Florida Aquifer Vulnerability Assessment (FAVA): Contamination potential of Florida’s principal aquifer systems. In Report Submitted to the Division of Water Resource Management, Florida Department of Environmental Protection. Tallahassee: Division of Resource Assessment and Management; Florida Geological Survey: Tallahassee, FL, USA, 2005. [Google Scholar]
- Sorichetta, A.; Ballabio, C.; Masetti, M.; Robinson Jr, G.R.; Sterlacchini, S. A Comparison of Data-Driven Groundwater Vulnerability Assessment Methods. Groundwater 2013, 51, 866–879. [Google Scholar] [CrossRef] [PubMed]
- Albinet, M.; Margat, J. Cartographie de la vulnerabilité à la pollution des nappes d’eau souterraines. Bull. BRGM 1970, 2ème série 3, 13–22. [Google Scholar]
- Coolbaugh, M.F.; Raines, G.L.; Zehner, R.E. Assessment of exploration bias in data-driven predictive models and the estimation of undiscovered resources. Nat. Resour. Res. 2007, 16, 199–207. [Google Scholar] [CrossRef]
- Sorichetta, A.; Robinson, G.R., Jr. Groundwater vulnerability assessment using positive and negative Weights-of-Evidence methods to correct for sampling bias. In Proceedings of the Flowpath 2012, Bologna, Italy, June 20–22 2012. [Google Scholar]
- Focazio, M.J. Assessing Ground-water Vulnerability to Contamination: Providing Scientifically Defensible Information for Decision Makers; US Dept. of the Interior, US Geological Survey: Reston, VA, USA, 2002; Volume 1224.
- Sorichetta, A.; Masetti, M.; Ballabio, C.; Sterlacchini, S.; Beretta, G.P. Reliability of groundwater vulnerability maps obtained through statistical methods. J. Environ. Manag. 2011, 92, 1215–1224. [Google Scholar] [CrossRef] [PubMed]
- Cowan, N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behav. Brain Sci. 2001, 24, 87–114. [Google Scholar] [CrossRef] [PubMed]
- Chung, C.-J.F.; Fabbri, A.G. Probabilistic prediction models for landslide hazard mapping. Photogramm. Eng. Remote Sens. 1999, 65, 1389–1399. [Google Scholar]
- Sawatzky, D.; Raines, G.; Bonham-Carter, G.; Looney, C. Spatial Data Modeller (SDM): ArcMAP 9.3 Geoprocessing Tools for Spatial Data Modelling Using Weights of Evidence, Logistic Regression, Fuzzy Logic and Neural Networks. 2009. Available online: http://www.ige.unicamp.br/sdm/ (accessed on 5 June 2019).
- Zámbó, L. Az Aggteleki-karszt felszínalaktani jellemzése. Geomorphological characterization of the Aggtelek Karst. Földrajzi értesitö 1998, 47, 359–378. [Google Scholar]
- Gessert, A. Geomorphology of the Slovak Karst (Eastern Part). J. Maps 2016, 12, 285–288. [Google Scholar] [CrossRef]
- Telbisz, T.; Gruber, P.; Mari, L.; Kőszegi, M.; Bottlik, Z.; Standovár, T. Geological Heritage, Geotourism and Local Development in Aggtelek National Park (NE Hungary). Geoheritage 2020, 12, 5. [Google Scholar] [CrossRef]
- Szentpétery, I.; Less, G. Az Aggtelek–Rudabányai-hegység Földtana. Magyarázó az Aggtelek–Rudabányai-Hegység 1988-ban Megjelent 1: 25 000 Méretarányú Fedetlen Földtani Térképéhez.(Geology of the Aggtelek–Rudabánya Hills. Explanatory Book to the Pre-Quaternary Geological Map of the Aggtelek–Rudabánya Hills, 1988, 1: 25 000.)—Magyarország Tájegységi Térképsorozata; Magyar Állami Földtani Intézet: Budapest, Hungary, 2006; p. 92. [Google Scholar]
- Hips, K. The structural setting of Lower Triassic formations in the Aggtelek-Rudabánya Mountains (northeastern Hungary) as revealed by geological mapping. Geol. Carpathica 2001, 52, 287–299. [Google Scholar]
- Sásdi, L. Vízföldtan és vízrajz [Hydrogeology and Hydrology]. In Az Aggteleki Nemzeti Park [The Aggtelek National Park]; Baross, G., Ed.; Mezőgazda Kiadó: Budapest, Hungary, 1998; pp. 118–159. [Google Scholar]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-filled SRTM for the globe Version 4. CGIAR-CSI 2008, 15, 25–54, CGIAR-CSI SRTM 90m Database. Available online: http://srtm.csi.cgiar.org (accessed on 5 June 2019).
- Less, G.; Mello, J.; Elecko, M.; Kovács, S.; Pelikán, P.; Pentelényi, L.; Pristaš, J.; Radócz, G.; Szentpétery, I.; Vass, D. Geological map of the Gemer-Bükk area 1: 100000; Hungarian Gelogical Institute: Budapest, Hungary, 2004. [Google Scholar]
- Wang, T.; Hamann, A.; Spittlehouse, D.; Carroll, C. Locally downscaled and spatially customizable climate data for historical and future periods for North America. PLoS ONE 2016, 11, e0156720. [Google Scholar] [CrossRef] [PubMed]
- Ghasemizadeh, R.; Hellweger, F.; Butscher, C.; Padilla, I.; Vesper, D.; Field, M.; Alshawabkeh, A. Review: Groundwater flow and transport modeling of karst aquifers, with particular reference to the North Coast Limestone aquifer system of Puerto Rico. Hydrogeol. J. 2012, 20, 1441–1461. [Google Scholar] [CrossRef]
- Mádl-Szőnyi, J.; Tóth, Á. Basin-scale conceptual groundwater flow model for an unconfined and confined thick carbonate region. Hydrogeol. J. 2015, 23, 1359–1380. [Google Scholar] [CrossRef]
- Caine, J.S.; Evans, J.P.; Forster, C.B. Fault zone architecture and permeability structure. Geology 1996, 24, 1025–1028. [Google Scholar] [CrossRef]
- Underschultz, J.; Otto, C.; Bartlett, R. Formation Fluids in Faulted Aquifers: Examples from the Foothills of Western Canada and the North West Shelf of Australia; American Association of Petroleum Geologists: Tulsa, OK, USA, 2005. [Google Scholar]
- Oravecz, É.; Héja, G.; Fodor, L. Triassic salt tectonics in the Inner Western Carpathians (Silica Nappe, Aggtelek Hills): The role of inherited salt structures during the Alpine deformation. In Proceedings of the 14th Workshop of the ILP Task Force Sedimentary basins, Hévíz, Hungary, 15–18 October 2019. [Google Scholar]
- Forkasiewicz, M.J.; Paloc, H. Régime de tarissement de la foux-de-la-vis (Gard) étude préliminaire. La Houille Blanche 1967, 1, 29–36. [Google Scholar] [CrossRef]
- Gunn, J. A conceptual model for conduit flow dominated karst aquifers. IAHS-AISH Publ. 1986, 161, 587–596. [Google Scholar]
- Bonacci, O. Karst springs hydrographs as indicators of karst aquifers. Hydrol. Sci. J. 1993, 38, 51–62. [Google Scholar] [CrossRef]
- Kiraly, L. Modelling karst aquifers by the combined discrete channel and continuum approach. Bulletin du Centre d’hydrogéologie 1998, 16, 77–98. [Google Scholar]
- Fiorillo, F. The recession of spring hydrographs, focused on karst aquifers. Water Resour. Manag. 2014, 28, 1781–1805. [Google Scholar] [CrossRef]
- Iván, V. Vulnerability mapping approaches of karst aquifers on the example of Gömör-Torna Karst. Ph.D. Thesis, Eötvös Loránd University, Budapest, Hungary, 2019. [Google Scholar]
- Pourtaghi, Z.S.; Pourghasemi, H.R. GIS-based groundwater spring potential assessment and mapping in the Birjand Township, southern Khorasan Province, Iran. Hydrogeol. J. 2014, 22, 643–662. [Google Scholar] [CrossRef]



| Concept | Definition | Operative Translation in... |
|---|---|---|
| Response variable | The phenomenon under consideration (e.g., mineral deposits). The location of occurrences is known. The occurrences are treated as points. Occurrences are subdivided into two sets used for generating the response themes (training set) or performing calibration and validation processes (control set) [17,18]. | Examples: mineral deposits (e.g., [17]), landslides (e.g., [19]), contaminated water wells (e.g., [23,31]). Occurrences can be either training points (TPs), being part of the training set, or control points (CPs), as part of the control set. |
| Evidential themes or predictors | Factors influencing the location and spatial distribution of the response variable. Evidential themes represent sets of continuous or categorical spatial data [17,18]. | Geological, geomorphological and physical factors influencing the presence and spatial distribution of the phenomenon under consideration, for example:
|
| Response theme or predictive probability map | The response theme (i.e., predictive probability map) is the result of the WofE [32]. | A response theme (i.e., predictive probability map) is an output data layer showing the distribution of posterior probability values [32]. It represents the relative probability of occurrence of the phenomenon under consideration (e.g., presence of mineral deposits, landslides risk, groundwater vulnerability). |
| Prior probability | The probability that a unit area contains an occurrence without considering any evidential themes [17,18]. | It is given by the ratio between the number of unit areas containing a TP and the total area [17]. |
| Posterior probability | The posterior probability represents the relative probability that a unit area contains an occurrence based on the evidences provided by the evidential themes [17,18]. | The posterior probability is calculated by adding a weight for each evidence class to the logit of the prior probability and converting the sum from logit to probability [17]. |
| Generalization of the evidential themes | Ordered evidential themes can be generalized during the analysis to improve model results relating the number and location of TPs and the presence of random effects [32]. | Generalizing an ordered evidential theme means defining ranges of values that can be grouped into evidence classes, which have a statistically significant spatial correlation with the location of TPs [32]. An objective (semi-guided) procedure has been developed by Sorichetta, Masetti, Ballabio and Sterlacchini [16]. |
| Weights | Weights establish a spatial association between TPs and evidential themes. Weights are the values assigned to each evidence class [18,32]. | Weights are calculated for each evidential theme based on the presence or absence of TPs [18,32]:
|
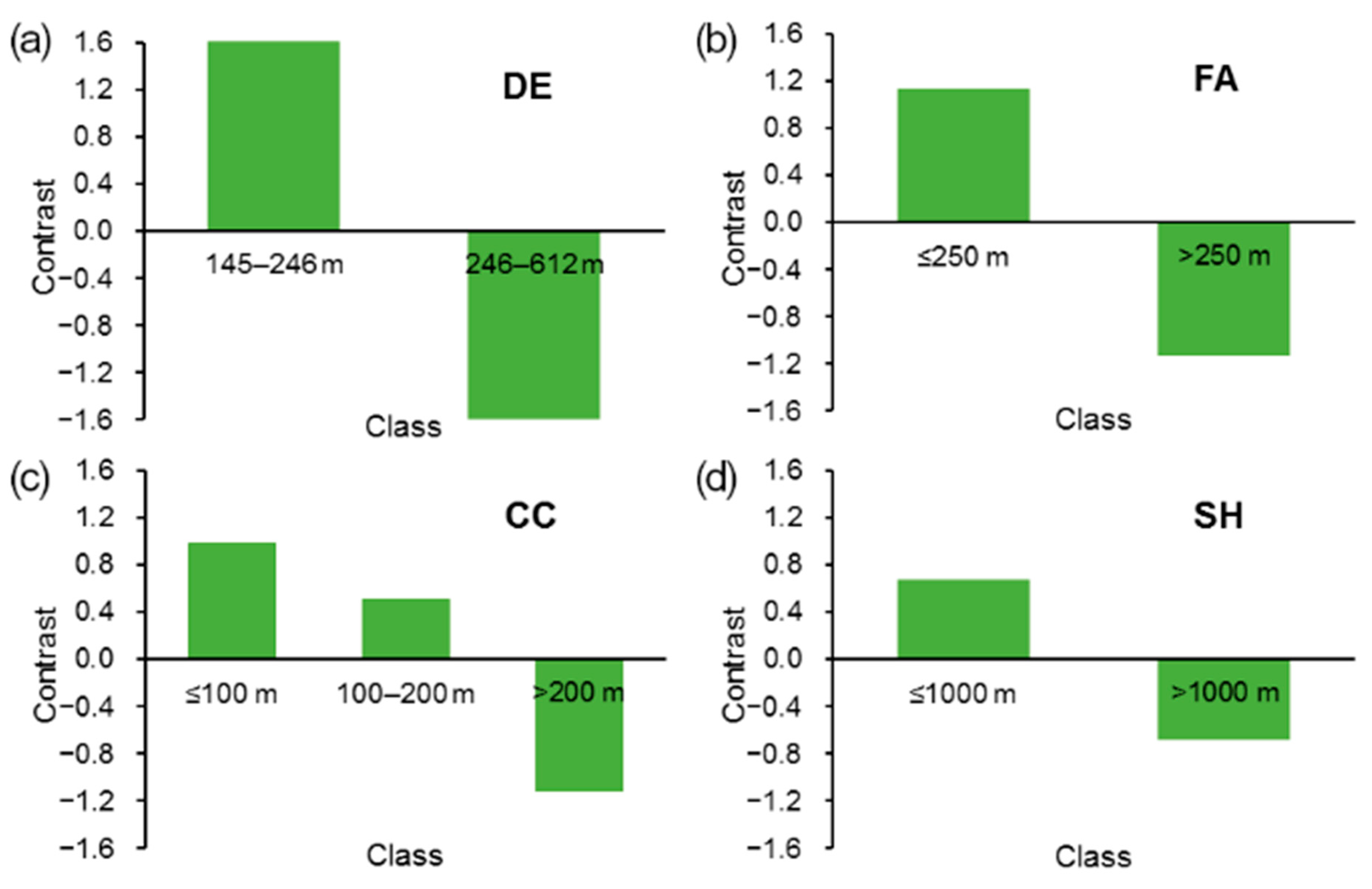
| Contrast | The contrast is a measure of the usefulness of each evidence class in predicting the location of the occurrences [17,18]. | For each class of each evidential theme, the contrast is calculated as the difference between the positive and the negative weight (C = W+ − W−). A positive contrast value means a direct correlation between the class and the TPs, and a negative value means an indirect correlation, whereas a value close to zero means low or no correlation [18] |
| Statistical significance | A level of significance needs to be established prior the generalization process. This is equivalent to a Student t-test [18,23]. | A confidence value for the ratio between the contrast and its standard deviation (i.e., normalized contrast) must be selected to provide a useful measure of the significance of the contrast and, thus, to the respective class of an evidential theme. See [23], for a complete list of confidence values and relative test values. |
| Scientific explanation | The pattern distribution of an evidential theme after the generalization process needs some justification by scientific reasoning [16,18,19,23,31,33]. | The pattern distribution needs to be justifiable from either a geological (e.g., [34]), geomorphological (e.g., [19]) or hydrogeological (e.g., [31]) point of view. |
| Bias | Statistical models generally require the use of random samples of a population. A bias could occur when the spatial distribution of occurrences differs greatly from an ideal random setting. Such condition could occur in mineral exploration researches or hydrogeological studies. For example, sources of exploration bias include land accessibility factors (location of outcrops, roads, lakes, swamps, property boundaries, political boundaries, etc.) and perceived exploration criteria (faults, alteration, geochemical anomalies, etc.); in most hydrogeological settings, biased distribution of monitoring wells is due to land accessibility factors and a tendency to site more monitoring wells in known contaminated areas than in other areas [35,36]. | Sorichetta, Masetti, Ballabio and Sterlacchini [16] developed a quantitative methodology that allows sampling bias to be recognized and contrast values to be corrected for sampling bias effects in hydrogeological studies. In an ideal random setting, contrasts calculated using all occurrences (both TPs and CPs) should have values of near zero for all evidence classes. If a bias occurs, the contrast is adjusted by subtracting the contrast calculated using all occurrences from the contrast calculated using either a) the TPs or b) the CPs. This procedure requires that the same classification of the Evidential Themes is used for both the analyses with all occurrences and either the TPs or the CPs. |
| Reclassified Predictive Probability Map | Scientifically defensible response themes, expressed as probability maps, require additional interpretation before being usable for most of the end-user purposes. This is due to the excessive number of classes, which is inappropriate in practical purposes (e.g., land use regulations) [37,38,39]. | Sorichetta, Masetti, Ballabio, Sterlacchini and Beretta [38], in their study on groundwater vulnerability assessment, have demonstrated the reliability and suitability of the geometrical interval classification method for reclassifying posterior probability values and obtain maps consisting of few classes (5). The geometrical interval classification method which ensures that each class has approximately the same number of different post probability values. |
| Calibration & Validation | The meaningfulness, reliability and accuracy of the probability maps need to be checked to improve defensibility of the results and facilitate implementation [19,23,38,40]. | Techniques: |
| Data | Use | Data Source |
|---|---|---|
| digital elevation model (SRTM, resolution of 3 arc-seconds) | evidential theme: DE | [48] |
| geological map (1:100,000) | evidential themes: FA and CC | [49] |
| sinkhole database (location) | evidential theme: SH | Cadastre of sinkholes (Aggtelek National Park) |
| modelled yearly average precipitation map (1000 m resolution) | evidential theme: PC | http://tinyurl.com/ClimateEU |
| spring database (location and activity: permanent or temporary) | response variables | [30]; Cadastre of springs (Aggtelek National Park) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iván, V.; Stevenazzi, S.; Pollicino, L.C.; Masetti, M.; Mádl-Szőnyi, J. An Enhanced Approach to the Spatial and Statistical Analysis of Factors Influencing Spring Distribution on a Transboundary Karst Aquifer. Water 2020, 12, 2133. https://doi.org/10.3390/w12082133
Iván V, Stevenazzi S, Pollicino LC, Masetti M, Mádl-Szőnyi J. An Enhanced Approach to the Spatial and Statistical Analysis of Factors Influencing Spring Distribution on a Transboundary Karst Aquifer. Water. 2020; 12(8):2133. https://doi.org/10.3390/w12082133
Chicago/Turabian StyleIván, Veronika, Stefania Stevenazzi, Licia C. Pollicino, Marco Masetti, and Judit Mádl-Szőnyi. 2020. "An Enhanced Approach to the Spatial and Statistical Analysis of Factors Influencing Spring Distribution on a Transboundary Karst Aquifer" Water 12, no. 8: 2133. https://doi.org/10.3390/w12082133
APA StyleIván, V., Stevenazzi, S., Pollicino, L. C., Masetti, M., & Mádl-Szőnyi, J. (2020). An Enhanced Approach to the Spatial and Statistical Analysis of Factors Influencing Spring Distribution on a Transboundary Karst Aquifer. Water, 12(8), 2133. https://doi.org/10.3390/w12082133