Modelling Hydrological Performance of a Bauxite Residue Profile for Deposition Management of a Storage Facility
Abstract
1. Introduction
2. Materials and Methods
2.1. Determining Physical Properties of Bauxite Residue
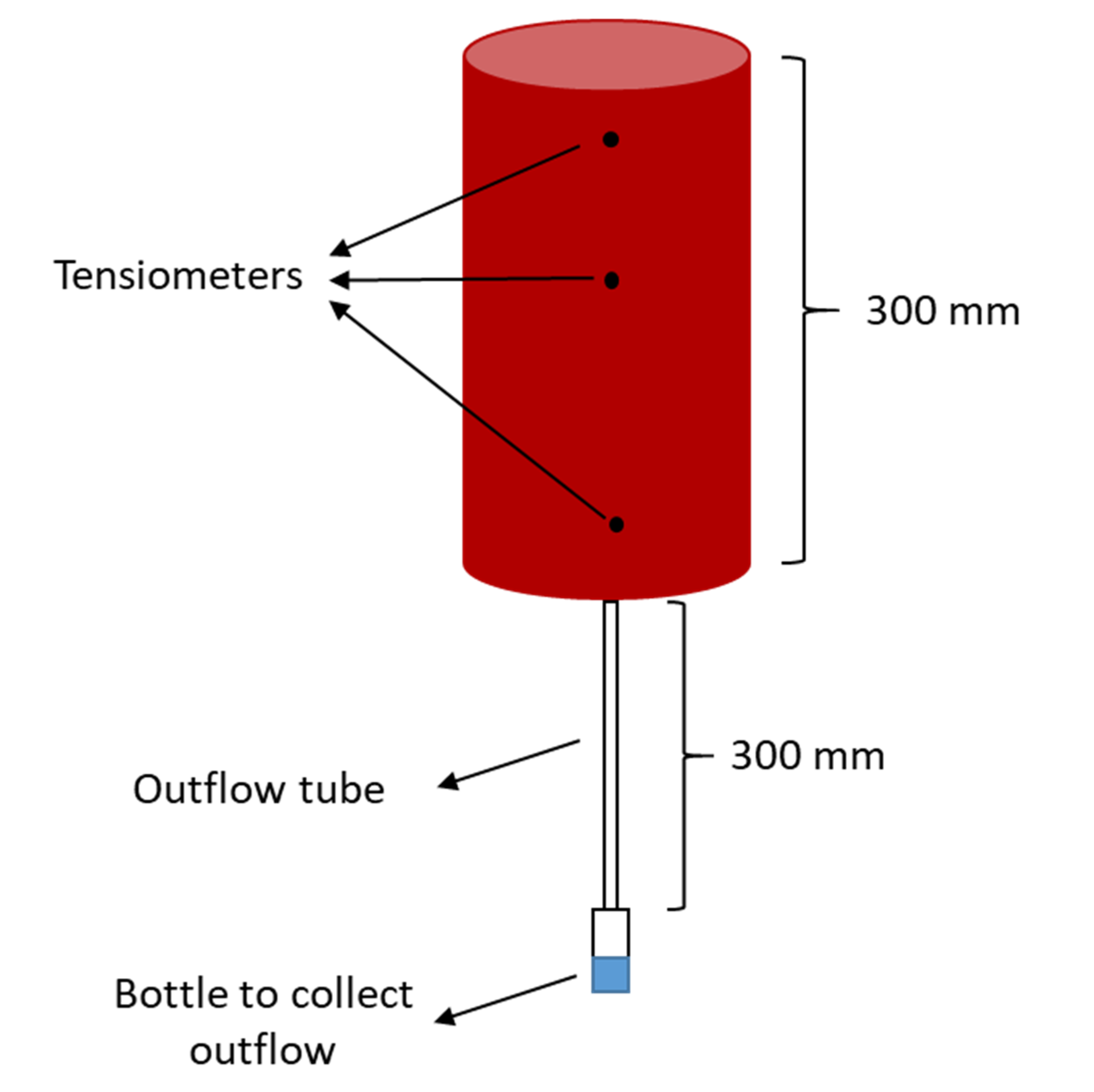
2.2. Laboratory Column Study
2.3. Inverse Solution Modelling
2.4. Validation of HYDRUS Model
2.5. Statistical Analyses
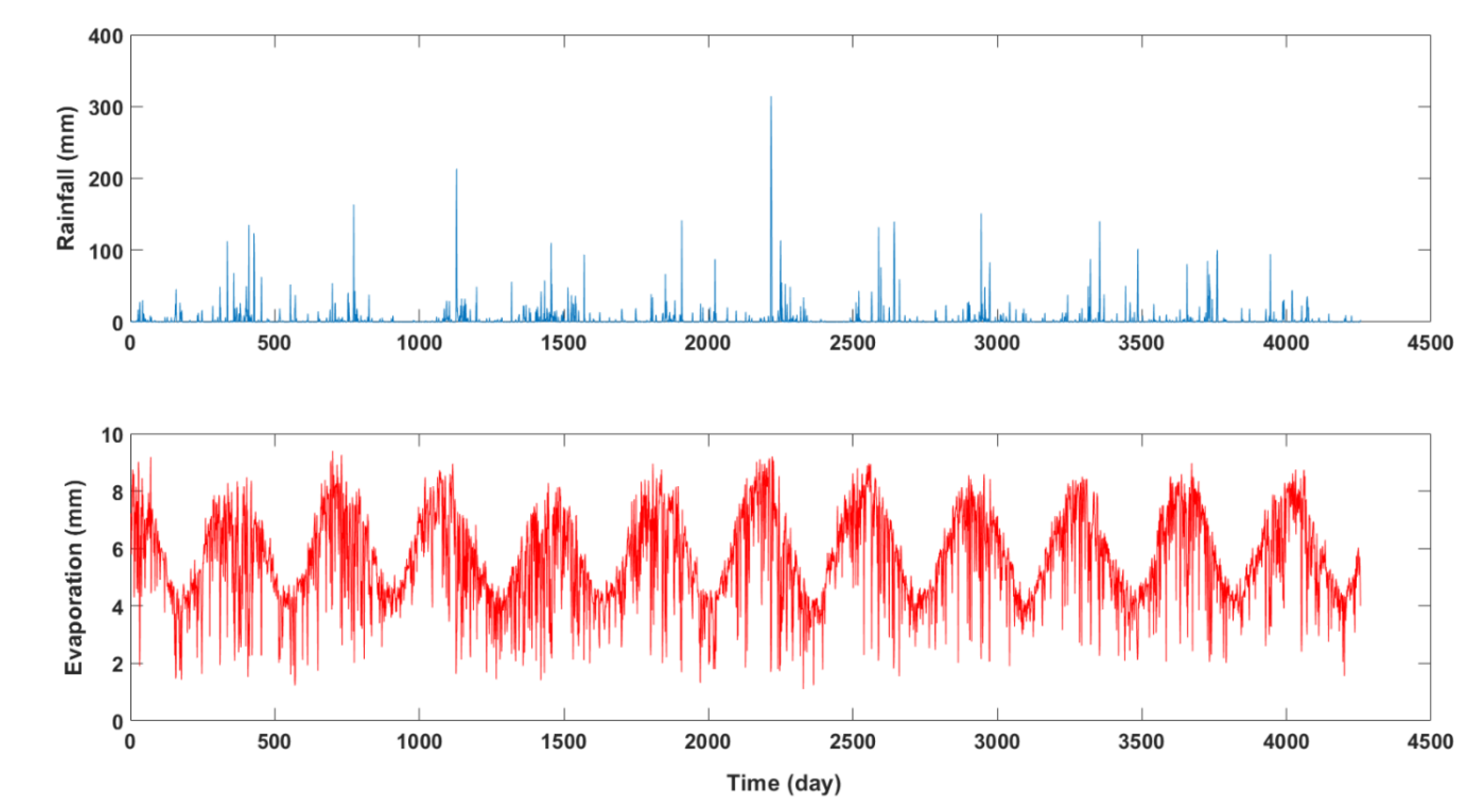
2.6. Simulation of Bauxite Residue Moisture Profile Using HYDRUS
3. Results and Discussion
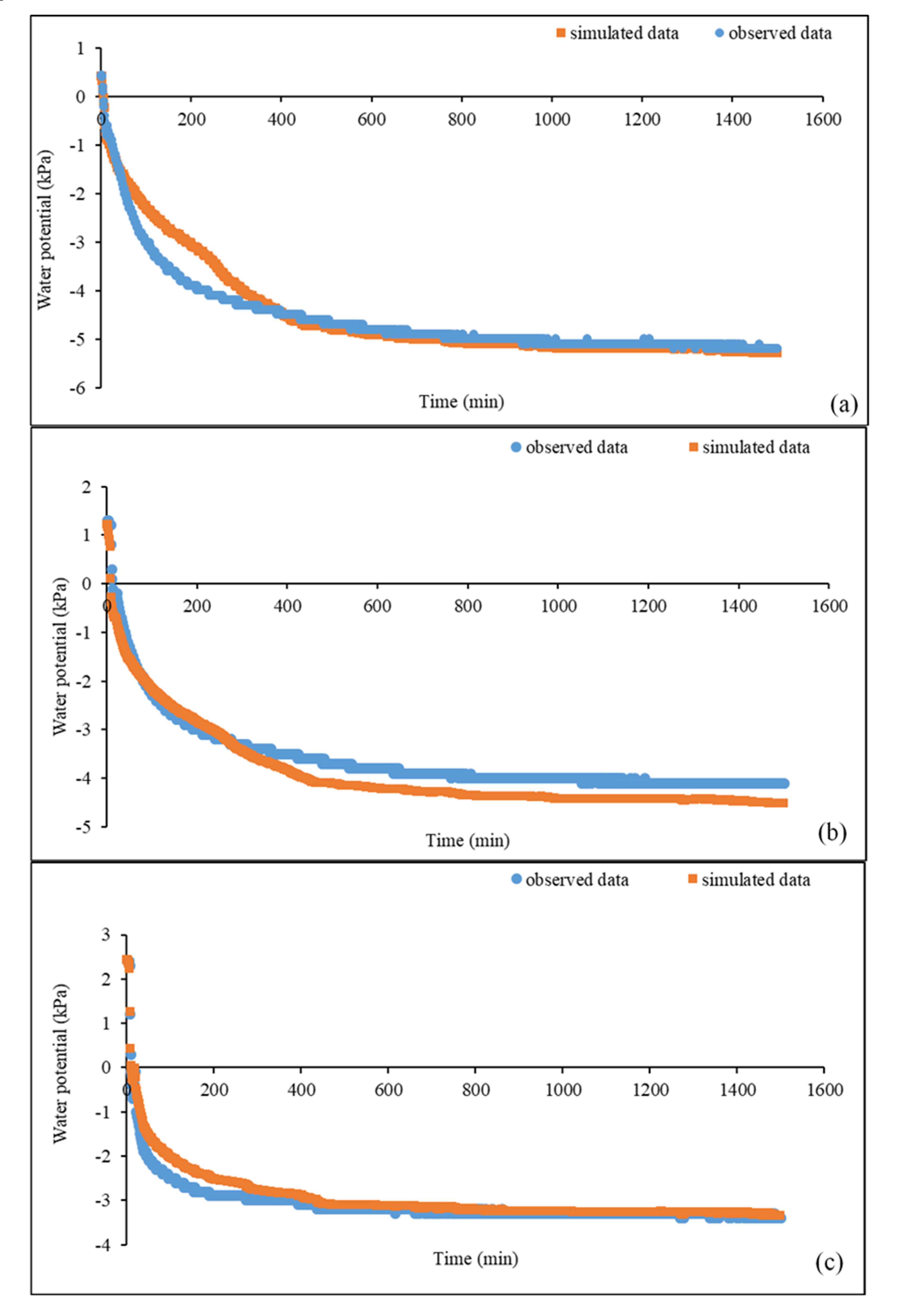
3.1. Evaluating the Performance of Inverse Modelling
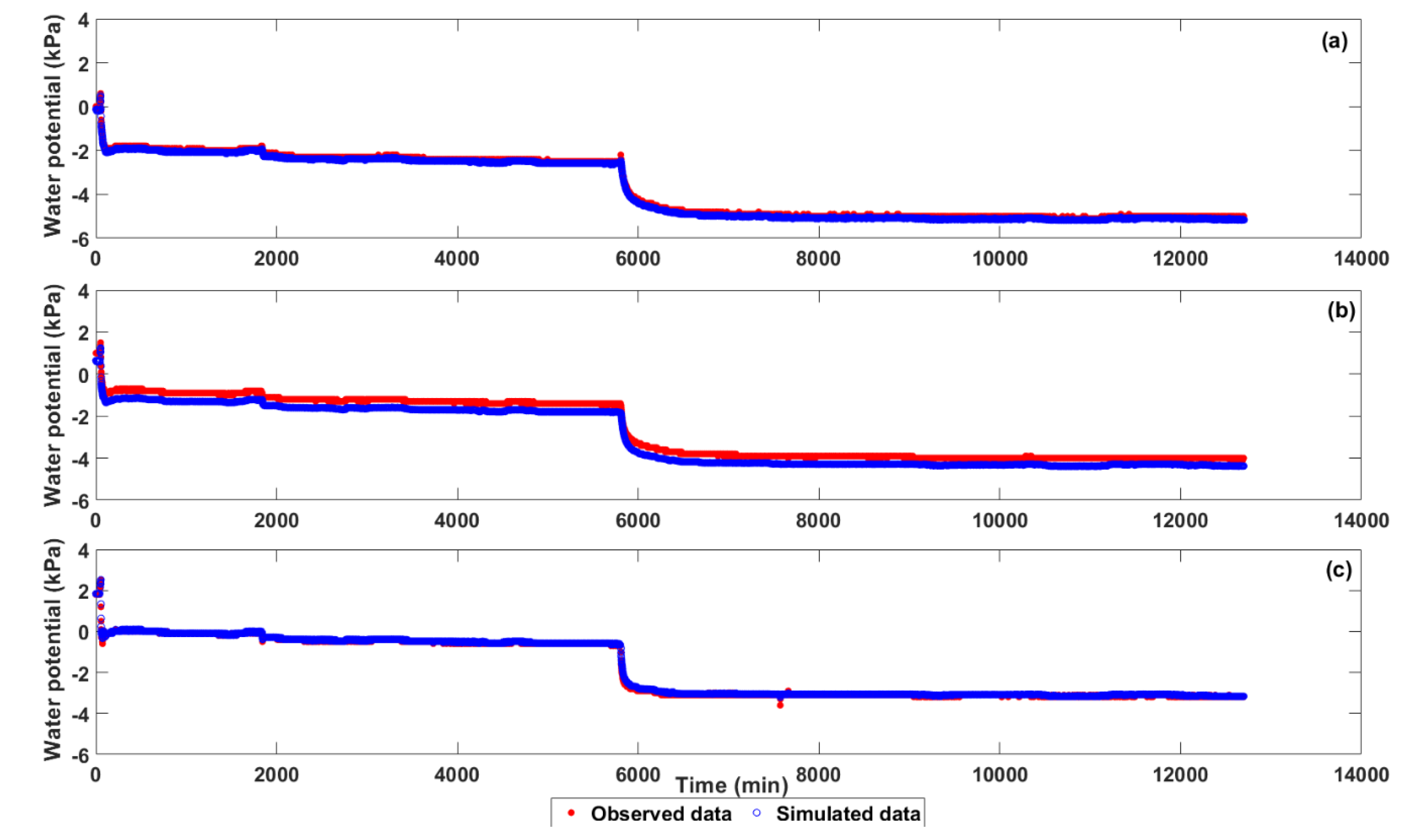
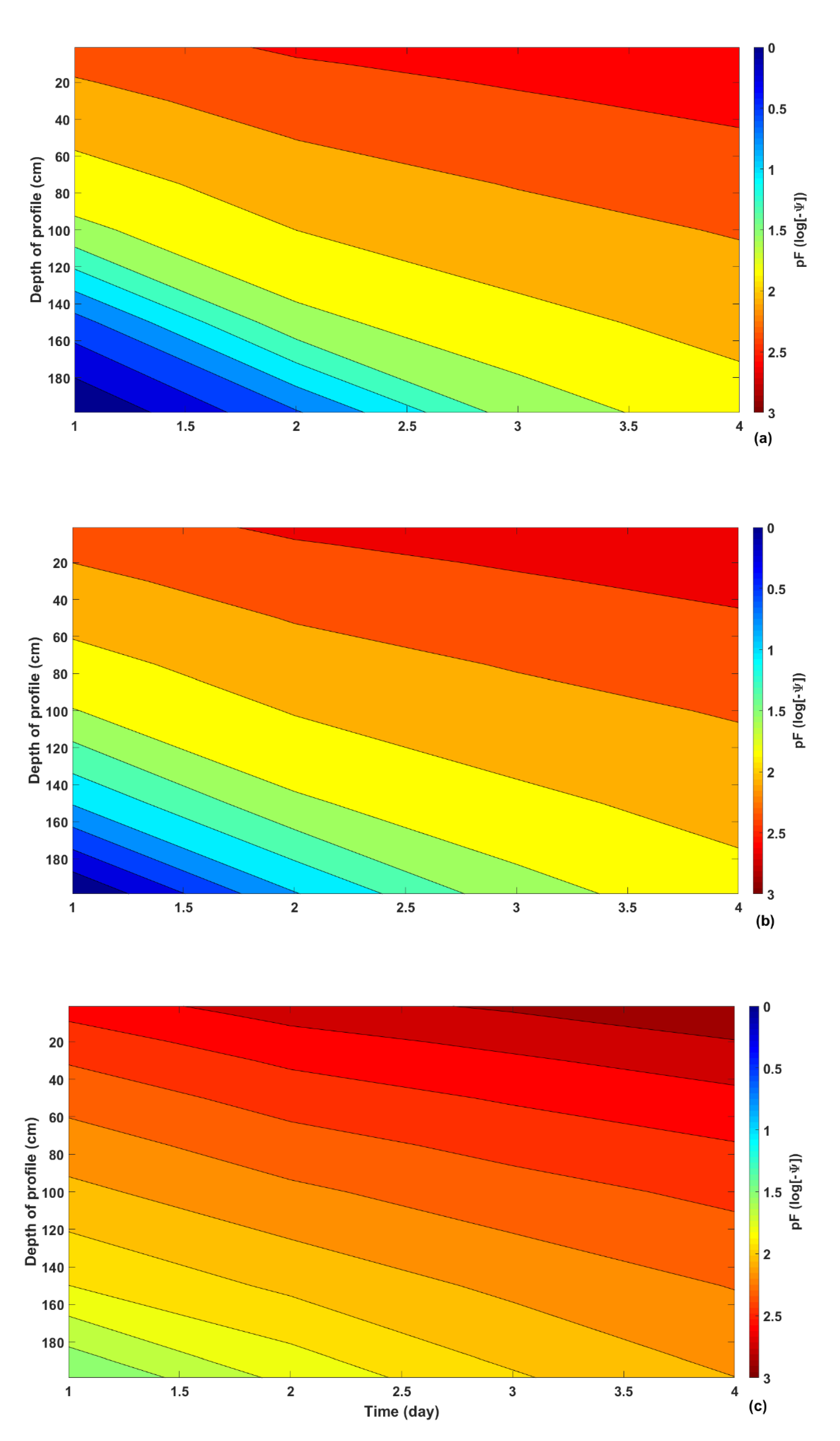
3.2. Investigating HYDRUS-1D’s Capability as a Predictive Tool for Estimating Bauxite Residue Moisture Profile
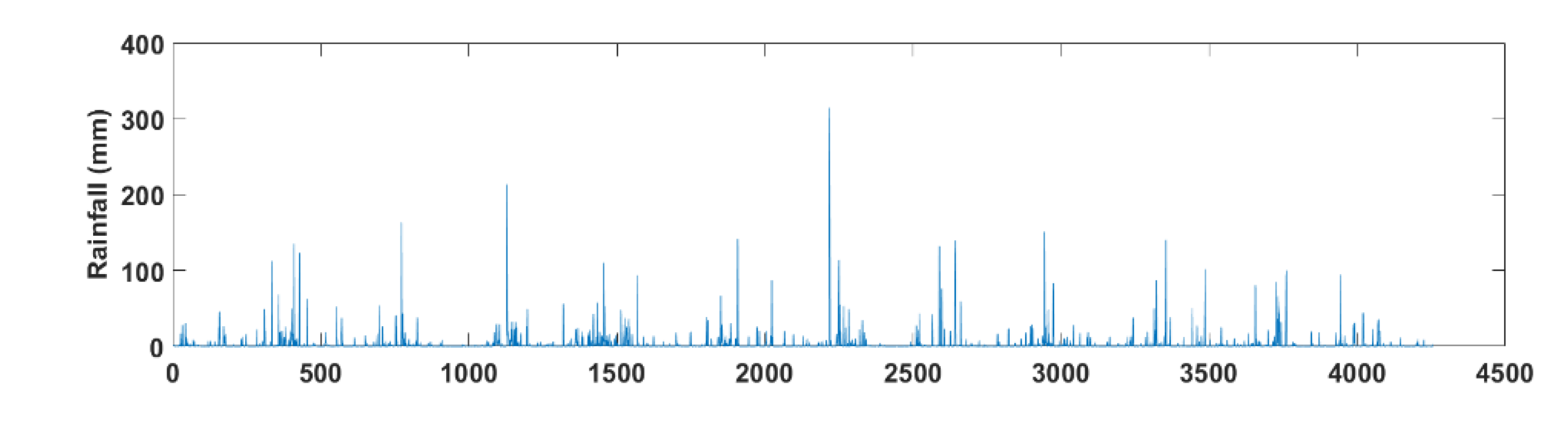
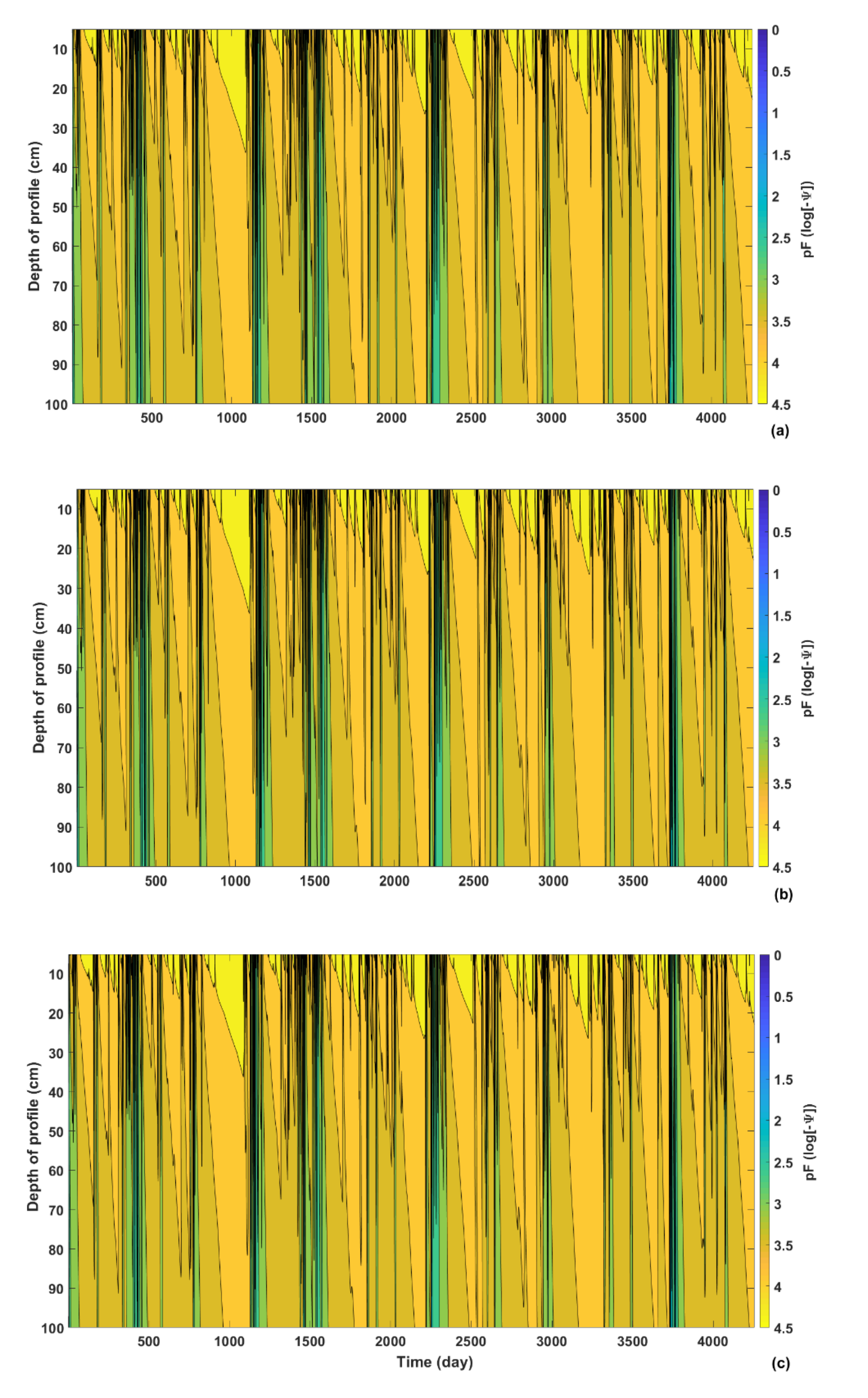
3.3. Application of HYDRUS-1D Modelling for Management of a Bauxite Residue Storage Facility
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Variable | Limit of Confidence at 95% | |
|---|---|---|
| WCR | −3.013 | 3.428 |
| WCS | −3.120 | 4.520 |
| α | −0.0033 | 0.0053 |
| n | 0.559 | 2.241 |
References
- Jones, B.E.H.; Haynes, R.J. Bauxite processing residue: A critical review of its formation, properties, storage, and revegetation. Crit. Rev. Environ. Sci. Technol. 2011, 41, 271–315. [Google Scholar] [CrossRef]
- Gräfe, M.; Power, G.; Klauber, C. Bauxite residue issues: III. Alkalinity and associated chemistry. Hydrometallurgy 2011, 108, 60–79. [Google Scholar] [CrossRef]
- Santini, T.C.; Fey, M.V.; Gilkes, R. Experimental simulation of long term weathering in alkaline bauxite residue tailings. Metals 2015, 5, 1241–1261. [Google Scholar] [CrossRef]
- Gräfe, M.; Klauber, C. Bauxite residue issues: IV. Old obstacles and new pathways for in situ residue bioremediation. Hydrometallurgy 2011, 108, 46–59. [Google Scholar] [CrossRef]
- Higgins, D.; Curtin, T.; Burke, I.; Courtney, R. The potential for constructed wetland mechanisms to treat alkaline bauxite residue leachate: Carbonation and precipitate characterisation. Environ. Sci. Pollut. Res. 2018, 25, 29451–29458. [Google Scholar] [CrossRef]
- Evans, K. The History, Challenges, and New Developments in the management and use of bauxite residue. J. Sustain. Metall. 2016, 2, 316–331. [Google Scholar] [CrossRef]
- Willan, M.; Ghataora, G. Management of bauxite residue in a temperate climate using mud-farming techniques. In Proceedings of the 18th International Seminar on Paste and Thickened Tailings, Australian Centre for Geomechanics, Perth, Australia, 5–7 May 2015; pp. 209–222. [Google Scholar]
- Kinnarinen, T.; Lubieniecki, B.; Holliday, L.; Helsto, J.-J.; Häkkinen, A. Enabling safe dry cake disposal of bauxite residue by deliquoring and washing with a membrane filter press. Waste Manag. Res. 2015, 33, 258–266. [Google Scholar] [CrossRef]
- Kaußen, F.M.; Friedrich, B. Methods for alkaline recovery of aluminum from bauxite residue. J. Sustain. Metall. 2016, 2, 353–364. [Google Scholar] [CrossRef]
- Doucet, J.; Paradis, R. Thickening/mud stacking technology—An environmental approach to residue management. In Proceedings of the Thirteenth International Seminar on Paste and Thickened Tailings, Australian Centre for Geomechanics, Toronto, ON, Canada, 3–6 May 2010; 2010; pp. 3–21. [Google Scholar]
- Cooling, D.J. Improving the sustainability of residue management practices-Alcoa World Alumina Australia. In Paste and Thickened Tailings: A Guide, Australian Centre for Geomechanics, Perth, Australia; Australian Centre for Geomechanics: Perth, Australia, 2007; pp. 3–16. [Google Scholar]
- Paramguru, R.K.; Rath, P.C.; Misra, V.N. Trends in red mud utilization—A review. Miner. Process. Extr. Metall. Rev. 2004, 26, 1–29. [Google Scholar] [CrossRef]
- Kossoff, D.; Dubbin, W.; Alfredsson, M.; Edwards, S.; Macklin, M.; Hudson-Edwards, K. Mine tailings dams: Characteristics, failure, environmental impacts, and remediation. Appl. Geochem. 2014, 51, 229–245. [Google Scholar] [CrossRef]
- Shaygan, M.; Baumgartl, T.; Arnold, S.; Reading, L.P. The effect of soil physical amendments on reclamation of a saline-sodic soil: Simulation of salt leaching using HYDRUS-1D. Soil Res. 2018, 56, 829. [Google Scholar] [CrossRef]
- Rasouli, F.; Pouya, A.K.; Šimůnek, J. Modeling the effects of saline water use in wheat-cultivated lands using the UNSATCHEM model. Irrig. Sci. 2012, 31, 1009–1024. [Google Scholar] [CrossRef]
- Shaygan, M.; Reading, L.P.; Arnold, S.; Baumgartl, T. Modeling the effect of soil physical amendments on reclamation and revegetation success of a saline-sodic soil in a semi-arid environment. Arid Land Res. Manag. 2018, 32, 379–406. [Google Scholar] [CrossRef]
- Zeng, W.; Xu, C.; Wu, J.-W.; Huang, J. Soil salt leaching under different irrigation regimes: HYDRUS-1D modelling and analysis. J. Arid Land 2013, 6, 44–58. [Google Scholar] [CrossRef]
- Gonçalves, M.; Simunek, J.; Ramos, T.; Martins, J.C.; Neves, M.J.; Pires, F.P. Multicomponent solute transport in soil lysimeters irrigated with waters of different quality. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Newson, T.; Dyer, T.; Adam, C.; Sharp, S.; Dyer, T.D. Effect of structure on the geotechnical properties of bauxite residue. J. Geotech. Geoenviron. Eng. 2006, 132, 143–151. [Google Scholar] [CrossRef]
- Smagin, A. Column-centrifugation method for determining water retention curves of soils and disperse sediments. Eurasian Soil Sci. 2012, 45, 416–422. [Google Scholar] [CrossRef]
- Rashid, N.S.A.; Askari, M.; Tanaka, T.; Simunek, J.; van Genuchten, M.T. Inverse estimation of soil hydraulic properties under oil palm trees. Geoderma 2015, 241, 306–312. [Google Scholar] [CrossRef]
- Ramos, T.; Gonçalves, M.; Martins, J.C.; Van Genuchten, M.T.; Pires, F.P. Estimation of soil hydraulic properties from numerical inversion of tension disk infiltrometer data. Vadose Zone J. 2006, 5, 684–696. [Google Scholar] [CrossRef]
- Schwartz, R.C.; Evett, S.R. Estimating hydraulic properties of a fine-textured soil using a disc infiltrometer. Soil Sci. Soc. Am. J. 2002, 66, 1409–1423. [Google Scholar] [CrossRef]
- Ventrella, D.; Losavio, N.; Vonella, A.; Leij, F. Estimating hydraulic conductivity of a fine-textured soil using tension infiltrometry. Geoderma 2005, 124, 267–277. [Google Scholar] [CrossRef]
- Lazarovitch, N.; Ben-Gal, A.; Šimunek, J.; Shani, U. Uniqueness of soil hydraulic parameters determined by a combined wooding inverse approach. Soil Sci. Soc. Am. J. 2007, 71, 860–865. [Google Scholar] [CrossRef]
- Botula, Y.-D.; Van Ranst, E.; Cornelis, W.M. Pedotransfer functions to predict water retention for soils of the humid tropics: A review. Rev. Bras. Cienc. Solo 2014, 38, 679–698. [Google Scholar] [CrossRef]
- Shaygan, M.; Reading, L.P.; Baumgartl, T. Effect of physical amendments on salt leaching characteristics for reclamation. Geoderma 2017, 292, 96–110. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Van Genuchten, M.T.; Leij, F.J.; Yates, S.R. The RETC Code for Quantifying the Hydraulic Functions of Unsaturated Soils; Version 1.0, EPA Report 600/2-91/065; US Salinity Laboratory, USDA-ARS: Riverside, CA, USA, 1991. [Google Scholar]
- Klute, A.; Dirksen, C. Hydraulic conductivity and diffusivity: Laboratory methods. In Methods of Soil Analysis-Physical and Mineralogical Methods; Klute, A., Ed.; American Society of Agronomy: Madison, WI, USA, 1982; Volume 2, pp. 687–734. [Google Scholar]
- Marshall, T.J.; Holmes, J.W.; Rose, C.W. Soil Physics; Cambridge University Press: New York, NY, USA, 1996. [Google Scholar]
- Assouline, S.; Tessier, D.; Tavares-Filho, J. Effect of compaction on soil physical and hydraulic properties: Experimental results and modeling. Soil Sci. Soc. Am. J. 1997, 61, 390. [Google Scholar] [CrossRef]
- Zhang, S.; Grip, H.; Lövdahl, L. Effect of soil compaction on hydraulic properties of two loess soils in China. Soil Tillage Res. 2006, 90, 117–125. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; van Genuchten, M. The Hydrus-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media; Version 4.16; Department of Environmental Sciences, University of California Riverside: Riverside, CA, USA, 2013; p. 340. [Google Scholar]
- Šimunek, J.; Van Genuchten, M.T.; Wendroth, O. Parameter estimation analysis of the evaporation method for determining soil hydraulic properties. Soil Sci. Soc. Am. J. 1998, 62, 894–905. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media; Version 4.0, Hydrus Software; Department of Environmental Sciences, University of California: Riverside, CA, USA, 2008. [Google Scholar]
- Saso, J.K.; Parkin, G.W.; Drury, C.F.; Lauzon, J.D.; Reynolds, W.D. Chloride leaching in two Ontario soils: Measurement and prediction using HYDRUS-1D. Can. J. Soil Sci. 2012, 92, 285–296. [Google Scholar] [CrossRef]
- LeGates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Ket, P.; Oeurng, C.; Degré, A. Estimating soil water retention curve by inverse modelling from combination of in situ dynamic soil water content and soil potential data. Soil Syst. 2018, 2, 55. [Google Scholar] [CrossRef]
- Schwartz, R.C.; Evett, S.R. Conjunctive use of tension infiltrometry and time-domain reflectometry for inverse estimation of soil hydraulic properties. Vadose Zone J. 2003, 2, 530–538. [Google Scholar] [CrossRef]
- Abbasi, F.; Simunek, J.; Feyen, J.; van Genuchten, M.T.; Shouse, P.J. Simultaneous inverse estimation of soil hydraulic and solute transport parameters from transient field experiments: Homogeneous soil. Trans. ASAE 2003, 46, 1085. [Google Scholar] [CrossRef]
- Abbasi, F.; Feyen, J.; Van Genuchten, M.; Van Genuchten, M.T. Two-dimensional simulation of water flow and solute transport below furrows: Model calibration and validation. J. Hydrol. 2004, 290, 63–79. [Google Scholar] [CrossRef]
- Shaygan, M.; Baumgartl, T. Simulation of the effect of climate variability on reclamation success of brine-affected soil in semi-arid environments. Sustainability 2020, 12, 371. [Google Scholar] [CrossRef]
- Schwartz, M.O.; Schippers, A.; Hahn, L. Hydrochemical models of the sulphidic tailings dumps at Matchless (Namibia) and Selebi-Phikwe (Botswana). Environ. Earth Sci. 2005, 49, 504–510. [Google Scholar] [CrossRef]
- Blanco, A.; Lloret, A.; Valhondo, C.; Olivella, S. Thermo-hydraulic behaviour of the vadose zone in sulphide tailings at Iberian Pyrite Belt: Waste characterization, monitoring and modelling. Eng. Geol. 2013, 165, 154–170. [Google Scholar] [CrossRef]
- Dawood, I.; Aubertin, M. Effect of dense material layers on unsaturated water flow inside a large waste rock pile: A numerical investigation. Mine Water Environ. 2013, 33, 24–38. [Google Scholar] [CrossRef]
- Fala, O.; Molson, J.; Aubertin, M.; Bussiere, B. Numerical modelling of flow and capillary barrier effects in unsaturated waste rock piles. Mine Water Environ. 2005, 24, 172–185. [Google Scholar] [CrossRef]
- Hadi, H.N.; Luo, M.K.; Li, S. Assessment of unsaturated flow for a large coal mine waste rock pile. Adv. Mater. Res. 2014, 955, 1179–1183. [Google Scholar] [CrossRef]
- Wissmeier, L.; Barry, D.; Phillips, I.R. Predictive hydrogeochemical modelling of bauxite residue sand in field conditions. J. Hazard. Mater. 2011, 191, 306–324. [Google Scholar] [CrossRef] [PubMed]
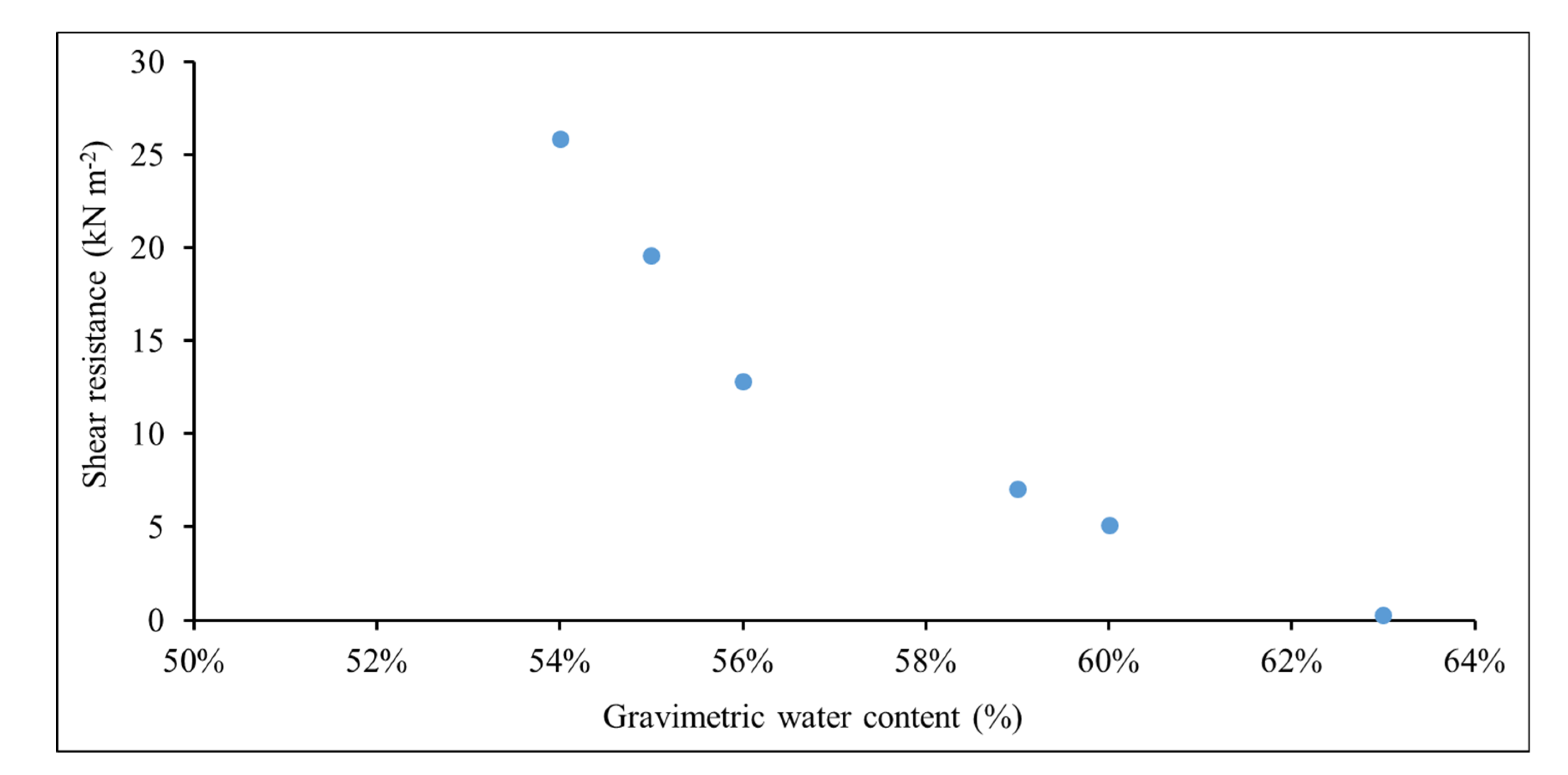
- Fredlund, D.G.; Morgenstern, N.R.; Widger, R.A. The shear strength of unsaturated soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]

| Parameters | θs (cm3 cm−3) | θr (cm3 cm−3) | α (cm−1) | n | Ksat (cm s−1) | Sand (%) | Silt (%) | Clay (%) |
|---|---|---|---|---|---|---|---|---|
| (n = 3) | 0.651 ± 0.01 | 0.336 ± 0.02 | 0.0356 ± 0.0007 | 1.384 ± 0.02 | 5.82 × 10−5 ± 0.2 × 10−5 | 4 ± 0.5 | 43 ± 1.02 | 53 ± 1.12 |
| Parameter | Value |
|---|---|
| Hydraulic parameters | |
| Saturated hydraulic conductivity (Ksat), cm s−1 | 5.66 × 10−5 |
| Residual volumetric water content (θr), cm3 cm−3 | 0.2 ⸸ |
| Saturated volumetric water content (θs), cm3 cm−3 | 0.699 ⸸ |
| Inverse of air entry suction α, cm−1 | 0.001 ⸸ |
| Measure of the pore size distribution n | 1.14 ⸸ |
| Pore connectivity parameter l | 0.5 |
| Discretisation | |
| Grid spacing, cm | 0.1 |
| Initial time step, second | 0.006 |
| Min. time step, second | 0.0012 |
| Max. time step, second | 60 |
| Statistical Analyses | Depth of the Bauxite Residue Profile | ||
|---|---|---|---|
| 35 mm | 120 mm | 250 mm | |
| RMSE (n = 1500) | 0.3050 | 0.3475 | 0.1936 |
| NSE (n = 1500) | 0.8887 | 0.8215 | 0.8895 |
| d (n = 1500) | 0.9766 | 0.9609 | 0.9757 |
| Statistical Analyses | Depth of the Bauxite Residue Profile | ||
|---|---|---|---|
| 35 mm | 120 mm | 250 mm | |
| RMSE (n = 12,701) | 0.08 | 0.37 | 0.04 |
| NSE (n = 12,701) | 0.99 | 0.92 | 0.99 |
| d (n = 12,701) | 0.99 | 0.98 | 0.99 |
| Initial Water Potential Content | Cumulative Run-Off (mm) | Cumulative Evaporation (mm) | Cumulative Rainfall (mm) | Cumulative Drainage (mm) | Water Balance Error (%) |
|---|---|---|---|---|---|
| −1 kPa | 2416.6 | 10,416 | 12,765.5 | 0.0001 | 0.057 |
| −2 kPa | 2416.6 | 10,415 | 12,765.5 | 0.0001 | 0.056 |
| −10 kPa | 2416.3 | 10,410 | 12,765.5 | 0.0004 | 0.048 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaygan, M.; Usher, B.; Baumgartl, T. Modelling Hydrological Performance of a Bauxite Residue Profile for Deposition Management of a Storage Facility. Water 2020, 12, 1988. https://doi.org/10.3390/w12071988
Shaygan M, Usher B, Baumgartl T. Modelling Hydrological Performance of a Bauxite Residue Profile for Deposition Management of a Storage Facility. Water. 2020; 12(7):1988. https://doi.org/10.3390/w12071988
Chicago/Turabian StyleShaygan, Mandana, Brent Usher, and Thomas Baumgartl. 2020. "Modelling Hydrological Performance of a Bauxite Residue Profile for Deposition Management of a Storage Facility" Water 12, no. 7: 1988. https://doi.org/10.3390/w12071988
APA StyleShaygan, M., Usher, B., & Baumgartl, T. (2020). Modelling Hydrological Performance of a Bauxite Residue Profile for Deposition Management of a Storage Facility. Water, 12(7), 1988. https://doi.org/10.3390/w12071988






