Efficient Urban Inundation Model for Live Flood Forecasting with Cellular Automata and Motion Cost Fields
Abstract
1. Introduction
2. Methodology
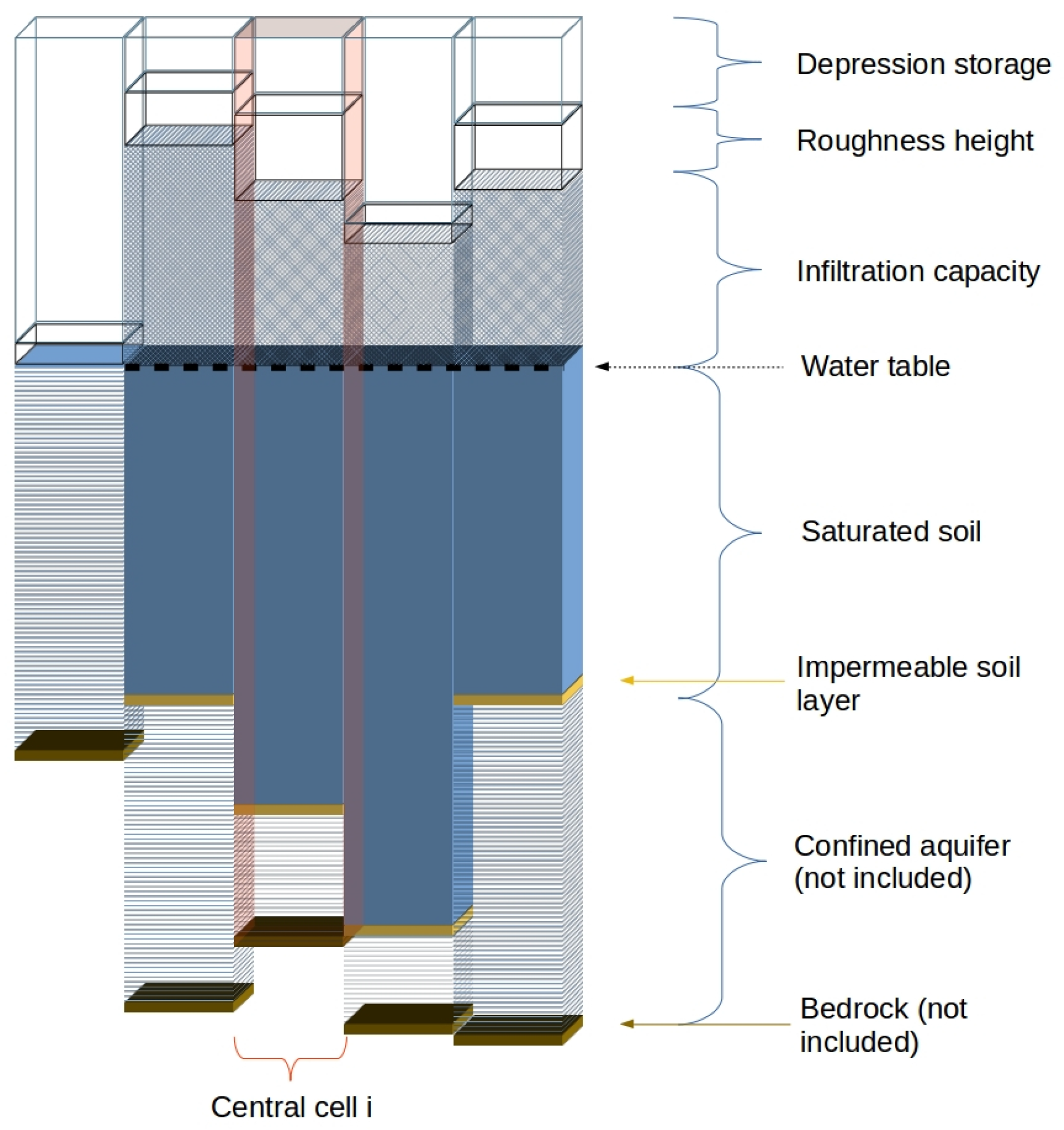
2.1. Cellular Automata
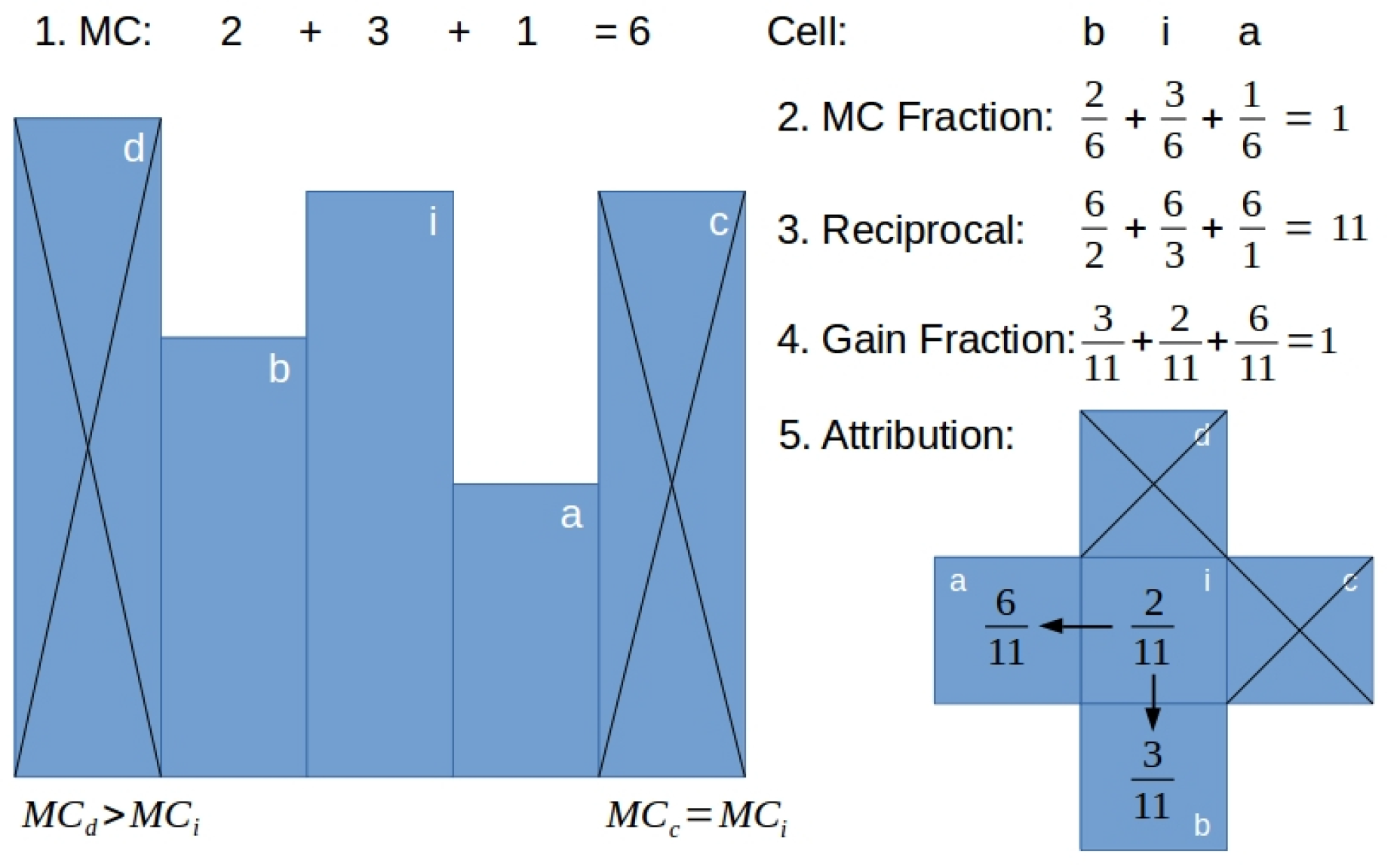
2.2. Motion Costs
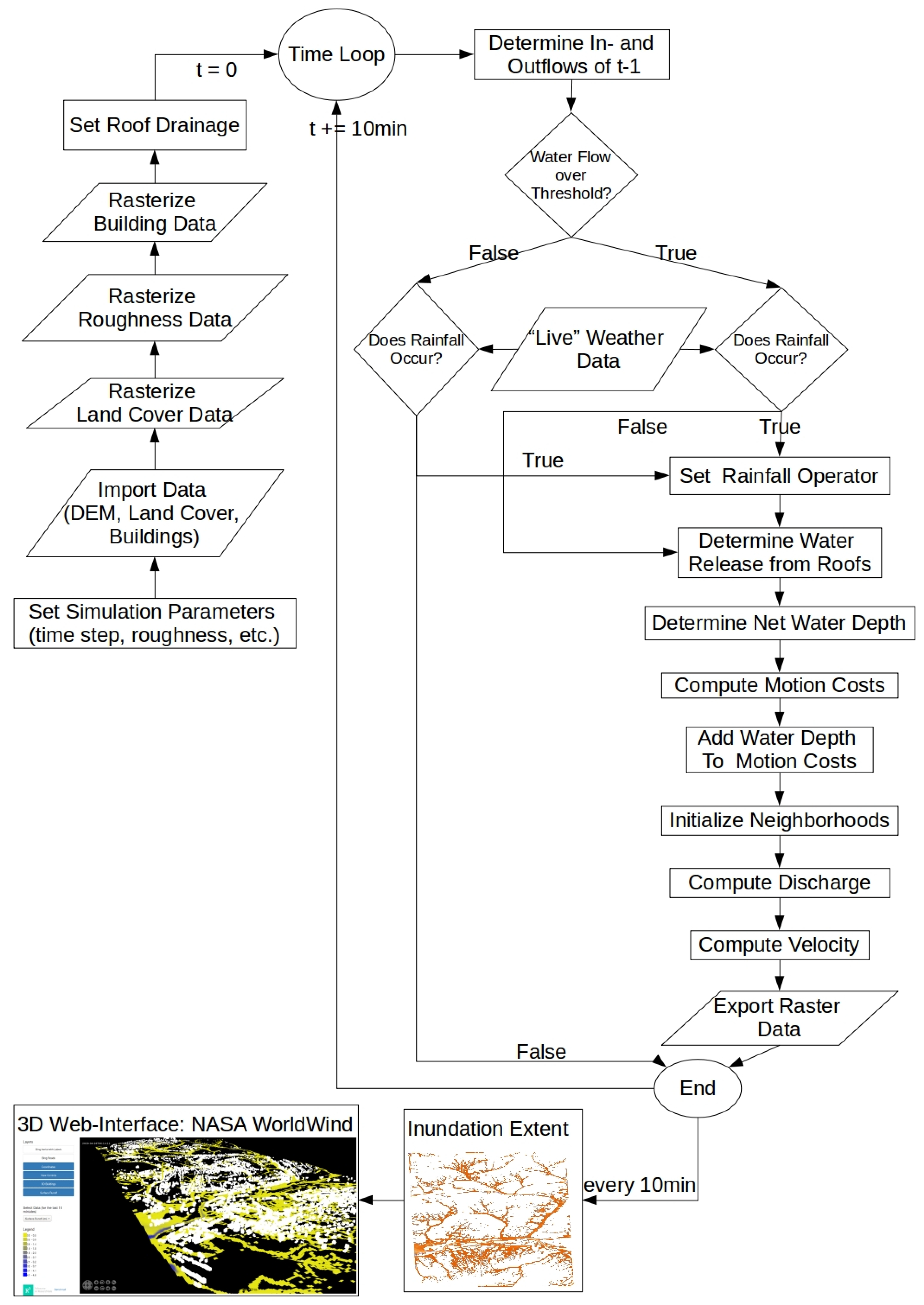
2.3. System Architecture
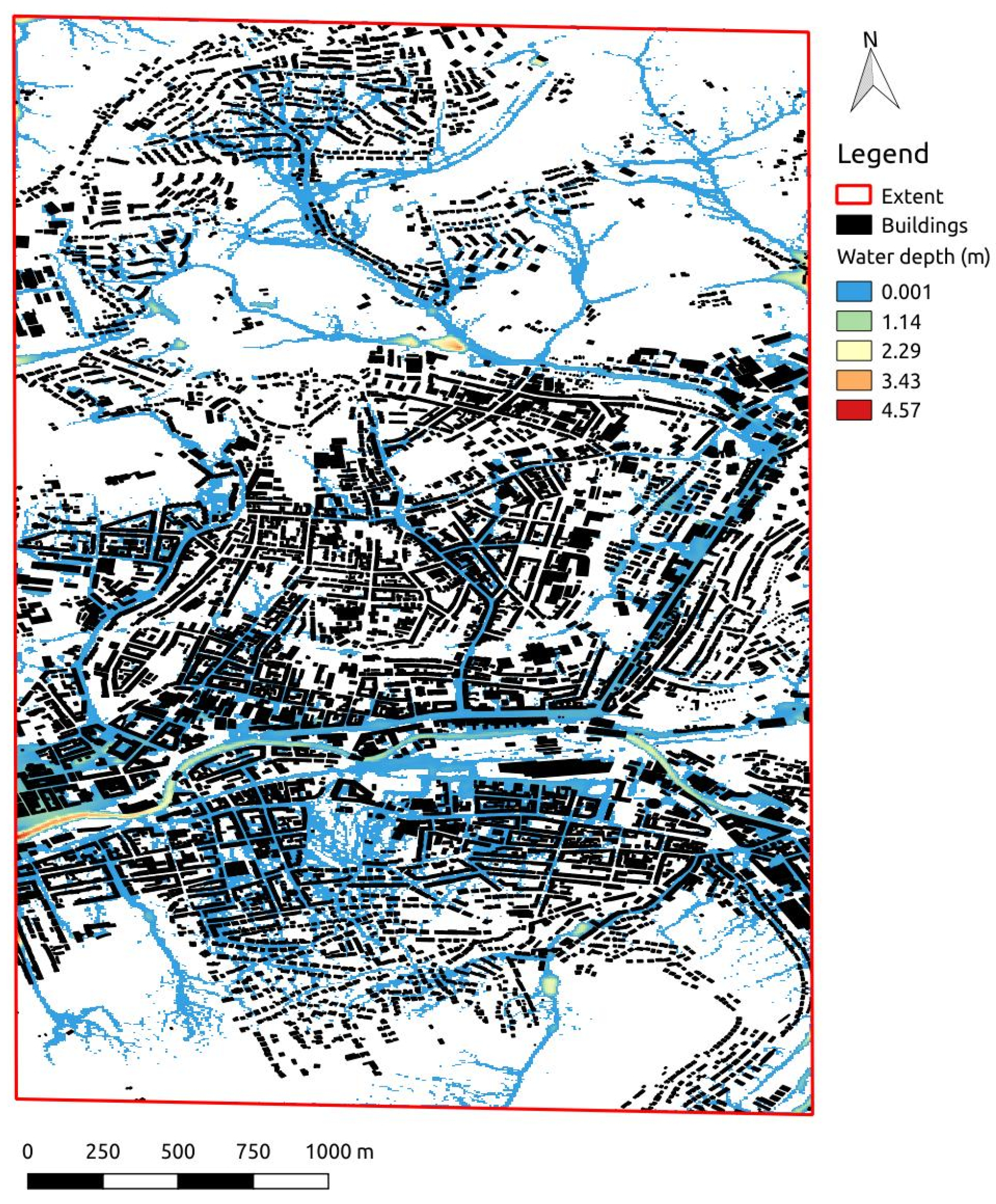
3. Case Study
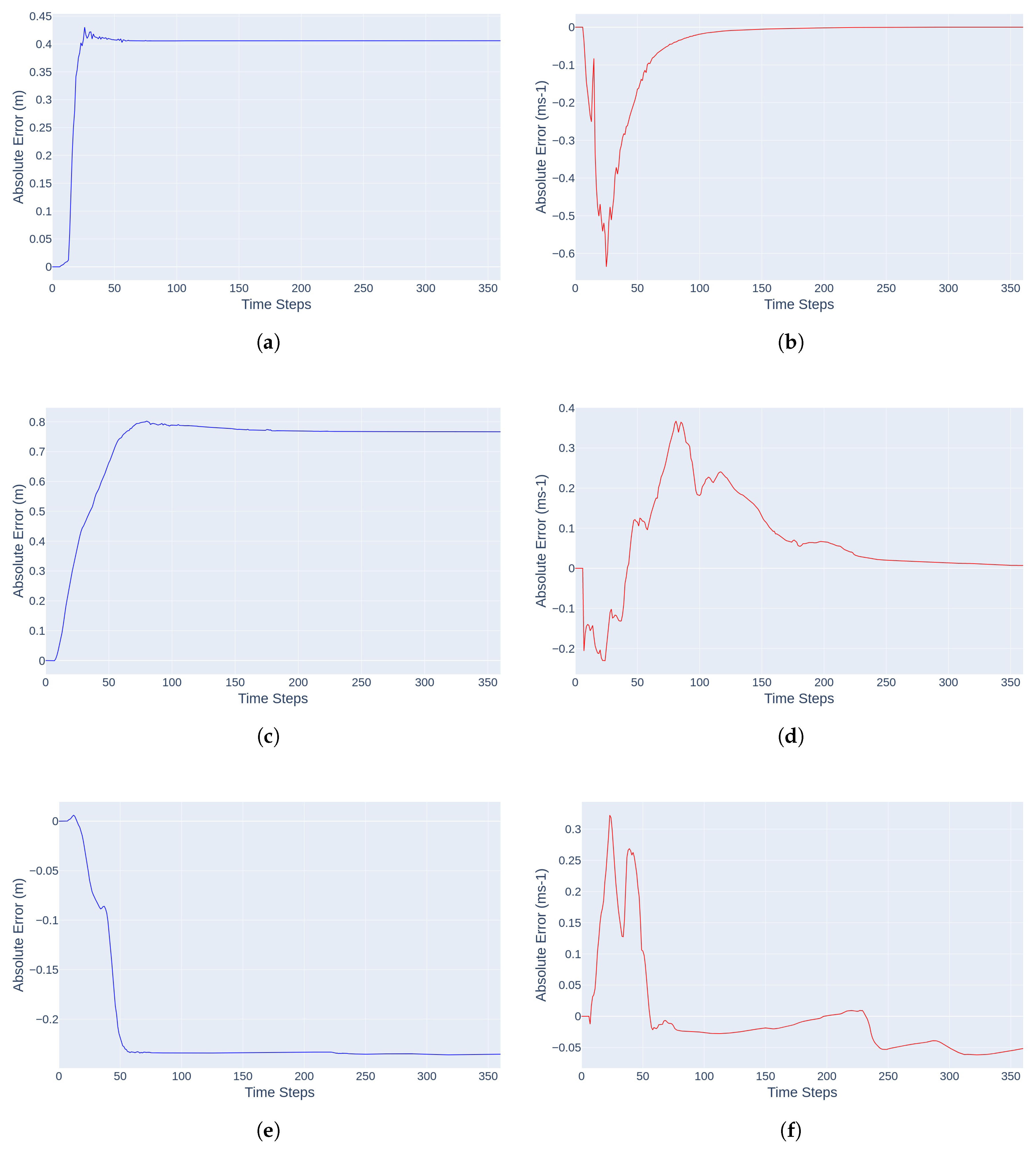
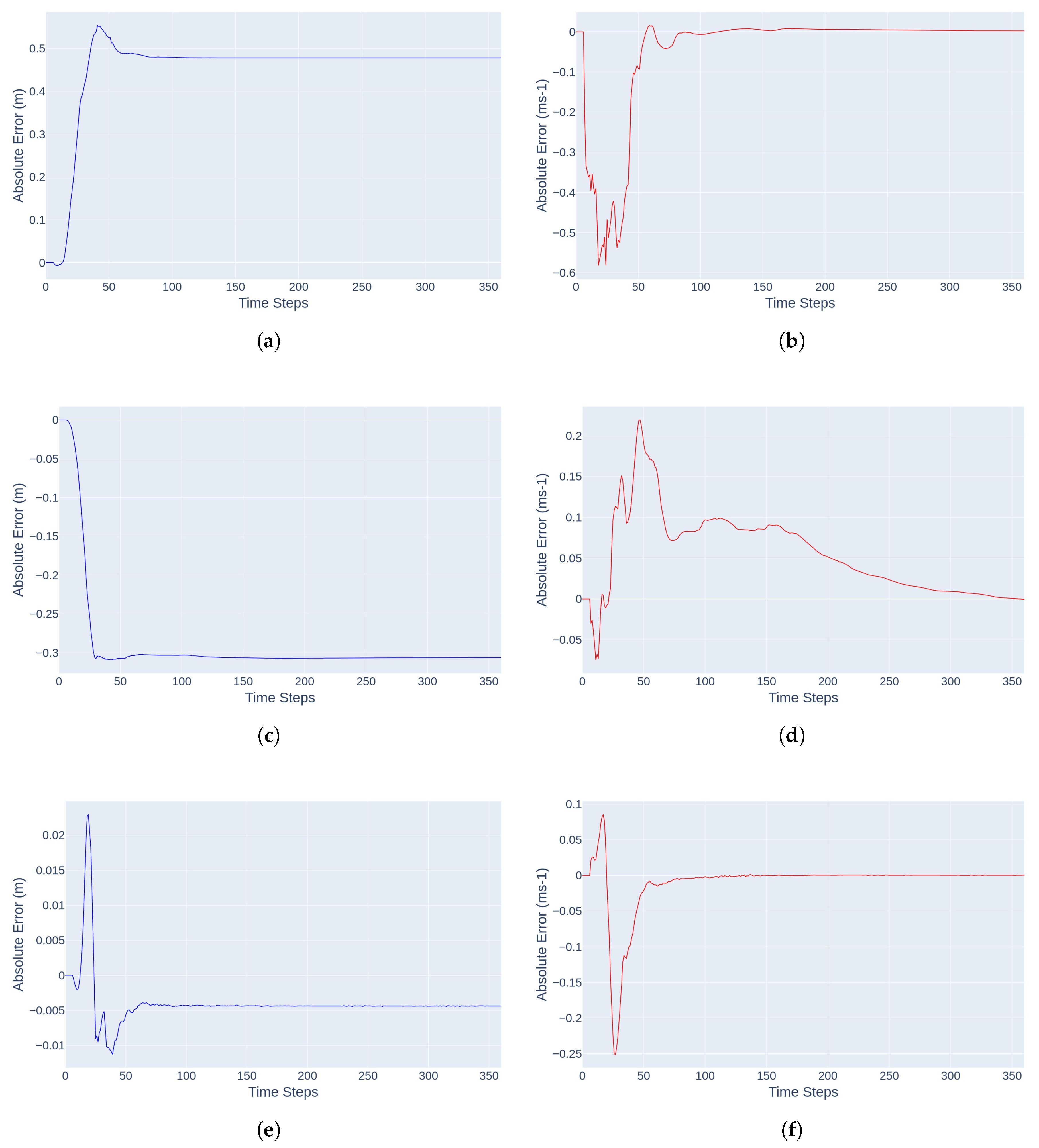
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jung, I.W.; Chang, H.; Moradkhani, H. Quantifying uncertainty in urban flooding analysis considering hydro-climatic projection and urban development effects. In Hydrology and Earth System Sciences; Copernicus Publications on behalf of the European Geosciences Union: Göttingen, Germany, 2011. [Google Scholar]
- Huong, H.T.L.; Pathirana, A. Urbanization and climate change impacts on future urban flooding in Can Tho city, Vietnam. Hydrol. Earth Syst. Sci. 2013, 17, 379. [Google Scholar] [CrossRef]
- Kim, Y.; Eisenberg, D.A.; Bondank, E.N.; Chester, M.V.; Mascaro, G.; Underwood, B.S. Fail-safe and safe-to-fail adaptation: Decision-making for urban flooding under climate change. Clim. Chang. 2017, 145, 397–412. [Google Scholar] [CrossRef]
- Miller, J.D.; Hutchins, M. The impacts of urbanisation and climate change on urban flooding and urban water quality: A review of the evidence concerning the United Kingdom. J. Hydrol. Regional Stud. 2017, 12, 345–362. [Google Scholar] [CrossRef]
- Zhang, D.L.; Lin, Y.; Zhao, P.; Yu, X.; Wang, S.; Kang, H.; Ding, Y. The Beijing extreme rainfall of 21 July 2012: “Right results” but for wrong reasons. Geophys. Res. Lett. 2013, 40, 1426–1431. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, S.; Cao, Q.; Hong, Y.; Wu, B.; Huang, M.; Qiao, L.; Zhang, Z.; Li, Z.; Li, W. Evaluation of version-7 TRMM multi-satellite precipitation analysis product during the Beijing extreme heavy rainfall event of 21 July 2012. Water 2014, 6, 32–44. [Google Scholar] [CrossRef]
- Hénonin, J.; Hongtao, M.; Zheng-Yu, Y.; Hartnack, J.; Havnø, K.; Gourbesville, P.; Mark, O. Citywide multi-grid urban flood modelling: The July 2012 flood in Beijing. Urban Water J. 2015, 12, 52–66. [Google Scholar] [CrossRef]
- Karamouz, M.; Zahmatkesh, Z.; Saad, T. Cloud computing in urban flood disaster management. World Environmental and Water Resources Congress 2013: Showcasing the Future; American Society of Civil Engineers: Reston, VA, USA, 2013; pp. 2747–2757. [Google Scholar]
- Albano, R.; Sole, A.; Adamowski, J.; Mancusi, L. A GIS-based model to estimate flood consequences and the degree of accessibility and operability of strategic emergency response structures in urban areas. Nat. Hazards Earth Syst. Sci. 2014, 14. [Google Scholar] [CrossRef]
- Muschalla, D.; Ostrowski, M.; Klawitter, A. Innovative simulation and optimisation tools for basinwide urban stormwater management. In Proceedings International Symposium on New Directions in Urban Water Management; UNESCO: Paris, France, 2016. [Google Scholar]
- Bournaski, E.G. Genetic Algorithm Techniques for Stormwater Runoff Source Control Planning and Design. In Advances in Urban Stormwater and Agricultural Runoff Source Controls; Springer: New York, NY, USA, 2001; pp. 245–254. [Google Scholar]
- Jia, H.; Yao, H.; Tang, Y.; Shaw, L.Y.; Field, R.; Tafuri, A.N. LID-BMPs planning for urban runoff control and the case study in China. J. Environ. Manag. 2015, 149, 65–76. [Google Scholar] [CrossRef]
- Hoang, L.; Fenner, R.A. System interactions of stormwater management using sustainable urban drainage systems and green infrastructure. Urban Water J. 2016, 13, 739–758. [Google Scholar] [CrossRef]
- McArdle, P.; Gleeson, J.; Hammond, T.; Heslop, E.; Holden, R.; Kuczera, G. Centralised urban stormwater harvesting for potable reuse. Water Sci. Technol. 2011, 63, 16–24. [Google Scholar] [CrossRef]
- Gaines, J.M. Water potential. Nature 2016, 531, S1. [Google Scholar] [CrossRef]
- Mungkasi, S.; Roberts, S.G. ANUGA software for numerical simulations of shallow water flows. J. Ilmu Komput. Inf. 2012, 5, 1–8. [Google Scholar]
- Roberts, S.; Nielsen, O.; Gray, D.; Sexton, J.; Davies, G. ANUGA. 2017. Available online: https://anuga.anu.edu.au/ (accessed on 12 July 2019).
- Néelz, S.; Pender, G. Benchmarking the Latest Generation of 2D Hydraulic Modelling Packages; Technical Report SC120002; UK Environment Agency: Rotherham, UK, 2013.
- Syme, B. 2D or not 2D?–an australian perspective. In Proceedings of the Defra Flood and Coastal Risk Management Conference, York, UK, 4–6 July 2006. [Google Scholar]
- Bates, P.; Trigg, M.; Neal, J.; Dabrowa, A. LISFLOOD-FP user manual. Code Release 2013, 5.9.5, 10–42. [Google Scholar]
- Scharffenberg, W.; Ely, P.; Daly, S.; Fleming, M.; Pak, J. Hydrologic modeling system (HEC-HMS): Physically-based simulation components. In Proceedings of the 2nd Joint Federal Interagency Conference, Las Vegas, NV, USA, 27 June–1 July 2010. [Google Scholar]
- Ji, X.; Li, D.; Cheng, T.; Wang, X.S.; Wang, Q. Parallelization of MODFLOW using a GPU library. Groundwater 2014, 52, 618–623. [Google Scholar] [CrossRef]
- Lacasta, A.; Morales-Hernández, M.; Murillo, J.; García-Navarro, P. GPU implementation of the 2D shallow water equations for the simulation of rainfall/runoff events. Environ. Earth Sci. 2015, 74, 7295–7305. [Google Scholar] [CrossRef]
- Le, P.V.; Kumar, P.; Valocchi, A.J.; Dang, H.V. GPU-based high-performance computing for integrated surface–sub-surface flow modeling. Environ. Model. Softw. 2015, 73, 1–13. [Google Scholar] [CrossRef]
- Noymanee, J.; Nikitin, N.O.; Kalyuzhnaya, A.V. Urban pluvial flood forecasting using open data with machine learning techniques in pattani basin. Procedia Comput. Sci. 2017, 119, 288–297. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Chang, F.J.; Hsu, K.; Chang, L.C. Flood Forecasting Using Machine Learning Methods; MDPI: Basel, Switzerland, 2019. [Google Scholar]
- Chang, F.J.; Chen, P.A.; Lu, Y.R.; Huang, E.; Chang, K.Y. Real-time multi-step-ahead water level forecasting by recurrent neural networks for urban flood control. J. Hydrol. 2014, 517, 836–846. [Google Scholar] [CrossRef]
- Doycheva, K.; Horn, G.; Koch, C.; Schumann, A.; König, M. Assessment and weighting of meteorological ensemble forecast members based on supervised machine learning with application to runoff simulations and flood warning. Adv. Eng. Inform. 2017, 33, 427–439. [Google Scholar] [CrossRef]
- Banks, V.A.; Plant, K.L.; Stanton, N.A. Driver error or designer error: Using the Perceptual Cycle Model to explore the circumstances surrounding the fatal Tesla crash on 7th May 2016. Safety Sci. 2018, 108, 278–285. [Google Scholar] [CrossRef]
- Wolfram, S. Cellular automata as models of complexity. Nature 1984, 311, 419–424. [Google Scholar] [CrossRef]
- Emerson, E. Crowd pathfinding and steering using flow field tiles. In Game AI Pro: Collected Wisdom of Game AI Professionals; CRC Press: Boca Raton, FL, USA, 2013; pp. 307–316. [Google Scholar]
- Dottori, F.; Todini, E. Developments of a flood inundation model based on the cellular automata approach: Testing different methods to improve model performance. Phys. Chem. Earth Parts A/B/C 2011, 36, 266–280. [Google Scholar] [CrossRef]
- Ghimire, B.; Chen, A.S.; Guidolin, M.; Keedwell, E.C.; Djordjević, S.; Savić, D.A. Formulation of a fast 2D urban pluvial flood model using a cellular automata approach. J. Hydroinformatics 2013, 15, 676–686. [Google Scholar] [CrossRef]
- Guidolin, M.; Chen, A.S.; Ghimire, B.; Keedwell, E.C.; Djordjević, S.; Savić, D.A. A weighted cellular automata 2D inundation model for rapid flood analysis. Environ. Model. Softw. 2016, 84, 378–394. [Google Scholar] [CrossRef]
- Jamali, B.; Bach, P.M.; Cunningham, L.; Deletic, A. A Cellular Automata Fast Flood Evaluation (CA-ffé) Model. Water Resour. Res. 2019, 55, 4936–4953. [Google Scholar] [CrossRef]
- Bernardini, G.; Postacchini, M.; Quagliarini, E.; D’Orazio, M.; Brocchini, M. Flooding pedestrians evacuation in historical urban scenario: A tool for risk assessment including human behaviors. In Structural Analysis of Historical Constructions; Springer: Cham, Switzerland, 2019; pp. 1152–1161. [Google Scholar]
- Schubert, J.E.; Sanders, B.F. Building treatments for urban flood inundation models and implications for predictive skill and modeling efficiency. Adv. Water Resour. 2012, 41, 49–64. [Google Scholar] [CrossRef]
- Ozdemir, H.; Sampson, C.; de Almeida, G.A.; Bates, P.D. Evaluating scale and roughness effects in urban flood modelling using terrestrial LIDAR data. Hydrol. Earth Syst. Sci. 2013, 10, 5903–5942. [Google Scholar] [CrossRef]
- Issermann, M. Wuppertal WorldWind Environmental Monitor. 2019. Available online: https://wupperwwem.github.io/ (accessed on 28 April 2020).
- Tariq, J.; Kumaravel, A. Construction of cellular automata over hexagonal and triangular tessellations for path planning of multi-robots. In Proceedings of the 2016 IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), Chennai, India, 15–17 December 2016; pp. 1–6. [Google Scholar]
- Encinas, L.H.; White, S.H.; Del Rey, A.M.; Sánchez, G.R. Modelling forest fire spread using hexagonal cellular automata. Appl. Math. Model. 2007, 31, 1213–1227. [Google Scholar] [CrossRef]
- Di Gregorio, S.; Iovine, G. Simulating debris flows through a hexagonal cellular automata model: SCIDDICA S 3? hex. Natural Hazards Earth Syst. Sci. 2003, 3, 545–559. [Google Scholar]
- Kier, L.B.; Seybold, P.G.; Cheng, C.K. Cellular automata. In Modeling Chemical Systems Using Cellular Automata: A Textbook and Laboratory Manual; Springer: Berlin/Heidelberg, Germany, 2005; pp. 9–38. [Google Scholar]
- Abtew, W.; Melesse, A. Evaporation and Evapotranspiration: Measurements and Estimations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kouwen, N. WATFLOOD/WATROUTE Hydrological Model Routing and Flood Forecasting System, User’s Manual; University of Waterloo: Waterloo, ON, Canada, 2016. [Google Scholar]
- Chanson, H. Hydraulics of Open Channel Flow; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Bell, D.G.; Kuehnel, F.; Maxwell, C.; Kim, R.; Kasraie, K.; Gaskins, T.; Hogan, P.; Coughlan, J. NASA World Wind: Opensource GIS for mission operations. In Proceedings of the 2007 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2007; pp. 1–9. [Google Scholar]
- Geobasis NRW. 3D-Messdaten Laserscanning – Paketierung: Gemeinden. Available online: https://www.opengeodata.nrw.de/produkte/geobasis/hm/3dm_l_las/3dm_l_las_paketiert/ (accessed on 10 March 2020).
- OpenStreetMap Contributors. Planet Dump. Available online: https://planet.osm.org (accessed on 12 December 2017).
- Openweather. OpenWeatherMap. Available online: https://openweathermap.org/api (accessed on 28 April 2020).
- Mungkasi, S.; Roberts, S.G. Validation of ANUGA hydraulic model using exact solutions to shallow water wave problems. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2013; Volume 423. [Google Scholar]
- Roberts, S.; Nielsen, O.; Gray, D.; Sexton, J.; Davies, G. ANUGA user manual. Geosci. Aust. 2010, 2.0.3, 1–79. [Google Scholar]
- Biondi, D.; Freni, G.; Iacobellis, V.; Mascaro, G.; Montanari, A. Validation of hydrological models: Conceptual basis, methodological approaches and a proposal for a code of practice. Phys. Chem. Earth Parts A/B/C 2012, 42, 70–76. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.; Guariso, G.; Guillaume, J.H.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.; Norton, J.P.; Perrin, C. Characterising performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Postacchini, M.; Zitti, G.; Giordano, E.; Clementi, F.; Darvini, G.; Lenci, S. Flood impact on masonry buildings: The effect of flow characteristics and incidence angle. J. Fluids Struct. 2019, 88, 48–70. [Google Scholar] [CrossRef]


| Name | Formula | Range | Ideal Value |
|---|---|---|---|
| Nash-Sutcliffe Model Efficiency (NSE) | (−∞, 1) | 1 | |
| Root Mean Square Error (RMSE) | (0, ∞) | 0 | |
| Index of Agreement (IoA) | (0, 1) | 1 | |
| n is the number of time steps; is the simulated output at time step t; | |||
| is the reference output at time step t; is the mean of the reference output | |||
| NSE | RMSE | IoA | ||
|---|---|---|---|---|
| Water depth | Mean | 0.61 | 0.39 m | 0.65 |
| Median | 0.67 | 0.25 m | 0.67 | |
| Velocity | Mean | 0.34 | 0.13 ms | 0.39 |
| Median | 0.38 | 0.11 ms | 0.42 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Issermann, M.; Chang, F.-J.; Jia, H. Efficient Urban Inundation Model for Live Flood Forecasting with Cellular Automata and Motion Cost Fields. Water 2020, 12, 1997. https://doi.org/10.3390/w12071997
Issermann M, Chang F-J, Jia H. Efficient Urban Inundation Model for Live Flood Forecasting with Cellular Automata and Motion Cost Fields. Water. 2020; 12(7):1997. https://doi.org/10.3390/w12071997
Chicago/Turabian StyleIssermann, Maikel, Fi-John Chang, and Haifeng Jia. 2020. "Efficient Urban Inundation Model for Live Flood Forecasting with Cellular Automata and Motion Cost Fields" Water 12, no. 7: 1997. https://doi.org/10.3390/w12071997
APA StyleIssermann, M., Chang, F.-J., & Jia, H. (2020). Efficient Urban Inundation Model for Live Flood Forecasting with Cellular Automata and Motion Cost Fields. Water, 12(7), 1997. https://doi.org/10.3390/w12071997







