Multi-Collocation-Based Estimation of Wave Climate in a Non-Tidal Bay: The Case Study of Bagnoli-Coroglio Bay (Tyrrhenian Sea)
Abstract
1. Introduction
1.1. Motivations and Perspective
- the presence of some missing values (the percentage of missing data can severely reduce the representativeness of the sample and disturb the conclusions drawn from the dataset) [5];
- the spatial resolution, the Italian Wave Network (IWN) consisting of only 15 stations positioned along the more than 7000 km of Italian coasts [6];
- highlight the discrepancies and errors in the use of different sources of wave data for both offshore and nearshore wave climate analysis from the perspective of coastal engineering measures and especially in the assessment of non-extreme wave conditions.
1.2. Approach and Challenges
2. Wave Data and Methodology
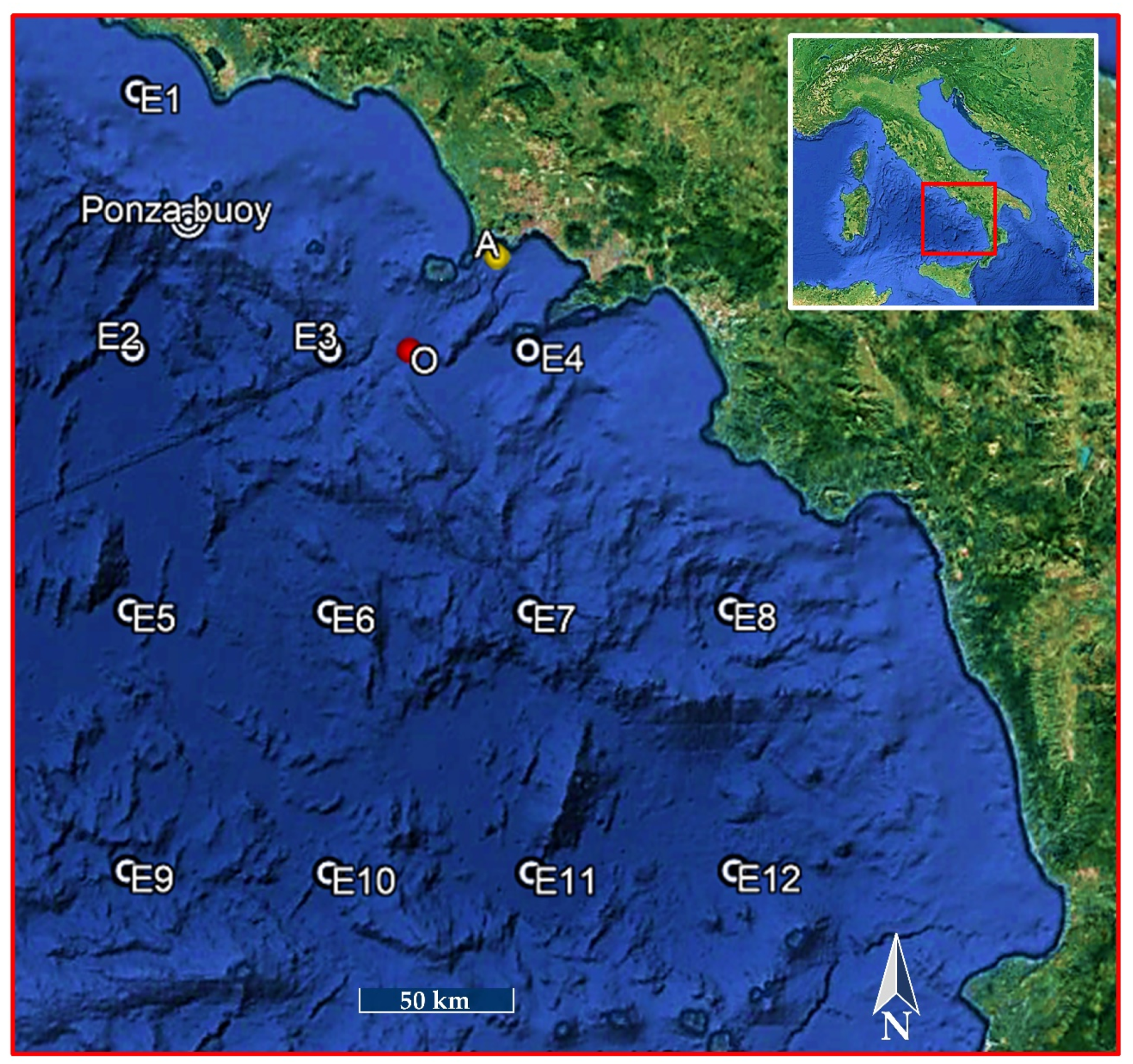
2.1. Offshore Wave Dataset
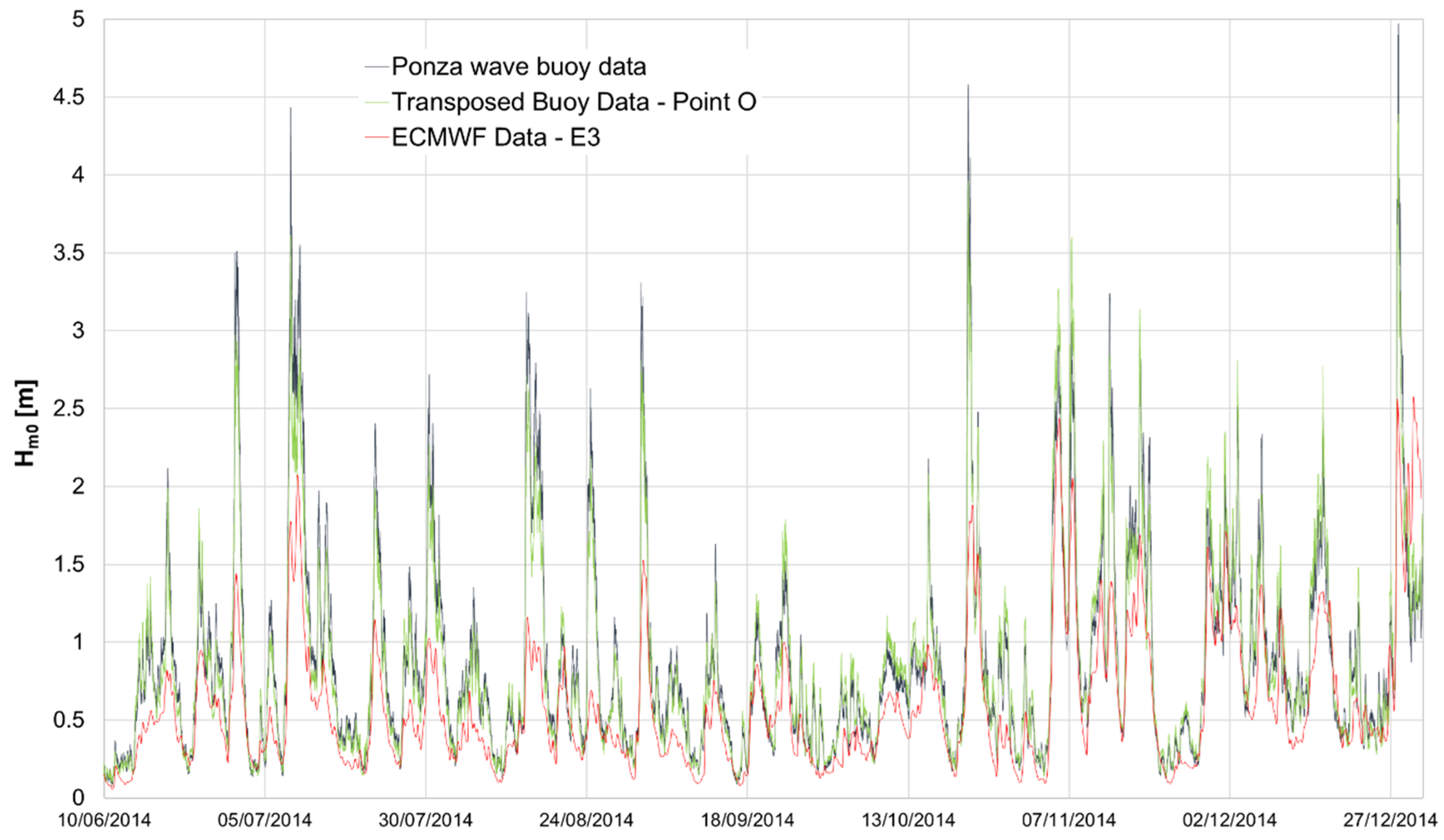
2.1.1. Comparison of Offshore Wave Data
- (a)
- the wind speed and direction are the same at both real and “virtual” (transposed) stations;
- (b)
- the extent of the wave generation region can be described by the effective fetches [97];
- (c)
- the wind blows over the fetch long enough to assume that wave conditions are independent of the wind duration (fetch-limited conditions);
- (d)
- both real and virtual stations are in deep water.
2.2. Study Site and Nearshore Wave Instrumentation
2.2.1. Acoustic Doppler Current Profiler
2.2.2. Directional Wave Spectra Drifter-Derived Wave Buoy
2.3. Wave Propagation and Model Calibration
- for the wave bathymetric breaking, the formulation proposed by Battjes and Janssen [121];
- the formulation of Kofoed-Hansen and Rasmussen [122] for bottom friction dissipation;
- the Komen et al. [123] dissipation model for whitecapping;
- for Snl parameterization, the discrete interaction approximation developed by Hasslmann et al. [126].
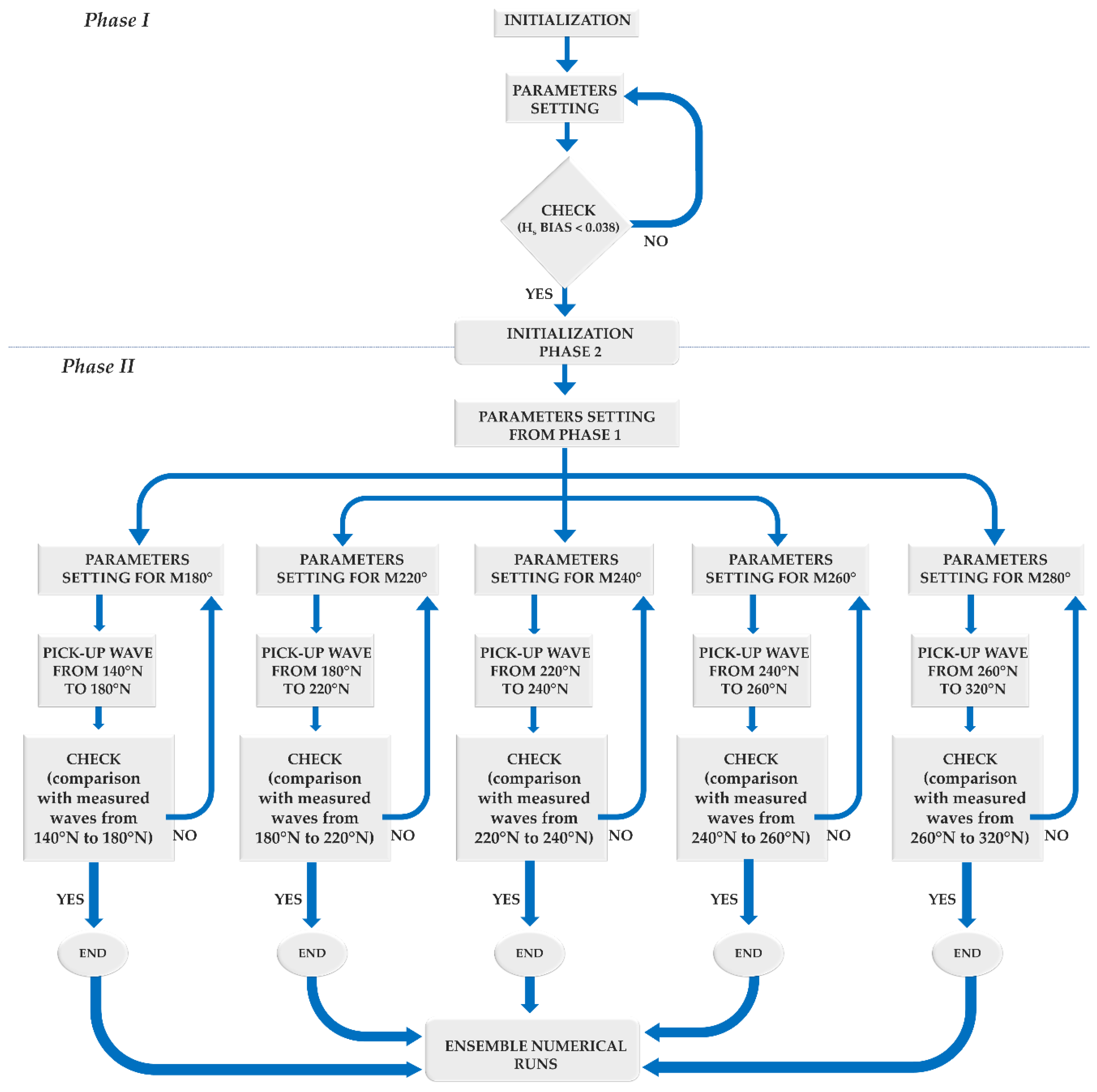
2.3.1. First Step: Triple Collocation
- firstly, qualitative evaluations of the input time series amount to cheap and almost instantaneous forward runs of a pretrained network of direct measurements;
- secondly, fast and accurate approximations of numerical output with respect to the model parameters returns, since short recordings by DWSD-B and ADCP-B are taken into account.
2.3.2. Second Step: Ensemble of Multiple Runs
3. Results
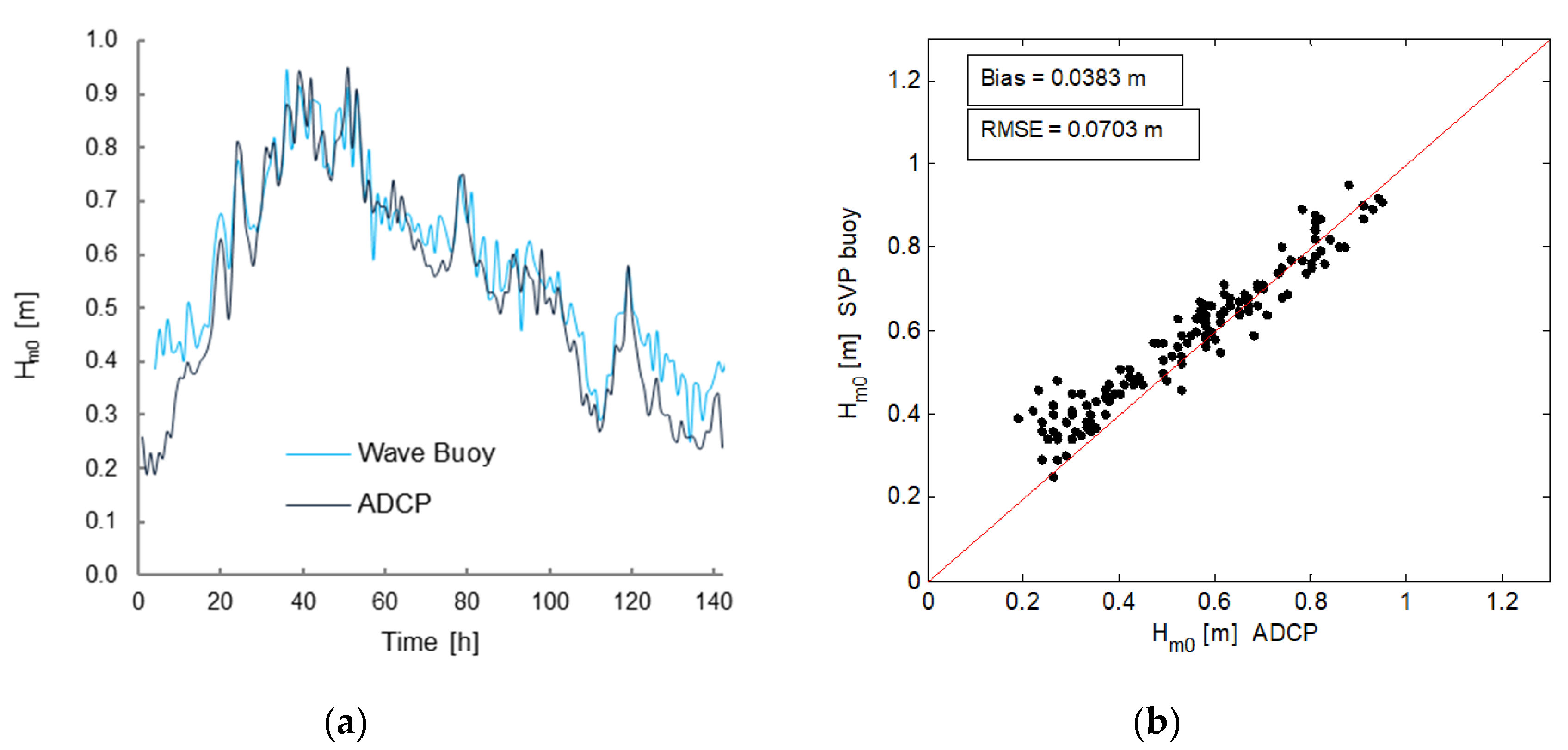
3.1. DWSD Buoy Compared to the ADCP
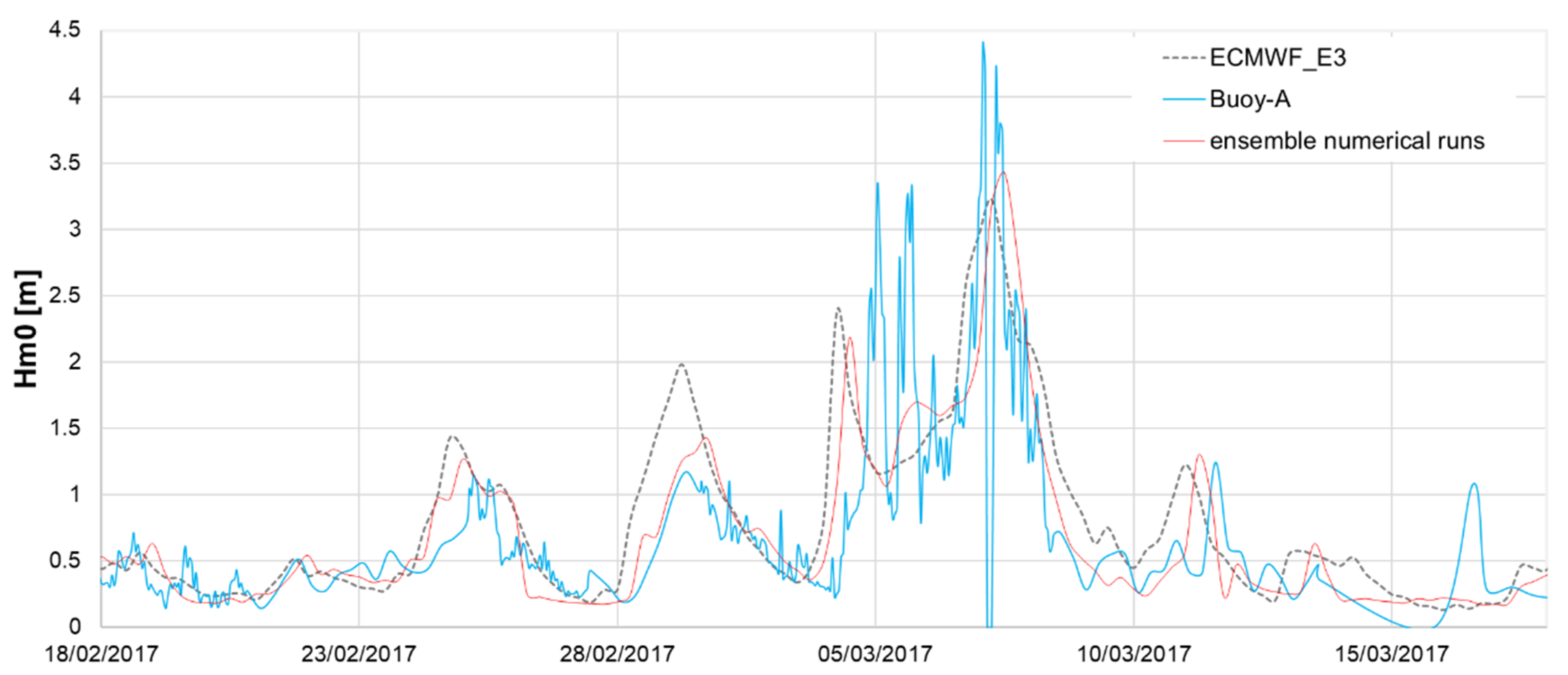
3.2. Triple Comparison
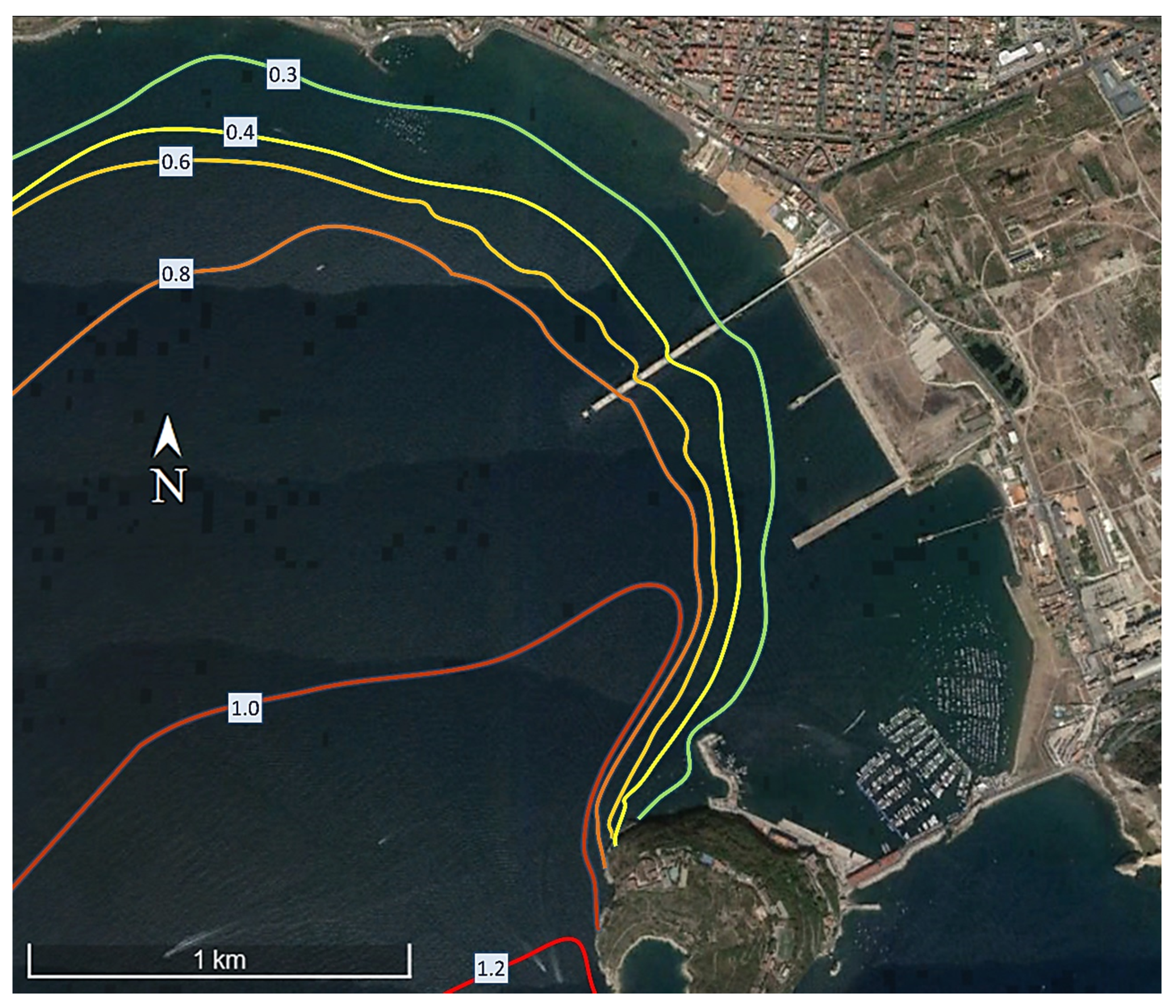
3.3. Final Calibration
4. Additional Considerations and Future Perspectives
5. Conclusions
- the procedure here proposed, in which every sea state is subject to five (one for each grid model orientation) numerical propagations by a simpler spectral wave model, allows researchers to reach a good level of accuracy, similarly to a more time-consuming Boussinesq-type wave model which, nowadays, represents a state-of-the-art modeling technique if a very detailed wave disturbance in an enclosed coastal area needs to be explored;
- the effectiveness of numerical model calibration by means of a short period of direct measurement, opening up opportunities to use low-cost GPS buoys. To bridge the gap of abundant direct measurements in the sea from traditional wave buoy networks, the capability of GPS-buoy clusters to provide data for assimilation, calibration and validation of both climate and weather models could be optimally leveraged.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Input |
|
|
| Result |
|
| Algorithm |
| For each n-th hourly sea state (n=1,…,N) if θECMWF,n ]0,190] then SEN,n = SM180°,n if θECMWF,n ]190,220] then SEN,n = SM220°,n if θECMWF,n ]220,250] then SEN,n = SM240°,n if θECMWF,n ]250,270] then SEN,n = SM260°,n if θECMWF,n ]270,360] then SEN,n = SM280°,n end |
References
- Dentale, F.; Furcolo, P.; Pugliese Carratelli, E.; Reale, F.; Contestabile, P.; Tomasicchio, G.R. Extreme wave analysis by integrating model and wave buoy data. Water 2018, 10, 373. [Google Scholar] [CrossRef]
- Fortunato, A.B.; Li, K.; Bertin, X.; Rodrigues, M.; Miguez, B.M. Determination of extreme sea levels along the Iberian Atlantic coast. Ocean Eng. 2016, 111, 471–482. [Google Scholar] [CrossRef]
- Franco, L. History of coastal engineering in Italy. In History and Heritage of Coastal Engineering; ASCE: Reston, VA, USA, 1996; pp. 275–335. [Google Scholar]
- European Centre for Medium-Range Weather Forecasts. Available online: http://www.ecmwf.int/ (accessed on 10 May 2020).
- Vicinanza, D.; Cappietti, L.; Ferrante, V.; Contestabile, P. Estimation of the wave energy in the Italian offshore. J. Coast. Res. 2011, 64, 613. [Google Scholar]
- Vicinanza, D.; Contestabile, P.; Ferrante, V. Wave energy potential in the north-west of Sardinia (Italy). Renew. Energy 2013, 50, 506–521. [Google Scholar] [CrossRef]
- Bencivenga, M.; Nardone, G.; Ruggiero, F.; Calore, D. The Italian Data Buoy Network. WTI Trans. Eng. Sci. 2012, 74, 321–332. [Google Scholar]
- Contestabile, P.; Ferrante, V.; Vicinanza, D. Wave energy resource along the coast of Santa Catarina (Brazil). Energies 2015, 8, 14219–14243. [Google Scholar] [CrossRef]
- Contestabile, P.; Lauro, E.D.; Galli, P.; Corselli, C.; Vicinanza, D. Offshore wind and wave energy assessment around Malè and Magoodhoo Island (Maldives). Sustainability 2017, 9, 613. [Google Scholar] [CrossRef]
- Shanas, P.R.; Kumar, V.S. Temporal variations in the wind and wave climate at a location in the eastern Arabian Sea based on ERA-Interim reanalysis data. Nat. Hazards Earth Syst. Sci. 2014, 14, 1371–1381. [Google Scholar] [CrossRef]
- Iuppa, C.; Cavallaro, L.; Vicinanza, D.; Foti, E. Investigation of suitable sites for wave energy converters around Sicily (Italy). Ocean Sci. 2015, 11, 543–557. [Google Scholar] [CrossRef]
- Contestabile, P.; Vicinanza, D. Coastal defence integrating wave-energy-based desalination: A case study in Madagascar. J. Mar. Sci. Eng. 2018, 6, 64. [Google Scholar] [CrossRef]
- Iuppa, C.; Cavallaro, L.; Foti, E.; Vicinanza, D. Potential wave energy production by different wave energy converters around Sicily. J. Renew. Sustain. Energy 2015, 7, 061701. [Google Scholar] [CrossRef]
- Caloiero, T.; Aristodemo, F.; Ferraro, D.A. Trend analysis of significant wave height and energy period in southern Italy. Theor. Appl. Climatol. 2019, 138, 917–930. [Google Scholar] [CrossRef]
- Sterl, A.; Komen, G.K.; Cotton, P.D. Fifteen years of global wave hindcasts using winds from the European Centre for Medium-Range Weather Forecasts reanalysis: Validating the reanalyzed winds and assessing the wave climate. J. Geophys. Res. Ocean. 1998, 103, 5477–5492. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M.; Bidlot, J.R.; Abdalla, S.; Hersbach, H. Progress in ocean wave forecasting at ECMWF. In ECMWF Technical Memory; ECMWF: Reading, UK, 2005; p. 27. [Google Scholar]
- Palm, S.P.; Benedetti, A.; Spinhirne, J. Validation of ECMWF global forecast model parameters using GLAS atmospheric channel measurements. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Klein, S.A.; Jakob, C. Validation and sensitivities of frontal clouds simulated by the ECMWF model. Mon. Weather Rev. 1999, 127, 2514–2531. [Google Scholar] [CrossRef]
- Molteni, F.; Buizza, R.; Palmer, T.N.; Petroliagis, T. The ECMWF ensemble prediction system: Methodology and validation. Q. J. R. Meteorol. Soc. 1996, 122, 73–119. [Google Scholar] [CrossRef]
- Hanna, E.; Valdes, P. Validation of ECMWF (re) analysis surface climate data, 1979–1998, for Greenland and implications for mass balance modelling of the ice sheet. Int. J. Climatol. A J. R. Meteorol. Soc. 2001, 21, 171–195. [Google Scholar] [CrossRef]
- Mace, G.G.; Jakob, C.; Moran, K.P. Validation of hydrometeor occurrence predicted by the ECMWF model using millimeter wave radar data. Geophys. Res. Lett. 1998, 25, 1645–1648. [Google Scholar] [CrossRef]
- King, J.C. Validation of ECMWF sea level pressure analyses over the Bellingshausen Sea, Antarctica. Weather Forecast. 2003, 18, 536–540. [Google Scholar] [CrossRef]
- Hagemann, S.; Gates, L.D. Validation of the hydrological cycle of ECMWF and NCEP reanalyses using the MPI hydrological discharge model. J. Geophys. Res. Atmos. 2001, 106, 1503–1510. [Google Scholar] [CrossRef]
- Janssen, P. ECMWF wave modeling and satellite altimeter wave data. In Satellites, Oceanography and Society; Halpern, D., Ed.; Elseviers Oceanography Series; Elsevier: Amsterdam, The Netherlands, 2000; Volume 63, pp. 35–56. [Google Scholar]
- Tokmakian, R.; Challenor, P.G. On the joint estimation of model and satellite sea surface height anomaly errors. Ocean Model. 1999, 1, 39–52. [Google Scholar] [CrossRef]
- Stopa, J.E.; Cheung, K.F. Intercomparison of wind and wave data from the ECMWF Reanalysis Interim and the NCEP Climate Forecast System Reanalysis. Ocean Model. 2014, 75, 65–83. [Google Scholar] [CrossRef]
- Sanil Kumar, V.; Naseef, T.M. Performance of ERA-Interim wave data in the nearshore waters around India. J. Atmos. Ocean. Technol. 2015, 32, 1257–1269. [Google Scholar] [CrossRef]
- Cavaleri, L.; Bertotti, L. Accuracy of the modelled wind and waves in enclosed seas. Tellus 2004, 56, 167–175. [Google Scholar] [CrossRef]
- Bertotti, L.; Cavaleri, L.; Soret, A.; Tolosana-Delgado, R. Performance of global and regional nested meteorological models. Cont. Shelf Res. 2014, 87, 17–27. [Google Scholar] [CrossRef]
- Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Performance evaluation of Wavewatch III in the Mediterranean Sea. Ocean Model. 2015, 90, 82–94. [Google Scholar] [CrossRef]
- Cavaleri, L. Wave modeling missing the peaks. J. Phys. Oceanogr. 2009, 39, 2757–2778. [Google Scholar] [CrossRef]
- Arena, F.; Laface, V.; Barbaro, G.; Romolo, A. Effects of Sampling between Data of SignificantWave Height for Intensity and Duration of Severe Sea Storms. Int. J. Geosci. 2013, 4, 240–248. [Google Scholar] [CrossRef][Green Version]
- Reale, F.; Dentale, F.; Pugliese Carratelli, E.; Torrisi, L. Remote Sensing of Small-Scale Storm Variations in Coastal Seas. J. Coast. Res. 2014, 30, 130–141. [Google Scholar] [CrossRef]
- Wang., J.; Li., B.; Gao., Z.; Wang., J. Comparison of ECMWF significant wave height forecasts in the China sea with buoy data. Weather Forecast. 2019, 34, 1693–1704. [Google Scholar] [CrossRef]
- Cavaleri, L.; Bertotti, L. The improvement of modelled wind and wave fields with increasing resolution. Ocean Eng. 2006, 33, 553–565. [Google Scholar] [CrossRef]
- Sartini, L.; Besio, G.; Dentale, F.; Reale, F. Wave Hindcast Resolution Reliability for Extreme Analysis. In Proceedings of the 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–2 July 2016. [Google Scholar]
- Contestabile, P.; Di Lauro, E.; Buccino, M.; Vicinanza, D. Economic assessment of Overtopping BReakwater for Energy Conversion (OBREC): A case study in Western Australia. Sustainability 2017, 9, 51. [Google Scholar] [CrossRef]
- Stoffelen, A. Toward the true near-surface wind speed: Error modeling and calibration using triple collocation. J. Geophys. Res. Ocean. 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- Nearing, G.S.; Yatheendradas, S.; Crow, W.T.; Bosch, D.D.; Cosh, M.H.; Goodrich, D.C.; Seyfried, M.S.; Starks, P.J. Nonparametric triple collocation. Water Resour. Res. 2017, 53, 5516–5530. [Google Scholar] [CrossRef]
- Janssen, P.A.; Abdalla, S.; Hersbach, H.; Bidlot, J.R. Error estimation of buoy, satellite, and model wave height data. J. Atmos. Ocean. Technol. 2007, 24, 1665–1677. [Google Scholar] [CrossRef]
- Caires, S.; Sterl, A. Validation of the ERA-40 ocean wave dataset using triple collocation. J. Geophys. Res. 2003. In Press. [Google Scholar] [CrossRef]
- Muraleedharan, G.; Rao, A.D.; Sinha, M.; Mahapatra, D.K. Analysis of Triple Collocation Method for validation of model predicted significant wave height data. J. Ind. Geophys. Union 2006, 10, 79–84. [Google Scholar]
- Schulz-Stellenfleth, J. A multi-collocation method for coastal zone observations with applications to Sentinel-3A altimeter wave height data. Ocean Sci. 2019, 15, 249–268. [Google Scholar] [CrossRef]
- Caires, S.; Sterl, A. A new nonparametric method to correct model data: Application to significant wave height from the ERA-40 re-analysis. J. Atmos. Ocean. Technol. 2005, 22, 443–459. [Google Scholar] [CrossRef]
- Robertson, B.; Lin, Y.; Buckham, B. Application of triple collocation technique to wave resource assessments and wave energy converter energy production. In Proceedings of the 14th Workshop on Wave Hindcasting and Forecasting, Key West, FL, USA, 8–13 November 2015; p. 23. [Google Scholar]
- McColl, K.A.; Vogelzang, J.; Konings, A.G.; Entekhabi, D.; Piles, M.; Stoffelen, A. Extended triple collocation: Estimating errors and correlation coefficients with respect to an unknown target. Geophys. Res. Lett. 2014, 41, 6229–6236. [Google Scholar] [CrossRef]
- Scipal, K.; Doubkova, M.; Hegyova, A.; Dorigo, W.; Wagner, W. An empirical understanding of triple collocation evaluation measure. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 7–12 April 2013; Volume 15. [Google Scholar]
- Wang, H.; Zhu, J.; Yang, J. Error analysis on ESA’s Envisat ASAR wave mode significant wave height retrievals using triple collocation model. Remote Sens. 2014, 6, 12217–12233. [Google Scholar] [CrossRef]
- Wang, H.; Shi, C.Y.; Zhu, J.H.; Huang, X.Q.; Chen, C.T. Validation of significant wave height product from Envisat ASAR using triple collocation. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Beijing, China, 22–26 April 2013; IOP Publishing: Bristol, UK, 2014; Volume 17, p. 012279. [Google Scholar]
- Bertocci, I.; Dell’Anno, A.; Musco, L.; Gambi, C.; Saggiomo, V.; Cannavacciuolo, M.; Lo Martire, M.; Passarelli, A.; Zazo, G.; Danovaro, R. Multiple human pressures in coastal habitats: Variation of meiofaunal assemblages associated with sewage discharge in a post-industrial area. Sci. Total Environ. 2019, 655, 1218–1231. [Google Scholar] [CrossRef] [PubMed]
- Morroni, L.; d’Errico, G.; Sacchi, M.; Molisso, F.; Armiento, G.; Chiavarini, S.; Rimauro, J.; Guida, M.; Siciliano, A.; Ceparano, M.; et al. Integrated characterization and risk management of marine sediments: The case study of the industrialized Bagnoli area (Naples, Italy). Mar. Environ. Res. 2020, 160, 104984. [Google Scholar] [CrossRef]
- Ruocco, N.; Bertocci, I.; Munari, M.; Musco, L.; Caramiello, D.; Danovaro, R.; Zupo, V.; Costantini, M. Morphological and molecular responses of the sea urchin Paracentrotus lividus to highly contaminated marine sediments: The case study of Bagnoli-Coroglio brownfield (Mediterranean Sea). Mar. Environ. Res. 2020, 154, 104865. [Google Scholar] [CrossRef] [PubMed]
- Ragozino, S.; Varriale, A.; De Vita, G.E. Self-organized practices for complex urban transformation. The case of Bagnoli in Naples, Italy. Tracce Urbane. Riv. Ital. Transdiscipl. Studi Urbani 2018, 2. [Google Scholar] [CrossRef]
- ABBaCo Project. Sperimentazioni pilota finalizzate al restauro ambientale e balneabilità del SIN Bagnoli-Coroglio. Italian Ministry for Education, University and Research Grant number C62F16000170001. 2018. Available online: http://www.szn.it/index.php/en/research/integrative-marine-ecology/research-projects-emi/abbaco (accessed on 6 July 2020).
- Musco, L.; Bertocci, I.; Buia, M.C.; Cannavacciuolo, M.; Conversano, F.; Gallo, A.; Gambi, M.C.; Ianora, A.; Iudicone, D.; Margiotta, F.; et al. Restauro ambientale e balneabilità a del SIN di Bagnoli Coroglio-Progetto ABBaCo Workshop SiCon2017. Siti contaminati. In Proceedings of the Esperienze Negli Interventi di Risanamento. Roma, Facoltà Ingegneria Civile ed Industriale. La Sapienza, Roma, Italy, 8–10 February 2017. [Google Scholar]
- Chatelain, M.; Guizien, K. Modelling coupled turbulence—Dissolved oxygen dynamics near the sediment–water interface under wind waves and sea swell. Water Res. 2010, 44, 1361–1372. [Google Scholar] [CrossRef]
- Semedo, A.; Weisse, R.; Behrens, A.; Sterl, A.; Bengtsson, L.; Günther, H. Projection of global wave climate change toward the end of the twenty-first century. J. Clim. 2012, 26, 8269–8288. [Google Scholar] [CrossRef]
- Casas-Prat, M.; Sierra, J.P. Projected future wave climate in the NW Mediterranean Sea. J. Geophys. Res. Ocean. 2013, 118, 3548–3568. [Google Scholar] [CrossRef]
- Valenti, D.; Denaro, G.; Spagnolo, B.; Mazzola, S.; Basilone, G.; Conversano, F.; Brunet, C.; Bonanno, A. Stochastic models for phytoplankton dynamics in Mediterranean Sea. Ecol. Complex. 2016, 27, 84–103. [Google Scholar] [CrossRef]
- Valenti, D.; Denaro, G.; Spagnolo, B.; Conversano, F.; Brunet, C. How diffusivity, thermocline and incident light intensity modulate the dynamics of deep chlorophyll maximum in Tyrrhenian sea. PLoS ONE 2015, 10, 1–31. [Google Scholar] [CrossRef]
- Van Dijk, M.A.; Passarelli, A.; Conversano, F.; Casotti, R. Phytoplankton dynamics by autonomous high-frequency flow cytometry from a floating buoy in the Gulf of Naples. In Proceedings of the IMEKO TC19 Workshop on Metrology for the Sea (MetroSea 2017), Naples, Italy, 11–13 October 2017. [Google Scholar]
- Fanelli, E.; Aguzzi, J.; Casotti, R.; Conversano, F.; D’Aiello, D.; Iudicone, D.; Marini, S.; Stefanni, S. NEREA, the Naples Ecological REsearch for Augmented observatories: Towards an end-to-end transdisciplinary approach for the study of marine ecosystems. In Proceedings of the 2019 IMEKO TC-19 International Workshop on Metrology for the Sea, Genova, Italy, 3–5 October 2019. [Google Scholar]
- Margiotta, F.; Balestra, C.; Buondonno, A.; Casotti, R.; D’Ambra, I.; Di Capua, I.; Gallia, R.; Mazzocchi, M.G.; Merquiol, L.; Pepi, M. Do plankton reflect the environmental quality status? The case of a post-industrial Mediterranean Bay. Mar. Environ. Res. 2020, 160, 104980. [Google Scholar] [CrossRef]
- Gerovasileiou, V.; Smith, C.W.J.; Sevastou, K.; Papadopoulou, N.; Dailianis, T.; Bekkby, T.; Fiorentino, D.; Mcowen, C.; Amaro, T.; Bengil, E.G.T. Habitat mapping in the European Seas-is it fit for purpose in the marine restoration agenda? Mar. Policy 2019, 106, 103521. [Google Scholar] [CrossRef]
- Azzellino, A.; Lanfredi, C.; D’amico, A.; Pavan, G.; Podestà, M.; Haun, J. Risk mapping for sensitive species to underwater anthropogenic sound emissions: Model development and validation in two Mediterranean areas. Mar. Pollut. Bull. 2011, 63, 56–70. [Google Scholar] [CrossRef] [PubMed]
- Azzellino, A.; Lanfredi, C.; Contestabile, P.; Ferrante, V.; Vicinanza, D. Strategic environmental assessment to evaluate WEC projects in the perspective of the environmental cost-benefit analysis. In Proceedings of the The Twenty-first International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2011. [Google Scholar]
- Azzellino, A.; Gaspari, S.A.; Airoldi, S.; Lanfredi, C. Biological consequences of global warming: Does sea surface temperature affect cetacean distribution in the western Ligurian Sea. J. Mar. Biol. Assoc. UK 2008, 88, 1145–1152. [Google Scholar] [CrossRef]
- Danovaro, R.; Fanelli, E.; Canals, M.; Ciuffardi, T.; Fabri, M.C.; Taviani, M.; Argyrouh, M.; Azzurrobi, E.; Bianchellia, S.; Cantafaroj, A.; et al. Towards a marine strategy for the deep Mediterranean Sea: Analysis of current ecological status. Mar. Policy 2020, 112, 103781. [Google Scholar] [CrossRef]
- Borsje, B.W.; Van Wesenbeeck, B.K.; Dekker, F.; Paalvast, P.; Bouma, T.J.; Van Katwijk, M.M.; de Vries, M.B. How ecological engineering can serve in coastal protection. Ecol. Eng. 2011, 37, 113–122. [Google Scholar] [CrossRef]
- Chung, C.H. Forty years of ecological engineering with Spartina plantations in China. Ecol. Eng. 2006, 27, 49–57. [Google Scholar] [CrossRef]
- Contestabile, P.; Aristodemo, F.; Vicinanza, D.; Ciavola, P. Laboratory study on a beach drainage system. Coast. Eng. 2012, 66, 50–64. [Google Scholar] [CrossRef]
- Cheong, S.M.; Silliman, B.; Wong, P.P.; Van Wesenbeeck, B.; Kim, C.K.; Guannel, G. Coastal adaptation with ecological engineering. Nat. Clim. Chang. 2013, 3, 787–791. [Google Scholar] [CrossRef]
- Temmerman, S.; Meire, P.; Bouma, T.J.; Herman, P.M.; Ysebaert, T.; De Vriend, H.J. Ecosystem-based coastal defence in the face of global change. Nature 2013, 504, 79–83. [Google Scholar] [CrossRef]
- Lagrangian Drifer Laboratory, SCRIPPS Institution of Oceanography. Available online: https://gdp.ucsd.edu/ldl/ (accessed on 15 May 2020).
- Longuet-Higgins, M.S.; Cartwright, D.E.; Smith, N.D. Observations of the directional spectrum of sea waves using the motion of a floating buoy. In Ocean Wave Spectra, 1st ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1963; pp. 111–132. [Google Scholar]
- Kuik, A.J.; Ph van Vledder, G.; Holthuijsen, L.H. A Method for the Routine Analysis of Pitch-and-Roll Buoy Wave Data. J. Phys. Oceanogr. 1988, 18, 1020–1034. [Google Scholar] [CrossRef]
- Krogstad, H.E.; Barstow, S.F.; Haug, O.; Markussen, P.Ø.; Ueland, G.; Rodriguez, I. SMART-800: A GPS based directional wave buoy. In Ocean Wave Measurement and Analysis; ASCE: Reston, VA, USA, 1997; pp. 1182–1195. [Google Scholar]
- Herbers, T.H.C.; Jessen, P.F.; Janssen, T.T.; Colbert, D.B.; MacMahan, J.H. Observing ocean surface waves with GPS-tracked buoys. J. Atmos. Ocean. Technol. 2012, 29, 944–959. [Google Scholar] [CrossRef]
- Kato, T.; Terada, Y.; Itoh, T.; Nagata, S.; Fujita, T.; Abe, T.; Miuake, T.; Nagai, T.; Koshimura, S.; Miyazaki, S. A new tsunami detection system using RTK-GPS. In Proceedings of the International Tsunami Symposium, Seattle, WA, USA, 7–10 August 2001; pp. 645–651. [Google Scholar]
- Nagai, T.; Satomi, S.; Terada, Y.; Kato, T.; Nukada, K.; Kudaka, M. GPS buoy and seabed installed wave gauge application to offshore tsunami observation. In Proceedings of the fifteenth International Offshore and Polar Engineering Conference, Seoul, Korea, 19–24 June 2005; pp. 292–299. [Google Scholar]
- De Vries, J.J.; Waldron, J.; Cunningham, V. Field tests of the new datawell dwr-g gpa wave buoy. Sea Technol. 2003, 44, 50–55. [Google Scholar]
- Colbert, D. Field Evaluation of Ocean Wave Measurements with GPS Buoy; NAVAL Postgraduate School: Monterey, CA, USA, 2010. [Google Scholar]
- Jeans, G.; Bellamy, I.; de Vries, J.J.; van Weert, P. Sea trial of the new Datawell GPS directional Waverider. In Proceedings of the IEEE/OES Seventh Working Conference on Current Measurement Technology, San Diego, CA, USA, 13–15 March 2003; pp. 145–147. [Google Scholar]
- Patra, S.K.; Jena, B.K. Inter-comparison of wave measurement by accelerometer and GPS wave buoy in shallow water off Cuddalore, East Coast of India. Indian J. Geo-Mar. Sci. 2014, 43, 45–49. [Google Scholar]
- Datawell, B.V. Mini Directional Waverider GPS Specifications. Haarlem, The Netherlands. Available online: http://www.datawell.nl (accessed on 15 May 2020).
- Centurioni, L.; Turton, J.; Lumpkin, R.; Braasch, L.J.; Brassington, G.B.; Chao, Y.; Charpentier, E.; Chen, Z.; Corlett, G.K.; Dohan, K.; et al. Global in situ Observations of Essential Climate and Ocean Variables at the Air–Sea Interface. Front. Mar. Sci. 2019, 6, 419. [Google Scholar] [CrossRef]
- Niiler, P.P. The world ocean surface circulation. In Ocean Circulation and Climate; Siedler, G., Church, J., Gould, J., Eds.; Academic Press: Cambridge, MA, USA, 2001; Volume 77, pp. 193–204. [Google Scholar]
- Maximenko, N.; Lumpking, R.; Centurioni, L. Chapter 12—Ocean Surface Circulation”. In International Geophysics; Griffies, S.M., Siedler, J.G.G., Church, A.J., Eds.; Academic Press: Cambridge, MA, USA, 2013; pp. 283–304. [Google Scholar]
- Centurioni, L.R. Drifter technology and impacts for sea surface temperature, sea-level pressure, and ocean circulation studies. In Observing the Oceans in Real Time; Venkatesan, R., Tandon, A., D’Asaro, E., Atmanand, M.A., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 37–57. [Google Scholar]
- MacMahan, J.; Brown, J.; Thornton, E. Low-cost handheld Global Positioning System for measuring surf-zone currents. J. Coast. Res. 2009, 25, 744–754. [Google Scholar] [CrossRef]
- Postacchini, M.; Centurioni, L.R.; Braasch, L.; Brocchini, M.; Vicinanza, D. Lagrangian Observations of Waves and Currents From the River Drifter. IEEE J. Ocean. Eng. 2016, 41, 94–104. [Google Scholar]
- Johnson, D.; Stocker, R.; Head, R.; Imberger, J.; Pattiaratchi, C. A compact, low-cost GPS drifter for use in the oceanic nearshore zone, lakes, and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 1880–1884. [Google Scholar] [CrossRef]
- Centurioni, L.; Braasch, L.; Di Lauro, E.; Contestabile, P.; De Leo, F.; Casotti, R.; Franco, L.; Vicinanza, D. A new strategic wave measurement station off Naples port main breakwater. Coast. Eng. 2017, 1, 36. [Google Scholar] [CrossRef]
- Piscopia, R.; Inghilesi, R.; Panizzo, A.; Corsini, S.; Franco, L. Analysis of 12-year wave measurements by the Italian Wave Network. In Coastal Engineering 2002, Cardiff, Wales, 7–12 July 2002; Smith, J.M., Ed.; World Scientific Publishing Company: Singapore, 2003; pp. 121–133. [Google Scholar]
- Corsini, S.; Franco, L.; Inghilesi, R.; Piscopia, R. Atlante delle onde nei mari Italiani–Italian Waves Atlas; Agenzia per la Protezione dell’Ambiente e per i Servizi Tecnici (APAT) and University of Rome: Rome, Italy, 2004; p. 3. [Google Scholar]
- Contini, P.; De Girolamo, P. Impatto morfologico di opere a mare: Casi di studio. In Proceedings of the Atti VIII Convegno AIOM, Lerici, Italy, 28–29 May 1998. (In Italian). [Google Scholar]
- Seymour, R.J. Estimating Wave Generation on Restricted Fetches. J. Waterw. Port Coast. Ocean Div. 1977, 103, 251–264. [Google Scholar]
- SPM. Shore Protection Manual; Waterways Experiment Station, Coastal Engineering Research Center, U.S. Army Corps of Engineers: Vicksburg, MS, USA, 1984. [Google Scholar]
- Gaglioti, M.; Vega Fernandez, T.; Musco, L.; Gambi, M.C. Habitat and benthic diversity in the bay of Bagnoli and surrounding areas (Gulf of Naples, Italy): A historical baseline for environmental restoration. Mar. Environ. Res. 2020, 157, 104925. [Google Scholar] [CrossRef] [PubMed]
- Groeben, C. The Stazione Zoologica: A clearing house for marine organisms. In Oceanographic History. The Pacific and Beyond; Benson, K.R., Rehbock, P.F., Eds.; University of Washington Press: Seattle, WA, USA, 2002; pp. 537–547. [Google Scholar]
- Somma, R.; Iuliano, S.; Matano, F.; Molisso, F.; Passaro, S.; Sacchi, M.; Troise, C.; de Natale, G. High-resolution morpho-bathymetry of Pozzuoli Bay, southern Italy. J. Maps 2016, 12, 222–230. [Google Scholar] [CrossRef]
- Pinkel, R.; Smith, J.A. Open ocean surface wave measurements using Doppler sonar. J. Geophys. Res. 1987, 92, 12967–12973. [Google Scholar] [CrossRef]
- Smith, J.A. Doppler sonar and surface waves: Range and resolution. J. Atmos. Ocean. Technol. 1989, 6, 680–696. [Google Scholar] [CrossRef][Green Version]
- Terray, E.A.; Brumley, B.H.; Strong, B. Measuring waves and currents with an upward-looking ADCP. In Proceedings of the IEEE 6th Working Conference on Current Measurement, San Diego, CA, USA, 13 March 1999; pp. 66–71. [Google Scholar]
- Strong, B.; Brumley, B.H.; Terray, E.A.; Stone, G.W. The performance of ADCP derived wave directional spectra and comparison with other independent measurements. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition, Providence, RI, USA, 11–14 September 2000; pp. 1195–1203. [Google Scholar]
- Teledyne Marine. Available online: http://www.teledynemarine.com/adcps/marine-measurements (accessed on 6 July 2020).
- Poulain, P.M.; Centurioni, L. Direct measurements of world ocean tidal currents with surface drifters. J. Geophys. Res. Ocean. 2015, 120, 6986–7003. [Google Scholar] [CrossRef]
- Centurioni, L.; Horányi, A.; Cardinali, C.; Charpentier, E.; Lumpkin, R. A global ocean observing system for measuring sea level atmospheric pressure: Effects and impacts on numerical weather prediction. Bull. Am. Meteorol. Soc. 2017, 98, 231–238. [Google Scholar] [CrossRef]
- DHI Water and Environment. Available online: https://www.dhigroup.com/ (accessed on 15 May 2020).
- Appendini, C.M.; Urano-Latorre, C.P.; Figueroa, B.; Dagua-Paz, C.J.; Torres-Freyermuth, A.; Salles, P. Wave energy potential assessment in the Caribbean Low Level Jet using wave hindcast information. Appl. Energy 2015, 137, 375–384. [Google Scholar] [CrossRef]
- Henfridsson, U.; Neimane, V.; Strand, K.; Kapper, R.; Bernhoff, H.; Danielsson, O. Wave energy potential in the Baltic sea and the Danish part of the North Sea, with reflections on the skagerrak. Renew. Energy 2007, 32, 2069–2084. [Google Scholar] [CrossRef]
- Venugopal, V.; Nemalidinne, R. Wave resource assessment for Scottish waters using a large scale North Atlantic spectral wave model. Renew. Energy 2015, 76, 503–525. [Google Scholar] [CrossRef]
- Aydogan, B.; Ayat, B.; Yüksel, Y. Black Sea wave energy atlas from 13 years hindcasted wave data. Renew. Energy 2013, 57, 436–447. [Google Scholar] [CrossRef]
- Strauss, D.; Mirferendesk, H.; Tomlinson, R. Comparison of two wave models for Gold Coast, Australia. J. Coast. Res. 2007, 50, 312–316. [Google Scholar]
- Samaras, A.G. High-resolution wave and hydrodynamics modelling in coastal areas: Operational applications for coastal planning, decision support and assessment. Nat. Hazards Earth Syst. Sci. 2016, 16, 1499. [Google Scholar] [CrossRef]
- Fonseca, R.B.; Gonçalves, M.; Guedes Soares, C. Comparing the performance of spectral wave models for coastal areas. J. Coast. Res. 2017, 33, 331–346. [Google Scholar] [CrossRef]
- Samaras, A.G.; Vacchi, M.; Archetti, R.; Lamberti, A. Wave and hydrodynamics modelling in coastal areas with TELEMAC and MIKE21. In Proceedings of the XXth TELEMAC-MASCARET User Conference, Karlsruhe, Germany, 16–18 October 2013; pp. 59–64. [Google Scholar]
- Ilia, A.; O’Donnell, J. An Assessment of Two Models of Wave Propagation in an Estuary Protected by Breakwaters. J. Mar. Sci. Eng. 2018, 6, 145. [Google Scholar] [CrossRef]
- Holthuijsen, L.H.; Booij, N.; Herbers, T.H.C. A prediction model for stationary, short-crested waves in shallow water with ambient currents. Coast. Eng. 1989, 13, 23–54. [Google Scholar] [CrossRef]
- Ozer, J.; Padillahernandez, R.; Monbaliu, J.; Fanjul, E.A.; Albiach, J.C.C.; Osuna, P.; Yu, J.C.S.; Wolf, J. A coupling module for tides, surges and waves. Coast. Eng. 2000, 41, 95–124. [Google Scholar] [CrossRef]
- Battjes, J.A.; Janssen, J.P.F.M. Energy loss and set-up due to breaking of random waves. In Proceedings of the 16th International Conference on Coastal Engineering, Hamburg, Germany, 27 August–3 September 1978; pp. 569–587. [Google Scholar]
- Kofoed-Hansen, H.; Rasmussen, J.H. Modelling of nonlinear shoaling based on stochastic evolution equations. Coast. Eng. 1998, 33, 203–232. [Google Scholar] [CrossRef]
- Komen, G.J.; Cavaleri, L.; Donelan, M.; Hasselmann, K.; Hasselmann, S.; Janssen, P.A.E.M. Dynamics and Modelling of Ocean Waves; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Eldeberky, Y. Parameterization of triad interaction in wave energy model. In Proceedings of the International Conference on Coastal Dynamics, Gdansk, Poland, 4–8 September 1995. [Google Scholar]
- Eldeberky, Y.; Battjes, J.A. Spectral modeling of wave breaking: Application to Boussinesq equations. J. Geophys. Res. Ocean. 1996, 101, 1253–1264. [Google Scholar] [CrossRef]
- Hasselmann, S.; Hasselmann, K.; Allender, J.H.; Barnett, T.P. Computations and parameterizations of the nonlinear energy transfer in a gravity-wave specturm. Part II: Parameterizations of the nonlinear energy transfer for application in wave models. J. Phys. Oceanogr. 1985, 15, 1378–1391. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Holthuijsen, L.H.; Herman, A.; Booij, N. Phase-decoupled refraction–diffraction for spectral wave models. Coast. Eng. 2003, 49, 291–305. [Google Scholar] [CrossRef]
- Berkhoff, J.C.W. Computation of combined refraction—Diffraction. In Proceedings of the 13th International Conference on Coastal Engineering, Vancouver, BC, Canada, 10–14 July 1972; pp. 471–490. [Google Scholar]
- Porter, D. The mild-slope equations. J. Fluid Mech. 2003, 494, 51–63. [Google Scholar] [CrossRef]
- MIKE 21 SM Scientific Documentation. Available online: https://manuals.mikepoweredbydhi.help/2017/Coast_and_Sea/M21SW_Scientific_Doc.pdf (accessed on 22 June 2020).
- Group, T.W. The WAM model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar] [CrossRef]
- Gunther, H.; Hasselmann, S.; Janssen, P.A.E.M. The WAM Model Cycle 4; Report No. 4; Modellberatungsgruppe: Hamburg, Germany, 1992. [Google Scholar]
- Janssen, P.; Janssen, P.A. The Interaction of Ocean Waves and Wind; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Monbaliu, J.; Padilla-Hernandez, R.; Hargreaves, J.C.; Albiach, J.C.C.; Luo, W.; Sclavo, M.; Guenther, H. The spectral wave model, WAM, adapted for applications with high spatial resolution. Coast. Eng. 2000, 41, 41–62. [Google Scholar] [CrossRef]
- General Bathymetric Chart of the Oceans. Available online: http://www.gebco.net/ (accessed on 15 May 2020).
- Klein, R. Hydrodynamic Simulation with Mike 21 of Mele Bay and Port Vila, Vanuatu; Technical Report 263; SOPAC: Suva, Fiji, 1998. [Google Scholar]
- Vogelzang, J.; Stoffelen, A. Triple Collocation; KNMI: De Bilt, the Netherlands, 2012. [Google Scholar] [CrossRef]
- Chakraborty, A.; Kumar, R.; Stoffelen, A. Validation of ocean surface winds from the OCEANSAT-2 scatterometer using triple collocation. Remote Sens. Lett. 2013, 4, 84–93. [Google Scholar] [CrossRef]
- Gettelman, A.; Rood, R.B. Climate change and global warming. In Demystifying Climate Models; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Ezer, T.; Atkinson, L.P. Accelerated flooding along the US East Coast: On the impact of sea-level rise, tides, storms, the Gulf Stream, and the North Atlantic Oscillations. Earths Future. 2014, 2, 362–382. [Google Scholar] [CrossRef]
- Giglioli, S.; Colombo, L.; Vicinanza, D.; Contestabile, P.; Musco, L.; Somma, R.; Azzellino, A. Source apportionment assessment of marine sediment contamination in a post-industrial area (Bagnoli, Naples). Water 2020. Submitted. [Google Scholar]








| Point | Latitude | Longitude | Depth |
|---|---|---|---|
| E1 | 41.25 N | 12.75 E | 122 |
| E2 | 40.50 N | 12.75 E | 3601 |
| E3 | 40.50 N | 13.50 E | 1688 |
| E4 | 40.50 N | 14.25 E | 1017 |
| E5 | 39.75 N | 12.75 E | 3591 |
| E6 | 39.75 N | 13.50 E | 3072 |
| E7 | 39.75 N | 14.25 E | 2377 |
| E8 | 39.75 N | 15.00 E | 1755 |
| E9 | 39.00 N | 12.75 E | 3020 |
| E10 | 39.00 N | 13.50 E | 3179 |
| E11 | 39.00 N | 14.25 E | 3438 |
| E12 | 39.00 N | 15.00 E | 2781 |
| Ponza buoy | 40°52′0.10″ N | 12°57′0.00″ E | 100 |
| O | 40°29′45.06″ N | 13°47′46.70″ E | 1037 |
| W | 40°45′56.49″ N | 14° 7′41.22″ E | 100 |
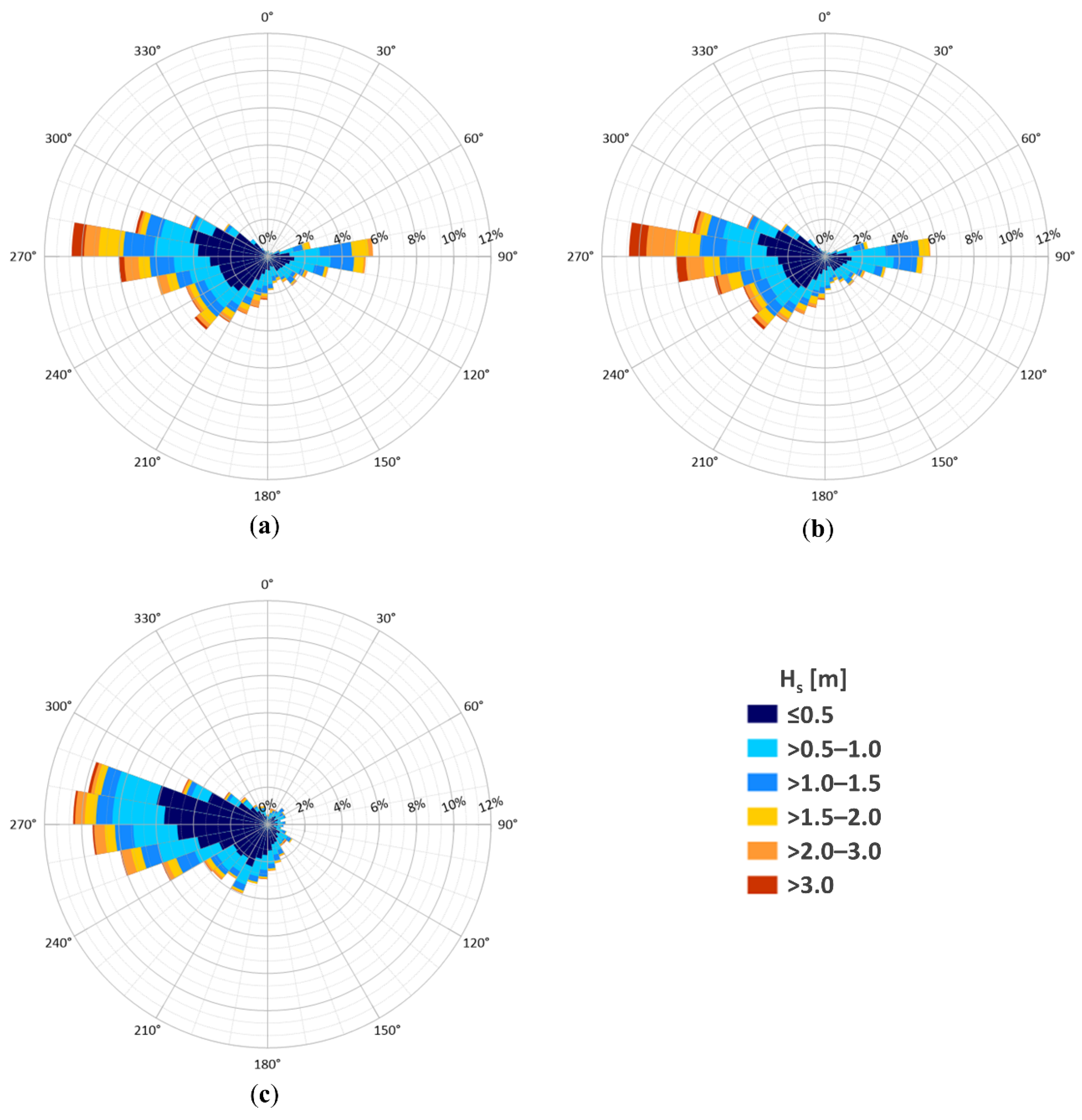
| Dataset | Hs,mean | Hs,max | σH | Tp, mean | Tp, mean | σT | θm | σθ | P,mean |
|---|---|---|---|---|---|---|---|---|---|
| (m) | (m) | (m) | (s) | (s) | (s) | (°) | (°) | (kW/m) | |
| Ponza buoy | 0.89 | 7.9 | 0.71 | 5.49 | 33.33 | 2.34 | 215.92 | 70.95 | 3.85 |
| Point O | 0.92 | 9.46 | 0.79 | 5.63 | 38.16 | 2.49 | 215.92 | 70.95 | 4.73 |
| E3 | 0.65 | 6.133 | 0.53 | 5.07 | 11.54 | 1.44 | 222.62 | 76.51 | 2.19 |
| Hs (m) | Hs,PONZA BUOY/Hs,ECMWF (m) | Hs,POINT O/Hs,ECMWF (m) |
|---|---|---|
| <0.5 | 1.04 | 1.06 |
| 0.5–0.75 | 1.75 | 1.77 |
| 0.75–1 | 1.47 | 1.50 |
| 1–2 | 1.41 | 1.43 |
| 2–3 | 1.35 | 1.37 |
| 3–4 | 1.21 | 1.36 |
| Mean | 1.37 | 1.42 |
| Point | Hs,mean (m) | Tm, mean (s) | θ, mean (°) | Pmean (kW/m) |
|---|---|---|---|---|
| E1 | 0.64 | 4.43 | 222.63 | 2.19 |
| E2 | 0.77 | 4.71 | 229.82 | 2.94 |
| E3 | 0.65 | 4.43 | 222.62 | 2.19 |
| E4 | 0.67 | 4.55 | 237.02 | 2.49 |
| E5 | 0.85 | 4.86 | 235.25 | 3.77 |
| E6 | 0.79 | 4.83 | 237.98 | 3.69 |
| E7 | 0.74 | 4.69 | 242.95 | 2.91 |
| E8 | 0.69 | 4.68 | 240.89 | 2.56 |
| E9 | 0.95 | 4.87 | 238.58 | 4.73 |
| E10 | 0.95 | 4.87 | 238.59 | 4.11 |
| E11 | 0.86 | 4.72 | 249.12 | 4.11 |
| E12 | 0.75 | 4.70 | 254.91 | 3.13 |
| Point | Latitude | Longitude | Depth |
|---|---|---|---|
| MEDA A | 40°49.668’ N | 14°13.984’ E | 19.0 |
| MEDA B | 40°48.550′ N | 14°09.300’ E | 17.5 |
| Time between Full Ensemble Records | (15 min) |
|---|---|
| Frequency | (600 kHz) |
| Size of the depth cell | (50 cm) |
| Number of bins in the current profile | (49 bins) |
| ADCP altitude above bottom | (50 cm) |
| Number of beams | (4 beams) |
| Frequency band width | (0.0078 Hz) |
| Maximum upper cutoff frequency | (0.5 Hz) |
| Sea-swell transition frequency | (0.11 Hz) |
| Minimum lower cutoff | (0.039 Hz) |
| Number of direction frequency bands | (128 bands) |
| Number of frequency bands | (128 bins) |
| Name of the Model | Wave Sector |
|---|---|
| M180° | From 0° N to 190° N |
| M220° | From 190° N to 220° N |
| M240° | From 220° N to 250° N |
| M260° | From 250° N to 270° N |
| M280° | From 270° N to 360° N |
| ECMWF | Ensemble | ADCP | |
|---|---|---|---|
| Hs | Hs | Hs | |
| (m) | (m) | (m) | |
| Mean | 0.62 | 0.38 | 0.39 |
| Median | 0.45 | 0.24 | 0.26 |
| Max | 3.95 | 2.96 | 3.27 |
| Min | 0.07 | 0.00 | 0.00 |
| Standard deviation | 0.5 | 0.41 | 0.38 |
| Tp | Tp | Tp | |
| (s) | (s) | (s) | |
| Mean | 5.14 | 4.54 | 5.47 |
| Median | 4.94 | 4.55 | 5.4 |
| Max | 10.33 | 10.16 | 28.1 |
| Min | 1.96 | 0.23 | 0.00 |
| Standard deviation | 1.71 | 2.61 | 2.27 |
| θ | θ | θ | |
| (°) | (°) | (°) | |
| Mean | 234.39 | 201.7 | 198.65 |
| Median | 262.39 | 202.21 | 203.00 |
| Max | 359.98 | 359.02 | 359.00 |
| Min | 0.03 | 0.00 | 0.00 |
| Standard deviation | 77.07 | 35.99 | 35.72 |
| P | P | P | |
| (kW/m) | (kW/m) | (kW/m) | |
| Mean | 1.73 | 0.93 | 0.96 |
| Median | 0.4 | 0.09 | 0.13 |
| Max | 67.88 | 33.95 | 43.19 |
| Min | 0 | 0 | 0 |
| Standard deviation | 4.18 | 2.70 | 2.80 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Contestabile, P.; Conversano, F.; Centurioni, L.; Golia, U.M.; Musco, L.; Danovaro, R.; Vicinanza, D. Multi-Collocation-Based Estimation of Wave Climate in a Non-Tidal Bay: The Case Study of Bagnoli-Coroglio Bay (Tyrrhenian Sea). Water 2020, 12, 1936. https://doi.org/10.3390/w12071936
Contestabile P, Conversano F, Centurioni L, Golia UM, Musco L, Danovaro R, Vicinanza D. Multi-Collocation-Based Estimation of Wave Climate in a Non-Tidal Bay: The Case Study of Bagnoli-Coroglio Bay (Tyrrhenian Sea). Water. 2020; 12(7):1936. https://doi.org/10.3390/w12071936
Chicago/Turabian StyleContestabile, Pasquale, Fabio Conversano, Luca Centurioni, Umberto Mario Golia, Luigi Musco, Roberto Danovaro, and Diego Vicinanza. 2020. "Multi-Collocation-Based Estimation of Wave Climate in a Non-Tidal Bay: The Case Study of Bagnoli-Coroglio Bay (Tyrrhenian Sea)" Water 12, no. 7: 1936. https://doi.org/10.3390/w12071936
APA StyleContestabile, P., Conversano, F., Centurioni, L., Golia, U. M., Musco, L., Danovaro, R., & Vicinanza, D. (2020). Multi-Collocation-Based Estimation of Wave Climate in a Non-Tidal Bay: The Case Study of Bagnoli-Coroglio Bay (Tyrrhenian Sea). Water, 12(7), 1936. https://doi.org/10.3390/w12071936








