Effect of Logarithmically Transformed IMERG Precipitation Observations in WRF 4D-Var Data Assimilation System
Abstract
1. Introduction
2. Materials and Methods
2.1. The 4D-Var Method
2.1.1. Cost Function with Nontransformed Observations
2.1.2. Cost Function with Logarithmically Transformed Observations
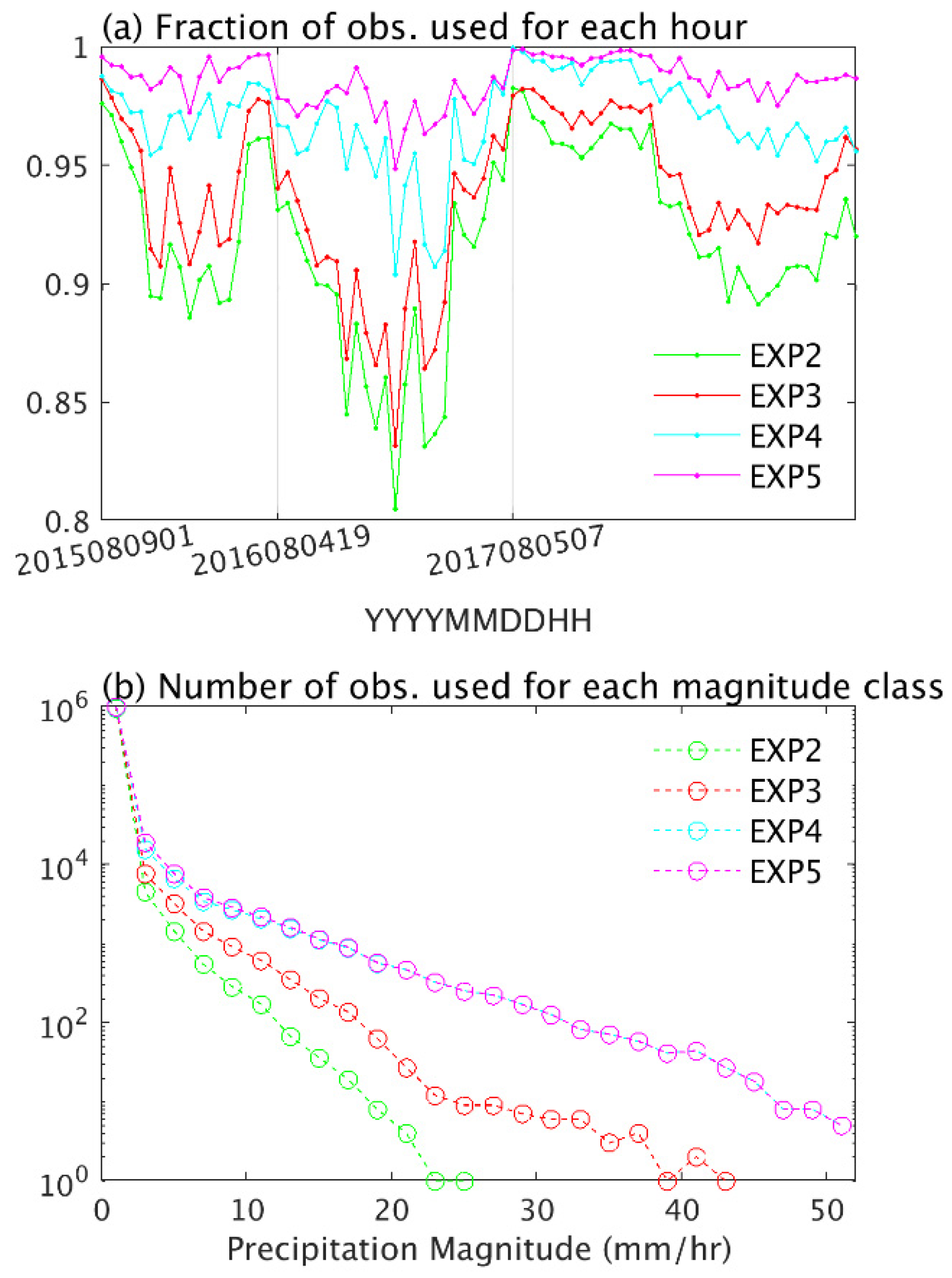
2.2. Precipitation Observations
2.3. Model Configurations
2.4. Experiments Design and Evaluation Metrics
3. Results
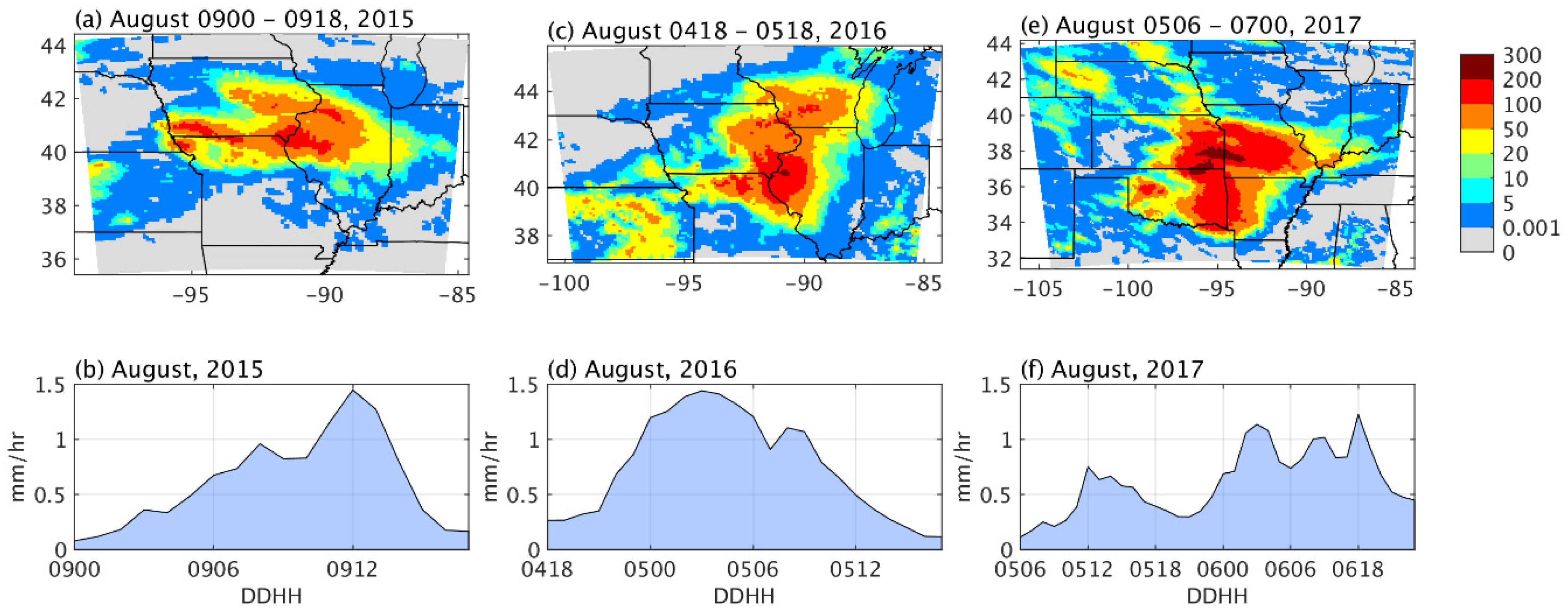
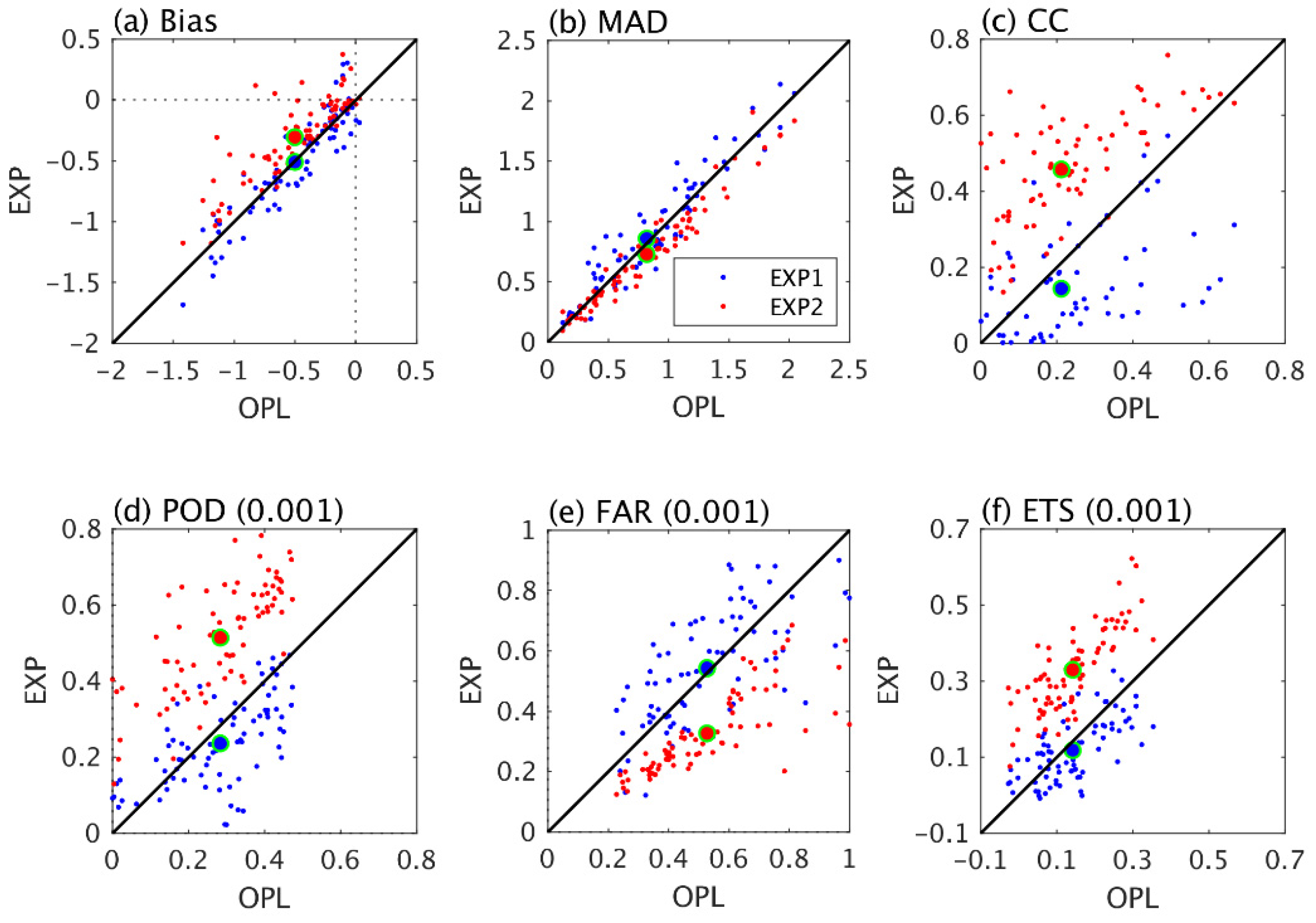
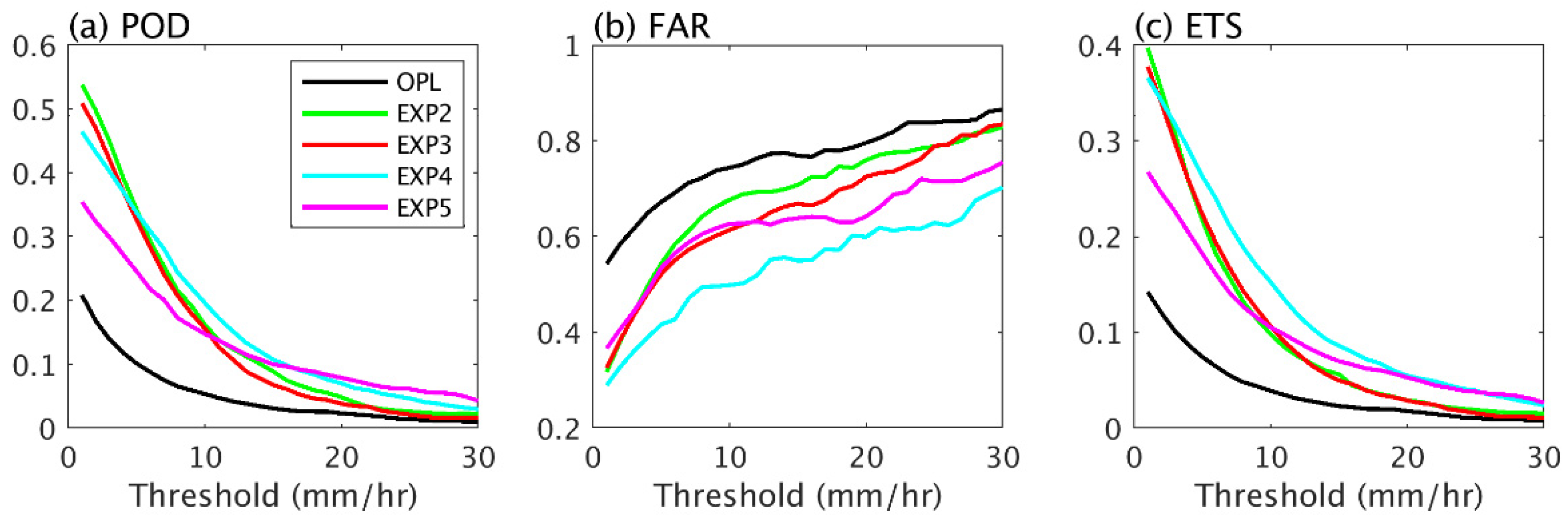
3.1. Evaluation of Precipitation Estimates from Six-Hour-Window and Hourly-Window Experiments
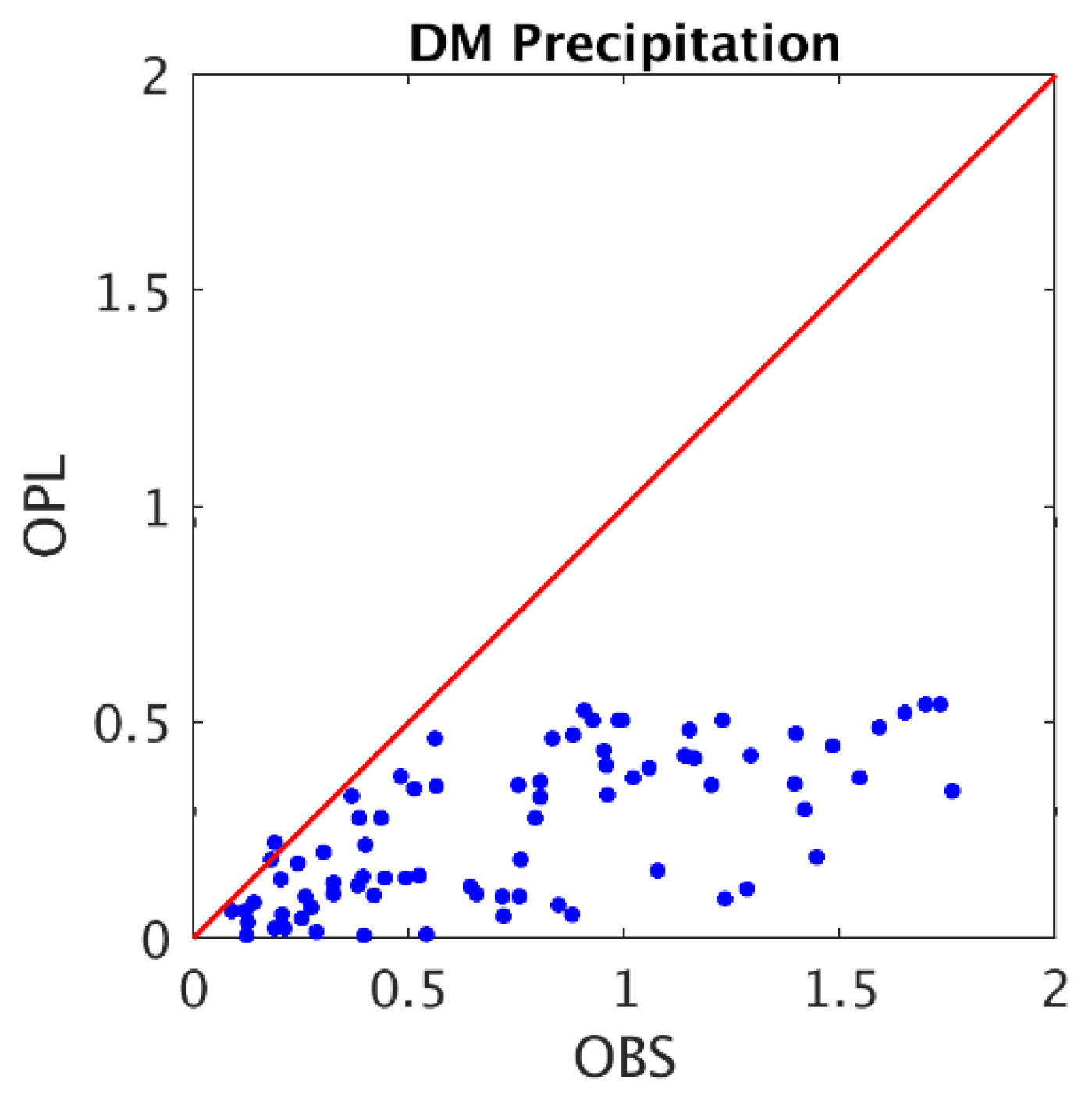
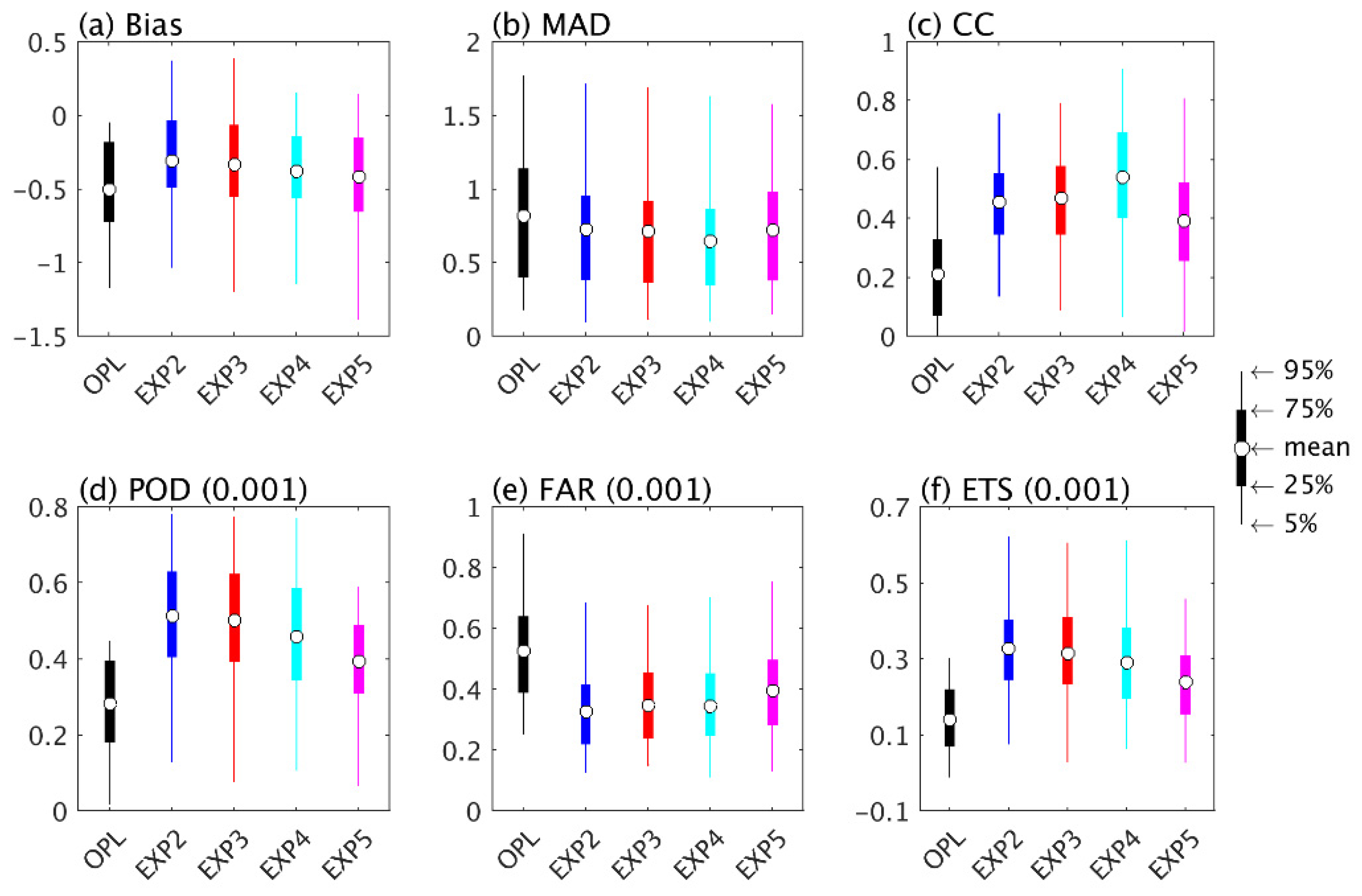
3.2. Evaluation of Precipitation Estimates from Nontransformed and Logarithmically Transformed Experiments
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Vidale, P.L.; Luthi, D.; Frei, C.; Seneviratne, S.I.; Schar, C. Predictability and uncertainty in a regional climate model. J. Geophys. Res. 2003, 108, 4586. [Google Scholar] [CrossRef]
- Roberts, N.M. Assessing the spatial and temporal variation in the skill of precipitation forecasts from an NWP model. Meteorol. Appl. 2008, 15, 163–169. [Google Scholar] [CrossRef]
- Slingo, J.; Palmer, T. Uncertainty in weather and climate prediction. Philos. Trans. R. Soc. A 2011, 369, 4751–4767. [Google Scholar] [CrossRef]
- Robinson, A.R.; Lermusiaux, P.F.J. Data assimilation in models. In Encyclopedia of Ocean Sciences; Academic Press: Cambridge, MA, USA, 2001; pp. 623–634. [Google Scholar]
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: New York, NY, USA, 2003; p. 369. [Google Scholar] [CrossRef]
- Zupanski, D.; Mesinger, F. Four-dimensional variational assimilation of precipitation data. Mon. Weather Rev. 1995, 123, 1112–1127. [Google Scholar] [CrossRef]
- Tsuyuki, T. Variational data assimilation in the tropics using precipitation data. Part III: Assimilation of SSM/I precipitation rates. Mon. Weather Rev. 1997, 125, 1447–1464. [Google Scholar] [CrossRef]
- Koizumi, K.; Ishikawa, Y.; Tsuyuki, T. Assimilation of precipitation data to the JMA mesoscale model with a four-dimensional variational method and its impact on precipitation forecasts. SOLA 2005, 1, 45–48. [Google Scholar] [CrossRef]
- Lopez, P. Direct 4D-Var assimilation of NCEP Stage IV radar and gauge precipitation data at ECMWF. Mon. Weather Rev. 2011, 139, 2098–2116. [Google Scholar] [CrossRef]
- Lin, L.-F.; Ebtehaj, A.M.; Bras, R.L.; Flores, A.N.; Wang, J. Dynamical precipitation downscaling for hydrologic applications using WRF 4D-Var data assimilation: Implications for GPM era. J. Hydrometeorol. 2015, 16, 811–829. [Google Scholar] [CrossRef]
- Lin, L.-F.; Ebtehaj, A.M.; Flores, A.N.; Bastola, S.; Bras, R.L. Combined assimilation of satellite precipitation and soil moisture: A case study using TRMM and SMOS data. Mon. Weather Rev. 2017, 145, 4997–5014. [Google Scholar] [CrossRef]
- Ban, J.; Liu, Z.; Zhang, X.; Huang, X.-Y.; Wang, H. Precipitation data assimilation in WRFDA 4D-Var: Implementation and application to convection permitting forecasts over United States. Tellus A Dyn. Meteorol. Oceanogrol. 2017, 69, 1368310. [Google Scholar] [CrossRef]
- Yi, L.; Zhang, W.; Wang, K. Evaluation of heavy precipitation simulated by the WRF model using 4D-Var data assimilation with TRMM 3B42 and GPM IMERG over the Huaihe River basin, China. Remote Sens. 2018, 10, 646. [Google Scholar] [CrossRef]
- Gebremichael, M.; Krajewski, W.F. Modeling distribution of temporal sampling errors in area–time-averaged rainfall estimates. Atmos. Res. 2005, 73, 243–259. [Google Scholar] [CrossRef]
- Lien, G.-Y.; Kalnay, E.; Miyoshi, T.; Huffman, G.J. Statistical properties of global precipitation in the NCEP GFS model and TMPA observations for data assimilation. Mon. Weather Rev. 2016, 144, 663–679. [Google Scholar] [CrossRef]
- Lien, G.-Y.; Miyoshi, T.; Kalney, E. Assimilation of TRMM multisatellite precipitation analysis with a low-resolution NCEP Global Forecast System. Mon. Weather Rev. 2016, 144, 643–662. [Google Scholar] [CrossRef]
- Kneifel, S.; Löhnert, U.; Battaglia, A.; Crewell, S.; Siebler, D. Snow scattering signals in ground-based passive microwave radiometer measurements. J. Geophys. Res. Atmos. 2010, 115, D16214. [Google Scholar] [CrossRef]
- Levizzani, V.; Laviola, S.; Cattani, E. Detection and measurement of snowfall from space. Remote Sens. 2011, 3, 145–166. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Liu, Z.; Ostrenga, D.; Vollmer, B.; Deshong, B.; Macritchie, K.; Greene, M.; Kempler, S. Global Precipitation Measurement mission products and services at the NASA GES DISC. Bull. Am. Meteorol. Soc. 2017, 98, 437–444. [Google Scholar] [CrossRef]
- Tan, J.; Petersen, W.A.; Tokay, A. A novel approach to identify sources of errors in IMERG for GPM ground validation. J. Hydrometeorol. 2016, 17, 2477–2491. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA version-7 legacy over mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and hydrological comparisons between TRMM and GPM Level-3 products over a midlatitude basin: Is Day-1 IMERG a good successor for TMPA 3B42V7? J. Hydrometeorol. 2016, 17, 121–137. [Google Scholar] [CrossRef]
- O, S.; Foelsche, U.; Kirchengast, G.; Fuchsberger, J.; Tan, J.; Petersen, W.A. Evaluation of GPM IMERG early, late, and final rainfall estimates with WegenerNet gauge data in southeast Austria. Hydrol. Earth Syst. Sci. Discuss. 2017, 21, 6559–6572. [Google Scholar] [CrossRef]
- Huang, X.-Y.; Xiao, Q.; Barker, D.M.; Zhang, X.; Michalakes, J.; Huang, W.; Henderson, T.; Bray, J.; Chen, Y.; Ma, Z.; et al. Four-dimensional variational data assimilation for WRF: Formulation and preliminary results. Mon. Weather Rev. 2009, 137, 299–314. [Google Scholar] [CrossRef]
- Courtier, P.; Thepaut, J.-N.; Hollingsworth, A. A strategy for operational implementation of 4D-Var, using an incremental approach. Q. J. R. Meteorol. Soc. 1994, 120, 1367–1387. [Google Scholar] [CrossRef]
- Errico, R.M.; Fillion, L.; Nychka, D.; Lu, Z.Q. Some statistical considerations associated with the data assimilation of precipitation observations. Q. J. R. Meteorol. Soc. 2000, 126, 339–359. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Xie, S. NASA Global Precipitation Measurement (GPM) Integrated Multi-Satellite Retrievals for GPM (IMERG). Algorithm Theoretical Basis Document (ATBD). Version 4.5; 2015; 30p. Available online: https://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V4.5.pdf (accessed on 31 March 2017).
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J.; et al. Integrated Multi-satellitE Retrievals for the Global Precipitation Measurement (GPM) mission (IMERG). Adv. Glob. Chang. Res. 2020, 67, 343–353. [Google Scholar]
- Lee, M.-I.; Choi, I.; Tao, W.-K.; Schubert, S.D.; Kang, I.-S. Mechanisms of diurnal precipitation over the US Great Plains: A cloud resolving model perspective. Clim. Dyn. 2009, 34, 419–437. [Google Scholar] [CrossRef]
- NCAR. Convection-Permitting Physics Suite for WRF. Available online: https://www2.mmm.ucar.edu/wrf/users/ncar_convection_suite.php (accessed on 13 June 2020).
- Hong, S.-Y.; Dudhia, J.; Chen, S.-H. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long–lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Tewari, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.A.; Mitchell, K.; Ek, M.; Gayno, G.; Wegiel, J.; Cuenca, R.H. Implementation and verification of the unified NOAH land surface model in the WRF model. In Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction, Seattle, WA, USA, 10–15 January 2004; American Meteorological Society: Boston, MA, USA, 2004; pp. 11–15. Available online: https://ams.confex.com/ams/84Annual/techprogram/paper_69061.htm (accessed on 12 June 2017).
- Monin, A.S.; Obukhov, A.M. Basic laws of turbulent mixing in the surface layer of the atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 1954, 151, 163–187. (In Russian) [Google Scholar]
- Janjic, Z.I. The step-mountain Eta coordinate model: Further developments of the convection, viscous sublayer and turbulence closure schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Janjic, Z.I. The surface layer in the NCEP Eta Model. In Proceedings of the Eleventh Conference on Numerical Weather Prediction, Norfolk, VA, USA, 19–23 August 1996; American Meteorological Society: Boston, MA, USA, 1996; pp. 354–355. Available online: https://www2.mmm.ucar.edu/wrf/users/phys_refs/SURFACE_LAYER/eta_part3.pdf (accessed on 12 June 2017).
- Janjic, Z.I. Nonsingular Implementation of the Mellor-Yamada Level 2.5 Scheme in the NCEP Meso Model; NCEP Office Note No. 437; NCEP: College Park, MD, USA, 2002; p. 61. Available online: https://repository.library.noaa.gov/view/noaa/11409/noaa_11409_DS1.pdf (accessed on 12 June 2017).
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- National Centers for Environmental Prediction/National Weather Service/NOAA/U.S. Department of Commerce: NCEP GDAS/FNL 0.25 Degree Global Tropospheric Analyses and Forecast Grids. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. 2015. Available online: https://doi.org/10.5065/D65Q4T4Z (accessed on 21 June 2017).
- Sun, J.; Xue, M.; Wilson, J.W.; Zawadzki, I.; Ballard, S.P.; Onvlee-Hooimeyer, J.; Joe, P.; Barker, D.M.; Li, P.-W.; Golding, B.; et al. Use of NWP for nowcasting convective precipitation: Recent progress and challenges. Bull. Am. Meteorol. Soc. 2014, 95, 409–426. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, L.-F.; Bras, R.L. Evaluation of the quality of precipitation products: A case study using WRF and IMERG data over the central United States. J. Hydrometeorol. 2018, 19, 2007–2020. [Google Scholar] [CrossRef]

| Experiment Name | Assimilation Window | Transformation of Precipitation | Errors in Regular Space (mm/h) | Errors in Log Space (mm/h) |
|---|---|---|---|---|
| EXP1 | 6-hour | No transformation | 2 (mm/6 h) | -- |
| EXP2 | Hourly | No transformation | 0.3 | 0.3/(yi + 1) |
| EXP3 | Hourly | Log transformation | 0.3 | 0.3/(yi + 1) |
| EXP4 | Hourly | No transformation | 0.3 × (yi + 1) | 0.3 |
| EXP5 | Hourly | Log transformation | 0.3 × (yi + 1) | 0.3 |
| Statistical Metrics | Equation | Perfect Value |
|---|---|---|
| Bias | Bias = Xe − Xr | 0 |
| Mean Absolute Difference (MAD) | MAD = |Xe − Xr| | 0 |
| Correlation Coefficient (CC) | CC = cov(Xe, Xr)/ (std(Xe)∙std(Xr)) | 1 |
| Probability of Detection (POD) | POD = a/(a + c) | 1 |
| False Alarm Ratio (FAR) | FAR = b/(a + b) | 0 |
| Equitable Threat Score (ETS) | ETS = (a − e)/(a + b + c − e), where e = (a + b)(a + c)/(a + b + c + d) | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Lin, L.-F.; Bras, R.L. Effect of Logarithmically Transformed IMERG Precipitation Observations in WRF 4D-Var Data Assimilation System. Water 2020, 12, 1918. https://doi.org/10.3390/w12071918
Zhang J, Lin L-F, Bras RL. Effect of Logarithmically Transformed IMERG Precipitation Observations in WRF 4D-Var Data Assimilation System. Water. 2020; 12(7):1918. https://doi.org/10.3390/w12071918
Chicago/Turabian StyleZhang, Jiaying, Liao-Fan Lin, and Rafael L. Bras. 2020. "Effect of Logarithmically Transformed IMERG Precipitation Observations in WRF 4D-Var Data Assimilation System" Water 12, no. 7: 1918. https://doi.org/10.3390/w12071918
APA StyleZhang, J., Lin, L.-F., & Bras, R. L. (2020). Effect of Logarithmically Transformed IMERG Precipitation Observations in WRF 4D-Var Data Assimilation System. Water, 12(7), 1918. https://doi.org/10.3390/w12071918






