Multi-Objective Model Predictive Control for Real-Time Operation of a Multi-Reservoir System
Abstract
1. Introduction
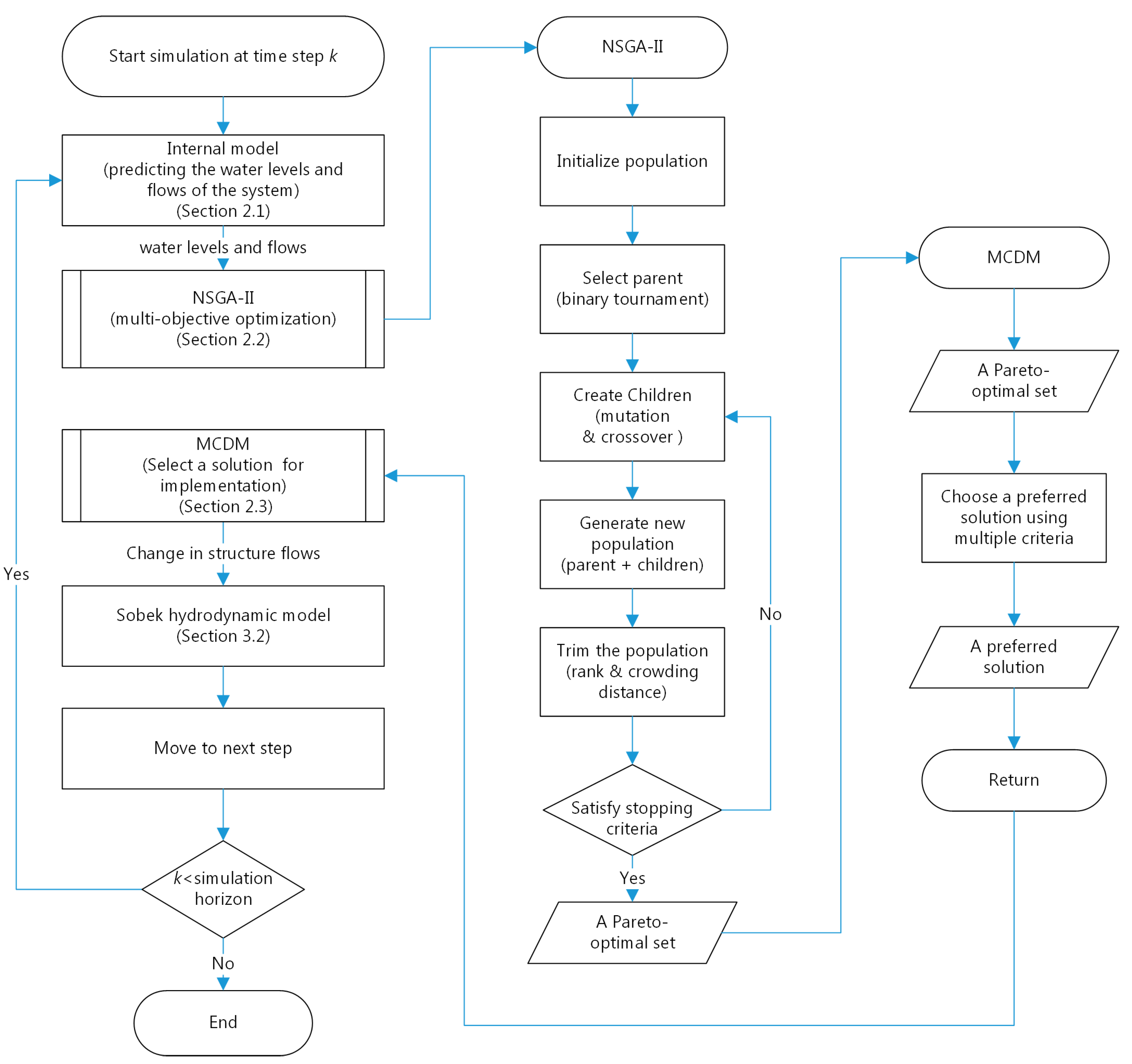
2. Methodology
2.1. Internal Model or Reservoir System Model
2.2. Multi-Objective Optimization
2.2.1. Multi-Objective Optimization in the Classical MPC
2.2.2. Multi-Objective Optimization in MOMPC
2.3. Multi-Criteria Decision Making
2.3.1. Weighted-Sum Method
2.3.2. Maximin Method
2.3.3. Maxisum Method
2.4. Performances of the System under Alternative Operating Rules
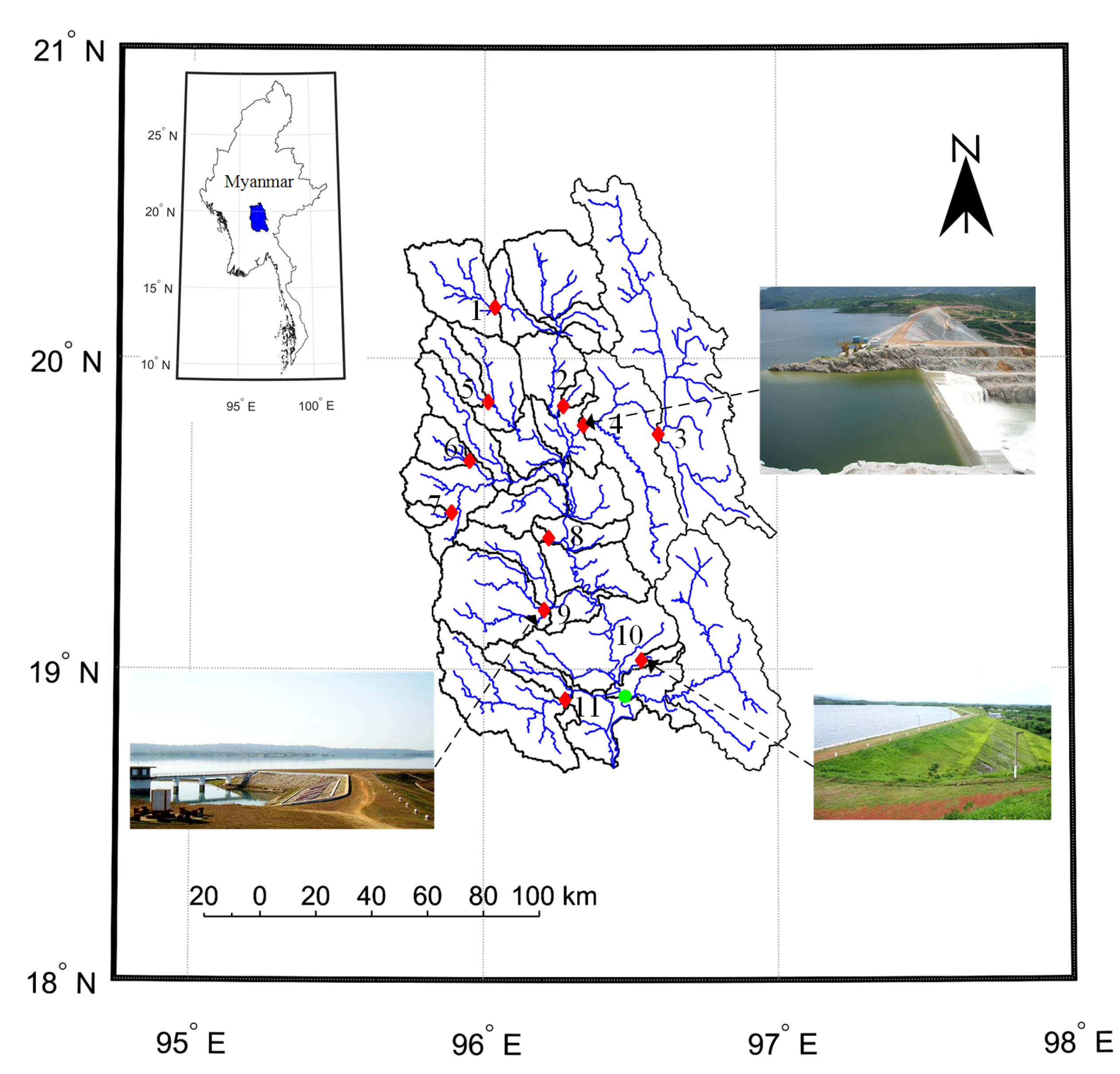
3. Case Study: A Multi-Reservoir System in the Sittaung River Basin
3.1. Control Objectives
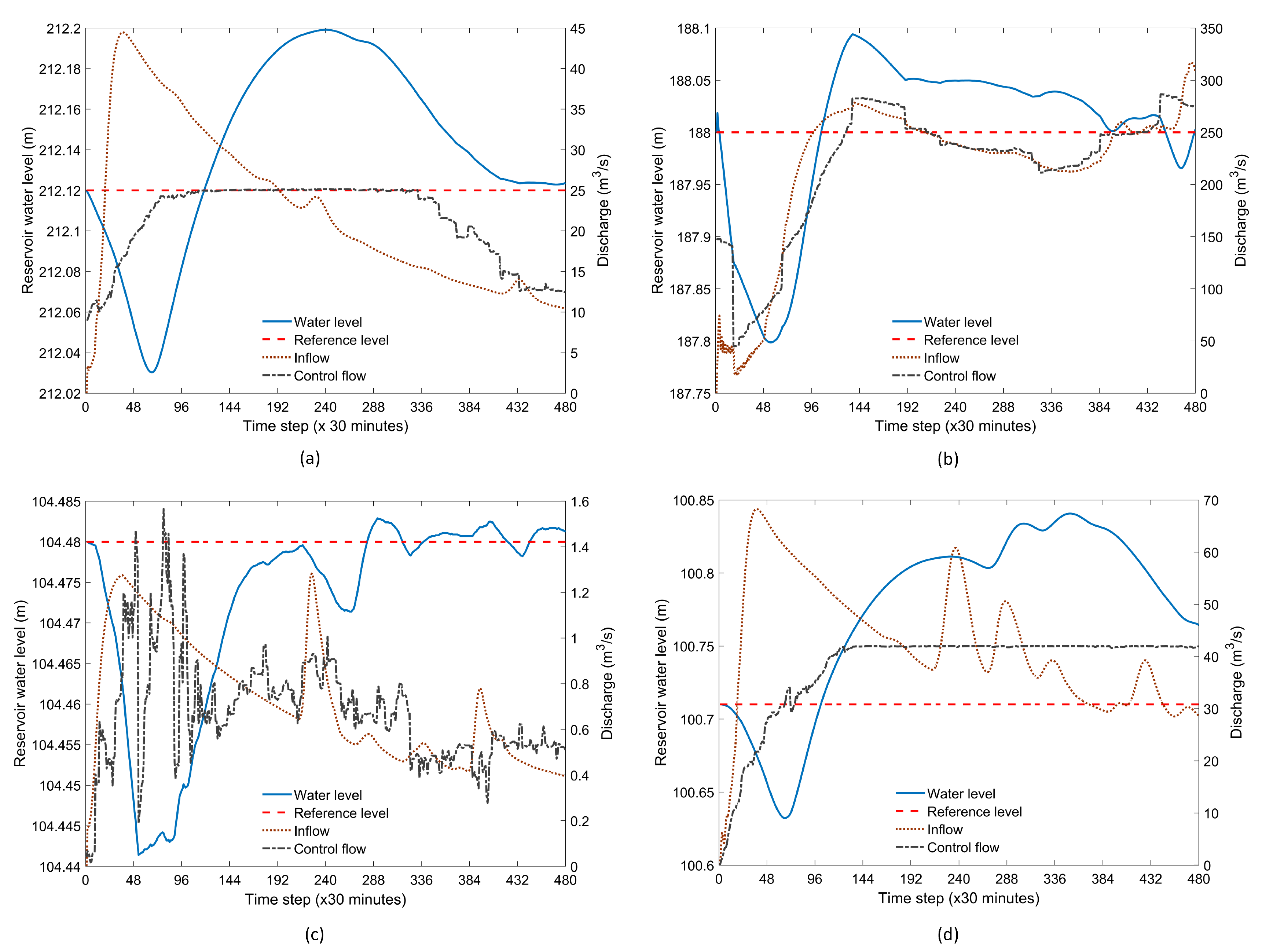
- The first objective () is to maintain the target water levels of reservoirs (or desired storage volume) for irrigation and hydropower generation in the dry season. Therefore, the deviations of reservoirs water level from its reference level are minimized by:where = water level at reservoir i (m), = reference water level of reservoir i (m), = controlled outflow at reservoir i (), = change of control flow at reservoir i (), = relative penalty on water level deviation for reservoir i, = relative penalty on the change of conduit flow at reservoir i, and = number of reservoirs (11 Nos.). The maximum allowed value estimate (MAVE) [29] was used to define the penalties on the change of water level and the conduit outflow. In this study, maximum allowed water level relative to reference level and maximum allowed discharge relative to the conduit capacity were used as MAVE of that variable. The penalties were defined to the reciprocal of the square of the MAVE of that variable.
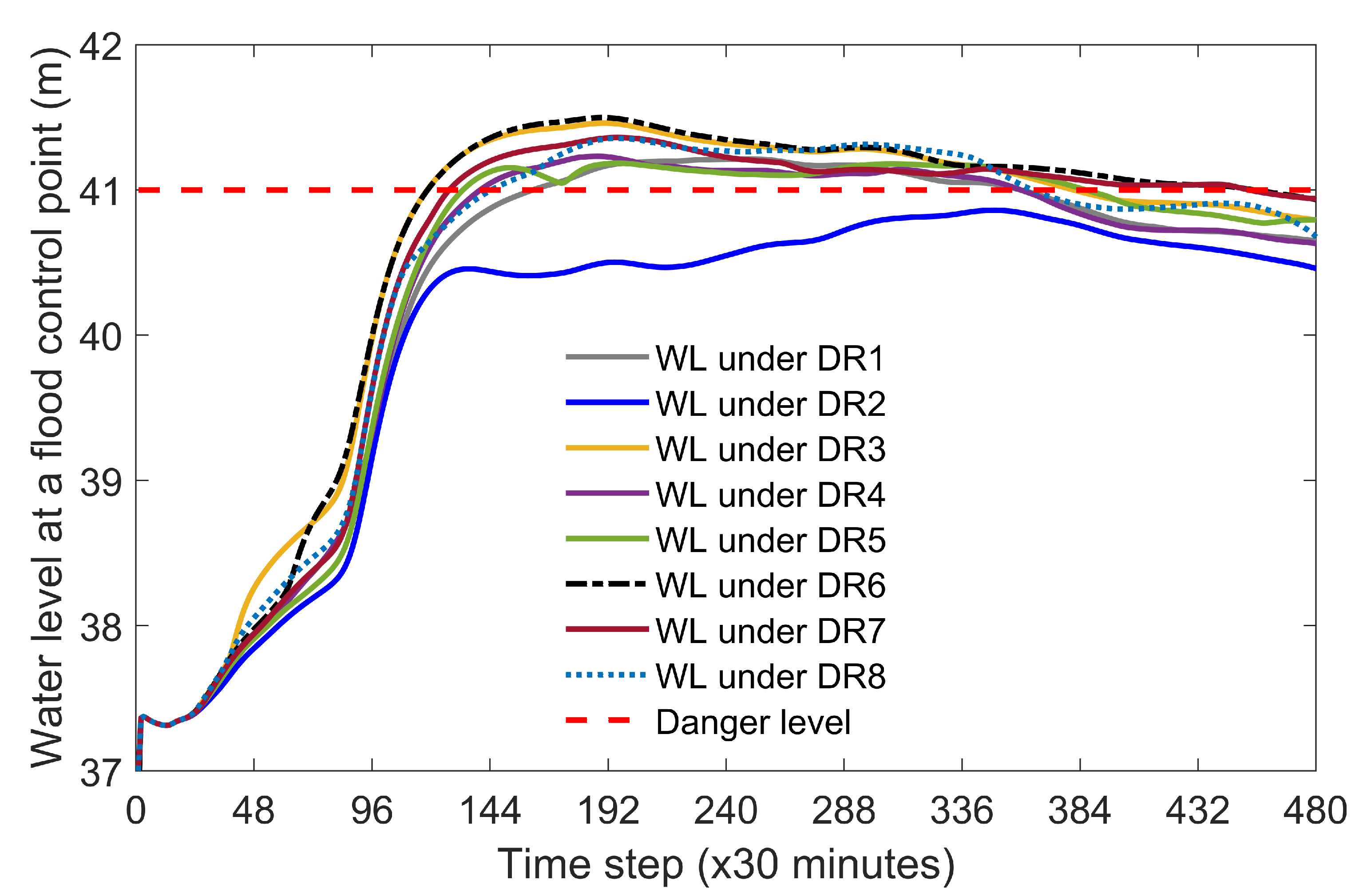
- The second objective () is to reduce the flood risk at the Taungoo city. A soft constraint [29] is implemented to minimize the water level deviations above the safety water level at a flood control station, which is defined as:where = water level at river reach p (m), = soft constraint [29] on water level at river reach p (m) and = safety water level at river reach p (m).
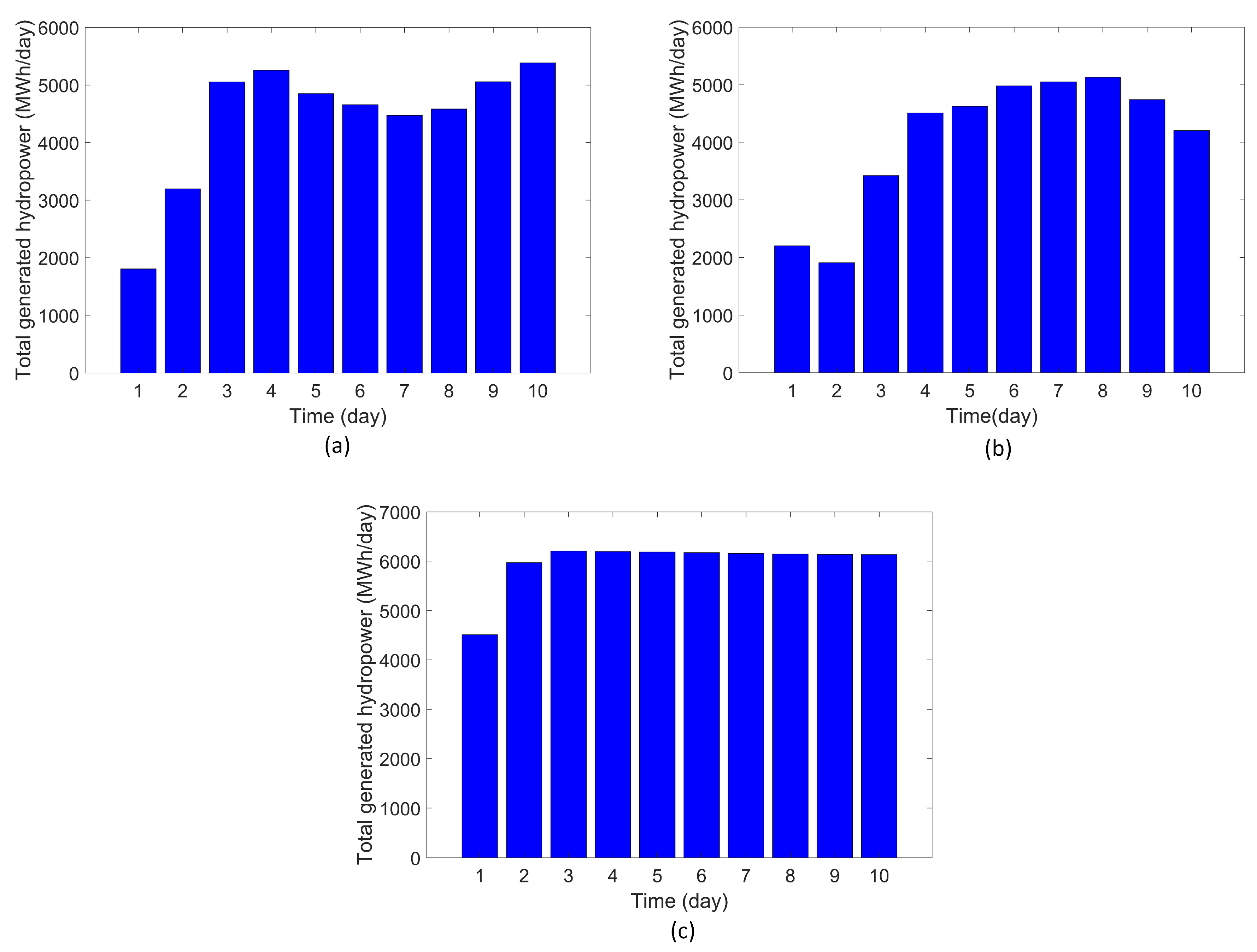
- The last objective () is to maximize electric energy production at the three reservoirs which is defined as [65]:where = tail water level at outlet structure i (m), = turbine efficiency ranging from 0 to 1 (0.6), g = acceleration due to gravity (9.81 ), = density of water (1000 ), and = 3.
3.2. Model Description
3.3. Simulation Settings
4. Results
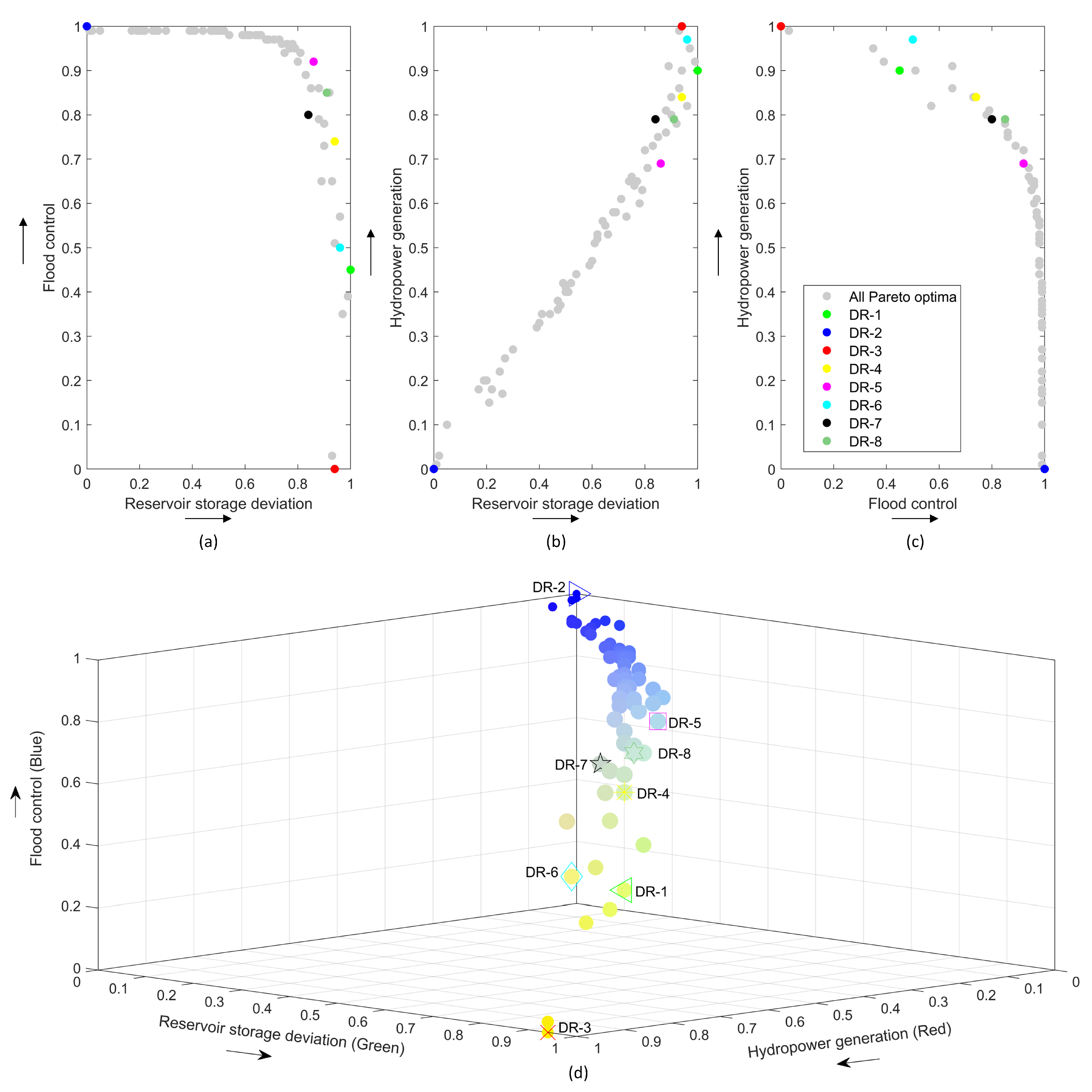
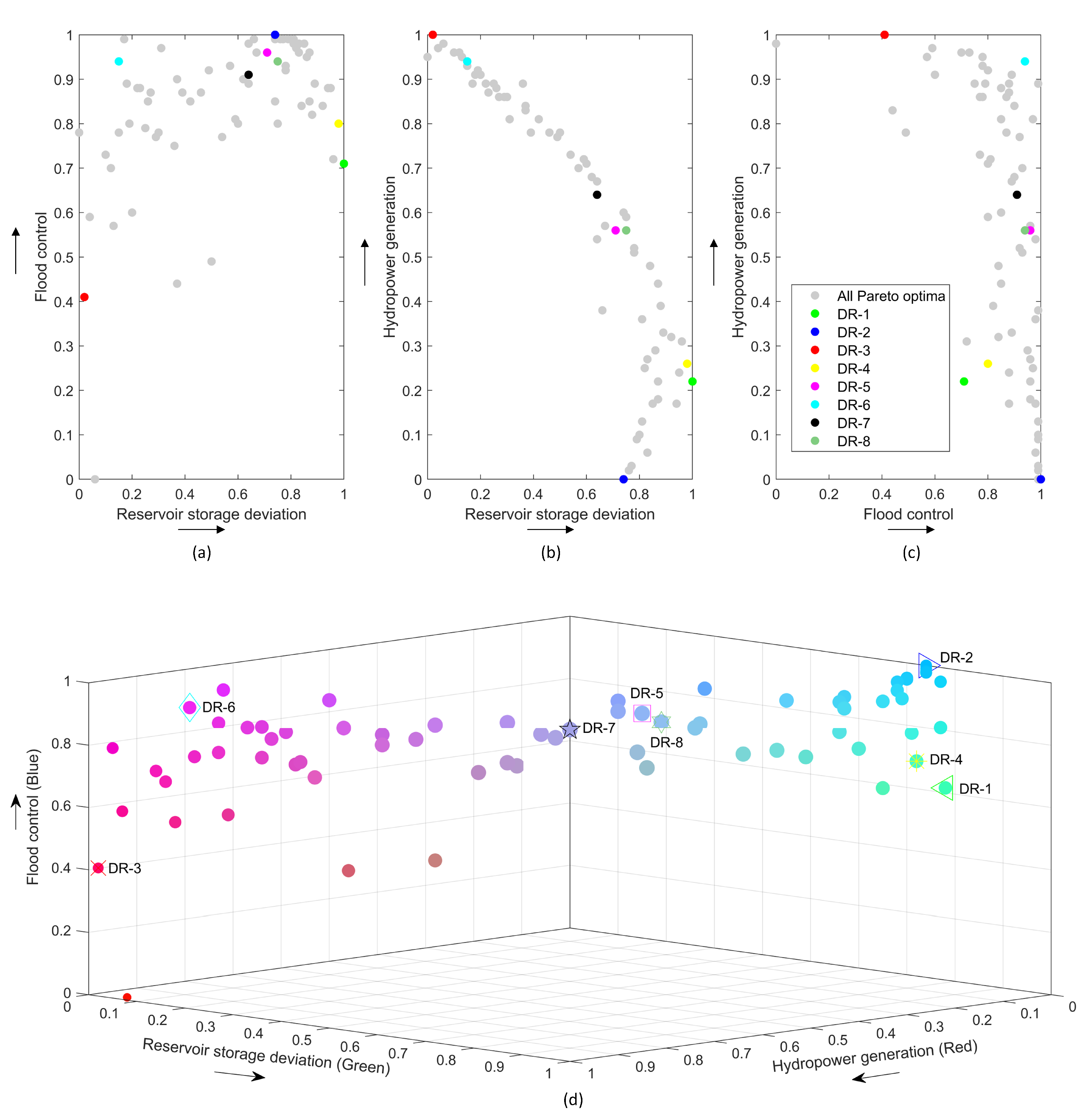
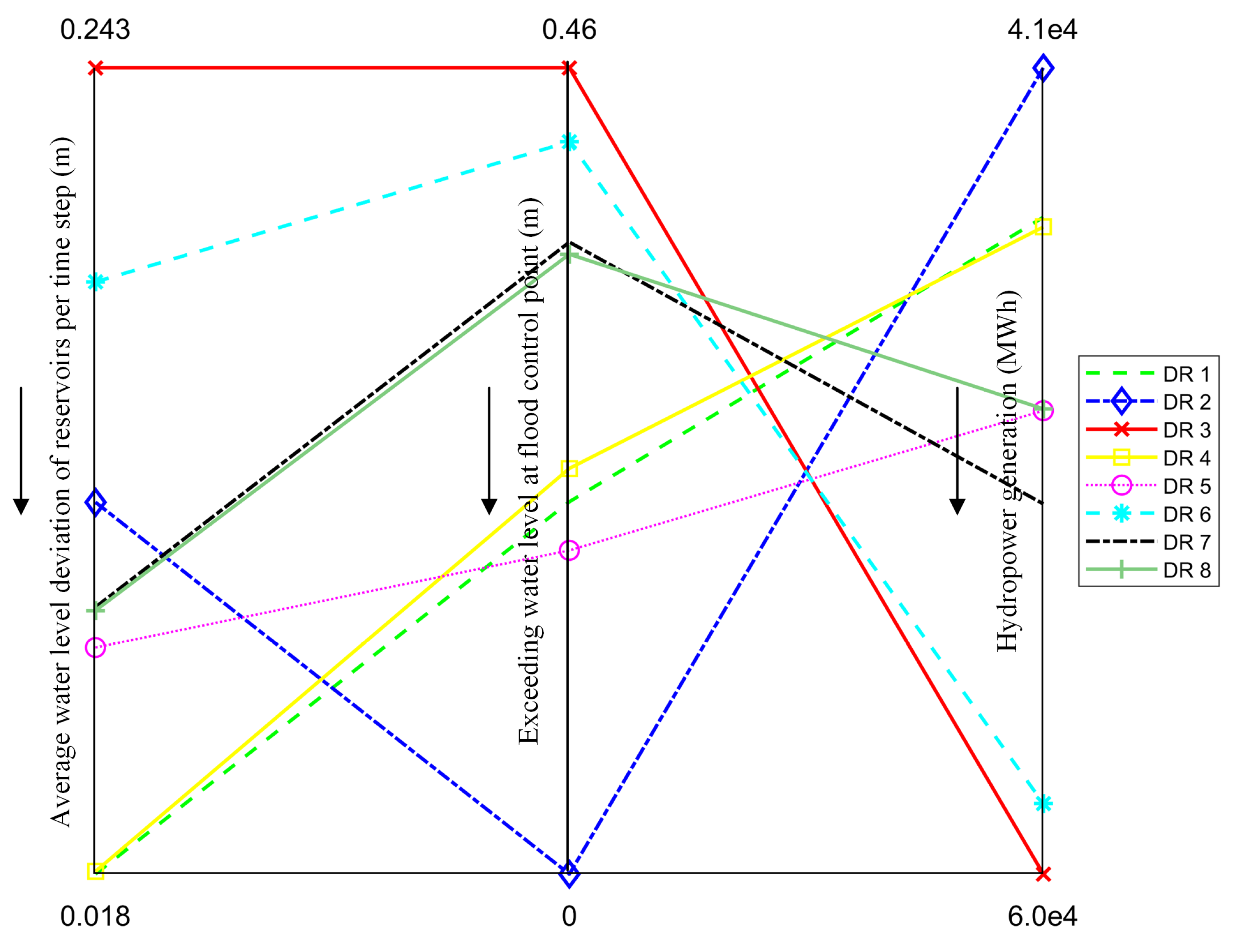
4.1. Pareto Fronts and Trade-Offs
4.2. Performance of the System
4.3. Overall Performance
4.4. Comparison of Results
5. Discussion
5.1. The Use of GA in MPC Formulation
5.2. Selection of a Decision-Making Method
5.3. Limitations of the Method
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lehner, B.; Liermann, C.R.; Revenga, C.; Vörösmarty, C.; Fekete, B.; Crouzet, P.; Döll, P.; Endejan, M.; Frenken, K.; Magome, J.; et al. High-resolution mapping of the world’s reservoirs and dams for sustainable river-flow management. Front. Ecol. Environ. 2011, 9, 494–502. [Google Scholar] [CrossRef]
- World Commission on Large Dams. Dams and Development; Technical Report November; World Commission on Large Dams: London, UK, 2000. [Google Scholar]
- Castelletti, A.; Yajima, H.; Giuliani, M.; Soncini-Sessa, R.; Weber, E. Planning the Optimal Operation of a Multioutlet Water Reservoir with Water Quality and Quantity Targets. J. Water Resour. Plan. Manag. 2014, 140, 496–510. [Google Scholar] [CrossRef]
- Ehsani, N.; Vörösmarty, C.J.; Fekete, B.M.; Stakhiv, E.Z. Reservoir operations under climate change: Storage capacity options to mitigate risk. J. Hydrol. 2017, 555, 435–446. [Google Scholar] [CrossRef]
- Oliveira, R.; Loucks, D.P. Operating rules for multireservoir systems. Water Resour. Res. 1997, 33, 839–852. [Google Scholar] [CrossRef]
- Lund, J.R.; Ferreira, I. Operating Rule Optimization for Missouri River Reservoir System. J. Water Resour. Plan. Manag. 1996, 122, 287–295. [Google Scholar] [CrossRef]
- Tian, X.; van Overloop, P.J.; Negenborn, R.R.; van de Giesen, N. Operational flood control of a low-lying delta system using large time step Model Predictive Control. Adv. Water Resour. 2015, 75, 1–13. [Google Scholar] [CrossRef]
- Myo Lin, N.; Rutten, M.; Tian, X. Flood Mitigation through Optimal Operation of a Multi-Reservoir System by Using Model Predictive Control: A Case Study in Myanmar. Water 2018, 10, 1371. [Google Scholar] [CrossRef]
- Becker, L.; Yeh, W.W.G. Optimization of Real Time Operation of a Multiple-Reservoir System. Water Resour. Res. 1974, I, 1107–1112. [Google Scholar] [CrossRef]
- Needham, J.T.; Watkins, D.W., Jr.; Lund, J.R.; Nanda, S.K. Linear Programming for Flood Control in the Iowa and Des Moines Rivers. J. Water Resour. Plan. Manag. 2000, 126, 118–127. [Google Scholar] [CrossRef]
- Wei, C.C.; Hsu, N.S. Multireservoir real-time operations for flood control using balanced water level index method. J. Environ. Manag. 2008, 88, 1624–1639. [Google Scholar] [CrossRef]
- Li, X.; Wei, J.; Li, T.; Wang, G.; Yeh, W.W.G. A parallel dynamic programming algorithm for multi-reservoir system optimization. Adv. Water Resour. 2014, 67, 1–15. [Google Scholar] [CrossRef]
- Yeh, W.W.G. Reservoir Management and Operations Models: A State-of-the-Art Review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Castelletti, A.; Pianosi, F.; Soncini-Sessa, R. Water reservoir control under economic, social and environmental constraints. Automatica 2008, 44, 1595–1607. [Google Scholar] [CrossRef]
- Wasimi, A.A.; Kitanidis, P.K. Real-Time Forecasting and Daily Operation of a Multireservoir System During Floods by Linear Quadratic Gaussian Control. Water Resour. Res. 1983, 19, 1511–1522. [Google Scholar] [CrossRef]
- Cervellera, C.; Chen, V.C.P.; Wen, A. Optimization of a large-scale water reservoir network by stochastic dynamic programming with efficient state space discretization. Eur. J. Oper. Res. 2006, 171, 1139–1151. [Google Scholar] [CrossRef]
- Yeh, W.W.; Becker, L. Multiobjective analysis of multireservoir operations. Water Resour. Res. 1982, 18, 1326–1336. [Google Scholar] [CrossRef]
- Joshi, G.S.; Gupta, K. A simulation model for the operation of multipurpose multireservoir system for River Narmada, India. J. Hydro-Environ. Res. 2009, 3, 96–108. [Google Scholar] [CrossRef]
- Seibert, S.; Skublics, D.; Ehret, U. The potential of coordinated reservoir operation for flood mitigation in large basins—A case study on the Bavarian Danube using coupled hydrological–hydrodynamic models. J. Hydrol. 2014, 517, 1128–1144. [Google Scholar] [CrossRef]
- Sigvaldson, O.T. A simulation model for operating a multipurpose multireservoir system. Water Resour. Res. 1976, 12, 263–278. [Google Scholar] [CrossRef]
- Fayaed, S.S.; El-Shafie, A.; Jaafar, O. Reservoir-system simulation and optimization techniques. Stoch. Environ. Res. Risk Assess. 2013, 27, 1751–1772. [Google Scholar] [CrossRef]
- Lin, N.M.; Rutten, M. Optimal Operation of a Network of Multi-purpose Reservoir: A Review. Procedia Eng. 2016, 154, 1376–1384. [Google Scholar] [CrossRef]
- Ngo, L.L.; Madsen, H.; Rosbjerg, D. Simulation and optimisation modelling approach for operation of the Hoa Binh reservoir, Vietnam. J. Hydrol. 2007, 336, 269–281. [Google Scholar] [CrossRef]
- Abou Rjeily, Y.; Abbas, O.; Sadek, M.; Shahrour, I.; Hage Chehade, F. Model Predictive Control for optimising the operation of Urban Drainage Systems. J. Hydrol. 2018, 566, 558–565. [Google Scholar] [CrossRef]
- Maestre, J.M.; Raso, L.; Overloop, P.J.V.; Schutter, B.D. Distributed tree-based model predictive control on a drainage water system. J. Hydroinform. 2013, 15, 335–347. [Google Scholar] [CrossRef]
- van Overloop, P.J.; Clemmens, A.J.; Strand, R.J.; Wagemaker, R.M.J.; Bautista, E. Real-Time Implementation of Model Predictive Control on Maricopa-Stanfield Irrigation and Drainage District’s WM Canal. J. Irrig. Drain. Eng. 2010, 136, 747–756. [Google Scholar] [CrossRef]
- Sankar, G.S.; Mohan Kumar, S.; Narasimhan, S.; Narasimhan, S.; Murty Bhallamudi, S. Optimal control of water distribution networks with storage facilities. J. Process. Control. 2015. [Google Scholar] [CrossRef]
- García, C.E.; Prett, D.M.; Morari, M. Model predictive control: Theory and practice—A survey. Automatica 1989, 25, 335–348. [Google Scholar] [CrossRef]
- van Overloop, P.J. Model Predictive Control on Open Water Systems. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2006. [Google Scholar]
- Camacho, E.F.; Bordons, C. Model Predictive Control; Advanced Textbooks in Control and Signal Processing; Springer: London, UK, 2007. [Google Scholar]
- Delgoda, D.K.; Saleem, S.K.; Halgamuge, M.N.; Malano, H. Multiple Model Predictive Flood Control in Regulated River Systems with Uncertain Inflows. Water Resour. Manag. 2013, 27, 765–790. [Google Scholar] [CrossRef]
- Ficchì, A.; Raso, L.; Dorchies, D.; Pianosi, F.; Malaterre, P.; van Overloop, P.J. Optimal Operation of the Multireservoir System in the Seine River Basin Using Deterministic and Ensemble Forecasts. J. Water Resour. Plan. Manag. 2016, 7, 1–12. [Google Scholar] [CrossRef]
- Galelli, S.; Goedbloed, A.; Schwanenberg, D.; van Overloop, P.J. Optimal Real-Time Operation of Multipurpose Urban Reservoirs: Case Study in Singapore. J. Water Resour. Plan. Manag. 2014, 140, 511–523. [Google Scholar] [CrossRef]
- Raso, L.; Malaterre, P.O. Combining Short-Term and Long-Term Reservoir Operation Using Infinite Horizon Model Predictive Control. J. Irrig. Drain. Eng. 2017, 143, B4016002. [Google Scholar] [CrossRef]
- Raso, L.; Schwanenberg, D.; van de Giesen, N.; van Overloop, P. Short-term optimal operation of water systems using ensemble forecasts. Adv. Water Resour. 2014, 71, 200–208. [Google Scholar] [CrossRef]
- Tian, X.; Negenborn, R.R.; van Overloop, P.J.; María Maestre, J.; Sadowska, A.; van de Giesen, N. Efficient multi-scenario Model Predictive Control for water resources management with ensemble streamflow forecasts. Adv. Water Resour. 2017, 109, 58–68. [Google Scholar] [CrossRef]
- Uysal, G.; Alvarado-Montero, R.; Schwanenberg, D.; Şensoy, A. Real-Time Flood Control by Tree-Based Model Predictive Control Including Forecast Uncertainty: A Case Study Reservoir in Turkey. Water 2018, 10, 340. [Google Scholar] [CrossRef]
- Schwanenberg, D.; Fan, F.M.; Naumann, S.; Kuwajima, J.I.; Montero, R.A.; Assis dos Reis, A. Short-Term Reservoir Optimization for Flood Mitigation under Meteorological and Hydrological Forecast Uncertainty. Water Resour. Manag. 2015, 29, 1635–1651. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization; Springer: Boston, MA, USA, 2014; pp. 403–449. [Google Scholar] [CrossRef]
- Reed, P.; Hadka, D.; Herman, J.; Kasprzyk, J.; Kollat, J. Evolutionary multiobjective optimization in water resources: The past, present, and future. Adv. Water Resour. 2013, 51, 438–456. [Google Scholar] [CrossRef]
- Nicklow, J.; Reed, P.; Savic, D.; Dessalegne, T.; Harrell, L.; Chan-Hilton, A.; Karamouz, M.; Minsker, B.; Ostfeld, A.; Singh, A.; et al. State of the Art for Genetic Algorithms and Beyond in Water Resources Planning and Management. J. Water Resour. Plan. Manag. 2010, 136, 412–432. [Google Scholar] [CrossRef]
- Reddy, M.J.; Kumar, D.N. Optimal Reservoir Operation Using Multi-Objective Evolutionary Algorithm. Water Resour. Manag. 2006, 20, 861–878. [Google Scholar] [CrossRef]
- Fu, G.; Kapelan, Z.; Kasprzyk, J.R.; Reed, P. Optimal Design of Water Distribution Systems Using Many-Objective Visual Analytics. J. Water Resour. Plan. Manag. 2013, 139, 624–633. [Google Scholar] [CrossRef]
- Reed, P.M.; Kollat, J.B. Visual analytics clarify the scalability and effectiveness of massively parallel many-objective optimization: A groundwater monitoring design example. Adv. Water Resour. 2013, 56, 1–13. [Google Scholar] [CrossRef]
- Kasprzyk, J.R.; Nataraj, S.; Reed, P.M.; Lempert, R.J. Many objective robust decision making for complex environmental systems undergoing change. Environ. Model. Softw. 2013, 42, 55–71. [Google Scholar] [CrossRef]
- Guo, Y.; Tian, X.; Fang, G.; Xu, Y.P. Many-objective optimization with improved shuffled frog leaping algorithm for inter-basin water transfers. Adv. Water Resour. 2020, 138. [Google Scholar] [CrossRef]
- Núñez, A.; Cortés, C.E.; Sáez, D.; De Schutter, B.; Gendreau, M. Multiobjective model predictive control for dynamic pickup and delivery problems. Control. Eng. Pract. 2014, 32, 73–86. [Google Scholar] [CrossRef]
- Chiang, P.K.; Willems, P. Combine Evolutionary Optimization with Model Predictive Control in Real-time Flood Control of a River System. Water Resour. Manag. 2015, 29, 2527–2542. [Google Scholar] [CrossRef]
- Vermuyten, E.; Meert, P.; Wolfs, V.; Willems, P. Combining Model Predictive Control with a Reduced Genetic Algorithm for Real-Time Flood Control. J. Water Resour. Plan. Manag. 2018, 144, 04017083. [Google Scholar] [CrossRef]
- Tian, X.; Guo, Y.; Negenborn, R.R.; Wei, L.; Lin, N.M.; Maestre, J.M. Multi-Scenario Model Predictive Control Based on Genetic Algorithms for Level Regulation of Open Water Systems under Ensemble Forecasts. Water Resour. Manag. 2019, 33, 3025–3040. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Morari, M.; Lee, J.H. Model predictive control: Past, present and future. Comput. Chem. Eng. 1999, 23, 667–682. [Google Scholar] [CrossRef]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1959. [Google Scholar]
- van Overloop, P.J. Drainage control in water management of polders in the Netherlands. Irrig. Drain. Syst. 2006, 20, 99–109. [Google Scholar] [CrossRef]
- Breckpot, M.; Agudelo, O.; Moor, B.D. Flood Control with Model Predictive Control for River Systems with Water Reservoirs. J. Irrig. Drain. Eng. 2013, 139, 532–541. [Google Scholar] [CrossRef]
- Xu, M.; van Overloop, P.; van de Giesen, N. On the study of control effectiveness and computational efficiency of reduced Saint-Venant model in model predictive control of open channel flow. Adv. Water Resour. 2011, 34, 282–290. [Google Scholar] [CrossRef]
- Xu, M.; Negenborn, R.; van Overloop, P.; van de Giesen, N. De Saint-Venant equations-based model assessment in model predictive control of open channel flow. Adv. Water Resour. 2012, 49, 37–45. [Google Scholar] [CrossRef]
- Tian, X. Model Predictive Control for Operational Water Management: A Case Study of the Dutch Water System. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2015. [Google Scholar]
- Xu, M. Real-Time Control of Combined Water Quantity & Quality in Open Channels. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar]
- Stelling, G.S.; Duinmeijer, S.P.A. A staggered conservative scheme for every Froude number in rapidly varied shallow water flows. Int. J. Numer. Method Fluids 2003, 1354, 1329–1354. [Google Scholar] [CrossRef]
- Marler, R.; Arora, J. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Giuliani, M.; Castelletti, A. Is robustness really robust? How different definitions of robustness impact decision-making under climate change. Clim. Chang. 2016, 135, 409–424. [Google Scholar] [CrossRef]
- McMahon, T.A.; Adeloye, A.J.; Zhou, S.L. Understanding performance measures of reservoirs. J. Hydrol. 2006, 324, 359–382. [Google Scholar] [CrossRef]
- Zatarain Salazar, J.; Reed, P.M.; Quinn, J.D.; Giuliani, M.; Castelletti, A. Balancing exploration, uncertainty and computational demands in many objective reservoir optimization. Adv. Water Resour. 2017, 109, 196–210. [Google Scholar] [CrossRef]
- Deltares. SOBEK 2.15 User Manual; Technical Report; Deltares: Delft, The Netherlands, 2016. [Google Scholar]
- Raso, L. Optimal Control of Water Systems Under Forecast Uncertainty. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar]
| NSGA-II Parameters | Setting Value |
|---|---|
| Population size | 200 |
| Maximum number of generations in each run | 1000 |
| Crossover rate | 0.80 |
| Mutation rate | 0.35 |
| Stopping criteria | 1. The average change in the spread of the Pareto front over generation (=100) is less than or equal to function tolerance (. |
| 2. The maximum number of generations is reached. |
| Decision Rule | Method | w |
|---|---|---|
| DR-1 | weighted-sum | [1,0,0] |
| DR-2 | weighted-sum | [0,1,0] |
| DR-3 | weighted-sum | [0,0,1] |
| DR-4 | weighted-sum | [0.6,0.2,0.2] |
| DR-5 | weighted-sum | [0.2,0.6,0.2] |
| DR-6 | weighted-sum | [0.2,0.2,0.6] |
| DR-7 | maximin | - |
| DR-8 | maxisum | - |
| Decision Rule (Weight) | Indicator | Overall Performance (Average) | ||
|---|---|---|---|---|
| Reliability of Meeting Storage Capacity V (%) | Reliability of Meeting Flood Control E (%) | Reliability of Maximizing Hydropower Generation P (%) | ||
| DR-1 (1,0,0) | 93 | 54 | 74 | 74 |
| DR-2 (0,1,0) | 50 | 100 | 68 | 73 |
| DR-3 (0,0,1) | 0 | 0 | 100 | 33 |
| DR-4 (0.6.0.2.0.2) | 92 | 50 | 74 | 72 |
| DR-5 (0.2,0.6.0.2) | 67 | 60 | 82 | 69 |
| DR-6 (0.2,0.2,0.6) | 25 | 9 | 97 | 44 |
| DR-7 | 62 | 22 | 85 | 56 |
| DR-8 | 62 | 23 | 82 | 56 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Myo Lin, N.; Tian, X.; Rutten, M.; Abraham, E.; Maestre, J.M.; van de Giesen, N. Multi-Objective Model Predictive Control for Real-Time Operation of a Multi-Reservoir System. Water 2020, 12, 1898. https://doi.org/10.3390/w12071898
Myo Lin N, Tian X, Rutten M, Abraham E, Maestre JM, van de Giesen N. Multi-Objective Model Predictive Control for Real-Time Operation of a Multi-Reservoir System. Water. 2020; 12(7):1898. https://doi.org/10.3390/w12071898
Chicago/Turabian StyleMyo Lin, Nay, Xin Tian, Martine Rutten, Edo Abraham, José M. Maestre, and Nick van de Giesen. 2020. "Multi-Objective Model Predictive Control for Real-Time Operation of a Multi-Reservoir System" Water 12, no. 7: 1898. https://doi.org/10.3390/w12071898
APA StyleMyo Lin, N., Tian, X., Rutten, M., Abraham, E., Maestre, J. M., & van de Giesen, N. (2020). Multi-Objective Model Predictive Control for Real-Time Operation of a Multi-Reservoir System. Water, 12(7), 1898. https://doi.org/10.3390/w12071898







