1. Introduction
Eroded by different forcing agents, soil is being lost at a rate that is orders-of-magnitude greater than its replenishment [
1]. Among all the erosive agents, water is the most prevalent and usually dominates. Moreover, due to the current climate change, the frequency, and the intensity of extreme rainfall events are projected to increase, which will lead to more intensive erosion [
2]. With this in mind, a lot of soil erosion models have been developed to mainly simulate water-induced erosion. Based on the numerical algorithms applied, these models can be classified as conceptual, empirical, and process-based models [
3]. The latter, with detailed representation of physical processes, is becoming the mainstream in both academia and industry [
4].
Depending on how processes and parameters are described, process-based models can be further grouped into semi-distributed and fully distributed models. Semi-distributed models, such as CREAMS (Chemical Runoff and Erosion from Agricultural Management Systems model [
5]), WEPP (Watershed Erosion Prediction Project [
6]), EUROSEM (EUROpean Soil Erosion Model [
7]), KINEROS (KINematic EROsion Simulation [
8]), and THREW (TsingHua Representative Elementary Watershed [
9]) break down the model domain (a watershed or a catchment) into a series of basic elements such as hillslopes, planes and channels, over which the algorithms are applied and physical parameters are represented [
10]. However, since hydrological parameters are lumped over the basic elements, semi-distributed models are not able to fully account for spatial heterogeneity. Fully distributed models divide a study domain into grid cells with certain sizes. The spatially distributed input data of fully distributed models are usually generated by the Geographical Information System (GIS). In this way, the physical heterogeneity is better represented. With the advances of scientific computation, several fully distributed, process-based models have been developed over the past three decades. Notable examples are LISEM (LImburg Soil Erosion Model [
11]), SHESED [
12] and CASC2D-SED (CASCade 2 dimensional sediment model [
13]). Recently, a physically based hydrological and soil erosion model has been developed by coupling the Soil Conservation Service model with a 2D fully Dynamic Wave model and a Hillslope Erosion model by Juez et al. [
2] The model is applied over a Mediterranean watershed to simulate the rainfall-runoff and soil erosion process during two rainfall events with satisfactory results generated. An efficient approach has been applied on the model for calibration process, which has largely reduced the computational cost. The model has demonstrated its potential applicability to large and long-term scale hydro-sedimentary process studies under climate change [
2]. In addition, the distributed model usually simulates the sedimentary processes in 2D mode. In the study of the replenishment of sediments in a water-worked channel using the 2D shallow water equation model coupled with Exner equation, Juez points out that the 2D distributed model can better resolve the bidimensional water and sediment flux compared to the 1D model [
14]. Moreover, the 2D model is more computationally efficient than the complicated 3D model while still meeting research and engineering requirements [
14].
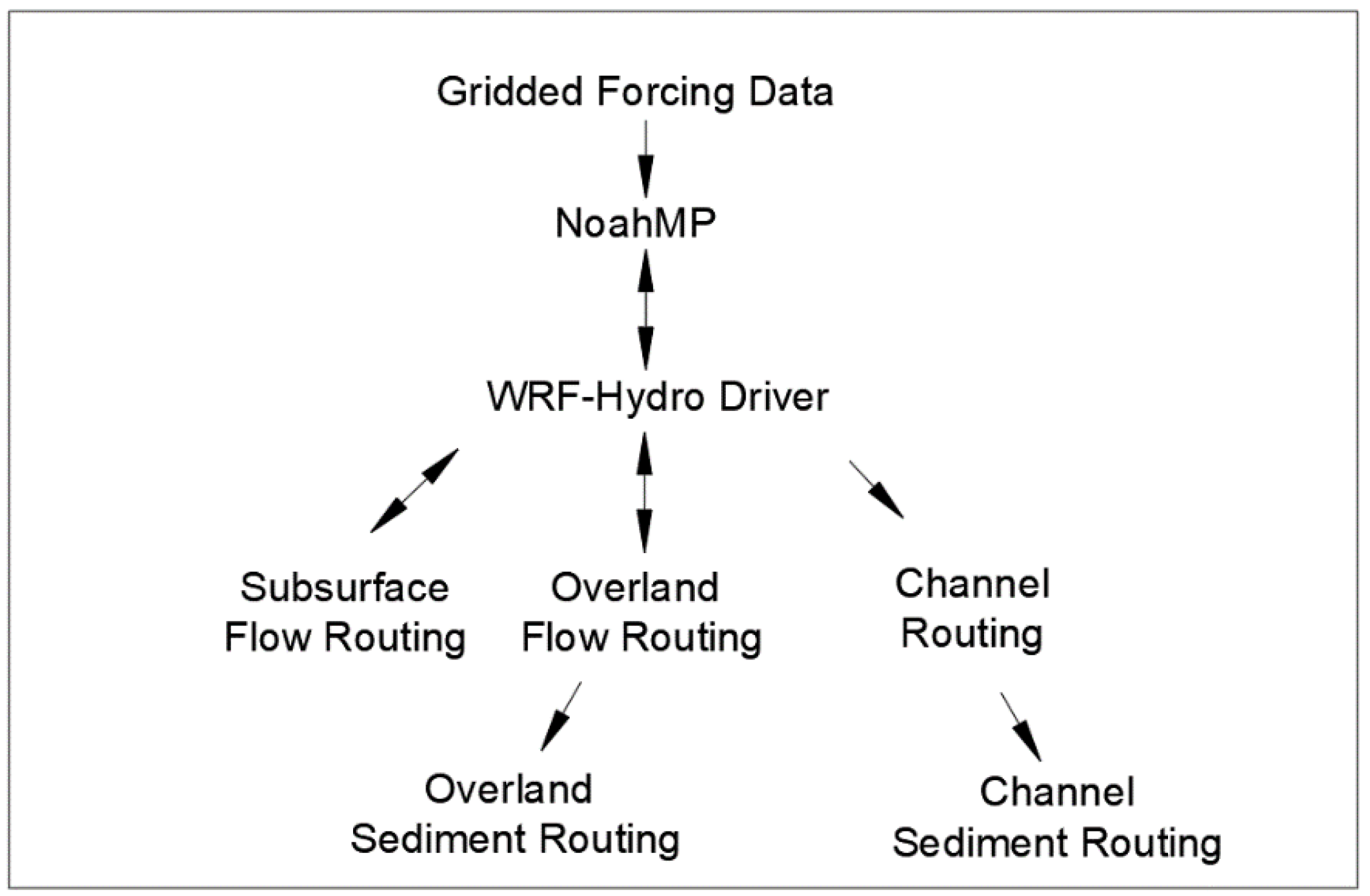
In this study, we present a newly developed, fully distributed, process-based soil erosion and sediment transport model. Our model is built on WRF-Hydro, which simulates the hydrological cycle and provides hydraulic parameters for soil erosion and transport. WRF-Hydro was developed as the hydrological modeling extension package of WRF at the National Center for Atmospheric Research in Boulder, Colorado [
15]. Compared to other hydrological models such as the Variable Infiltration Capacity model (VIC, [
16]) and the Soil and Water Assessment Tool (SWAT, [
17]) model, WRF-Hydro’s advantage is its capability of simulating multi-processes at multi-scales while considering the spatial distribution of hydrological variables. Besides, WRF-Hydro takes advantage of various available meteorological and terrain datasets and has been fully coupled with meteorological and climate models such as WRF. WRF-Hydro’s performance has been evaluated by its applications in flooding [
18], water resource management [
19], water budget estimation [
20], decadal scale hydroclimatic change [
21], and others. Currently, an instance of WRF-Hydro is running operationally as the National Oceanic and Atmospheric Administration’s (NOAA) National Water Model, which provides streamflow forecasts on 2.7 million river reaches of the contiguous United States. However, until this study, WRF-Hydro does not include a sediment module, which limits its capability in water quality-related forecasts and studies.
In this paper, the architecture and algorithms of the WRF-Hydro-Sed model, the study area, and datasets used as well as the calibration method are presented in
Section 2. Results of model calibration and validation are detailed in
Section 3.
Section 4 discusses the model’s uncertainty, the validity of applying calibrated parameters to different events, the relationship between landscape patterns and soil erosion as well as the limitation of current model regarding long-term simulation under climate change. A conclusion is given in
Section 5.
5. Conclusions
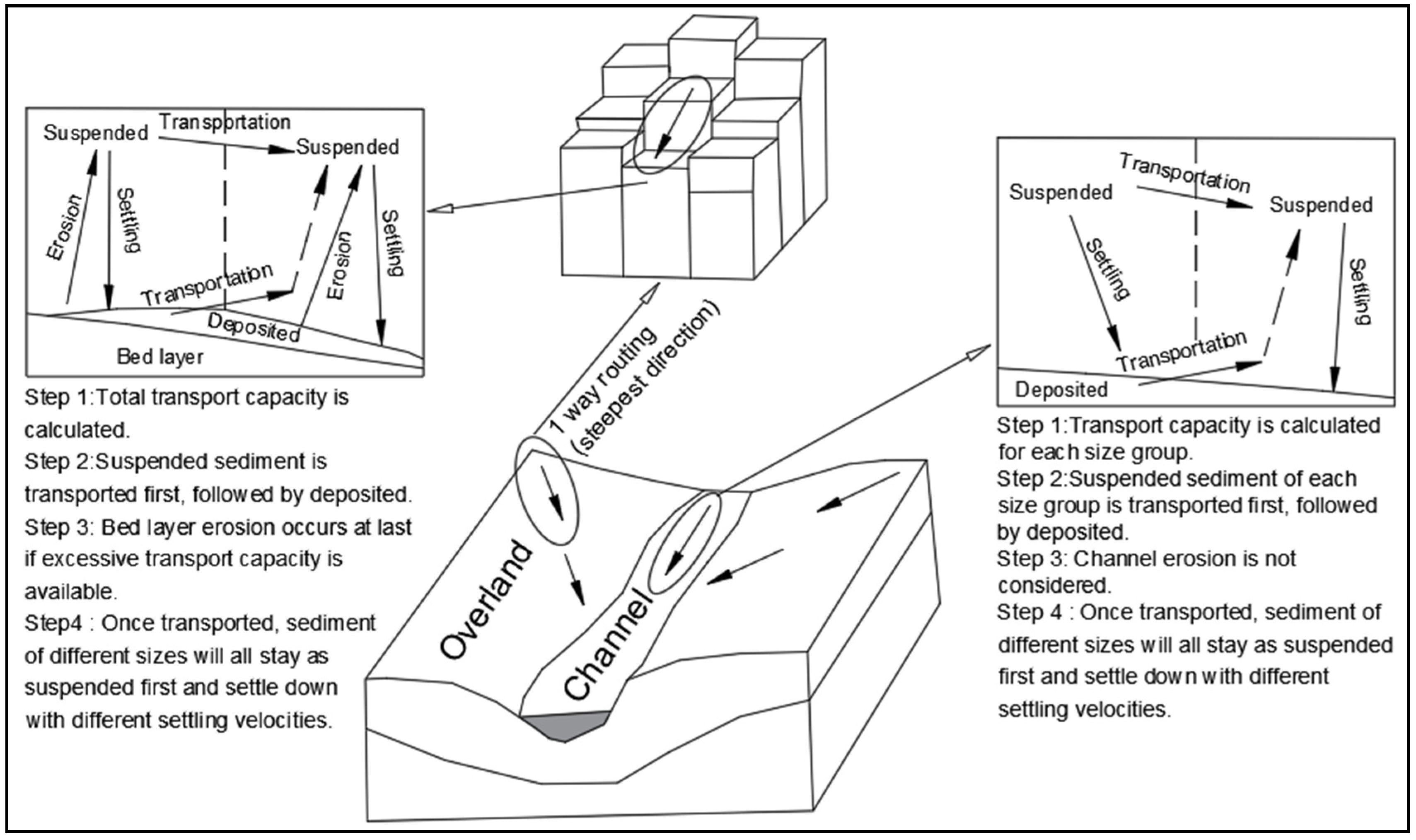
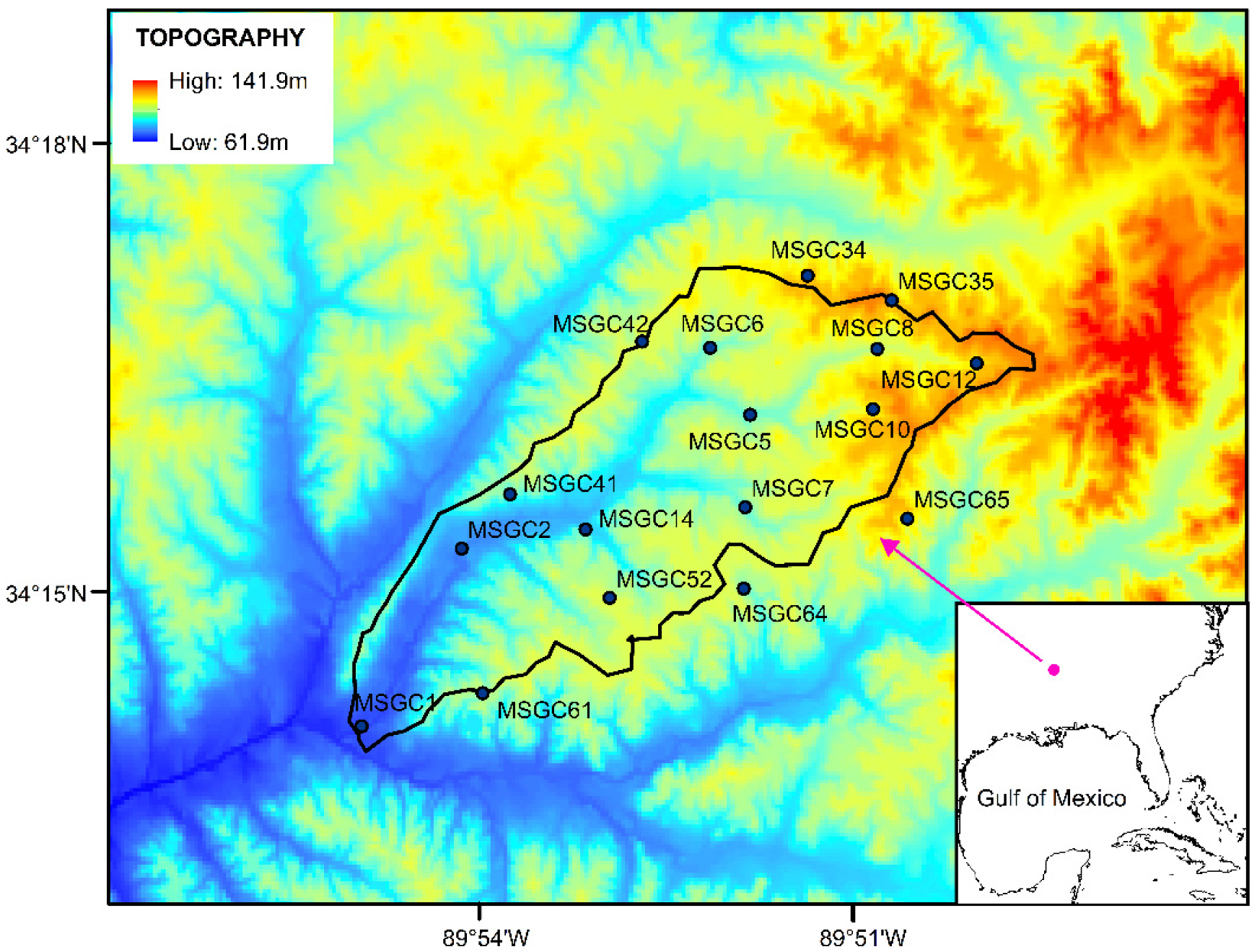
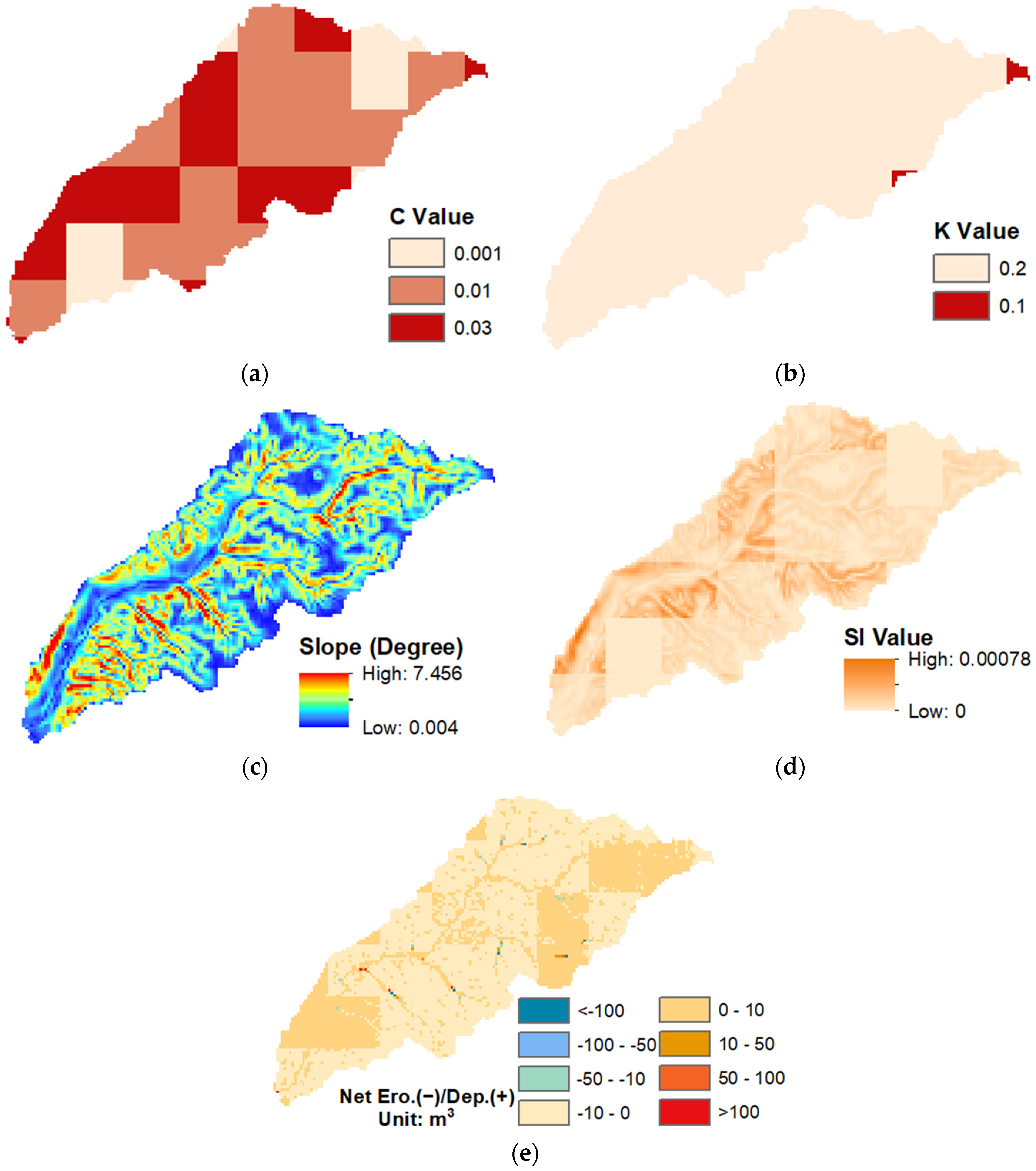
In this study, by adapting the sediment algorithm from CASC2D-Sed, we introduced a sediment module into the WRF-Hydro platform, allowing for the development of a fully distributed, process-based soil erosion and sediment transport model (WRF-Hydro-Sed). The model’s performance was evaluated via a comparison with the observed streamflow and sediment concentration data at the Goodwin Creek Experimental Watershed during rainfall events.
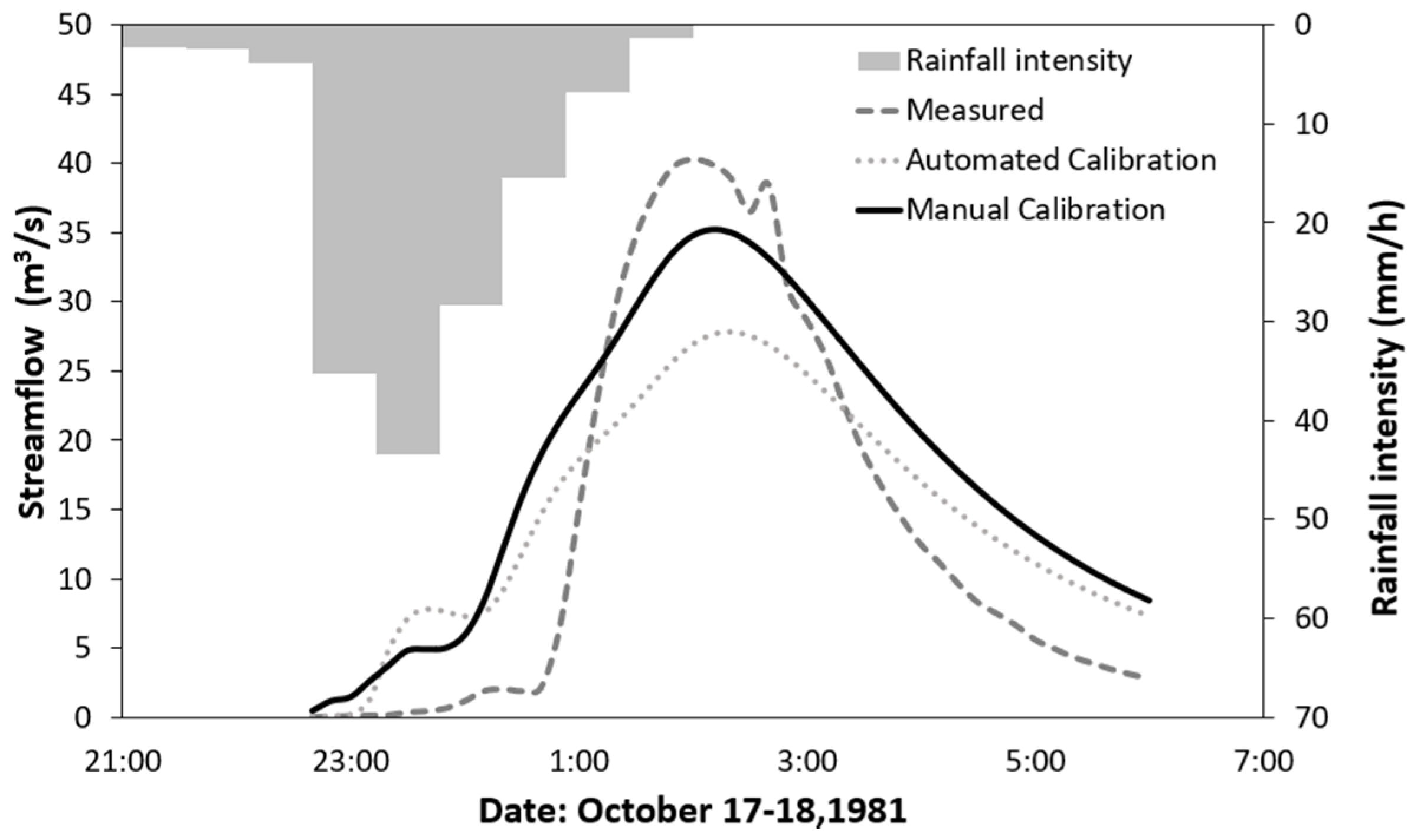
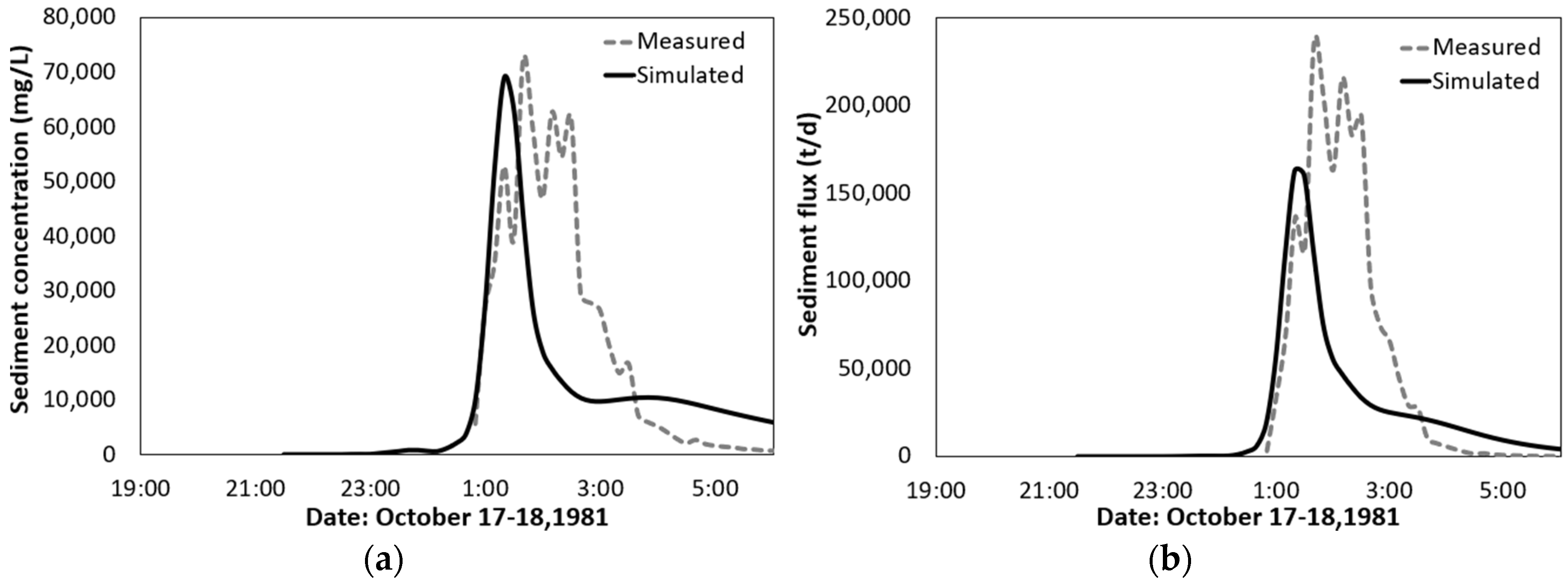
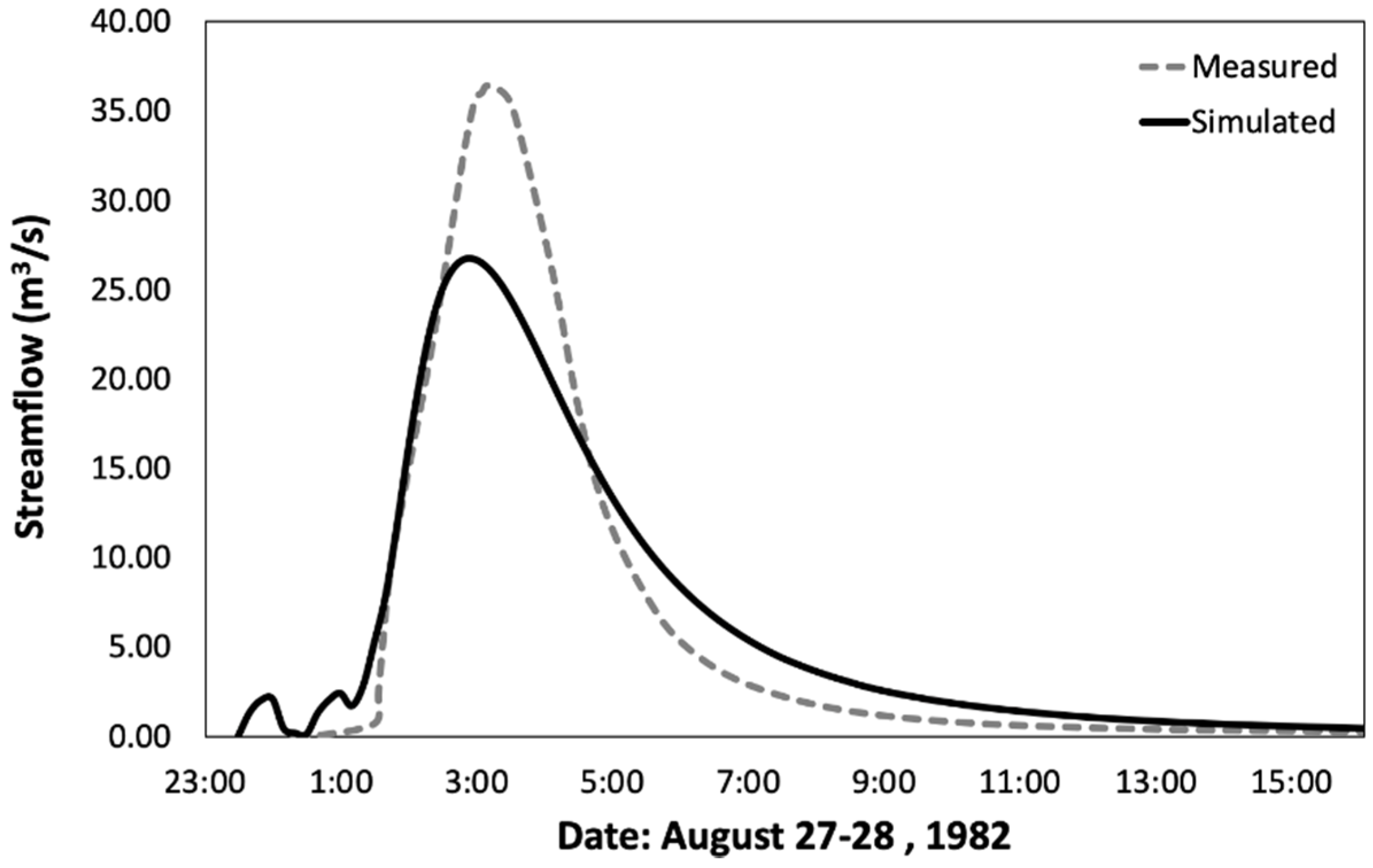
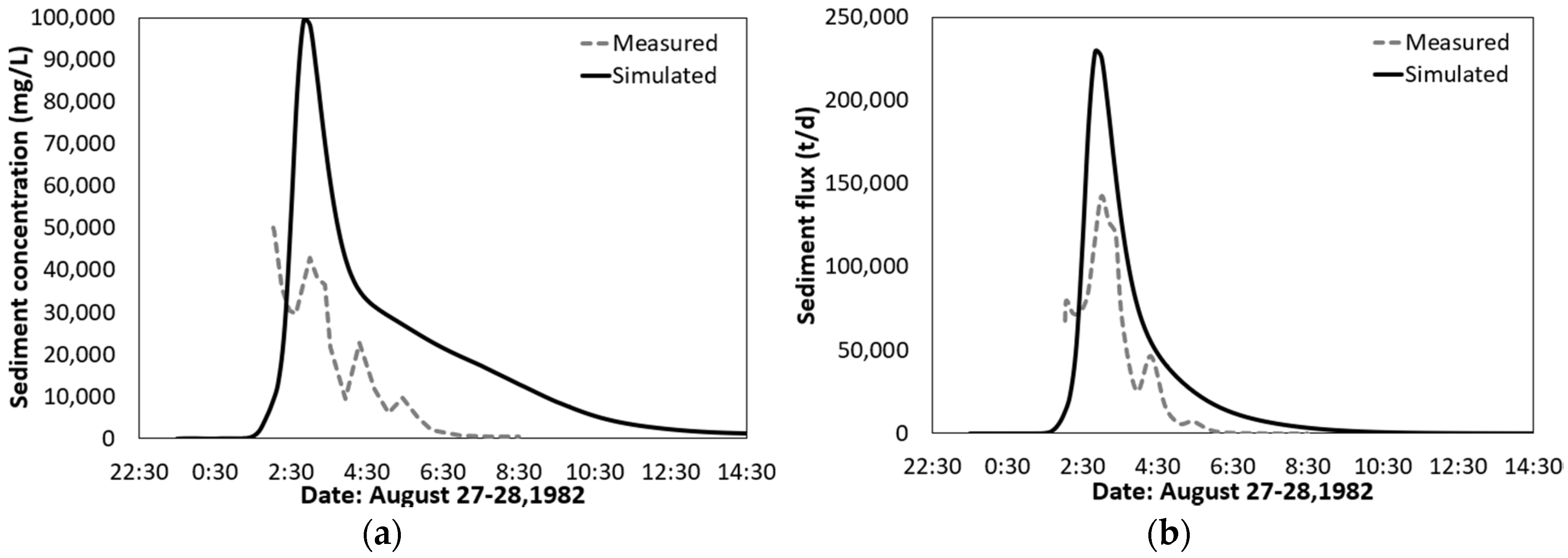
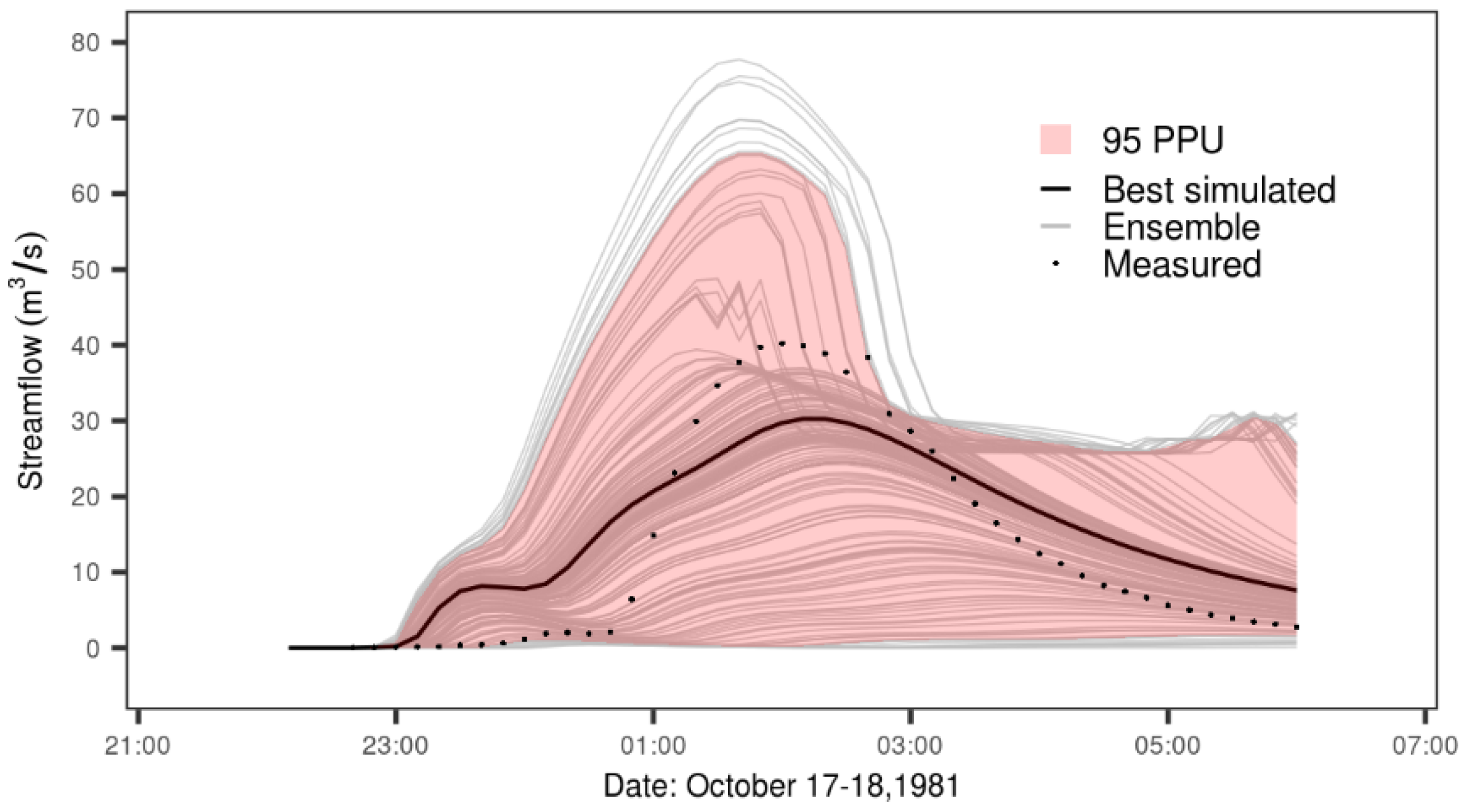
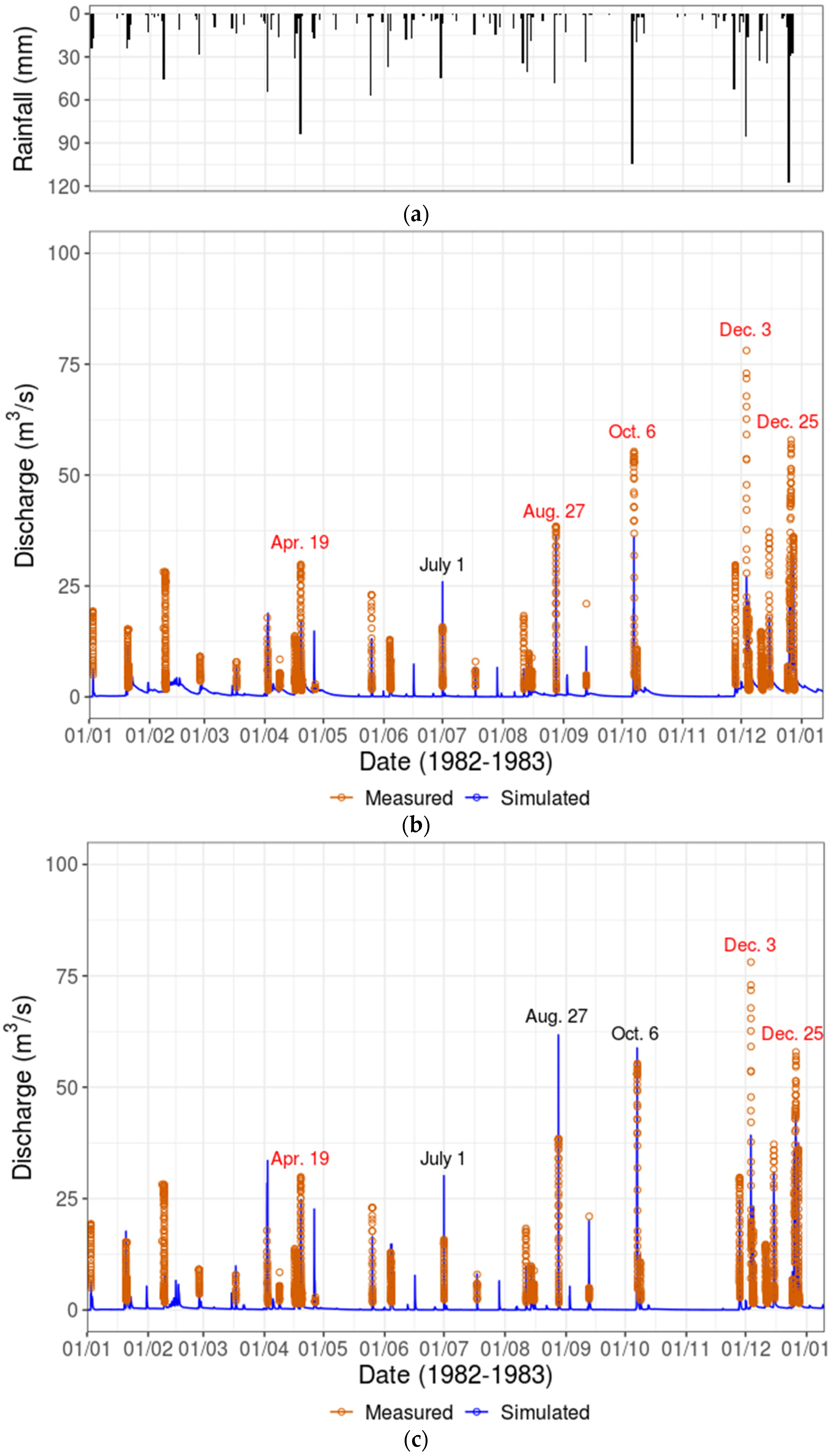
WRF-Hydro-Sed is able to generate satisfactory results of streamflow and sediment yield during rainfall events. The streamflow can be calibrated successfully based on a single rainfall event with the adjustment of a few hydro-parameters including refkdt (the parameter that controls runoff–infiltration partition) and channel geometries. With the single event calibrated hydro-parameters, the model can also perform satisfactorily in simulating the hydrograph during a validation event. Based on calibrated hydro-parameters, sediment concentration, sediment flux, as well as sediment yield can also be calibrated successfully at watershed scale by adjusting sediment parameters related to land use and soil category. Satisfactory results are also generated for a validation event using calibrated sediment parameters. The model’s performance in simulating sediment yield is better than sediment concentration and flux.
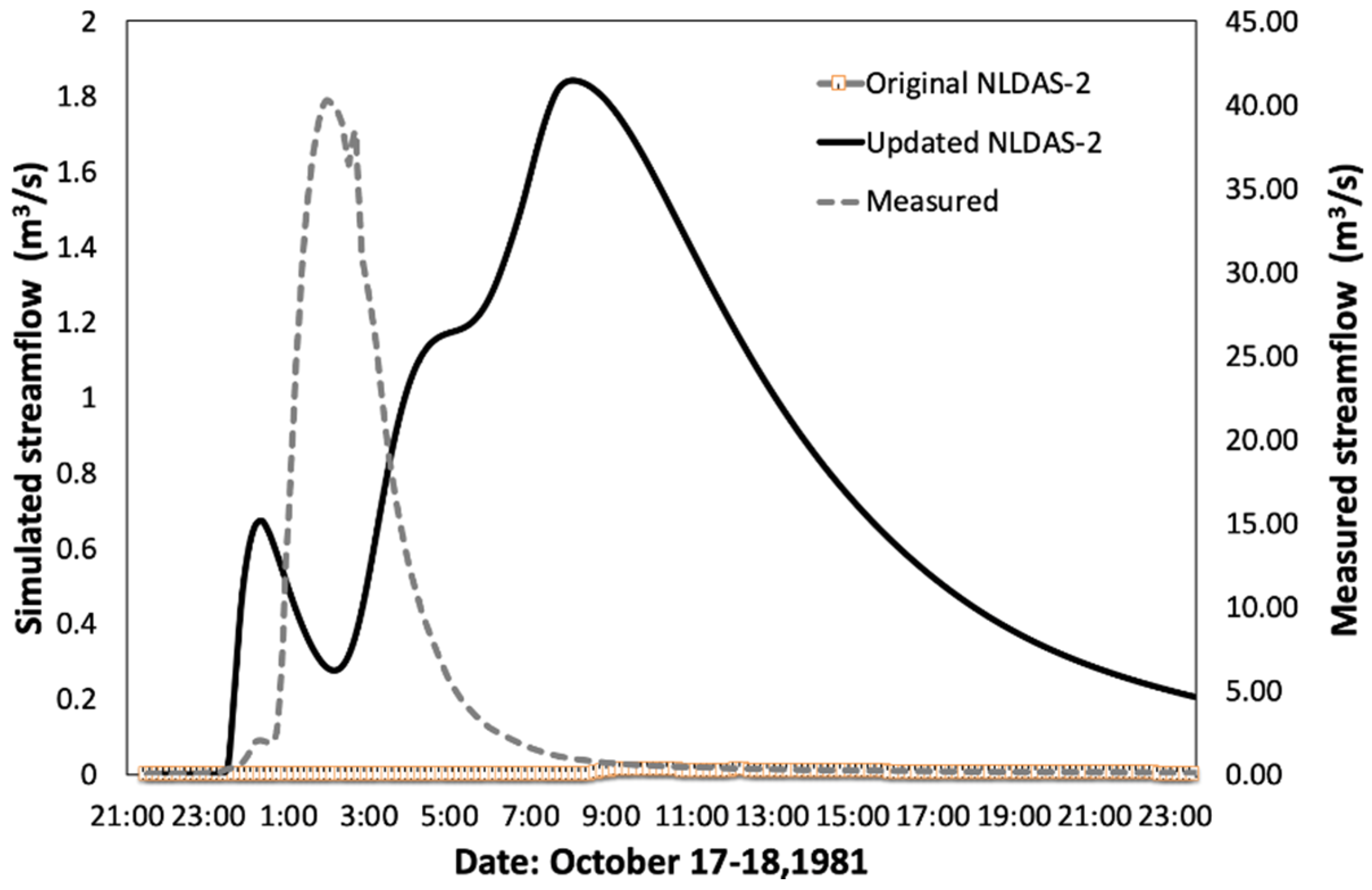
The model’s performance in streamflow simulation is sensitive to forcing data. The original NLDAS-2, given its 1/8 degree coarse resolution, may not be an optimal choice to provide rainfall forcing for simulation over a relatively small watershed like the Goodwin Creek under local storm events. High resolution meteorological forcing data is recommended for application of the WRF-Hydro-Sed on a small watershed.
Calibrated hydro-parameters based on a single event can be applied to different rainfall events to reproduce the hydrograph. While it might not be practical to have a set of parameters that can be suitable for any rainfall event, an intensive calibration based on multiple events can improve the model’s performance to a certain degree, but with extensive computational efforts. In this case, intensive calibration over a long time scale might not be an optimal strategy if computational cost is a major concern and if the model performance based on a single event calibration is acceptable. With the calibrated sediment parameters based on a single event, the sediment yield over different events can be simulated within the same magnitude observed. Moreover, the model shows promising potential in simulating annual soil erosion on a watershed scale. While simulated sediment yield is considered acceptable for 71% of the events (12 out of 17), substantial bias can be found during certain events mainly due to the bias transferred from the streamflow simulation. Future development of the model by including the bank and channel erosion algorithm is expected to further improve model performance.