Hybrid Model for Short-Term Water Demand Forecasting Based on Error Correction Using Chaotic Time Series
Abstract
1. Introduction
- Present the framework, methods, and performance indicators of the hybrid forecasting model,
- Test the hybrid model’s accuracy based on case studies of three real-world DMAs in Beijing WDSs,
- Verify the effectiveness of the model by comparing it with the results of other models, including ARIMA, LSSVM without error correction, and LSSVM using Fourier series for error correction.
2. Methodology
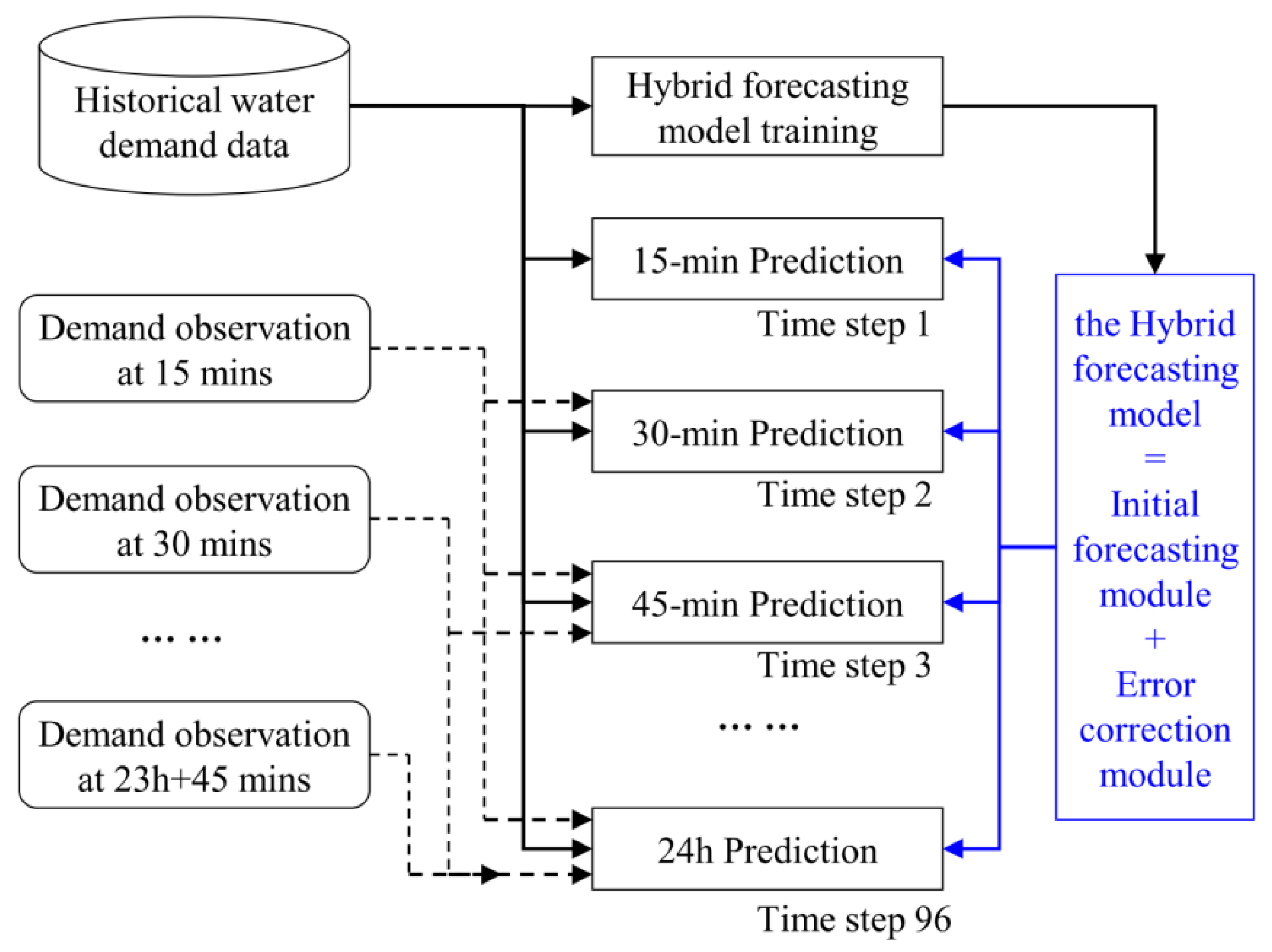
2.1. Research Framework
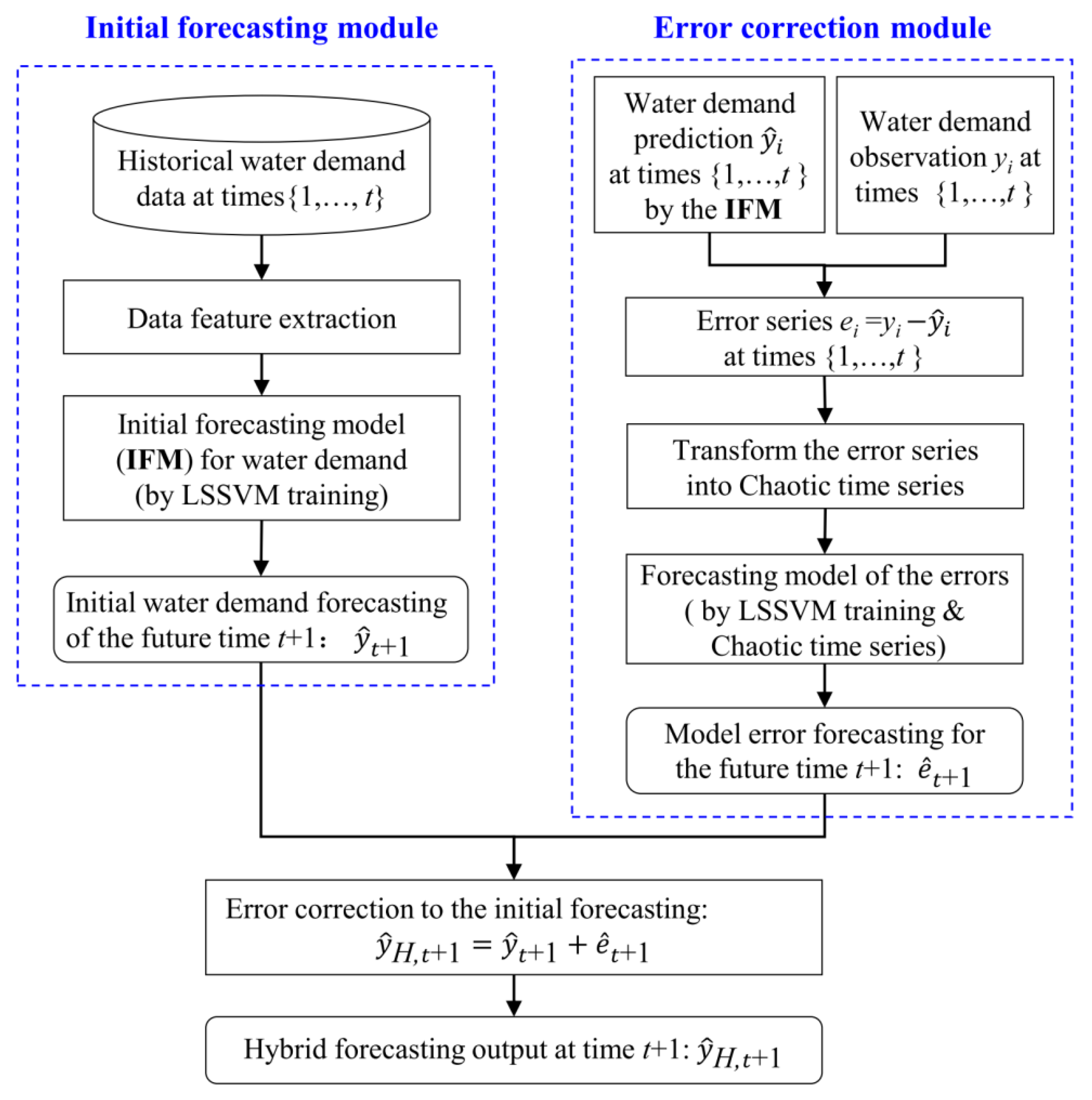
2.2. Initial Forecasting Model by LSSVM
2.3. Error Forecasting Model Based on Chaotic Time Series
2.4. Performance Indicators of Forecasting Models
3. Case Study
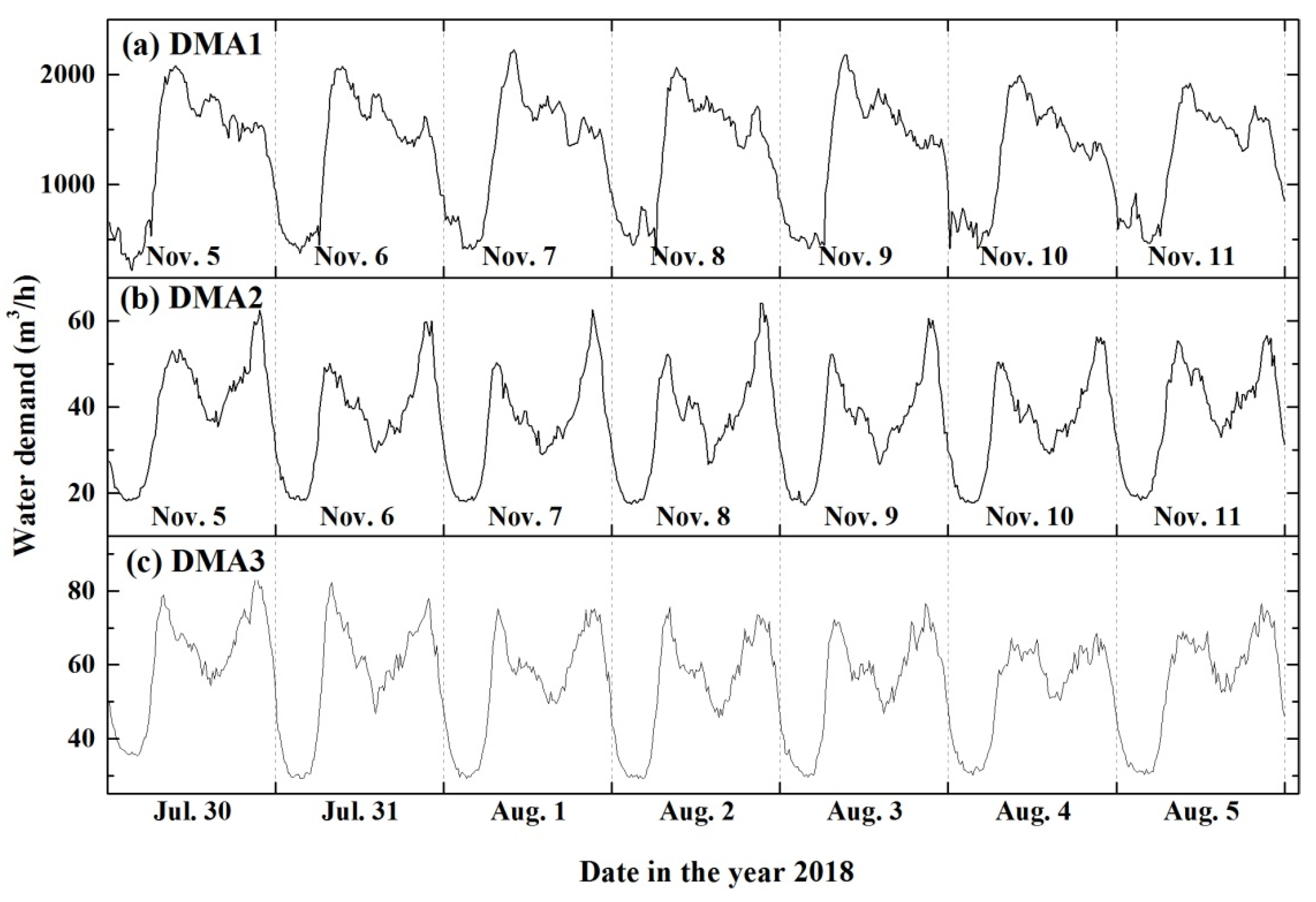
3.1. Data Feature Extraction and Model Inputs
3.2. Model Setup
3.3. Application Results
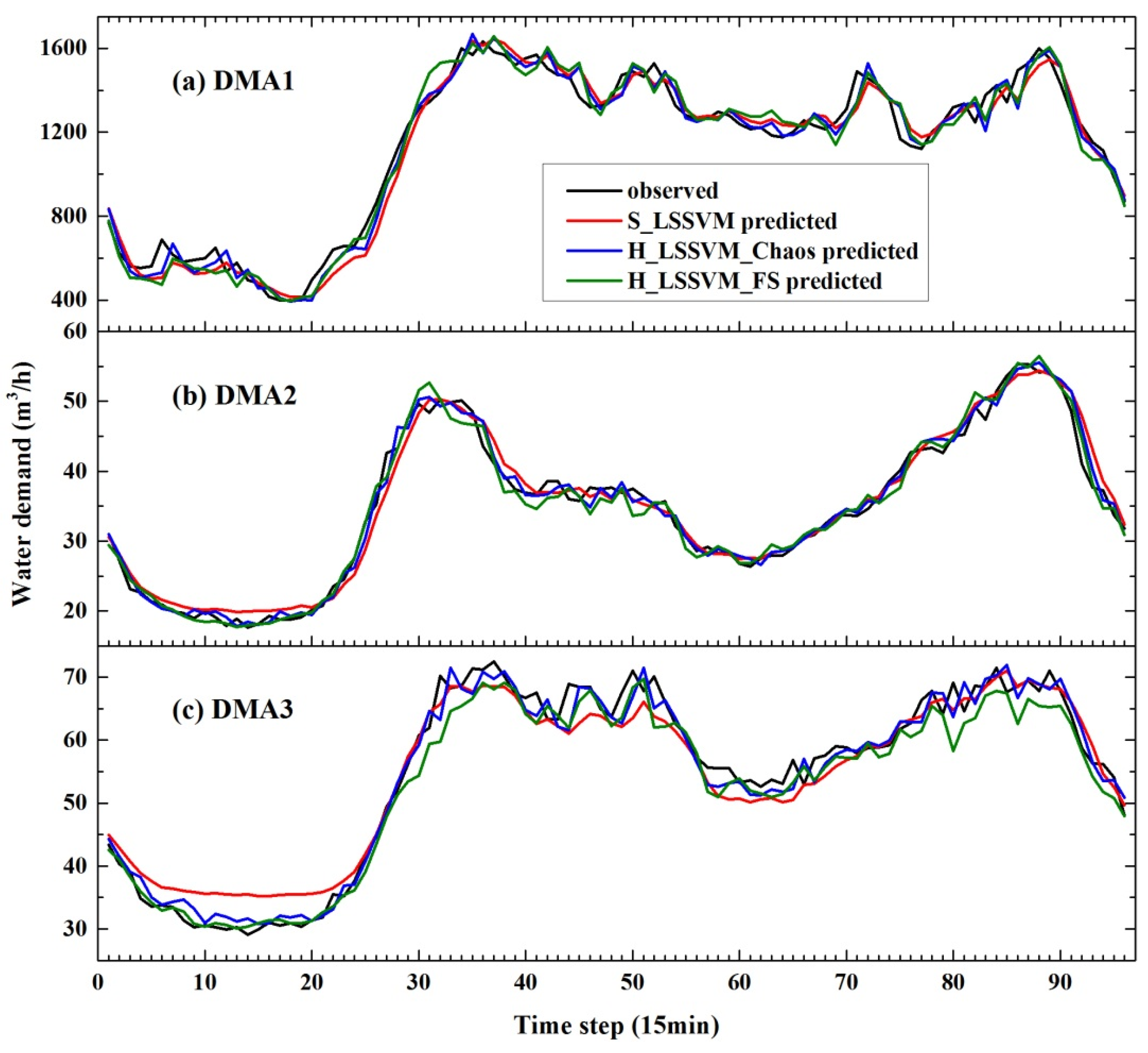
3.3.1. Overall Performance
3.3.2. Comparisons Between the Hybrid Forecasting Models
- The error forecasting models based on the chaos method and the FS method can both obtain more reasonable prediction results in some periods where the error data changes mildly, such as time steps 5 to 23 and 60 to 72 in DMA2, and 10 to 24 in DMA3.
- The prediction accuracy of the two methods is relatively low in the periods where the error data change frequently, such as time steps 33 to 55 in DMA1, 24 to 34 in DMA2, and 35 to 53 in DMA3. It should be noted that even in these hardly predictable time steps, however, the predictions from the chaos method is closer to the errors of the initial prediction than the FS model, e.g., for the error predictions at time steps 30 to 55 in the three DMAs, the MAEs obtained by chaos method and FS model are (47.54, 1.17, 2.40) and (64.53, 1.84, 3.15), respectively.
- At some time steps, the error predictions from the FS method are larger than the errors of initial prediction, which leads to misleading corrections to the initial forecasting, such as the time steps 32, 33, and 62 to 64 in DMA1; time steps 32, 46, 55 and 50 in DMA2; time steps 30 to 35, 80 and 86 in DMA3. While this kind of misleading correction is not much in the chaos method.
3.4. Discussion
4. Conclusions
- In most instances, the hybrid models perform better than the forecasting model without error correction. The error correction module performs better in the short-term water demand forecasting than the DMAs whose composition of customers is simple. A simple composition of customers indicates a simple water consumption pattern and less peak fluctuations in the water consumption curves.
- Due to the capability of detecting the underlying instability characteristics of time series, the error correction module using chaotic time series performs better than the Fourier series in predicting a complex disordered time series of errors.
- For the periods of frequent and disordered peak fluctuations in the error time series, the performance of the error correction module is not good, and the error forecasting model based on Fourier series may lead to unreasonable forecasts by misleading the corrections to the initial forecasting. As a result, more attention should be paid to the features of the error time series when using the error correction module.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Herrera, M.; Torgo, L.; Izquierdo, J.; Pérez-García, R. Predictive models for forecasting hourly urban water demand. J. Hydrol. 2010, 387, 141–150. [Google Scholar] [CrossRef]
- Anele, A.; Hamam, Y.; Abu-Mahfouz, A.; Todini, E. Overview, comparative assessment and recommendations of forecasting models for short-term water demand prediction. Water 2017, 9, 887–898. [Google Scholar] [CrossRef]
- Chen, J.; Boccelli, D.L. Demand forecasting for water distribution systems. Procedia Eng. 2014, 70, 339–342. [Google Scholar] [CrossRef]
- Qin, T.; Boccelli, D.L. Estimating distribution system water demands using Markov chain Monte Carlo. J. Water Resour. Plan. Manag. 2019, 145, 04019023. [Google Scholar] [CrossRef]
- Donkor, E.A.; Mazzuchi, T.A.; Soyer, R.; Alan Roberson, J. Urban water demand forecasting: Review of methods and models. J. Water Resour. Plan. Manag. 2014, 140, 146–159. [Google Scholar] [CrossRef]
- Chen, J.; Boccelli, D.L. Forecasting hourly water demands with seasonal autoregressive models for real-time application. Water Resour. Res. 2018, 54, 879–894. [Google Scholar] [CrossRef]
- Odan, F.K.; Reis, L.F.R. Hybrid water demand forecasting model associating artificial neural network with Fourier series. J. Water Resour. Plan. Manag. 2012, 138, 245–256. [Google Scholar] [CrossRef]
- Pacchin, E.; Gagliardi, F.; Alvisi, S.; Franchini, M. A comparison of short-term water demand forecasting models. Water Resour. Manag. 2019, 33, 1481–1497. [Google Scholar] [CrossRef]
- Guo, G.; Liu, S.; Wu, Y.; Li, J.; Zhou, R.; Zhu, X. Short-term water demand forecast based on deep learning method. J. Water Resour. Plan. Manag. 2018, 144, 04018076. [Google Scholar] [CrossRef]
- Crommelynck, V.; Duquesne, C.; Mercier, M. Daily and Hourly Water Consumption Forecasting Tools Using Neural Networks. In Proceeding of the AWWA’s Annual Computer Specialty Conference, Nashville, TN, USA, 12–15 April 1999; pp. 665–676. [Google Scholar]
- Jain, A.; Ormsbee, L. Short-term water demand forecast modeling techniques—Conventional Methods Versus AI. Am. Water Work. Assoc. 2002, 94, 64–72. [Google Scholar] [CrossRef]
- Bougadis, J.; Adamowski, K.; Diduch, R. Short-term municipal water demand forecasting. Hydrol. Process. 2005, 19, 137–148. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, T.Q. Hourly water demand forecast model based on Bayesian least squares support vector machine. J. Tianjin Univ. 2006, 39, 1037–1042. [Google Scholar]
- Chen, L.; Zhang, T.Q. Hourly water demand forecast model based on least squares support vector machine. J. Harbin Inst. Technol. 2006, 38, 1528–1530. [Google Scholar]
- Khan, M.S.; Coulibaly, P. Application of support vector machine in lake water level prediction. J. Hydrol. Eng. 2006, 11, 199–205. [Google Scholar] [CrossRef]
- Braun, M.; Bernard, T.; Piller, O.; Sedehizade, F. 24-Hours demand forecasting based on SARIMA and support vector machines. Procedia Eng. 2014, 89, 926–933. [Google Scholar] [CrossRef]
- Dahl, C.M.; Hylleberg, S. Flexible regression models and relative forecast performance. Int. J. Forecast. 2004, 20, 201–217. [Google Scholar] [CrossRef]
- Chen, G.; Long, T.; Xiong, J.; Bai, Y. Multiple random forests modelling for urban water consumption forecasting. Water Resour. Manag. 2017, 31, 4715–4729. [Google Scholar] [CrossRef]
- Tripathi, S.; Srinivas, V.V.; Nanjundiah, R.S. Downscaling of precipitation for climate change scenarios: A support vector machine approach. J. Hydrol. 2006, 330, 621–640. [Google Scholar] [CrossRef]
- Ghalehkhondabi, I.; Ardjmand, E.; Young, W.A.; Weckman, G.R. Water demand forecasting: Review of soft computing methods. Env. Monit Assess. 2017, 189, 313. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; De Brabanter, J.; Lukas, L.; Vandewalle, J. Weighted least squares support vector machines robustness and sparse approximation. Neurocomputing 2002, 48, 85–105. [Google Scholar] [CrossRef]
- Vijai, P.; Bagavathi Sivakumar, P. Performance comparison of techniques for water demand forecasting. Procedia Comput. Sci. 2018, 143, 258–266. [Google Scholar] [CrossRef]
- Samsudin, R.; Saad, P.; Shabri, A. River flow time series using least squares support vector machines. Hydrol. Earth Syst. Sci. 2011, 15, 1835–1852. [Google Scholar] [CrossRef]
- Kisi, O. Modeling discharge-suspended sediment relationship using least square support vector machine. J. Hydrol. 2012, 456–457, 110–120. [Google Scholar] [CrossRef]
- Aydogdu, M.; Firat, M. Estimation of failure rate in water distribution network using fuzzy clustering and LS-SVM methods. Water Resour. Manag. 2014, 29, 1575–1590. [Google Scholar] [CrossRef]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2004, 17, 113–126. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Brentan, B.M.; Luvizottom, E.; Herrera, M.; Izquierdo, J.; Pérez-García, R. Hybrid regression model for near real-time urban water demand forecasting. J. Comput. Appl. Math. 2017, 309, 532–541. [Google Scholar] [CrossRef]
- Dhanya, C.T.; Nagesh Kumar, D. Multivariate nonlinear ensemble prediction of daily chaotic rainfall with climate inputs. J. Hydrol. 2011, 403, 292–306. [Google Scholar] [CrossRef]
- Liu, X.; Fang, X.; Qin, Z.; Ye, C.; Xie, M. A Short-term forecasting algorithm for network traffic based on Chaos theory and SVM. J. Netw. Syst. Manag. 2010, 19, 427–447. [Google Scholar] [CrossRef]
- Yang, H.Y.; Ye, H.; Wang, G.; Khan, J.; Hu, T. Fuzzy neural very-short-term load forecasting based on chaotic dynamics reconstruction. Chaos Solitons Fractals 2006, 29, 462–469. [Google Scholar] [CrossRef]
- Bakker, M.; Vreeburg, J.H.G.; van Schagen, K.M.; Rietveld, L.C. A fully adaptive forecasting model for short-term drinking water demand. Environ. Model. Softw. 2013, 48, 141–151. [Google Scholar] [CrossRef]
- Cutore, P.; Campisano, A.; Kapelan, Z.; Modica, C.; Savic, D. Probabilistic prediction of urban water consumption using the SCEM-UA algorithm. Urban. Water J. 2008, 5, 125–132. [Google Scholar] [CrossRef]
- Al-Zahrani, M.A.; Abo-Monasar, A. Urban residential water demand prediction based on artificial neural networks and time series models. Water Resour. Manag. 2015, 29, 3651–3662. [Google Scholar] [CrossRef]
- Van Gestel, T.; Suykens, J.A.; Baesens, B.; Viaene, S.; Vanthienen, J.; Dedene, G. Benchmarking least squares support vector machine classifiers. Mach. Learn. 2004, 54, 5–32. [Google Scholar] [CrossRef]
- Van Gestel, T.; Suykens, J.A.; Baestaens, D.E.; Lambrechts, A.; Lanckriet, G.; Vandaele, B. Financial time series prediction using least squares support vector machines within the evidence framework. IEEE Trans. Neural Netw. 2001, 4, 809–821. [Google Scholar] [CrossRef]
- Li, D.; Han, M.; Wang, J. Chaotic time series prediction based on a novel robust echo state network. Trans. Neural Netw. Learn. Syst. 2012, 23, 787–799. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Lecture Notes in Mathematics; Rand, D.A., Young, L.S., Eds.; Springer: Berlin, Germany, 1981; Volume 898, pp. 366–381. [Google Scholar] [CrossRef]
- Lai, Y.C.; Ye, N. Recent developments in chaotic time series analysis. World Sci. Publ. Co. 2003, 13, 1383–1422. [Google Scholar] [CrossRef]
- Kim, H.S.; Eykholt, R.; Salas, J.D. Nonlinear dynamics, delay times, and embedding windows. Phys. D Nonlinear Phenom. 1999, 127, 48–60. [Google Scholar] [CrossRef]
- Dhanya, C.T.; Nagesh Kumar, D. Nonlinear ensemble prediction of chaotic daily rainfall. Adv. Water Resour. 2010, 33, 327–347. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- De Brabanter, K.; Karsmakers, P.; Ojeda, F. LS-SVMlab Toolbox User’s Guide Version 1.8; Katholieke Universiteit Leuven: Leuven, Belgium, 2011; p. 115. [Google Scholar]
- Adamowski, J.F. Development of a short-term river flood forecasting method for snowmelt driven floods based on wavelet and cross-wavelet analysis. J. Hydrol. 2008, 353, 247–266. [Google Scholar] [CrossRef]
- Wang, X.; Sun, Y.; Song, L.; Mei, C. An eco-environmental water demand based model for optimising water resources using hybrid genetic simulated annealing algorithm. Part II: Model application and results. J. Environ. Manag. 2009, 19, 2612–2619. [Google Scholar] [CrossRef] [PubMed]


| DMAs | Date of Data | Minimum (m³/h) | Maximum (m³/h) | Mean (m³/h) | Standard Deviation (m³/h) | Coefficient of Variation |
|---|---|---|---|---|---|---|
| DMA1 | 1 November–26 December | 120.00 | 2224.00 | 1192.03 | 467.81 | 0.39 |
| DMA2 | 1 November–26 December | 16.88 | 67.04 | 35.85 | 19.97 | 0.30 |
| DMA3 | 17 June–11 August | 28.48 | 95.12 | 63.45 | 15.14 | 0.24 |
| Models | Forecasting Category | Model Inputs |
|---|---|---|
| S_LSSVM | Single forecasting | Feature values of historical water demand data |
| H_LSSVM_Chaos | Hybrid forecasting | Chaotic time series of the errors of the initial forecasting |
| H_LSSVM_FS | Hybrid forecasting | Scalar time series of the errors of the initial forecasting |
| Models | DMA ID | γ | δ2 | m | τ |
|---|---|---|---|---|---|
| S_LSSVM | 1 | 0.1431 | 5.7407 | - | - |
| 2 | 0.0378 | 12.5104 | - | - | |
| 3 | 0.0457 | 13.4042 | - | - | |
| H_LSSVM_Chaos | 1 | 0.5827 | 5.7680 | 4 | 9 |
| 2 | 2.7872 | 4.5586 | 4 | 8 | |
| 3 | 3.1269 | 6.1330 | 3 | 11 |
| Models | DMA ID | R2 | MAE (m3/h) | MAPE (%) | RMSE (m3/h) |
|---|---|---|---|---|---|
| S_LSSVM | 1 | 0.9654 | 54.43 | 5.64 | 68.61 |
| 2 | 0.9722 | 1.31 | 4.06 | 1.76 | |
| 3 | 0.9447 | 2.70 | 5.84 | 3.31 | |
| H_LSSVM_Chaos | 1 | 0.9711 | 47.92 | 4.84 | 62.66 |
| 2 | 0.9817 | 1.08 | 3.15 | 1.43 | |
| 3 | 0.9701 | 1.86 | 3.47 | 2.44 | |
| H_LSSVM_FS | 1 | 0.9626 | 56.35 | 5.44 | 71.30 |
| 2 | 0.9782 | 1.18 | 3.33 | 1.56 | |
| 3 | 0.9533 | 2.20 | 3.72 | 3.05 |
| Methods | Model Parameters | Model Performance Indicators | Computation Time (s) | ||||
|---|---|---|---|---|---|---|---|
| γ | δ2 | R2 | MAE (m3/h) | MAPE (%) | RMSE (m3/h) | ||
| 1-level Bayesian inferring | 0.0183 | 13.6763 | 0.9632 | 1.56 | 4.98 | 2.03 | 179 |
| 3-level Bayesian inferring | 0.0378 | 12.5104 | 0.9722 | 1.31 | 4.06 | 1.76 | 1253 |
| Grid search | 0.1097 | 0.7515 | 0.9809 | 1.13 | 3.38 | 1.46 | 3685 |
| DMA ID | Forecasting Date | Forecasting Models | R2 | MAE (m3/h) | MAPE (%) | RMSE (m3/h) |
|---|---|---|---|---|---|---|
| 1 | 26 December | ARIMA | 0.9656 | 55.43 | 5.53 | 68.34 |
| H_LSSVM_Chaos | 0.9711 | 47.92 | 4.84 | 62.66 | ||
| 2 | 26 December | ARIMA | 0.9723 | 1.31 | 3.83 | 1.76 |
| H_LSSVM_Chaos | 0.9817 | 1.08 | 3.15 | 1.43 | ||
| 3 | 11 August | ARIMA | 0.9687 | 1.92 | 3.44 | 2.50 |
| H_LSSVM_Chaos | 0.9701 | 1.86 | 3.47 | 2.44 | ||
| 8–10 August (mean values) | ARIMA | 0.9687 | 1.90 | 3.49 | 2.44 | |
| H_LSSVM_Chaos | 0.9772 | 1.64 | 3.00 | 2.08 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Han, H.; Hou, B.; Diao, K. Hybrid Model for Short-Term Water Demand Forecasting Based on Error Correction Using Chaotic Time Series. Water 2020, 12, 1683. https://doi.org/10.3390/w12061683
Wu S, Han H, Hou B, Diao K. Hybrid Model for Short-Term Water Demand Forecasting Based on Error Correction Using Chaotic Time Series. Water. 2020; 12(6):1683. https://doi.org/10.3390/w12061683
Chicago/Turabian StyleWu, Shan, Hongquan Han, Benwei Hou, and Kegong Diao. 2020. "Hybrid Model for Short-Term Water Demand Forecasting Based on Error Correction Using Chaotic Time Series" Water 12, no. 6: 1683. https://doi.org/10.3390/w12061683
APA StyleWu, S., Han, H., Hou, B., & Diao, K. (2020). Hybrid Model for Short-Term Water Demand Forecasting Based on Error Correction Using Chaotic Time Series. Water, 12(6), 1683. https://doi.org/10.3390/w12061683






