Analysis of Streamflow Variability and Trends in the Meta River, Colombia
Abstract
:1. Introduction
2. Materials and Methods
2.1. Case Study: Meta River
2.2. Gauging Stations and Data Preprocessing
2.3. Statistical Analysis of Trends
2.3.1. MK Test
2.3.2. Modified Mann–Kendall (MMK) Test
2.3.3. Sen’s Slope Estimation
3. Results
3.1. Trend Analysis Results for the Average Monthly Streamflow
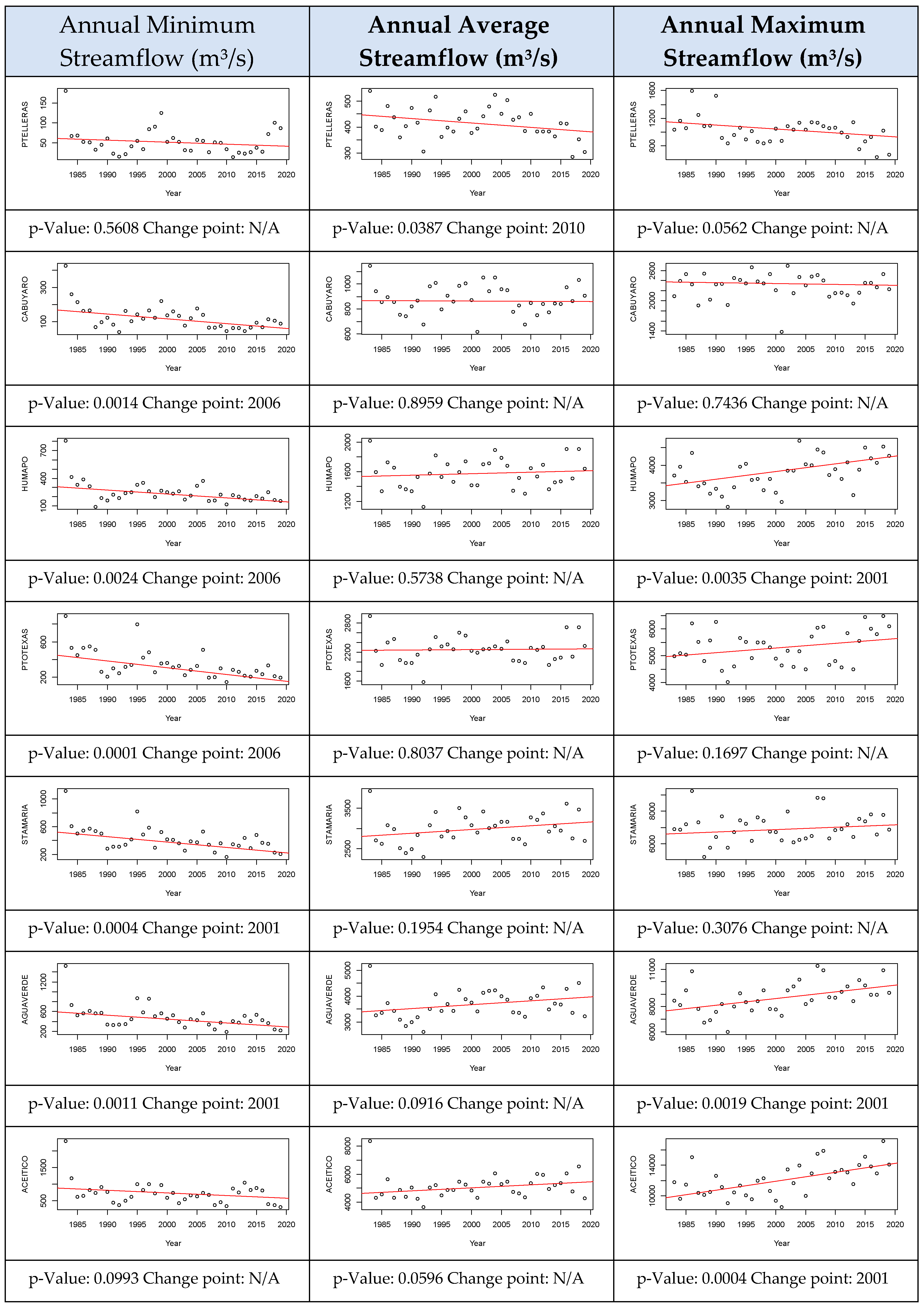
3.2. Trend Analysis Results for the Maximum Annual Streamflow
3.3. Trend Analysis Results for the Minimum Annual Streamflow
3.4. Trend Analysis Results for the Annual Average Streamflow
4. Discussion
4.1. Analysis of Trends Based on Their Spatial Distribution
4.2. Site-Specific Analysis of Trends
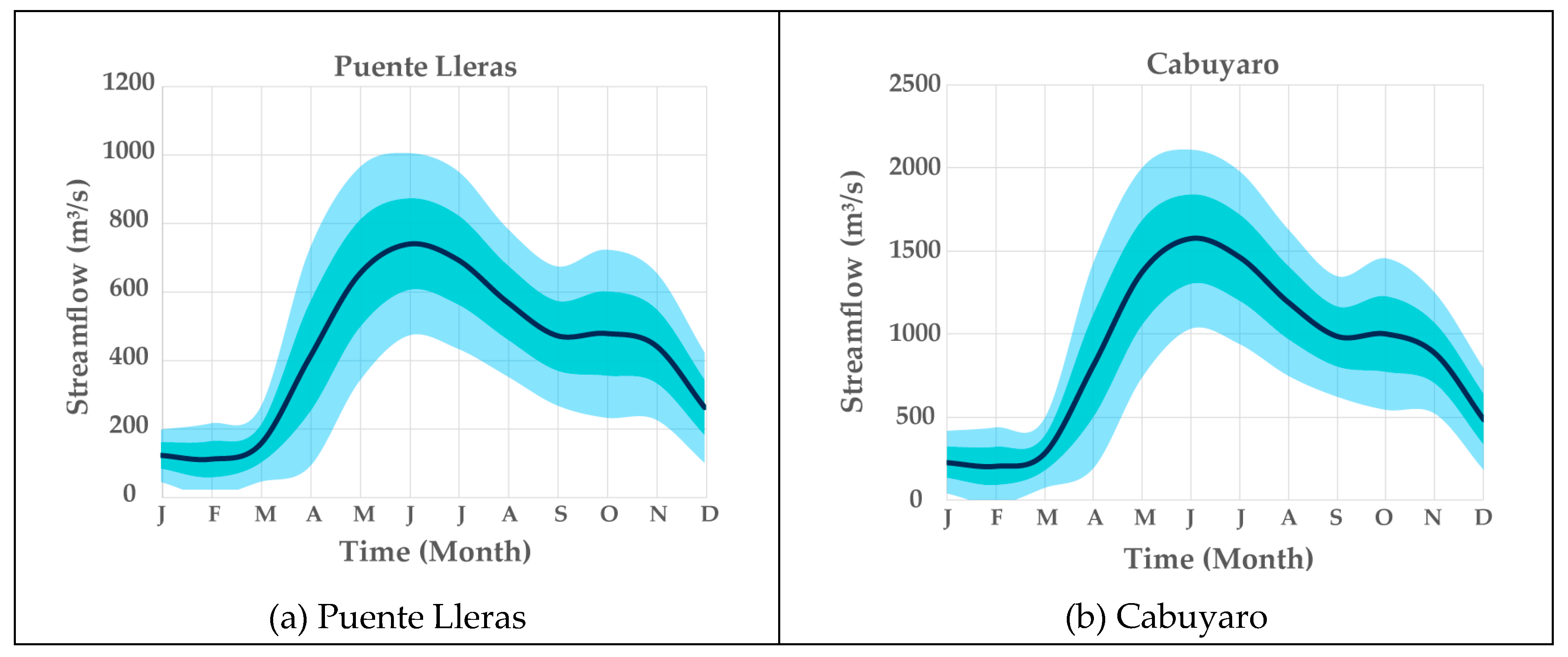
- Puente Lleras: The most upstream gauging station is the only station than exhibited significant trends in its annual average streamflow. Additionally, the annual maximum streamflow in this station also presents a downward trend; however, this represents less than 0.6% of the current average of the annual maximum streamflows in this station.
- Cabuyaro: The results for this gauging station indicate only two statistically significant trends for the monthly averages in February (downward) and April (upward), as well as in the annual minimum streamflow (downward).
- Humapo: This gauging station presented a significant downward trend for the average monthly streamflow for February and upward trends for the middle months of the wet season. As a noteworthy feature, this station, along with Aguaverde, exhibit significant trends that suggest decreasing annual minimum streamflows and increasing annual maximum discharges.
- Puerto Texas: The trend analysis for station indicated significant trends for the average streamflows of three months, two of them in the dry season (downward), and one increasing in the wet season. In terms of its annual features, only the minimum streamflow in this station presents a significant downward trend.
- Santa Maria: This gauging station showed a statistically significant downward trend for the monthly average of February, and upward trends at a 95% level of confidence for the monthly average streamflow for April, May, June, and November. This behavior does not seem to have an impact on the annual maximum and annual average streamflow, as they do not show significant trends.
- Aguaverde: The results for this station indicate the existence of statistically significant trends at a 95% level of confidence for the annual maximum (upward) and annual minimum streamflow (downward). The increase is more evident, and it can be explained by the behavior of the average monthly streamflow during the wet season, where most of these months show some of the steepest slopes of the entire set. Additionally, for November, the MMK test detected a significant trend, while the MK did not, evidencing the effects of correlation in trend detection.
- Aceitico: The most downstream gauging station exhibited increasing annual maximum streamflows, also presenting the steepest slope of the whole set of results. The trend detection through the MMK test differed from the MK test in the monthly averages of June and November. A previous study indicated that the average annual streamflow for the period between 1970 and 2000 displayed a downward trend [57], suggesting a change in the direction of the trend occurring over the last two decades.
5. Conclusions
- The hydrographs of the seven stations evidenced a unimodal distribution over the year, with peak flows occurring between June and July, and two clearly defined seasons.
- All of the seven streamflow gauging stations under analysis presented statistically significant trends for at least one of their annual variables (minimum, average, maximum). Perhaps the most relevant change is observed in the annual minima, as there are five consecutive stations in the upper and middle section of the river exhibiting significant decreasing trends at a 95% level of confidence. However, the specific streamflow changes corresponding to this variation are less than 0.2 l/s/km², which is well within the range of uncertainty associated with the IDEAM measurement processes. Similarly, the two most downstream stations exhibited significant upward trends for their annual maximum streamflow, corresponding to a change between 0.7 l/s/km² and 1.1 l/s/km², also within the estimated range of uncertainty.
- The Pettitt’s test was conducted for determining breakpoints in the time-series, in order to assess possible sources of change in the streamflow regimes of the Meta River, and the years 2001 and 2006 were found as the most common significant change points. However, power spectral density analysis and land cover change assessments conducted in this research suggest that there is no evidence for accepting the hypothesis that macroclimatic phenomena or anthropic actions on the local scale are the main cause of the trends for these time-series. Therefore, a future research direction is to conduct a multivariate analysis, including additional hydroclimatic parameters for evaluating if they contribute to the observed changes.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Grizzetti, B.; Lanzanova, D.; Liquete, C.; Reynaud, A.; Cardoso, A.C. Assessing water ecosystem services for water resource management. Environ. Sci. Policy 2016, 61, 194–203. [Google Scholar] [CrossRef]
- Silva, A.T. Introduction to Nonstationary Analysis and Modeling of Hydrologic Variables. In Fundamentals of Statistical Hydrology; Naghettini, M., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 537–577. [Google Scholar]
- Arfan, M.; Lund, J.; Hassan, D.; Saleem, M.; Ahmad, A. Assessment of Spatial and Temporal Flow Variability of the Indus River. Resources 2019, 8, 103. [Google Scholar] [CrossRef] [Green Version]
- Ali, R.; Ismael, A.; Heryansyah, A.; Nawaz, N. Long Term Historic Changes in the Flow of Lesser Zab River, Iraq. Hydrology 2019, 6, 22. [Google Scholar] [CrossRef] [Green Version]
- Tadese, M.T.; Kumar, L.; Koech, R.; Zemadim, B. Hydro-Climatic Variability: A Characterisation and Trend Study of the Awash River Basin, Ethiopia. Hydrology 2019, 6, 35. [Google Scholar] [CrossRef] [Green Version]
- Langat, P.; Kumar, L.; Koech, R. Temporal Variability and Trends of Rainfall and Streamflow in Tana River Basin, Kenya. Sustainability 2017, 9, 1963. [Google Scholar] [CrossRef] [Green Version]
- Yilmaz, A.G.; Perera, B.J.C. Spatiotemporal Trend Analysis of Extreme Rainfall Events in Victoria, Australia. Water Resour. Manag. 2015, 29, 4465–4480. [Google Scholar] [CrossRef]
- Wdowikowski, M.; Kaźmierczak, B.; Ledvinka, O. Maximum daily rainfall analysis at selected meteorological stations in the upper Lusatian Neisse River basin. Meteorol. Hydrol. Water Manag. 2016, 4, 53–63. [Google Scholar] [CrossRef] [Green Version]
- Pellicciotti, F.; Burlando, P.; Van Vliet, K. Recent trends in precipitation and streamflow in the Aconcagua River Basin, central Chile. In IAHS Assembly; IAHS Publ.: Foz do Iguaçu, Brazil, 2007; pp. 1–22. [Google Scholar]
- Su, L.; Miao, C.; Kong, D.; Duan, Q.; Lei, X.; Hou, Q.; Li, H. Long-term trends in global river flow and the causal relationships between river flow and ocean signals. J. Hydrol. 2018, 563, 818–833. [Google Scholar] [CrossRef]
- Feng, J.; Li, D.; Wang, T.; Liu, Q.; Deng, L.; Zhao, L. Acceleration of the Extreme Sea Level Rise Along the Chinese Coast. Earth Space Sci. 2019, 6, 1942–1956. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.V. Methods for Analysis of Trends and Changes in Hydroclimatological Time-Series. In Trends and Changes in Hydroclimatic Variables; Teegavarapu, R.S.V., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–89. [Google Scholar]
- Şener, Ş.; Şener, E.; Davraz, A. Evaluation of water quality using water quality index (WQI) method and GIS in Aksu River (SW-Turkey). Sci. Total Environ. 2017, 584–585, 131–144. [Google Scholar] [CrossRef]
- Ndehedehe, C.E.; Ferreira, V.G. Assessing land water storage dynamics over South America. J. Hydrol. 2020, 580, 124339. [Google Scholar] [CrossRef]
- Vega-Jácome, F.; Lavado-Casimiro, W.S.; Felipe-Obando, O.G. Assessing hydrological changes in a regulated river system over the last 90 years in Rimac Basin (Peru). Theor. Appl. Climatol. 2018, 132, 347–362. [Google Scholar] [CrossRef] [Green Version]
- Morán-Tejeda, E.; Bazo, J.; López-Moreno, J.I.; Aguilar, E.; Azorín-Molina, C.; Sanchez-Lorenzo, A.; Martínez, R.; Nieto, J.J.; Mejía, R.; Martín-Hernández, N.; et al. Climate trends and variability in Ecuador (1966–2011). Int. J. Climatol. 2016, 36, 3839–3855. [Google Scholar] [CrossRef] [Green Version]
- Seoane, R.; López, P. Assessing the effects of climate change on the hydrological regime of the Limay River basin. GeoJournal 2007, 70, 251–256. [Google Scholar] [CrossRef]
- Vich, A.I.J.; López, P.M.; Schumacher, M.C. Trend detection in the water regime of the main rivers of the Province of Mendoza, Argentina. GeoJournal 2007, 70, 233–243. [Google Scholar] [CrossRef]
- De Santos, V.O.; Nishiyama, L. Tendências Hidrológicas no Alto Curso da Bacia Hidrográfica do Rio Uberaba, em Minas Gerais. Caminhos Geogr. 2016, 17, 196–212. [Google Scholar] [CrossRef]
- De Alcântara, L.R.P.; de Costa, I.R.A.; de Barros, V.H.O.; Santos Neto, S.M.; Coutinho, A.P.; Antonino, A.C.D. Análise de tendência para dados pluviométricos no município de Toritama-PE. J. Environ. Anal. Prog. 2019, 4, 130. [Google Scholar] [CrossRef] [Green Version]
- De Quadros, L.E.; de Mello, E.L.; Gomes, B.M.; Araujo, F.C. Rainfall trends for the State of Paraná: Present and future climate. Ambient. Agua Interdiscip. J. Appl. Sci. 2019, 14, 1. [Google Scholar] [CrossRef]
- Rodrigues, A.L.M.; Reis, G.B.; dos Santos, M.T.; da Silva, D.D.; dos Santos, V.J.; de Siqueira Castro, J.; Calijuri, M.L. Influence of land use and land cover’s change on the hydrological regime at a Brazilian southeast urbanized watershed. Environ. Earth Sci. 2019, 78, 595. [Google Scholar] [CrossRef]
- De Santos, V.O.; de Naves, J.G.P. Low flow diagnosis on upper course of Uberaba river basin. Ambiência 2016, 12, 859–868. [Google Scholar] [CrossRef]
- Trindade, A.L.C.; de Almeida, K.C.B.; Barbosa, P.E.; Oliveira, S.M.A.C. Tendências temporais e espaciais da qualidade das águas superficiais da sub-bacia do Rio das Velhas, estado de Minas Gerais. Eng. Sanit. Ambient. 2016, 22, 13–24. [Google Scholar] [CrossRef] [Green Version]
- Restrepo, J.C.; Ortíz, J.C.; Maza, M.; Otero, L.; Alvarado, M.; Aguirre, J. Estimating fluvial discharge in the Caribbean seaboard of Colombia: Magnitude, variability and extreme events. Coast. Eng. Proc. 2012, 1, 44. [Google Scholar] [CrossRef] [Green Version]
- Restrepo, J.C.; Ortíz, J.C.; Pierini, J.; Schrottke, K.; Maza, M.; Otero, L.; Aguirre, J. Freshwater discharge into the Caribbean Sea from the rivers of Northwestern South America (Colombia): Magnitude, variability and recent changes. J. Hydrol. 2014, 509, 266–281. [Google Scholar] [CrossRef]
- Restrepo, J.D.; Escobar, H.A. Sediment load trends in the Magdalena River basin (1980–2010): Anthropogenic and climate-induced causes. Geomorphology 2018, 302, 76–91. [Google Scholar] [CrossRef]
- Restrepo, J.D.; Escobar, R.; Tosic, M. Fluvial fluxes from the Magdalena River into Cartagena Bay, Caribbean Colombia: Trends, future scenarios, and connections with upstream human impacts. Geomorphology 2018, 302, 92–105. [Google Scholar] [CrossRef]
- Ávila, Á.; Guerrero, F.; Escobar, Y.; Justino, F. Recent Precipitation Trends and Floods in the Colombian Andes. Water 2019, 11, 379. [Google Scholar] [CrossRef] [Green Version]
- Puertas-Orozco, O.L.; Carvajal-Escobar, Y.; Quintero-Angel, M. Estudio de tendencias de la precipitación mensual en la cuenca alta-media del río Cauca, Colombia. DYNA 2011, 78, 112–120. [Google Scholar]
- Carmona, A.M.; Poveda, G. Detection of long-term trends in monthly hydro-climatic series of Colombia through Empirical Mode Decomposition. Clim. Change 2014, 123, 301–313. [Google Scholar] [CrossRef]
- Ardila Luna, D.C. El río Meta y los proyectos para la integración de los Llanos Orientales colombianos, desde la Colonia hasta el siglo XXI. Anu. Hist. Reg. Front. 2016, 21, 265–283. [Google Scholar]
- Ministerio de Transporte Plan Maestro Fluvial de Colombia 2015. 2015; 108. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=2ahUKEwi7x8zh4MHpAhVNCqYKHQb1C6EQFjAAegQIAxAB&url=https%3A%2F%2Fwww.mintransporte.gov.co%2Fdescargar.php%3FidFile%3D13276&usg=AOvVaw2Eky0KTUsR1_G0JSnb7I_1 (accessed on 15 May 2020).
- Liu, L.; Wen, Y.; Liang, Y.; Zhang, F.; Yang, T. Extreme weather impacts on inland waterways transport of Yangtze River. Atmosphere (Basel) 2019, 10, 133. [Google Scholar] [CrossRef] [Green Version]
- Actualización de los Estudios y Diseños para la Navegabilidad del río Meta entre Cabuyaro (K804) y Puerto Carreño (K0); Universidad del Norte: Barranquilla, Colombia, 2013.
- Acuña, G.J.; Ávila, H.; Canales, F.A. River Model Calibration Based on Design of Experiments Theory. A Case Study: Meta River, Colombia. Water 2019, 11, 1382. [Google Scholar] [CrossRef] [Green Version]
- Warne, A.G.; Meade, R.H.; White, W.A.; Guevara, E.H.; Gibeaut, J.; Smyth, R.C.; Aslan, A.; Tremblay, T. Regional controls on geomorphology, hydrology, and ecosystem integrity in the Orinoco Delta, Venezuela. Geomorphology 2002, 44, 273–307. [Google Scholar] [CrossRef] [Green Version]
- IDEAM. Estudio Nacional del Agua; Instituto de Hidrología, Meteorología y Estudios Ambientales: Bogotá DC, Colombia, 2010.
- IDEAM. Consulta y Descarga de Datos Hidrometeorológicos. Available online: http://dhime.ideam.gov.co/atencionciudadano/ (accessed on 10 October 2019).
- Umar, D.A.; Ramli, M.F.; Aris, A.Z.; Jamil, N.R.; Aderemi, A.A. Evidence of climate variability from rainfall and temperature fluctuations in semi-arid region of the tropics. Atmos. Res. 2019, 224, 52–64. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Chung, E.-S.; Al-Abadi, A.M. Long-term trends in daily temperature extremes in Iraq. Atmos. Res. 2017, 198, 97–107. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Kibria, K.N.; Ahiablame, L.; Hay, C.; Djira, G. Streamflow trends and responses to climate variability and land cover change in South Dakota. Hydrology 2016, 3, 2. [Google Scholar] [CrossRef] [Green Version]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Winslow, L.A.; Read, J.S.; Hansen, G.J.A.; Hanson, P.C. Small lakes show muted climate change signal in deepwater temperatures. Geophys. Res. Lett. 2015, 42, 355–361. [Google Scholar] [CrossRef]
- Mohd Razali, N.; Bee Wah, Y. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Lozano Blanco, L.J.; Meseguer Zapata, V.F.; De Juan García, D. Statistical analysis of laboratory results of Zn wastes leaching. Hydrometallurgy 1999, 54, 41–48. [Google Scholar] [CrossRef]
- Ahmad, I.; Tang, D.; Wang, T.; Wang, M.; Wagan, B. Precipitation trends over time using Mann-Kendall and spearman’s Rho tests in swat river basin, Pakistan. Adv. Meteorol. 2015, 2015, 15. [Google Scholar] [CrossRef] [Green Version]
- Pohlert, T. Package “Trend”: Non-Parametric Trend Tests and Change-Point Detection. Available online: https://cran.r-project.org/package=trend (accessed on 3 March 2020).
- Xu, S.; Qin, M.; Ding, S.; Zhao, Q.; Liu, H.; Li, C.; Yang, X.; Li, Y.; Yang, J.; Ji, X. The impacts of climate variation and land use changes on streamflow in the Yihe River, China. Water (Switzerland) 2019, 11, 887. [Google Scholar] [CrossRef] [Green Version]
- Guarín Giraldo, G.W.; Poveda, G. Variabilidad espacial y temporal del almacenamiento de agua en el suelo en Colombia. Rev. Acad. Colomb. Ciencias Exactas Físicas Nat. 2013, 37, 89–113. [Google Scholar]
- Estudio Nacional del Agua 2018; IDEAM: Bogota, Colombia, 2019.
- Guse, B.; Kail, J.; Radinger, J.; Schröder, M.; Kiesel, J.; Hering, D.; Wolter, C.; Fohrer, N. Eco-hydrologic model cascades: Simulating land use and climate change impacts on hydrology, hydraulics and habitats for fish and macroinvertebrates. Sci. Total Environ. 2015, 533, 542–556. [Google Scholar] [CrossRef]
- IDEAM. Leyenda Nacional de Coberturas de la Tierra. Metodología CORINE Land Cover Adaptada para Colombia Escala 1:100.000; Instituto de Hidrología, Meteorología y Estudios Ambientales: Bogota, DC, Colombia, 2010.
- Armenteras, D.; González, T.; Meza, M.; Ramírez-Delgado, J.P.; Cabrera, E.; Galindo, G.; Yepes, A. Causas de Degradación Forestal en Colombia: Una Primera Aproximación; Universidad Nacional de Colombia Sede Bogotá, Instituto de Hidrología, Meteorología y Estudios Ambientales de Colombia-IDEAM, Programa ONU-REDD: Bogota, DC, Colombia, 2018.
- Food and Agriculture Organization of the United Nations FAOSTAT. Available online: http://www.fao.org/faostat/en/#data/LC/visualize (accessed on 20 April 2020).
- IDEAM. Informe Anual Sobre el Estado del Medio Ambiente y los Recursos Naturales Renovables de Colombia; Imprenta Nacional: Bogota, Colombia, 2004.
- Torres Pungo, K.; Rivera, H.G.; Rivera, M.; Fuentes Bacca, J.B.; León Alvarez, M.A. Identificación de la incertidumbre en el proceso estocástico de caudales medios en el río Fonce (San Gil–Santander). Av. Investig. Ing. 2015, 12, 1. [Google Scholar] [CrossRef] [Green Version]
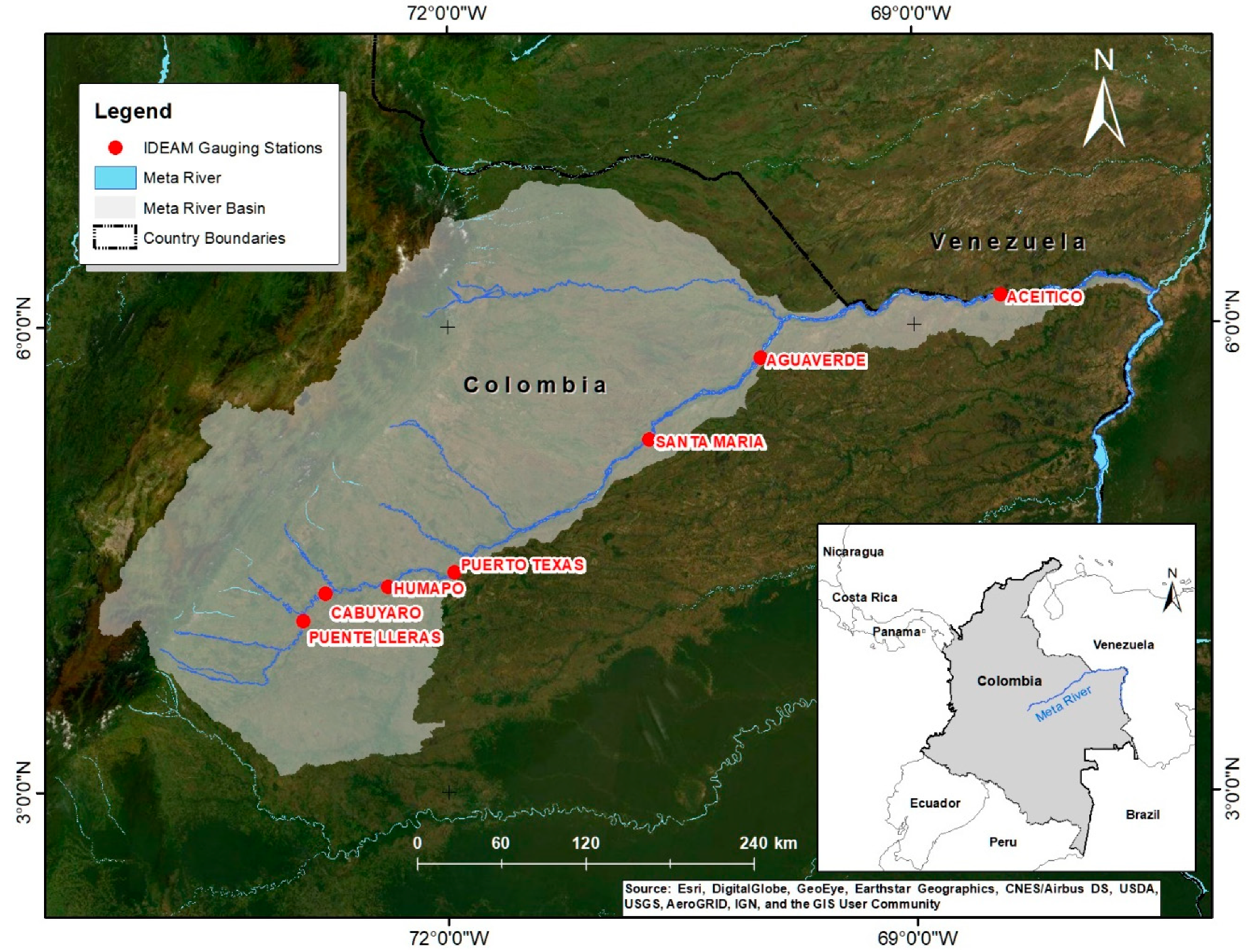



| Site No. | Station Code | Station Name | Type | Location Coordinates | Area (km²) | Records Available |
|---|---|---|---|---|---|---|
| 1 | 35017020 | Puente Lleras | AUTO | 4°06′10.9″, –72°56′11.0″ | 8170 | 01/1977 to 10/2019 |
| 2 | 35107030 | Cabuyaro | CONV | 4°16′51.6″, –72°47′35.9″ | 13,951 | 01/1977 to 10/2019 |
| 3 | 35117010 | Humapo | AUTO | 4°19′40.0″, –72°23′29.7″ | 23,033 | 04/1978 to 10/2019 |
| 4 | 35177020 | Puerto Texas | CONV | 4°25′06.2″, –71°57′39.5″ | 40,373 | 04/1978 to10/2019 |
| 5 | 35267030 | Santa María | CONV | 5°16′15.0″, –70°42′20.1″ | 67,325 | 02/1983 to 08/2019 |
| 6 | 35267080 | Aguaverde | AUTO | 5°47′31.0″, –69°59′16.4″ | 76,137 | 06/1983 to 08/2019 |
| 7 | 35257040 | Aceitico | CONV | 6°11′00.8″, –68°26′29.3″ | 104,135 | 02/1983 to 08/2019 |
| Test | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PUENTE LLERAS | ||||||||||||
| Normality | YES | NO | YES | YES | YES | YES | YES | YES | YES | NO | YES | YES |
| MK ZS | 0.68 | −0.72 | 0.31 | 2.22 | −0.37 | −1.69 | −2.11 | −1.40 | −2.11 | −2.47 | −0.12 | −0.04 |
| MMK ZS | 0.68 | −0.72 | 0.31 | 5.25 | −0.37 | −1.91 | −2.55 | −1.40 | −2.42 | −2.47 | −0.12 | −0.04 |
| SS (m³/s) | 0.47 | −0.54 | 0.30 | 5.27 | −0.78 | −3.79 | −4.48 | −2.34 | −3.42 | −3.96 | −0.15 | −0.20 |
| CABUYARO | ||||||||||||
| Normality | NO | NO | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES |
| MK ZS | −1.29 | −2.33 | −1.38 | 2.41 | 1.65 | 0.64 | −0.46 | −1.57 | −1.02 | −1.02 | 1.35 | −0.23 |
| MMK ZS | −1.63 | −2.33 | −1.38 | 3.89 | 1.65 | 0.82 | −0.46 | −1.57 | −1.02 | −1.02 | 1.35 | −0.23 |
| SS (m³/s) | −1.89 | −3.71 | −2.20 | 11.96 | 9.51 | 3.70 | −2.47 | −6.31 | −3.69 | −4.01 | 4.16 | −0.56 |
| HUMAPO | ||||||||||||
| Normality | YES | NO | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES |
| MK ZS | −1.08 | −2.68 | −1.62 | 1.78 | 2.14 | 2.42 | 1.32 | −0.31 | −1.35 | −0.86 | 0.99 | −0.59 |
| MMK ZS | −1.08 | −3.73 | −1.62 | 1.78 | 2.14 | 3.07 | 1.16 | −0.42 | −1.35 | −0.86 | 1.45 | −0.59 |
| SS (m³/s) | −2.45 | −5.18 | −4.65 | 15.62 | 20.18 | 17.53 | 9.86 | −2.60 | −7.78 | −6.86 | 4.53 | −2.21 |
| PUERTO TEXAS | ||||||||||||
| Normality | YES | NO | YES | NO | YES | YES | YES | YES | YES | YES | YES | YES |
| MK ZS | −1.89 | −3.26 | −1.81 | 2.00 | 1.78 | 1.32 | 0.85 | −0.29 | −2.00 | −1.21 | 1.08 | −0.23 |
| MMK ZS | −1.89 | −4.42 | −1.81 | 2.00 | 1.78 | 1.32 | 1.01 | −0.38 | −2.27 | −1.21 | 1.32 | −0.19 |
| SS (m³/s) | −5.94 | −8.76 | −5.76 | 20.69 | 27.00 | 11.91 | 8.72 | −4.66 | −14.40 | −13.11 | 7.26 | −1.09 |
| SANTA MARIA | ||||||||||||
| Normality | YES | YES | YES | NO | YES | YES | YES | YES | YES | YES | NO | NO |
| MK ZS | −0.31 | −2.79 | −1.51 | 2.36 | 2.82 | 2.55 | 1.19 | 0.67 | 0.56 | 0.07 | 2.25 | 0.94 |
| MMK ZS | −0.36 | −3.66 | −1.51 | 2.36 | 3.06 | 3.44 | 1.86 | 0.67 | 0.73 | 0.07 | 2.08 | 1.02 |
| SS (m³/s) | −1.27 | −8.41 | −4.74 | 27.24 | 52.47 | 32.14 | 16.43 | 11.28 | 3.41 | 1.11 | 21.13 | 6.97 |
| AGUAVERDE | ||||||||||||
| Normality | YES | YES | YES | NO | NO | YES | YES | YES | YES | YES | NO | YES |
| MK ZS | −0.42 | −2.78 | −1.57 | 2.00 | 2.82 | 2.81 | 2.63 | 1.02 | 0.01 | −0.10 | 1.40 | 0.12 |
| MMK ZS | −0.42 | −13.88 | −1.57 | 2.00 | 4.37 | 6.81 | 4.05 | 1.02 | 0.01 | −0.10 | 2.14 | 0.10 |
| SS (m³/s) | −1.63 | −10.19 | −6.44 | 29.89 | 66.88 | 60.55 | 49.64 | 19.88 | −0.04 | −2.47 | 17.51 | 1.51 |
| ACEITICO | ||||||||||||
| Normality | YES | YES | YES | NO | YES | YES | YES | NO | YES | YES | NO | YES |
| MK ZS | 0.07 | −1.29 | −1.43 | 2.30 | 2.30 | 1.79 | 3.02 | 1.19 | −0.04 | 0.10 | 1.46 | 0.78 |
| MMK ZS | 0.07 | −1.29 | −1.43 | 2.30 | 3.62 | 3.70 | 2.47 | 1.19 | −0.04 | 0.10 | 2.41 | 1.00 |
| SS (m³/s) | 1.05 | −7.43 | −9.02 | 36.95 | 68.33 | 67.31 | 87.42 | 34.36 | −0.97 | 1.92 | 24.06 | 8.96 |
| No | Station | Mean (m³/s) | Std.Dev (m³/s) | Normal Dist. | MK ZS | MMK ZS | SS (m³/s) | AC |
|---|---|---|---|---|---|---|---|---|
| 1 | Puente Lleras | 1019.81 | 189.18 | NO | −2.09 | −1.98 | −5.59 | NO |
| 2 | Cabuyaro | 2282.23 | 249.88 | NO | −0.33 | −0.48 | −1.66 | NO |
| 3 | Humapo | 3775.44 | 471.11 | YES | 2.92 | 3.42 | 21.91 | YES |
| 4 | Puerto Texas | 5308.08 | 642.27 | YES | 1.37 | 1.48 | 17.34 | NO |
| 5 | Santa Maria | 6995.69 | 861.26 | YES | 1.02 | 1.02 | 14.15 | NO |
| 6 | Aguaverde | 8765.48 | 1202.21 | YES | 3.10 | 3.10 | 53.15 | YES |
| 7 | Aceitico | 12163.66 | 2090.51 | YES | 3.52 | 3.00 | 115.74 | YES |
| No | Station | Mean (m³/s) | Std.Dev (m³/s) | Normal Dist. | MK ZS | MMK ZS | SS (m³/s) | AC |
|---|---|---|---|---|---|---|---|---|
| 1 | Puente Lleras | 53.103 | 32.934 | NO | −1.190 | −1.027 | −0.508 | YES |
| 2 | Cabuyaro | 123.700 | 72.895 | NO | −3.335 | −3.230 | −2.811 | YES |
| 3 | Humapo | 246.449 | 121.936 | NO | −3.047 | −3.855 | −4.175 | YES |
| 4 | Puerto Texas | 347.865 | 162.288 | NO | −3.924 | −3.924 | −7.623 | YES |
| 5 | Santa Maria | 420.324 | 177.590 | NO | −3.518 | −3.518 | −7.705 | NO |
| 6 | Aguaverde | 486.232 | 235.372 | NO | −3.270 | −2.810 | −7.794 | NO |
| 7 | Aceitico | 727.595 | 346.999 | NO | −1.648 | −1.216 | −8.270 | NO |
| No | Station | Mean (m³/s) | Std.Dev (m³/s) | Normal Dist. | MK ZS | MMK ZS | SS (m³/s) | AC |
|---|---|---|---|---|---|---|---|---|
| 1 | Puente Lleras | 415.24 | 59.90 | YES | −2.05 | −2.05 | −1.71 | NO |
| 2 | Cabuyaro | 877.79 | 115.65 | YES | −0.12 | −0.12 | −0.25 | NO |
| 3 | Humapo | 1578.73 | 200.03 | YES | 0.56 | 0.56 | 2.11 | NO |
| 4 | Puerto Texas | 2252.54 | 260.18 | YES | 0.25 | 0.25 | 0.87 | YES |
| 5 | Santa Maria | 2996.25 | 355.98 | YES | 1.55 | 1.29 | 9.18 | YES |
| 6 | Aguaverde | 3673.22 | 515.11 | YES | 1.69 | 1.69 | 15.19 | NO |
| 7 | Aceitico | 5126.50 | 829.72 | YES | 1.90 | 1.90 | 21.81 | NO |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arrieta-Castro, M.; Donado-Rodríguez, A.; Acuña, G.J.; Canales, F.A.; Teegavarapu, R.S.V.; Kaźmierczak, B. Analysis of Streamflow Variability and Trends in the Meta River, Colombia. Water 2020, 12, 1451. https://doi.org/10.3390/w12051451
Arrieta-Castro M, Donado-Rodríguez A, Acuña GJ, Canales FA, Teegavarapu RSV, Kaźmierczak B. Analysis of Streamflow Variability and Trends in the Meta River, Colombia. Water. 2020; 12(5):1451. https://doi.org/10.3390/w12051451
Chicago/Turabian StyleArrieta-Castro, Marco, Adriana Donado-Rodríguez, Guillermo J. Acuña, Fausto A. Canales, Ramesh S. V. Teegavarapu, and Bartosz Kaźmierczak. 2020. "Analysis of Streamflow Variability and Trends in the Meta River, Colombia" Water 12, no. 5: 1451. https://doi.org/10.3390/w12051451
APA StyleArrieta-Castro, M., Donado-Rodríguez, A., Acuña, G. J., Canales, F. A., Teegavarapu, R. S. V., & Kaźmierczak, B. (2020). Analysis of Streamflow Variability and Trends in the Meta River, Colombia. Water, 12(5), 1451. https://doi.org/10.3390/w12051451







