Uncertainty Assessment of Urban Hydrological Modelling from a Multiple Objective Perspective
Abstract
1. Introduction
2. Methods
- The performance of the parameter sets was comprehensively investigated by considering the threshold of each objective function. Only the parameter sets for which all objective function values exceeded their threshold were considered as behavioral.
- An integrated likelihood measure was carried out using TOPSIS, which was used as a weighting factor to derive the posterior probability density functions for both the parameters and the predictions. The prominent advantage of TOPSIS is that different types of objective functions can be easily integrated into a unified evaluation index by setting the benefit criteria and loss criteria.
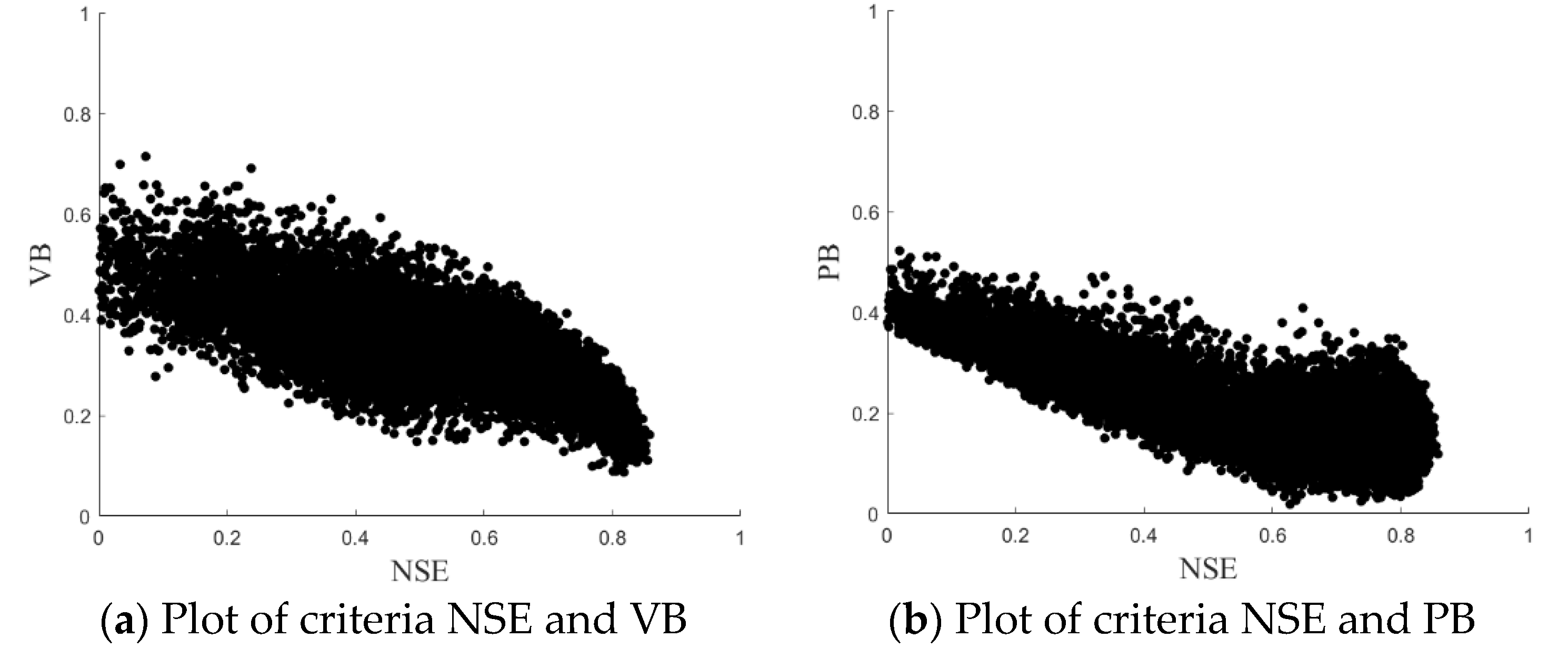
- Instead of a unique likelihood measure, multiple thresholds from multiple criteria are used to determine the behavioral parameter sets. In urban stormwater management, not only the precision of the flood process but also the precision of the flood volume and flood peak is considered by the modeler [31]. A behavior parameter set should be able to achieve these objectives. The criteria typically used in flood prediction are as follows:andwhere is the observed flow, is the simulated flow, is the average measured flow, is the average simulated flow, and n is the number of the observed flow points.In the above formula, NSE is the widely used Nash–Sutcliffe efficiency index [32]. The flood volume bias (VB) and flood peak bias (PB) are the modified expressions for the flood volume and flood peak deviation [18,33], respectively. The parameter R represents the consistency between the observed flow and the simulated flow [34]. The threshold of these criteria can be defined with reference to practical demand [35]. The reasonable range of the four criteria is between 0 to 1. The optimum value of NSE and R is 1, and optimum value of VB and PB is 0, which means the simulation results of the model completely fit the measured results. In this study, the behavioral parameter sets whose likelihood values of the four criteria were greater than the corresponding thresholds were chosen for further analysis.
- TOPSIS, which is a well-known MCDA method and can provide the ranking order of all alternatives [36,37], was employed in the calculation of the aggregate likelihood value L() of the behavioral parameter set .In the TOPSIS method, the four criteria of all parameter sets should be normalized by the classification of the benefit and cost criterion, where the benefit criterion means that a larger value is more valuable, and vice-versa for the cost criterion [37]. In this study, NSE and R are benefit criteria, while VB and PB are cost criteria; xij is the ith criterion of the jth parameter set. For the benefit criteria, the normalized value (rij) is calculated as follows:For the cost criteria, the normalized value (rij) is calculated as follows:In many situations, the criterion should be weighted according its importance [36]. Because it is difficult to identify which criterion is more important, we assume that all criteria are equally important. The ideal solution and negative-ideal solution can be calculated as follows:Then, the separation of each alternative from the ideal and negative-ideal solutions are expressed, respectively, as follows:The aggregate likelihood value L() is evaluated by comparing the distance from the ideal solution and the distance from the negative-ideal solution:
- Finally, the predictions from the behavioral parameter sets are ranked in the order of the likelihood weights W(i), which is defined as follows:where N is the number of behavioral parameter sets. Additionally, the cumulative probability distribution for the ranked discharge predictions can be obtained as follows:where Q denotes the discharge, and Qi is the discharge prediction ranked at the ith position; n has the same meaning as in Equation (2). According to the cumulative probability distribution, the uncertainty bound can be obtained for a given certainty level.
3. Study Area and SWMM Model
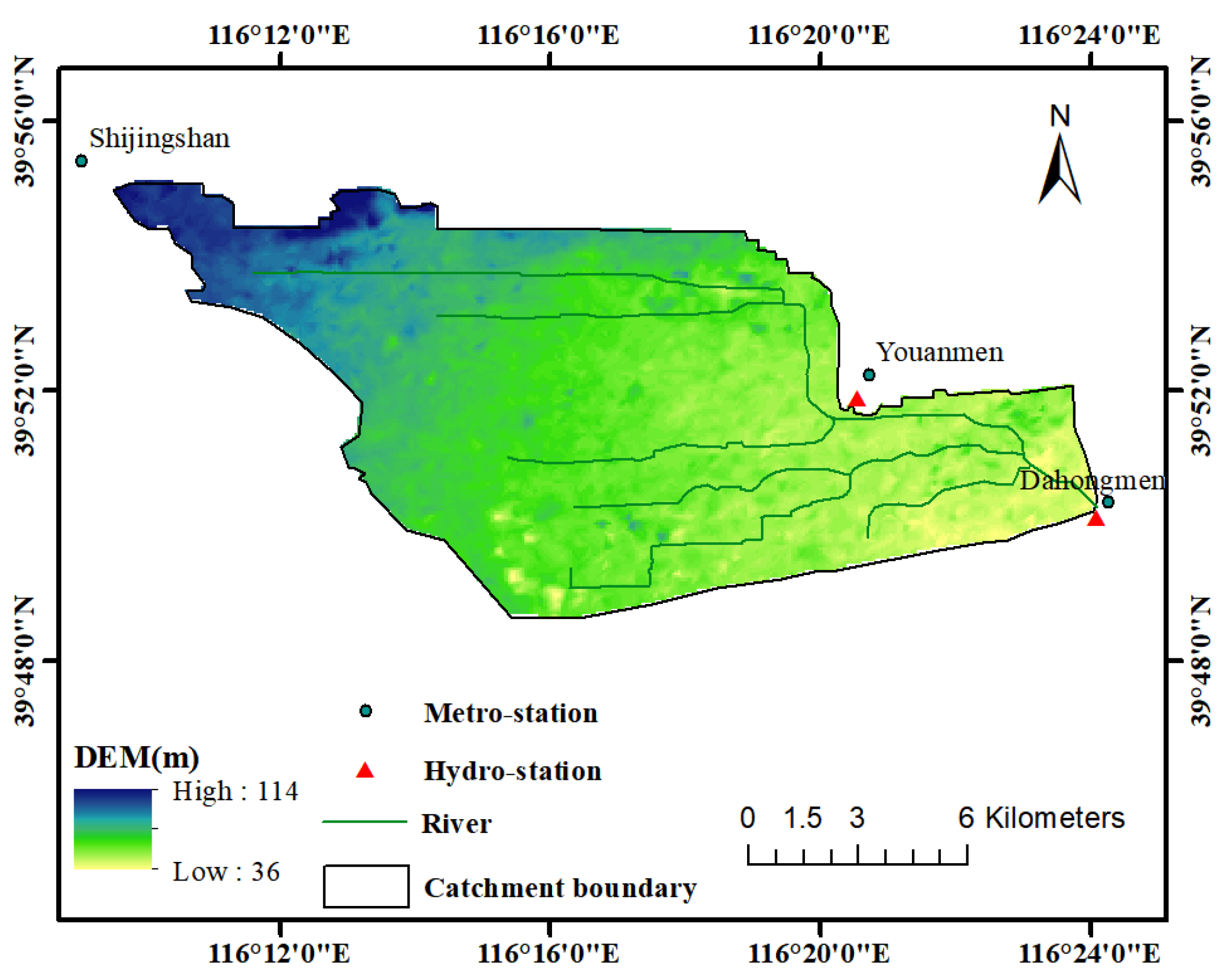
3.1. Study Area
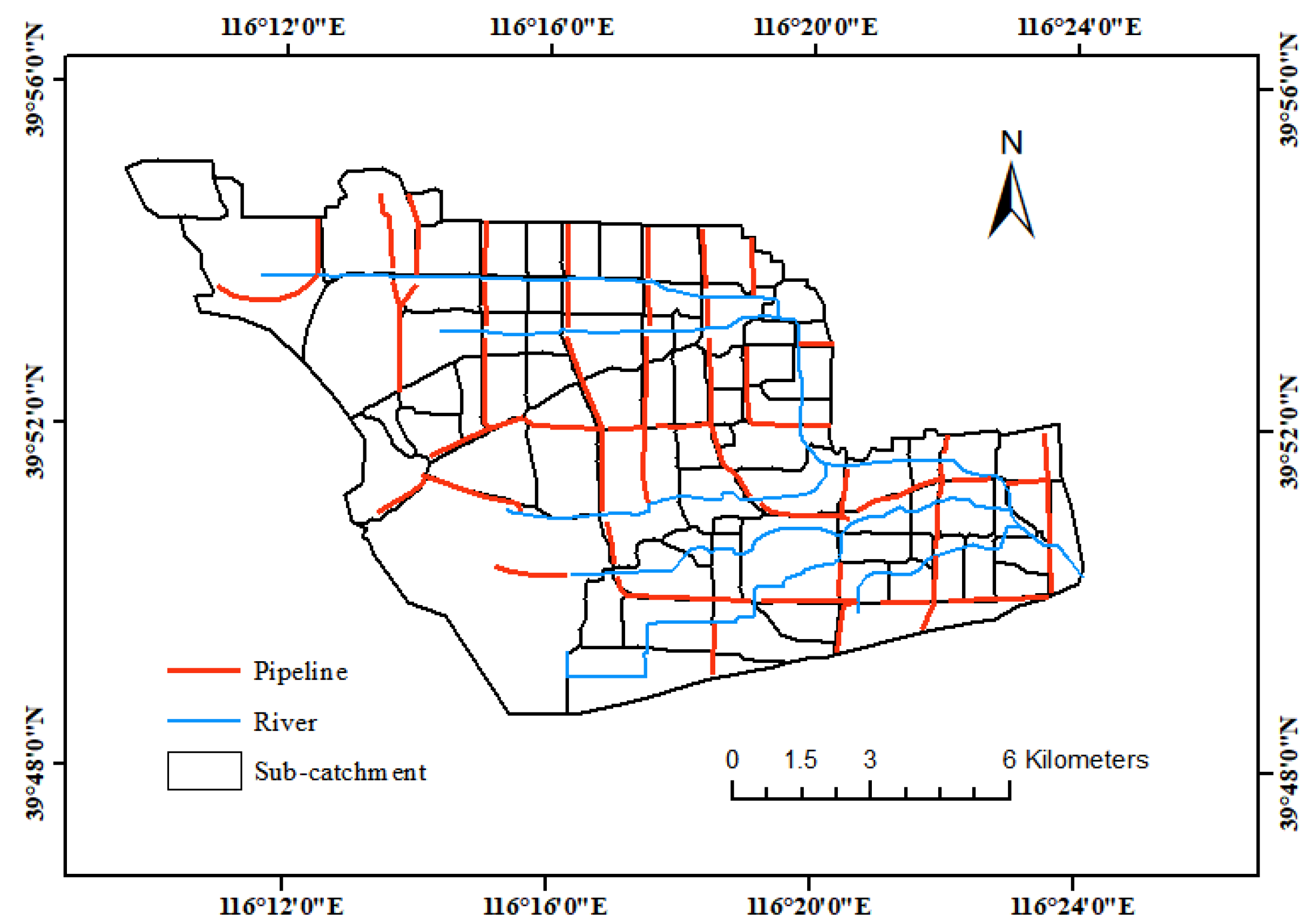
3.2. SWMM Model
3.3. Interval Evaluation Index
4. Results
4.1. Comparison of Different Acceptability Thresholds
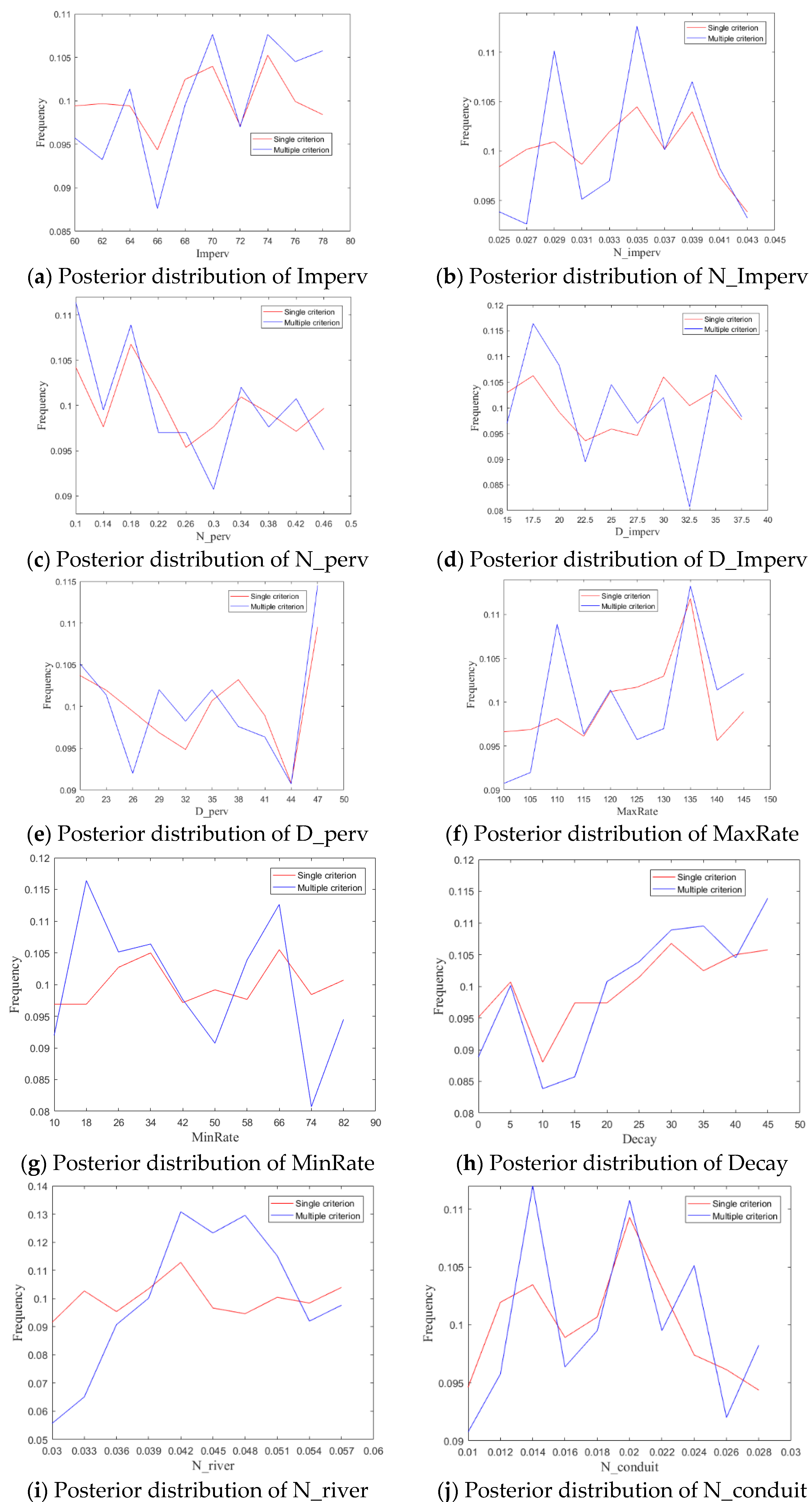
4.2. Comparison of Posterior Distribution
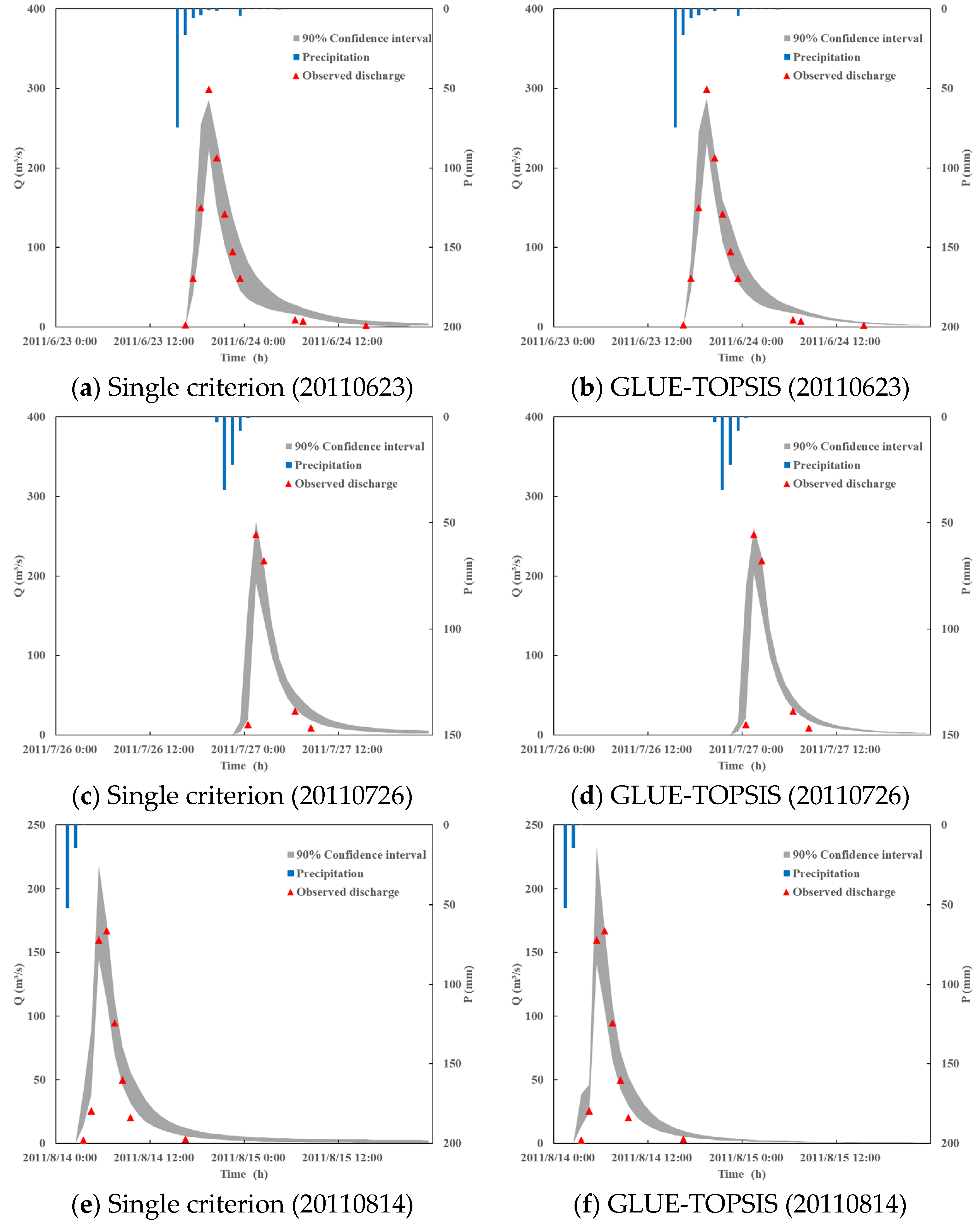
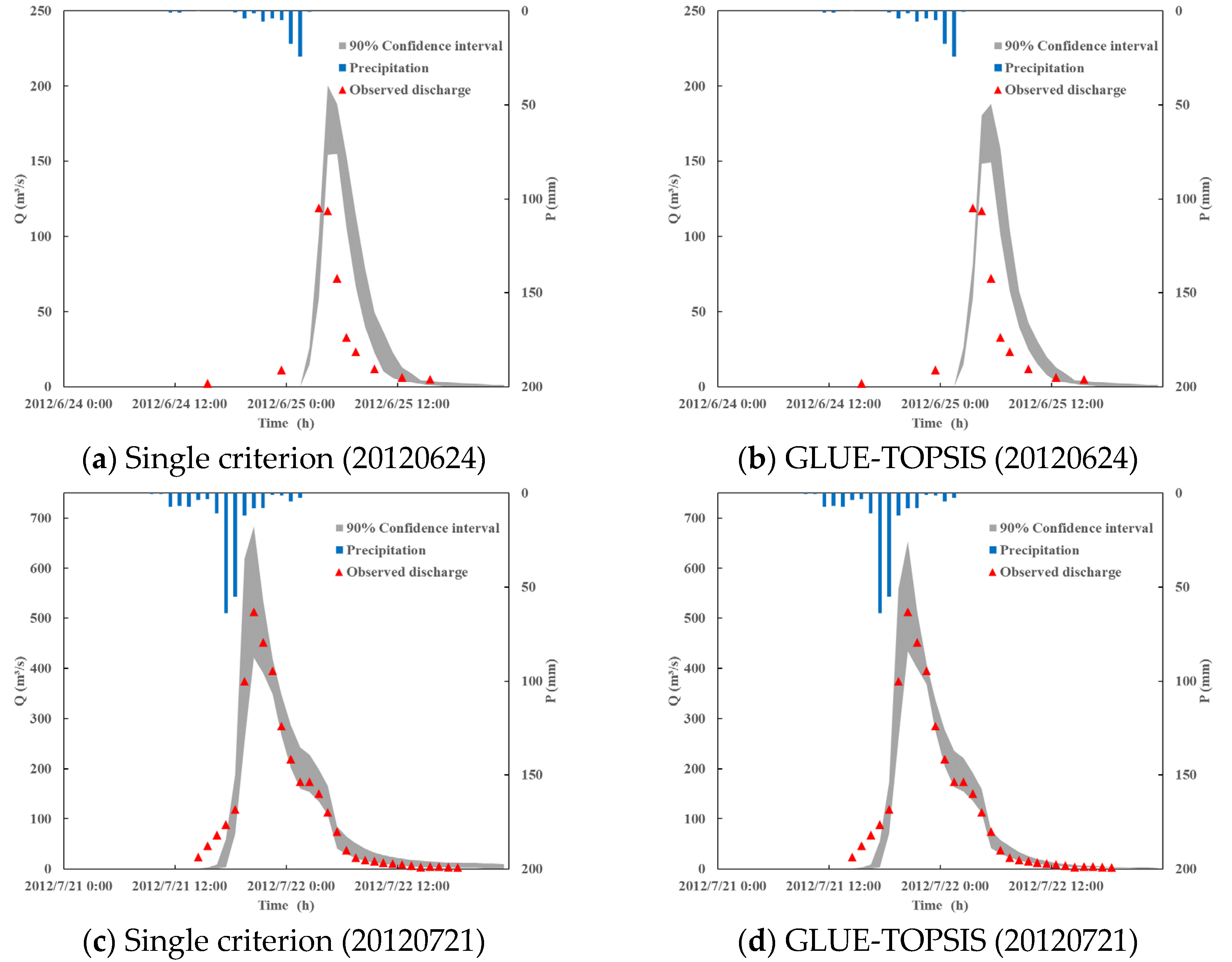
4.3. Uncertainty Estimation of Discharge Simulation
5. Discussion
6. Conclusions
- 10,000 parameter sets generated by the Monte Carlo sampling in GLUE framework revealed that none of the four commonly used objective criteria could fully represent the urban flow process. Notably, the NSE, which is widely used in assessing the performance of hydrological models also cannot describe the flow characteristics alone, which highlights the need for adopting multi-criteria methods.
- The GLUE-TOPSIS method provided more precise uncertainty bounds and median estimates than traditional GLUE method which used NSE as single criterion. The GLUE-TOPSIS method reduced the bandwidth and deviation of the uncertainty bounds with a higher coverage than these from single criterion. The median estimates of GLUE-TOPSIS are also superior to these from single criterion according to the four objective criteria.
- The SWMM model performed well in the flood simulation of Dahongmen catchment in Beijing, PRC. Most observed flows fell within the 90% uncertainty interval, which suggests that the parameter uncertainty analysis has a relatively high contribution toward improving the simulation accuracy of flood prediction. The comparison results for the posterior distribution revealed that the parameters characterizing the impervious area had obvious high frequency intervals, owing to the large impervious area of Dahongmen catchment.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shukla, S.; Gedam, S. Assessing the impacts of urbanization on hydrological processes in a semi-arid river basin of Maharashtra, India. Modell. Earth Sys. Environ. 2018, 4, 699–728. [Google Scholar] [CrossRef]
- Barbosa, A.E.; Fernandes, J.N.; David, L.M. Key issues for sustainable urban stormwater management. Water Res. 2012, 46, 6787–6798. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.P.; Wang, Q.J.; Pagano, T.C. A review of advances in flash flood forecasting. Hydrol. Process. 2011, 25, 2771–2784. [Google Scholar] [CrossRef]
- Hallegatte, S.; Green, C.; Nicholls, R.J.; Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802–806. [Google Scholar] [CrossRef]
- Suttles, K.M.; Singh, N.K.; Vose, J.M.; Martin, K.L.; Emanuel, R.E.; Coulston, J.W.; Saia, S.M.; Crump, M.T. Assessment of hydrologic vulnerability to urbanization and climate change in a rapidly changing watershed in the Southeast US. Sci. Total Environ. 2018, 645, 806–816. [Google Scholar] [CrossRef]
- Cristiano, E.; Ten Veldhuis, M.; van de Giesen, N. Spatial and temporal variability of rainfall and their effects on hydrological response in urban areas—a review. Hydrol. Earth Syst. Sc. 2017, 21, 3859–3878. [Google Scholar] [CrossRef]
- Cullmann, J.; Krausse, T.; Philipp, A. Enhancing flood forecasting with the help of processed based calibration. Phys. Chem. Earth 2008, 33, 1111–1116. [Google Scholar] [CrossRef]
- Xu, Z. Hydrological Models: Past, present and feature. J. Beijing Normal Univ. Nat. Sci. 2010, 46, 278–289. [Google Scholar]
- Fonseca, A.; Ames, D.P.; Yang, P.; Botelho, C.; Boaventura, R.; Vilar, V. Watershed model parameter estimation and uncertainty in data-limited environments. Environ. Modell. Softw. 2014, 51, 84–93. [Google Scholar] [CrossRef]
- Zahmatkesh, Z.; Karamouz, M.; Nazif, S. Uncertainty based modeling of rainfall-runoff: Combined differential evolution adaptive Metropolis (DREAM) and K-means clustering. Adv. Water Resour. 2015, 83, 405–420. [Google Scholar] [CrossRef]
- Blasone, R.; Vrugt, J.A.; Madsen, H.; Rosbjerg, D.; Robinson, B.A.; Zyvoloski, G.A. Generalized likelihood uncertainty estimation (GLUE) using adaptive Markov chain Monte Carlo sampling. Adv. Water Resour. 2008, 31, 630–648. [Google Scholar] [CrossRef]
- Lindblom, E.; Madsen, H.; Mikkelsen, P.S. Comparative uncertainty analysis of copper loads in stormwater systems using GLUE and grey-box modeling. Water Sci. Technol. 2007, 56, 11–18. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Liu, Y.R.; Li, Y.P.; Huang, G.H.; Zhang, J.L.; Fan, Y.R. A Bayesian-based multilevel factorial analysis method for analyzing parameter uncertainty of hydrological model. J. Hydrol. 2017, 553, 750–762. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Thorndahl, S.; Beven, K.J.; Jensen, J.B.; Schaarup-Jensen, K. Event based uncertainty assessment in urban drainage modelling, applying the GLUE methodology. J. Hydrol. 2008, 357, 421–437. [Google Scholar] [CrossRef]
- Setegn, S.G.; Srinivasan, R.; Melesse, A.M.; Dargahi, B. SWAT model application and prediction uncertainty analysis in the Lake Tana Basin, Ethiopia. Hydrol. Process. 2010, 24, 357–367. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Toward improved calibration of hydrologic models: Multiple and noncommensurable measures of information. Water Resour. Res. 1998, 34, 751–763. [Google Scholar] [CrossRef]
- Madsen, H. Automatic Calibration of a Conceptual Rainfall-Runoff Model Using Multiple Objectives. J. Hydrol. 2000, 235, 276–288. [Google Scholar] [CrossRef]
- Fenicia, F.; Savenije, H.H.G.; Matgen, P.; Pfister, L. A comparison of alternative multiobjective calibration strategies for hydrological modeling. Water Resour. Res. 2007, 43, 93–99. [Google Scholar] [CrossRef]
- Gill, M.K.; Kaheil, Y.H.; Khalil, A.; Mckee, M.; Bastidas, L. Multiobjective particle swarm optimization for parameter estimation in hydrology. Water Resour. Res. 2006, 42, 257–271. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. GLUE: 20 years on. Hydrol. Process. 2014, 28, 5897–5918. [Google Scholar] [CrossRef]
- Hwang, C.L.; Lai, Y.J.; Liu, T.Y. A new approach for multiple-objective decision-making. Comput. Oper. Res. 1993, 20, 889–899. [Google Scholar] [CrossRef]
- Hwang, C.; Yoon, K. Methods for Multiple Attribute Decision Making, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. [Google Scholar]
- Beven, K.; Binley, A. The future of distribute models-model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Mantovan, P.; Todini, E. Hydrological forecasting uncertainty assessment: Incoherence of the GLUE methodology. J. Hydrol. 2006, 330, 368–381. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Vogel, R.M.; Lee, S.U.; Batchelder, R. Appraisal of the Generalized Likelihood Uncertainty Estimation (GLUE) Method. Water Resour. Res. 2009, 42. [Google Scholar] [CrossRef]
- Clark, M.P.; Kavetski, D.; Fenicia, F. Pursuing the method of multiple working hypotheses for hydrological modeling. Water Resour. Res. 2011, 47, 178–187. [Google Scholar] [CrossRef]
- Freer, J.; Beven, K.; Ambroise, B. Bayesian Estimation of Uncertainty in Runoff Prediction and the Value of Data: An Application of the GLUE Approach. Water Resour. Res. 1996, 32, 2161–2173. [Google Scholar] [CrossRef]
- Beven, K.; Smith, P.; Freer, J. Comment on “Hydrological forecasting uncertainty assessment: Incoherence of the GLUE methodology” by Pietro Mantovan and Ezio Todini. J. Hydrol. 2007, 338, 315–318. [Google Scholar] [CrossRef]
- Loperfido, J.V.; Noe, G.B.; Jarnagin, S.T.; Hogan, D.M. Effects of distributed and centralized stormwater best management practices and land cover on urban stream hydrology at the catchment scale. J. Hydrol. 2014, 519, 2584–2595. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 290. [Google Scholar] [CrossRef]
- Pang, B.; Guo, S.; Xiong, L.; Li, C. A nonlinear perturbation model based on artificial neural network. J. Hydrol. 2007, 333, 504–516. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. T. Asabe 2015, 58, 1763–1785. [Google Scholar]
- Yilmaz, K.K.; Gupta, H.V.; Wagener, T. A multi-criteria penalty function approach for evaluating a priori model parameter estimates. J. Hydrol. 2015, 525, 165–177. [Google Scholar] [CrossRef]
- Cheng, K.; Lien, Y.; Wu, Y.; Su, Y. On the criteria of model performance evaluation for real-time flood forecasting. Stoch. Env. Res. Risk A. 2017, 31, 1123–1146. [Google Scholar] [CrossRef]
- Zanakis, S.H.; Solomon, A.; Wishart, N.; Dublish, S. Multi-attribute decision making: A simulation comparison of select methods. Eur. J. Oper. Res. 1998, 107, 507–529. [Google Scholar] [CrossRef]
- Zoppou, C. Review of urban storm water models. Environ. Modell. Softw. 2001, 16, 195–231. [Google Scholar] [CrossRef]
- Gironas, J.; Roesner, L.A.; Rossman, L.A.; Davis, J. A new applications manual for the Storm Water Management Model (SWMM). Environ. Modell. Softw. 2010, 25, 813–814. [Google Scholar] [CrossRef]
- Rossman, L.A. Storm Water Management Model User’s Manual, 5th ed.; Environment Protection Agency: Cincinnati, OH, USA, 2005; pp. 125–137. [Google Scholar]
- Xu, Z.; Zhao, G. Impact of urbanization on rainfall-runoff processes: Case study in the Liangshui River Basin in Beijing, China. Proc. Int. Assoc. Hydrol. Sci. 2016, 373, 7–12. [Google Scholar] [CrossRef]
- Zhao, G.; Pang, B.; Xu, Z.; Du, L.; Zhong, Y. Simulation of urban storm an Dahongmen drainage area by SWMM. J. Beijing Normal Univ. Nat. Sci. 2014, 50, 452–455. [Google Scholar]
- Shi, R.; Zhao, G.; Pang, B.; Jinag, Q.; Zhen, T. Uncertainty Analysis of SWMM Model Parameters Based on GLUE Method. J. China Hydrol. 2016, 36, 1–6. [Google Scholar]
- Xiong, L.; Wan, M.; Wei, X.; O’Connor, K.M. Indices for assessing the prediction bounds of hydrological models and application by generalised likelihood uncertainty estimation. Hydrolog. Sci. J. 2009, 54, 852–871. [Google Scholar] [CrossRef]
- Zhao, D.; Chen, J.; Wang, H.; Tong, Q. Application of a Sampling Based on the Combined Objectives of Parameter Identification and Uncertainty Analysis of an Urban Rainfall-Runoff Model. J. Irrig. Drain. Eng. 2013, 139, 66–74. [Google Scholar] [CrossRef]
- Wagner, B.; Reyes-Silva, J.D.; Forster, C.; Benisch, J.; Helm, B.; Krebs, P. Automatic Calibration Approach for Multiple Rain Events in SWMM Using Latin Hypercube Sampling. In Green Energy and Technology; Mannina, G., Ed.; Springer: Cham, Switzerland, 2019; Volume 23, pp. 435–440. [Google Scholar]
- Sun, N.; Hall, M.; Hong, B.; Zhang, L. Impact of SWMM Catchment Discretization: Case Study in Syracuse, New York. J. Hydrol. Eng. 2014, 19, 223–234. [Google Scholar] [CrossRef]
- Zhang, W.; Li, T. The Influence of Objective Function and Acceptability Threshold on Uncertainty Assessment of an Urban Drainage Hydraulic Model with Generalized Likelihood Uncertainty Estimation Methodology. Water Resour. Manag. 2015, 29, 2059–2072. [Google Scholar] [CrossRef]
- Sun, N.; Hong, B.; Hall, M. Assessment of the SWMM model uncertainties within the generalized likelihood uncertainty estimation (GLUE) framework for a high-resolution urban sewershed. Hydrol. Process. 2014, 28, 3018–3034. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, X. Evaluating the Effects of Low Impact Development Practices on Urban Flooding under Different Rainfall Intensities. Water 2017, 9, 548. [Google Scholar] [CrossRef]
- Elliott, A.H.; Trowsdale, S.A. A review of models for low impact urban stormwater drainage. Environ. Modell. Softw. 2007, 22, 394–405. [Google Scholar] [CrossRef]
| Category | Parameter | Description | Units | Distribution |
|---|---|---|---|---|
| Basic characteristic | %Imperv | Percent of impervious area | % | 60–80 |
| Manning roughness | N-Imperv | Manning coefficient for impervious area | 0.025–0.045 | |
| N-perv | Manning coefficient for pervious area | 0.1–0.5 | ||
| N-river | Manning coefficient for riverway | 0.03–0.06 | ||
| N-conduit | Manning coefficient for conduit | 0.01–0.03 | ||
| Reservoir in depressions | D-imperv | Depth of depression storage on impervious area | mm | 15–40 |
| D-perv | Depth of depression storage on pervious area | mm | 20–50 | |
| Infiltration parameters | MaxRate | Maximum rate on Horton infiltration curve | mm/h | 100–150 |
| MinRate | Minimum rate on Horton infiltration curve | mm/h | 10–90 | |
| Decay | Decay constant for the Horton infiltration curve | h−1 | 0–50 |
| Criterion | Number | Criterion | Number | Criterion | Number | Criterion | Number |
|---|---|---|---|---|---|---|---|
| NSE ≥ 0.7 | 2506 | NSE ≥ 0.7 and VB ≤ 0.3 | 2226 | NSE ≥ 0.7 and VB ≤ 0.3 and PB ≤ 0.2 | 1598 | NSE ≥ 0.7 and VB ≤ 0.3 and PB ≤ 0.2 and R ≥ 0.8 | 1598 |
| VB ≤ 0.3 | 3958 | NSE ≥ 0.7 and PB ≤ 0.2 | 1772 | NSE ≥ 0.7 and VB ≤ 0.3 and R ≥ 0.8 | 2226 | ||
| PB ≤ 0.2 | 4215 | NSE ≥ 0.7 and R ≥ 0.8 | 2506 | NSE ≥ 0.7 and PB ≤ 0.2 and R ≥ 0.8 | 1772 | ||
| R ≥ 0.8 | 6918 | VB ≤ 0.3 and PB ≤ 0.2 | 2557 | VB ≤ 0.3 and PB ≤ 0.2 and R ≥ 0.8 | 2396 | ||
| VB ≤ 0.3 and R ≥ 0.8 | 3413 | ||||||
| PB ≤ 0.2 and R ≥ 0.8 | 3927 |
| Method | Criteria | B(m³/s) | CR (%) | RD (m³/s) | |
|---|---|---|---|---|---|
| Calibration period | 20110623 | Single criteria | 48.308 | 54.5 | 13.606 |
| GLUE-TOPSIS | 35.17 | 54.5 | 12.804 | ||
| 20110726 | Single criteria | 50.563 | 20.0 | 41.454 | |
| GLUE-TOPSIS | 43.723 | 40.0 | 40.551 | ||
| 20110814 | Single criteria | 39.829 | 50.0 | 18.995 | |
| GLUE-TOPSIS | 37.908 | 62.5 | 16.276 | ||
| Average | Single criteria | 46.233 | 41.5 | 24.685 | |
| GLUE-TOPSIS | 38.934 | 52.3 | 23.211 | ||
| Validation period | 20120624 | Single criteria | 17.100 | 10.0 | 17.100 |
| GLUE-TOPSIS | 14.100 | 10.0 | 14.150 | ||
| 20120721 | Single criteria | 53.953 | 81.8 | 17.140 | |
| GLUE-TOPSIS | 41.839 | 84.8 | 13.358 | ||
| Average | Single criteria | 35.526 | 45.9 | 17.120 | |
| GLUE-TOPSIS | 27.970 | 47.4 | 13.754 | ||
| Method | Criteria | NSE | VB | PB | R | |
|---|---|---|---|---|---|---|
| Calibration period | 20110623 | Single criteria | 0.863 | 0.003 | 0.118 | 0.994 |
| GLUE-TOPSIS | 0.876 | 0.02 | 0.112 | 0.995 | ||
| 20110726 | Single criteria | 0.936 | 0.086 | 0.096 | 0.955 | |
| GLUE-TOPSIS | 0.949 | 0.123 | 0.077 | 0.941 | ||
| 20110814 | Single criteria | 0.966 | 0.184 | 0.085 | 0.962 | |
| GLUE-TOPSIS | 0.982 | 0.103 | 0.138 | 0.991 | ||
| Average | Single criteria | 0.921 | 0.091 | 0.099 | 0.970 | |
| GLUE-TOPSIS | 0.936 | 0.082 | 0.109 | 0.975 | ||
| Validation period | 20120624 | Single criteria | 0.429 | 0.402 | 0.375 | 0.790 |
| GLUE-TOPSIS | 0.530 | 0.300 | 0.428 | 0.663 | ||
| 20120721 | Single criteria | 0.936 | 0.041 | 0.077 | 0.989 | |
| GLUE-TOPSIS | 0.974 | 0.005 | 0.059 | 0.962 | ||
| Average | Single criteria | 0.683 | 0.222 | 0.226 | 0.890 | |
| GLUE-TOPSIS | 0.752 | 0.153 | 0.244 | 0.812 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, B.; Shi, S.; Zhao, G.; Shi, R.; Peng, D.; Zhu, Z. Uncertainty Assessment of Urban Hydrological Modelling from a Multiple Objective Perspective. Water 2020, 12, 1393. https://doi.org/10.3390/w12051393
Pang B, Shi S, Zhao G, Shi R, Peng D, Zhu Z. Uncertainty Assessment of Urban Hydrological Modelling from a Multiple Objective Perspective. Water. 2020; 12(5):1393. https://doi.org/10.3390/w12051393
Chicago/Turabian StylePang, Bo, Shulan Shi, Gang Zhao, Rong Shi, Dingzhi Peng, and Zhongfan Zhu. 2020. "Uncertainty Assessment of Urban Hydrological Modelling from a Multiple Objective Perspective" Water 12, no. 5: 1393. https://doi.org/10.3390/w12051393
APA StylePang, B., Shi, S., Zhao, G., Shi, R., Peng, D., & Zhu, Z. (2020). Uncertainty Assessment of Urban Hydrological Modelling from a Multiple Objective Perspective. Water, 12(5), 1393. https://doi.org/10.3390/w12051393








