A Two-Stage LP-NLP Methodology for the Least-Cost Design and Operation of Water Distribution Systems
Abstract
:1. Introduction
2. Definitions and Notation
3. Model Formulation
3.1. The Original NLP Model Formulation
3.1.1. Objective Function
3.1.2. Constraints
3.2. NLP Model Formulation
4. Simplification of the NLP Constraints Using Reformulated Co-Tree Flows Method (RCTM)
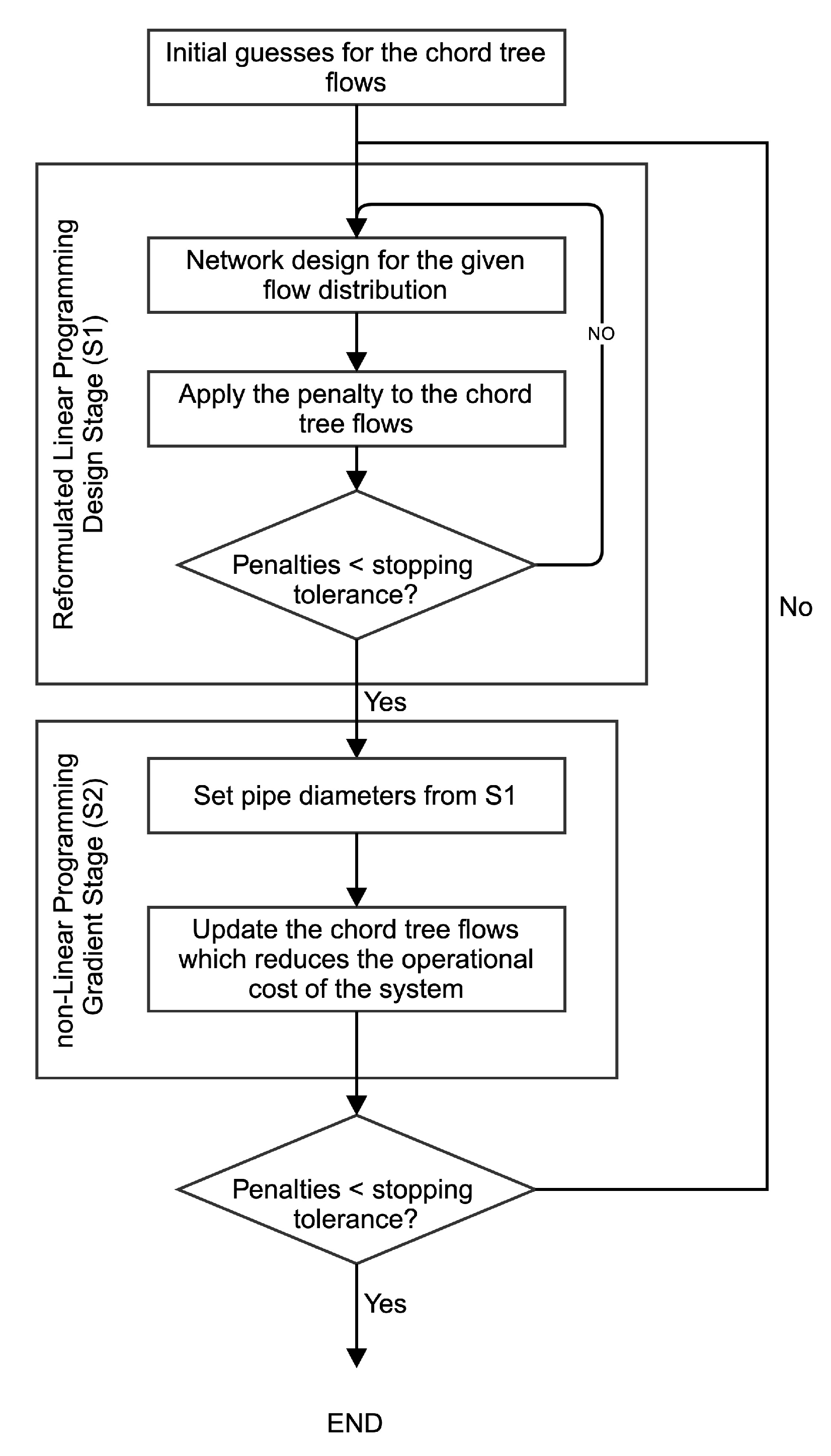
5. The Two-Stage Solution Method
5.1. Stage 0—The Identification of the Chord Tree and Spanning Tree of a WDS
5.2. Stage 1—Iterative LP Design Stage
Penalty Reduction
5.3. Stage 2—NLP Descending Stage
6. Relation of the Proposed Method to Other LP Methods
7. Applications
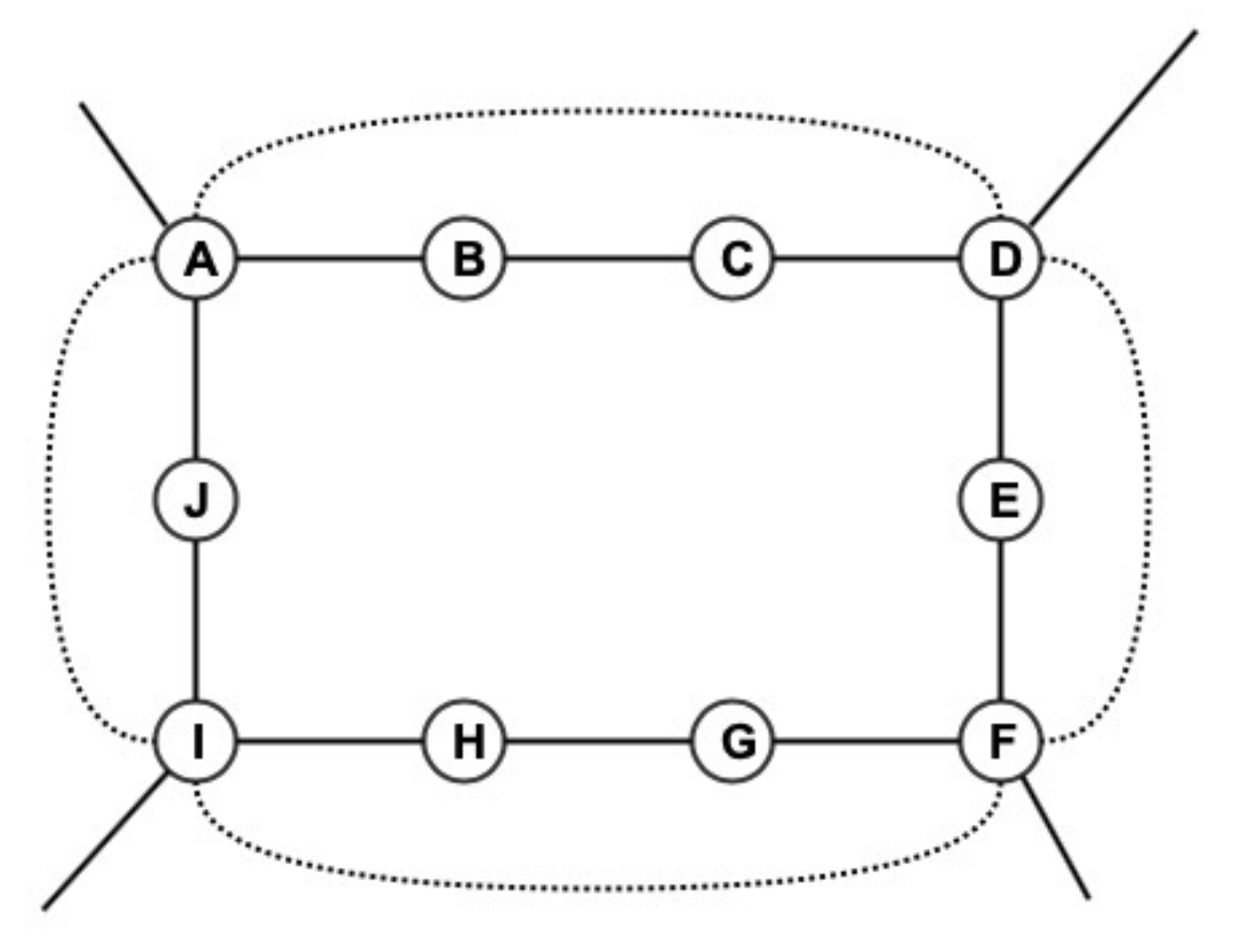
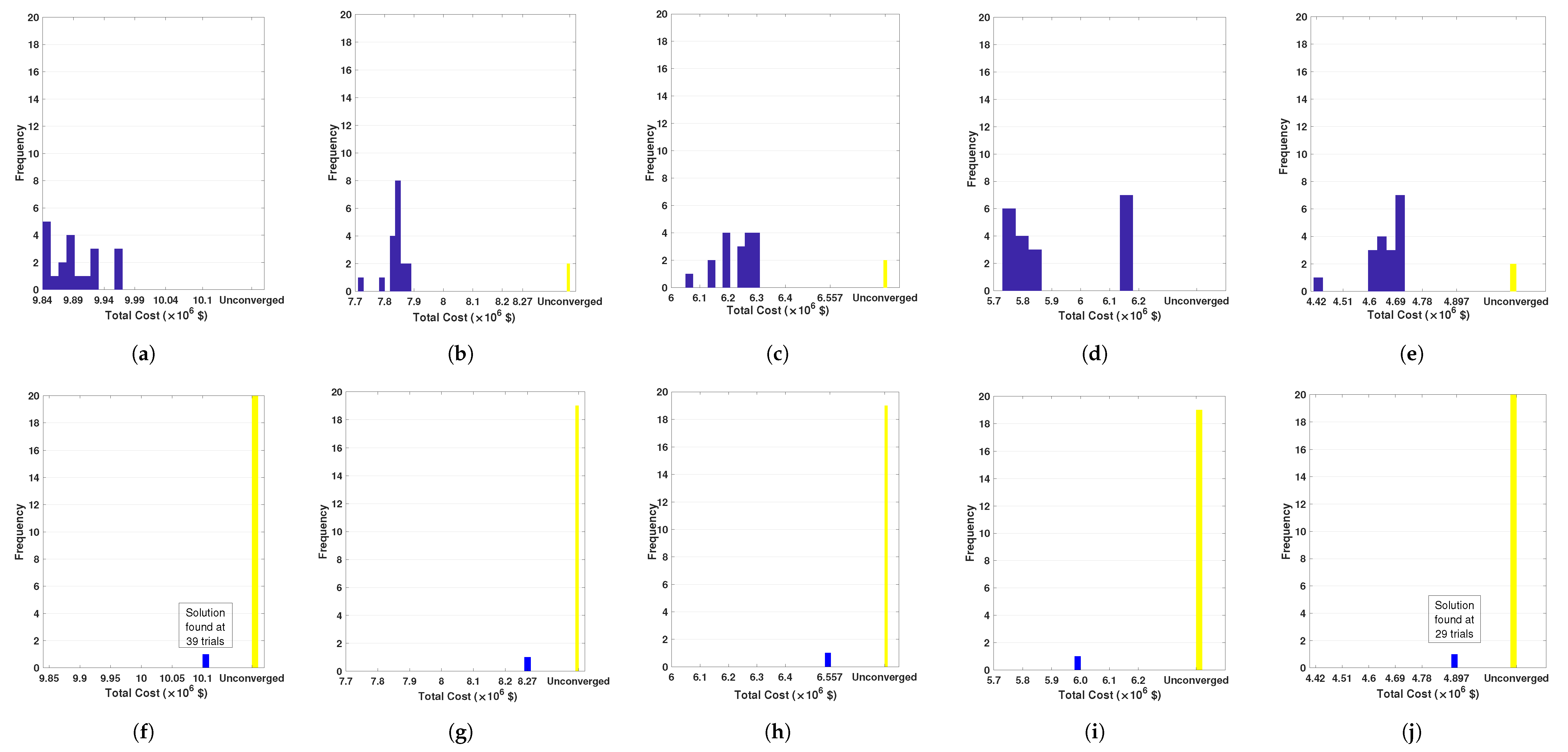
7.1. Case Study 1
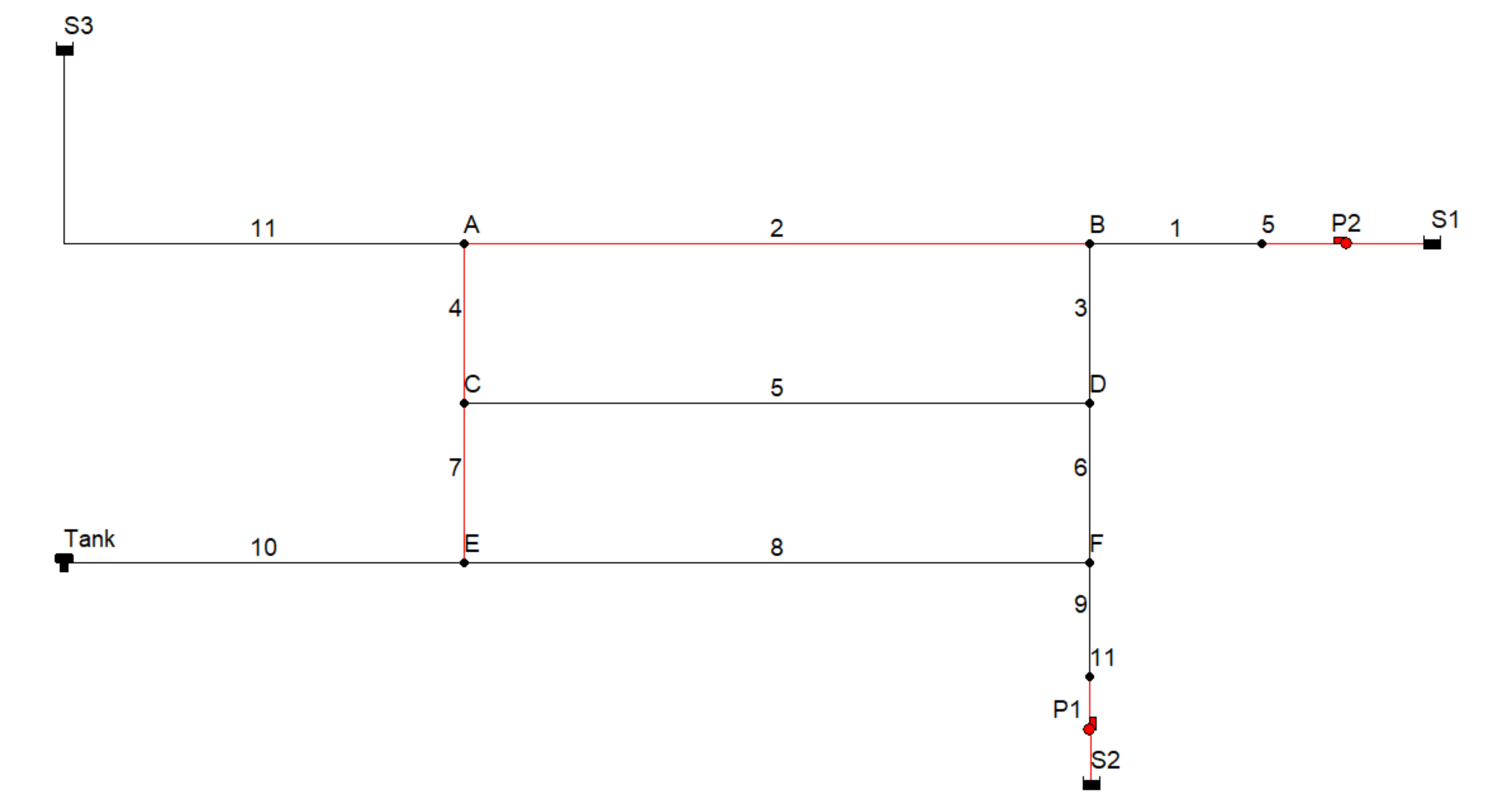
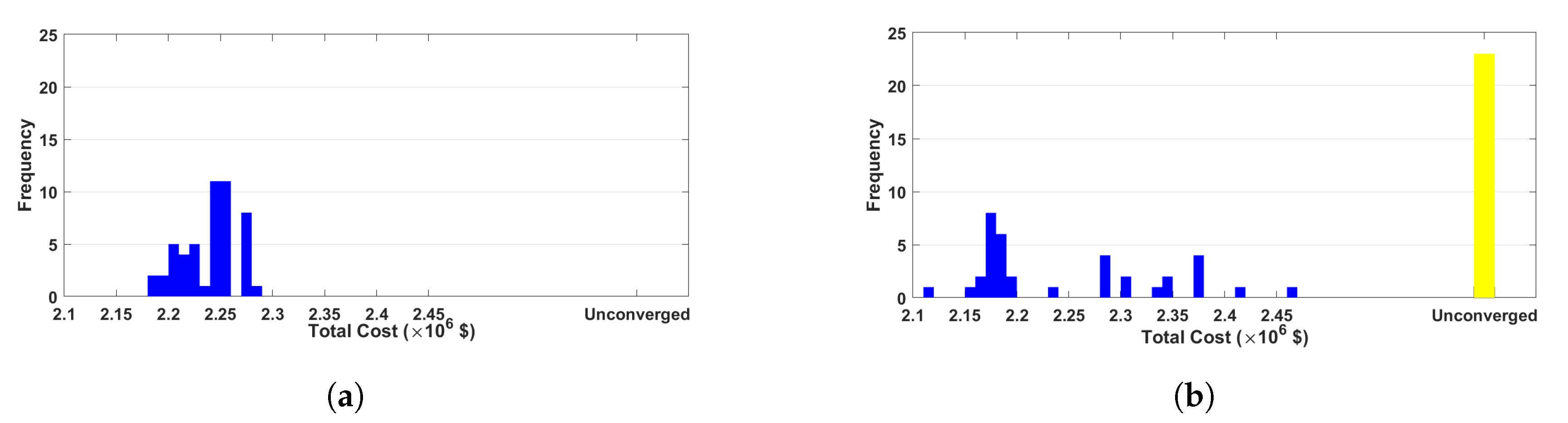
7.2. Case Study 2
8. Conclusions
- the iterative LP stage can consistently find a feasible design for a WDS with multiple loading conditions without the need to add additional network elements (such as valves) to the network;
- it exhibits a higher robustness to the increase of the number of loading conditions and the change of the elevations of the reservoir nodes when compared to the NLP formulation and meta-heuristics algorithms (ant colony optimization);
- its performance is not affected by the parameters used so that no parameter tuning is required;
- it is significantly less computational-intensive when compared to evolutionary algorithms, such as genetic algorithm, differential evolution, ant colony optimization, and particle swarm optimization.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zessler, U.; Shamir, U. Optimal operation of water distribution systems. J. Water Resour. Plan. Manag. 1989, 115, 735–752. [Google Scholar] [CrossRef]
- Alperovits, E.; Shamir, U. Design of optimal water distribution systems. Water Resour. Res. 1977, 13, 885–900. [Google Scholar] [CrossRef]
- Kessler, A.; Shamir, U. Analysis of the linear programming gradient method for optimal design of water supply networks. Water Resour. Res. 1989, 25, 1469–1480. [Google Scholar] [CrossRef]
- Quindry, G.E.; Liebman, J.C.; Brill, E.D. Optimization of looped water distribution systems. J. Environ. Eng. Div. 1981, 107, 665–679. [Google Scholar]
- Shamir, U. Optimal design and operation of water distribution systems. Water Resour. Res. 1974, 10, 27–36. [Google Scholar] [CrossRef]
- Murphy, L.; Simpson, A.; Dandy, G. Pipe Network Optimization Using an Improved Genetic Algorithm; Department of Civil and Environmental Engineering, University of Adelaide: Adelaide, Australia, 1993. [Google Scholar]
- Simpson, A.; Dandy, G.; Murphy, L. Genetic algorithms compared to other techniques for pipe optimization. J. Water Resour. Plan. Manag. 1994, 120, 423–443. [Google Scholar] [CrossRef] [Green Version]
- Dandy, G.; Simpson, A.; Murphy, L. An improved genetic algorithm for pipe network optimization. Water Resour. Res. 1996, 32, 449–458. [Google Scholar] [CrossRef] [Green Version]
- Savic, D.; Walters, G. Genetic algorithms for least-cost design of water distribution networks. J. Water Resour. Plan. Manag. 1997, 123, 67–77. [Google Scholar] [CrossRef]
- Loganathan, G.; Greene, J.; Ahn, T. Design heuristic for globally minimum cost water-distribution systems. J. Water Resour. Plan. Manag. 1995, 121, 182–192. [Google Scholar] [CrossRef]
- Cunha, M.; Sousa, J. Water distribution network design optimization: Simulated annealing approach. J. Water Resour. Plan. Manag. 1999, 125, 215–221. [Google Scholar] [CrossRef]
- Lippai, I.; Heaney, J.; Laguna, M. Robust water system design with commercial intelligent search optimizers. J. Comput. Civ. Eng. 1999, 13, 135–143. [Google Scholar] [CrossRef]
- Geem, Z.; Kim, J.; Loganathan, G. Harmony search optimization: Application to pipe network design. Int. J. Model. Simul. 2002, 22, 125–133. [Google Scholar] [CrossRef]
- Geem, Z. Optimal cost design of water distribution networks using harmony search. Eng. Optim. 2006, 38, 259–277. [Google Scholar] [CrossRef]
- Eusuff, M.; Lansey, K. Optimization of water distribution network design using the shuffled frog leaping algorithm. J. Water Resour. Plan. Manag. 2003, 129, 210–225. [Google Scholar] [CrossRef]
- Suribabu, C.; Neelakantan, T. Design of water distribution networks using particle swarm optimization. Urban Water J. 2006, 3, 111–120. [Google Scholar] [CrossRef]
- Montalvo, I.; Izquierdo, J.; Pérez, R.; Tung, M. Particle swarm optimization applied to the design of water supply systems. Comput. Math. Appl. 2008, 56, 769–776. [Google Scholar] [CrossRef] [Green Version]
- Maier, H.; Simpson, A.; Zecchin, A.; Foong, W.; Phang, K.; Seah, H.; Tan, C. Ant colony optimization for design of water distribution systems. J. Water Resour. Plan. Manag. 2003, 129, 200–209. [Google Scholar] [CrossRef] [Green Version]
- Zecchin, A.; Simpson, A.; Maier, H.; Leonard, M.; Roberts, A.; Berrisford, M. Application of two ant colony optimisation algorithms to water distribution system optimisation. Math. Comput. Model. 2006, 44, 451–468. [Google Scholar] [CrossRef] [Green Version]
- Zecchin, A.; Maier, H.; Simpson, A.; Leonard, M.; Nixon, J. Ant colony optimization applied to water distribution system design: Comparative study of five algorithms. J. Water Resour. Plan. Manag. 2007, 133, 87–92. [Google Scholar] [CrossRef] [Green Version]
- Ostfeld, A.; Tubaltzev, A. Ant colony optimization for least-cost design and operation of pumping water distribution systems. J. Water Resour. Plan. Manag. 2008, 134, 107–118. [Google Scholar] [CrossRef]
- Baños, R.; Gil, C.; Agulleiro, J.; Reca, J. A memetic algorithm for water distribution network design. In Soft Computing in Industrial Applications; Springer: Berlin/Heidelberg, Germany, 2007; pp. 279–289. [Google Scholar]
- Suribabu, C. Differential evolution algorithm for optimal design of water distribution networks. J. Hydroinformatics 2010, 12, 66–82. [Google Scholar] [CrossRef]
- Vasan, A.; Simonovic, S. Optimization of water distribution network design using differential evolution. J. Water Resour. Plan. Manag. 2010, 136, 279–287. [Google Scholar] [CrossRef]
- Zheng, F.; Zecchin, A.; Simpson, A. Self-adaptive differential evolution algorithm applied to water distribution system optimization. J. Comput. Civ. Eng. 2012, 27, 148–158. [Google Scholar] [CrossRef] [Green Version]
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in optimisation of water distribution systems? A literature review of system operation. Environ. Model. Softw. 2017, 93, 209–254. [Google Scholar] [CrossRef] [Green Version]
- Krapivka, A.; Ostfeld, A. Coupled genetic algorithm—Linear programming scheme for least-cost pipe sizing of water-distribution systems. J. Water Resour. Plan. Manag. 2009, 135, 298–302. [Google Scholar] [CrossRef]
- Zheng, F.; Simpson, A.R.; Zecchin, A.C. A combined NLP-differential evolution algorithm approach for the optimization of looped water distribution systems. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Elhay, S.; Simpson, A.R.; Deuerlein, J.; Alexander, B.; Schilders, W.H. Reformulated co-tree flows method competitive with the global gradient algorithm for solving water distribution system equations. J. Water Resour. Plan. Manag. 2014, 140, 04014040. [Google Scholar] [CrossRef] [Green Version]
- Schilders, W. Solution of indefinite linear systems using an LQ decomposition for the linear constraints. Linear Algebra Its Appl. 2009, 431, 381–395. [Google Scholar] [CrossRef] [Green Version]
- Qiu, M.; Alexander, B.; Simpson, A.; Elhay, S. WDSLib: A Water Distribution System Simulation Test Bed. Environ. Model. Softw. submitted.
- Löfberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the CACSD Conference, Taipei, Taiwan, 2–4 September 2004; Volume 3. [Google Scholar]
- Berkelaar, M.; Eikland, K.; Notebaert, P. Lpsolve: Open Source (Mixed-Integer) Linear Programming System; Eindhoven University of Technology: Eindhoven, The Netherlands, 2004; Volume 63. [Google Scholar]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Cohon, J.L. Multiobjective Programming and Planning; Courier Corporation: Chelmsford, MA, USA, 2004; Volume 140. [Google Scholar]
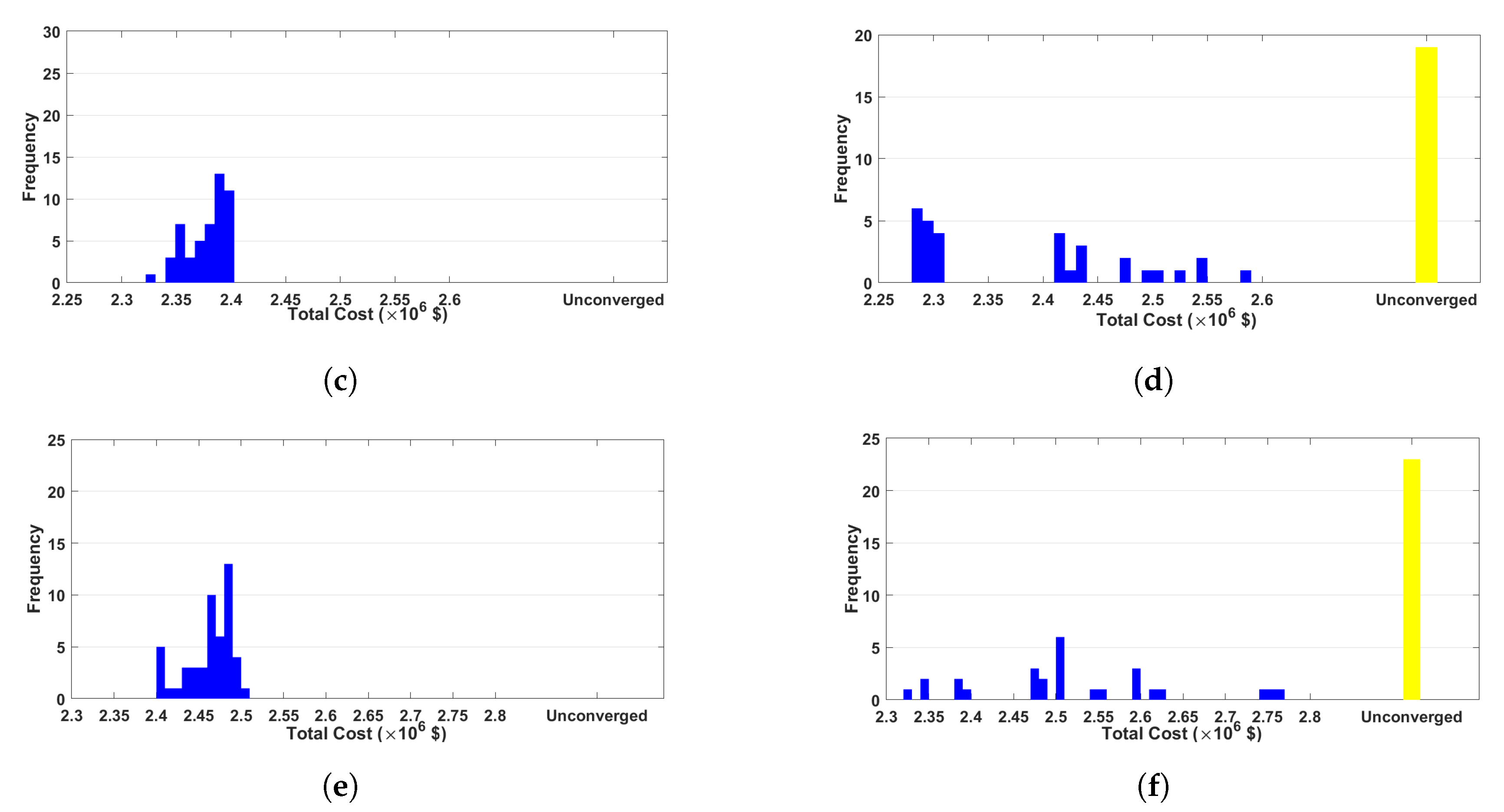
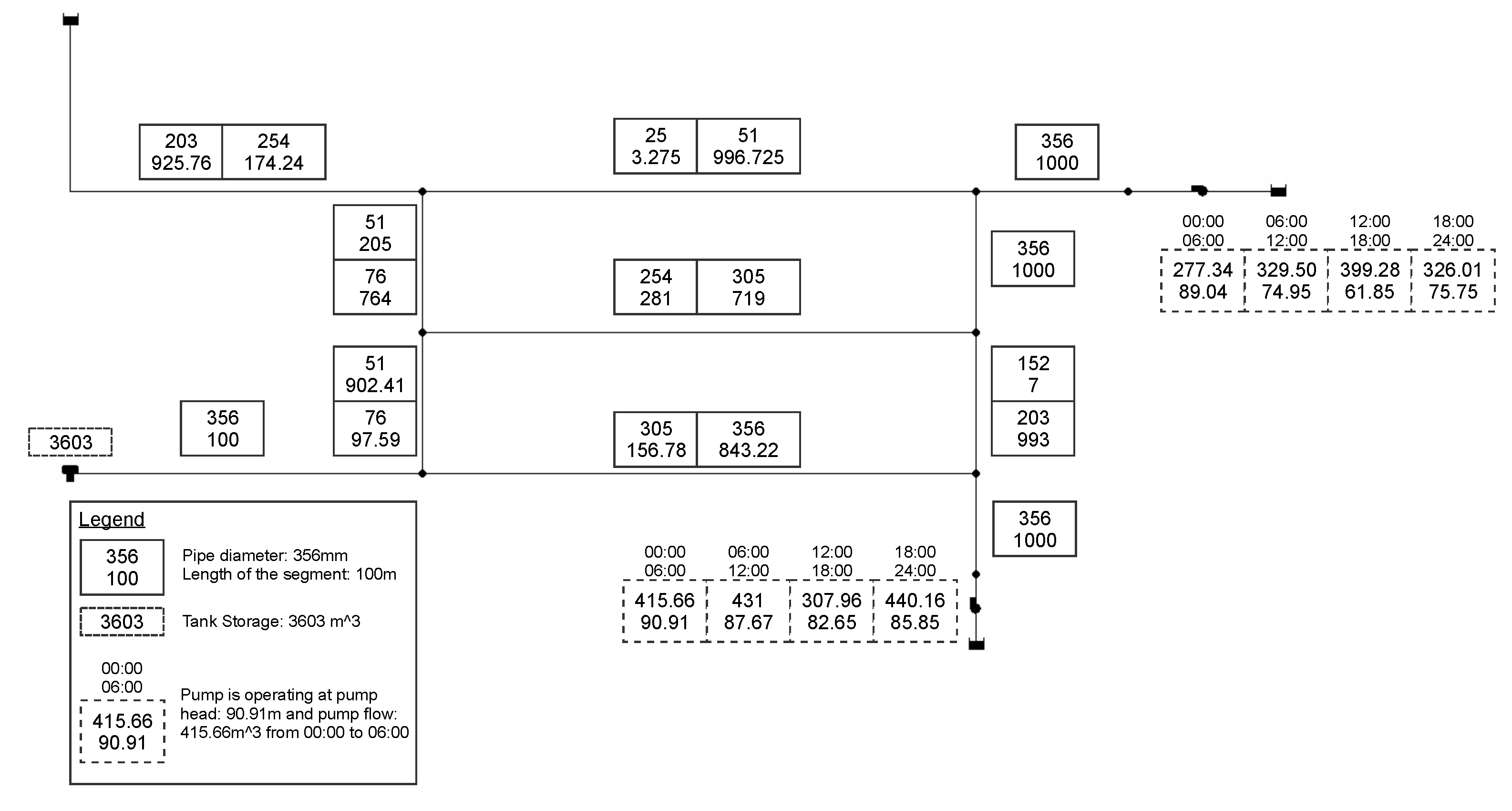
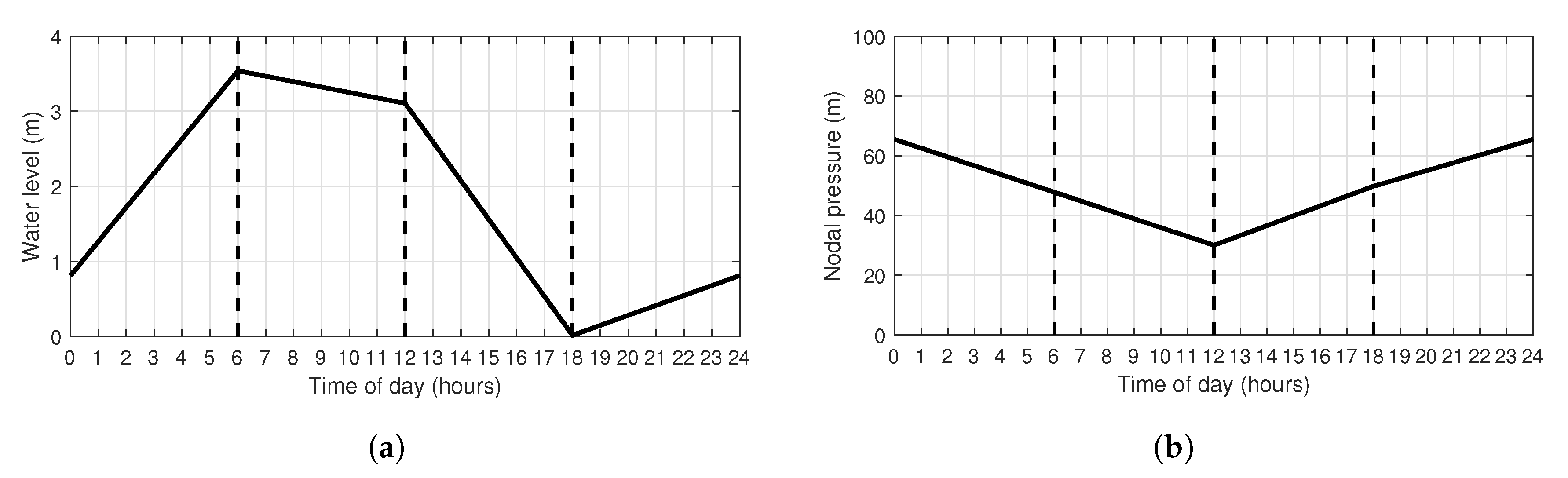
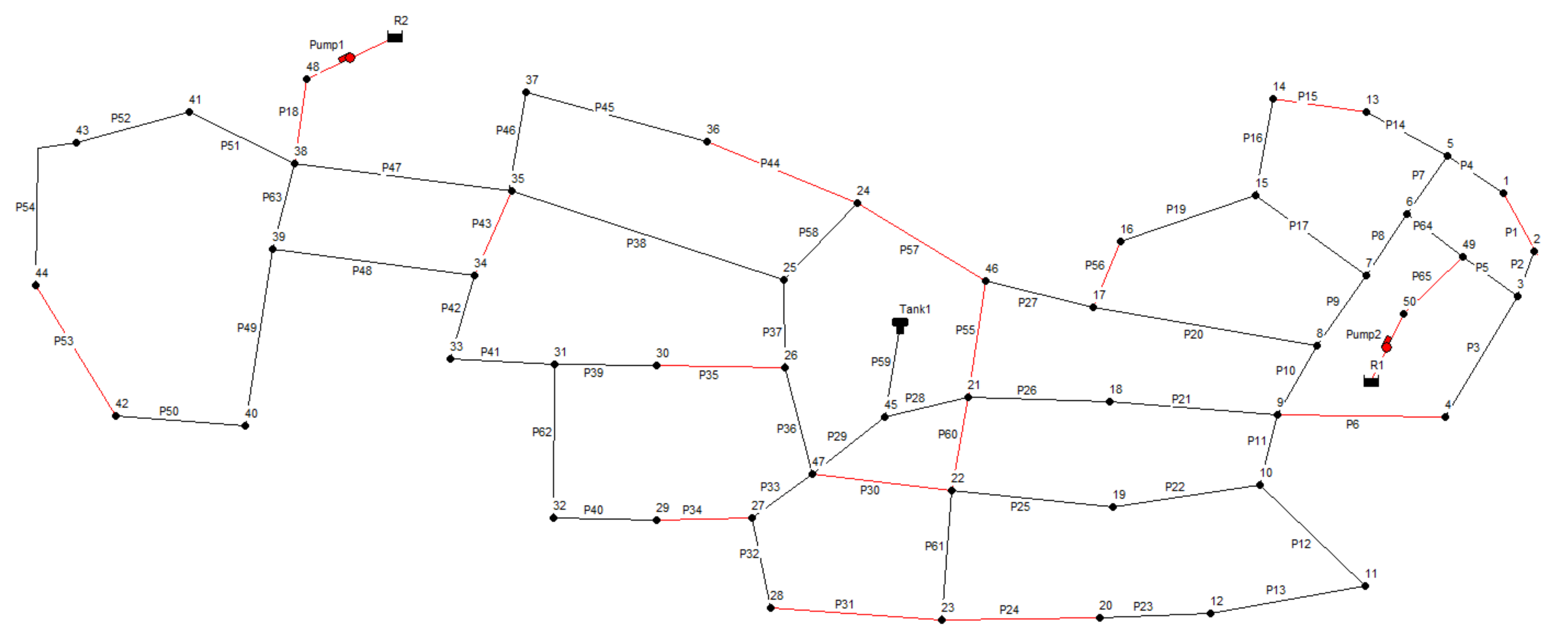
| Pipe Diameter (mm) | Cost ($/m) |
|---|---|
| 25 | 2 |
| 51 | 5 |
| 76 | 8 |
| 102 | 11 |
| 152 | 16 |
| 203 | 23 |
| 254 | 32 |
| 305 | 50 |
| 356 | 60 |
| 406 | 90 |
| 457 | 130 |
| 508 | 170 |
| 559 | 300 |
| 610 | 550 |
| Time of Day | Demand Multiplier - | Energy Tariff ($/kWh) | ||||
|---|---|---|---|---|---|---|
| 00:00–02:00 | - | - | 0.2 | - | - | 0.02 |
| 02:00–04:00 | - | 0.15 | 0.1 | - | 0.015 | 0.01 |
| 04:00–06:00 | 0.2 | - | 0.3 | 0.02 | - | 0.03 |
| 06:00–08:00 | - | 0.7 | 1.1 | - | 0.07 | 0.11 |
| 08:00–10:00 | - | - | 0.9 | - | - | 0.09 |
| 10:00–12:00 | 0.8 | 0.65 | 0.4 | 0.064 | 0.065 | 0.04 |
| 12:00–14:00 | - | - | 0.8 | - | - | 0.08 |
| 14:00–16:00 | - | 1.0 | 1.2 | - | 0.1 | 0.12 |
| 16:00–18:00 | 1.2 | - | 1.6 | 0.12 | - | 0.16 |
| 18:00–20:00 | - | 1.2 | 0.8 | - | 0.12 | 0.08 |
| 20:00–22:00 | - | - | 0.7 | - | - | 0.07 |
| 22:00–24:00 | 0.6 | 0.5 | 0.3 | 0.048 | 0.05 | 0.03 |
| (a) | ||||||
|---|---|---|---|---|---|---|
| Statistical Properties ($ × 105) | ||||||
| Min | Max | Mean (%) | Median | Std. Dev | Std. Err | |
| Pipe Cost | 3.52 | 4.15 | 3.82 (17%) | 3.80 | 0.19 | 0.03 |
| Tank Cost | 1.26 | 1.72 | 1.46 (7%) | 1.45 | 0.10 | 0.01 |
| Pump Cost | 5.18 | 5.94 | 5.4 (24%) | 5.38 | 0.19 | 0.03 |
| Energy Cost | 10.85 | 12.18 | 11.68 (52%) | 11.76 | 0.36 | 0.05 |
| Total Cost | 21.78 | 22.91 | 22.37 | 22.42 | 0.28 | 0.04 |
| (b) | ||||||
| Statistical Properties ($ × 105) | ||||||
| Min | Max | Mean(%) | Median | Std. Dev | Std. Err | |
| Pipe Cost | 2.63 | 4.43 | 3.23 (14%) | 3.19 | 0.31 | 0.05 |
| Tank Cost | 0.65 | 1.40 | 1.10 (5%) | 1.25 | 0.30 | 0.05 |
| Pump Cost | 5.10 | 6.72 | 5.88 (26%) | 5.66 | 0.42 | 0.07 |
| Energy Cost | 11.40 | 13.39 | 12.25 (55%) | 12.10 | 0.55 | 0.09 |
| Total Cost | 21.14 | 24.65 | 22.46 | 21.87 | 0.90 | 0.15 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, M.; Housh, M.; Ostfeld, A. A Two-Stage LP-NLP Methodology for the Least-Cost Design and Operation of Water Distribution Systems. Water 2020, 12, 1364. https://doi.org/10.3390/w12051364
Qiu M, Housh M, Ostfeld A. A Two-Stage LP-NLP Methodology for the Least-Cost Design and Operation of Water Distribution Systems. Water. 2020; 12(5):1364. https://doi.org/10.3390/w12051364
Chicago/Turabian StyleQiu, Mengning, Mashor Housh, and Avi Ostfeld. 2020. "A Two-Stage LP-NLP Methodology for the Least-Cost Design and Operation of Water Distribution Systems" Water 12, no. 5: 1364. https://doi.org/10.3390/w12051364
APA StyleQiu, M., Housh, M., & Ostfeld, A. (2020). A Two-Stage LP-NLP Methodology for the Least-Cost Design and Operation of Water Distribution Systems. Water, 12(5), 1364. https://doi.org/10.3390/w12051364







