Effect of Plastic Film Residue on Vertical Infiltration Under Different Initial Soil Moisture Contents and Dry Bulk Densities
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Site
2.2. Experimental Materials and Devices
2.3. Design and Methods
2.3.1. Experimental Design
2.3.2. Data Analysis
Testing of the Regression Equation
Testing of the Fitting Degree of the Equation
3. Results
3.1. Analysis of the MF
3.2. Analysis of theAccumulative Infiltration (AI)
3.3. Analysis of the MC
4. Discussion
4.1. Burial Depth of RPF
4.2. The RPFC
4.3. The IMCand DBD
4.4. Interaction Effects Between Two Factors
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Lament, W.J. Plastic mulches for the production of vegetable crops. In A Guide to the Manufacture Performance and Potential of Plastics in Agriculture; Elsevier: Amsterdam, The Netherlands, 2017; pp. 45–60. [Google Scholar]
- Lamont, W.J. Plastics: Modifying the microclimate for the production of vegetable crops. Hort. Technol. 2005, 15, 477–481. [Google Scholar] [CrossRef]
- Gan, Y.T.; Siddique, K.H.M.; Turner, N.C.; Li, X.G.; Niu, J.Y.; Yang, C.; Liu, L.P.; Chai, Q. Ridge-Furrow Mulching Systems-An Innovative Technique for Boosting Crop Productivity in Semiarid Rain-Fed Environments. Adv. Agro. 2013, 118, 429–476. [Google Scholar]
- Gu, X.B.; Li, Y.N.; Du, Y.D. Effects of ridge-furrow film mulching and nitrogen fertilization on growth, seed yield and water productivity of winter oilseed rape (Brassica napus L.) in Northwestern China. Agric. Water Manag. 2018, 200, 60–70. [Google Scholar] [CrossRef]
- Enrique, G.S.; Braud, I.; Jean-Louis, T.; Michel, V.; Pierre, B.; Jean-Christophe, C. Modelling heat and water exchanges of fallow land covered with plant-residue mulch. Agricul. Forest Meteorol. 1999, 97, 151–169. [Google Scholar] [CrossRef]
- Gu, X.B.; Li, Y.N.; Du, Y.D. Optimized nitrogen fertilizer application improves yield, water and nitrogen use efficiencies of winter rapeseed cultivated under continuous ridges with film mulching. Ind. Crops Prod. 2017, 109, 233–240. [Google Scholar] [CrossRef]
- Kasirajan, S.; Ngouajio, M. Polyethylene and biodegradable mulches for agri-cultural applications: A review. Agron. Sustain. Dev. 2012, 32, 501–529. [Google Scholar] [CrossRef]
- Gu, X.B.; Cai, H.J.; Du, Y.D.; Li, Y.N. Effects of film mulching and nitrogen fertilization on rhizosphere soil environment, root growth and nutrient uptake of winter oilseed rape in northwest China. Soil Till. Res. 2019, 187, 194–203. [Google Scholar] [CrossRef]
- Ma, D.D.; Chen, L.; Qu, H.C.; Wang, L.Y.; Misselbrook, T.; Jiang, R. Impacts of plastic film mulching on crop yields, soil water, nitrate, and organic carbon in Northwestern China: Ameta-analysis. Agric. Water Manag. 2018, 202, 166–173. [Google Scholar] [CrossRef]
- O’Loughlin, J.; Finnan, J.; Mcdonnell, K. Accelerating early growth in miscanthus with the application of plastic mulch film. Biomass Bioenergy. 2017, 100, 52–61. [Google Scholar] [CrossRef]
- Daryanto, S.; Wang, L.X.; Jacinthe, P.A. Can ridge-furrow plastic mulching replace irrigation in dryland wheat and maize cropping systems? Agricul. Water Manag. 2017, 190, 1–5. [Google Scholar] [CrossRef]
- Al-Shammary, A.A.G.; Kouzani, A.; Gyasi-Agyei, Y.; Gates, W.; Rodrigo-Comino, J. Effects of solarisation on soil thermal-physical properties under different soil treatments: A review. Geoderma 2020, 363, 114137. [Google Scholar] [CrossRef]
- Yang, N.; Sun, Z.X.; Feng, L.S.; Zheng, M.Z.; Chi, D.C.; Meng, W.Z.; Hou, Z.Y.; Bai, W.; Li, K.Y. Plastic film mulching for water-efficient agricultural applications and degradable films materials development research. Adv. Manuf. Process. 2015, 30, 143–154. [Google Scholar] [CrossRef]
- Yan, C.; He, W.; Xue, Y.; Liu, Q. Application of biodegradable plastic film to reduce plastic film residual pollution in Chinese agriculture. Chinese J. Biotechnol. 2016, 32, 748–760. [Google Scholar]
- Picuno, P. Innovative material and improved technical design for a sustainable exploitation of agricultural plastic film. Polym. Plast. Technol. Eng. 2014, 53, 1000–1011. [Google Scholar] [CrossRef]
- Li, Y.Q.; Zhao, C.X.; Yan, C.R.; Mao, L.L.; Liu, Q.; Li, Z.; He, W.Q. Effects of agricultural plastic film residues on transportation and distribution of water and nitrate in soil. Chemosphere. 2020, 242, 125131. [Google Scholar]
- Brodhagen, M.; Goldberger, J.R.; Hayes, D.G.; Inglis, D.A.; Marsh, T.L.; Miles, C. Policy considerations for limiting unintended residual plastic in agricultural soils. Environ. Sci. Policy. 2017, 69, 81–84. [Google Scholar] [CrossRef]
- Guo, B.Y.; Meng, J.; Wang, X.Y.; Yin, C.N.; Hao, W.Y.; Ma, B.W.; Tao, Z. Quantification of pesticide residues on plastic mulching films in typical farmlands of the north China. Front. Env. Eng. 2019, 14. [Google Scholar] [CrossRef]
- Zou, X.Y.; Niu, W.Q.; Liu, J.J.; Li, Y.; Liang, B.H.; Guo, L.L.; Guan, Y.H. Effects of residual mulch film on the growth and fruit quality of tomato (Lycopersicon esculentummill.). Water Air Soil Pollut. 2017, 228, 71. [Google Scholar] [CrossRef]
- Chen, Y.S.; Wu, C.F.; Zhang, H.B.; Lin, Q.Y.; Hong, Y.W.; Luo, Y.M. Empirical estimation of pollution load and contamination levels of phthalate esters in agricultural soils from plastic film mulching in China. Environ. Earth Sci. 2013, 70, 239–247. [Google Scholar] [CrossRef]
- Gao, H.H.; Yan, C.R.; Liu, Q.; Chen, B.Q.; Li, Z. Effects of plastic mulching and plastic residue on agricultural production: A meta-analysis. Sci. Total Environ. 2018, 651, 484–492. [Google Scholar] [CrossRef]
- Qiuyan, Y.; Richard, S.; Jan, O. Poly hydroxyl butyrate production from municipal wastewater activated sludge with different carbon sources. Air Soil Water Res. 2015, 853–858. [Google Scholar] [CrossRef]
- Ibarra-Jiménez, L.; Lira-Saldivar, R.H.; Valdez-Aguilar, L.A.; Lozano-Del Rio, J. Colored plastic mulches affect soil temperature and tuber production of potato. Acta Agricul. Scandinav. Sect. b-Soil Plant Sci. 2011, 61, 365–371. [Google Scholar] [CrossRef]
- Liu, E.K.; He, W.Q.; Yan, C.R. ‘White revolution’ to ‘white pollution’—Agricultural plastic film mulch in China. Environ. Res. Lett. 2014, 9, 091001. [Google Scholar] [CrossRef]
- Zhang, D.; Ng, E.L.; Hu, W.L.; Wang, H.Y.; Galaviz, P.; Yang, H.; Sun, W.; Li, C.; Ma, X.; Fu, B.; et al. Plastic pollution in croplands threatens long-term food security. Global Chang. Biol. 2020. [Google Scholar] [CrossRef]
- Shi, M.; Sun, Y.Y.; Wang, Z.H.; He, G.; Quan, H.X.; He, H.X. Plastic film mulching increased the accumulation and human health risks of phthalate esters in wheat grains. Environ. Poll. 2019, 250, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Gu, X.B.; Li, Y.N.; Du, Y.D. Biodegradable film mulching improves soil temperature, moisture and seed yield of winter oilseed rape (Brassica napus L.). Soil Till. Res. 2017, 171, 42–50. [Google Scholar] [CrossRef]
- Ren, X.L.; Chen, X.L.; Cai, T.; Wei, T.; Wu, Y.; Ali, S.; Zhang, P.; Jia, Z.K. Effects of ridge-furrow system combined with different degradable mulching materials on soil water conservation and crop production in semi-humid areas of China. Front. Plant Sci. 2017, 8, 1877. [Google Scholar] [CrossRef]
- Chiellini, E.; Cinelli, P.; D’Antone, S.; Ilieva, V.I. Environmentally degradable polymeric materials (edpm) in agricultural applications—An overview. Polimery. 2002, 47, 538–544. [Google Scholar] [CrossRef]
- Abidli, S.; Antunes, J.C.; Ferreira, J.L.; Lahbib, Y.; Sobral, P.; El Menif, N.T. Micro plastics in sediments from the littoral zone of the north Tunisian coast (Mediterranean Sea). Estuarine Coastal Shelf Sci. 2018, 205, 1–9. [Google Scholar] [CrossRef]
- Han, W.; Ren, J.Y.; Xuan, H.Y.; Ge, L.Q. Controllable degradation rates, antibacterial, free-standing and highly transparent films based on polylactic acid and chitosan. Colloids Surf. A Physicochem. Eng. Asp. 2018, 514, 128–136. [Google Scholar] [CrossRef]
- Hazarika, P.; Chowdhury, D.; Chattopadhyay, A. Fabrication of submicron scale patterned plastic thin film fluidic devices with controllable thickness. Lab Chip 2003, 3, 128. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.F.; Chen, Y.; Liu, Y.; Wen, X.X.; Liao, Y.C. Coupling effects of plastic film mulching and urea types on water use efficiency and grain yield of maize in the Loess Plateau, China. Soil Till. Res. 2016, 157, 1–10. [Google Scholar] [CrossRef]
- Gong, D.Z.; Hao, W.P.; Mei, X.R.; Gao, X.; Liu, Q.; Caylor, K. Warmer and wetter soil stimulates assimilation more than respiration in rainfed agricultural ecosystem on the China Loess Plateau: The role of partial plastic film mulching tillage. PlosOne. 2015, 10, e0136578. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Shi, H.; Ye, L.; Wang, Z.; Lin, Y.; Xin, L. Effects of different residual plastic film quantities in soil on drip infiltration and its uncertainty analysis. Trans. Chin. Soc. Agric. Eng. 2013, 29, 84–90, (In Chinese with English abstract). [Google Scholar]
- Zou, X.; Niu, W.; Liu, J.; Xu, J.; Zhang, M.; Li, Y. Ability of Retarding Water Horizontal Movement for Residual Plastic Film Mixed in Soil. J. Soil Water Conserv. 2016, 30, 96–102, 108, (In Chinese with English abstract). [Google Scholar]
- Xing, X.G.; Li, Y.B.; Ma, X.Y. Water retention curve correction using changes in bulk density during data collection. Eng. Geol. 2018, 233, 231–237. [Google Scholar] [CrossRef]
- Bauters, T.W.J.; DiCarlo, D.A.; Steenhuis, T.S.; Parlange, J.Y. Soil water content dependent wetting front characteristics in sands. J. Hydrol. 2000, 231, 244–254. [Google Scholar] [CrossRef]
- Fan, Y.W.; Huang, N.; Gong, J.G.; Shao, X.X.; Zhang, J.; Zhao, T. A simplified infiltration model for predicting cumulative infiltration during vertical line source irrigation. Water. 2018, 10, 89. [Google Scholar] [CrossRef]
- Lekshmi, S.U.S.; Singh, D.N.; Baghini, M.S.A. critical review of soil moisture measurement. Measurement 2014, 54, 92–105. [Google Scholar]
- Wang, Z.C.; Li, X.Y.; Shi, H.B.; Lin, Y.X.; Li, X.; Liang, J.C. Study on effect of plastic film residue at different buried depths on silt loam drip infiltration. Soils. 2014, 46, 710–715, (In Chinese with English abstract). [Google Scholar]
- Li, Y.; He, Q.; Yan, C. Effect of residual film on soil infiltration under drip irrigation. Trans. Chin. Soc. Agric. Eng. 2015, 31, 145–149, (In Chinese with English abstract). [Google Scholar]
- Grismer, M.E.; Orang, M.N.; Clausnitzer, V.; Kinney, K. Effects of air compression and counter flow on infiltration into soils. J. Irrig. Drainage Eng. 1994, 120, 775–795. [Google Scholar] [CrossRef]



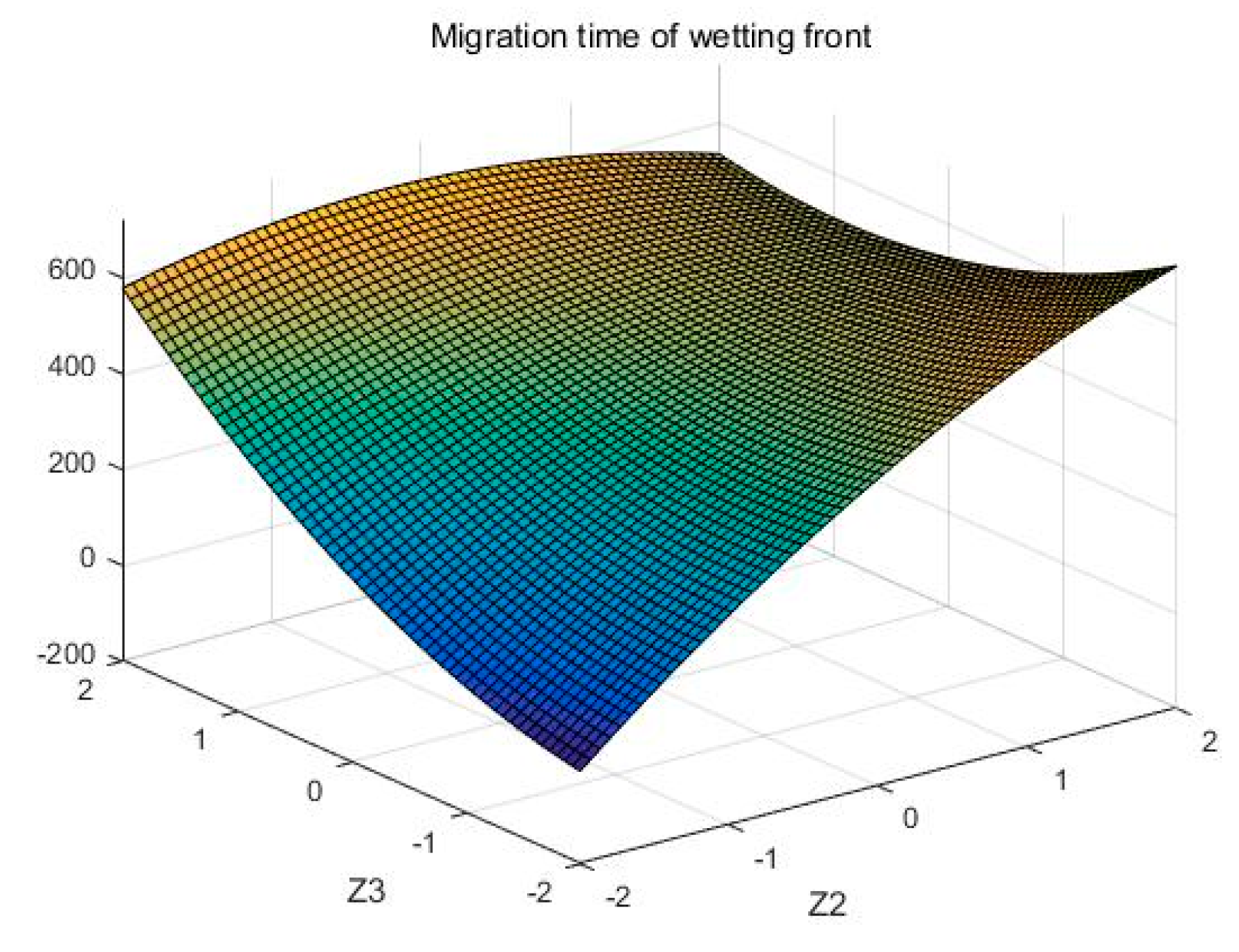
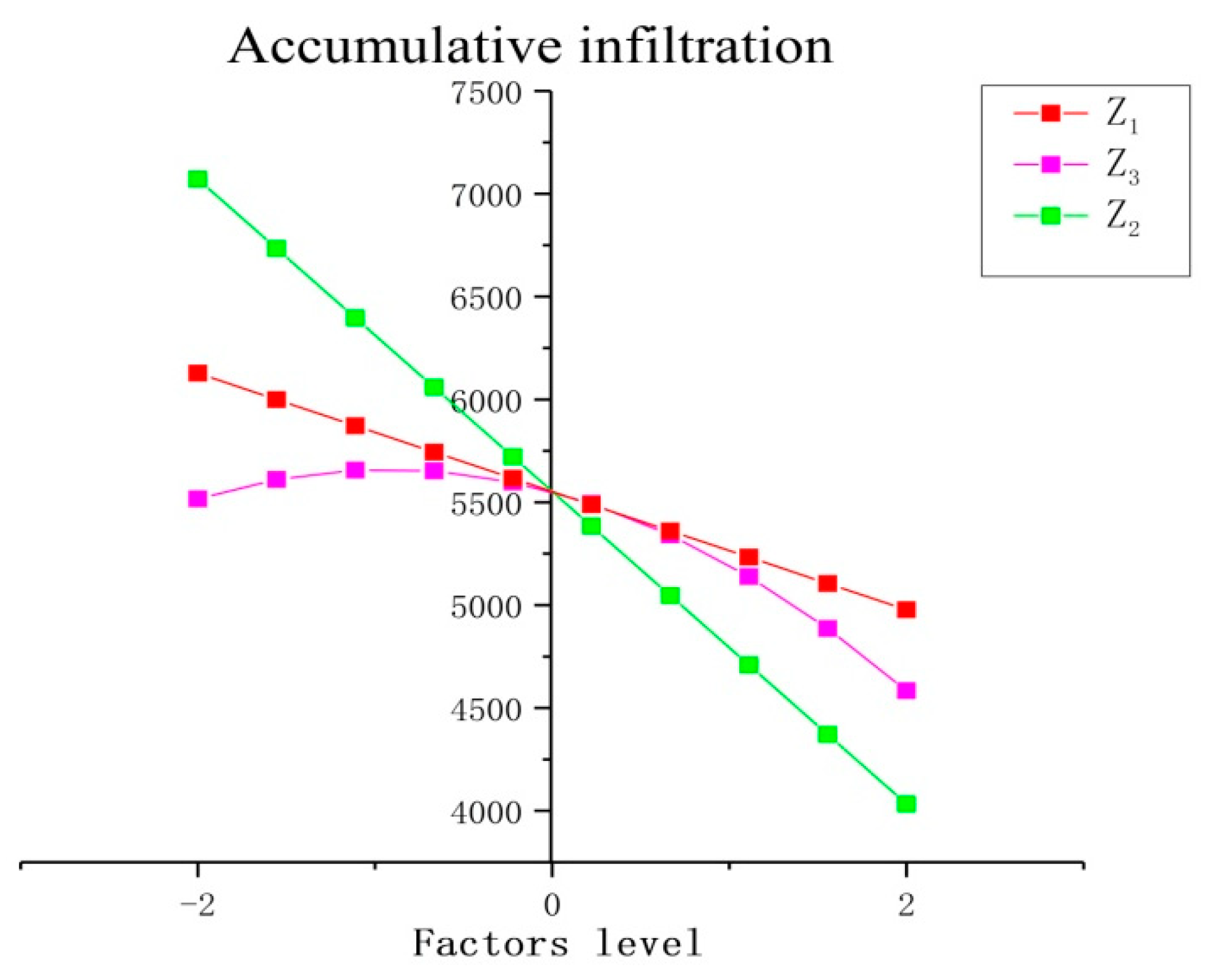


| Zj | IMC Z1/% | DBD Z2/(g/cm³) | RPFC Z3/(kg/hm²) | Burial Depth of RPFZ4/cm |
|---|---|---|---|---|
| r (2) | 16 | 1.45 | 200 | 30~40 |
| 1 | 14 | 1.41 | 150 | 20~30 |
| 0 | 11 | 1.35 | 100 | 10~20 |
| −1 | 8 | 1.29 | 50 | 0~10 |
| r (−2) | 6 | 1.25 | 0 | 0 |
| Variance Source | Sum of Squares | Degree of Freedom | Mean Square | Partial Correlation | F-Ratio | P |
|---|---|---|---|---|---|---|
| Z1 | 430,408.2 | 1 | 430,408.2 | −0.9648 | 282.3304 | 0.0001 |
| Z2 | 175,788.2 | 1 | 175,788.2 | 0.9197 | 115.3099 | 0.0001 |
| Z3 | 58,608.17 | 1 | 58,608.17 | 0.8042 | 38.4446 | 0.0001 |
| Z4 | 80.6667 | 1 | 80.6667 | −0.0501 | 0.0529 | 0.8203 |
| Z12 | 62.3472 | 1 | 62.3472 | 0.0441 | 0.0409 | 0.8417 |
| Z22 | 14,252.35 | 1 | 14,252.35 | −0.555 | 9.349 | 0.006 |
| Z32 | 20,234.01 | 1 | 20,234.01 | 0.6223 | 13.2727 | 0.0015 |
| Z42 | 5390.681 | 1 | 5390.681 | −0.3796 | 3.5361 | 0.074 |
| Z1Z2 | 28,392.25 | 1 | 28,392.25 | −0.6856 | 18.6242 | 0.0003 |
| Z1Z3 | 12.25 | 1 | 12.25 | 0.0196 | 0.008 | 0.9294 |
| Z1Z4 | 72.25 | 1 | 72.25 | 0.0475 | 0.0474 | 0.8298 |
| Z2Z3 | 37,442.25 | 1 | 37,442.25 | −0.7342 | 24.5606 | 0.0001 |
| Z2Z4 | 2652.25 | 1 | 2652.25 | 0.2766 | 1.7398 | 0.2014 |
| Z3Z4 | 702.25 | 1 | 702.25 | −0.1465 | 0.4606 | 0.5047 |
| Regression | 774,098.1 | 14 | 55,292.72 | F2 = 36.26979 | 0.0001 | |
| Residual | 32,014.17 | 21 | 1524.484 | |||
| Lack of fit | 22,307.92 | 10 | 2230.792 | F1 = 2.52813 | 0.0001 | |
| Error | 9706.25 | 11 | 882.3864 | |||
| Sum | 806,112.2 | 35 | ||||
| Factors | Sum of Squares | Degree of Freedom | Mean Square | Partial Correlation | F-Ratio | P |
|---|---|---|---|---|---|---|
| Z1 | 1,985,291 | 1 | 1,985,291 | −0.7791 | 32.4444 | 0.0001 |
| Z2 | 13,841,432 | 1 | 13,841,432 | −0.9566 | 226.2023 | 0.0001 |
| Z3 | 1,303,728 | 1 | 1,303,728 | −0.7097 | 21.3061 | 0.0001 |
| Z4 | 9680.97 | 1 | 9680.97 | −0.0865 | 0.1582 | 0.6948 |
| Z12 | 129,160.7 | 1 | 129,160.7 | −0.3022 | 2.1108 | 0.161 |
| Z22 | 484,006.6 | 1 | 484,006.6 | 0.5231 | 7.9098 | 0.0104 |
| Z32 | 503,850.7 | 1 | 503,850.7 | −0.5307 | 8.2341 | 0.0092 |
| Z42 | 87,288.17 | 1 | 87,288.17 | −0.2522 | 1.4265 | 0.2457 |
| Z1Z2 | 58,888.73 | 1 | 58,888.73 | −0.2093 | 0.9624 | 0.3378 |
| Z1Z3 | 104,022.4 | 1 | 104,022.4 | 0.2737 | 1.7 | 0.2064 |
| Z1Z4 | 26,511.98 | 1 | 26,511.98 | 0.1422 | 0.4333 | 0.5175 |
| Z2Z3 | 2,447,723 | 1 | 2,447,723 | 0.8098 | 40.0017 | 0.0001 |
| Z2Z4 | 20,067.56 | 1 | 20,067.56 | 0.124 | 0.328 | 0.5729 |
| Z3Z4 | 14,174.09 | 1 | 14,174.09 | 0.1045 | 0.2316 | 0.6353 |
| Regression | 21,015,826 | 14 | 1,501,130 | F2 = 24.53208 | 0.0001 | |
| Residual | 1,285,001 | 21 | 61,190.51 | |||
| Lack of fit | 1,244,848 | 10 | 124,484.8 | F1 = 34.10330 | 0.0001 | |
| Error | 40,152.51 | 11 | 3650.228 | |||
| Sum | 22,300,827 | 35 | ||||
| Factors | Sum of Squares | Degree of Freedom | Mean Square | Partial Correlation | F-Ratio | P |
|---|---|---|---|---|---|---|
| Z1 | 40.3782 | 1 | 40.3782 | −0.89 | 79.9942 | 0.0001 |
| Z2 | 78.9525 | 1 | 78.9525 | −0.939 | 156.4148 | 0.0001 |
| Z3 | 5.0508 | 1 | 5.0508 | −0.5681 | 10.0063 | 0.0047 |
| Z4 | 0.0002 | 1 | 0.0002 | −0.0044 | 0.0004 | 0.9841 |
| Z12 | 0.0458 | 1 | 0.0458 | 0.0656 | 0.0906 | 0.7663 |
| Z22 | 3.8157 | 1 | 3.8157 | 0.5145 | 7.5594 | 0.012 |
| Z32 | 6.1864 | 1 | 6.1864 | −0.6071 | 12.256 | 0.0021 |
| Z42 | 2.2103 | 1 | 2.2103 | 0.4154 | 4.3788 | 0.0487 |
| Z1Z2 | 0.8236 | 1 | 0.8236 | 0.2685 | 1.6316 | 0.2154 |
| Z1Z3 | 0.6765 | 1 | 0.6765 | −0.2449 | 1.3402 | 0.26 |
| Z1Z4 | 2.4571 | 1 | 2.4571 | −0.4338 | 4.8677 | 0.0386 |
| Z2Z3 | 1.8701 | 1 | 1.8701 | 0.3873 | 3.7048 | 0.0679 |
| Z2Z4 | 0.2377 | 1 | 0.2377 | −0.1481 | 0.4708 | 0.5001 |
| Z3Z4 | 1.2939 | 1 | 1.2939 | −0.3298 | 2.5634 | 0.1243 |
| Regression | 143.9986 | 14 | 10.2856 | F2 = 20.37708 | 0.0001 | |
| Residual | 10.6 | 21 | 0.5048 | |||
| Lack of fit | 10.3697 | 10 | 1.037 | F1 = 49.52981 | 0.0001 | |
| Error | 0.2303 | 11 | 0.0209 | |||
| Sum | 154.5987 | 35 | ||||
| Factors | Sum of Squares | Degree of Freedom | Mean Square | Partial Correlation | F-Ratio | P |
|---|---|---|---|---|---|---|
| Z1 | 41.554 | 1 | 41.554 | −0.851 | 55.1587 | 0.0001 |
| Z2 | 102.0113 | 1 | 102.0113 | −0.9304 | 135.4094 | 0.0001 |
| Z3 | 7.5264 | 1 | 7.5264 | −0.5678 | 9.9905 | 0.0047 |
| Z4 | 0.1442 | 1 | 0.1442 | −0.095 | 0.1913 | 0.6663 |
| Z12 | 1.4706 | 1 | 1.4706 | 0.2916 | 1.9521 | 0.177 |
| Z22 | 0.5778 | 1 | 0.5778 | 0.1877 | 0.767 | 0.3911 |
| Z32 | 6.2481 | 1 | 6.2481 | −0.5321 | 8.2937 | 0.009 |
| Z42 | 0.3828 | 1 | 0.3828 | 0.1537 | 0.5081 | 0.4838 |
| Z1Z2 | 0.6241 | 1 | 0.6241 | 0.1948 | 0.8284 | 0.3731 |
| Z1Z3 | 1.092 | 1 | 1.092 | −0.2541 | 1.4496 | 0.242 |
| Z1Z4 | 1.199 | 1 | 1.199 | −0.2654 | 1.5916 | 0.2209 |
| Z2Z3 | 1.3924 | 1 | 1.3924 | 0.2844 | 1.8483 | 0.1884 |
| Z2Z4 | 0.0625 | 1 | 0.0625 | −0.0627 | 0.083 | 0.7761 |
| Z3Z4 | 0.7656 | 1 | 0.7656 | −0.2149 | 1.0163 | 0.3249 |
| Regression | 165.0509 | 14 | 11.7893 | F2 = 15.64914 | 0.0001 | |
| Residual | 15.8204 | 21 | 0.7534 | |||
| Lack of fit | 14.5316 | 10 | 1.4532 | F1 = 12.40190 | 0.0001 | |
| Error | 1.2889 | 11 | 0.1172 | |||
| Sum | 180.8713 | 35 | ||||
| Factors | Sum of Squares | Degree of Freedom | Mean Square | Partial Correlation | F-Ratio | P |
|---|---|---|---|---|---|---|
| Z1 | 24.8067 | 1 | 24.8067 | −0.7409 | 25.5609 | 0.0001 |
| Z2 | 99.5523 | 1 | 99.5523 | −0.9111 | 102.5792 | 0.0001 |
| Z3 | 7.958 | 1 | 7.958 | −0.5299 | 8.2 | 0.0093 |
| Z4 | 0.028 | 1 | 0.028 | −0.0371 | 0.0289 | 0.8667 |
| Z12 | 0.091 | 1 | 0.091 | 0.0667 | 0.0938 | 0.7624 |
| Z22 | 0.9614 | 1 | 0.9614 | 0.2122 | 0.9907 | 0.3309 |
| Z32 | 7.854 | 1 | 7.854 | −0.5274 | 8.0928 | 0.0097 |
| Z42 | 0.2568 | 1 | 0.2568 | 0.1116 | 0.2646 | 0.6123 |
| Z1Z2 | 0.6006 | 1 | 0.6006 | 0.1692 | 0.6189 | 0.4402 |
| Z1Z3 | 0.0042 | 1 | 0.0042 | 0.0144 | 0.0044 | 0.948 |
| Z1Z4 | 0.5256 | 1 | 0.5256 | −0.1586 | 0.5416 | 0.4699 |
| Z2Z3 | 1.113 | 1 | 1.113 | 0.2276 | 1.1469 | 0.2964 |
| Z2Z4 | 3.441 | 1 | 3.441 | −0.3801 | 3.5457 | 0.0736 |
| Z3Z4 | 0.3906 | 1 | 0.3906 | −0.1371 | 0.4025 | 0.5327 |
| Regression | 147.5834 | 14 | 10.5417 | F2 = 10.86219 | 0.0001 | |
| Residual | 20.3803 | 21 | 0.9705 | |||
| Lack of fit | 19.9954 | 10 | 1.9995 | F1 = 57.14589 | 0.0001 | |
| Error | 0.3849 | 11 | 0.035 | |||
| Sum | 167.9637 | 35 | ||||
| Factors | Sum of Squares | Degree of Freedom | Mean Square | Partial Correlation | F-Ratio | P |
|---|---|---|---|---|---|---|
| Z1 | 24.9492 | 1 | 24.9492 | −0.8376 | 49.3765 | 0.0001 |
| Z2 | 67.0338 | 1 | 67.0338 | −0.9292 | 132.6653 | 0.0001 |
| Z3 | 8.9426 | 1 | 8.9426 | −0.6763 | 17.6981 | 0.0004 |
| Z4 | 0.0925 | 1 | 0.0925 | −0.093 | 0.1831 | 0.6731 |
| Z12 | 1.2813 | 1 | 1.2813 | 0.3282 | 2.5359 | 0.1262 |
| Z22 | 3.3822 | 1 | 3.3822 | 0.4916 | 6.6936 | 0.0172 |
| Z32 | 4.4377 | 1 | 4.4377 | −0.543 | 8.7826 | 0.0074 |
| Z42 | 2.858 | 1 | 2.858 | 0.4606 | 5.6563 | 0.027 |
| Z1Z2 | 0.5006 | 1 | 0.5006 | 0.2122 | 0.9906 | 0.3309 |
| Z1Z3 | 0.6521 | 1 | 0.6521 | −0.2406 | 1.2905 | 0.2688 |
| Z1Z4 | 1.9113 | 1 | 1.9113 | −0.3907 | 3.7826 | 0.0653 |
| Z2Z3 | 0.015 | 1 | 0.015 | 0.0376 | 0.0297 | 0.8648 |
| Z2Z4 | 3.3948 | 1 | 3.3948 | −0.4923 | 6.7186 | 0.017 |
| Z3Z4 | 0.1351 | 1 | 0.1351 | −0.1121 | 0.2673 | 0.6106 |
| Regression | 119.5862 | 14 | 8.5419 | F2 = 16.90505 | 0.0001 | |
| Residual | 10.611 | 21 | 0.5053 | |||
| Lack of fit | 10.5042 | 10 | 1.0504 | F1 = 108.22336 | 0.0001 | |
| Error | 0.1068 | 11 | 0.0097 | |||
| Sum | 130.1972 | 35 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Chen, P.; Li, Y.; Fang, H.; Gu, X.; Li, Y. Effect of Plastic Film Residue on Vertical Infiltration Under Different Initial Soil Moisture Contents and Dry Bulk Densities. Water 2020, 12, 1346. https://doi.org/10.3390/w12051346
Cao J, Chen P, Li Y, Fang H, Gu X, Li Y. Effect of Plastic Film Residue on Vertical Infiltration Under Different Initial Soil Moisture Contents and Dry Bulk Densities. Water. 2020; 12(5):1346. https://doi.org/10.3390/w12051346
Chicago/Turabian StyleCao, Junhao, Pengpeng Chen, Yupeng Li, Heng Fang, Xiaobo Gu, and Yuannong Li. 2020. "Effect of Plastic Film Residue on Vertical Infiltration Under Different Initial Soil Moisture Contents and Dry Bulk Densities" Water 12, no. 5: 1346. https://doi.org/10.3390/w12051346
APA StyleCao, J., Chen, P., Li, Y., Fang, H., Gu, X., & Li, Y. (2020). Effect of Plastic Film Residue on Vertical Infiltration Under Different Initial Soil Moisture Contents and Dry Bulk Densities. Water, 12(5), 1346. https://doi.org/10.3390/w12051346






