Pressure Regulation vs. Water Aging in Water Distribution Networks
Abstract
:1. Introduction
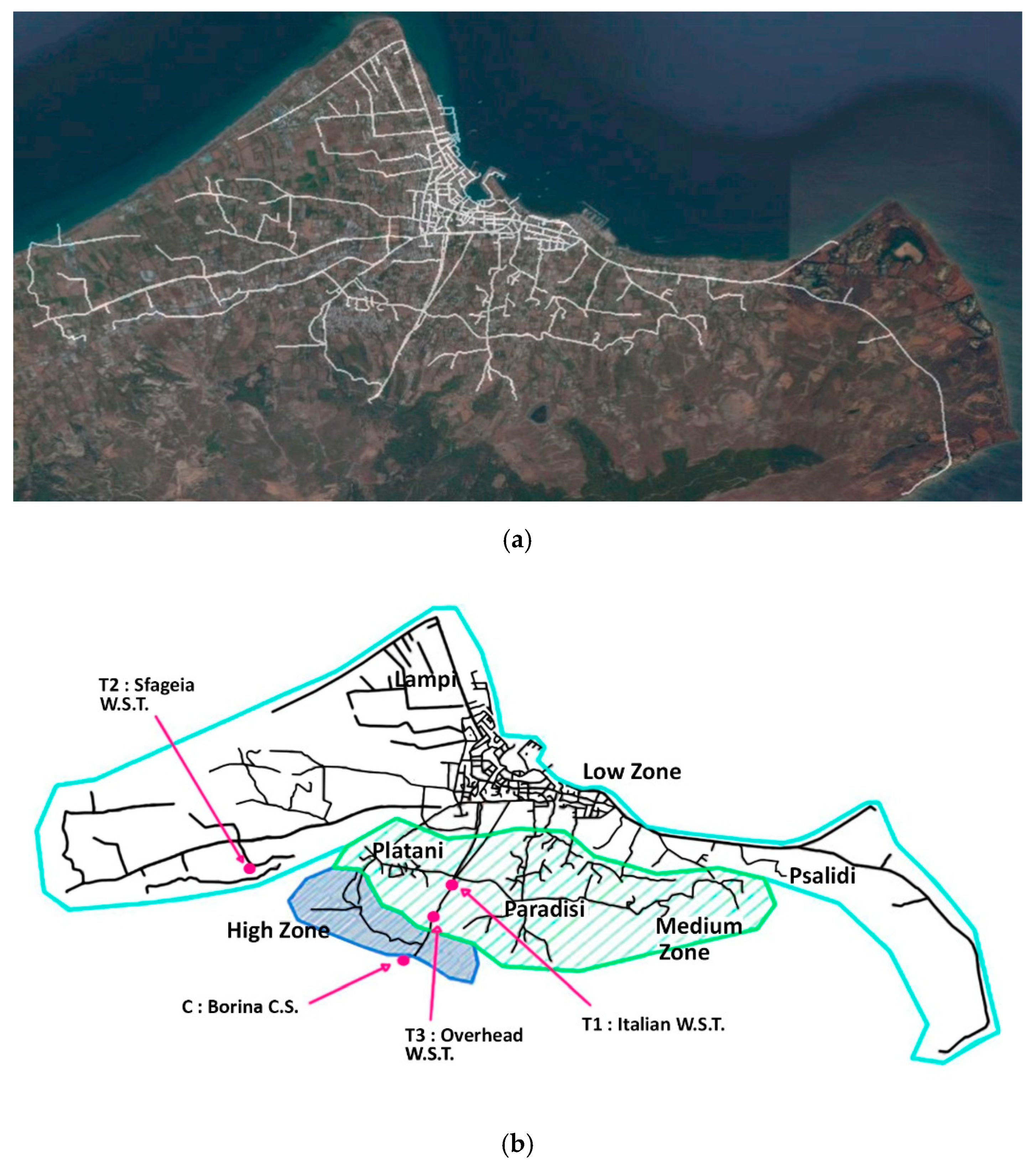
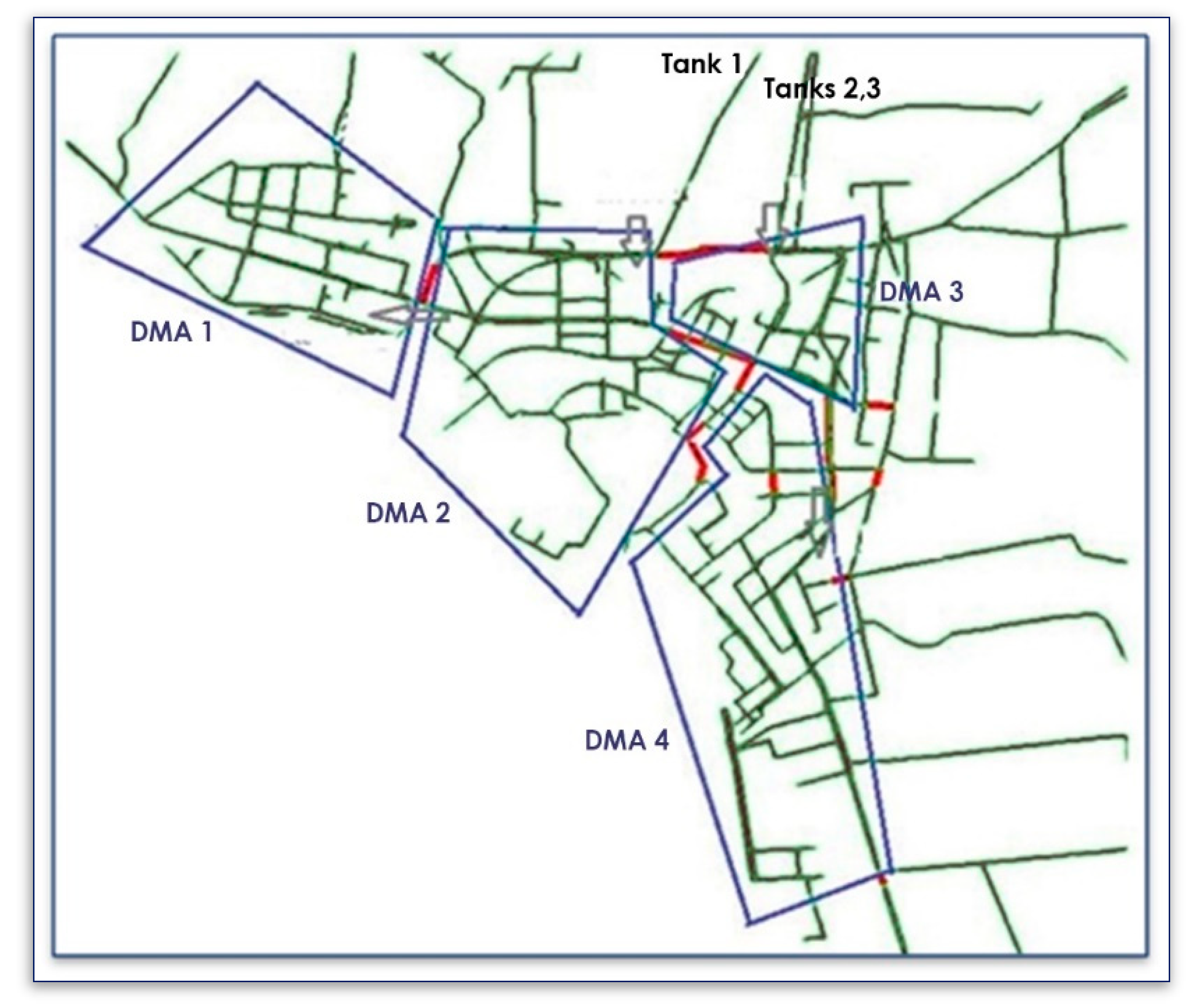
2. Case Study Network
3. Hydraulic Model Simulation
- Scenario No1 (no DMAs_no PRVs): the base scenario with no DMAs formed and no PRVs installed;
- Scenario No2 (with DMAs_no PRVs): DMAs are formed based on well-known specific criteria (size, population served, topography, physical barriers etc.) [1] in the network by closing some pipes (pipe status = closed) in order to separate the entire network in several sub-areas. No PRVs were installed;
- Scenario No3 (with DMAs_with PRVs): a PRV is added in the entering node of each DMA to reduce the average pressure in it as much as possible. The reduction accomplished depends on the actual location (i.e., distance from the entering node) of the critical node in each DMA (i.e., the node with the lowest pressure) as, by law, the Water Utility has to supply water at a pressure of at least 200 kPa (same as 2 atm) measured at the level of the customer’s water meter.
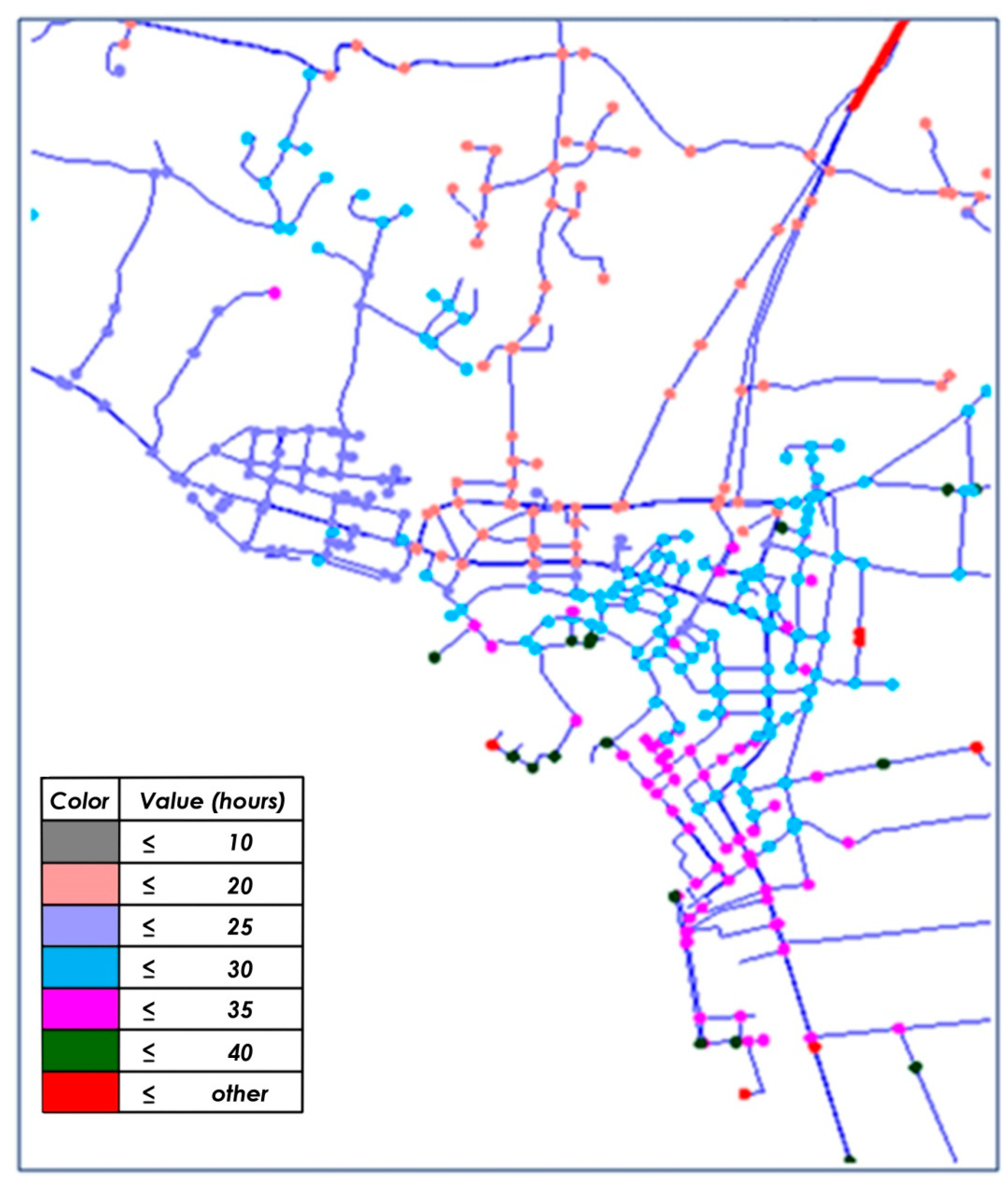
3.1. Water Age Definition
3.2. First Step Analysis and Results
3.3. Water Age Reduction after Regulation of the PRVs
3.4. Proposed Formation of DMAs Based on Minimization of the Water Age
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Charalambous, B. Experience in DMA redesign at water board of Lemesos, Cyprus. In Proceedings of the IWA Specialized Conference Leakage, Halifax, NS, Canada, 12–14 September 2005. [Google Scholar]
- MacDonald, G.; Yates, C. DMA design and implementation, an American context. In Proceedings of the IWA Specialized Conference Leakage, Halifax, NS, Canada, 12–14 September 2005. [Google Scholar]
- Rogers, D. Reducing leakage in Jakarta, Indonesia. In Proceedings of the IWA Specialized Conference Leakage, Halifax, NS, Canada, 12–14 September 2005. [Google Scholar]
- Araujo, L.; Ramos, H.; Coelho, S. Pressure Control for Leakage minimization in Water Distribution Systems Management. Water Resour. Manag. 2006, 1, 133–149. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Muhammetoglu, H. Urban water pipe networks management towards NRW reduction: Two case studies from Greece & Turkey. CLEAN Soil Air Water 2014, 2, 880–892. [Google Scholar]
- Kanakoudis, V.; Gonelas, K. Applying pressure management to reduce water losses in two Greek cities’ Water Distribution Systems: Expectations, problems, results and revisions. Procedia Eng. 2014, 89, 318–325. [Google Scholar] [CrossRef] [Green Version]
- Savic, D.; Ferrari, G. Economic Performance of DMAs in Water Distribution Systems. Procedia Eng. 2015, 189–195. [Google Scholar]
- Kanakoudis, V.; Gonelas, K. The joint effect of water price changes and pressure management, at the economic annual real losses level, on the system input volume of a water distribution system. Water Sci. Technol. Water Suppl. 2015, 15, 1069–1078. [Google Scholar] [CrossRef]
- Wright, R.; Abraham, E.; Parpas, P.; Stoianov, I. Control of water distribution networks with dynamic DMA topology using strictly feasible sequential convex programming. Water Resour. Res. 2015, 51, 9925–9941. [Google Scholar] [CrossRef] [Green Version]
- Kanakoudis, V.; Gonelas, K. The optimal balance point between NRW reduction measures, full water costing and water pricing in water distribution systems. Alternative scenarios forecasting Κozani’s WDS optimal balance point. Procedia Eng. 2015, 119, 1278–1287. [Google Scholar] [CrossRef] [Green Version]
- Vicente, J.; Garrote, L.; Sánchez, R.; Santillán, D. Pressure Management in Water Distribution Systems Current Status, Proposals, and Future Trends. Water Resour. Plann. Manag. 2016, 142, 4015061. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Gonelas, K. Non-revenue water reduction through pressure management in Kozani’s water distribution network: From theory to practice. Desalin. Water Treat. 2016, 57, 11436–11446. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Gonelas, K. Assessing the results of a virtual pressure management project applied in Kos Town water distribution network. Desalin. Water Treat. 2016, 57, 11472–11483. [Google Scholar] [CrossRef]
- Gonelas, K.; Kanakoudis, V. Reaching Economic Leakage Level through Pressure Management. Water Sci. Technol. Water Suppl. 2016, 16, 756–765. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Gonelas, K. Analysis and calculation of the short and long run economic leakage level in a water distribution system. Water Util. 2016, 12, 57–66. [Google Scholar]
- Kanakoudis, V.; Tsitsifli, S.; Demetriou, D. Applying an integrated methodology toward non-revenue water reduction: The case of Nicosia, Cyprus. Desalin. Water Treat. 2016, 57, 11447–11461. [Google Scholar] [CrossRef]
- Patelis, M.; Kanakoudis, V.; Gonelas, K. Combining pressure management and energy recovery benefits in a water distribution system installing PATs. Water Supply Res. Technol. AQUA 2017, 66, 520–527. [Google Scholar] [CrossRef] [Green Version]
- Korkana, P.; Kanakoudis, V.; Patelis, M.; Gonelas, K. Forming district metered areas in a water distribution network using genetic algorithms. Procedia Eng. 2016, 162, 511–520. [Google Scholar] [CrossRef] [Green Version]
- Korkana, P.; Kanakoudis, V.; Makrysopoulos, A.; Patelis, M.; Gonelas, K. Developing an optimization algorithm to form district metered areas in a water distribution system. Procedia Eng. 2016, 162, 530–536. [Google Scholar] [CrossRef] [Green Version]
- Gonelas, K.; Chondronasios, A.; Kanakoudis, V.; Patelis, M.; Korkana, P. Forming DMAs in a water distribution network considering the operating pressure and the chlorine residual concentration as the design parameters. Hydroinformatics 2017, 19, 900–910. [Google Scholar] [CrossRef] [Green Version]
- Chatzivasili, S.; Papadimitriou, K.; Kanakoudis, V.; Patelis, M. Optimizing the formation of DMAs in a water distribution network applying Geometric Partitioning (GP) and Gaussian Mixture Models (GMMs). Proceedings 2018, 2, 601. [Google Scholar] [CrossRef] [Green Version]
- Chatzivasili, S.; Papadimitriou, K.; Kanakoudis, V. Optimizing the formation of DMAs in a water distribution network through advanced modelling. Water 2019, 11, 278. [Google Scholar] [CrossRef] [Green Version]
- Chondronasios, A.; Gonelas, K.; Kanakoudis, V.; Patelis, M.; Korkana, P. Optimizing DMAs’ formation in a water pipe network: The water aging and the operating pressure factors. Hydroinformatics 2017, 19, 890–899. [Google Scholar] [CrossRef] [Green Version]
- Shamsaei, H.; Jaafar, O.; Basri, N. Disadvantage pressure changes on the decline of water quality in water distribution systems. Engineering 2013, 5, 97–105. [Google Scholar] [CrossRef] [Green Version]
- Dan Barr, P.E. Dealing with high water age in a water distribution system. In Ohio AWWA Southeast District Fall Meeting; 2013; Available online: https://www.slideserve.com/pier/dealing-with-high-water-age-in-a-water-distribution-system (accessed on 2 February 2020).
- AWWA. Effects of Water Age on Distribution System Water Quality, Office of Water (4601M) Prepared for U.S.; Environmental Protection Agency: Washington, DC, USA, 2002. Available online: https://www.epa.gov/sites/production/files/2015-09/documents/2007_05_18_disinfection_tcr_whitepaper_tcr_waterdistribution.pdf (accessed on 2 January 2020).
- The National Academic Press. Drinking Water Distribution Systems: Assessing and Reducing Risks, Chapter 5: Hydraulic Integrity; National Research Council: Washington DC, USA, 2006; Available online: https://doi.org/10.17226/11728 (accessed on 2 January 2020).
- Robinson, L.; Edwards, J.; Willnow, L. Computer Modeling of Water Distribution Systems; Manual M32; AWWA: Denver, CO, USA, 2012. [Google Scholar]
- Cruickshank, R. Hydraulic Models Shed Light on Water Age. Opflow 2010, 36, 18–21. [Google Scholar] [CrossRef]
- EPA. Water Quality in Small Community Distribution Systems—A Reference Guide for Operators; EPA: Cincinnati, OH, USA, 2008.
- Rowling, J. Introduction to Water Distribution: A Basic/Intermediate Course for Water System Operators (Principles and Practices of Water Supply Operations, V. 3); AWWA: Denver, CO, USA, 1986. [Google Scholar]
- Fu, G.; Kapelan, Z.; Kasprzyk, J.R.; Reed, P. Optimal design of water distribution systems using many-objective visual analytics. J. Water Resour. Plan. Manag. 2013, 139, 624–633. [Google Scholar] [CrossRef] [Green Version]
- Ghorbanian, V.; Karney, B.W.; Guo, Y. Minimum pressure criterion in water distribution systems: Challenges and consequences. In Proceedings of the World Environmental and Water Resources Congress 2015, Austin, TX, USA, 17–21 May 2015; pp. 777–791. [Google Scholar]
- Kravvari, A.; Kanakoudis, V.; Patelis, M. The impact of pressure management techniques on the water age in an urban pipe network-The case of Kos city network. Proceedings 2018, 2, 699. [Google Scholar] [CrossRef] [Green Version]
- Kanakoudis, V.; Gonelas, K. Properly allocating the urban waters meters’ readings to the nodes of a waterpipe network simulation model in a developing water utility. Desalin. Water Treat. 2015, 54, 2190–2203. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Gonelas, K. Accurate water demand spatial allocation for water networks modeling using a new approach. Urban Water 2015, 12, 362–379. [Google Scholar] [CrossRef]
- Rak, J.; Pietrucha-Urbanik, K. An approach to determine risk indices for drinking water—Study investigation. Sustainability 2019, 11, 3189. [Google Scholar] [CrossRef] [Green Version]
- Kanakoudis, V.; Tsitsifli, S. Using the Bimonthly WB of a Non-Fully Monitored Water Distribution Network with Seasonal Water Demand Peaks to define its Actual NRW Level: The case of Kos Town, Greece. Urban Water 2014, 11, 348–360. [Google Scholar] [CrossRef]
- TOTEE 2411/1986. Infrastructures in Buildings and Plots of Land, Delivery of Cold-Hot Water. Governmental Gazette 834B/16-11-1988. 1988. Available online: http://portal.tee.gr/portal/page/portal/SCIENTIFIC_WORK/tech_odigies_totee/totee_2411_86.pdf (accessed on 2 February 2020). (In Greek).

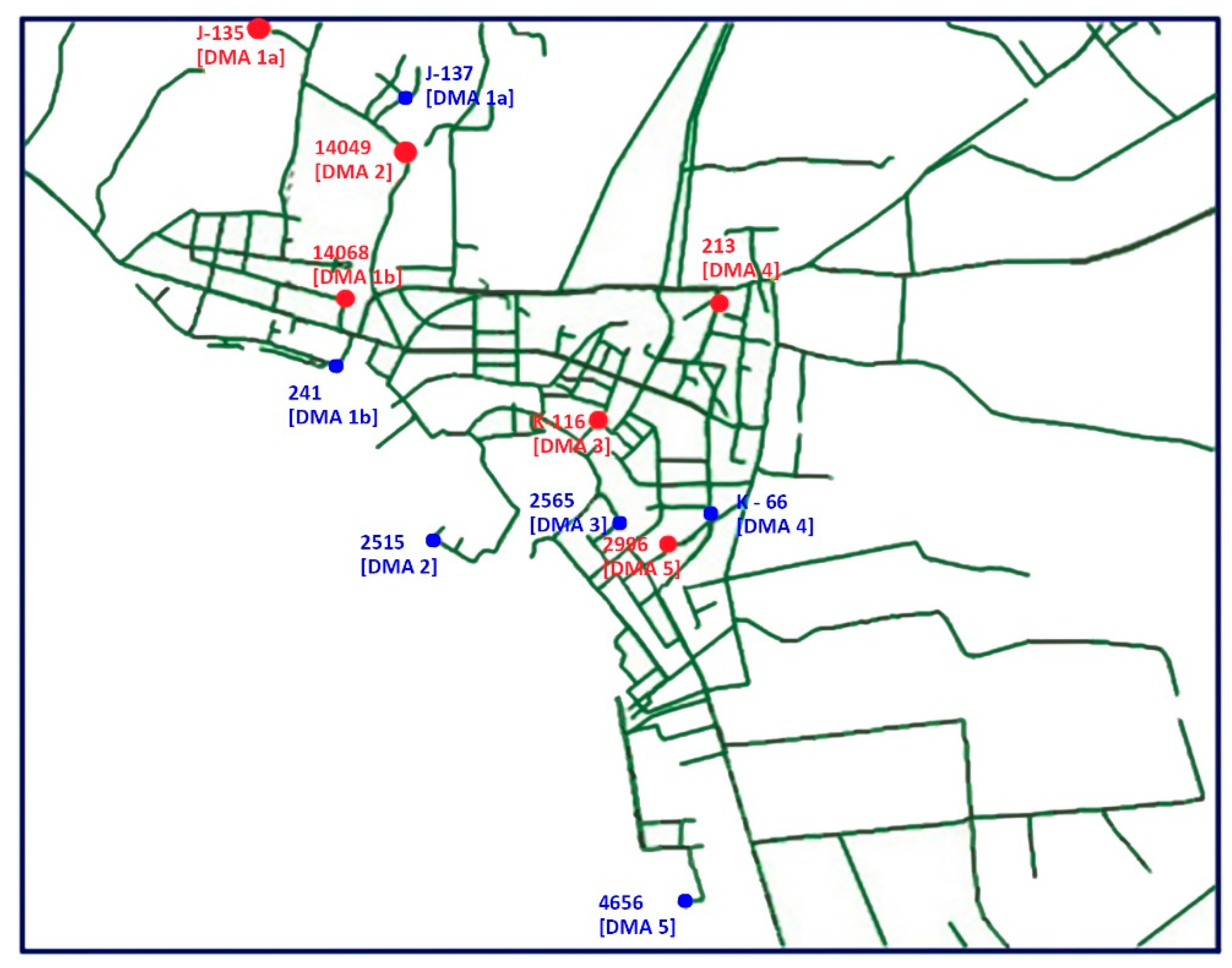
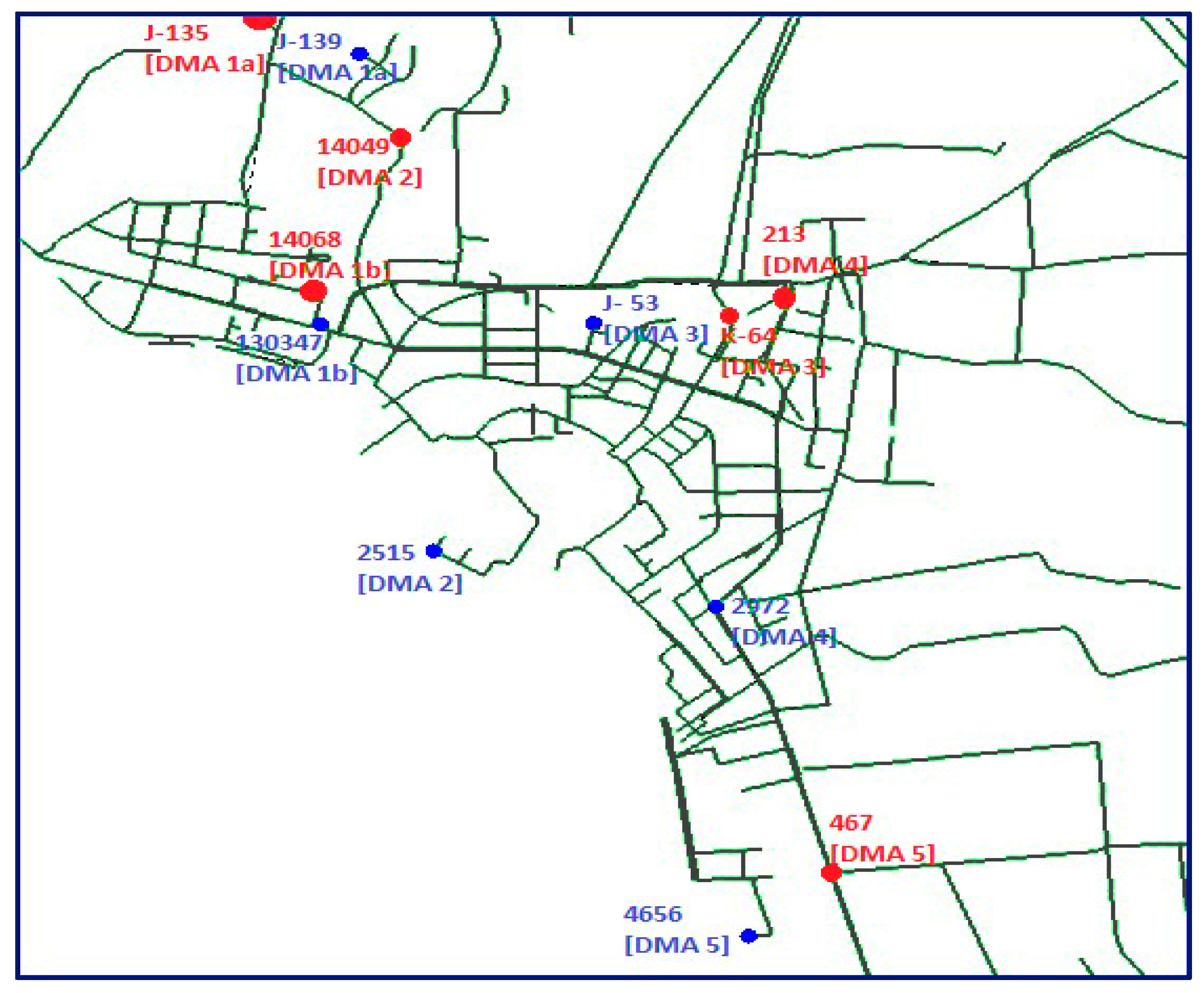
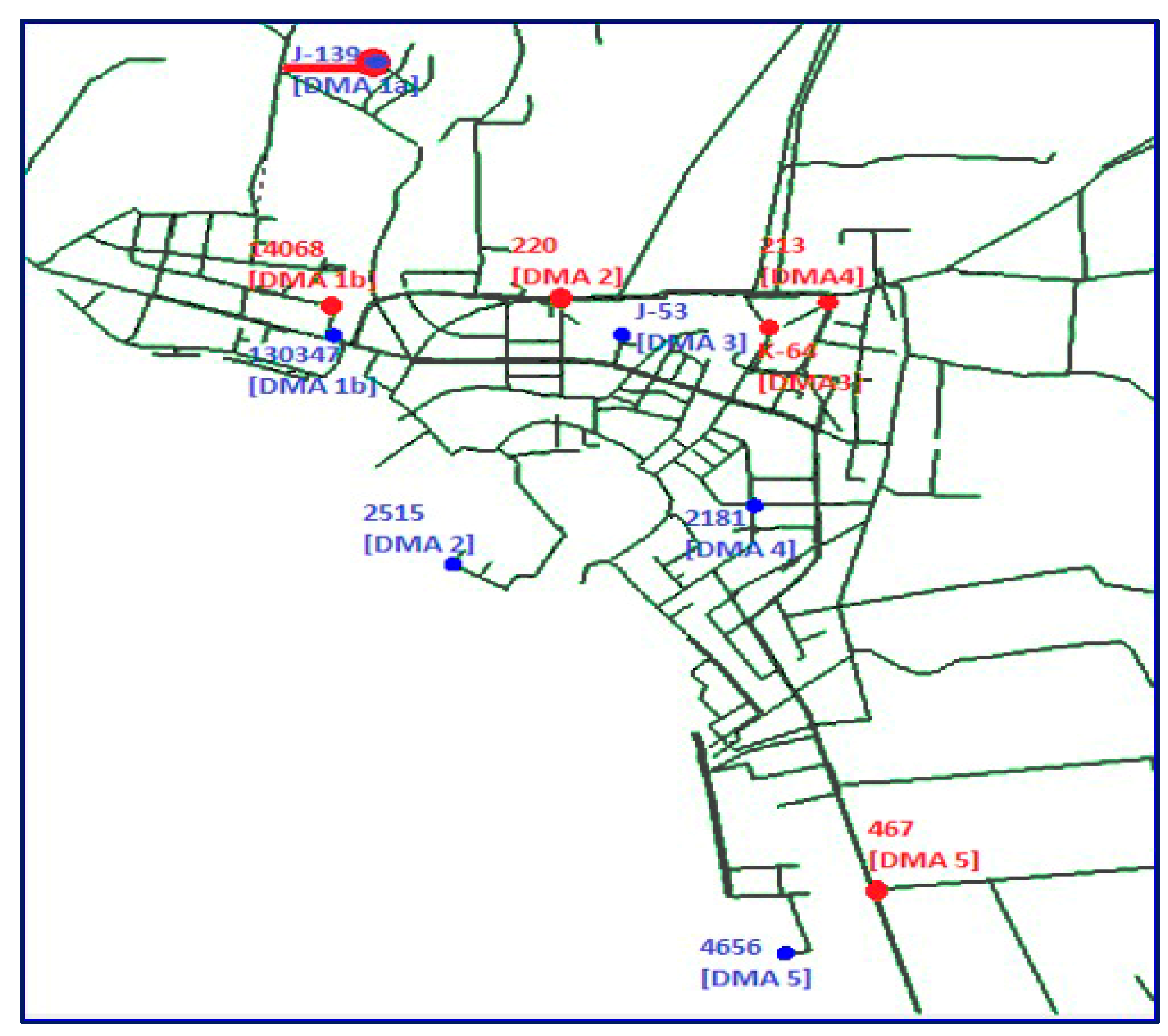
| Scenario No1: noDMAs_no PRVs | |||||||
|---|---|---|---|---|---|---|---|
| Critical Nodes Per DMA Based on the Water Pressure | |||||||
| Pressure (kPa) | Age (h) | Demand (m3/h) | |||||
| DMAs | Critical Node | Mean value per DMA | Mean value at critical node | Mean value per DMA | Mean value at critical node | MAX value at critical node | MAX value at critical node |
| DMA 1a | J-135 | 460.09 | 401.93 | 13.49 | 15.59 | 22.16 | 20.26 |
| DMA 1b | 14068 | 494.02 | 473.88 | 12.27 | 11.91 | 16.86 | 40.48 |
| DMA 2 | 14049 | 484.01 | 457.19 | 9.76 | 12.97 | 18.03 | 37.14 |
| DMA 3 | K-116 | 482.94 | 489.77 | 13.62 | 13.78 | 21.67 | 7.06 |
| DMA 4 | 213 | 474.05 | 430.67 | 10.65 | 9.66 | 12.50 | 69.24 |
| DMA 5 | 2996 | 500.15 | 492.57 | 15.88 | 13.24 | 20.85 | 32.1 |
| Critical Nodes Per DMA Based on the Water Age | |||||||
| DMA 1a | J-137 | 460.09 | 407.81 | 13.49 | 16.31 | 23.13 | 10.1 |
| DMA 1b | 241 | 494.02 | 494.06 | 12.27 | 13.27 | 24.3 | 15.22 |
| DMA 2 | 2515 | 484.01 | 503.87 | 9.76 | 21.77 | 33.65 | 1.76 |
| DMA 3 | 2565 | 482.94 | 494.68 | 13.62 | 15.67 | 22.96 | 6.82 |
| DMA 4 | K-66 | 474.05 | 487.68 | 10.65 | 17.17 | 22.33 | 16.92 |
| DMA 5 | 4656 | 500.15 | 497.14 | 15.88 | 20.65 | 33.9 | 3.32 |
| Scenario No2: with DMAs_no PRVs | |||||||
|---|---|---|---|---|---|---|---|
| Critical Nodes Per DMA Based on the Water Pressure | |||||||
| Pressure (kPa) | Age (h) | Demand (m3/h) | |||||
| DMAs | Critical Node | Mean value per DMA | Mean value at critical node | Mean value per DMA | Mean value at critical node | MAX value at critical node | MAX value at critical node |
| DMA 1a | J-135 | 450.01 | 391.75 | 14.82 | 15.91 | 25.26 | 20.26 |
| DMA 1b | 14068 | 482.91 | 463.78 | 13.45 | 12.07 | 20.09 | 40.48 |
| DMA 2 | 14049 | 457.24 | 430.57 | 10.56 | 12.99 | 18.78 | 37.14 |
| DMA 3 | K-64 | 470.95 | 451.58 | 14.13 | 14.36 | 22.13 | 10.08 |
| DMA 4 | 213 | 465.53 | 422.11 | 11.51 | 10.51 | 12.74 | 69.24 |
| DMA 5 | 467 | 480.40 | 466.75 | 15.90 | 16.10 | 24.53 | 43.92 |
| Critical Nodes Per DMA Based on the Water Age | |||||||
| DMA 1a | J-137 | 460.09 | 407.81 | 14.82 | 15.47 | 25.69 | 10.1 |
| DMA 1b | 241 | 494.02 | 494.06 | 13.45 | 16.37 | 27.50 | 15.22 |
| DMA 2 | 2515 | 484.01 | 503.87 | 10.56 | 22.75 | 34.92 | 1.76 |
| DMA 3 | 2565 | 482.94 | 494.68 | 14.36 | 15.69 | 26.11 | 6.82 |
| DMA 4 | K-66 | 474.05 | 487.68 | 11.51 | 14.07 | 23.85 | 16.92 |
| DMA 5 | 4656 | 500.15 | 497.14 | 15.90 | 20.76 | 33.54 | 3.32 |
| Scenario No3: with DMAs_with PRVs | |||||||
|---|---|---|---|---|---|---|---|
| Critical Nodes Per DMA Based on the Water Pressure | |||||||
| Pressure (kPa) | Age (h) | Demand (m3/h) | |||||
| DMAs | Critical Node | Mean value per DMA | Mean value at critical node | Mean value per DMA | Mean value at critical node | MAX value at critical node | MAX value at critical node |
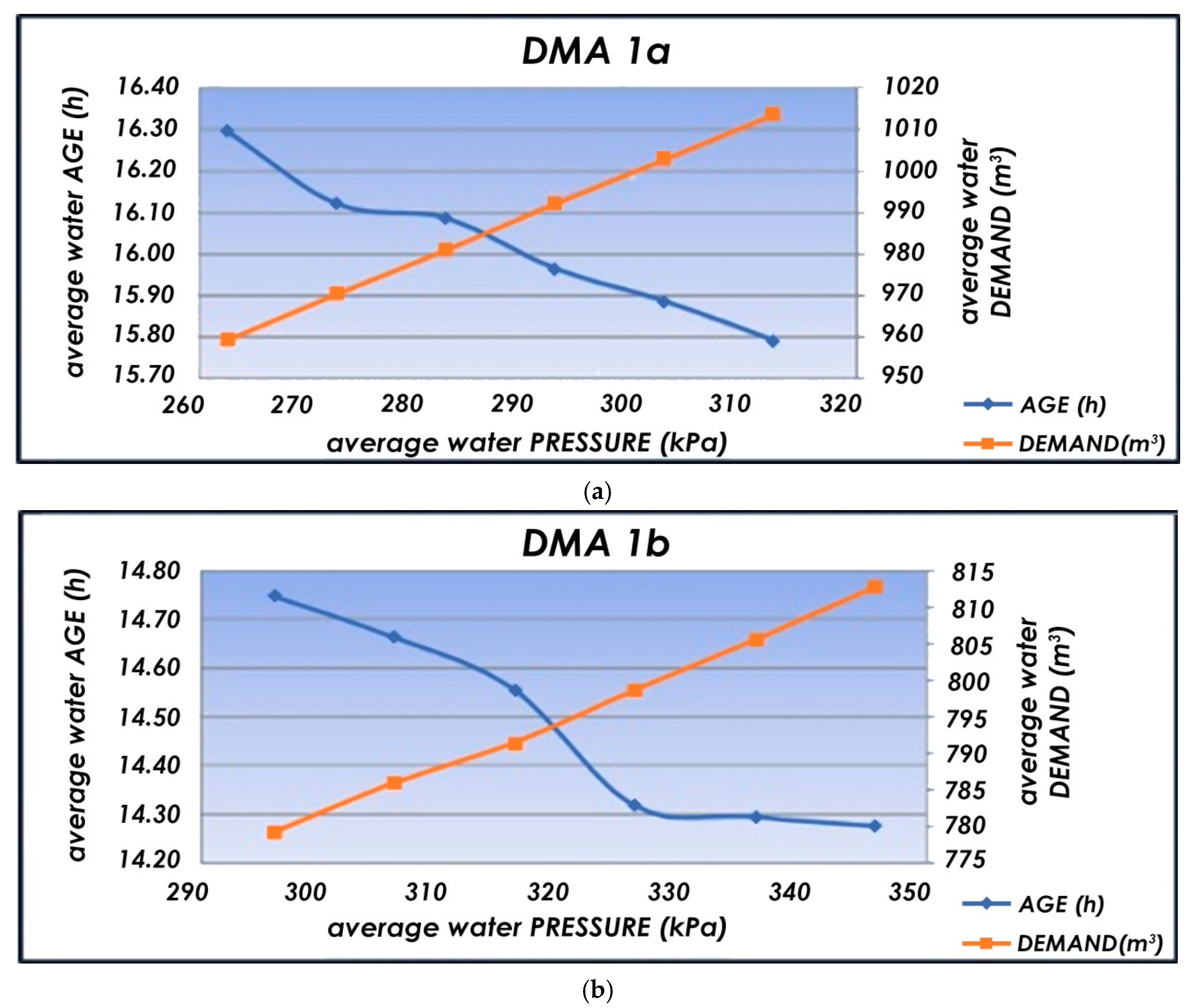
| DMA 1a | J-139 | 262.58 | 200.38 | 16.29 | 19.43 | 27.33 | 8.16 |
| DMA 1b | 14068 | 296.02 | 276.74 | 14.74 | 14.17 | 20.86 | 34.1 |
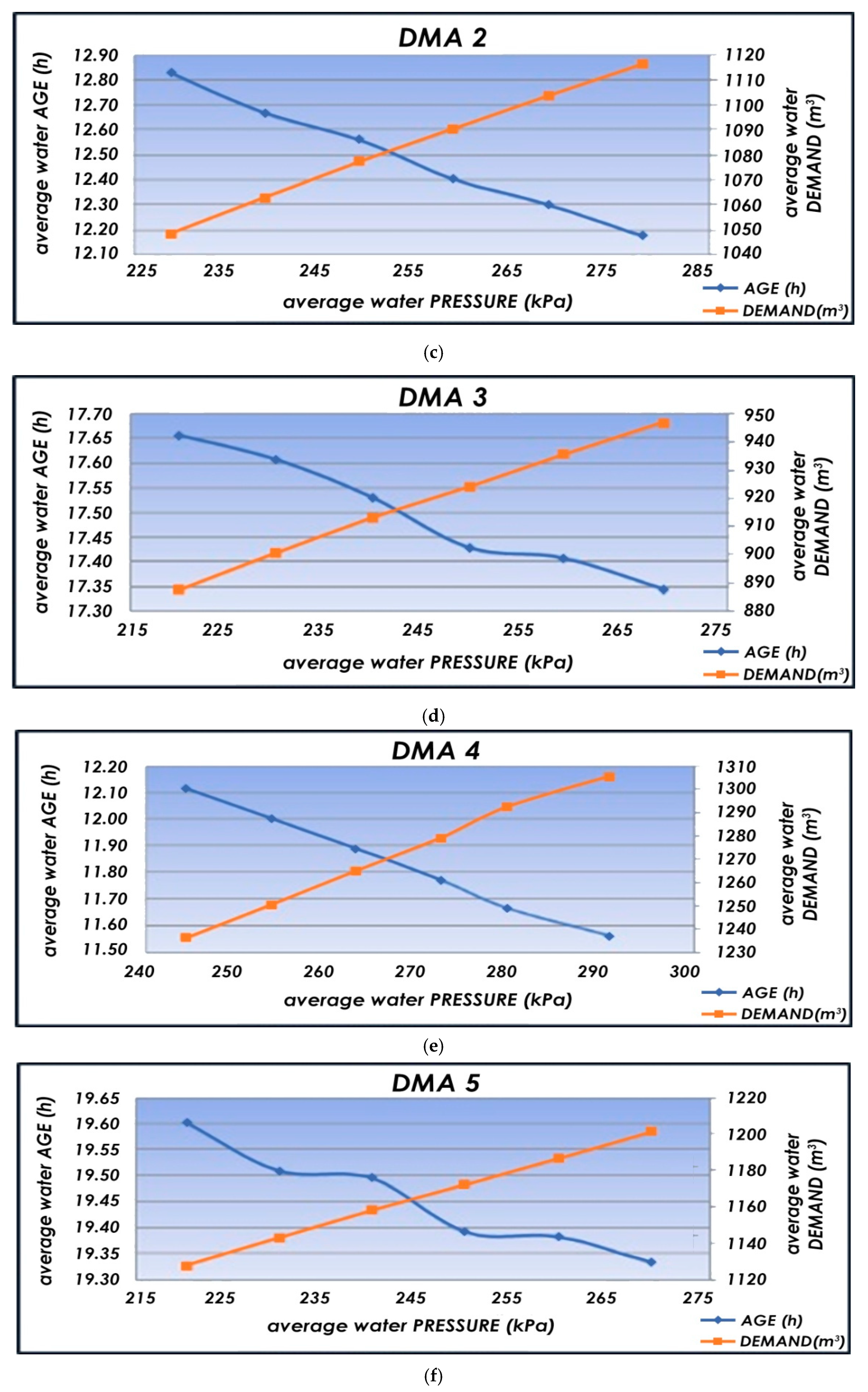
| DMA 2 | 220 | 228.92 | 201.22 | 12.82 | 9.35 | 11.63 | 19.5 |
| DMA 3 | K-64 | 219.76 | 203.44 | 17.65 | 17.83 | 23.96 | 7.86 |
| DMA 4 | 213 | 244.45 | 208.84 | 12.11 | 11.07 | 12.96 | 55.16 |
| DMA 5 | 467 | 220.24 | 212.39 | 19.60 | 20.00 | 27.11 | 33.64 |
| Critical Nodes Per DMA Based on the Water Age | |||||||
| DMA 1a | J-139 | 262.58 | 200.38 | 16.29 | 19.43 | 27.33 | 8.16 |
| DMA 1b | 130347 | 296.02 | 305.41 | 14.74 | 20.71 | 29.56 | 2.84 |
| DMA 2 | 2515 | 228.92 | 248.57 | 12.82 | 25.35 | 35.66 | 1.38 |
| DMA 3 | J-53 | 219.76 | 209.54 | 17.65 | 19.73 | 27.92 | 19.54 |
| DMA 4 | 2181 | 244.45 | 251.87 | 12.11 | 12.14 | 31.58 | 20.32 |
| DMA 5 | 4656 | 220.24 | 212.87 | 19.60 | 25.51 | 39.11 | 2.56 |
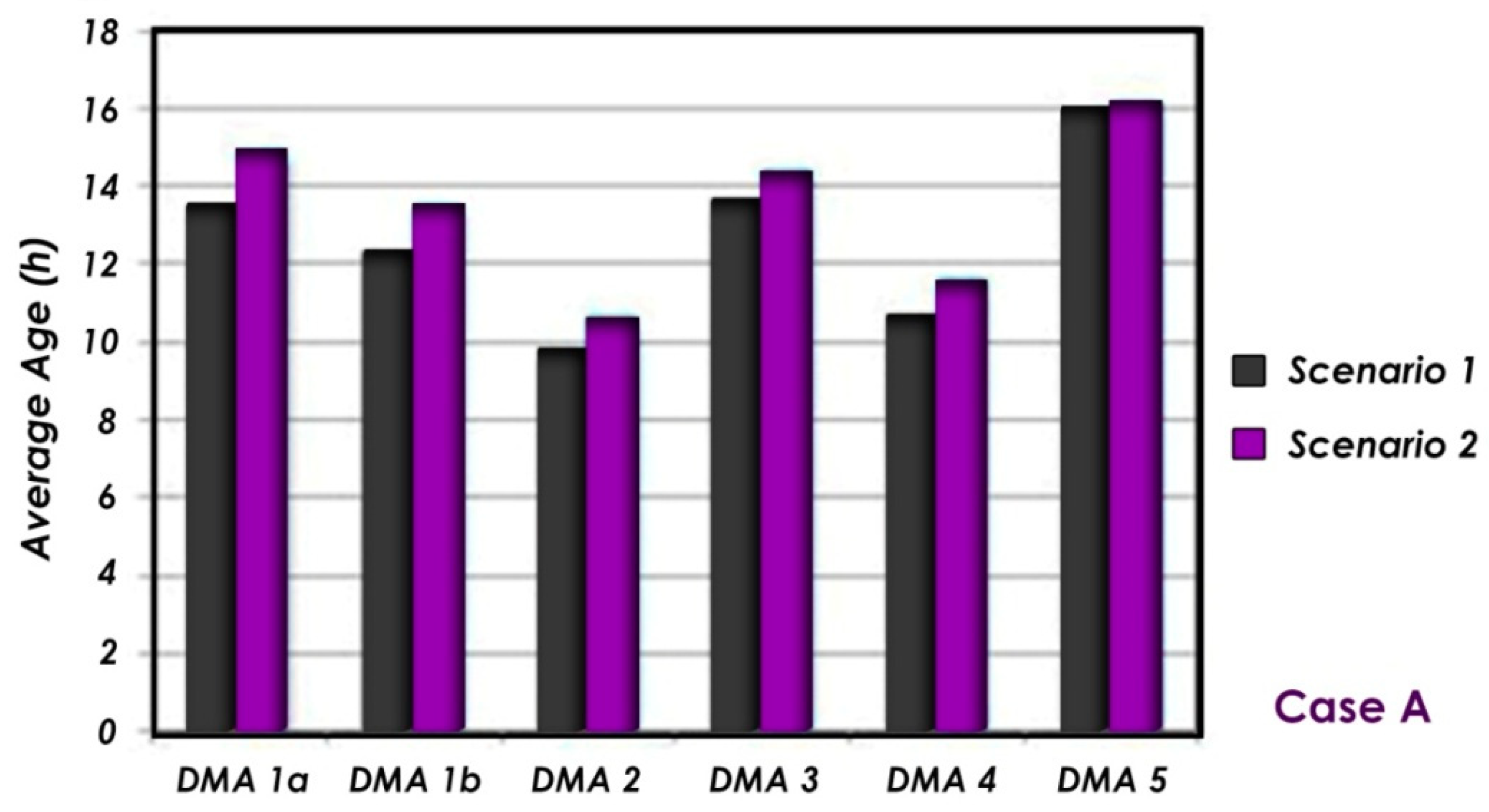
| Scenario No1: no DMAs_no PRVs | ||||||
| DMA1a | DMA1b | DMA2 | DMA3 | DMA4 | DMA5 | |
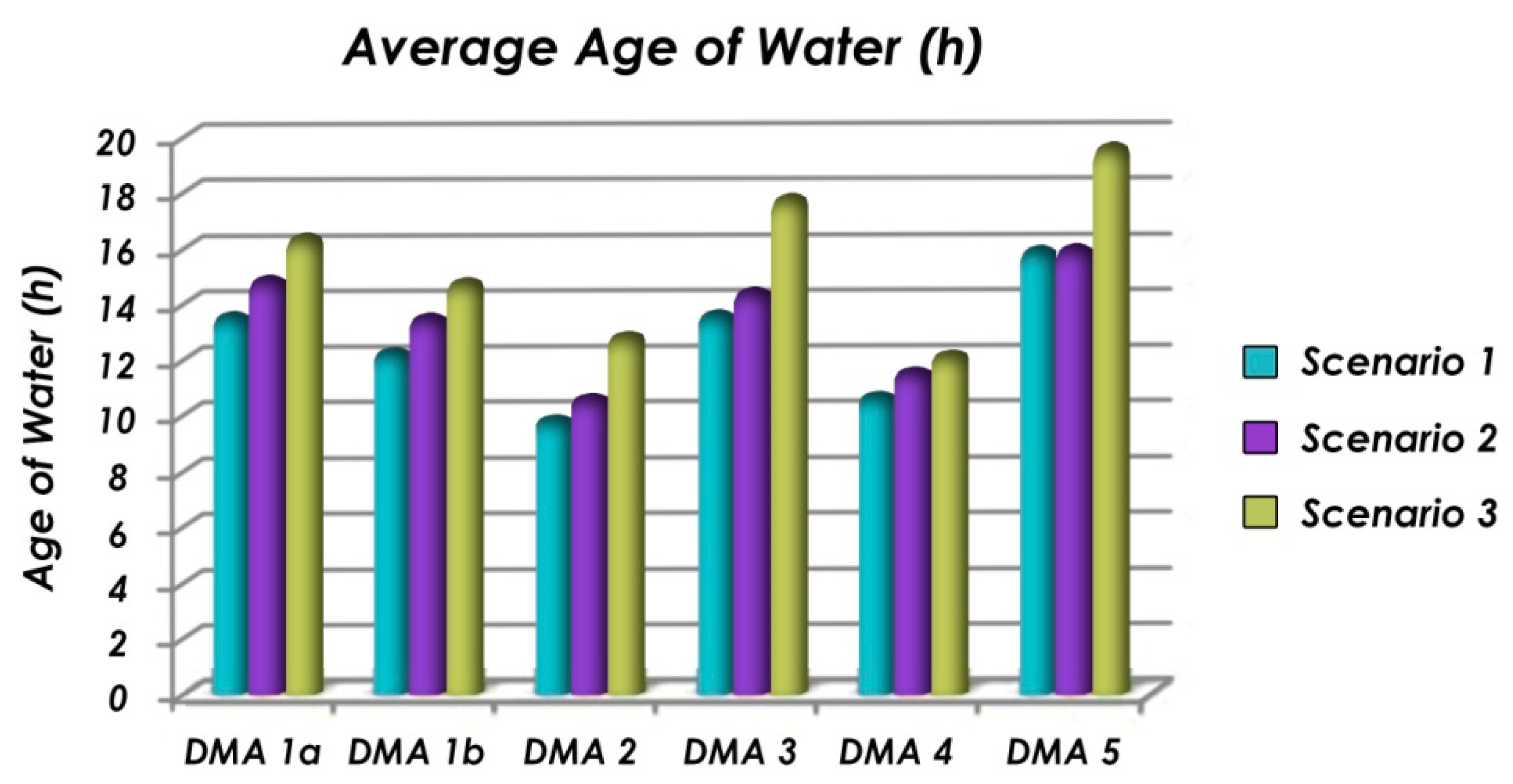
| Max water age (h) | 23.13 | 24.32 | 33.66 | 22.96 | 22.33 | 33.94 |
| Average max water age (h) | 18.98 | 17.45 | 12.15 | 21.36 | 14.32 | 24.49 |
| Average water age (h) | 13.49 | 12.28 | 9.77 | 13.62 | 10.66 | 15.89 |
| Average water age for the entire WDN (h) | 12.62 | |||||
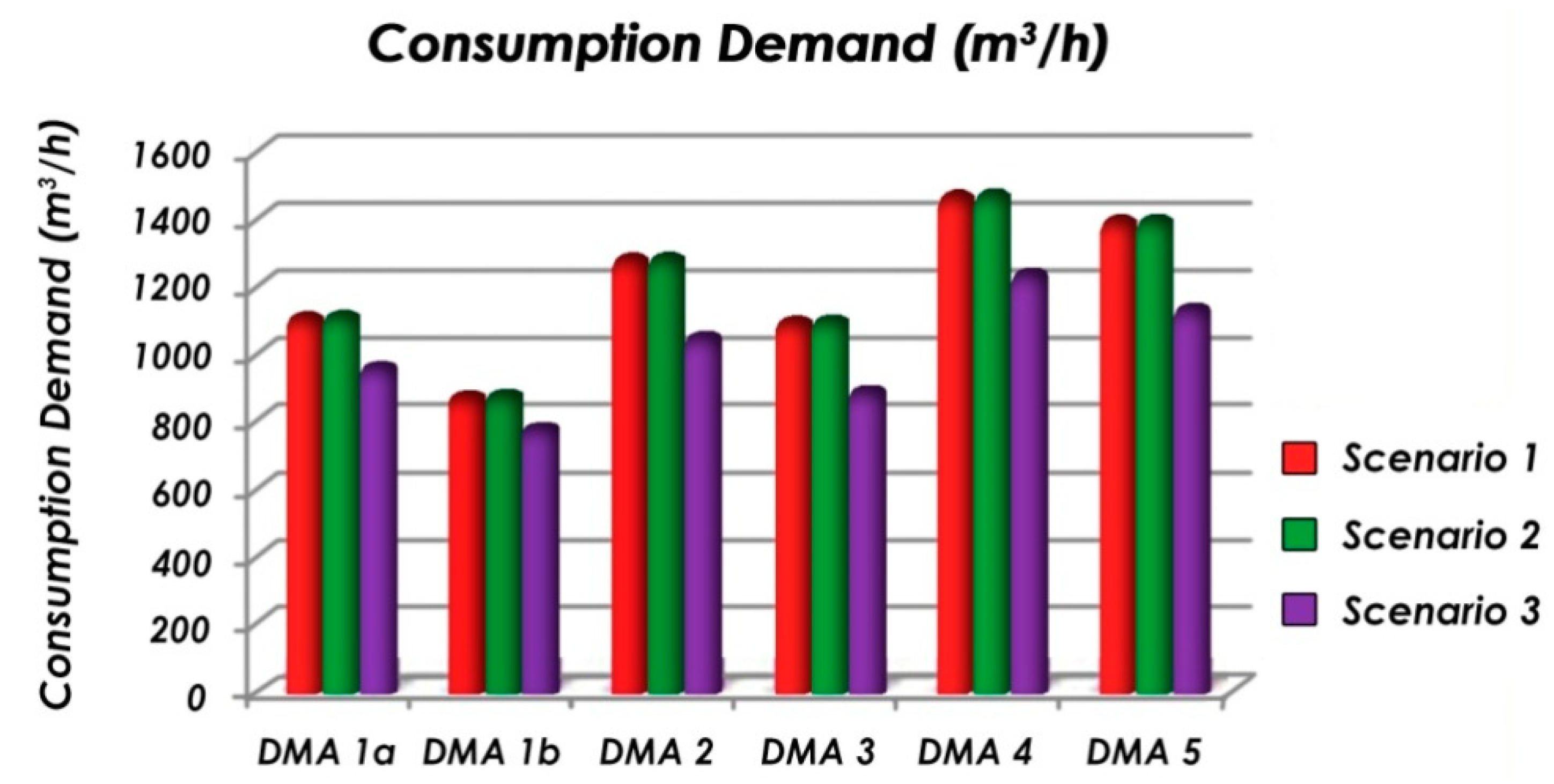
| Water demand (48 h) (m3) | 1105.50 | 872.93 | 1280.42 | 1092.15 | 1467.65 | 1395.11 |
| Total water demand for the entire WDN (m3) | 7213.76 | |||||
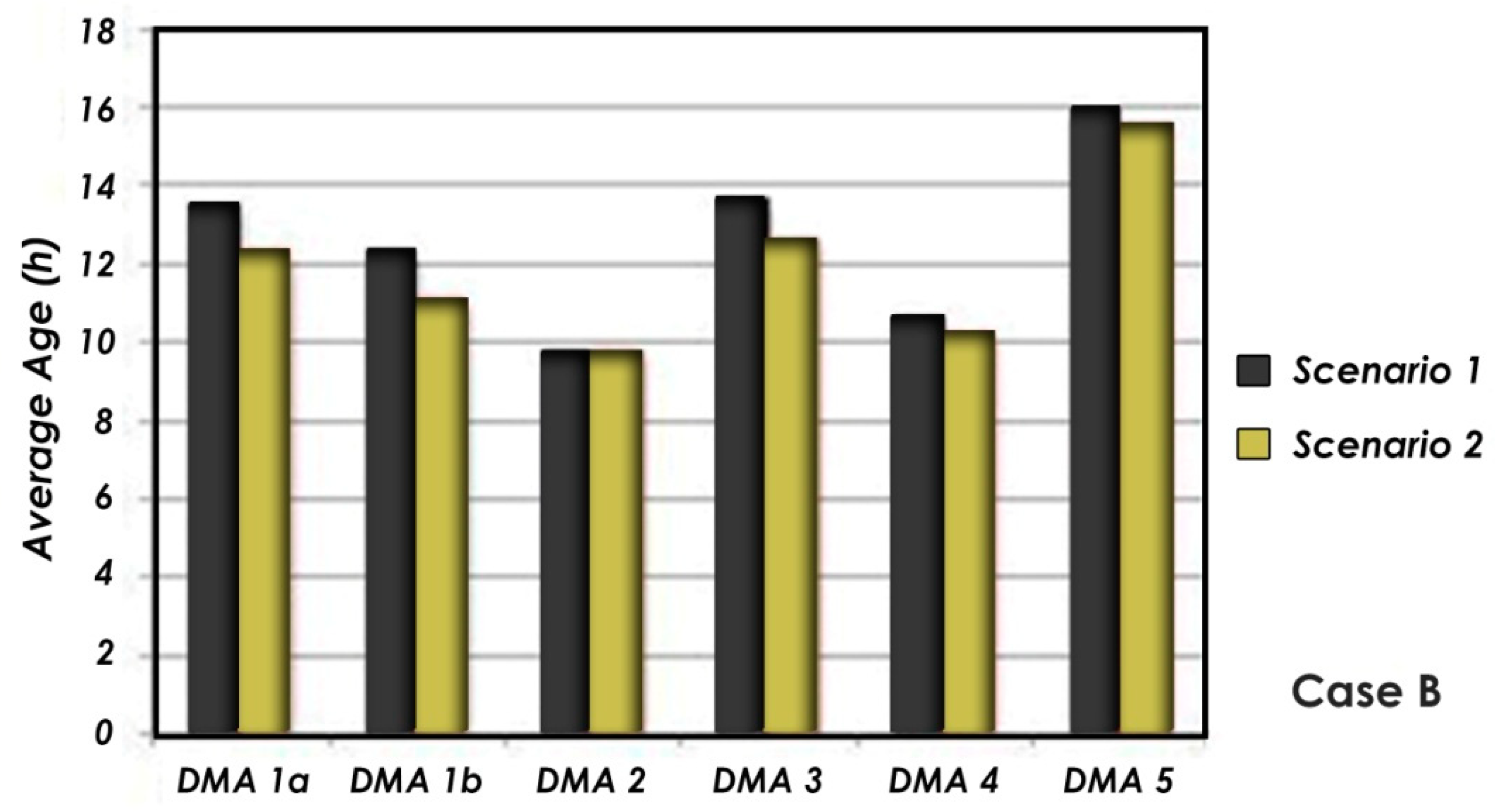
| Scenario No2: with DMAs_no PRVs | ||||||
| DMA1a | DMA1b | DMA2 | DMA3 | DMA4 | DMA5 | |
| Max water age (h) | 25.70 | 27.51 | 34.93 | 26.12 | 23.85 | 33.55 |
| Average max water age (h) | 22.04 | 20.52 | 14.75 | 22.70 | 16.58 | 24.98 |
| Average water age (h) | 14.82 | 13.46 | 10.56 | 14.37 | 11.51 | 15.90 |
| Average water age for the entire WDN (h) | 13.44 | |||||
| Water demand (48 h) (m3) | 1105.50 | 872.93 | 1280.42 | 1092.15 | 1467.65 | 1395.11 |
| Total water demand for the entire WDN (m3) | 7213.76 | |||||
| Scenario No3: with DMAs_with PRVs | ||||||
| DMA1a | DMA1b | DMA2 | DMA3 | DMA4 | DMA5 | |
| Max water age (h) | 27.33 | 29.57 | 35.66 | 27.93 | 31.58 | 39.11 |
| Average max water age (h) | 23.31 | 21.36 | 17.41 | 23.38 | 18.90 | 26.99 |
| Average water age (h) | 16.29 | 14.75 | 12.83 | 17.66 | 12.11 | 19.60 |
| Average water age for the entire WDN (h) | 15.54 | |||||
| Water demand (48 h) (m3) | 959.22 | 779.17 | 1048.4 | 887.49 | 1236.13 | 1127.53 |
| Total water demand for the entire WDN (m3) | 6037.94 | |||||
| Case a (Base Values) | Case b | Case c | Case d | Case e | Case f | |
|---|---|---|---|---|---|---|
| PRV label | Pressure (kPa) | Pressure (kPa) | Pressure (kPa) | Pressure (kPa) | Pressure (kPa) | Pressure (kPa) |
| PRV-1 | 350 | Scenario a (base scenario) + 10 kPa | Scenario a (base scenario) + 20 kPa | Scenario a (base scenario) + 30 kPa | Scenario a (base scenario) + 40 kPa | Scenario a (base scenario) + 50 kPa |
| PRV-2 | 232 | |||||
| PRV-3 | 205 | |||||
| PRV-4 | 213.5 | |||||
| PRV-5 | 226 | |||||
| PRV-6 | 227 | |||||
| PRV-7 | 300 | |||||
| PRV-8 | 227 | |||||
| PRV-9 | 350 | |||||
| PRV-10 | 225 | |||||
| PRV-11 | 289.5 | |||||
| PRV-12 | 299.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patelis, M.; Kanakoudis, V.; Kravvari, A. Pressure Regulation vs. Water Aging in Water Distribution Networks. Water 2020, 12, 1323. https://doi.org/10.3390/w12051323
Patelis M, Kanakoudis V, Kravvari A. Pressure Regulation vs. Water Aging in Water Distribution Networks. Water. 2020; 12(5):1323. https://doi.org/10.3390/w12051323
Chicago/Turabian StylePatelis, Menelaos, Vasilis Kanakoudis, and Anastasia Kravvari. 2020. "Pressure Regulation vs. Water Aging in Water Distribution Networks" Water 12, no. 5: 1323. https://doi.org/10.3390/w12051323
APA StylePatelis, M., Kanakoudis, V., & Kravvari, A. (2020). Pressure Regulation vs. Water Aging in Water Distribution Networks. Water, 12(5), 1323. https://doi.org/10.3390/w12051323






