1. Introduction
According to the recent reports published by United Nations, the population of the world has been estimated at 7.7 billion people in 2019 and projected to continue its increasing trend to around 8.5 billion in 2030, 9.7 billion in 2050, and 10.9 billion in 2100 [
1]. Furthermore, it is predicted that most of the world population will live in urban regions rather than rural areas. The growth of the urban population faces some challenges, including unsuitable urban planning and management, insufficient public services, social and cultural anomalies, economic problems associated with urban poverty, environmental contamination, and supplying secure and sustainable water [
1,
2].
Amongst the aforementioned urban challenges, the water supply is one of the most serious. Concerning water supply, water withdrawal from renewable resources, water transfer, treatment of wastewater, water allocation for several demands, satisfying security and sustainability, and consensus-seeking among urban stakeholders with different preferences are the main issues [
2,
3]. Therefore, the water supply issues should be met by implementing desirable water strategies, which consider multiple sustainable development criteria [
4]. Additionally, the several preferences of multiple stakeholders regarding the relevant water demands should be satisfied and group consensus could be achieved [
5]. Accordingly, Parkinson et al. have presented the integrated urban watershed management (IUWM) approach, which has been developed for better management of water and wastewater strategies in an urban setting [
6].
One of the most complicated challenges for implementing IUWM is increasing the variety of sustainable development objectives, including water resources sustainability, environmental sustainability, socio-economic sustainability, and the related criteria [
4,
7]. This has led to a serious problem for selecting the more desirable urban water strategy, by which the sustainable development objectives and the important relevant criteria should be satisfied, in addition to achieving the group consensus among the stakeholders. Accordingly, implementing IUWM requires evaluation of the water strategies for supplying the urban demands, while considering the sustainable development criteria and the final group agreement [
8,
9].
The other significant challenge for implementing IUWM is related to the variety of risk-taking attitudes of stakeholders’ groups [
10]. The risk-taking attitudes represent the number of criteria that should be satisfied by the urban water strategies [
11,
12]. The risk-taking cases, which are identified by the risk-taking degrees, are expressed by some linguistic phrases such as “selecting the more desirable strategy for satisfying all criteria” in the completely risk-averse viewpoint, “selecting the more desirable strategy for satisfying at least one criterion” in the completely risk-prone standpoint, and the other cases between these two limits [
13,
14].
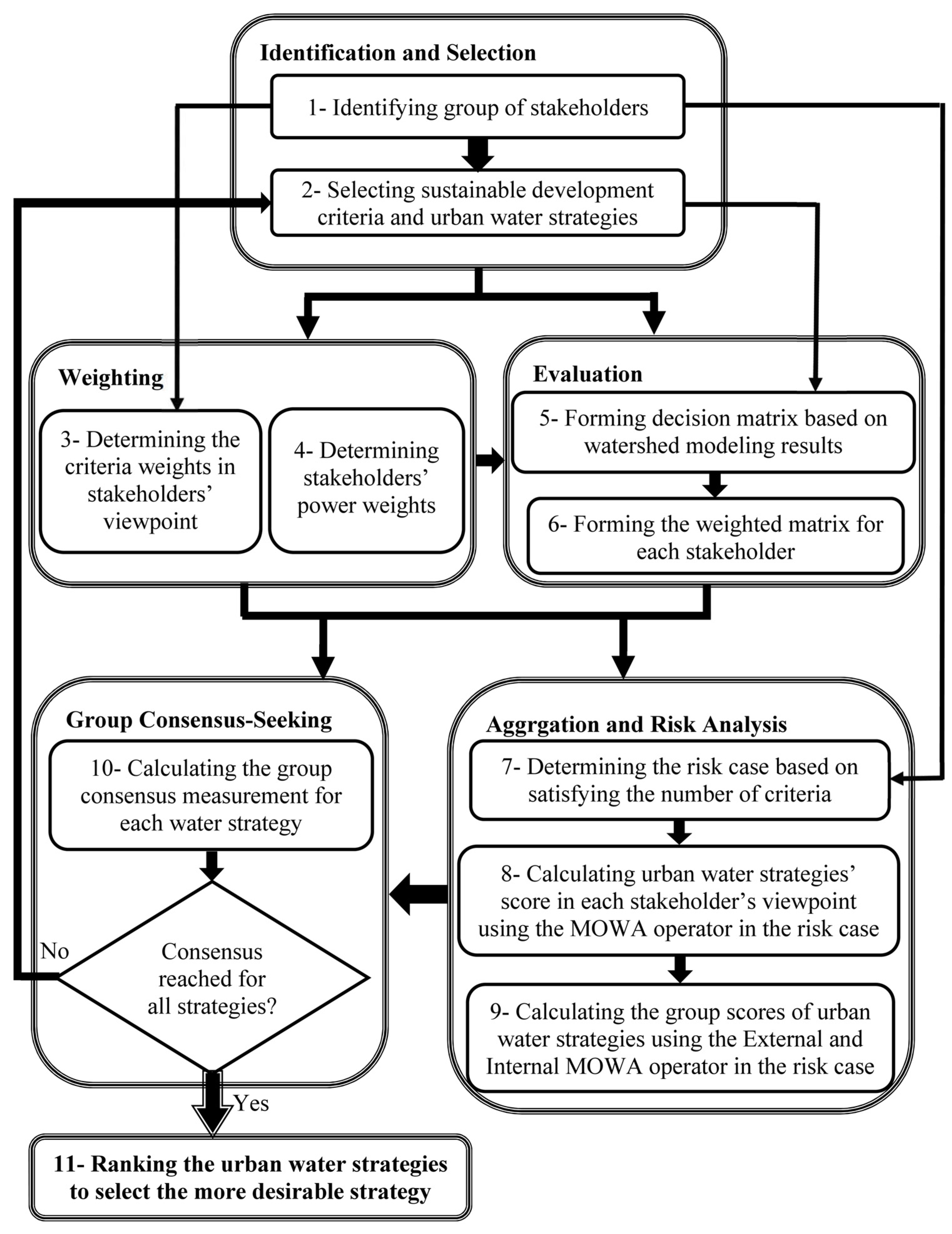
In order to take on the aforementioned challenges, an appropriate model for IUWM should be developed to consider the sustainable development objectives, risk-taking attitudes of stakeholders, and a final group consensus in evaluation of urban water strategies. Simonovic and Bender analyzed the collaborative planning-support system (CPSS) model, as the subset of the decision-support system (DSS) model, which considers all relevant aspects of sustainable water resources planning and management, especially in the process of criteria selection [
15]. In the group decision support system (GDSS) approach, the main three issues, such as selection of criteria, generation of alternatives, and evaluation of alternatives based on the criteria are considered based on the balancing and reinforcing aspects for better decision analysis [
16,
17,
18]. Accordingly, developing a group decision-support system (GDSS) model within an urban watershed needs to analyze a multiple criteria decision-making (MCDM) process, in which the final criteria and water strategies are selected, the strategies are evaluated with respect to the criteria, and the water strategies are ranked for several risk-taking cases.
For analyzing the MCDM process in a GDSS model, a large variety of methodologies have been utilized, of which the most frequently used methods have been well demonstrated in the literature [
19]. The most important methods are classified into four categories, including: scoring methods [
20], distance-based methods [
20,
21,
22,
23], outranking methods [
20,
24,
25,
26], and pair-wise comparisons methods [
27,
28]. The differences between these methods are related to their strategies for solving MCDM problems.
For risk analysis in the MCDM process, some of the risk-based methodologies have been utilized. The most commonly used method is using the family of the ordered weighted averaging (OWA) operator, which considers the risk analysis in the decision-making process [
4,
8,
9]. The OWA family includes a group of operators with several properties. In this family, the most frequently used operators are the OWA, induced ordered weighted averaging (IOWA), and hybrid weighted averaging (HWA). The OWA operator considers only the risk-taking attitudes and disregards the criteria weights. The IOWA operator considers the risk-taking attitudes and the importance orders of criteria, whereas it ignores the criteria weights. The HWA operator considers the risk-taking attitudes and criteria weights, while disregards the stakeholders’ power weights [
11,
12].
In recent years, related to the context of urban water management, several studies have been done based on MCDM methodologies [
29,
30,
31,
32,
33,
34,
35,
36,
37]. However, in this paper, a risk-based consensus-based GDSS model is developed for IUWM within the study area of an urban watershed. Accordingly, the following improvements are performed in this study that are distinctive comparing to similar works in IUWM:
Developing a comprehensive GDSS model for IUWM based on group risk considerations and group consensus measuring.
Improving the OWA operator properties, considering the risk-taking attitudes of decision-making, importance degrees of criteria, and the stakeholders’ power weights simultaneously.
Considering the two types of aggregation, including the external modified ordered weighted averaging (EMOWA) and the internal modified ordered weighted averaging (IMOWA), for selecting the more desirable urban water strategy in several risk-taking attitudes of stakeholders.
Selecting final criteria for the MCDM process by use of a risk-based group consensus method.
Seeking group consensus among stakeholders during the GDSS process by use of a risk-based weighted Minkowski’s method.
Accordingly, in order for sustainable water resources management, this research makes the connection between the outputs of watershed modeling and the inputs of a GDSS model for analyzing the risk-based MCDM process. This paper can be used to select the most effective sustainable development criteria of watershed by the stakeholders of the watershed. Additionally, it can assist water scientists and analysts of water resources management to analyze the several impacts of implementing water strategies on the selected sustainable development criteria. Furthermore, it can help all stakeholders to identify the conditions of watershed including several demands, probable water supply resources, and the related impacts on the criteria, which result in better decision making for a sustainable watershed. Ultimately, this study leads to a collaborative group consensus among stakeholders and, consequently, facilitates integrated watershed management.
This paper is organized as follows:
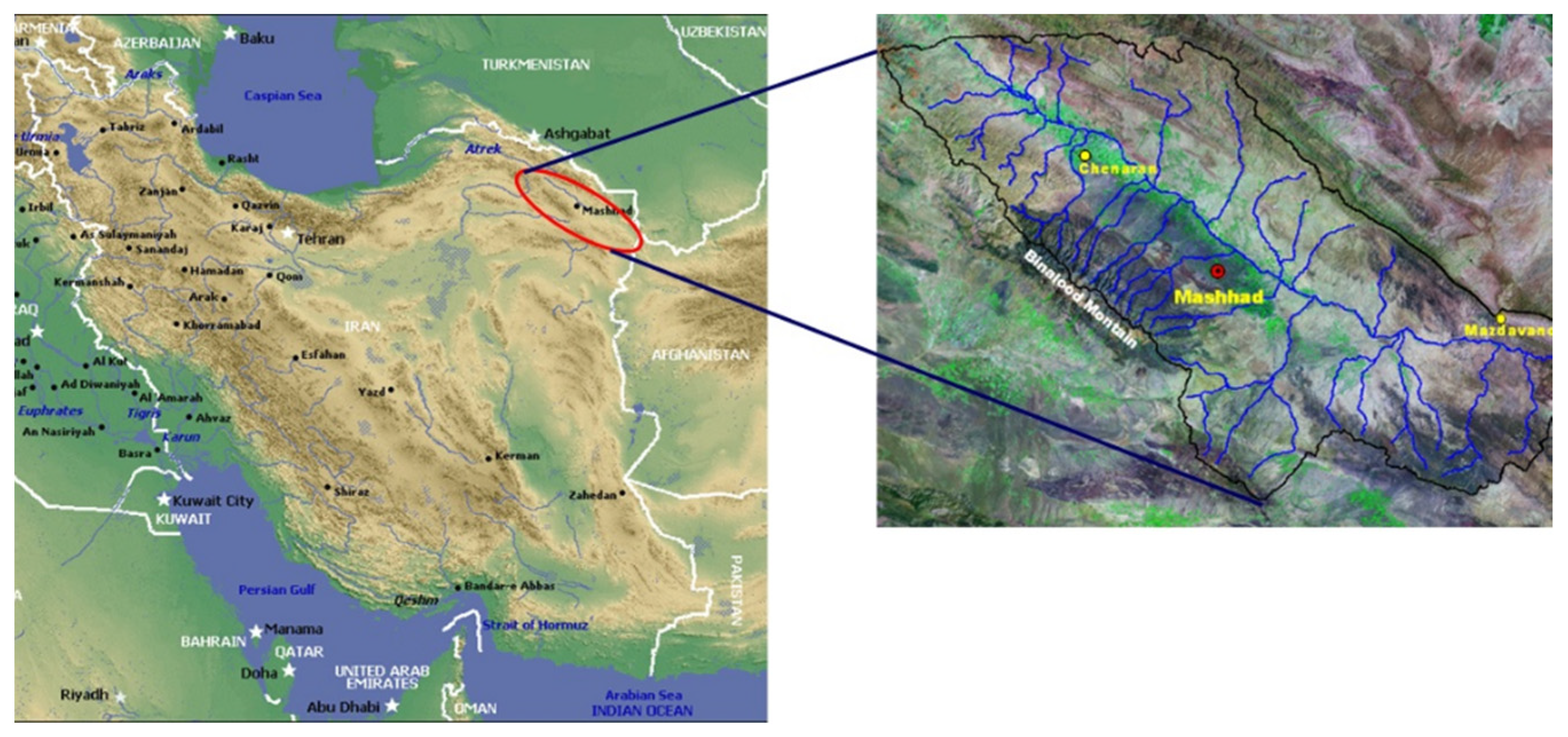
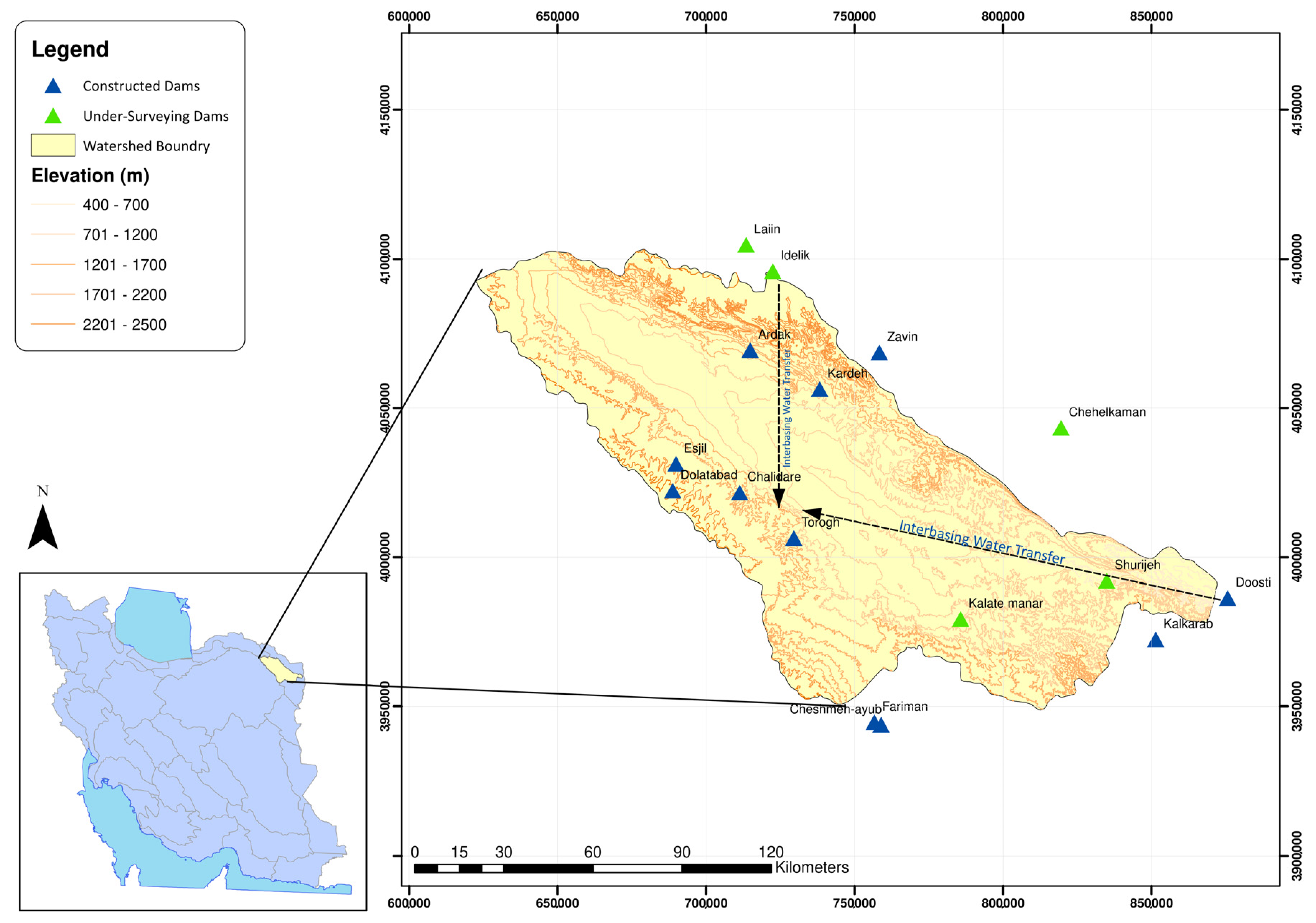
Section 2 proposes the flow diagram and explains the complete analysis of the risk-based consensus-based GDSS model for the urban watershed. In addition, this section introduces the study area of the urban watershed, the criteria, the urban water strategies, and the participating stakeholders in the decision-making process. The methodology is also applied for IUWM of the study area. In
Section 3, the results, including the scores of urban water strategies, the group consensus measurements, and the final ranking of strategies, are obtained in several risk-taking cases.
Section 4 discusses the results and effects of several risk-taking cases on the scores and ranking of the strategies. Finally,
Section 5 concludes this paper and proposes future research.
4. Discussion
Discussion about the results of the risk-based consensus-based GDSS modeling for the Kashafroud urban watershed is illustrated in four subjects, including 1—importance degrees of the criteria in the viewpoints of the group of stakeholders, 2—scores of water strategies in each stakeholder’s viewpoint and the group of stakeholders’ opinions, 3—group consensus measurements for the strategies, and 4—final ranking of the water strategies.
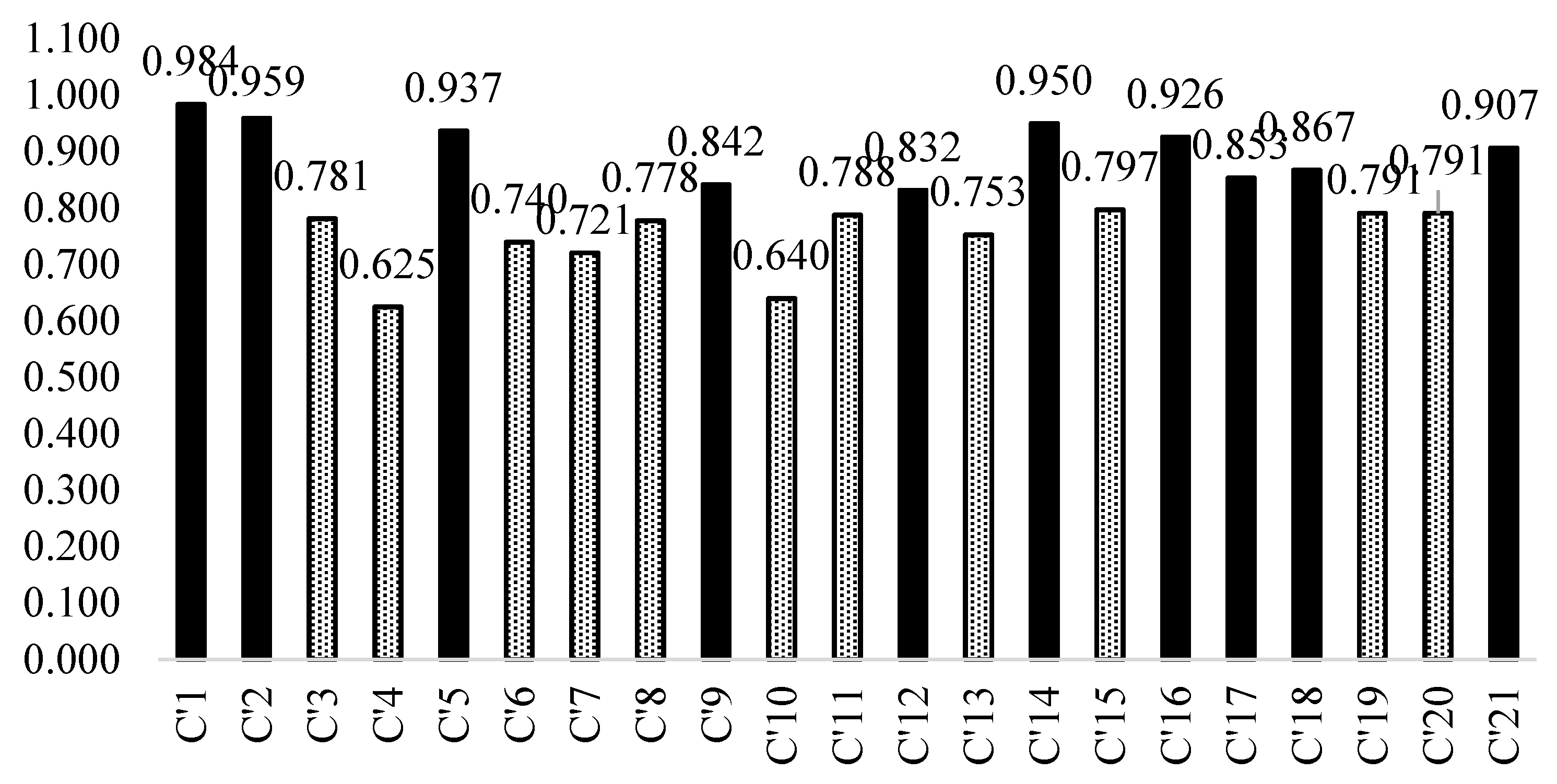
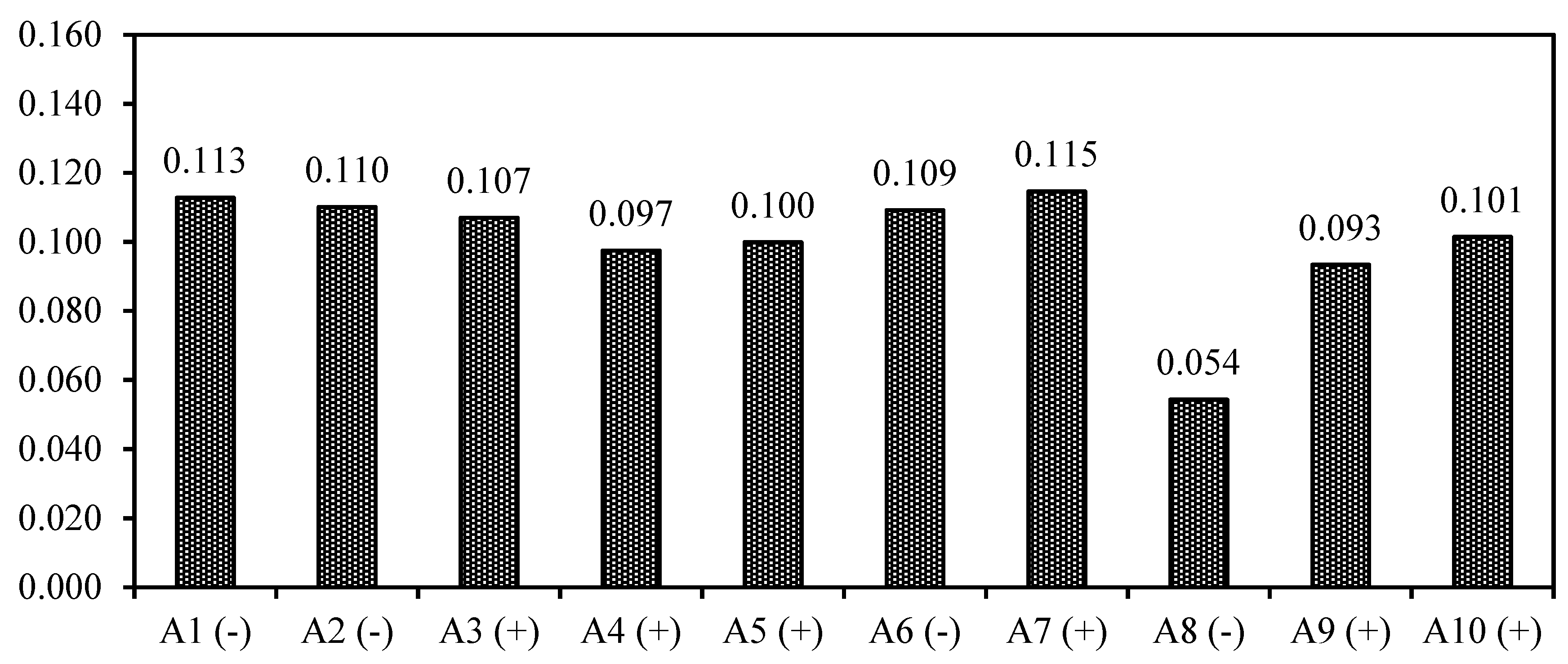
According to the results of criteria weights in group viewpoint (
Figure 9), the stakeholders’ group assigned the most weight to the criteria
and
, respectively. In the viewpoint of the group, the priority of the criterion
(purified sewerage ratio) in comparison with the other criteria shows that utilization of purified wastewater for some agricultural demands could reduce its withdrawal from groundwater resources, which instead be used to supply the increasing urban potable demand. Additionally, the relative priority of
(water stress) emphasizes the importance of a close ratio between water withdrawal and renewable water resources in a semi-arid climate in order to control the withdrawal from other water resources. On the other hand, the group of stakeholders assigns the least weight for the criterion
(potable water losses), because the criterion
has no significant effect on water stress in comparison with the other factors.
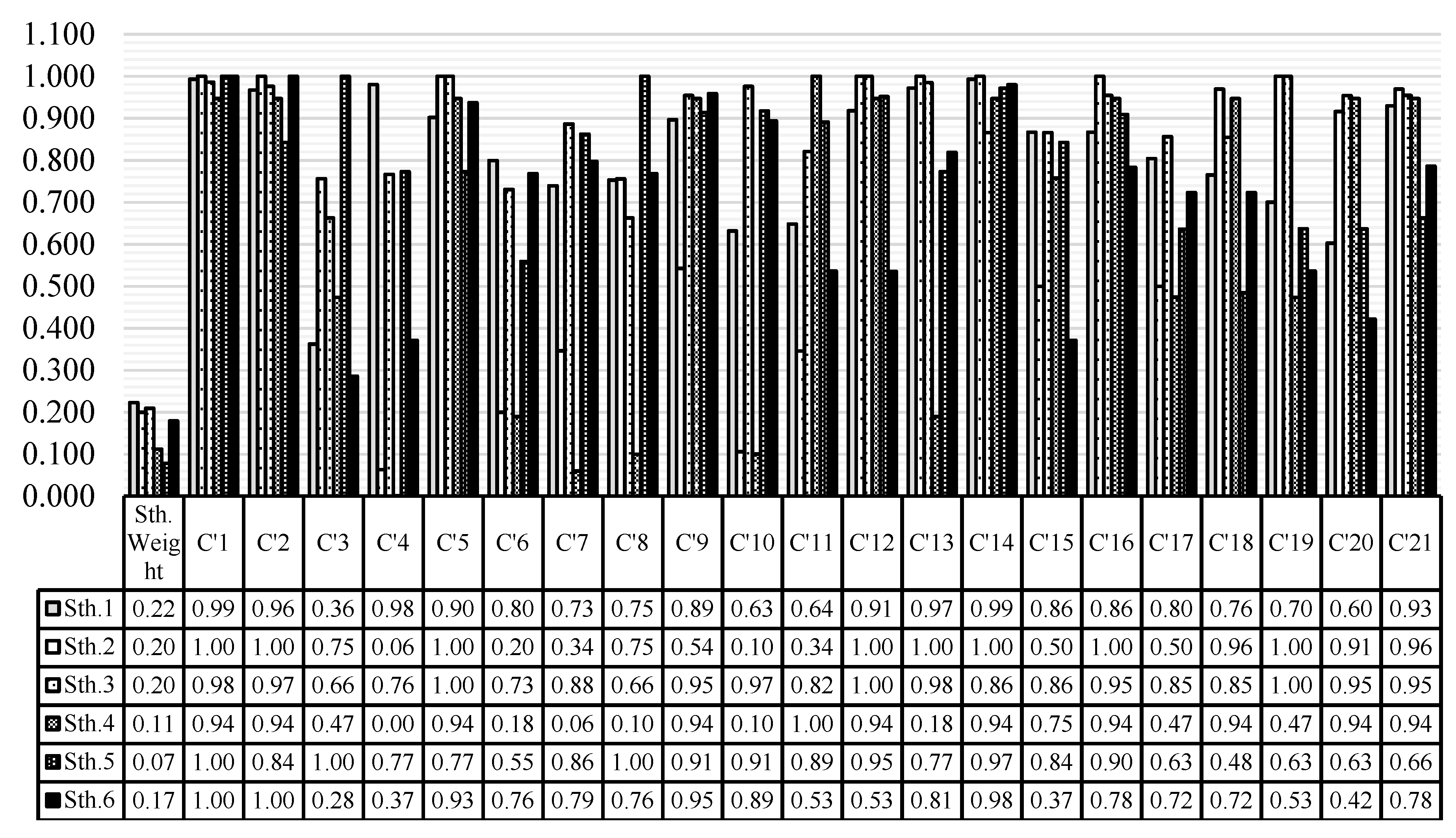
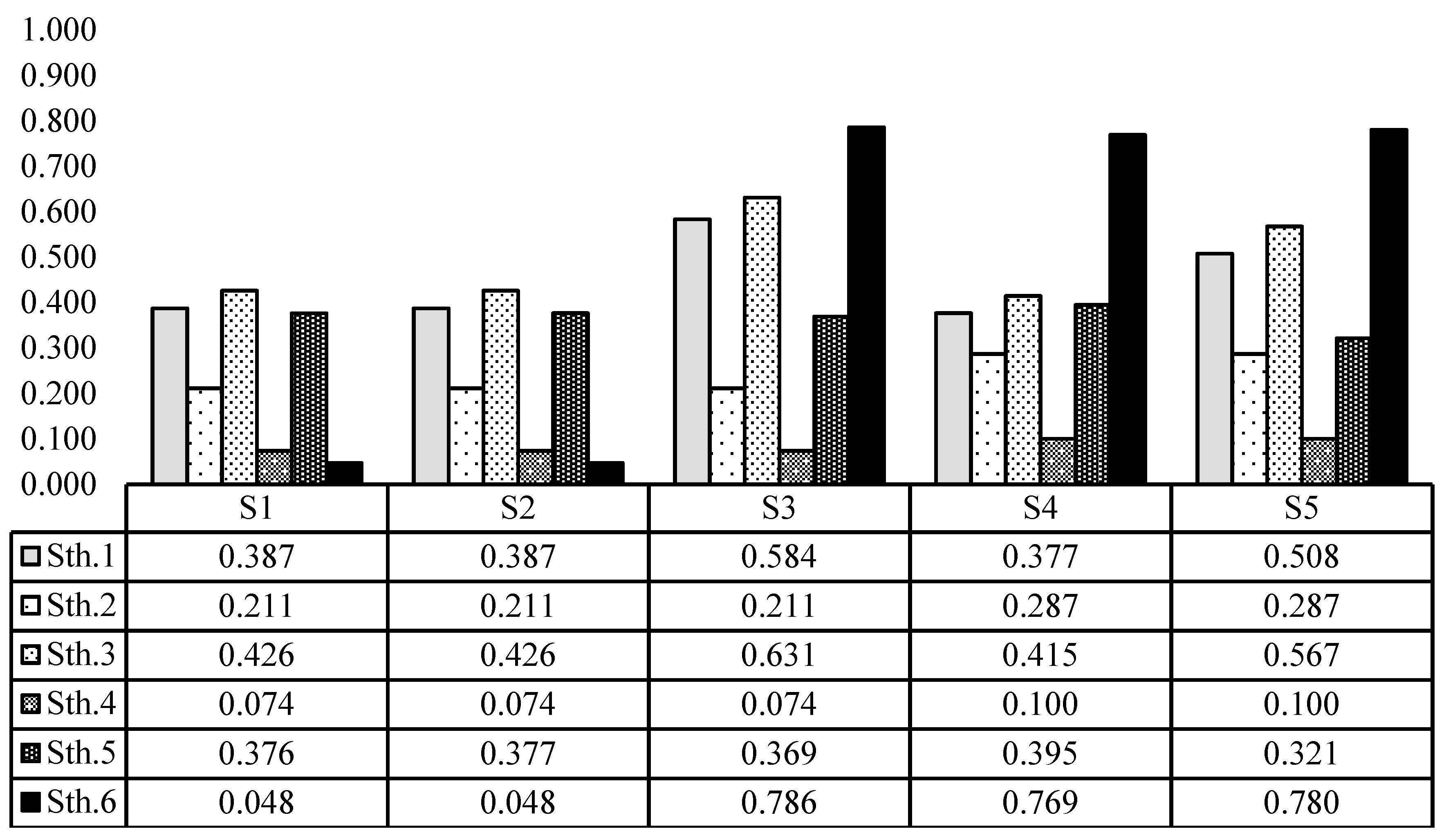
Regarding the results related to the scores of water strategies in each stakeholder’s viewpoint (
Figure 10 and
Figure 11), in the completely risk-averse case, each stakeholder desires to select the strategy that satisfies all criteria. In this conservative viewpoint, half of the stakeholders choose the strategy
as the more desirable strategy. These stakeholders have the supply management approach with an emphasis on utilization of purified wastewater for agricultural irrigation and dependency on water transfer from the Doosti Dam. Vice versa, in the completely risk-prone standpoint, each stakeholder desires to select the strategy that satisfies at least one criterion. Therefore, in this nonconservative standpoint, half of the stakeholders choose the strategy
as the more desirable strategy. These stakeholders have just the demand management approach while considering the water transfer from the Doosti Dam. As it is expected from the risk analysis results, the scores of strategies in each stakeholder’s viewpoint in the completely risk-prone viewpoint (completely optimistic viewpoint) are greater than the scores in the completely risk-averse viewpoint (completely pessimistic viewpoint). The completely optimistic viewpoint emphasizes on a fully positive and fully nonconservative approach of each stakeholder, while the completely pessimistic standpoint emphasizes on a fully negative and a fully conservative approach of each stakeholder.
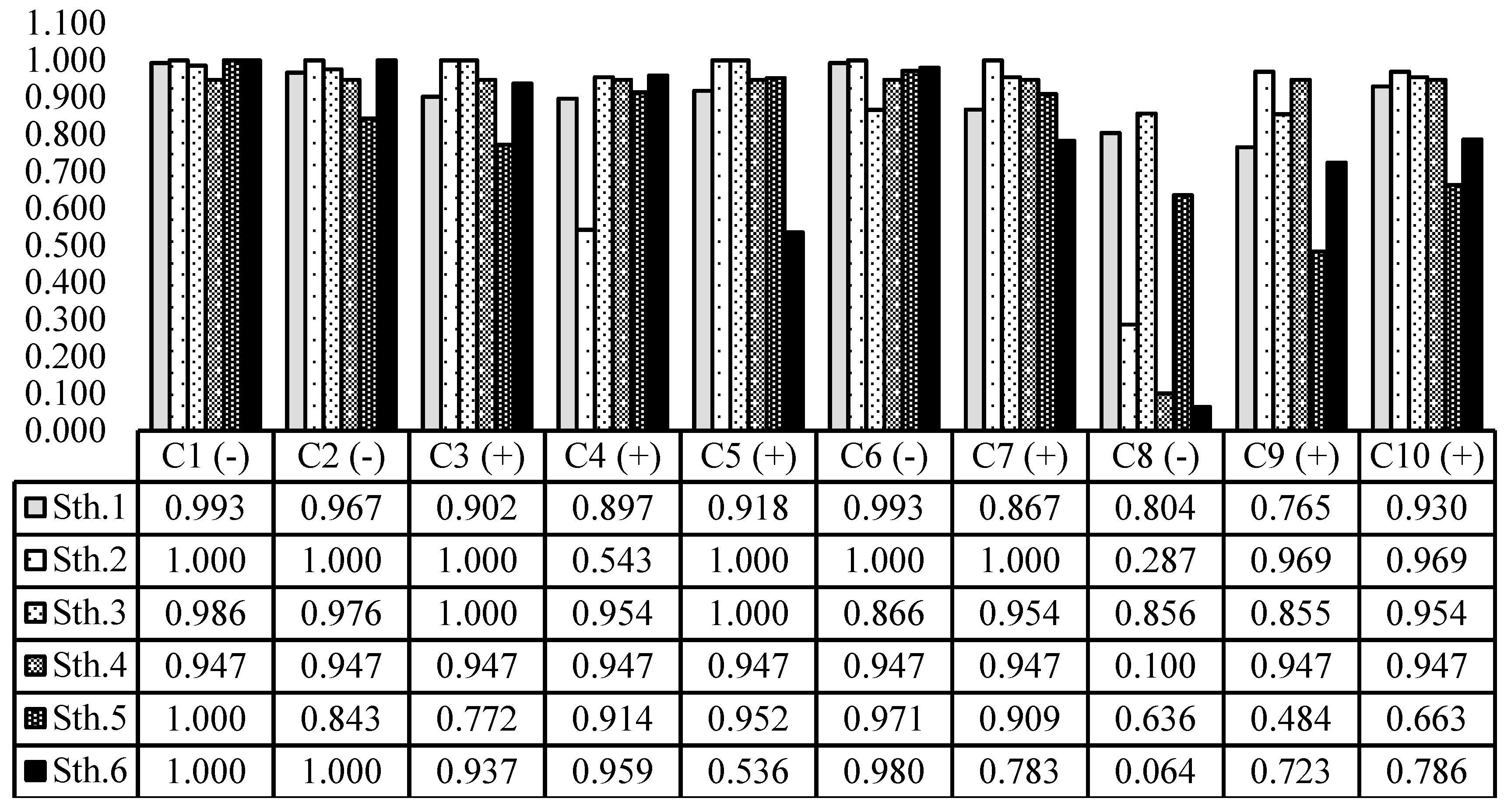
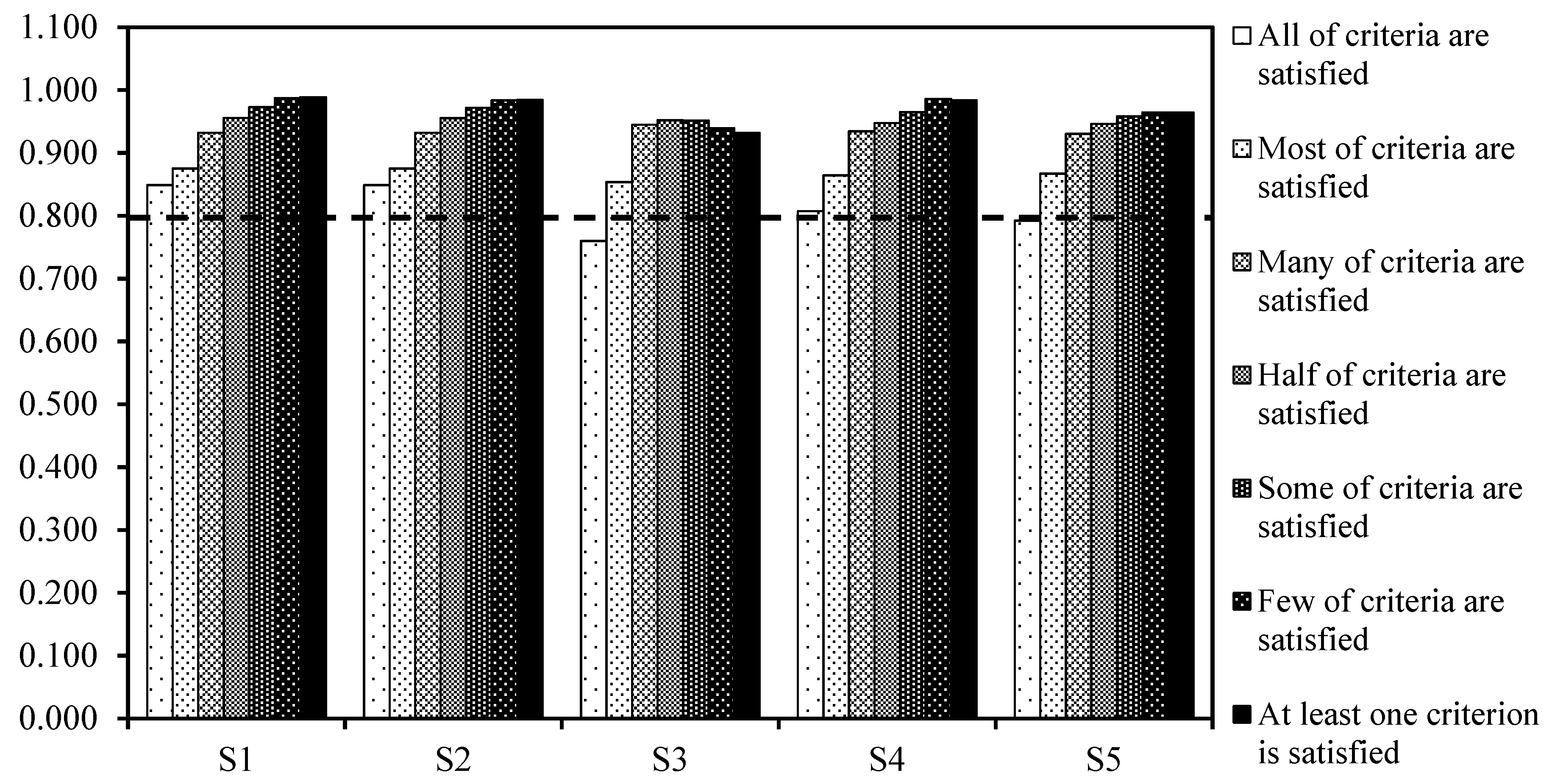
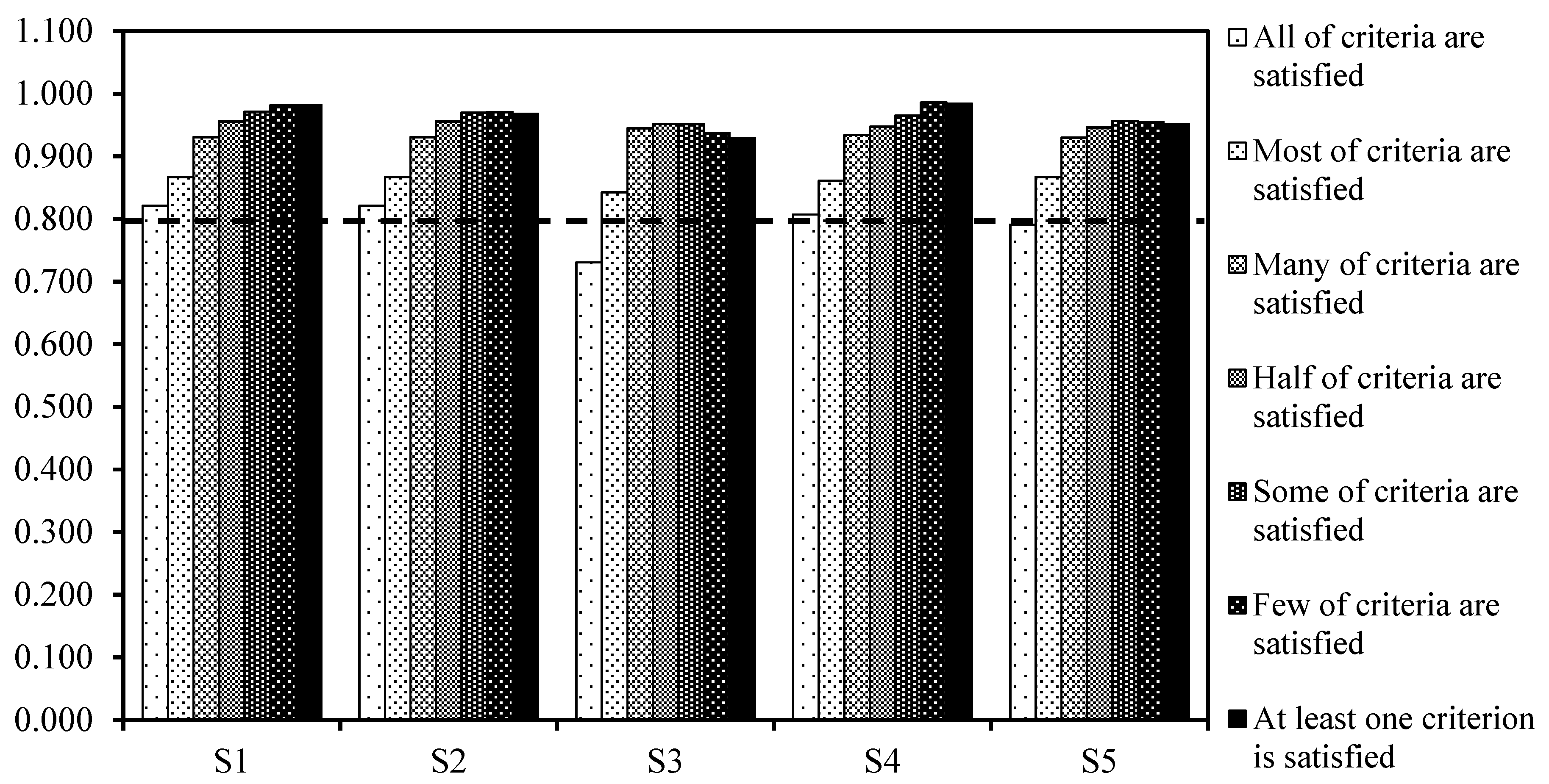
With respect to the results of the group scores of water strategies (
Figure 12 and
Figure 13), the group scores of strategies are increased from the completely risk-averse viewpoint to the completely risk-prone standpoint. Risk-averse cases have a conservative viewpoint and emphasize a pessimistic approach from stakeholders in the GDSS process, while the risk-prone cases have a nonconservative standpoint and emphasize an optimistic approach from stakeholders. For several risk-taking cases, the trend of changes for EMOWA scores is almost the same as the trend of changes for IMOWA scores, except for the completely risk-averse case. According to the EMOWA results, in the completely risk-averse viewpoint, strategy
is selected as the more desirable strategy by the group. On the other hand, in the completely risk-averse viewpoint of the IMOWA results, strategy
is chosen as the more desirable strategy by the group. It means that, for the Kashafroud watershed, the completely risk-averse viewpoint of the EMOWA operator emphasizes a supply management approach with dependency on water transfer from the Doosti Dam, whereas the completely risk-averse viewpoint of the IMOWA operator emphasizes a combined supply-demand management approach with no dependency on water transfer from the Doosti Dam. On the other hand, in accordance with the EMOWA and IMOWA results, in the completely risk-prone standpoint, strategy
is chosen as the more desirable strategy by the group. For this watershed, the completely risk-prone viewpoint of the EMOWA and IMOWA operators emphasizes a demand management approach with dependency on the water transfer from the Doosti Dam.
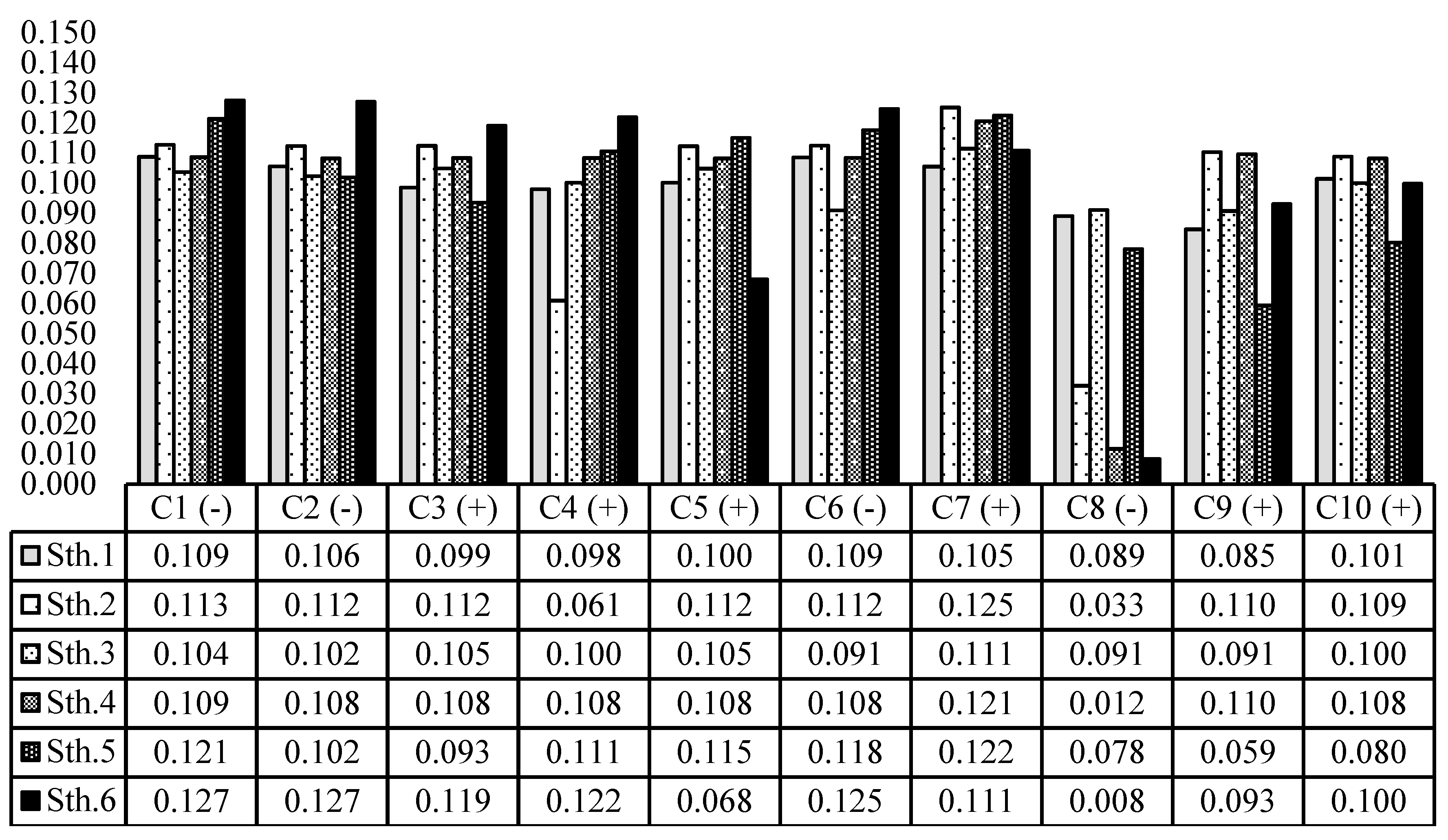
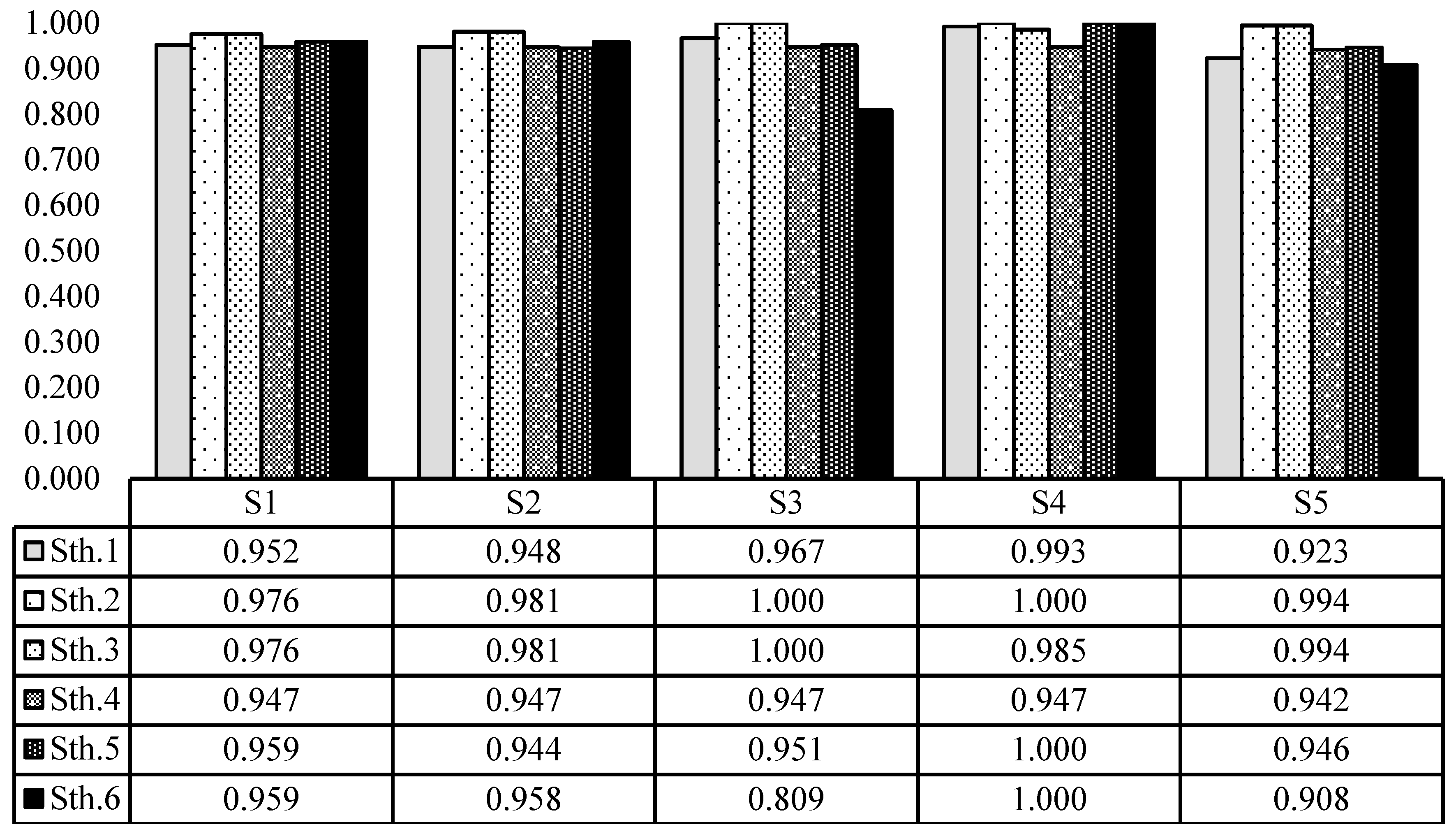
Following the results of group consensus measurements (
Figure 14 and
Figure 15), the consensus measurements of all water strategies in several risk-taking cases are higher than the selected TLA, except for the strategy
in the completely risk-averse viewpoint (which has a consensus measurement with a really small distance to the selected TLA of 0.800). Therefore, a final group agreement amongst the stakeholders was reached. Additionally, according to the results of
Figure 14 and
Figure 15, it is observed that the group consensus measurements have an increasing trend from a completely risk-averse viewpoint to a completely risk-prone standpoint. It is therefore more difficult to achieve group consensus by satisfying all criteria by the water strategies in the completely risk-averse viewpoint than accomplishing a group consensus by satisfying just one criterion by the strategies in the completely risk-prone standpoint. In addition, changing the Minkowski’s parameter of
from 1 to infinity, the deviation and conflict between the individual and group viewpoints about the water strategies increased, which caused a decrease of group consensus measurements on strategies. After the achievement of the group consensus, the final ranking of water strategies can be implemented to determine the more desirable strategy in several risk-taking cases in both the EMOWA and IMOWA operators.
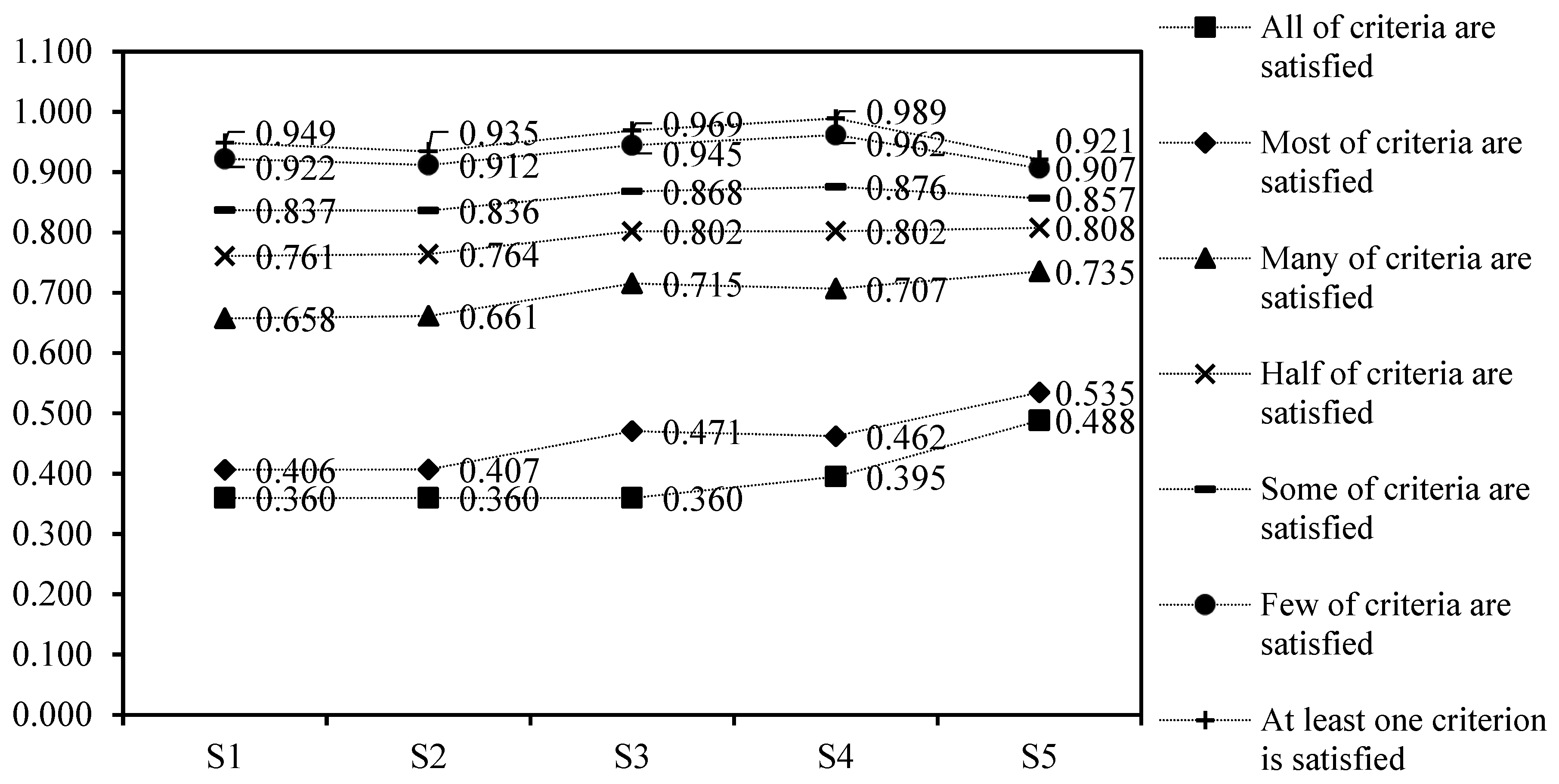
Consequently, according to the results of group scores achieved by the EMOWA and IMOWA operators, the final ranking of water strategies is determined in several risk-taking cases (
Table 8). Regarding the EMOWA results, in the three risk-prone cases, the strategy
is selected as the more desirable water strategy. In the neutral risk and the two risk-averse cases, the strategy
is chosen as the more desirable strategy. Additionally, in the completely risk-averse case, the strategy
is selected as the more desirable strategy. In accordance with the IMOWA results, in the three risk-prone cases, the strategy
is selected as the more desirable water strategy, while, in the neutral risk and the three risk-averse cases, the strategy
is chosen as the more desirable strategy.
5. Conclusions
In modeling the GDSS for effective urban watershed management, there are numerous stakeholders and beneficiaries with several opinions and preferences that should be used to evaluate water strategies with respect to sustainable development criteria for selecting the more desirable water strategy. The stakeholders’ group may have several risk-taking attitudes, each of which risk-taking cases is related to satisfying the number of criteria by water strategies. The risk-taking attitudes vary from a completely risk-averse viewpoint to a completely risk-prone standpoint. The completely risk-averse viewpoint (completely conservative opinion) believes that all criteria should be satisfied by water strategies, while the completely risk-prone standpoint (completely nonconservative opinion) believes that at least one criterion can be satisfied by strategies. The other risk-taking attitudes are expressed between these two limited risk-taking cases. Accordingly, for analyzing the effect of risk-taking cases on the selection of the more desirable water strategy, the risk-based consensus-based GDSS model should be developed for effective urban watershed management.
In this research, in order to select the more desirable water strategy for the Kashafroud watershed, the risk-based EMOWA and IMOWA operators were proposed in the two types of external and internal aggregations to calculate the group scores of water strategies with respect to the criteria. These operators consider the importance degrees of criteria, the risk-taking degrees of the stakeholders’ group, and the stakeholders’ power weights simultaneously. Additionally, the group consensus-seeking process was implemented based on the weighted Minkowski’s method, in which the group consensus measurements for strategies have been calculated using the squared mean deviation between the individual and group viewpoints of stakeholders. Finally, the ranking of the water strategies was determined in several risk-taking attitudes of the group of stakeholders with respect to the EMOWA and IMOWA scores for the strategies.
Therefore, the proposed methodology, including the main phases of water strategies’ scoring, group consensus measuring, and the water strategies’ ranking, was successfully developed for the study area of the Kashafroud watershed. The scoring results related to the EMOWA and IMOWA operators represents that the group scores of the water strategies are dependent on the risk-taking attitudes of the stakeholders within the watershed. Accordingly, for each strategy, the group scores in the risk-prone cases (at least one, a few, and some of the criteria satisfied by the strategies) are greater than the group scores in the risk-averse situations (many, most, and all of the criteria satisfied by the strategies). In addition, the group consensus measuring results shows that the final agreement among the stakeholders for all strategies was almost fully achieved. According to the findings of each strategy, the group consensus measurements in the risk-prone cases are greater than the group consensus measurements in the risk-averse situations. Finally, regarding the ranking results of strategies, for the risk-averse viewpoint in the EMOWA results, the group of stakeholders has a conservative approach and tend to select the strategy of as a supply management strategy, which satisfies all sustainable development criteria, while, in the IMOWA results with the risk-averse viewpoint, the group of stakeholders tends to choose the strategy of as a combined supply-demand management strategy. For the risk-prone standpoint in both EMOWA and IMOWA results, the group of stakeholders have a nonconservative approach and like to select the strategy of as a demand management strategy, which satisfies at least one sustainable development criteria.
Besides the advantages of the proposed risk-based consensus-based GDSS model in this study, there are some issues that should be improved in future studies, which include:
Improving the GDSS model for use of the other input variables in the MCDM process, including the combination of crisp and linguistic data, as well as fuzzy interval valued data.
Considering the alternative generation process during the GDSS modeling by use of the design theory, such as the K-C and K-C-P methodologies.
Modeling the other probable water strategies such as climate changes strategies; additionally, changes in the percentage of water supply for the agricultural demand with respect to more several criteria.
Resolving probable conflicts among stakeholders within the GDSS model using the game-theoretical Nash Bargaining solution.
For future studies, it is suggested to develop this proposed risk-based consensus-based GDSS model for any other watershed management by generating several water strategies based on the stakeholders’ group consensus, which considers the combination of agricultural, industrial, and environmental demands and climate changes conditions. Furthermore, a conflict resolution process among stakeholders within the risk-based consensus-based GDSS process for resolving the probable conflicts of preferences among the watershed stakeholders should be analyzed. Additionally, an analysis of the varieties of the Minkowski’s parameter and its effect on the group consensus measurement should be studied for future research.