Evaluation of Snowmelt Estimation Techniques for Enhanced Spring Peak Flow Prediction
Abstract
:1. Introduction
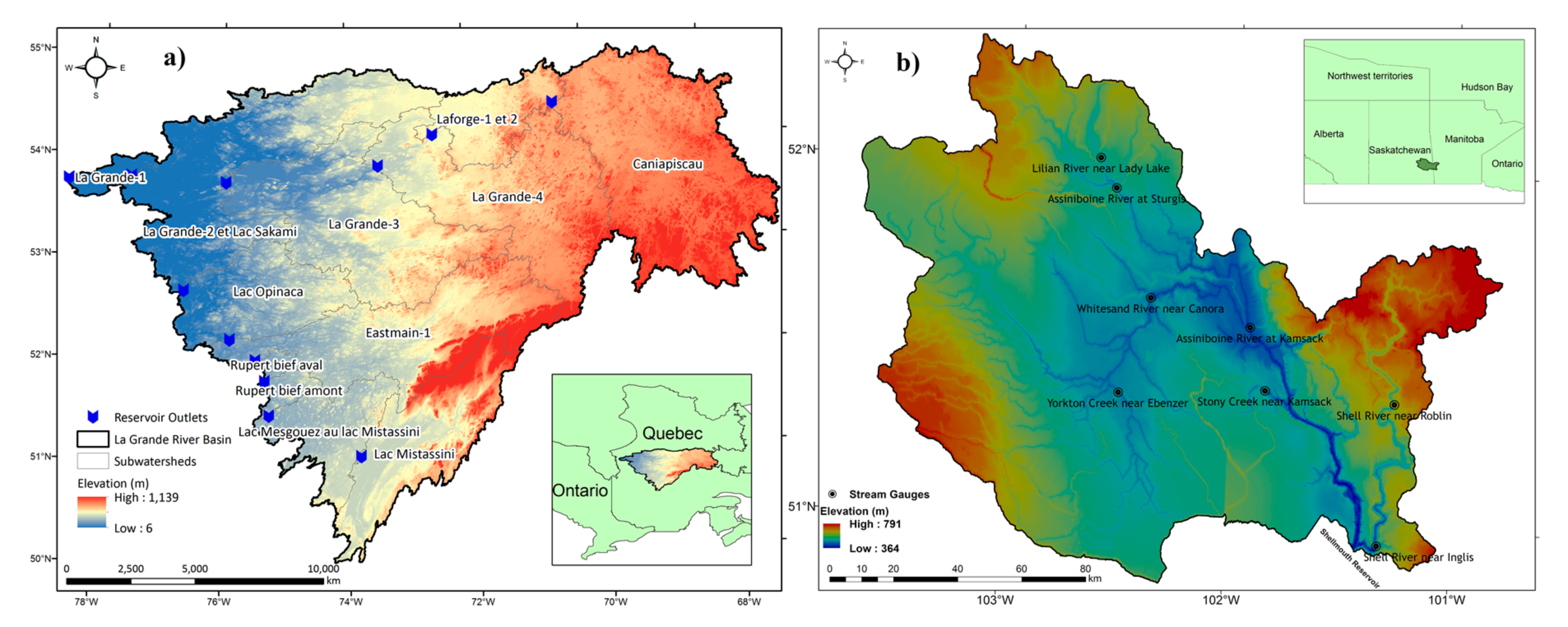
2. Materials
3. Methods
3.1. Hydrological Models
3.1.1. MAC-HBV Model
3.1.2. SAC-SMA Model
3.2. Snowmelt Estimation Methods
3.2.1. Degree-Day Method
3.2.2. SNOW-17 Model
3.3. Model Optimization
3.4. Model Performance Criteria
4. Results
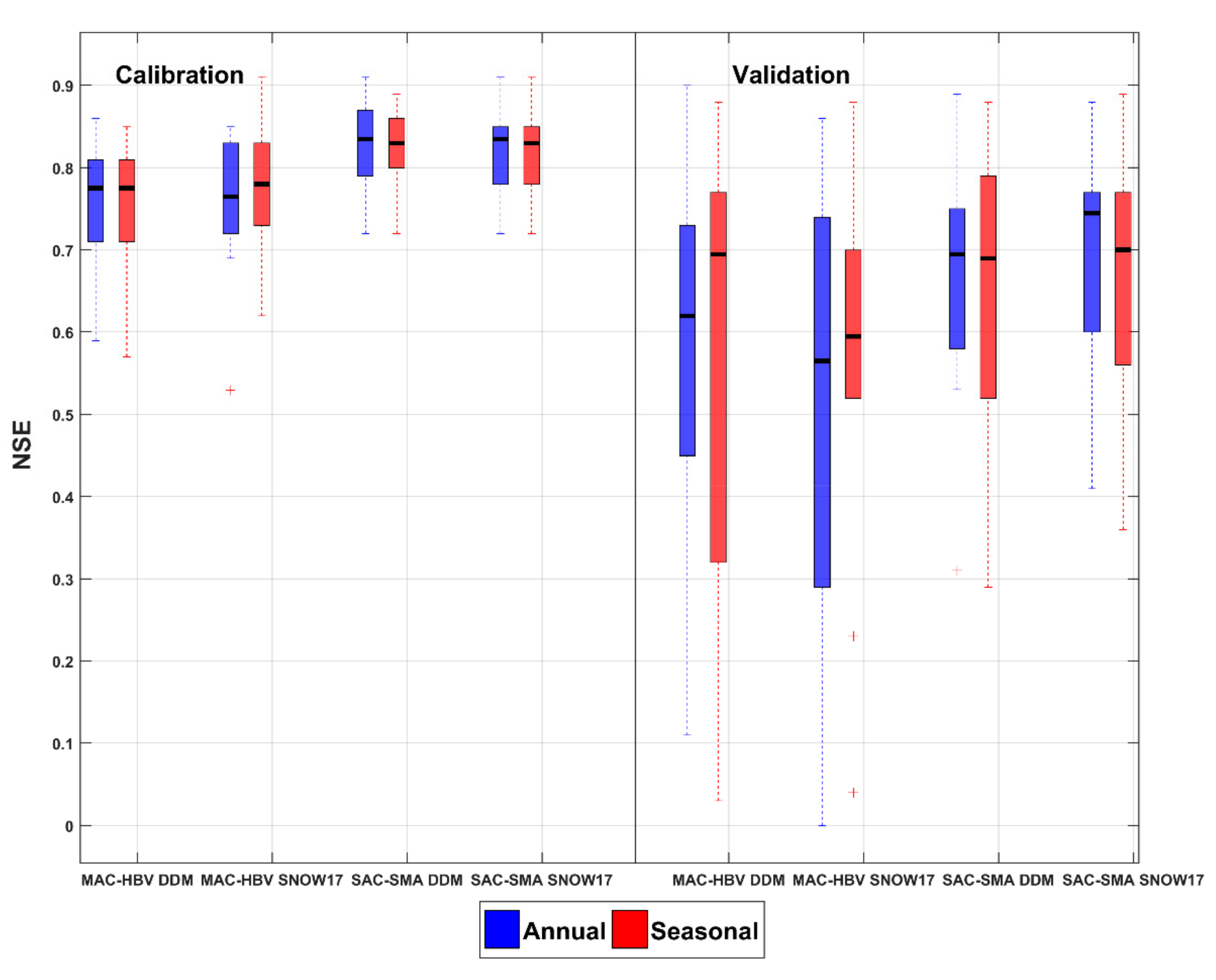
4.1. Evaluation of Snowmelt Estimation Methods: DDM and SNOW-17 Model
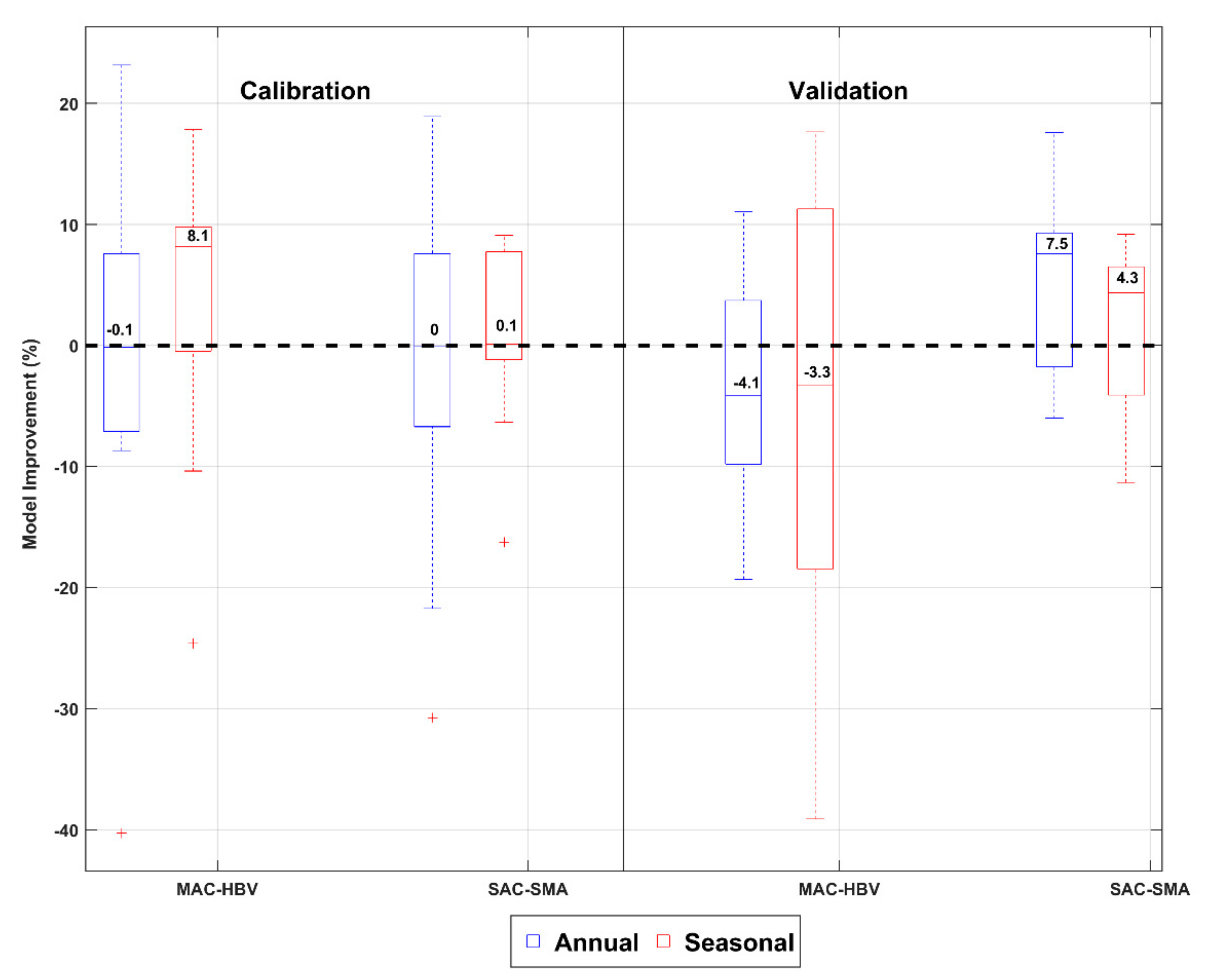
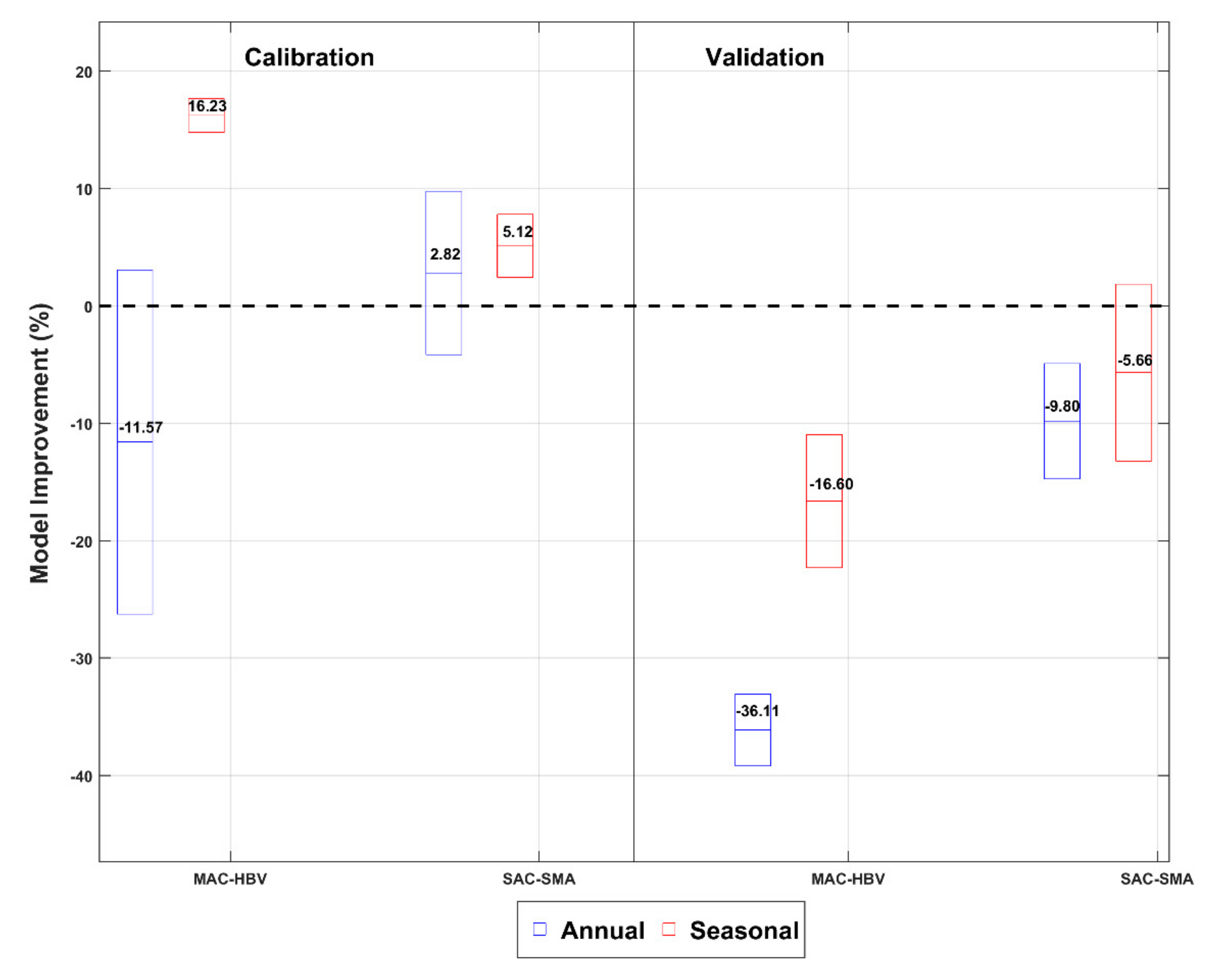
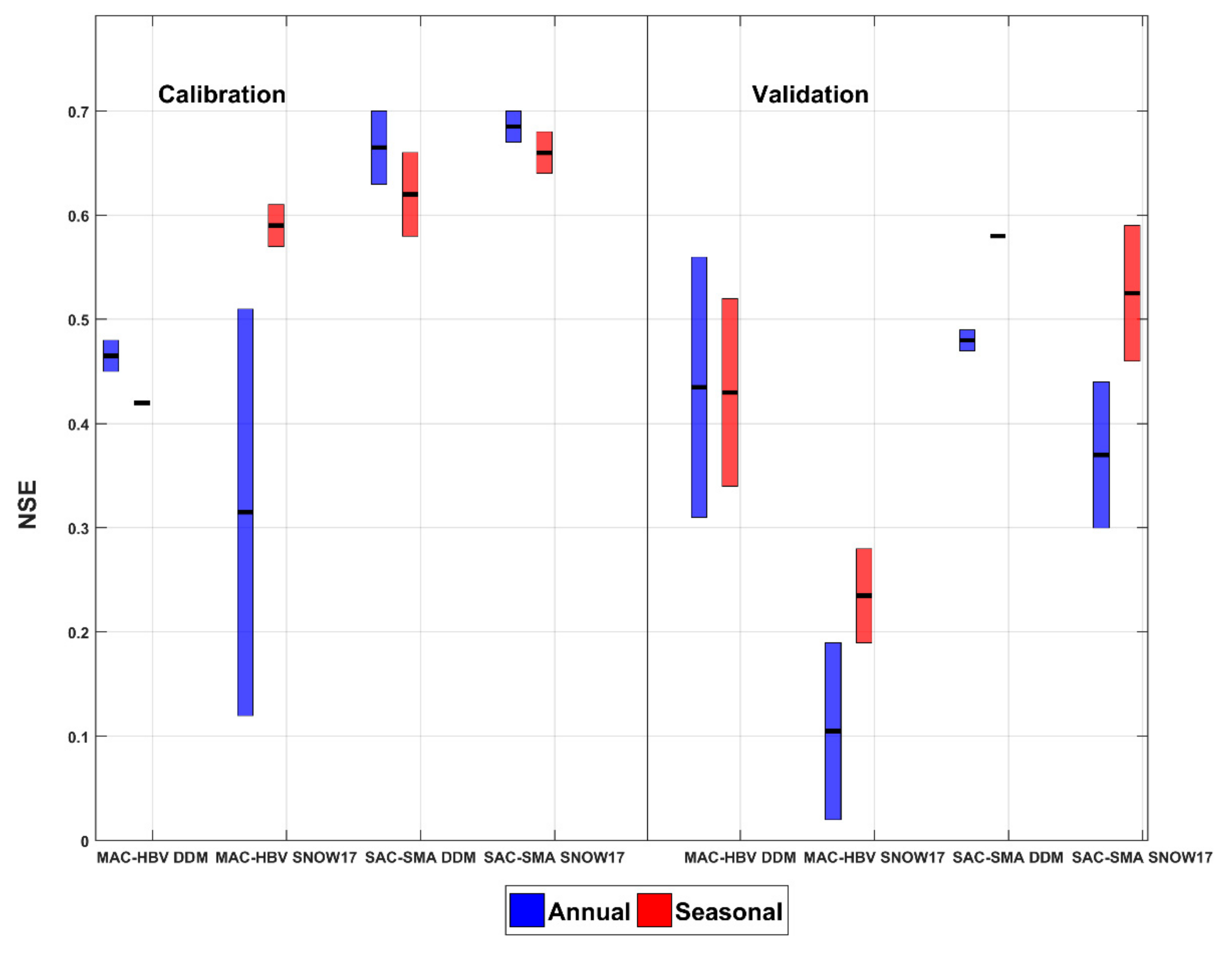
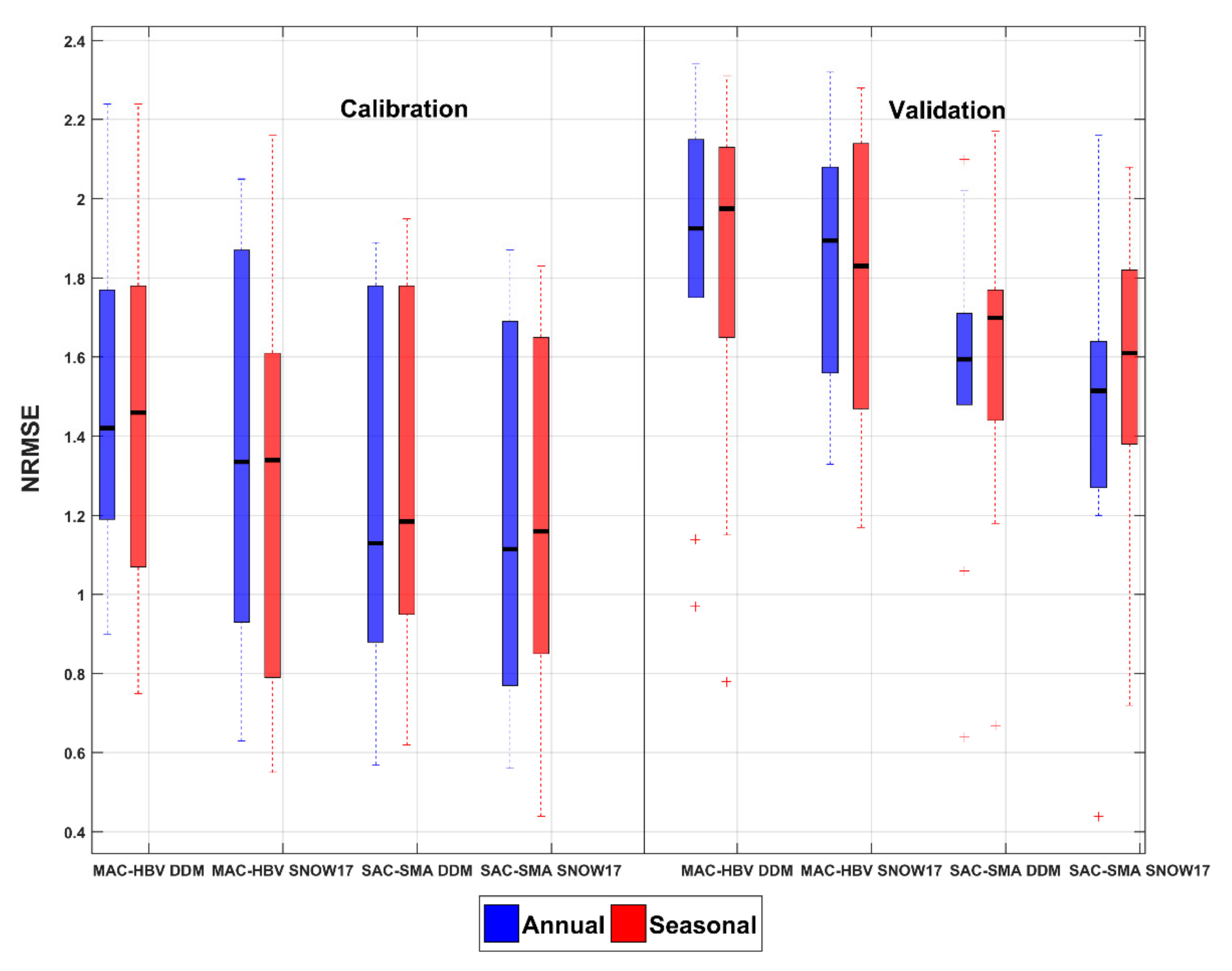
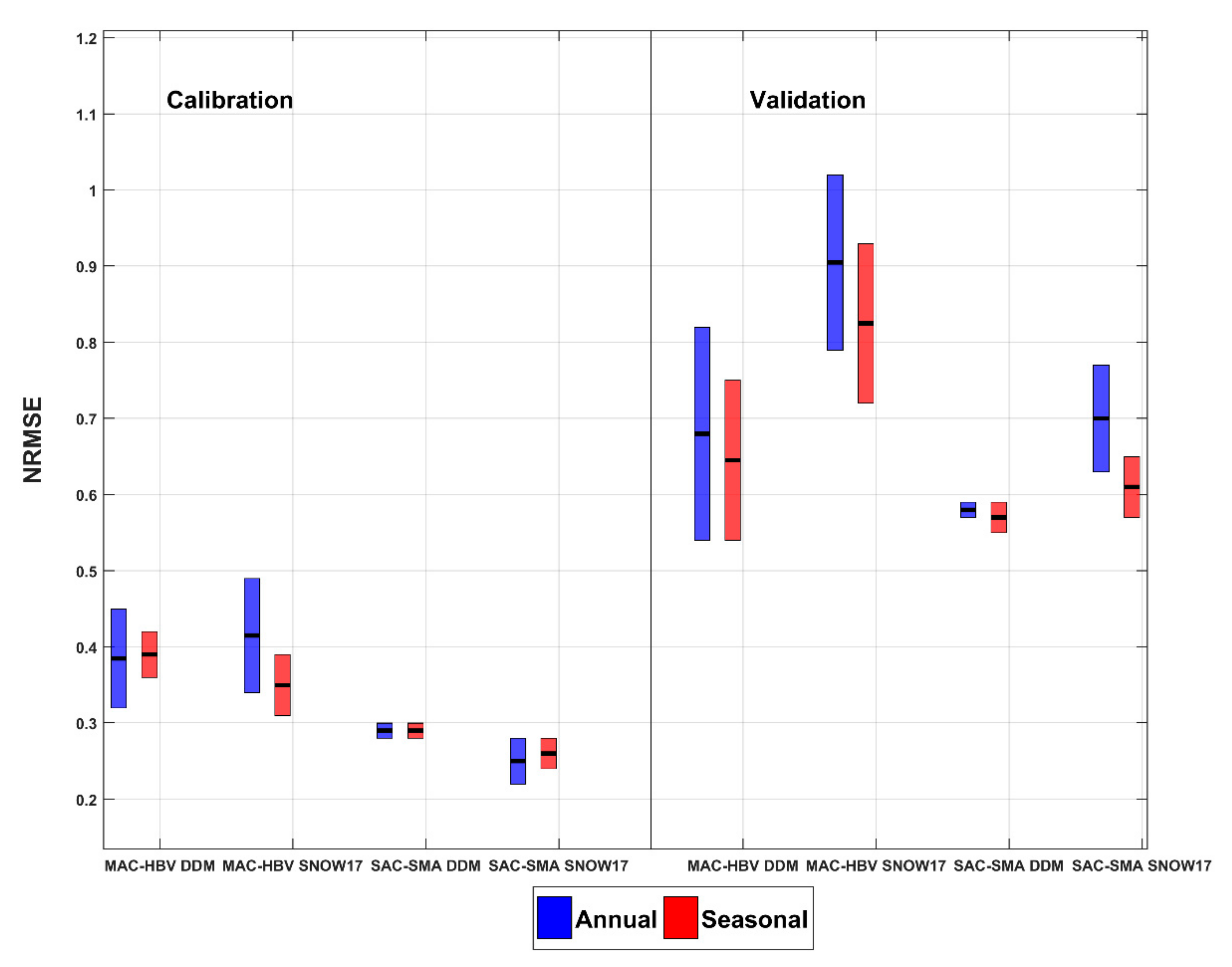
4.2. Results of Annually and Seasonally Calibrated Models
4.3. Comparison between Hydrological Models: MAC-HBV and SAC-SMA
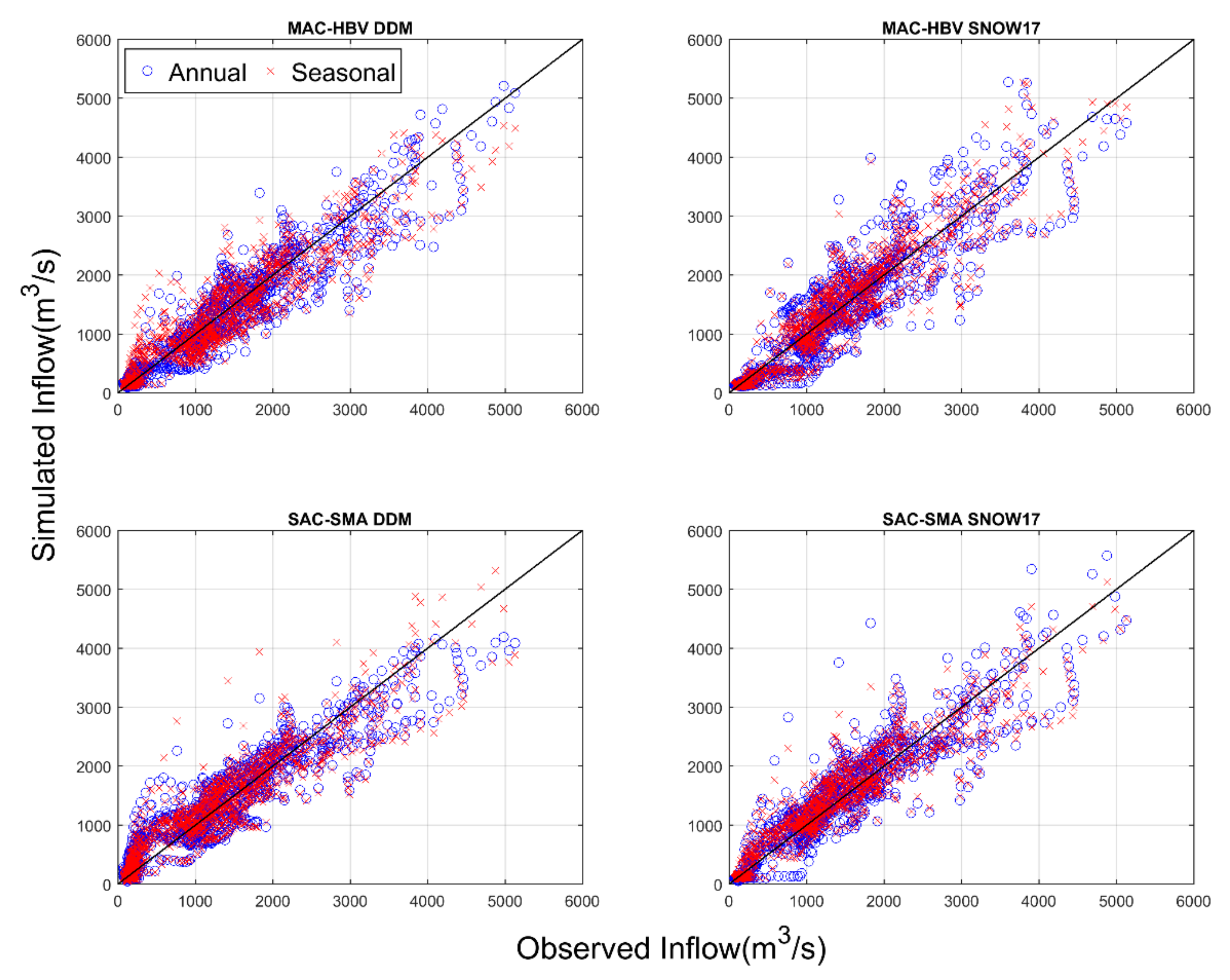
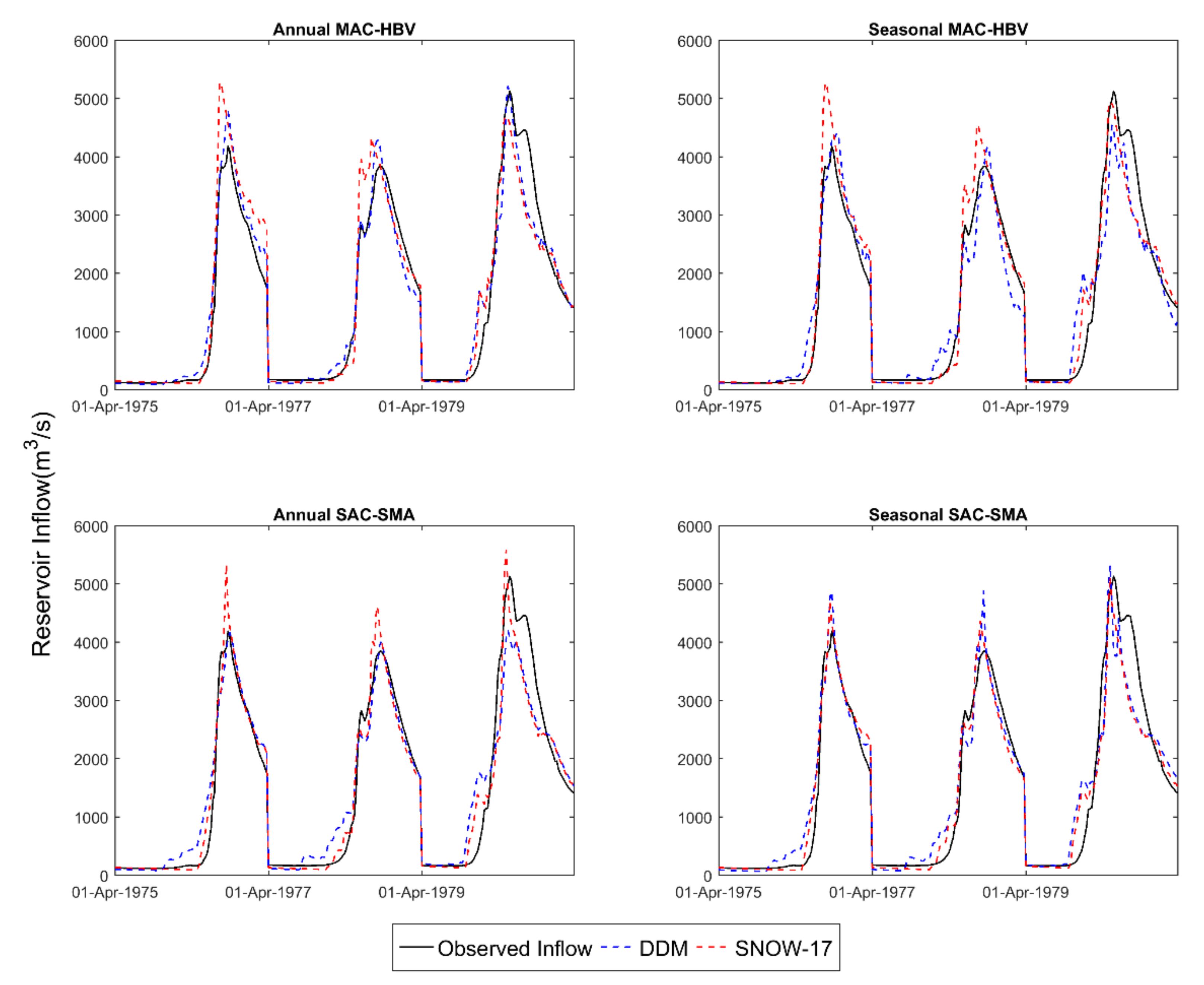
4.4. Visual Inspection of Model Performance
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ahmed, S.; Coulibaly, P.; Tsanis, I. Improved spring peak-flow forecasting using ensemble meteorological predictions. J. Hydrol. Eng. 2015, 20, 04014044. [Google Scholar] [CrossRef]
- Coulibaly, P. Impact of meteorological predictions on real-time spring flow forecasting. Hydrol. Process. 2003, 17, 3791–3801. [Google Scholar] [CrossRef]
- Awol, F.S.; Coulibaly, P.; Tolson, B.A. Event-based model calibration approaches for selecting representative distributed parameters in semi-urban watersheds. Adv. Water Resour. 2018, 118, 12–27. [Google Scholar] [CrossRef]
- Krauße, T.; Cullmann, J.; Saile, P.; Schmitz, G.H. Hydrology and Earth System Sciences Robust multi-objective calibration strategies-possibilities for improving flood forecasting. Hydrol. Earth Syst. Sci. 2012, 16, 3579–3606. [Google Scholar] [CrossRef] [Green Version]
- Etchevers, P.; Martin, E.; Brown, R.; Fierz, C.; Lejeune, Y.; Bazile, E.; Boone, A.; Dai, Y.-J.; Essery, R.; Fernandez, A.; et al. Validation of the Energy Budget of an Alpine Snowpack Simulated by Several Snow Models (SnowMIP project). Ann. Glaciol. 2004, 38, 150–158. [Google Scholar] [CrossRef] [Green Version]
- Mahanama, S.; Livneh, B.; Koster, R.; Lettenmaier, D.; Reichle, R. Soil Moisture, Snow, and Seasonal Streamflow Forecasts in the United States. J. Hydrometeorol. 2012, 13, 189–203. [Google Scholar] [CrossRef]
- Troin, M.; Arsenault, R.; Brissette, F. Performance and Uncertainty Evaluation of Snow Models on Snowmelt Flow Simulations over a Nordic Catchment (Mistassibi, Canada). Hydrology 2015, 2, 289–317. [Google Scholar] [CrossRef] [Green Version]
- Debele, B.; Srinivasan, R.; Gosain, A.K. Comparison of Process-Based and Temperature-Index Snowmelt Modeling in SWAT Conflict Resolution and Equitable Apportionment in Transboundary Basins View project Hydrological modeling View project Comparison of Process-Based and Temperature-Index Snowmelt. Water Resour. Manag. 2010, 24, 1065–1088. [Google Scholar] [CrossRef]
- Rango, A.; Martinec, J. Revisiting the degree-day method for snowmelt computations. J. Am. Water Resour. Assoc. 1995, 31, 657–669. [Google Scholar] [CrossRef]
- Pomeroy, J.W.; De Boer, D.; Martz, L.W. Hydrology and Water Resources of Saskatchewan, Centre for Hydrology; University of Saskatchewan: Saskatoon, SK, Canada, 2005. [Google Scholar]
- Essery, R.; Rutter, N.; Pomeroy, J.; Baxter, R.; Stahli, M.; Gustafsson, D.; Barr, A.; Bartlett, P.; Elder, K. An Evaluation of Forest Snow Process Simulations. Bull. Am. Meteorol. Soc. 2009, 90, 1120–1135. [Google Scholar] [CrossRef] [Green Version]
- Valeo, C.; Ho, C.L.I. Modelling urban snowmelt runoff. J. Hydrol. 2004, 299, 237–251. [Google Scholar] [CrossRef]
- Raleigh, M.S.; Lundquist, J.D. Comparing and combining SWE estimates from the SNOW-17 model using PRISM and SWE reconstruction. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Bokhorst, S.; Pedersen, S.H.; Brucker, L.; Anisimov, O.; Bjerke, J.W.; Brown, R.D.; Ehrich, D.; Essery, R.L.H.; Heilig, A.; Ingvander, S.; et al. Changing Arctic snow cover: A review of recent developments and assessment of future needs for observations, modelling, and impacts. Ambio 2016, 45, 516–537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moghadas, S.; Gustafsson, A.M.; Muthanna, T.M.; Marsalek, J.; Viklander, M. Review of models and procedures for modelling urban snowmelt. Urban Water J. 2016, 13, 396–411. [Google Scholar] [CrossRef]
- Essery, R.; Morin, S.; Lejeune, Y.; Ménard, C.B. A comparison of 1701 snow models using observations from an alpine site. Adv. Water Resour. 2013, 55, 131–148. [Google Scholar] [CrossRef] [Green Version]
- Rutter, N.; Essery, R.; Pomeroy, J.; Altimir, N.; Andreadis, K.; Baker, I.; Barr, A.; Bartlett, P.; Boone, A.; Deng, H.; et al. Evaluation of forest snow processes models (SnowMIP2). J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Bowling, L.; Lettenmaier, D.; Nijssen, B. Simulation of high-latitude hydrological processes in the Torne–Kalix basin: PILPS Phase 2 (e): 1: Experiment description and summary intercomparisons. Glob. Planet. Chang. 2003, 38, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Raleigh, M.S.; Livneh, B.; Lapo, K.; Lundquist, J.D. How does availability of meteorological forcing data impact physically based snowpack simulations? J. Hydrometeorol. 2016, 17, 99–120. [Google Scholar] [CrossRef]
- Förster, K.; Meon, G.; Marke, T.; Strasser, U. Effect of meteorological forcing and snow model complexity on hydrological simulations in the Sieber catchment (Harz Mountains, Germany). Hydrol. Earth Syst. Sci. 2014, 18, 4703–4720. [Google Scholar] [CrossRef] [Green Version]
- World Meteorological Organization. Intercomparison of Models of Snowmelt Runoff; Operational Hydrology Report No. 23; WMO No: 646; WMO: Geneva, Switzerland, 1986. [Google Scholar]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Kustas, W.P.; Rango, A.; Uijlenhoet, R. A simple energy budget algorithm for the snowmelt runoff model. Water Resour. Res. 1994, 30, 1515–1527. [Google Scholar] [CrossRef]
- Nijssen, B.; Bowling, L.; Lettenmaier, D. Simulation of high latitude hydrological processes in the Torne–Kalix basin: PILPS Phase 2 (e): 2: Comparison of model results with observations. Glob. Planet. Chang. 2003, 38, 31–53. [Google Scholar] [CrossRef] [Green Version]
- Franz, K.J.; Butcher, P.; Ajami, N.K. Addressing snow model uncertainty for hydrologic prediction. Adv. Water Resour. 2010, 33, 820–832. [Google Scholar] [CrossRef]
- Kumar, M.; Marks, D.; Dozier, J.; Reba, M.; Winstral, A. Evaluation of distributed hydrologic impacts of temperature-index and energy-based snow models. Adv. Water Resour. 2013, 56, 77–89. [Google Scholar] [CrossRef]
- Hernández-Henríquez, M.A.; Mlynowski, T.J.; Déry, S.J. Reconstructing the natural streamflow of a regulated river: A case study of la grande rivière, Québec, Canada. Can. Water Resour. J. 2010, 35, 301–316. [Google Scholar] [CrossRef] [Green Version]
- Coulibaly, P.; Keum, J. Snow Network Design and Evaluation for La Grande River Basin; Technical Report to Hydro-Quebec; McMaster University: Hamilton, ON, Canada, 2016. [Google Scholar]
- Blais, E.L.; Greshuk, J.; Stadnyk, T. The 2011 flood event in the Assiniboine River Basin: Causes, assessment and damages. Can. Water Resour. J. 2016, 41, 74–84. [Google Scholar] [CrossRef]
- Fang, X.; Minke, A.; Pomeroy, J.; Brown, T.; Westbrook, C.; Guo, X.; Guangul, S. A Review of Canadian Prairie Hydrology: Principles, Modelling and Response to Land Use and Drainage Change; Centre for Hydrology Report #2, Version 2; University of Saskatchewan: Saskatoon, SK, Canada, 2007. [Google Scholar]
- Shrestha, R.R.; Dibike, Y.B.; Prowse, T.D. Modeling Climate Change Impacts on Hydrology and Nutrient Loading in the Upper Assiniboine Catchment1. JAWRA J. Am. Water Resour. Assoc. 2012, 48, 74–89. [Google Scholar] [CrossRef]
- Samuel, J.; Coulibaly, P.; Metcalfe, R.A. Estimation of continuous streamflow in ontario ungauged basins: Comparison of regionalization methods. J. Hydrol. Eng. 2011, 16, 447–459. [Google Scholar] [CrossRef]
- Bergström, S. Development and Application of a Conceptual Runoff Model for Scandinavian Catchments; Technical Report No. RHO7; Swedish Meteorological and Hydrological Institute: Norrköping, Sweden, 1976. [Google Scholar]
- Razavi, T.; Coulibaly, P. Improving streamflow estimation in ungauged basins using a multi-modelling approach. Hydrol. Sci. J. 2016, 61, 2668–2679. [Google Scholar] [CrossRef] [Green Version]
- Samuel, J.; Coulibaly, P.; Metcalfe, R.A. Identification of rainfall-runoff model for improved baseflow estimation in ungauged basins. Hydrol. Process. 2012, 26, 356–366. [Google Scholar] [CrossRef]
- Sharma, M.; Coulibaly, P.; Dibike, Y. Assessing the need for downscaling RCM data for hydrologic impact study. J. Hydrol. Eng. 2011, 16, 534–539. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Gupta, H.V.; Nualláin, B.; Bouten, W. Real-Time Data Assimilation for Operational Ensemble Streamflow Forecasting. J. Hydrometeorol. 2006, 7, 548–565. [Google Scholar] [CrossRef]
- Anderson, E. Snow Accumulation and Ablation Model–SNOW-17; US National Weather Service: Silver Spring, MD, USA, 2006.
- He, M.; Hogue, T.S.; Franz, K.J.; Margulis, S.A.; Vrugt, J.A. Corruption of parameter behavior and regionalization by model and forcing data errors: A Bayesian example using the SNOW17 model. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Anderson, E. National Weather Service River Forecast System: Snow Accumulation and Ablation Model; NOAA Tech. Memo., NWS Hydro-17; National Weather Service (NWS): Silver Spring, MD, USA, 1973.
- Burnash, R.; Ferral, R.; McGuire, R. A Generalized Streamflow Simulation System: Conceptual Modeling for Digital Computers; Dept. of Water Resources, State of California: Sacramento, CA, USA, 1973.
- Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.J. Overall distributed model intercomparison project results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
- Day, G.N. Extended streamflow forecasting using NWSRFS. J. Water Resour. Plan. Manag. 1985, 111, 157–170. [Google Scholar] [CrossRef]
- Ohmura, A. Physical Basis for the Temperature-Based Melt-Index Method. J. Appl. Meteorol. 2001, 40, 753–761. [Google Scholar] [CrossRef]
- Hogue, T.S.; Gupta, H.; Sorooshian, S. A “User-Friendly” approach to parameter estimation in hydrologic models. J. Hydrol. 2006, 320, 202–217. [Google Scholar] [CrossRef]
- Tang, Y. Advancing Hydrologic Model Evaluation and Identification Using Multiobejctive Calibration, Sensitivity Analysis and Parallel Computation. Ph.D. Thesis, The Graduate School, The Pennsylvania State University, State College, PA, USA, 2007. [Google Scholar]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall-runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef] [Green Version]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995. [Google Scholar]
- Razavi, T.; Coulibaly, P. An evaluation of regionalization and watershed classification schemes for continuous daily streamflow prediction in ungauged watersheds. Can. Water Resour. J. 2017, 42, 2–20. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Coulibaly, P.; Anctil, F.; Bobée, B. Multivariate reservoir inflow forecasting using temporal neural networks. J. Hydrol. Eng. 2001, 6, 367–376. [Google Scholar] [CrossRef]
- Singh, P.; Jain, S.K. Modelling of streamflow and its components for a large Himalayan basin with predominant snowmelt yields. Hydrol. Sci. J. 2003, 48, 257–276. [Google Scholar] [CrossRef]
- Réveillet, M.; Six, D.; Vincent, C.; Rabatel, A.; Dumont, M.; Lafaysse, M.; Morin, S.; Vionnet, V.; Litt, M. Relative performance of empirical and physical models in assessing the seasonal and annual glacier surface mass balance of Saint-Sorlin Glacier (French Alps). Cryosphere 2018, 12, 1367–1386. [Google Scholar] [CrossRef] [Green Version]
- Melloh, R.A. A Synopsis and Comparison of Selected Snowmelt Algorithms; CRREL Report 99-8; US Army Corps of Engineers: Hanover, NH, USA, 1999.
- Unduche, F.; Tolossa, H.; Senbeta, D.; Zhu, E. Evaluation of four hydrological models for operational flood forecasting in a Canadian Prairie watershed. Hydrol. Sci. J. 2018, 63, 1133–1149. [Google Scholar] [CrossRef] [Green Version]
- Lundquist, J.D.; Flint, A.L. Onset of snowmelt and streamflow in 2004 in the Western Unites States: How shading may affect spring streamflow timing in a warmer world. J. Hydrometeorol. 2006, 7, 1199–1217. [Google Scholar] [CrossRef] [Green Version]
- Paik, K.; Kim, J.H.; Kim, H.S.; Lee, D.R. A conceptual rainfall-runoff model considering seasonal variation. Hydrol. Process. 2005, 19, 3837–3850. [Google Scholar] [CrossRef]
- Kim, H.S.; Lee, S. Assessment of a seasonal calibration technique using multiple objectives in rainfall-runoff analysis. Hydrol. Process. 2014, 28, 2159–2173. [Google Scholar] [CrossRef]
- Muhammad, A.; Stadnyk, T.; Unduche, F.; Coulibaly, P. Multi-Model Approaches for Improving Seasonal Ensemble Streamflow Prediction Scheme with Various Statistical Post-Processing Techniques in the Canadian Prairie Region. Water 2018, 10, 1604. [Google Scholar] [CrossRef] [Green Version]
- Awol, F.S.; Coulibaly, P.; Tsanis, I.; Unduche, F. Identification of hydrological models for enhanced ensemble reservoir inflow forecasting in a large complex prairiewatershed. Water 2019, 11, 2201. [Google Scholar] [CrossRef] [Green Version]


| Parameter Code | Description | Unit | Ranges |
|---|---|---|---|
| SAC-SMA | |||
| UZTWM | Upper-zone tension water maximum storage | mm | 1–150 |
| UZFWM | Upper-zone free water maximum storage | mm | 1–150 |
| UZK | Upper-zone free water lateral depletion rate | day−1 | 0.1–0.5 |
| PCTIM | Impervious fraction of the watershed area | - | 0–0.1 |
| ADIMP | Additional impervious area | - | 0–0.4 |
| ZPERC | Maximum percolation rate | - | 1–250 |
| REXP | Exponent of the percolation equation | - | 1–5 |
| LZTWM | Lower-zone tension water maximum storage | mm | 1–500 |
| LZFSM | Lower-zone free water supplemental maximum storage | mm | 1–1000 |
| LZFPM | Lower-zone free water primary maximum storage | mm | 1–1000 |
| LZSK | Lower-zone supplemental free water lateral depletion rate | day−1 | 0.01–0.25 |
| LZPK | Lower-zone primary free water lateral depletion rate | day−1 | 0.0001–0.025 |
| PFREE | Fraction percolating from upper to lower zone free water storage | - | 0–0.6 |
| Rq | Routing coefficient | - | 0.5–1.5 |
| MAC-HBV | |||
| athorn | Constant for Thornthwaite’s equation | - | 0.1–0.3 |
| fc | Maximum soil box water content | mm | 50–800 |
| lp | Limit for potential evaporation | mm/mm | 0.1*fc–0.9*fc |
| beta | Non-linear parameter controlling runoff generation | - | 0–10 |
| k0 | Flow recession coefficient in an upper soil reservoir | days | 1–30 |
| lsuz | A threshold value used to control response routing on an upper soil reservoir | mm | 1–100 |
| k1 | Flow recession coefficient in an upper soil reservoir | days | 30–100 |
| cperc | A constant percolation rate parameter | mm/day | 0.01–6 |
| k2 | Flow recession coefficient in a lower soil reservoir | days | 100–500 |
| alpha1 | An exponent in relation between outflow and storage representing non-linearity of storage – discharge relationship of lower reservoir | - | 0.5–1.25 |
| maxbas | A triangle weighting function for modelling a channel routing routine | days | 1–20 |
| DDM | |||
| tr | Upper threshold temperature to distinguish between rainfall and snowfall | °C | 0–2.5 |
| scf | Snowfall correction factor | - | 0.4–1.6 |
| ddf | Degree day factor | mm/day°C | 0–5.0 |
| rcr | Rainfall correction factor | - | 0.5–1.5 |
| SNOW17 | |||
| scf | Snowfall correction factor | - | 0.7–1.6 |
| uadj | Average wind function during rain-on-snow events | mm/mb/6 h | 0.03–0.19 |
| mbase | Base temperature for non-rain melt factor | °C | 0–1.0 |
| mfmax | Maximum melt factor considered to occur on Jun 21 | mm/6 h/°C | 0.5–2.0 |
| mfmin | Minimum melt factor considered to occur on Dec 21 | mm/6 h/°C | 0.05–0.49 |
| tipm | Antecedent snow temperature index | - | 0.01–1.0 |
| nmf | Maximum negative melt factor | mm/6 h/°C | 0.05–0.50 |
| plwhc | Percent liquid-water holding capacity | - | 0.02–0.3 |
| pxtemp1 | Lower limit temperature dividing transition from snow | °C | −2–0 |
| pxtemp2 | Upper limit temperature dividing rain from transition | °C | 1–3 |
| Model Calibration Mean | Model Validation Mean | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Models | NSE | KGE | NRMSE (mm/d) | PFC | Model Improvement (%) | NSE | KGE | NRMSE (mm/d) | PFC | Model Improvement (%) |
| MAC DDM | 0.76 | 0.83 | 1.49 | 0.40 | 1.13 | 0.56 | 0.68 | 1.83 | 0.46 | -4.21 |
| MAC SNOW-17 | 0.75 | 0.84 | 1.37 | 0.40 | 0.53 | 0.65 | 1.85 | 0.45 | ||
| SAC DDM | 0.82 | 0.87 | 1.24 | 0.35 | 0.83 | 0.66 | 0.72 | 1.54 | 0.42 | 4.27 |
| SAC SNOW-17 | 0.82 | 0.88 | 1.20 | 0.37 | 0.70 | 0.77 | 1.45 | 0.39 | ||
| Model Calibration Mean | Model Validation Mean | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Models | NSE | KGE | NRMSE (mm/d) | PFC | Model Improvement (%) | NSE | KGE | NRMSE (mm/d) | PFC | Model Improvement (%) |
| MAC DDM | 0.75 | 0.83 | 1.45 | 0.39 | 6.10 | 0.58 | 0.65 | 1.80 | 0.42 | 1.76 |
| MAC SNOW-17 | 0.78 | 0.85 | 1.28 | 0.35 | 0.55 | 0.66 | 1.78 | 0.45 | ||
| SAC DDM | 0.82 | 0.85 | 1.25 | 0.35 | 1.71 | 0.66 | 0.71 | 1.60 | 0.42 | 2.90 |
| SAC SNOW-17 | 0.82 | 0.87 | 1.19 | 0.32 | 0.66 | 0.75 | 1.54 | 0.43 | ||
| Calibration | Validation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | NSE | KGE | NRMSE (mm/d) | PFC | Model Improvement (%) | NSE | KGE | NRMSE (mm/d) | PFC | Model Improvement (%) |
| MAC DDM | 0.48 | 0.74 | 0.32 | 0.47 | 3.07 | 0.56 | 0.57 | 0.54 | 0.53 | -39.17 |
| MAC SNOW-17 | 0.51 | 0.73 | 0.34 | 0.48 | 0.19 | 0.23 | 0.79 | 0.62 | ||
| SAC DDM | 0.7 | 0.82 | 0.28 | 0.43 | -4.14 | 0.49 | 0.52 | 0.59 | 0.57 | -4.89 |
| SAC SNOW-17 | 0.67 | 0.80 | 0.22 | 0.38 | 0.44 | 0.49 | 0.63 | 0.6 | ||
| Calibration | Validation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | NSE | KGE | NRMSE (mm/d) | PFC | Model Improvement (%) | NSE | KGE | NRMSE (mm/d) | PFC | Model Improvement (%) |
| MAC DDM | 0.42 | 0.72 | 0.36 | 0.49 | 17.67 | 0.52 | 0.6 | 0.54 | 0.52 | -22.28 |
| MAC SNOW-17 | 0.61 | 0.78 | 0.31 | 0.45 | 0.28 | 0.35 | 0.72 | 0.61 | ||
| SAC DDM | 0.66 | 0.73 | 0.28 | 0.44 | 2.44 | 0.58 | 0.5 | 0.55 | 0.55 | -13.20 |
| SAC SNOW-17 | 0.68 | 0.73 | 0.28 | 0.46 | 0.46 | 0.48 | 0.65 | 0.59 | ||
| Percentage of Sub-Basins Performing Better/Comparable with DDM Than SNOW-17 Model | Percentage of Sub-Basins Performing Better/Comparable with SEASONAL Models than ANNUAL Models | Percentage of Sub-Basins Performing Better/Comparable with SAC-SMA Than MAC-HBV Hydrologic Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| LGRB | NSE | PFC | MI | NSE | KGE | PFC | NRMSE | NSE | KGE | PFC | NRMSE |
| Entire Study Period | 51 | 56 | 46 | 54 | 51 | 51 | 53 | 92 | 79 | 74 | 86 |
| UASR | NSE | PFC | MI | NSE | KGE | PFC | NRMSE | NSE | KGE | PFC | NRMSE |
| Entire Study Period | 56 | 62 | 56 | 62 | 38 | 62 | 75 | 94 | 69 | 75 | 87 |
| Sum (LGRB+ UASR) | 52 | 57 | 48 | 55 | 49 | 53 | 57 | 93 | 77 | 74 | 86 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agnihotri, J.; Coulibaly, P. Evaluation of Snowmelt Estimation Techniques for Enhanced Spring Peak Flow Prediction. Water 2020, 12, 1290. https://doi.org/10.3390/w12051290
Agnihotri J, Coulibaly P. Evaluation of Snowmelt Estimation Techniques for Enhanced Spring Peak Flow Prediction. Water. 2020; 12(5):1290. https://doi.org/10.3390/w12051290
Chicago/Turabian StyleAgnihotri, Jetal, and Paulin Coulibaly. 2020. "Evaluation of Snowmelt Estimation Techniques for Enhanced Spring Peak Flow Prediction" Water 12, no. 5: 1290. https://doi.org/10.3390/w12051290
APA StyleAgnihotri, J., & Coulibaly, P. (2020). Evaluation of Snowmelt Estimation Techniques for Enhanced Spring Peak Flow Prediction. Water, 12(5), 1290. https://doi.org/10.3390/w12051290




