Decision-Making Tools to Manage the Microbiology of Drinking Water Distribution Systems
Abstract
1. Introduction
1.1. Microbial Quality of Drinking Water
1.2. Multi Criteria Decision-Making
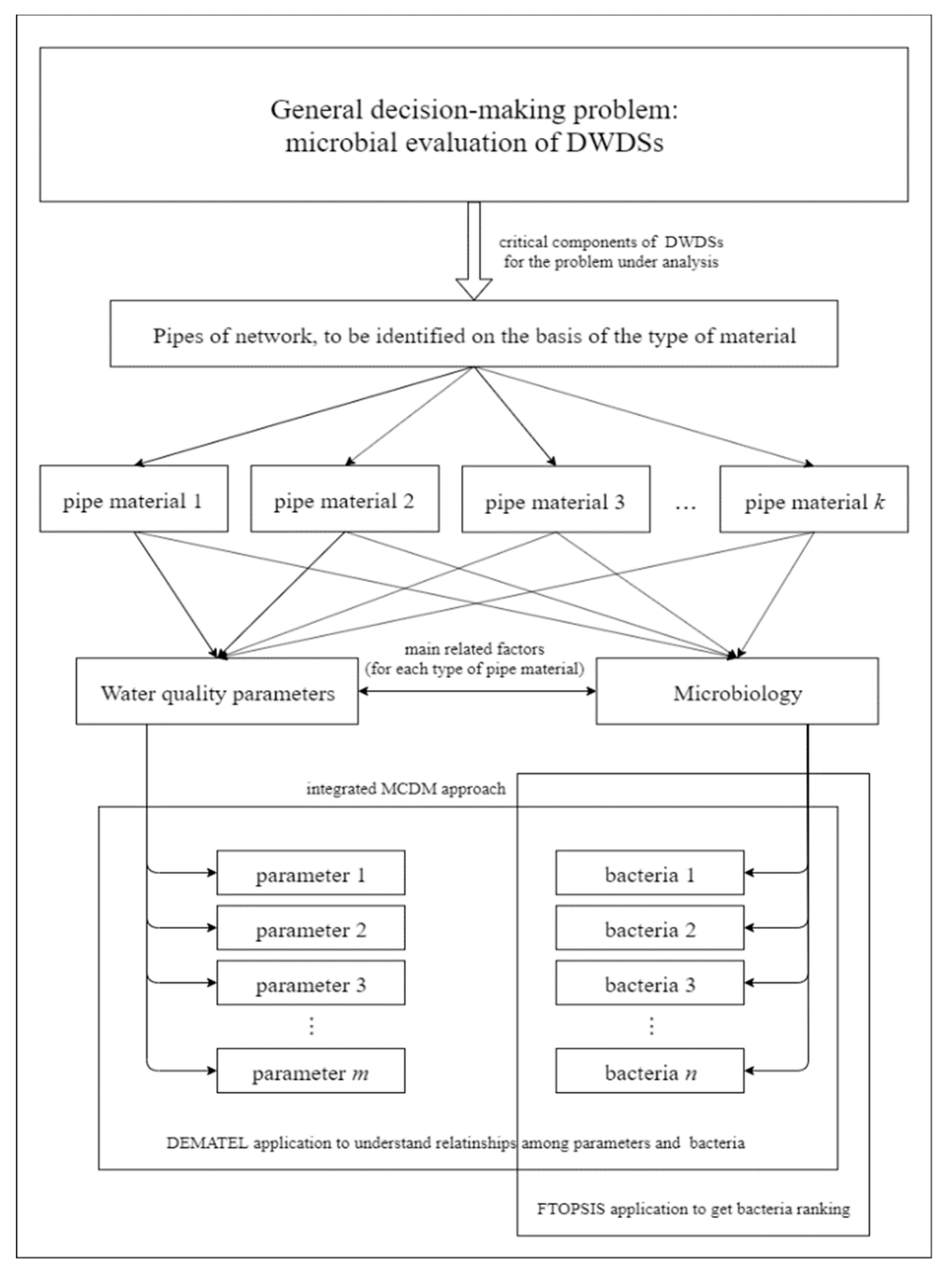
2. Aim and Structure
3. Materials and Methods
3.1. The Problem of Microbial Evaluation for DWDSs
3.2. Integrated MCDM Approach
3.2.1. Modified DEMATEL to Establish Relationships of Influence among Elements
- Collecting the non-negative input matrix, , whose cells give the relation of influence of one element, , over another one, , according to the following linguistic evaluation scale: 0 (no influence), 1 (very low influence), 2 (low influence), 3 (high influence), 4 (very high influence). The main diagonal of the matrix will be zeroes, since one element has no influence on itself.
- According to the traditional DEMATEL procedure [29,30], the previous stage is carried out by involving a decision-making group and by asking each expert to fill in their own input matrix. All these matrices are then aggregated into one, the so called direct relation matrix, (output of the third stage of the procedure), with the aim to treat the set of input data in a way as balanced and reliably as possible. In this paper, a single input matrix is used, in which, instead of subjective expert evaluations, the relations of influence for each pair of elements are derived from the related values of measured Spearman correlations. Hence, the direct relation matrix coincides with a single input matrix .
- Calculating the normalised direct relation matrix as:being a positive number slightly smaller thanMatrix shows the initial influence that elements exert on and receive from the others. The next step consists of obtaining a continuous decrease of indirect effects among factors in terms of consecutive powers of .
- Obtaining the total relation matrix, , which collects the total interrelation, including both direct and indirect effects among elements, which can be calculated as the sum of the powers of the normalised direct relation matrix , given by:where is the identity matrix. As observed, for example, in [46], since the spectral radius of is smaller than 1, being bounded by the maximum row and column sum. Then, as shown for instance by Meyer [47], the power series of the normalised direct relation matrix converges to –. Moreover, it has to be noticed that, whereas the main diagonal of matrix is filled with zeroes (expression of no direct effect of each element on itself), the diagonal entries of the total relation matrix collect all the non-direct effects related to their corresponding factors.
- Defining the two vectors and , respectively representing the and vectors of sums of the rows and sums of the columns in the total relation matrix . From these two vectors it is possible to calculate the prominence as the sum , reflecting the general effect of element on all the other elements, and the relation as the subtraction , helping in dividing the elements into classes of cause (if positive) and effect (if negative).
- Drawing up the final ranking of elements, ordered according to their decreasing values of prominence.
3.2.2. FTOPSIS to Rank Bacteria according to the Type of Pipe Material
- Defining the fuzzy decision matrix collecting input data:where the generic fuzzy number represents the rating of alternative under criterion j. In the present case, TFNs characterized by ordered triples are taken into account:
- Obtaining matrix by weighting and normalising the fuzzy decision matrix of input with relation to each criterion. Elements of matrix are calculated as:where is the subset of criteria to be maximised, the subset of criteria to be minimised, expresses the weight of criterion , and and are calculated as:
- Computing distances between each alternative and two fuzzy ideal solutions, namely the fuzzy positive ideal solution and the fuzzy negative ideal solution :where and . Chen (2000) proposed to compute distances between each alternative and these points through the vertex method, for which the distance between two TFNs and corresponds to the following crisp value:Then, aggregating with respect to the set of considered criteria, the distances of each alternative from and are:
- Calculating the closeness coefficient to get the final ranking. The mentioned closeness coefficient is calculated as:To get the final ranking it is necessary to sort the values of the closeness coefficient related to each alternative in a decreasing way. The elements with higher values will be selected.
3.3. Case Study
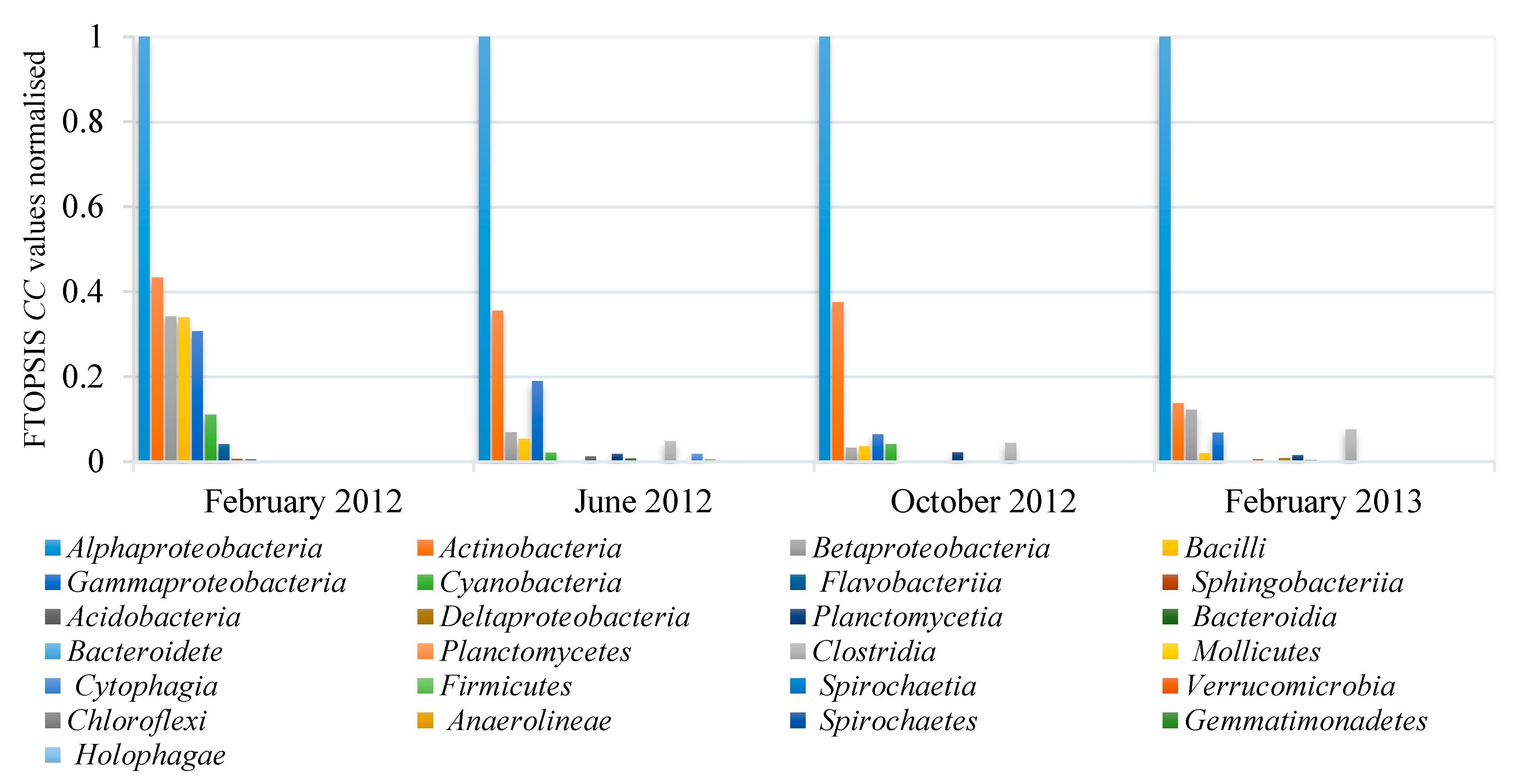
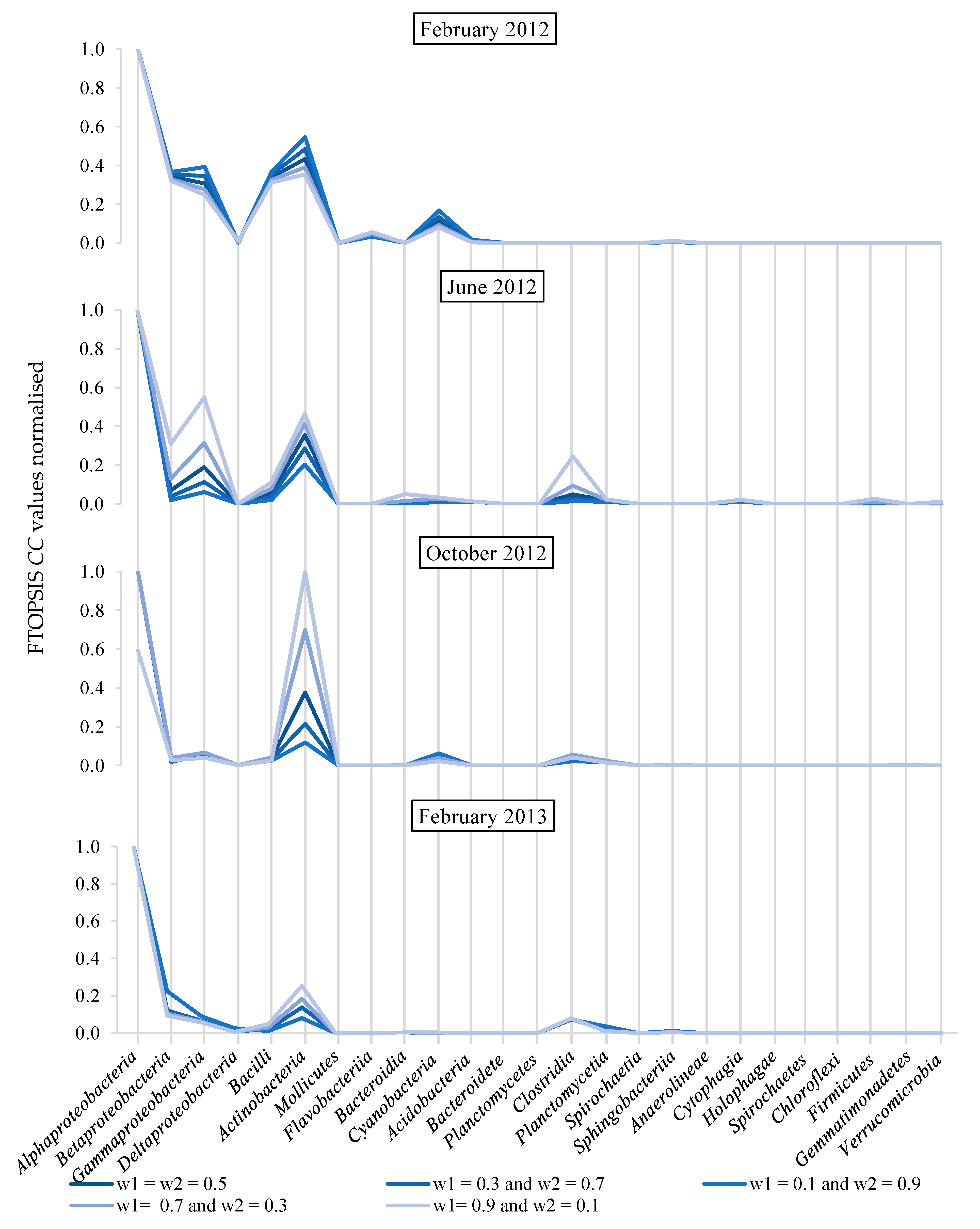
4. Results and Discussion
5. Conclusions
- Mutual interdependencies existing among water quality parameters (e.g., iron, chlorine, phosphate etc.,) and bacterial class can be determined by the decision-making trial and evaluation laboratory, also removing the need for reliance on expert judgement.
- Bacterial classes can be ranked according to their relative abundance depending on pipe materials using the fuzzy technique for order preference by similarity to ideal solution.
- The method reveals that the critical bacterial classes, those that have the most inter-dependencies and therefore potential management impact, may not be the most abundant.
- Initial application of the approach generated new knowledge of the physicochemical and biological parameters that are most likely to influence the presence and relative abundance of bacterial classes, for the limited data set available. Such knowledge will allow water companies to inform management strategies to promote favourable bacterial communities and hence help to safeguard drinking water quality.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. DEMATEL and FTOPSIS Results
| Factor | r = c | Prominence | Order | Ranking | |
|---|---|---|---|---|---|
| P1 | 1.437216965 | 2.87443393 | 37 | P12 | Iron |
| P2 | 2.973143464 | 5.946286928 | 6 | P3 | Phosphate |
| P3 | 3.17935789 | 6.358715781 | 4 | P9 | Betaproteobacteria |
| P4 | 2.345268204 | 4.690536408 | 17 | P10 | Turbidity |
| P5 | 1.726788409 | 3.453576818 | 32 | B2 | Manganese |
| P6 | 2.251308008 | 4.502616016 | 23 | B8 | Diversity |
| P7 | 2.030897355 | 4.06179471 | 27 | B4 | Spirochaetia |
| P8 | 2.640276655 | 5.280553311 | 12 | B16 | Gammaproteobacteri |
| P9 | 3.448076894 | 6.896153789 | 1 | P2 | Flavobacteriia |
| P10 | 3.137029854 | 6.274059707 | 5 | B15 | Gemmatimonadetes |
| P11 | 2.240798202 | 4.481596404 | 24 | B3 | Deltaproteobacteria |
| P12 | 3.424555671 | 6.849111342 | 2 | B5 | Aluminium |
| P13 | 1.509733521 | 3.019467042 | 36 | P8 | Acidobacteria |
| B1 | 1.58008322 | 3.160166439 | 34 | B21 | Bacilli |
| B2 | 3.393248734 | 6.786497469 | 3 | B9 | Anaerolineae |
| B3 | 2.895992476 | 5.791984953 | 8 | B25 | Holophagae |
| B4 | 2.653556974 | 5.307113947 | 11 | B19 | Total organic carbon |
| B5 | 2.511551785 | 5.02310357 | 14 | B24 | Bacteroidete |
| B6 | 1.395898146 | 2.791796292 | 38 | P4 | Sphingobacteriia |
| B7 | 1.927236046 | 3.854472092 | 29 | B11 | Firmicutes |
| B8 | 2.815970477 | 5.631940955 | 9 | B23 | Bacteroidia |
| B9 | 2.303522588 | 4.607045176 | 21 | B12 | Chloroflexi |
| B10 | 1.953345677 | 3.906691354 | 28 | B7 | pH |
| B11 | 2.528074142 | 5.056148284 | 13 | B10 | Nitrate |
| B12 | 2.341968998 | 4.683937996 | 18 | P6 | Planctomycetia |
| B13 | 1.548426935 | 3.09685387 | 35 | P11 | Cytophagia |
| B14 | 1.835317607 | 3.670635214 | 30 | B17 | Chlorine |
| B15 | 2.201492206 | 4.402984412 | 25 | B20 | Cyanobacteria |
| B16 | 2.93537933 | 5.870758661 | 7 | P7 | Mollicutes |
| B17 | 2.320906655 | 4.64181331 | 19 | B14 | Clostridia |
| B18 | 2.369284818 | 4.738569635 | 15 | B22 | Spirochaetes |
| B19 | 2.112981146 | 4.225962291 | 26 | B13 | Temperature |
| B20 | 2.351855933 | 4.703711866 | 16 | P5 | Verrucomicrobia |
| B21 | 1.752601241 | 3.505202483 | 31 | B26 | Alphaproteobacteria |
| B22 | 2.266608635 | 4.533217271 | 22 | P13 | Planctomycetes |
| B23 | 2.314947689 | 4.629895379 | 20 | P1 | Sulphate |
| B24 | 2.711514009 | 5.423028017 | 10 | B1 | Richness |
| B25 | 1.652805885 | 3.305611769 | 33 | B6 | Actinobacteria |
| ID | ||||||
|---|---|---|---|---|---|---|
| B1 | 20.49107931 | 22.98176432 | 35.19847571 | 17.49200859 | 24.68045308 | 25.27149145 |
| B2 | 6.999646706 | 7.151476659 | 9.267970455 | 5.299802556 | 11.94256668 | 15.4431105 |
| B3 | 4.560177834 | 5.074191839 | 15.04694037 | 6.692299699 | 10.77111383 | 13.02206152 |
| B4 | 0.393775802 | 3.161985515 | 3.85331385 | 0.020783539 | 1.1318975 | 1.666710071 |
| B5 | 4.930240006 | 9.649355238 | 21.37821531 | 6.791843538 | 8.375766393 | 9.982707122 |
| B6 | 6.66573253 | 8.351857733 | 11.1596891 | 10.72682492 | 10.88049168 | 22.21760366 |
| B7 | 0 | 0.232199692 | 7.138774214 | 0 | 0.639312477 | 11.86228808 |
| B8 | 1.258611553 | 1.431230859 | 2.229279136 | 0.539747419 | 0.572931587 | 6.131144134 |
| B9 | 0.176647235 | 1.144984687 | 1.390917752 | 0 | 1.582560394 | 12.63639198 |
| B10 | 1.174976183 | 2.40606922 | 8.386327504 | 3.153727962 | 4.574752397 | 5.840174582 |
| B11 | 0 | 0 | 0.749444268 | 0 | 0 | 1.203156332 |
| B12 | 0.039745628 | 0.527151477 | 3.342874872 | 0.463553738 | 0.654681492 | 2.814022952 |
| B13 | 0.080068859 | 0.387424579 | 0.463698993 | 0 | 1.013047215 | 3.018393334 |
| B14 | 0.018015493 | 0.225225225 | 0.381073357 | 0 | 0.317716607 | 1.62972279 |
| B15 | 0.368370911 | 2.295974538 | 5.272919979 | 0 | 0 | 0.005240266 |
| B16 | 0.317561131 | 1.175010509 | 4.107048225 | 0 | 3.143311024 | 5.502279516 |
| B17 | 0.260400127 | 0.980392157 | 1.937666393 | 0 | 0 | 0 |
| B18 | 0.02540489 | 1.801801802 | 2.259943551 | 0 | 1.828172609 | 1.844573704 |
| B19 | 0 | 0.174149769 | 0.251722311 | 0 | 0 | 0 |
| B20 | 0 | 0.04857799 | 0.058049923 | 0 | 0 | 0 |
| B21 | 0 | 0.379791556 | 1.373180936 | 0 | 0.01039177 | 1.294345753 |
| B22 | 0 | 0 | 0 | 0 | 0 | 0 |
| B23 | 0 | 0.002001721 | 0.587352058 | 0 | 0 | 0 |
| B24 | 0 | 0.05404648 | 1.519166225 | 0 | 0 | 0 |
| B25 | 0 | 0.438377004 | 0.507860802 | 0 | 0 | 0.282974375 |
| ID | ||||||
|---|---|---|---|---|---|---|
| B1 | 0.000014205 | 0.000021756 | 0.000024401 | 0.000019785 | 0.000020259 | 0.000028584 |
| B2 | 0.000053949 | 0.000069915 | 0.000071432 | 0.000032377 | 0.000041867 | 0.000094343 |
| B3 | 0.000033229 | 0.000098537 | 0.000109645 | 0.000038396 | 0.000046420 | 0.000074713 |
| B4 | 0.000129758 | 0.000158128 | 0.001269758 | 0.000299992 | 0.000441736 | 0.0240575 |
| B5 | 0.000023388 | 0.000051817 | 0.000101415 | 0.000050087 | 0.000059696 | 0.000073618 |
| B6 | 0.000044804 | 0.000059867 | 0.000075010 | 0.000022504 | 0.000045954 | 0.000046612 |
| B7 | 0.000070040 | 0.002153319 | 1 | 0.000042150 | 0.00078209 | 1 |
| B8 | 0.000224288 | 0.00034935 | 0.000397263 | 0.000081551 | 0.000872705 | 0.000926359 |
| B9 | 0.000359475 | 0.000436687 | 0.0028305 | 0.000039568 | 0.000315944 | 1 |
| B10 | 0.000059621 | 0.000207808 | 0.000425541 | 0.000085614 | 0.000109296 | 0.000158543 |
| B11 | 0.000667161 | 1 | 1 | 0.000415574 | 1 | 1 |
| B12 | 0.000149572 | 0.000948494 | 0.01258 | 0.000177682 | 0.00076373 | 0.001078624 |
| B13 | 0.001078286 | 0.001290574 | 0.006244625 | 0.000165651 | 0.00049356 | 1 |
| B14 | 0.001312083 | 0.00222 | 0.027753889 | 0.000306801 | 0.00157373 | 1 |
| B15 | 0.000094824 | 0.000217772 | 0.001357328 | 0.095415 | 1 | 1 |
| B16 | 0.000121742 | 0.000425528 | 0.0015745 | 0.000090871 | 0.000159068 | 1 |
| B17 | 0.000258042 | 0.00051 | 0.001920122 | 1 | 1 | 1 |
| B18 | 0.000221244 | 0.0002775 | 0.01968125 | 0.000271065 | 0.000273497 | 1 |
| B19 | 0.001986316 | 0.002871092 | 1 | 1 | 1 | 1 |
| B20 | 0.008613276 | 0.010292727 | 1 | 1 | 1 | 1 |
| B21 | 0.000364118 | 0.001316512 | 1 | 0.000386296 | 0.048115 | 1 |
| B22 | 1 | 1 | 1 | 1 | 1 | 1 |
| B23 | 0.000851278 | 0.249785 | 1 | 1 | 1 | 1 |
| B24 | 0.000329128 | 0.009251296 | 1 | 1 | 1 | 1 |
| B25 | 0.000984522 | 0.001140571 | 1 | 0.001766944 | 1 | 1 |
| February 2012 | June 2012 | October 2012 | February 2013 | ||||
|---|---|---|---|---|---|---|---|
| Ranking | Ranking | Ranking | Ranking | ||||
| 0.000021904 | B1 | 0.000032782 | B1 | 0.000020284 | B1 | 0.000018493 | B1 |
| 0.000050556 | B6 | 0.000092323 | B6 | 0.000054029 | B6 | 0.000134639 | B6 |
| 0.000064015 | B2 | 0.000173322 | B3 | 0.000314969 | B3 | 0.000151797 | B2 |
| 0.000064507 | B5 | 0.000473575 | B2 | 0.000460293 | B14 | 0.000242965 | B14 |
| 0.000071328 | B3 | 0.000609658 | B5 | 0.000489808 | B10 | 0.000273064 | B3 |
| 0.000198617 | B10 | 0.000679344 | B14 | 0.000551176 | B5 | 0.000915538 | B5 |
| 0.000533991 | B8 | 0.001587454 | B10 | 0.000618129 | B2 | 0.001244508 | B15 |
| 0.003518699 | B17 | 0.001798972 | B15 | 0.000916142 | B15 | 0.00212396 | B4 |
| 0.004021346 | B11 | 0.001857045 | B19 | 0.012192723 | B17 | 0.003477588 | B17 |
| 0.007296215 | B4 | 0.002647 | B11 | 0.012280875 | B9 | 0.005532909 | B9 |
| 0.241561775 | B15 | 0.004477637 | B9 | 0.014121489 | B24 | 0.028684001 | B10 |
| 0.241845487 | B9 | 0.006075334 | B23 | 0.014330545 | B4 | 0.241510047 | B19 |
| 0.242680267 | B12 | 0.011889233 | B25 | 0.061908005 | B13 | 0.243271905 | B11 |
| 0.24738986 | B13 | 0.241329775 | B16 | 0.24315878 | B11 | 0.243461954 | B12 |
| 0.349935656 | B14 | 0.241336195 | B4 | 0.2644993 | B8 | 0.243912411 | B8 |
| 0.414398757 | B7 | 0.241677682 | B8 | 0.419032998 | B16 | 0.342153911 | B20 |
| 0.41738494 | B19 | 0.242711521 | B17 | 0.426324756 | B25 | 0.342212028 | B25 |
| 0.50033904 | B23 | 0.414485803 | B20 | 0.432738399 | B19 | 0.342907479 | B22 |
| 0.500513044 | B16 | 0.416274632 | B13 | 0.501509865 | B23 | 0.346318664 | B13 |
| 0.501015736 | B25 | 0.422019615 | B24 | 0.505008398 | B12 | 0.346642736 | B16 |
| 0.659998225 | B22 | 0.500396692 | B12 | 0.506825384 | B18 | 0.500423791 | B18 |
| 0.661057314 | B18 | 0.502661286 | B18 | 0.511728433 | B7 | 0.501795598 | B24 |
| 0.688589598 | B21 | 0.503899708 | B7 | 0.594284831 | B20 | 0.667389964 | B21 |
| 0.763948195 | B24 | 0.659464916 | B22 | 0.660197068 | B22 | 0.759022559 | B23 |
| 1 | B20 | 0.659802486 | B21 | 1 | B21 | 0.759056766 | B7 |
References
- WHO. Guidelines for Drinking Water Quality, 4th Edition, Incorporating the 1st Addendum 2017. Available online: https://www.who.int/water_sanitation_health/publications/drinking-water-quality-guidelines-4-including-1st-addendum/en/ (accessed on 4 November 2019).
- ISO 5667-5:2006. Water Quality-Sampling-Part 5: Guidance on Sampling of Drinking Water from Treatment Works and Piped Distribution Systems. Available online: https://www.iso.org/obp/ui/#iso:std:iso:5667:-5:ed-2:v1:en (accessed on 22 November 2019).
- Deng, W.; Wang, G. A novel water quality data analysis framework based on time-series data mining. J. Environ. 2017, 196, 365–375. [Google Scholar] [CrossRef] [PubMed]
- Bos, R.; Alves, D.; Latorre, C.; Macleod, N.; Payen, G.; Roaf, V.; Rouse, M. Manual on the Human Rights to Safe Drinking Water and Sanitation for Practitioners; IWA Publishing: London, UK, 2016. [Google Scholar]
- McClymont, K.; Keedwell, E.; Savic, D. An analysis of the interface between evolutionary algorithm operators and problem features for water resources problems. A case study in water distribution network design. Environ. Model. Softw. 2015, 69, 414–424. [Google Scholar] [CrossRef]
- Izquierdo, J.; Montalvo, I.; Pérez-García, R.; Matías, A. On the Complexities of the Design of Water Distribution Networks. Math. Probl. Eng. 2011, 2012, 1–25. [Google Scholar] [CrossRef]
- Fox, S.; Shepherd, W.; Collins, R.; Boxall, J. Experimental Quantification of Contaminant Ingress into a Buried Leaking Pipe during Transient Events. J. Hydraul. Eng. 2016, 142, 04015036. [Google Scholar] [CrossRef]
- Mounce, S.; Mounce, R.; Boxall, J. Novelty detection for time series data analysis in water distribution systems using support vector machines. J. Hydroinform. 2011, 13, 672–686. [Google Scholar] [CrossRef]
- Vališ, D.; Hasilová, K.; Forbelská, M.; Vintr, Z. Reliability modelling and analysis of water distribution network based on backpropagation recursive processes with real field data. Measurement 2020, 149, 107026. [Google Scholar] [CrossRef]
- Liu, G.; Bakker, G.L.; Li, S.; Vreeburg, J.H.G.; Verberk, J.Q.J.C.; Medema, G.J.; Liu, W.T.; Van Dijk, J.C. Pyrosequencing reveals bacterial communities in unchlorinated drinking water distribution system: An integral study of bulk water, suspended solids, loose deposits, and pipe wall biofilm. Environ. Sci. Technol. 2014, 48, 5467–5476. [Google Scholar] [CrossRef]
- Donlan, R.M.; Costerton, J.W. Biofilms: Survival mechanisms of clinically relevant microorganisms. Clin. Microbiol. Rev. 2002, 15, 167–193. [Google Scholar] [CrossRef]
- Douterelo, I.; Husband, S.; Loza, V.; Boxall, J. Dynamics of Biofilm Regrowth in Drinking Water Distribution Systems. Appl. Environ. Microbiol. 2016, 82, 4155–4168. [Google Scholar] [CrossRef]
- Wang, H.; Hu, C.; Hu, X.; Yang, M.; Qu, J. Effects of disinfectant and biofilm on the corrosion of cast iron pipes in a reclaimed water distribution system. Water Res. 2012, 46, 1070–1078. [Google Scholar] [CrossRef]
- Husband, S.; Fish, K.E.; Douterelo, I.; Boxall, J.B. Linking discolouration modelling and biofilm behaviour within drinking water distribution systems. Water Sci. Technol. Water Supply 2016, 16, 942–950. [Google Scholar] [CrossRef]
- Wingender, J.; Flemming, H.C. Biofilms in drinking water and their role as reservoir for pathogens. Int. J. Hyg. Environ. Health 2011, 214, 417–423. [Google Scholar] [CrossRef]
- Douterelo, I.; Boxall, J.B.; Deines, P.; Sekar, R.; Fish, K.E.; Biggs, C.A. Methodological approaches for studying the microbial ecology of drinking water distribution systems. Water Res. 2014, 65, 134–156. [Google Scholar] [CrossRef]
- Prakash, B.; Veeregowda, B.M.; Krishnappa, G. Biofilms: A survival strategy of bacteria. Curr. Sci. 2003, 85, 1299–1307. [Google Scholar]
- Douterelo, I.; Sharpe, R.L.; Boxall, J.B. Influence of hydraulic regimes on bacterial community structure and composition in an experimental drinking water distribution system. Water Res. 2013, 47, 503–516. [Google Scholar] [CrossRef] [PubMed]
- European Commission. Council Directive 98/83/EC on the quality of water intended for human consumption. Off. J. Eur. Commun. 1998, 41, 32–54. [Google Scholar]
- Harwani, D. The Great Plate Count Anomaly and the Unculturable Bacteria. Int. J. Sci. 2012, 2, 350–351. [Google Scholar] [CrossRef]
- Ikonen, J.; Pitkänen, T.; Kosse, P.; Ciszek, R.; Kolehmainen, M.; Miettinen, I.T. On-line detection of Escherichia coli intrusion in a pilot-scale drinking water distribution system. J. Environ. Manag. 2017, 198, 384–392. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Q.; Zhang, J.; Dong, J.; Yan, H.; Chen, C.; Feng, R. Characterization and source identification of tetracycline antibiotics in the drinking water sources of the lower Yangtze River. J. Environ. Manag. 2019, 244, 13–22. [Google Scholar] [CrossRef]
- Yu, J.; Kim, D.; Lee, T. Microbial diversity in biofilms on water distribution pipes of different materials. Water Sci. Technol. 2010, 61, 163–171. [Google Scholar] [CrossRef]
- Rogers, J.W.; Louis, G.E. Risk and opportunity in upgrading the US drinking water infrastructure system. J. Environ. Manag. 2008, 87, 26–36. [Google Scholar] [CrossRef] [PubMed]
- Henriques, J.J.; Louis, G.E. A decision model for selecting sustainable drinking water supply and greywater reuse systems for developing communities with a case study in Cimahi, Indonesia. J. Environ. Manag. 2011, 92, 214–222. [Google Scholar] [CrossRef] [PubMed]
- Ramos-Martínez, E.; Herrera, M.; Gutiérrez-Pérez, J.; Izquierdo, J.; Pérez-García, R. Rehabilitation actions in water supply systems: Effects on biofilm susceptibility. Procedia Eng. 2014, 89, 225–231. [Google Scholar] [CrossRef]
- Ramos-Martínez, E.; Herrera, M.; Izquierdo, J.; Pérez-García, R. Multi-Agent Approach to Biofilm Development in Water Supply Systems. In Proceedings of the Atiner’s Conference Paper Series; Athens Institute for Education and Research: Athina, Greece, 2015; Volume 1693, pp. 3–9. [Google Scholar]
- Ramos-Martínez, E.; Herrera, M.; Izquierdo, J.; Pérez-García, R. A multi-disciplinary procedure to ascertain biofilm formation in drinking water pipes. In Proceedings of the 8th International Congress on Environmental Modelling and Software, Toulouse, France, 10–14 July 2016; Volume 3, pp. 619–626. [Google Scholar]
- Fontela, E.; Gabus, A. DEMATEL, Innovative Methods, Technical Report no. 2, Structural Analysis of the World Problematique; Battelle Geneva Research Institute: Geneva, Switzerland, 1974. [Google Scholar]
- Fontela, E.; Gabus, A. The DEMATEL Observe; Battelle Institute, Geneva Research Center: Geneva, Switzerland, 1976. [Google Scholar]
- Dalvi-Esfahani, M.; Niknafs, A.; Kuss, D.J.; Nilashi, M.; Afrough, S. Social media addiction: Applying the DEMATEL approach. Telemat. Inform. 2019, 43, 101250. [Google Scholar] [CrossRef]
- Si, S.-L.; You, X.-Y.; Liu, H.-C.; Zhang, P. Dematel Technique: A Systematic Review of the State-of-the-Art Literature on Methodologies and Applications. Math. Probl. Eng. 2018, 2018, 3696457. [Google Scholar] [CrossRef]
- Chen, C. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Set. Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer: New York, NY, USA, 1981. [Google Scholar]
- Gul, M.; Ak, M.F. A comparative outline for quantifying risk ratings in occupational health and safety risk assessment. J. Clean. Prod. 2018, 196, 653–664. [Google Scholar] [CrossRef]
- Carpitella, S.; Certa, A.; Izquierdo, J.; La Fata, C.M. A combined multi-criteria approach to support FMECA analyses: A real-world case. Reliab. Eng. Syst. Safe 2018, 169, 394–402. [Google Scholar] [CrossRef]
- Palczewski, K.; Sałabun, W. The fuzzy TOPSIS applications in the last decade. Procedia Comput. Sci. 2019, 159, 2294–2303. [Google Scholar] [CrossRef]
- Sarkar, S.; Pratihar, D.K.; Sarkar, B. An integrated fuzzy multiple criteria supplier selection approach and its application in a welding company. J. Manuf. Syst. 2018, 46, 163–178. [Google Scholar] [CrossRef]
- Dinçer, H.; Yüksel, S.; Martínez, L. Interval type 2-based hybrid fuzzy evaluation of financial services in E7 economies with DEMATEL-ANP and MOORA methods. Appl. Soft Comput. 2019, 79, 186–202. [Google Scholar] [CrossRef]
- Chen, J.-K.; Chen, I.-S. Using a novel conjunctive MCDM approach based on DEMATEL, fuzzy ANP, and TOPSIS as an innovation support system for Taiwanese higher education. Expert Syst. Appl. 2010, 37, 1981–1990. [Google Scholar] [CrossRef]
- Nilashi, M.; Samad, S.; Manaf, A.A.; Ahmadi, H.; Rashid, T.A.; Munshi, A.; Almukadi, W.; Ibrahim, O.; Ahmed, O.H. Factors influencing medical tourism adoption in Malaysia: A DEMATEL-Fuzzy TOPSIS approach. Comput. Ind. Eng. 2019, 137, 106005. [Google Scholar] [CrossRef]
- Li, G.; Ma, X.; Chen, R.; Yu, Y.; Tao, H.; Shi, B. Field studies of manganese deposition and release in drinking water distribution systems: Insight into deposit control. Water Res. 2019, 163, 114897. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Wang, H.; Li, X.; Hu, C.; Yang, M.; Qu, J. Characterization of biofilm and corrosion of cast iron pipes in drinking water distribution system with UV/Cl2 disinfection. Water Res. 2014, 60, 174–181. [Google Scholar] [CrossRef]
- Chiu, Y.J.; Chen, H.C.; Tzeng, G.H.; Shyu, J.Z. Marketing strategy based on customer behavior for the LCD-TV. Int. J. Manag. Decis. Mak. 2006, 7, 143–165. [Google Scholar]
- Du, Y.-W.; Zhou, W. New improved DEMATEL method based on both subjective experience and objective data. Eng. Appl. Artif. Intell. 2019, 83, 57–71. [Google Scholar] [CrossRef]
- Carpitella, S.; Carpitella, F.; Certa, A.; Benítez, J.; Izquierdo, J. Managing human factors to reduce organisational risk in industry. Math. Comput. Appl. 2018, 23, 67. [Google Scholar] [CrossRef]
- Meyer, C. Matrix Analysis and Applied Linear Algebra; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Gerami Seresht, N.; Fayek, A.R. Computational method for fuzzy arithmetic operations on triangular fuzzy numbers by extension principle. Int. J. Approx. Reason. 2019, 106, 172–193. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Prokopowicz, P. The use of Ordered Fuzzy Numbers for modelling changes in dynamic processes. Inf. Sci. 2019, 470, 1–14. [Google Scholar] [CrossRef]
- Okunuki, S.; Kawaharasaki, M.; Tanaka, H.; Kanagawa, T. Changes in phosphorus removing performance and bacterial community structure in an enhanced biological phosphorus removal reactor. Water Res. 2004, 38, 2433–2439. [Google Scholar] [CrossRef] [PubMed]
- Rofner, C.; Sommaruga, R.; Pérez, M.T. Phosphate and ATP uptake by lake bacteria: Does taxonomical identity matter? Environ. Microbiol. 2016, 18, 4782–4793. [Google Scholar] [CrossRef] [PubMed]
- Ferro, P.; Vaz-Moreira, I.; Manaia, C.M. Betaproteobacteria are predominant in drinking water: Are there reasons for concern? Crit. Rev. Microbiol. 2019, 45, 649–667. [Google Scholar] [CrossRef]
- Ertekin, E.; Hatt, J.K.; Konstantinidis, K.T.; Tezel, U. Similar microbial consortia and genes are involved in the biodegradation of benzalkonium chlorides in different environments. Environ. Sci. Technol. 2016, 50, 4304–4313. [Google Scholar] [CrossRef]

| Water Quality Parameter | Bacterial Class | ||||
|---|---|---|---|---|---|
| P1 | Richness | B1 | Alphaproteobacteria | B14 | Clostridia |
| P2 | Diversity | B2 | Betaproteobacteria | B15 | Planctomycetia |
| P3 | Turbidity | B3 | Gammaproteobacteri | B16 | Spirochaetia |
| P4 | Total organic carbon | B4 | Deltaproteobacteria | B17 | Sphingobacteriia |
| P5 | Temperature | B5 | Bacilli | B18 | Anaerolineae |
| P6 | pH | B6 | Actinobacteria | B19 | Cytophagia |
| P7 | Chlorine | B7 | Mollicutes | B20 | Holophagae |
| P8 | Aluminium | B8 | Flavobacteriia | B21 | Spirochaetes |
| P9 | Iron | B9 | Bacteroidia | B22 | Chloroflexi |
| P10 | Manganese | B10 | Cyanobacteria | B23 | Firmicutes |
| P11 | Nitrate | B11 | Acidobacteria | B24 | Gemmatimonadetes |
| P12 | Phosphate | B12 | Bacteroidete | B25 | Verrucomicrobia |
| P13 | Sulphate | B13 | Planctomycetes | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carpitella, S.; Del Olmo, G.; Izquierdo, J.; Husband, S.; Boxall, J.; Douterelo, I. Decision-Making Tools to Manage the Microbiology of Drinking Water Distribution Systems. Water 2020, 12, 1247. https://doi.org/10.3390/w12051247
Carpitella S, Del Olmo G, Izquierdo J, Husband S, Boxall J, Douterelo I. Decision-Making Tools to Manage the Microbiology of Drinking Water Distribution Systems. Water. 2020; 12(5):1247. https://doi.org/10.3390/w12051247
Chicago/Turabian StyleCarpitella, Silvia, Gonzalo Del Olmo, Joaquín Izquierdo, Stewart Husband, Joby Boxall, and Isabel Douterelo. 2020. "Decision-Making Tools to Manage the Microbiology of Drinking Water Distribution Systems" Water 12, no. 5: 1247. https://doi.org/10.3390/w12051247
APA StyleCarpitella, S., Del Olmo, G., Izquierdo, J., Husband, S., Boxall, J., & Douterelo, I. (2020). Decision-Making Tools to Manage the Microbiology of Drinking Water Distribution Systems. Water, 12(5), 1247. https://doi.org/10.3390/w12051247







