Web-Based Tool for the Development of Intensity Duration Frequency Curves under Changing Climate at Gauged and Ungauged Locations
Abstract
1. Introduction
2. Methodology
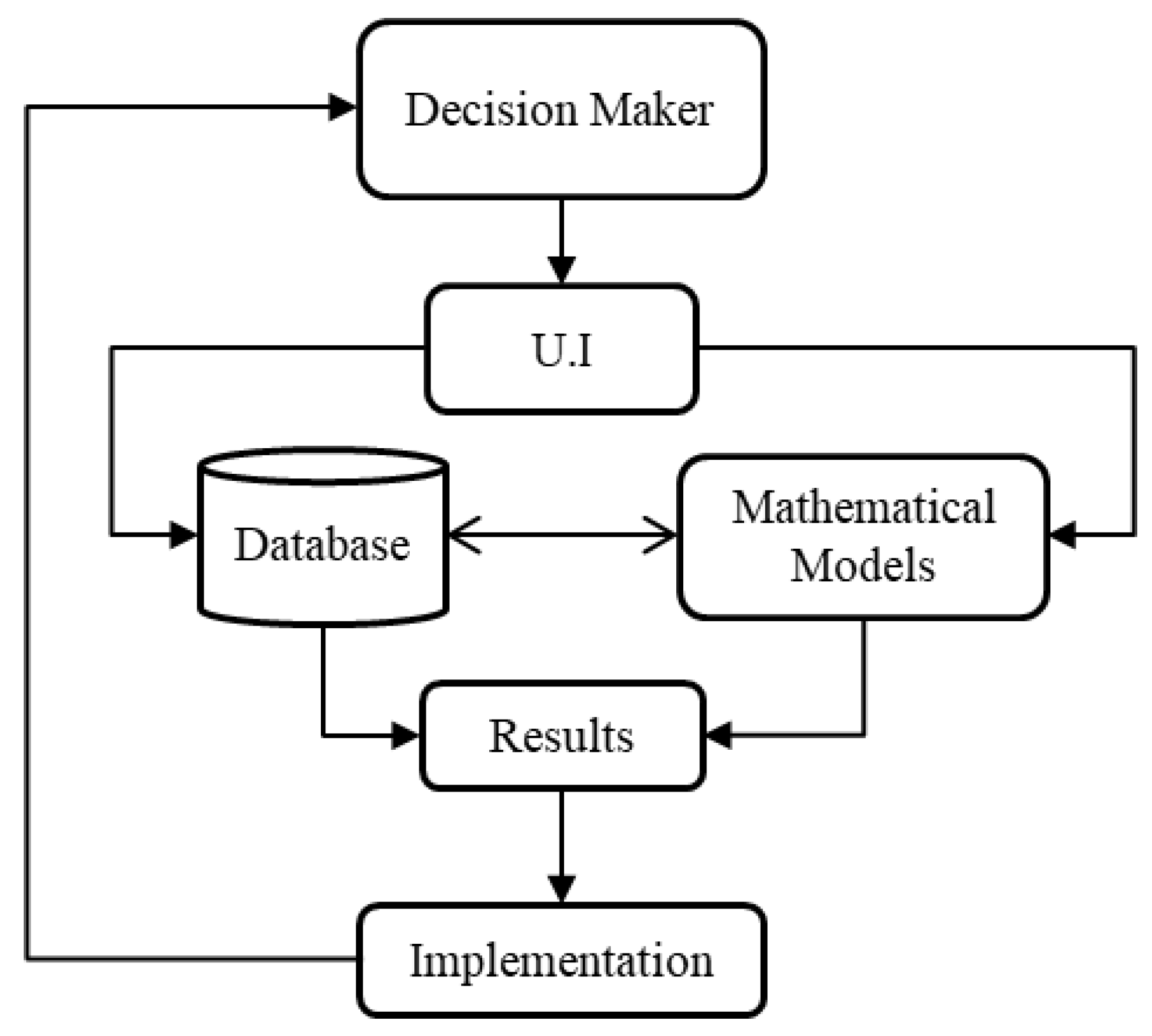
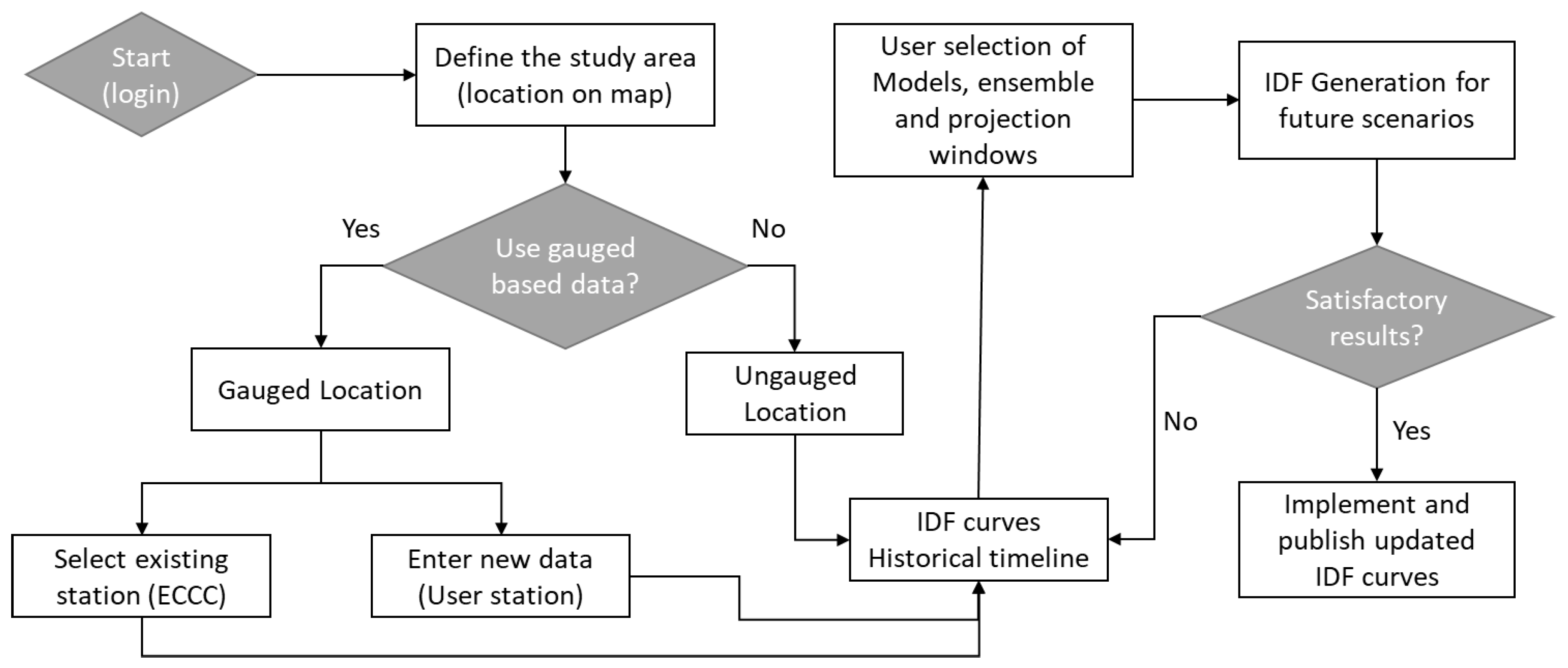
2.1. IDF_CC Tool
- Implementation of the General Extreme Value (GEV) distribution with the L-moments methods (described in Section 2.2).
- Introduction of the module for development of IDF curves for ungauged locations (described in Section 2.3).
- Update of the database with the stations from the Environment and Climate Change Canada (ECCC) IDF engineering dataset [31].
- Update of the climate models data base with second version of bias corrected climate models from the Pacific Climate Impacts Consortium [32].
2.2. Statistical Distributions
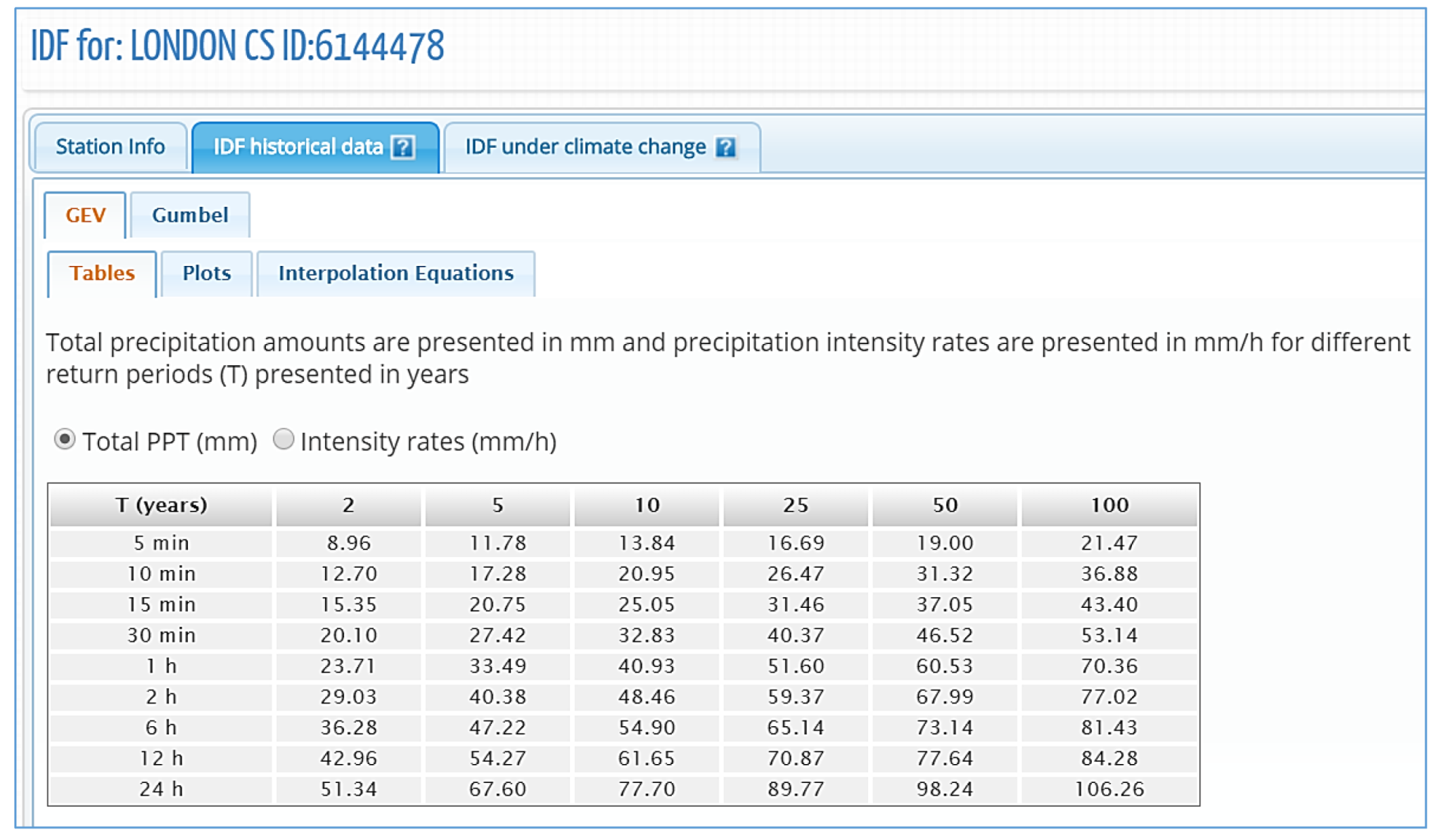
2.2.1. Gumbel Distributions
2.2.2. GEV Distribution
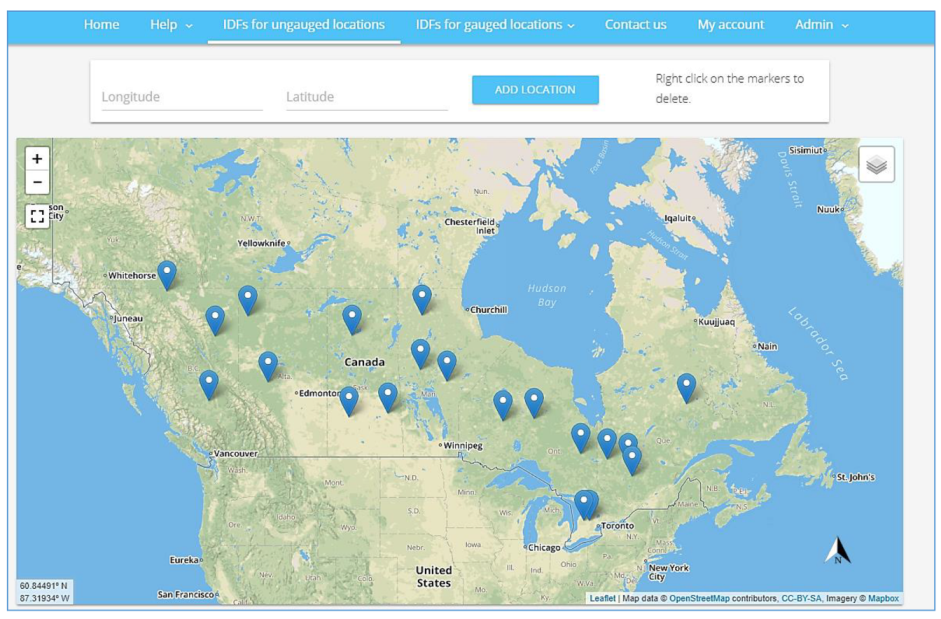
2.3. IDF Curves for Ungauged Locations
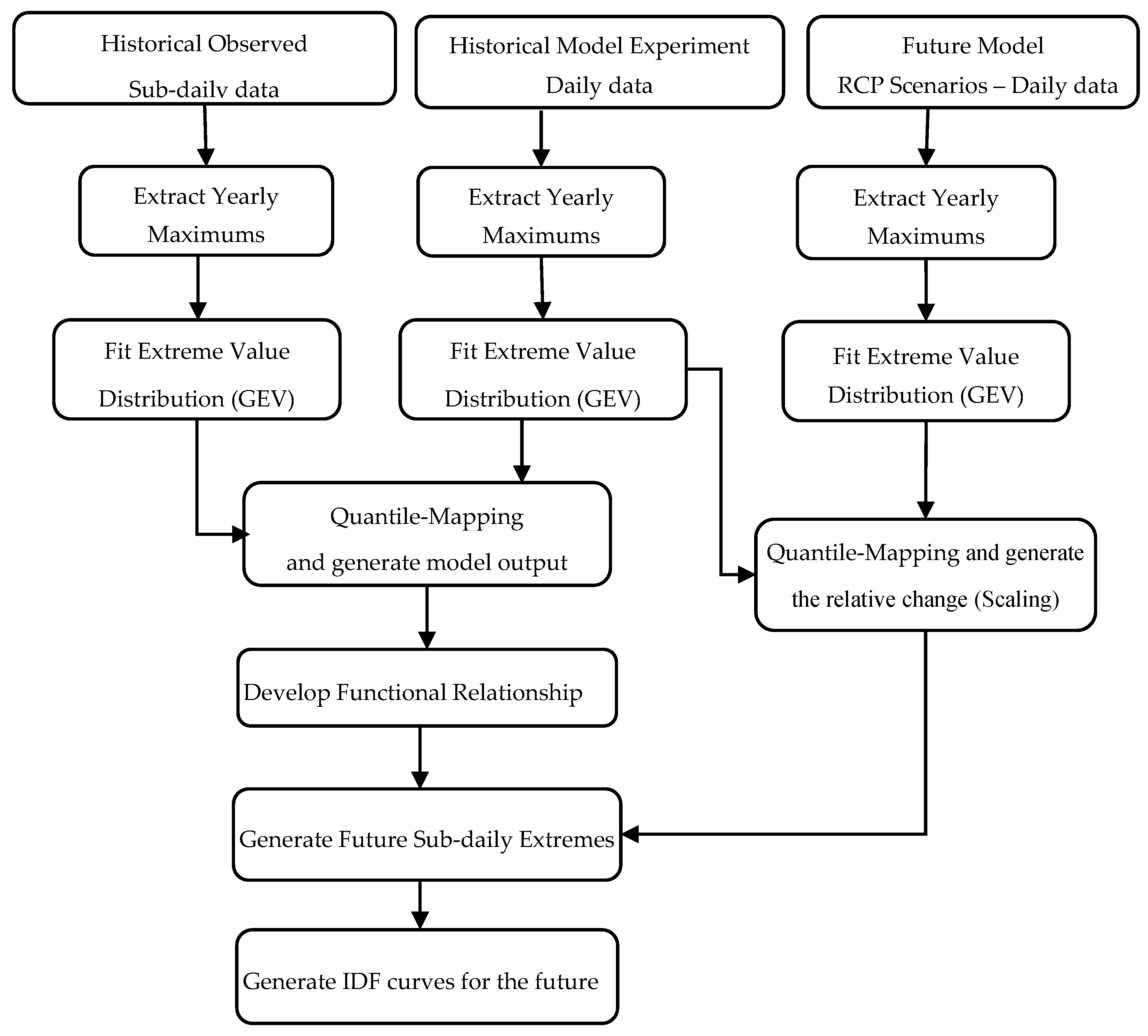
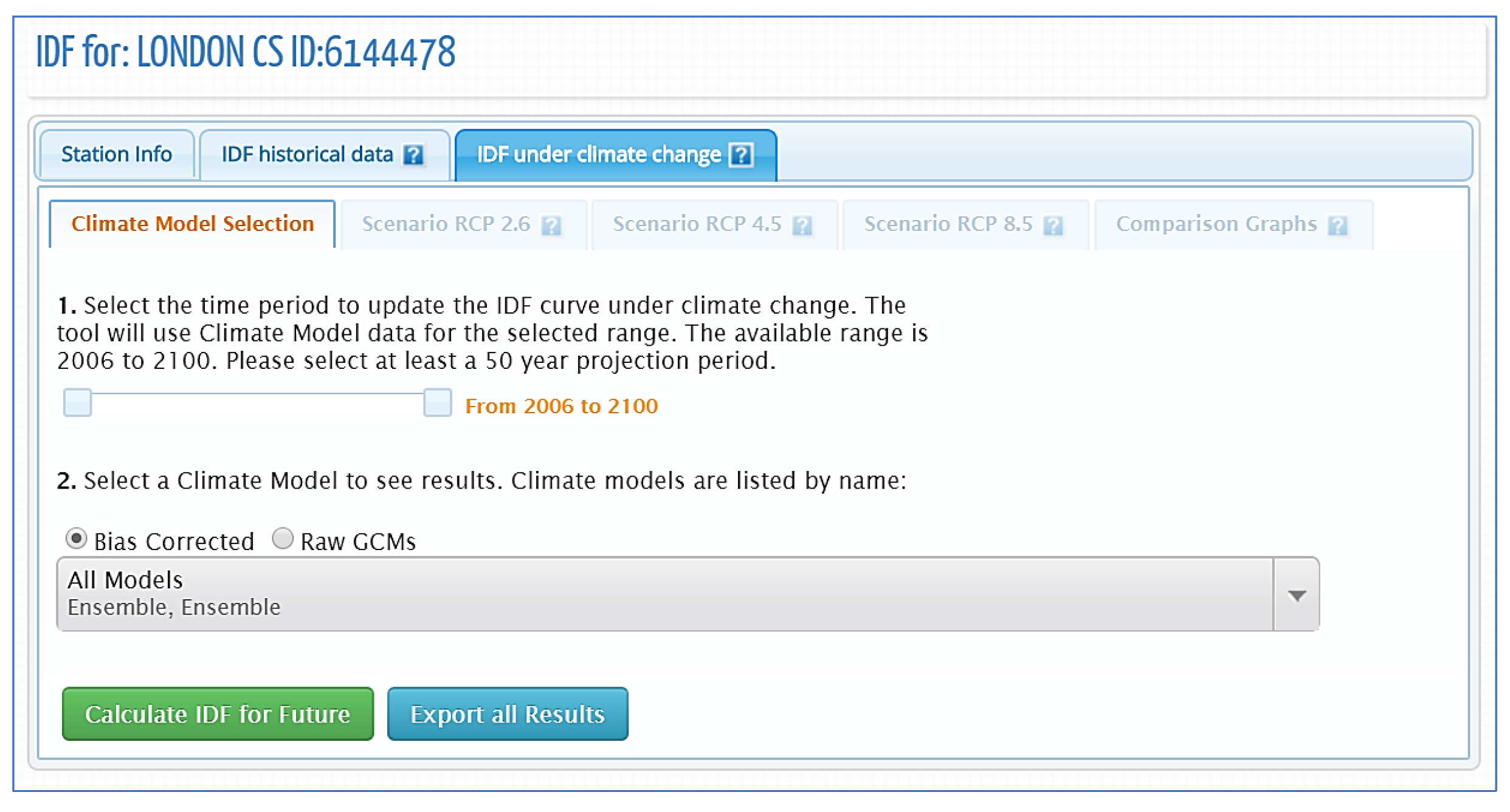
2.4. IDF Curves under Changing Climate
2.4.1. Equidistant Quantile Matching Method with GEV
- 1.
- Extract sub-daily maximums from the observed data at a given location (i.e., maximums of 5, 10, 15 min, 1, 2, 6, 12, 24 h precipitation data).
- 2.
- Extract daily maximums for the historical baseline period from the selected GCMs, .
- 3.
- Fit the GEV probability distribution to maxima series extracted in (i) for each sub-daily duration, , and for the GCM series from step (ii), .
- 4.
- Based on sampling technique proposed by [22], generate random numbers for non-exceedance probability in the [0, 1] range. The quantiles extracted from the GEV fitted to each pair and are equated to establish a statistical relationship in the following form:where corresponds to the AMP quantiles at the station scale and , are the adjusted coefficients of the equation for each sub-daily duration j. A Differential Evolution (DE) optimization algorithm is used to fit the coefficients .
- 5.
- Extract daily maximums from the RCP Scenarios used in the IDF_CC tool (i.e., RCP 2.6, RCP 4.5, RCP 8.5) for the selected GCM model, .
- 6.
- Fit the GEV probability distribution to the daily maximums from the GCM model for each of the future scenarios .
- 7.
- For each projected future precipitation series , calculate the non-exceedance probability from the fitted GEV . Find the corresponding quantile ( at the GCM historical baseline by entering the value of in the inverse CDF . This is a scaling step introduced to incorporate the future projections in the updated IDF and uses the concepts of quantile delta mapping [54,56]. The relative change , is calculated using Equation (20):
- 8.
- To generate the projected future maximum sub-daily series at the station scale (, use (17) by replacing to and multiplying by the relative change from Equation (20).
- 9.
- Generate IDF curves for the future sub-daily data and compare the same with the historically observed IDF curves to observe the change in intensities.
2.4.2. Spatial Interpolation of GCM Data
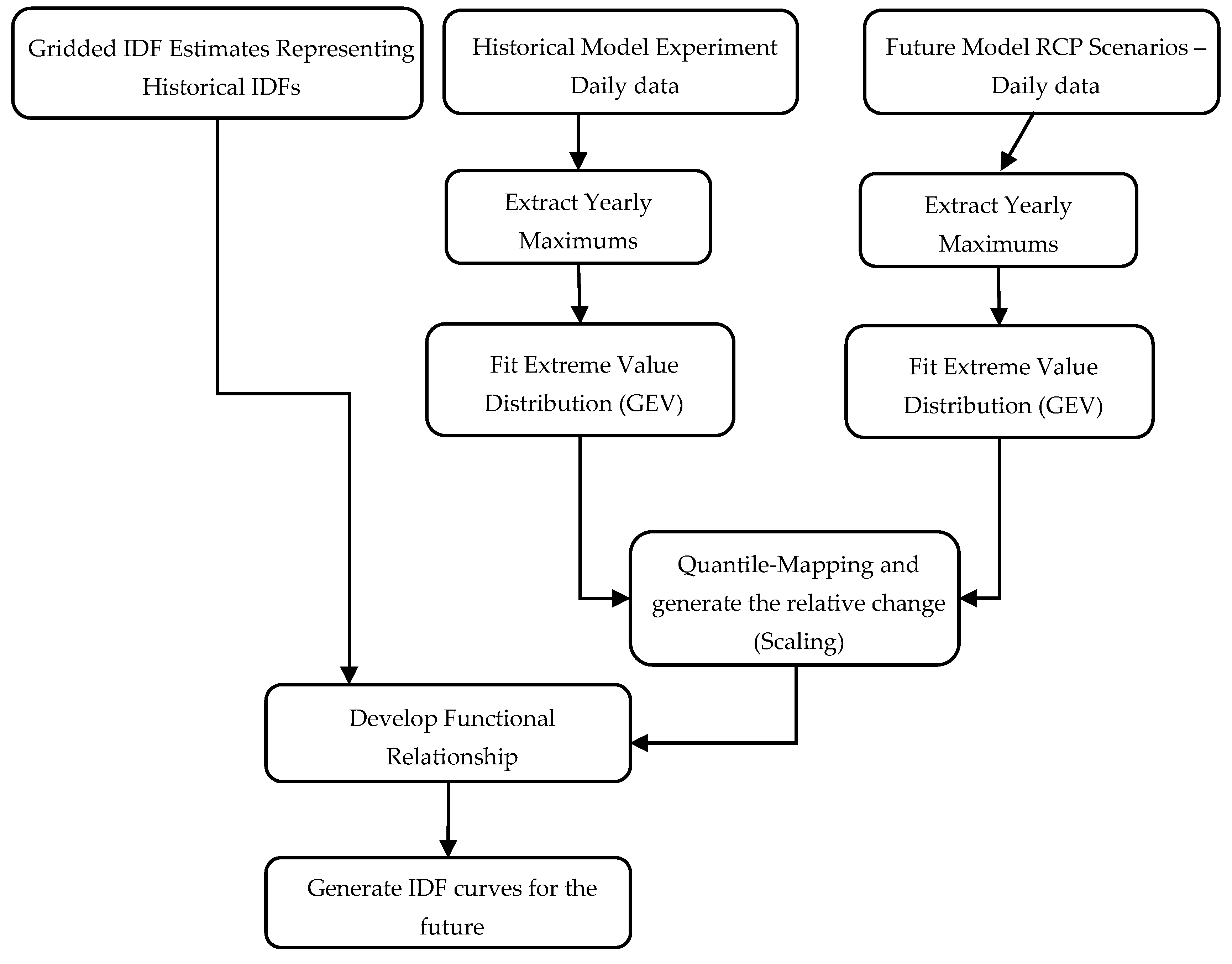
2.5. Updating IDFs for Ungauged Locations
- 10.
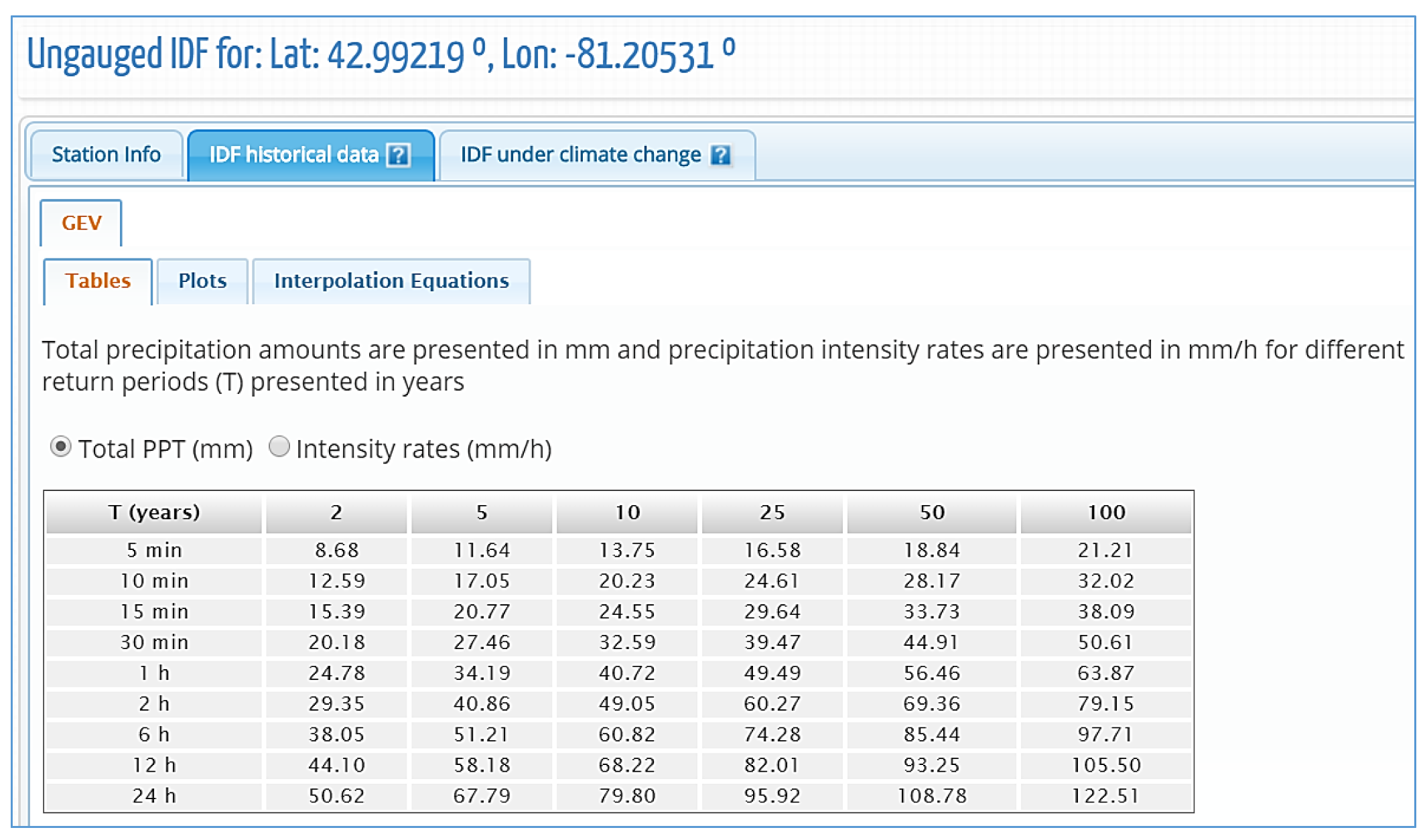
- Extract the IDF curves, representing the historical IDF, from the gridded dataset for all durations (5 min, 10 min, 15 min, 1 h, 2 h, 6 h, 12 h, 24 h) and all return periods (2, 5, 10, 25, 50 and 100 years) at the selected location.
- 11.
- Extract daily maximums for the historical baseline period from the selected GCMs, .
- 12.
- Fit the GEV probability distribution to maxima series extracted for the GCM series in (ii), .
- 13.
- Extract daily maximums from the RCP Scenarios (i.e., RCP 2.6, RCP 4.5, RCP 8.5) for the selected GCM model, .
- 14.
- Fit the GEV probability distribution to the daily maximums from the GCM model for each of the future scenarios .
- 15.
- For each projected future precipitation series, calculate the quantiles () using the non-exceedance probability () for each T (2, 5, 10, 25, 50 and 100 years) from the inverse CDF of the fitted GEV, . Similarly, calculate the quantiles () at the GCM historical baseline by entering the value of the non-exceedance probability for each T in the inverse CDF . This is a scaling step introduced to incorporate the future projections in the updated IDF and mimics the concepts of quantile delta mapping [54,56]. The relative change is calculated using (25), for each T 2, 5, 10, 25, 50 and 100 years.
- 16.
- To generate the projected future IDF curves for each duration and T, at the selected location, use and multiple by the relative change from (25).
2.6. Statistically Downscaled Global Climate Models
3. IDF_CC Tool Implementation
3.1. IDF_CC Tool Components
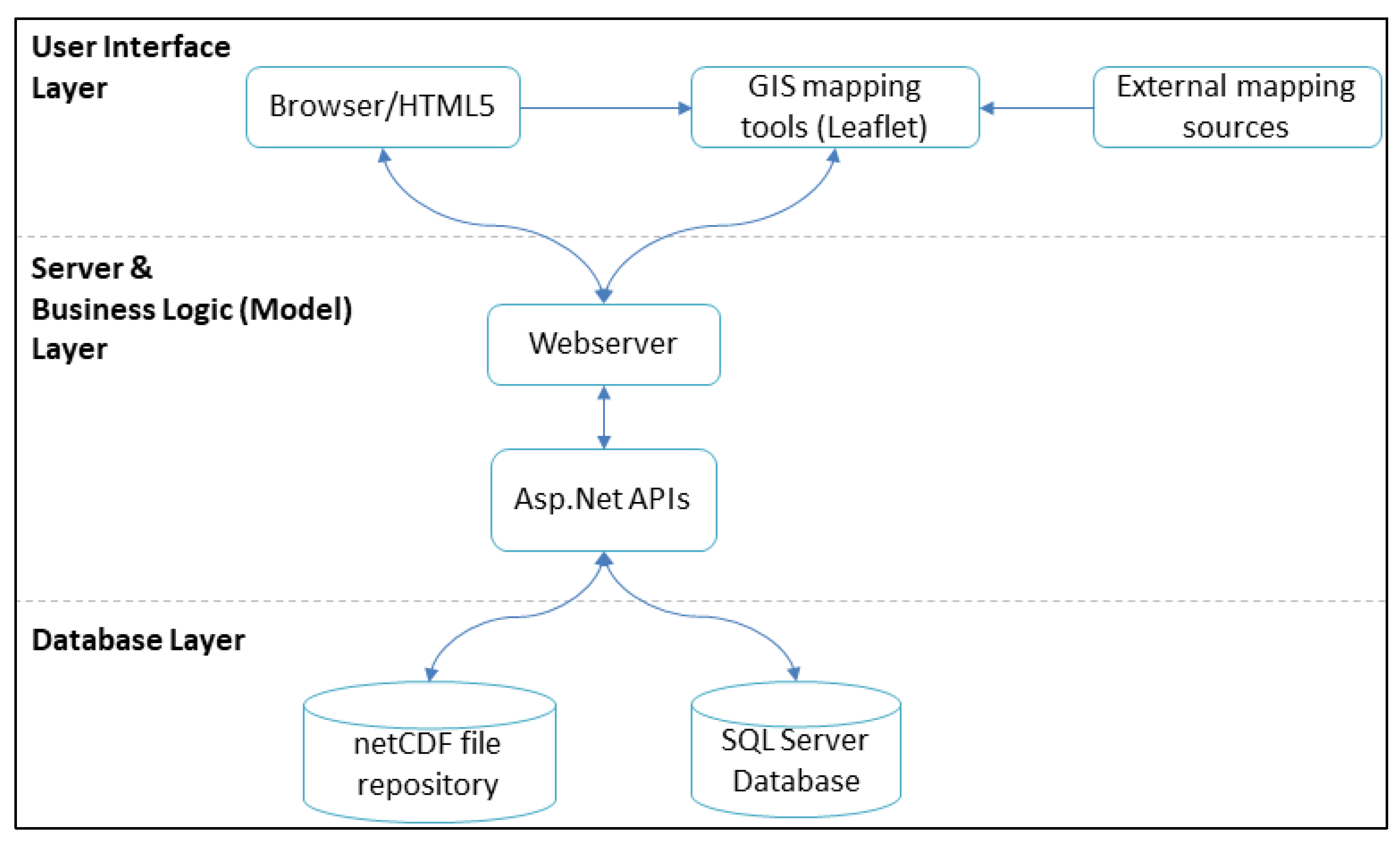
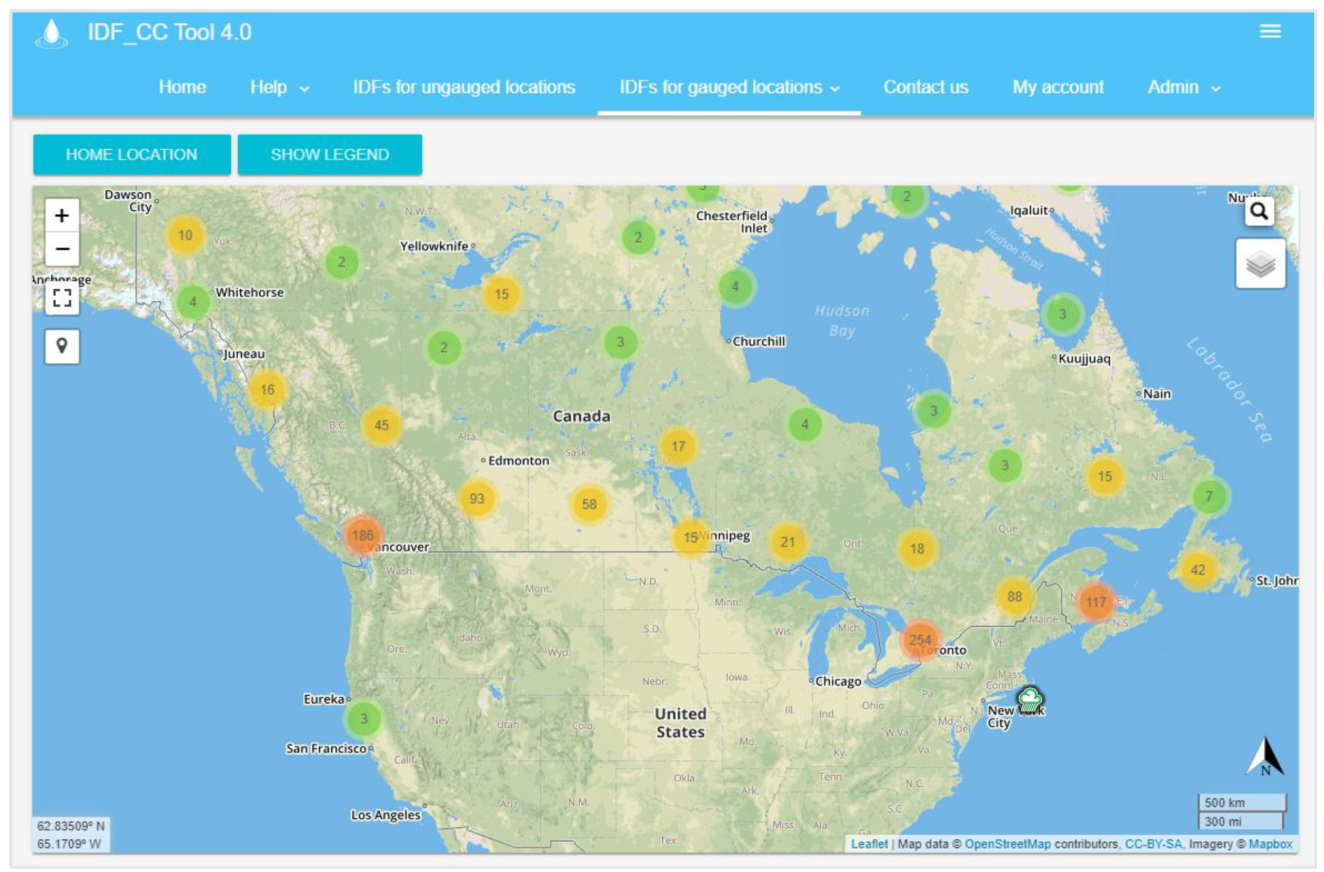
3.2. User Interface
3.3. Model Base
- Statistical analysis algorithm is applied to fit the selected theoretical distribution to both historical (Gumbel and GEV) and future precipitation data (GEV) using the method of moments to estimate the parameters of the Gumbel distribution and L-moments method for the GEV.
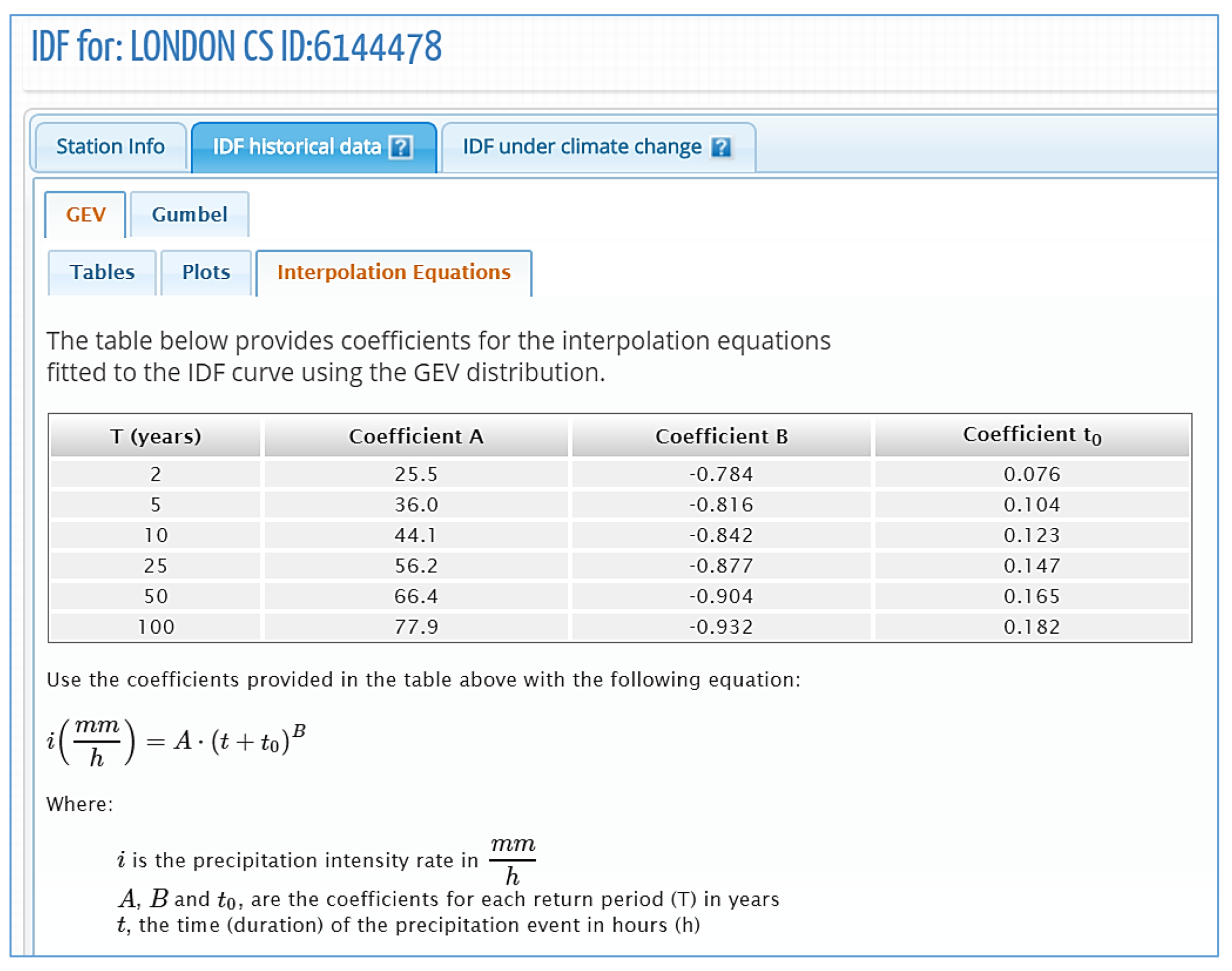
- An optimization algorithm using a differential evolution (DE) optimization algorithm introduced by [67] is used on the equidistant quantile matching. The DE algorithm is used to find the coefficients of the equation to establish a statistical relationship between historical observed data and the model’s baseline, as described in Section 2.4.1. The optimization algorithm is also used to fit the analytical relationships in the IDF curves. For each return period (T), an equation is fitted by finding the coefficients of the IDF equation through minimization of the sum of the root square errors between the IDF curve and equation calculated values.
- The updated equidistant quantile matching (EQM) algorithm is applied to the IDF curve updating procedure. This algorithm combines historical precipitation data with data from the climate data to develop the IDF for future periods (Section 2.4.1).
3.4. Database
- Repository of ECCC IDF curves dataset: the IDF_CC tool’s database stores the latest records from the hydro-meteorological station information available from ECCC stations across the country. There are approximately 700 stations throughout the country. Only publicly available data from the ECCC stations are stored in the tool’s database, including station name, location, coordinates, station ID, sub-daily AMP records and daily precipitation data.
- Dataset of gridded IDF curves for the ungauged location module. The dataset is stored in the database of the IDF_CC tool as another physical table in the database associating the coordinates with the estimates of the IDF using the methodology described in Section 2.3.
- Climate projections in the form of Global Climate Models (GCM) output files are converted from the netCDF format to an MSSQL database structure created for the IDF_CC tool that is more efficient for use with the tool’s algorithms. The GCM data is available in a gridded format. For each grid point, precipitation series are available. These points cover the globe and are represented by a pair of coordinates (longitude and latitude). The database structure was created in order to allow the grid points to be stored with geographic information and the associated series in tabular form. The selection of the grid points from the GCMs and associated series is made with the use of nearest neighbor query available in MSSQL, which adds to the tool’s IDF updating procedure efficiency.
- Some user information is required to access the IDF_CC tool’s functionalities, and the user must create an account and provide data that are stored in the database, including their name, email, institution/municipality, the intent of use and password.
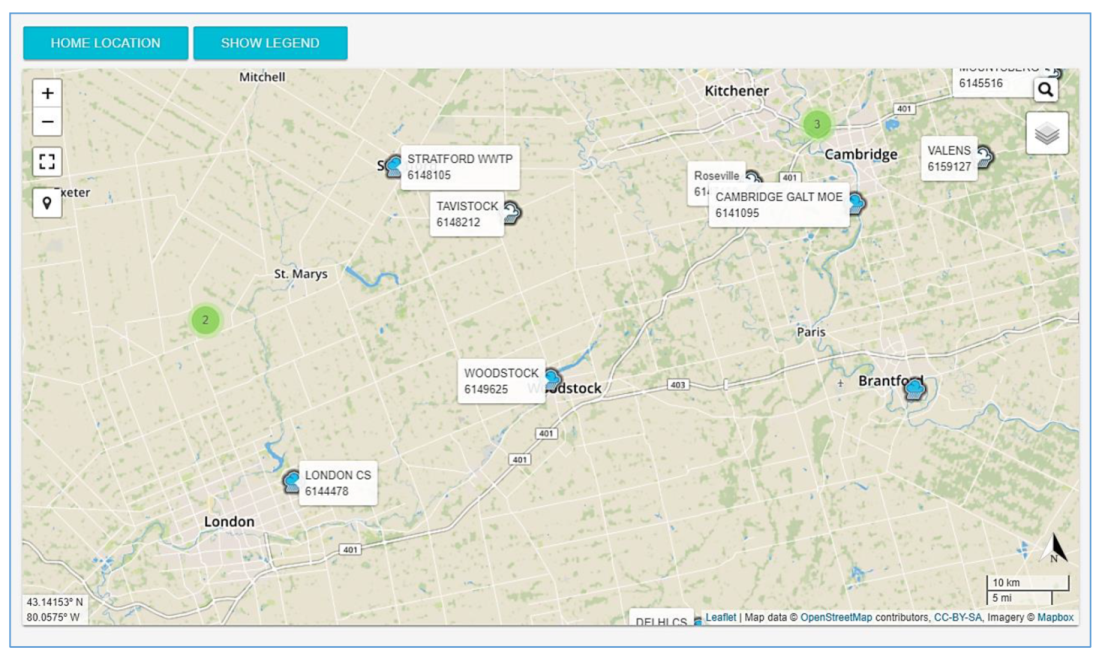
- User-provided stations and data: any registered user of IDF_CC can create stations and provide data for them. The type of data and input options are discussed in Section 4 of the paper. User-created stations can be shared among other users registered with the IDF_CC tool. Stations created by users will contain the same basic data as EC stations, including name, ID, coordinates and location. The coordinates will allow the tool to plot the station on the map with different colors for easier identification. Users are allowed to provide data for their station by including pre-processed sub-daily annual maximum precipitation (AMP) series or raw for-the-day-maximums series. The tool can identify the type of data provided and process the IDF curves calculation accordingly. There are several sub-daily durations that the user can choose from 5, 10, 15, 20 and 30 min, 1, 2, 3, 6, 12, 18 and 24 h.
- Users can upload files that are related to a specific station. The files are also stored in the database and can be either text documents, spreadsheets and/or pdf files.
3.5. IDF_CC Tool—Technical Implementation Details
4. Use of IDF_CC Tool and Results
4.1. IDF Curves for Gauged Locations
4.2. IDF Curves for the Ungauged Locations
4.3. Use of IDF_CC Tool for Developing IDF Curves for Future Conditions
4.4. Sensitivity Analysis and Comparison of Results
4.5. Discussion of Uncertainty
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. List of Bias Corrected and Raw Models
| Country | Centre Acronym | Model | Centre Name | Original (Longitude vs. Latitude) | Bias corrected (Longitude vs. Latitude) |
|---|---|---|---|---|---|
| China | BCC | bcc_csm1_1 | Beijing Climate Center, China Meteorological Administration | 2.8 × 2.8 | 0.0833 × 0.0833 |
| China | BCC | bcc_csm1_1 m | Beijing Climate Center, China Meteorological Administration | ||
| China | BNU | BNU-ESM | College of Global Change and Earth System Science | 2.8 × 2.8 | |
| Canada | CCCma | CanESM2 | Canadian Centre for Climate Modeling and Analysis | 2.8 × 2.8 | |
| USA | CCSM | CCSM4 | National Center of Atmospheric Research | 1.25 × 0.94 | |
| France | CNRM | CNRM-CM5 | Centre National de Recherches Meteorologiques and Centre Europeen de Recherches et de Formation Avancee en Calcul Scientifique | 1.4 × 1.4 | |
| Australia | CSIRO3.6 | CSIRO-Mk3-6-0 | Australian Commonwealth Scientific and Industrial Research Organization in collaboration with the Queensland Climate Change Centre of Excellence | 1.8 × 1.8 | |
| USA | CESM | CESM1-CAM5 | National Center of Atmospheric Research | 1.25 × 0.94 | |
| China | LASG-CESS | FGOALS_g2 | IAP (Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing, China) and THU (Tsinghua University) | 2.55 × 2.48 | |
| USA | NOAA GFDL | GFDL-CM3 | National Oceanic and Atmospheric Administration’s Geophysical Fluid Dynamic Laboratory | 2.5 × 2.0 | |
| USA | NOAA GFDL | GFDL-ESM2G | National Oceanic and Atmospheric Administration’s Geophysical Fluid Dynamic Laboratory | 2.5 × 2.0 | |
| USA | NOAA GFDL | GFDL-ESM2M | National Oceanic and Atmospheric Administration’s Geophysical Fluid Dynamic Laboratory | 2.5 × 2.0 | |
| United Kingdom | MOHC | HadGEM2-AO | Met Office Hadley Centre | 1.25 × 1.875 | |
| United Kingdom | MOHC | HadGEM2-ES | Met Office Hadley Centre | 1.25 × 1.875 | |
| France | IPSL | IPSL-CM5A-LR | Institut Pierre Simon Laplace | 3.75 × 1.8 | |
| France | IPSL | IPSL-CM5A-MR | Institut Pierre Simon Laplace | 3.75 × 1.8 | |
| Japan | MIROC | MIROC5 | Japan Agency for Marine-Earth Science and Technology | 1.4 × 1.41 | |
| Japan | MIROC | MIROC-ESM | Japan Agency for Marine-Earth Science and Technology | 2.8 × 2.8 | |
| Japan | MIROC | MIROC-ESM-CHEM | Japan Agency for Marine-Earth Science and Technology | 2.8 × 2.8 | |
| Germany | MPI-M | MPI-ESM-LR | Max Planck Institute for Meteorology | 1.88 × 1.87 | |
| Germany | MPI-M | MPI-ESM-MR | Max Planck Institute for Meteorology | 1.88 × 1.87 | |
| Japan | MRI | MRI-CGCM3 | Meteorological Research Institute | 1.1 × 1.1 | |
| Norway | NOR | NorESM1-M | Norwegian Climate Center | 2.5 × 1.9 | |
| Norway | NOR | NorESM1-ME | Norwegian Climate Center | 2.5 × 1.9 |
| Country | Centre Acronym | Model | Centre Name | Number of Ensembles | GCM Resolutions |
|---|---|---|---|---|---|
| (Longitude vs. Latitude) | |||||
| China | BCC | bcc_csm1_1 | Beijing Climate Center, China Meteorological Administration | 1 | 2.8 × 2.8 |
| China | BCC | bcc_csm1_1 m | Beijing Climate Center, China Meteorological Administration | 1 | |
| China | BNU | BNU-ESM | College of Global Change and Earth System Science | 1 | 2.8 × 2.8 |
| Canada | CCCma | CanESM2 | Canadian Centre for Climate Modeling and Analysis | 5 | 2.8 × 2.8 |
| USA | CCSM | CCSM4 | National Center of Atmospheric Research | 1 | 1.25 × 0.94 |
| France | CNRM | CNRM-CM5 | Centre National de Recherches Meteorologiques and Centre Europeen de Recherches et de Formation Avancee en Calcul Scientifique | 1 | 1.4 × 1.4 |
| Australia | CSIRO3.6 | CSIRO-Mk3-6-0 | Australian Commonwealth Scientific and Industrial Research Organization in collaboration with the Queensland Climate Change Centre of Excellence | 10 | 1.8 × 1.8 |
| USA | CESM | CESM1-CAM5 | National Center of Atmospheric Research | 1 | 1.25 × 0.94 |
| E.U. | EC-EARTH | EC-EARTH | EC-EARTH | 1 | 1.125 × 1.125 |
| China | LASG-CESS | FGOALS_g2 | IAP (Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing, China) and THU (Tsinghua University) | 1 | 2.55 × 2.48 |
| USA | NOAA GFDL | GFDL-CM3 | National Oceanic and Atmospheric Administration’s Geophysical Fluid Dynamic Laboratory | 1 | 2.5 × 2.0 |
| USA | NOAA GFDL | GFDL-ESM2G | National Oceanic and Atmospheric Administration’s Geophysical Fluid Dynamic Laboratory | 1 | 2.5 × 2.0 |
| USA | NOAA GFDL | GFDL-ESM2M | National Oceanic and Atmospheric Administration’s Geophysical Fluid Dynamic Laboratory | 2.5 × 2.0 | |
| United Kingdom | MOHC | HadGEM2-AO | Met Office Hadley Centre | 1 | 1.25 × 1.875 |
| United Kingdom | MOHC | HadGEM2-ES | Met Office Hadley Centre | 2 | 1.25 × 1.875 |
| France | IPSL | IPSL-CM5A-LR | Institut Pierre Simon Laplace | 4 | 3.75 × 1.8 |
| France | IPSL | IPSL-CM5A-MR | Institut Pierre Simon Laplace | 4 | 3.75 × 1.8 |
| Japan | MIROC | MIROC5 | Japan Agency for Marine-Earth Science and Technology | 3 | 1.4 × 1.41 |
| Japan | MIROC | MIROC-ESM | Japan Agency for Marine-Earth Science and Technology | 1 | 2.8 × 2.8 |
| Japan | MIROC | MIROC-ESM-CHEM | Japan Agency for Marine-Earth Science and Technology | 1 | 2.8 × 2.8 |
| Germany | MPI-M | MPI-ESM-LR | Max Planck Institute for Meteorology | 3 | 1.88 × 1.87 |
| Germany | MPI-M | MPI-ESM-MR | Max Planck Institute for Meteorology | 3 | 1.88 × 1.87 |
| Japan | MRI | MRI-CGCM3 | Meteorological Research Institute | 1 | 1.1 × 1.1 |
| Norway | NOR | NorESM1-M | Norwegian Climate Center | 3 | 2.5 × 1.9 |
References
- CSA (Canadian Standards Association). Technical Guide: Development, Interpretation, and Use of Rainfall Intensity-Duration-Frequency (IDF) Information: Guideline for Canadian Water Resources Practitioners; Canadian Standards Association: Mississauga, ON, Canada, 2012. [Google Scholar]
- Trenberth, K.E. Changes in precipitation with climate change. Clim. Res. 2011, 47, 1231–1238. [Google Scholar] [CrossRef]
- Warren, F.J.; Lemmen, D.S. (Eds.) Canada in a Changing Climate: Sector Perspectives on Impacts and Adaptation; Government of Canada: Ottawa, ON, Canada, 2014; p. 286.
- Simonovic, S.P.; Schardong, A.; Sandink, D.; Srivastav, R. A Web-based Tool for the Development of Intensity Duration Frequency Curves under Changing Climate. Environ. Model. Softw. J. 2016, 81, 136–153. [Google Scholar] [CrossRef]
- Eum, H.I.; Simonovic, S.P. Assessment on variability of extreme climate events for the Upper Thames River basin in Canada. Hydrol. Process. 2011, 26, 485–499. [Google Scholar] [CrossRef]
- Kao, S.C.; Ganguly, A.R. Intensity, duration, and frequency of precipitation extremes under 21st-century warming scenarios. J. Geophys. Res. 2011, 116, D16119. [Google Scholar] [CrossRef]
- Mladjic, B.; Sushama, L.; Khaliq, M.; Laprise, R.; Caya, D.; Roy, R. Canadian RCM projected changes to extreme precipitation characteristics over Canada. J. Clim. 2011, 24, 2565–2584. [Google Scholar] [CrossRef]
- Mailhot, A.; Kingumbi, A.; Talbot, G.; Poulin, A. Future changes in intensity and seasonal pattern of occurrence of daily and multi-day annual maximum precipitation over Canada. J. Hydrol. 2010, 388, 1731–1785. [Google Scholar] [CrossRef]
- Katz, R.W. Statistics of extremes in climate change. Clim. Chang. 2010, 100, 71–76. [Google Scholar] [CrossRef]
- Cunderlik, J.; Simonovic, S.P. Hydrologic extremes in South-western Ontario under future climate projections. J. Hydrol. Sci. 2005, 50, 631–654. [Google Scholar]
- Forster, P.M.; Andrews, T.; Good, P.; Gregory, J.M.; Jackson, L.S.; Zelinka, M. Evaluating adjusted forcing and model spread for historical and future scenarios in the CMIP5 generation of climate models. J. Geophys. Res. Atmos. 2013, 118. [Google Scholar] [CrossRef]
- Myhre, G.; Forster, P.M.; Samset, B.H.; Hodnebrog, Ø.; Sillmann, J.; Aalbergsjø, S.G.; Andrews, T.; Boucher, O.; Faluvegi, G.; Fläschner, D.; et al. PDRMIP: A Precipitation Driver and Response Model Intercomparison Project—Protocol and preliminary results. Bull. Am. Meteorol. Soc. 2017, 98, 1185–1198. [Google Scholar] [CrossRef]
- Richardson, T.B.; Forster, P.M.; Smith, C.J.; Maycock, A.C.; Wood, T.; Andrews, T.; Boucher, O.; Faluvegi, G.; Fläschner, D.; Hodnebrog, Ø.; et al. Efficacy of Climate Forcings in PDRMIP Models. J. Geophys. Res. Atmos. 2019, 124, 12824–12844. [Google Scholar] [CrossRef] [PubMed]
- Insurance Bureau of Canada. Facts of the Property and Casualty Insurance Industry in Canada; Insurance Bureau of Canada: Toronto, ON, Canada, 2018. [Google Scholar]
- Sandink, D. Urban flooding and ground-related homes in Canada: An overview. J. Flood Risk Manag. 2015, 9, 208–223. [Google Scholar] [CrossRef]
- Crabbe, P.; Robin, M. Institutional adaptation of water resource infrastructures to climate change in eastern Ontario. Clim. Chang. 2006, 78, 103–133. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Clim. Chang. 2013, 1535. [Google Scholar] [CrossRef]
- Sugahara, S.; Rocha, R.P.; Silveira, R. Non-stationary frequency analysis of extreme daily rainfall in Sao Paulo, Brazil. Int. J. Climatol. 2009, 29, 1339–1349. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity Is Dead: Whither Water Management? Science 2008, 319, 5735–5774. [Google Scholar] [CrossRef]
- Srivastav, R.K.; Schardong, A.; Simonovic, S.P. Equidistance Quantile Matching Method for Updating IDF Curves under Climate Change. Water Resour. Manag. 2014, 28, 25392–25562. [Google Scholar] [CrossRef]
- Cheng, L.; AghaKouchak, A. Nonstationary precipitation Intensity-Duration-Frequency curves for infrastructure design in a changing climate. Sci. Rep. 2014, 4, 7093. [Google Scholar] [CrossRef]
- Hassanzadeh, E.; Nazemi, A.; Elshorbagy, A. Quantile-Based Downscaling of Precipitation using Genetic Programming: Application to IDF Curves in the City of Saskatoon. J. Hydrol. Eng. 2014, 19, 9439–9455. [Google Scholar] [CrossRef]
- Peck, A.; Prodanovic, P.; Simonovic, S.P. Rainfall Intensity Duration Frequency Curves Under Climate Change: City of London, Ontario, Canada. Can. Water Resour. J. 2012, 37, 177–189. [Google Scholar] [CrossRef]
- Solaiman, T.A.; King, L.M.; Simonovic, S.P. Extreme precipitation vulnerability in the Upper Thames River basin: Uncertainty in climate model projections. Int. J. Climatol. 2011, 31, 2350–2364. [Google Scholar] [CrossRef]
- Mailhot, A.; Duchesne, S.; Caya, D.; Talbot, G. Assessment of future change in intensity-duration-frequency (IDF) curves for Southern Quebec using the Canadian Regional Climate Model (CRCM). J. Hydrol. 2007, 347, 197–210. [Google Scholar] [CrossRef]
- Sandink, D.; Simonovic, S.P.; Schardong, A.; Srivastav, R. A Decision Support System for Updating and Incorporating Climate Change Impacts into Rainfall Intensity-Duration-Frequency Curves: Review of the Stakeholder Involvement Process. Environ. Model. Softw. J. 2016, 84, 193–209. [Google Scholar] [CrossRef]
- Chang, K.B.; Lai, S.H.; Faridah, O. RainIDF: Automated derivation of rainfall intensity-duration-frequency relationship from annual maxima and partial duration series. J. Hydroinform. 2013, 15, 1224–1233. [Google Scholar] [CrossRef][Green Version]
- Grasso., S.; Libertino, A.; Claps, P. MultiRain: A GIS-based tool for multi-model estimation of regional design rainfall for scientists and practitioners. J. Hydroinform. 2019, 16. [Google Scholar] [CrossRef]
- Simonovic, S.P.; Schardong, A.; Sandink, D. Mapping Extreme Rainfall Statistics for Canada Under Climate Change Using Updated Intensity-Duration-Frequency Curves. ASCE J. Water Resour. Plan. Manag. 2017, 143. [Google Scholar] [CrossRef]
- Schardong, A.; Gaur, A.; Simonovic, S.P. Comparison of the theoretical Clausius-Clapeyron scaling and IDF_CC tool for updating Intensity-Duration-Frequency Curves under climate change for Canada. J. Hydrol. Eng. 2018, 23, 04018036. [Google Scholar] [CrossRef]
- Environmental Canada and Climate Change (ECCC). Engineering Climate Datasets. 2019. Available online: https://climate.weather.gc.ca/prods_servs/engineering_e.html (accessed on 15 September 2019).
- Pacific Climate Impacts Consortium (PCIC). Statistically Downscaled Climate Scenarios Version 2. 2019. Available online: https://pacificclimate.org/data/statistically-downscaled-climate-scenarios (accessed on 15 September 2019).
- Hogg, W.D.; Carr, D.A.; Routledge, B. Rainfall Intensity-Duration-Frequency Values for Canadian Locations; Environment Canada, Atmospheric Environment Service: Ottawa, ON, Canada, 1989. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Overeem, A.; Buishand, A.; Holleman, I. Rainfall depth-duration-frequency curves and their uncertainties. J. Hydrol. 2007, 348, 124–134. [Google Scholar] [CrossRef]
- Millington, N.; Das, S.; Simonovic, S.P. The Comparison of GEV, Log-Pearson Type 3 and Gumbel Distributions in the Upper Thames River Watershed under Global Climate Models; Water Resources Research Report no. 077; Facility for Intelligent Decision Support, Department of Civil and Environmental Engineering: London, ON, Canada, 2011; p. 53, ISBN: (print) 978-0-7714-2898-2; (online) 978-0-7714-2905-7. [Google Scholar]
- Provost, S.B.; Saboor, A.; Cordeiro, G.M.; Mansoor, M. On the q-Generalized Extreme Value Distribution REVSTAT. Stat. J. 2018, 16, 45–70. [Google Scholar]
- Nguyen, V.T.V.; Nguye, T.D.; Cung, A. A statistical approach to downscaling of sub-daily extreme rainfall processes for climate-related impact studies in urban areas. Water Sci. Technol. Water Supply 2007, 7, 1831–1892. [Google Scholar] [CrossRef]
- Paixao, E.; Auld, H.; Mirza, M.M.Q.; Klaassen, J.; Shephard, M.W. Regionalization of heavy rainfall to improve climatic design values for infrastructure: Case study in Southern Ontario, Canada. Hydrol. Sci. J. 2011, 56, 1067–1089. [Google Scholar] [CrossRef]
- Coulibaly, P.; Burn, D.; Switzman, H.; Henderson, J.; Fausto, E. A comparison of future IDF curves for Southern Ontario, Technical Report, McMaster University, Hamilton. 2015. Available online: https://climateconnections.ca/wp-content/uploads/2014/01/IDF-Comparison-Report-and-Addendum.pdf (accessed on 9 December 2018).
- Ganguli, P.; Coulibaly, P. Does nonstationarity in rainfall require nonstationary intensity–duration–frequency curves? Hydrol. Earth Syst. Sci. 2017, 21, 6461–6483. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R.; Wood, E.F. Estimation of the Generalized Extreme-Value Distribution by the Method of Probability-Weighted Moments. Technometrics 1985, 27, 251–261. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. Ser. B 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Gaur, A.; Schardong, A.; Simonovic, S.P. Gridded extreme precipitation Intensity—Duration-Frequency estimates for the Canadian landmass. J. Hydrol. Eng. 2020, 25. [Google Scholar] [CrossRef]
- Mesinger, F.; DiMego, G.; Kalnay, E.; Shafran, P.C.; Ebisuzaki, W.; Jović, D.; Woollen, J.; Rogers, E.; Berbery, E.H.; Ek, M.B.; et al. North American regional reanalysis. Bull. Am. Meteorol. Soc. 2006, 87, 343–360. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Van de Vyver, H. Spatial regression models for extreme precipitation in Belgium. Water Resour. Res. 2012, 48, W09549. [Google Scholar] [CrossRef]
- Faulkner, D.S.; Prudhomme, C. Mapping an index of extreme rainfall across the UK. Hydrol. Earth Syst. Sci. 1998, 2, 183–194. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273. [Google Scholar] [CrossRef]
- Karatzoglou, A.; Smola, A.; Hornik, K. R Package Kernlab; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Platt, J.C. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines; Technical Report MSR-TR-98-14; Microsoft Research: Albuquerque, NM, USA, 1998. [Google Scholar]
- Olsson, J.; Berggren, K.; Olofsson, M.; Viklander, M. Applying climate model precipitation scenarios for urban hydrological assessment: A case study in Kalmar City, Sweden. Atmos. Res. 2009, 92, 364–375. [Google Scholar] [CrossRef]
- Bürger, G.; Sobie, S.R.; Cannon, A.J.; Werner, A.T.; Murdock, T.Q. Downscaling extremes—An intercomparison of multiple methods for future climate. J. Clim. 2013, 26, 34293–34449. [Google Scholar] [CrossRef]
- Cannon, A.J.; Sobie, S.R.; Murdock, T.Q. Bias Correction of GCM Precipitation by Quantile Mapping: How Well Do Methods Preserve Changes in Quantiles and Extremes? J. Clim. 2015, 28, 69386–69959. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Available online: http://www.ipcc.ch/report/ar5/wg1/ (accessed on 29 September 2019).
- Werner, A.T.; Cannon, A.J. Hydrologic extremes—An intercomparison of multiple gridded statistical downscaling methods. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 6179–6239. [Google Scholar] [CrossRef]
- Maurer, E.; Hidalgo, H.; Das, T.; Dettinger, M.; Cayan, D. The utility of daily large-scale climate data in the assessment of climate change impacts on daily streamflow in California (link is external). Hydrol. Earth Syst. Sci. 2010, 14, 1125–1138. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Technical Note: Downscaling RCM precipitation to the station scale using statistical transformations—A comparison of methods (link is external). Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D.P. Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Maurer, E.P.; Hidalgo, H.G. Utility of daily vs. monthly large-scale climate data: An intercomparison of two statistical downscaling methods. Hydrol. Earth Syst. Sci. 2008, 12, 551–563. [Google Scholar] [CrossRef]
- Werner, A.T. BCSD Downscaled Transient Climate Projections for Eight Select GCMs over British Columbia; Pacific Climate Impacts Consortium, University of Victoria: Victoria, BC, Canada, 2011; p. 63. [Google Scholar]
- Hunter, R.D.; Meentemeyer, R.K. Climatologically Aided Mapping of Daily Precipitation and Temperature. J. Appl. Meteorol. 2005, 44, 1501–1510. [Google Scholar] [CrossRef]
- Myhre, G.; Shindell, D.; Bréon, F.M.; Collins, W.; Fuglestvedt, J.; Huang, J.; Koch, D.; Lamarque, J.F.; Lee, D.; Mendoza, B.; et al. Anthropogenic and Natural Radiative Forcing. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 659–740. [Google Scholar] [CrossRef]
- Checa-Garcia, R.; Shine, K.P.; Hegglin, M.I. The Contribution of Greenhouse Gases to the Recent Slowdown in Global-Mean Temperature Trends. Environ. Res. Lett. 2016, 11, 094018. [Google Scholar] [CrossRef]
- Schardong, A.; Gaur, A.; Simonovic, S.P.; Sandink, D. (a). Computerized Tool for the Development of Intensity-Duration-Frequency Curves Under a Changing Climate: Technical Manual v.3; Water Resources Research Report no. 103; Facility for Intelligent Decision Support, Department of Civil and Environmental Engineering: London, UK; London, ON, Canada, 2018; p. 67. ISBN 978-0-7714-3107-4. [Google Scholar]
- Schardong, A.; Gaur, A.; Simonovic, S.P.; Sandink, D. (b). Computerized Tool for the Development of Intensity-Duration-Frequency Curves Under a Changing Climate: User’s Manual v.3; Water Resources Research Report no. 104; Facility for Intelligent Decision Support, Department of Civil and Environmental Engineering: London, UK; London, ON, Canada, 2018; p. 80. ISBN 978-0-7714-3108-1. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Statistics of extremes and estimation of extreme rainfall: II. Empirical investigation of long rainfall records. Hydrol. Sci. J. 2004, 49, 610. [Google Scholar] [CrossRef]
- Cai, X.; Hames, D. Minimum Sample Size Determination for Generalized Extreme Value Distribution. Commun. Stat. Simul. Comput. 2010, 40, 87–98. [Google Scholar] [CrossRef]
- Ragulina, G.; Reitan, T. Generalized extreme value shape parameter and its nature for extreme precipitation using long time series and the Bayesian approach. Hydrol. Sci. J. 2017, 62, 8638–8679. [Google Scholar] [CrossRef]
- MTO—Ontario Ministry of Transportation. MTO IDF Curves Finder Tool. 2020. Available online: http://www.mto.gov.on.ca/IDF_Curves/database_status.shtml (accessed on 10 January 2020).

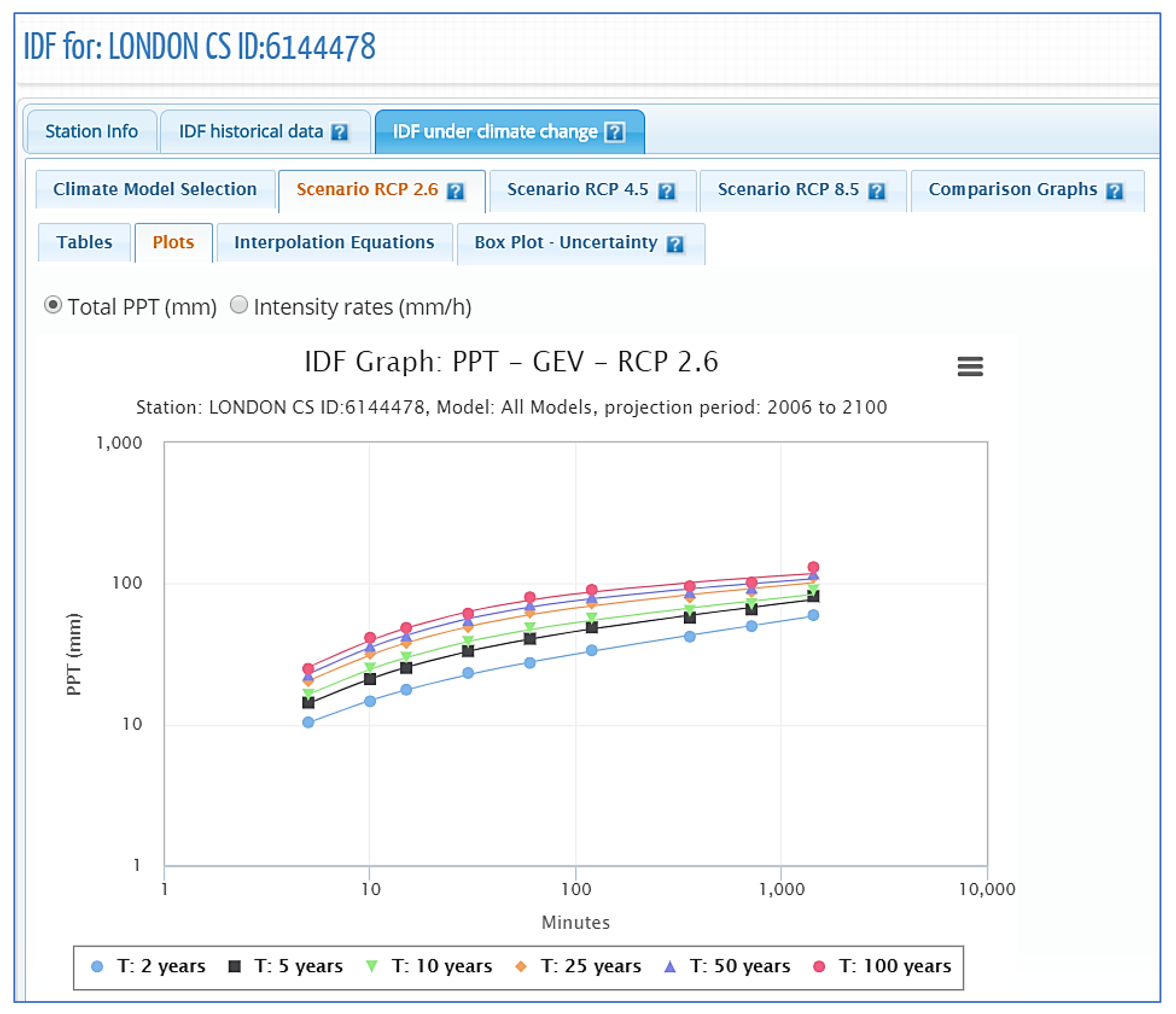
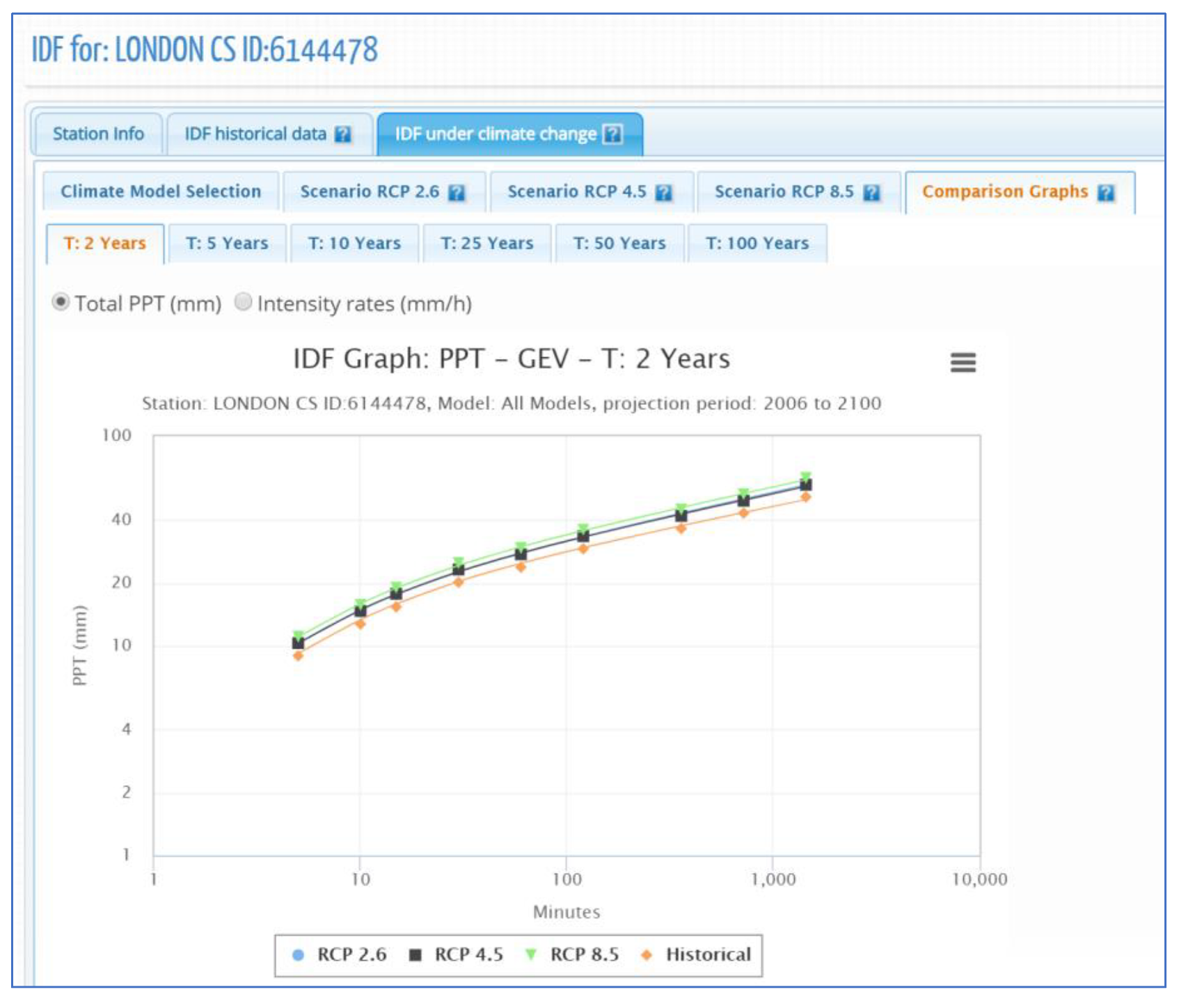
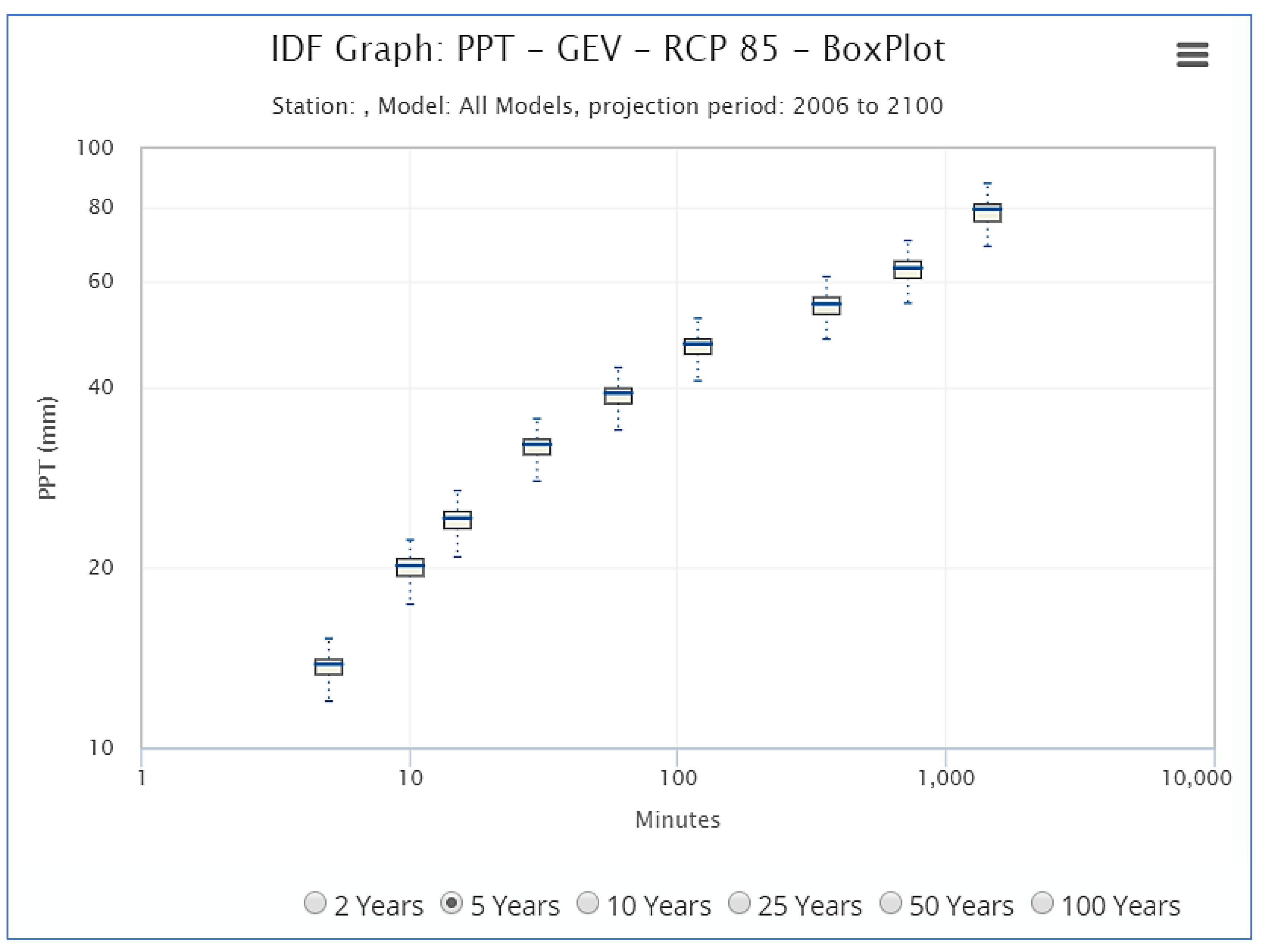
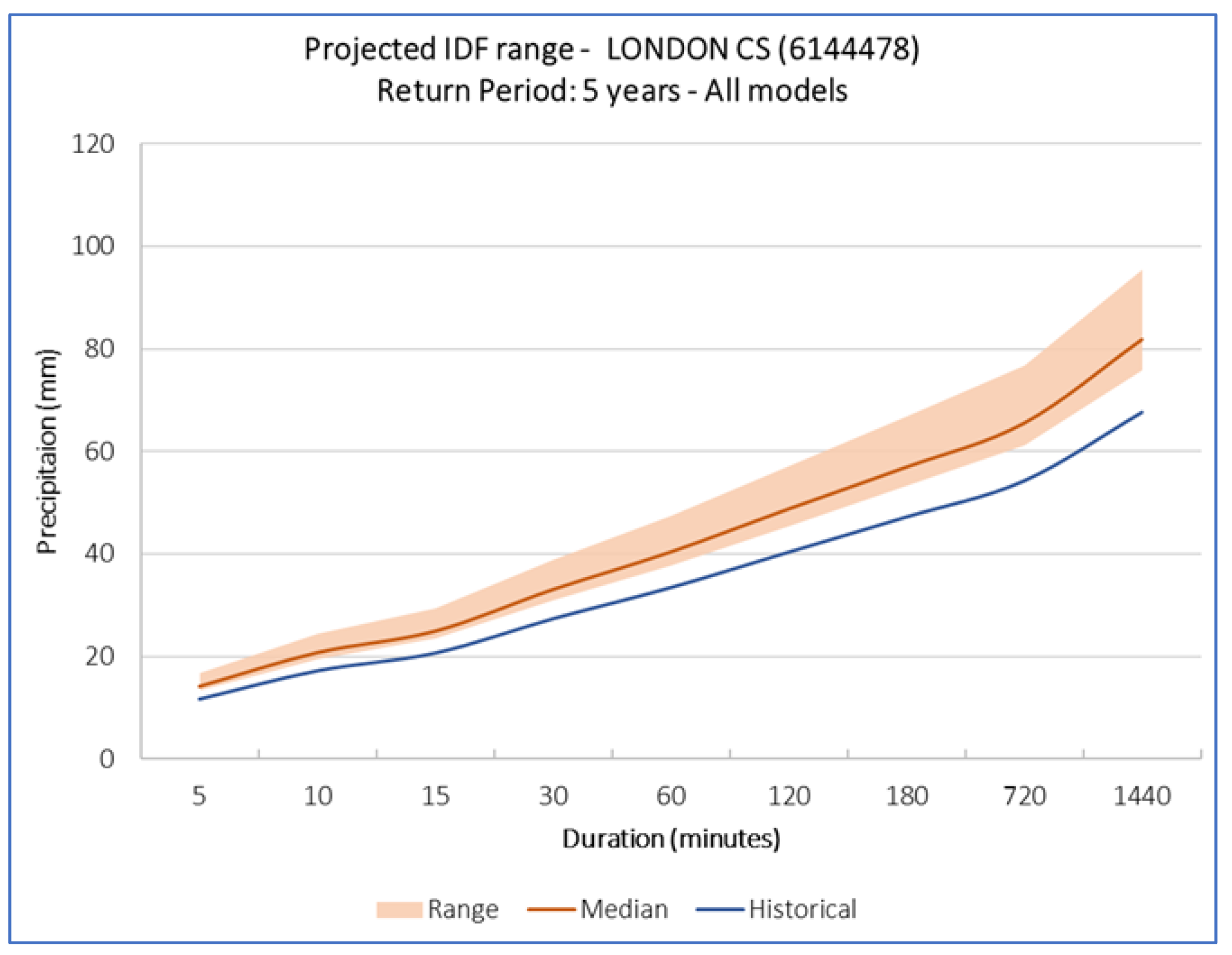
| Duration\T (Years) | Bias Correct Climate Models | Raw Climate Models | ||
|---|---|---|---|---|
| 50 Years | 100 Years | 50 Years | 100 Years | |
| 5 min | 26.4% | 30.1% | 26.5% | 25.0% |
| 10 min | 25.3% | 27.0% | 28.4% | 27.5% |
| 15 min | 25.8% | 28.6% | 27.9% | 26.1% |
| 30 min | 26.3% | 29.3% | 26.1% | 25.8% |
| 1 h | 26.0% | 29.1% | 27.0% | 25.5% |
| 2 h | 26.3% | 29.1% | 26.2% | 25.9% |
| 6 h | 26.5% | 30.1% | 25.9% | 26.1% |
| 12 h | 26.7% | 30.2% | 26.7% | 27.1% |
| 24 h | 26.4% | 29.1% | 33.9% | 33.5% |
| Duration\T (Years) | MTO Tool for Year 2085 | IDF CC Tool | ||||
|---|---|---|---|---|---|---|
| Bias Correct Models | Raw Models | |||||
| 50 Years | 100 Years | 50 Years | 100 Years | 50 Years | 100 Years | |
| 5 min | 22.7 | 24.8 | 23.1 | 26.7 | 23.2 | 25.7 |
| 10 min | 28.1 | 30.7 | 37.9 | 44.6 | 38.8 | 44.8 |
| 15 min | 31.8 | 34.8 | 45.0 | 52.9 | 45.8 | 51.8 |
| 30 min | 39.4 | 43.0 | 57.5 | 65.9 | 57.4 | 64.1 |
| 1 h | 48.8 | 53.3 | 74.5 | 87.2 | 75.1 | 84.8 |
| 2 h | 60.4 | 66.0 | 83.5 | 95.5 | 83.4 | 93.2 |
| 6 h | 85.2 | 93.0 | 91.9 | 104.8 | 91.4 | 101.6 |
| 12 h | 105.6 | 115.2 | 102.0 | 114.8 | 102.0 | 112.0 |
| 24 h | 132.0 | 144.0 | 127.0 | 141.7 | 134.5 | 146.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schardong, A.; Simonovic, S.P.; Gaur, A.; Sandink, D. Web-Based Tool for the Development of Intensity Duration Frequency Curves under Changing Climate at Gauged and Ungauged Locations. Water 2020, 12, 1243. https://doi.org/10.3390/w12051243
Schardong A, Simonovic SP, Gaur A, Sandink D. Web-Based Tool for the Development of Intensity Duration Frequency Curves under Changing Climate at Gauged and Ungauged Locations. Water. 2020; 12(5):1243. https://doi.org/10.3390/w12051243
Chicago/Turabian StyleSchardong, Andre, Slobodan P. Simonovic, Abhishek Gaur, and Dan Sandink. 2020. "Web-Based Tool for the Development of Intensity Duration Frequency Curves under Changing Climate at Gauged and Ungauged Locations" Water 12, no. 5: 1243. https://doi.org/10.3390/w12051243
APA StyleSchardong, A., Simonovic, S. P., Gaur, A., & Sandink, D. (2020). Web-Based Tool for the Development of Intensity Duration Frequency Curves under Changing Climate at Gauged and Ungauged Locations. Water, 12(5), 1243. https://doi.org/10.3390/w12051243






