Potential Fields in Fluid Mechanics: A Review of Two Classical Approaches and Related Recent Advances
Abstract
:1. Introduction
- A reduction in the number of equations and unknowns;
- Self-adjointness of the equations;
- A full decoupling of the equations;
- Transformation of the equations to a known mathematical type.
- The so-called Clebsch transformation [19,20,23] and related methodologies enabling, in the first instance, Euler’s equation to be reformulated as a generalised Bernoulli equation complemented with two transport equations for the Clebsch potentials. The approach was subsequently generalised to encompass baroclinic flow by Seliger and Witham [24], but still with the restriction that the flow is inviscid and heat conduction absent. Note that the Clebsch transformation has been applied to physical problems beyond fluid mechanics including Maxwell theory in classical electrodynamics [25], the field of Magnetohydrodynamics [26], relativistic dynamical systems [27] and even in relation to quantum theory within the context of (a) the quantisation of vortex tubes Madelung [28], Schoenberg [29], (b) generalised membranes [30] and (c) relativistic quantum vorticity [31].
- The complex variable method, developed in the first half of the 20th century and originally related to problems in plane linear elasticity [32,33]. The method was subsequently adopted by the fluid mechanics community: in the case of 2D Stokes flow () it has led to solutions based on a complex-valued Goursat representation of the stream function in terms of two analytic functions, which has been generalised incrementally, starting with Legendre [34] and followed by Coleman [35], Ranger [36], and Scholle et al. [37], Marner et al. [38], resulting finally in an exact complex-valued first integral of the 2D unsteady NS equations, based on the introduction of an auxiliary potential field. A further generalisation to 3D viscous flow has been achieved only recently using a tensor potential in place of the complex potential field employed in two-dimensions [39].
2. Clebsch Transformation Approach
2.1. The Clebsch Transformation for Inviscid Flows
2.2. A Note on the Global Existence of the Clebsch Variables
Derivation of a Clebsch-Like Form by Galilean Invariance and Self-Adjointness
- time translations:
- space translations:
- rigid rotations:
- Galilei boosts:
- Its dynamics are deducible from Hamilton’s Principle (30),
- Equivalenceof momentum density and mass flux density is given,
2.3. An Extended Clebsch Transformation for Viscous Flow
2.4. Axisymmetric Stagnation Flow
3. Complex Variable and Tensor Potential Approach
3.1. The Classical Complex Variable Method
3.2. Integration of the Full 2D Navier–Stokes Equations
3.3. Integration of the Dynamic Boundary Condition
3.4. Particular Flow Geometries as Exemplars
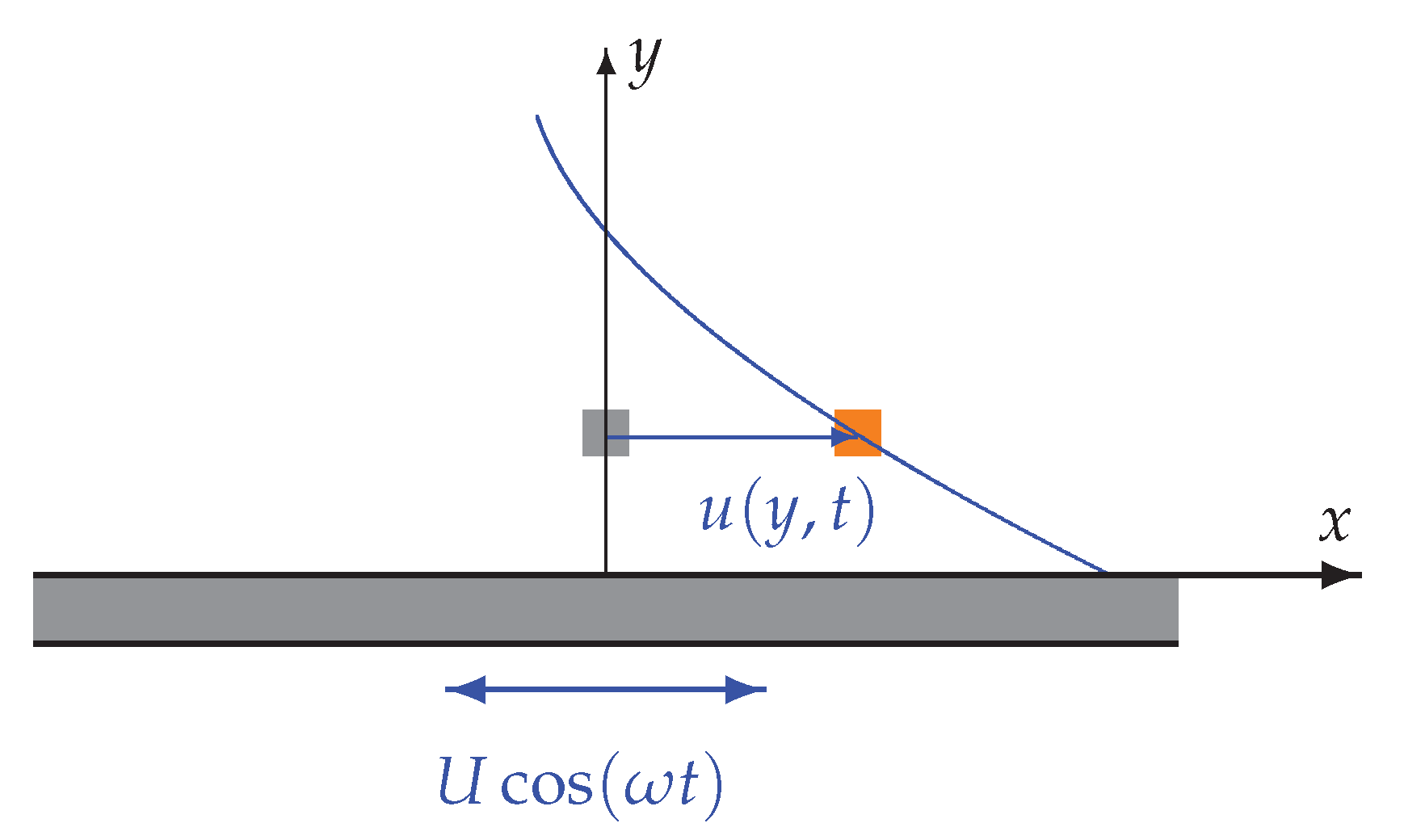
3.4.1. Uniaxial Flow: Flow over an Oscillating Plate
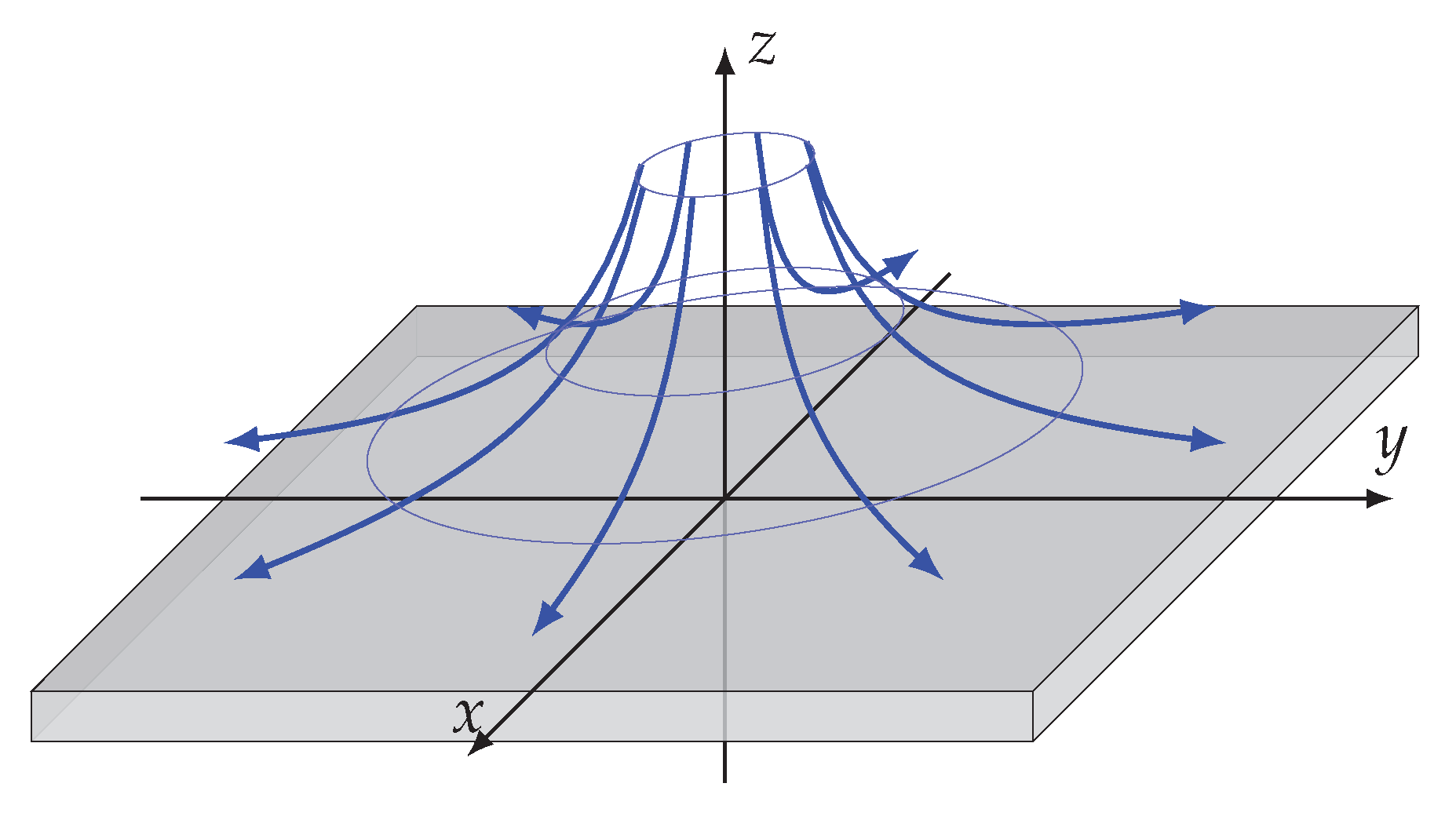
3.4.2. Axisymmetric Flow: The Lamb-Oseen Vortex
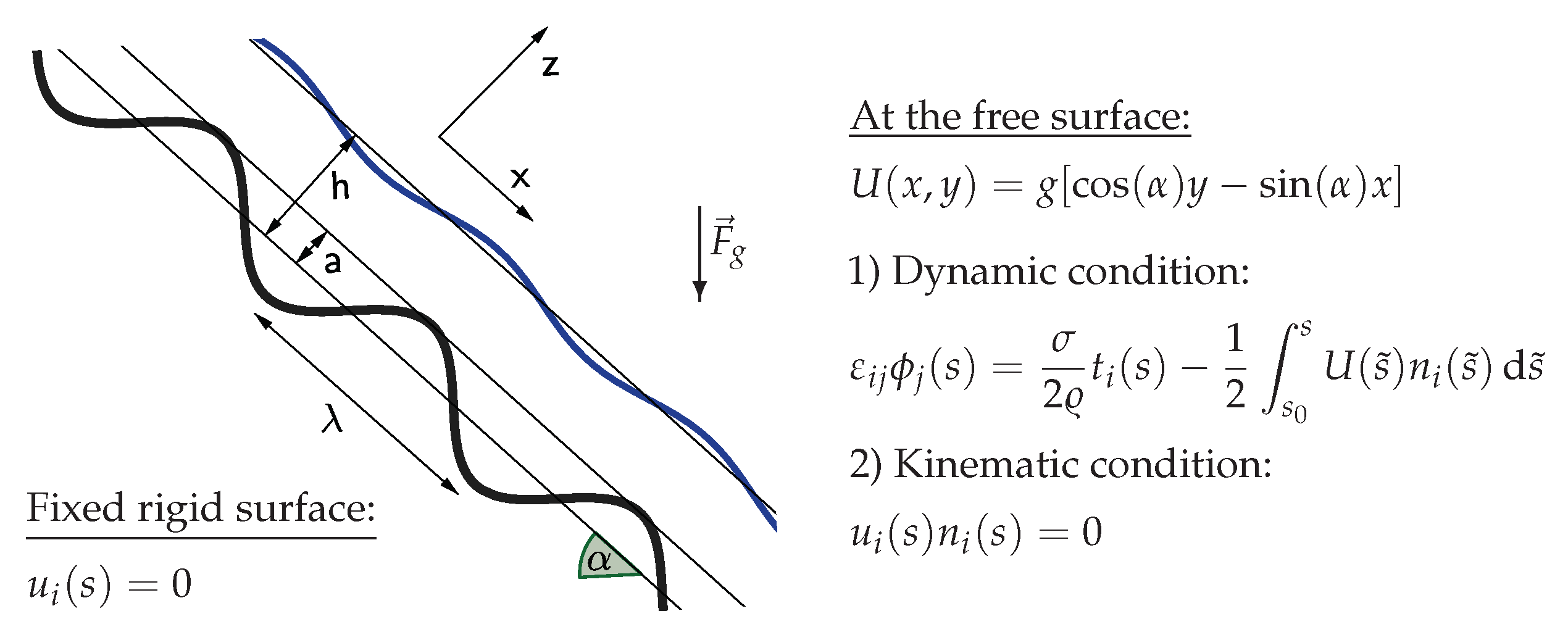
3.4.3. Steady Film Flow over Topography
3.5. Tensor Potential Approach
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| 2/3/4D | two-/three-/four-dimensional |
| LSFEM | least square finite element method |
| NS | Navier–Stokes |
| ODE | ordinary differential equation |
| PDE | partial differential equation |
Appendix A. Proof of the Existence of a Representation with Two Pairs of Clebsch Variables
References
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Heaviside, O. Electrical Papers (2 Volumes, Collected Works); The Electrician Printing and Publishing Co.: London, UK, 1892. [Google Scholar]
- Heaviside, O. Electromagnetic Theory; The Electrician Printing and Publishing Co.: London, UK, 1894; Volume 1. [Google Scholar]
- Wu, A.; Yang, C.N. Evolution of the concept of the vector potential in the description of fundamental interactions. Int. J. Mod. Phys. A 2006, 21, 3235–3277. [Google Scholar] [CrossRef]
- Jackson, J.D.; Okun, L.B. Historical roots of gauge invariance. Rev. Mod. Phys. 2001, 73, 663–680. [Google Scholar] [CrossRef] [Green Version]
- Marner, F. Potential-Based Formulations of the Navier-Stokes Equations and Their Application. Ph.D. Thesis, Durham University, Durham, UK, 2019. [Google Scholar]
- Kaku, M. Quantum Field Theory: A Modern Introduction; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Lanczos, C. The Splitting of the Riemann Tensor. Rev. Mod. Phys. 1962, 34, 379–389. [Google Scholar] [CrossRef]
- Roberts, M.D. The Lanczos Potential for Bianchi Spacetime. arXiv 2019, arXiv:1910.00416. [Google Scholar]
- Ehrenberg, W.; Siday, R.E. The Refractive Index in Electron Optics and the Principles of Dynamics. Proc. Phys. Soc. B 1949, 62, 8–21. [Google Scholar] [CrossRef]
- Aharonov, Y.; Bohm, D. Significance of Electromagnetic Potentials in the Quantum Theory. Phys. Rev. 1959, 115, 485–491. [Google Scholar] [CrossRef]
- Boyer, T.H. Does the Aharonov–Bohm Effect Exist? Found. Phys. 2000, 30, 893–905. [Google Scholar] [CrossRef]
- Boyer, T.H. Comment on Experiments Related to the Aharonov–Bohm Phase Shift. Found. Phys. 2008, 38, 498–505. [Google Scholar] [CrossRef] [Green Version]
- Vaidman, L. Role of potentials in the Aharonov-Bohm effect. Phys. Rev. A 2012, 86, 040101. [Google Scholar] [CrossRef] [Green Version]
- Aharonov, Y.; Cohen, E.; Rohrlich, D. Comment on “Role of potentials in the Aharonov-Bohm effect”. Phys. Rev. A 2015, 92. [Google Scholar] [CrossRef] [Green Version]
- Vaidman, L. Reply to “Comment on ‘Role of potentials in the Aharonov-Bohm effect”’. Phys. Rev. A 2015, 92, 026102. [Google Scholar] [CrossRef] [Green Version]
- Aharonov, Y.; Cohen, E.; Rohrlich, D. Nonlocality of the Aharonov-Bohm effect. Phys. Rev. A 2016, 93, 042110. [Google Scholar] [CrossRef] [Green Version]
- De Oliveira, C.R.; Romano, R.G. A New Version of the Aharonov-Bohm Effect. Found. Phys. 2020, 50, 137–146. [Google Scholar] [CrossRef] [Green Version]
- Lamb, H. Hydrodynamics; Cambridge University Press: Cambridge, UK, 1974. [Google Scholar]
- Panton, R.L. Incompressible Flow; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge Mathematical Library, Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Spurk, J.H.; Aksel, N. Fluid Mechanics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Clebsch, A. Ueber die Integration der hydrodynamischen Gleichungen. Journal für die Reine und Angewandte Mathematik 1859, 56, 1–10. [Google Scholar]
- Seliger, R.; Witham, G.B. Variational principles in continuum mechanics. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1968, 305, 1–25. [Google Scholar] [CrossRef]
- Wagner, H.J. Das Inverse Problem der Lagrangeschen Feldtheorie in Hydrodynamik, Plasmaphysik und Hydrodynamischem Bild der Quantenmechanik. Ph.D. Thesis, University of Paderborn, Paderborn, Germany, 1997. [Google Scholar]
- Calkin, M.G. An action principle for magnetohydrodynamics. Can. J. Phys. 1963, 41, 2241–2251. [Google Scholar] [CrossRef]
- Rund, H. Clebsch representations and relativistic dynamical systems. Arch. Ration. Mech. Anal. 1979, 71, 199–220. [Google Scholar] [CrossRef]
- Madelung, E. Quantentheorie in hydrodynamischer Form. Zeitschrift für Physik 1927, 40, 322–326. [Google Scholar] [CrossRef]
- Schoenberg, M. Vortex Motions of the Madelung Fluid. Nuovo Cimento 1955, 1, 543–580. [Google Scholar] [CrossRef]
- Roberts, M. A fluid generalization of membranes. Open Phys. 2011, 9, 1016–1021. [Google Scholar] [CrossRef] [Green Version]
- Asenjo, F.A.; Mahajan, S.M. Relativistic quantum vorticity of the quadratic form of the Dirac equation. Phys. Scr. 2015, 90, 015001. [Google Scholar] [CrossRef]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity; Noordhoff: Groningen, The Netherlands, 1953. [Google Scholar]
- Mikhlin, S.G. Integral Equations and Their Applications to Certain Problems in Mechanics, Mathematical Physics and Technology; Pergamon Press: New York, NY, USA, 1957. [Google Scholar]
- Legendre, R. Solutions plus complète du problème Blasius. Comptes Rendus Hebdomadaires des Seances de l Academie des Sciences 1949, 228, 2008–2010. [Google Scholar]
- Coleman, C.J. On the use of complex variables in the analysis of flows of an elastic fluid. J. Non-Newtonian Fluid Mech. 1984, 15, 227–238. [Google Scholar] [CrossRef]
- Ranger, K.B. Parametrization of general solutions for the Navier-Stokes equations. Q. J. Appl. Math. 1994, 52, 335–341. [Google Scholar] [CrossRef] [Green Version]
- Scholle, M.; Haas, A.; Gaskell, P.H. A first integral of Navier-Stokes equations and its applications. Proc. R. Soc. A 2011, 467, 127–143. [Google Scholar] [CrossRef] [Green Version]
- Marner, F.; Gaskell, P.H.; Scholle, M. On a potential-velocity formulation of Navier-Stokes equations. Phys. Mesomech. 2014, 17, 341–348. [Google Scholar] [CrossRef]
- Scholle, M.; Gaskell, P.H.; Marner, F. Exact integration of the unsteady incompressible Navier-Stokes equations, gauge criteria, and applications. J. Math. Phys. 2018, 59, 043101. [Google Scholar] [CrossRef] [Green Version]
- Neuber, H. Ein neuer Ansatz zur Lösung räumlicher Probleme der Elastizitätstheorie. J. Appl. Math. Mech. 1934, 14, 2008–2010. [Google Scholar]
- Lee, S.; Ryi, S.; Lim, H. About vortex equations of two dimensional flows. Indian J. Phys. 2017, 91, 1089–1094. [Google Scholar] [CrossRef]
- Greengard, L.; Jiang, S. A New Mixed Potential Representation for Unsteady, Incompressible Flow. SIAM Rev. 2019, 61, 733–755. [Google Scholar] [CrossRef]
- Prakash, J.; Lavrenteva, O.M.; Nir, A. Application of Clebsch variables to fluid-body interaction in presence of non-uniform vorticity. Phys. Fluids 2014, 26, 077102. [Google Scholar] [CrossRef]
- Lin, C.C. Hydrodynamics of Liquid Helium II. Phys. Rev. Lett. 1959, 2, 245–246. [Google Scholar] [CrossRef]
- Eckart, C. Variation Principles of Hydrodynamics. Phys. Fluids 1960, 3, 421–427. [Google Scholar] [CrossRef]
- Lin, C.C. Hydrodynamics of Helium II. In Proceedings of the International School of Physics of Physics “Enrico Fermi”, Varenna, Italy, 19–31 August 1963; Academic Press: New York, NY, USA, 1963; Volume 21. [Google Scholar]
- Moreau, J.J. Constantes d’un îlot tourbillonnaire en fluide parfait barotrope. Comptes Rendus Hebdomadaires des Séances de l’Académie des Sciences 1961, 252, 2810–2812. [Google Scholar]
- Moffatt, H.K. The degree of knottedness of tangled vortex lines. J. Fluid Mech. 1969, 35, 117–129. [Google Scholar] [CrossRef]
- Yahalom, A. Using Fluid Variational Variables to Obtain New Analytic Solutions of Self-Gravitating Flows with Nonzero Helicity. Procedia IUTAM 2013, 7, 223–232. [Google Scholar] [CrossRef] [Green Version]
- Yahalom, A.; Lynden-Bell, D. Variational principles for topological barotropic fluid dynamics. Geophys. Astrophys. Fluid Dyn. 2014, 108, 667–685. [Google Scholar] [CrossRef]
- Balkovsky, E. Some notes on the Clebsch representation for incompressible fluids. Phys. Lett. A 1994, 186, 135–136. [Google Scholar] [CrossRef]
- Yoshida, Z. Clebsch parameterization: Basic properties and remarks on its applications. J. Math. Phys. 2009, 50, 113101. [Google Scholar] [CrossRef]
- Ohkitani, K.; Constantin, P. Numerical study on the Eulerian–Lagrangian analysis of Navier–Stokes turbulence. Phys. Fluids 2008, 20, 075102. [Google Scholar] [CrossRef] [Green Version]
- Cartes, C.; Bustamante, M.D.; Brachet, M.E. Generalized Eulerian-Lagrangian description of Navier-Stokes dynamics. Phys. Fluids 2007, 19, 077101. [Google Scholar] [CrossRef] [Green Version]
- Ohkitani, K. Study of the 3D Euler equations using Clebsch potentials: Dual mechanisms for geometric depletion. Nonlinearity 2018, 31, R25. [Google Scholar] [CrossRef] [Green Version]
- Scholle, M. Construction of Lagrangians in continuum theories. Proc. R. Soc. Lond. A 2004, 460, 3241–3260. [Google Scholar] [CrossRef]
- Schmutzer, E. Symmetrien und Erhaltungssätze der Physik; 75: Reihe Mathematik und Physik; Akademie-Verlag: Berlin, Germany, 1972; 165p. [Google Scholar]
- Corson, E.M. Introduction to Tensors, Spinors and Relativistic Wave-Equations: Relation Structure; Hafner: New York, NY, USA, 1953. [Google Scholar]
- Noether, E. Invariant variation problems. Transp. Theory Stat. Phys. 1971, 1, 186–207. [Google Scholar] [CrossRef] [Green Version]
- Scholle, M.; Marner, F. A generalized Clebsch transformation leading to a first integral of Navier-Stokes equations. Phys. Lett. A 2016, 380, 3258–3261. [Google Scholar] [CrossRef]
- Mayes, C.; Schlichting, H.; Krause, E.; Oertel, H.; Gersten, K. Boundary-Layer Theory; Physic and Astronomy; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Mikhlin, S.; Morozov, N.; Paukshto, M.; Gajewski, H. The Integral Equations of the Theory of Elasticity; Teubner-Texte zur Mathematik, Vieweg+Teubner Verlag: Berlin, Germany, 2013. [Google Scholar]
- Lauricella, G. Sur l’intégration de l’équation relative àl’équilibre des plaques élastiques encastrées. Acta Math. 1909, 32, 201. [Google Scholar] [CrossRef]
- Sherman, D.I. On the solution of the theory of elasticity static plane problem under given external loading. Doklady Akademii Nauk SSSR 1940, 26, 25–28. [Google Scholar]
- Greengard, L.; Kropinski, M.C.; Mayo, A. Integral equation methods for Stokes flow and isotropic elasticity in the plane. J. Comput. Phys. 1996, 125, 403–404. [Google Scholar] [CrossRef]
- Richardson, S. On the no-slip boundary condition. J. Fluid Mech. 1973, 59, 707–719. [Google Scholar] [CrossRef]
- Howison, S.D. Complex variable methods in Hele–Shaw moving boundary problems. Eur. J. Appl. Math. 1992, 3, 209–224. [Google Scholar] [CrossRef] [Green Version]
- Siegel, M. Cusp formation for time-evolving bubbles in two-dimensional Stokes flow. J. Fluid Mech. 2000, 412, 227–257. [Google Scholar] [CrossRef]
- Cummings, L.J. Steady solutions for bubbles in dipole-driven Stokes flows. Phys. Fluids 2000, 12, 2162–2168. [Google Scholar] [CrossRef]
- Scholle, M.; Wierschem, A.; Aksel, N. Creeping films with vortices over strongly undulated bottoms. Acta Mech. 2004, 168, 167–193. [Google Scholar] [CrossRef]
- Scholle, M. Creeping Couette flow over an undulated plate. Arch. Appl. Mech. 2004, 73, 823–840. [Google Scholar] [CrossRef]
- Scholle, M.; Haas, A.; Aksel, N.; Wilson, M.C.T.; Thompson, H.M.; Gaskell, P.H. Competing geometric and inertial effects on local flow structure in thick gravity-driven fluid films. Phys. Fluids 2008, 20, 123101. [Google Scholar] [CrossRef]
- Marner, F.; Gaskell, P.H.; Scholle, M. A complex-valued first integral of Navier-Stokes equations: Unsteady Couette flow in a corrugated channel system. J. Math. Phys. 2017, 58, 043102. [Google Scholar] [CrossRef] [Green Version]
- Scholle, M.; Gaskell, P.H.; Marner, F. A Potential Field Description for Gravity-Driven Film Flow over Piece-Wise Planar Topography. Fluids 2019, 4. [Google Scholar] [CrossRef] [Green Version]
- Cassidy, M. A Spectral Method for Viscoelastic Extrudate Swell. Ph.D. Thesis, University of Wales, Aberystwyth, UK, 1996. [Google Scholar]
- Thatcher, R.W. A least squares method for Stokes flow based on stress and stream functions. In Manchester Centre for Computational Mathematics; Report 330; University of Manchester: Manchester, UK, 1998. [Google Scholar]
- Bolton, P.; Thatcher, R.W. A least-squares finite element method for the Navier-Stokes equations. J. Comput. Phys. 2006, 213, 174–183. [Google Scholar] [CrossRef]
- Bochev, P.B.; Gunzburger, M.D. Least-Squares Finite Element Methods; Applied Mathematical Sciences; Springer: New York, NY, USA, 2009; Volume 166. [Google Scholar]
- Schörner, M.; Reck, D.; Aksel, N. Does the topography’s specific shape matter in general for the stability of film flows? Phys. Fluids 2015, 27, 042103. [Google Scholar] [CrossRef]
- Scholle, M.; Marner, F.; Gaskell, P.H. A first integral form of the energy-momentum equations for viscous flow, with comparisons drawn to classical fluid flow theory. Eur. J. Mech. B Fluids 2020. under review. [Google Scholar]
- Anthony, K.H. Hamilton’s action principle and thermodynamics of irreversible processes—A unifying procedure for reversible and irreversible processes. J. Non-Newton. Fluid Mech. 2001, 96, 291–339. [Google Scholar] [CrossRef]
- Zuckerwar, A.J.; Ash, R.L. Variational approach to the volume viscosity of fluids. Phys. Fluids 2006, 18, 047101. [Google Scholar] [CrossRef] [Green Version]
- Zuckerwar, A.J.; Ash, R.L. Volume viscosity in fluids with multiple dissipative processes. Phys. Fluids 2009, 21, 033105. [Google Scholar] [CrossRef] [Green Version]
- Olsson, P. Transport Phenomena in Newtonian Fluids—A Concise Primer; Springer Briefs in Applied Sciences and Technology; Springer International Publishing: Cham, Switzerland, 2013. [Google Scholar] [CrossRef]
- Belevich, M. Classical Fluid Mechanics; Bentham Science Publishers: Sharjah, UAE, 2017. [Google Scholar]
- Scholle, M.; Marner, F. A non-conventional discontinuous Lagrangian for viscous flow. R. Soc. Open Sci. 2017, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marner, F.; Scholle, M.; Herrmann, D.; Gaskell, P.H. Competing Lagrangians for incompressible and compressible viscous flow. R. Soc. Open Sci. 2019, 6, 181595. [Google Scholar] [CrossRef] [Green Version]
- Cipriano, F.; Cruzeiro, A.B. Navier-Stokes Equation and Diffusions on the Group of Homeomorphisms of the Torus. Commun. Math. Phys. 2007, 275, 255–269. [Google Scholar] [CrossRef]
- Arnaudon, M.; Cruzeiro, A.B.; Galamba, N. Lagrangian Navier-Stokes flows: A stochastic model. J. Phys. A 2011, 44, 175501. [Google Scholar] [CrossRef] [Green Version]
- Arnaudon, M.; Cruzeiro, A.B. Lagrangian Navier-Stokes diffusions on manifolds: Variational principle and stability. Bulletin des Sciences Mathématiques 2012, 136, 857–881. [Google Scholar] [CrossRef] [Green Version]
- Arnaudon, M.; Cruzeiro, A.B. Stochastic Lagrangian Flows and the Navier-Stokes Equations. In Stochastic Analysis: A Series of Lectures; Springer: Berlin, Germany, 2015; pp. 55–75. [Google Scholar]
- Arnaudon, M.; Chen, X.; Cruzeiro, A.B. Stochastic Euler-Poincaré reduction. J. Math. Phys. 2014, 55, 081507. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Cruzeiro, A.B.; Ratiu, T.S. Constrained and stochastic variational principles for dissipative equations with advected quantities. arXiv 2015, arXiv:1506.05024. [Google Scholar]
- Roberts, M.D. The Clebsch potential approach to fluid Lagrangians. J. Geom. Phys. 2017, 117, 60–67. [Google Scholar] [CrossRef] [Green Version]
- Lightman, A.; Press, W.; Price, R.; Teukolsky, S. Problem Book in Relativity and Gravitation; Princeton University Press: Princeton, NJ, USA, 1975. [Google Scholar]
- Kuipers, J.B. Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace, and Virtual Reality; Princeton University Press: Princeton, NJ, USA, 1999. [Google Scholar]
- Arribas, M.; Elipe, A.; Palacios, M. Quaternions and the rotation of a rigid body. Celest. Mech. Dyn. Astron. 2006, 96, 239–251. [Google Scholar] [CrossRef]
- Haupt, P. Continuum Mechanics and Theory of Materials. Appl. Mech. Rev. 2002, 55, B23. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scholle, M.; Marner, F.; Gaskell, P.H. Potential Fields in Fluid Mechanics: A Review of Two Classical Approaches and Related Recent Advances. Water 2020, 12, 1241. https://doi.org/10.3390/w12051241
Scholle M, Marner F, Gaskell PH. Potential Fields in Fluid Mechanics: A Review of Two Classical Approaches and Related Recent Advances. Water. 2020; 12(5):1241. https://doi.org/10.3390/w12051241
Chicago/Turabian StyleScholle, Markus, Florian Marner, and Philip H. Gaskell. 2020. "Potential Fields in Fluid Mechanics: A Review of Two Classical Approaches and Related Recent Advances" Water 12, no. 5: 1241. https://doi.org/10.3390/w12051241
APA StyleScholle, M., Marner, F., & Gaskell, P. H. (2020). Potential Fields in Fluid Mechanics: A Review of Two Classical Approaches and Related Recent Advances. Water, 12(5), 1241. https://doi.org/10.3390/w12051241





