Time-Lapse Seismic and Electrical Monitoring of the Vadose Zone during a Controlled Infiltration Experiment at the Ploemeur Hydrological Observatory, France
Abstract
:1. Introduction
2. Materials and Methods
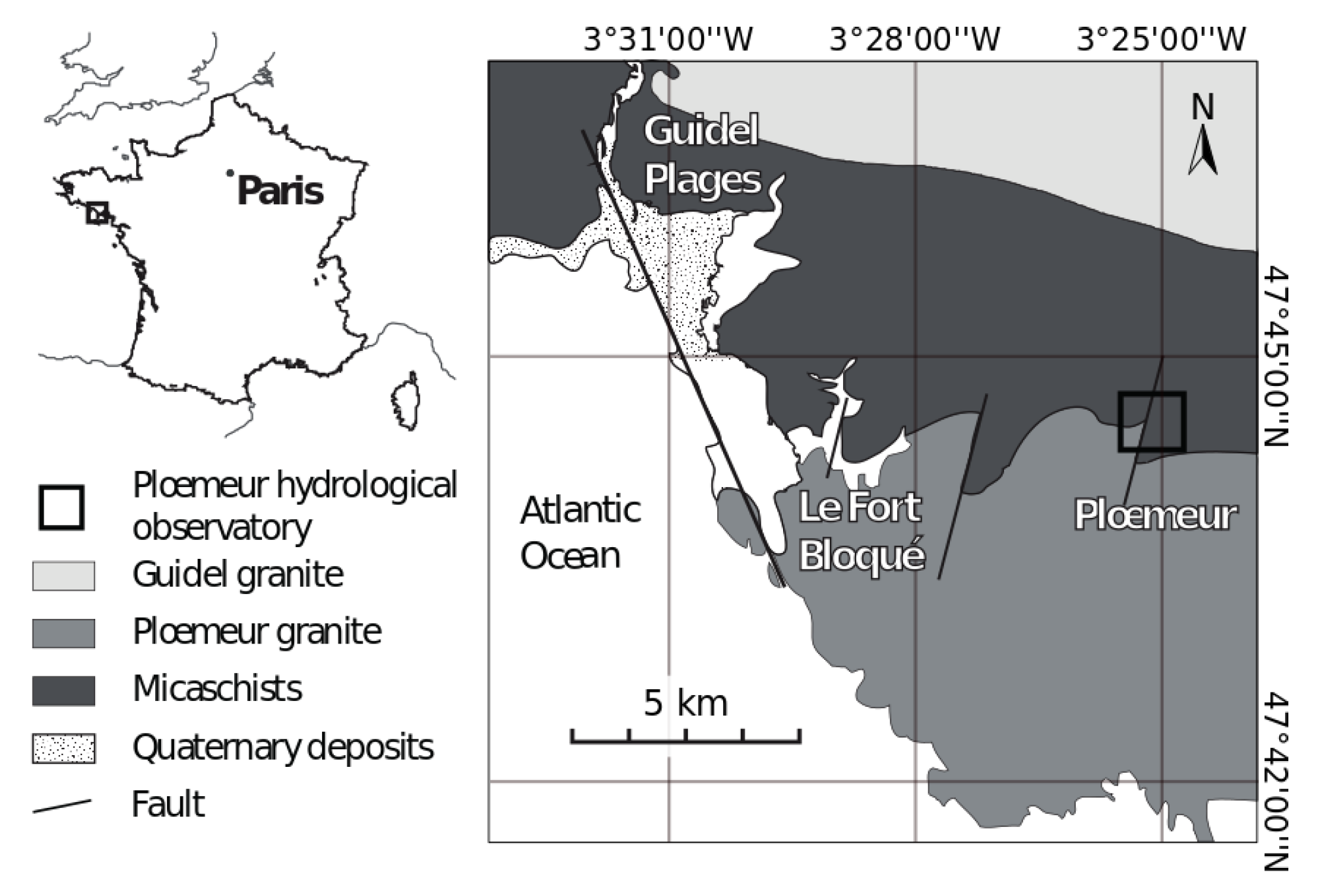
2.1. Site Description
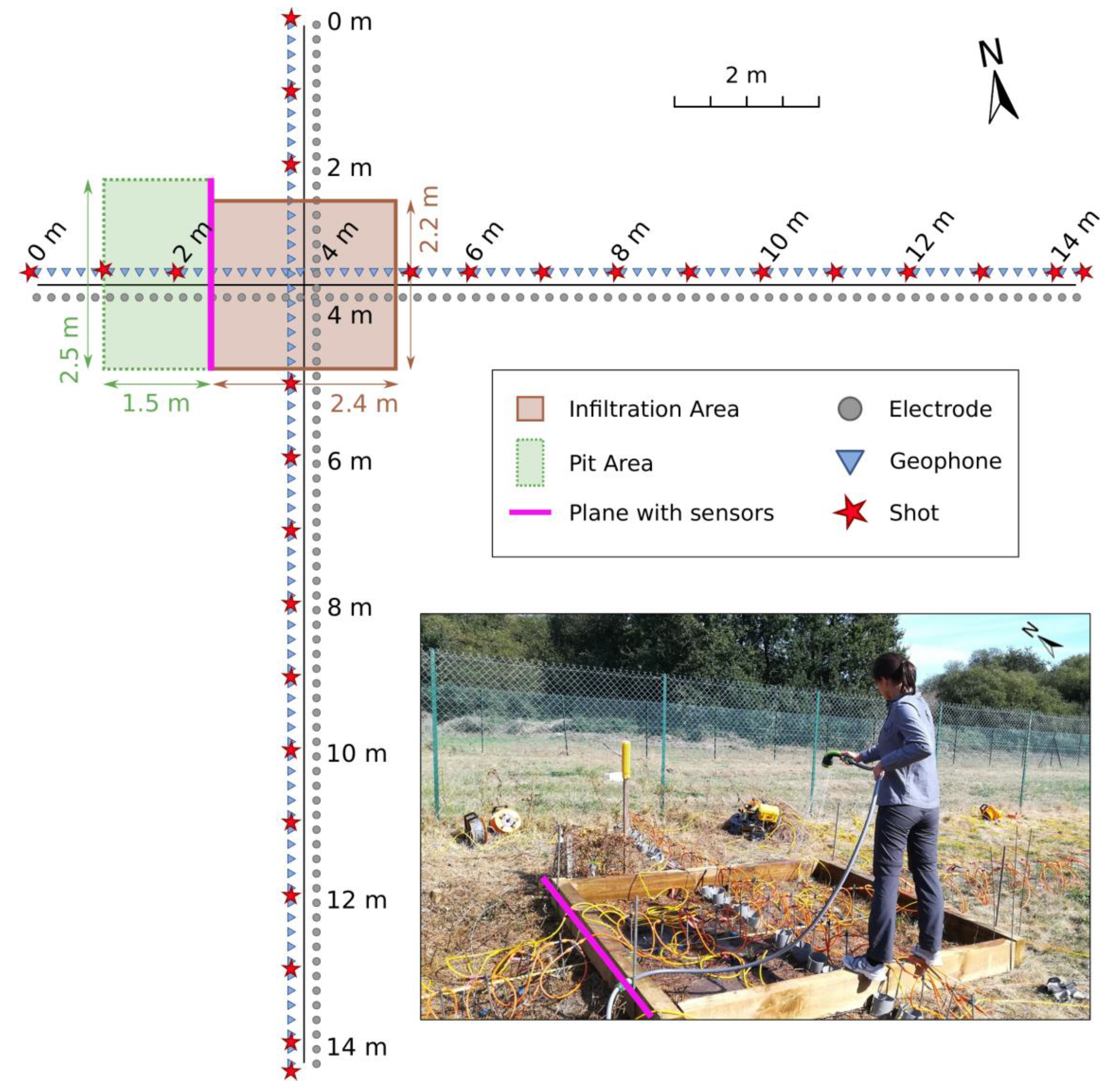
2.2. Acquisition Setup
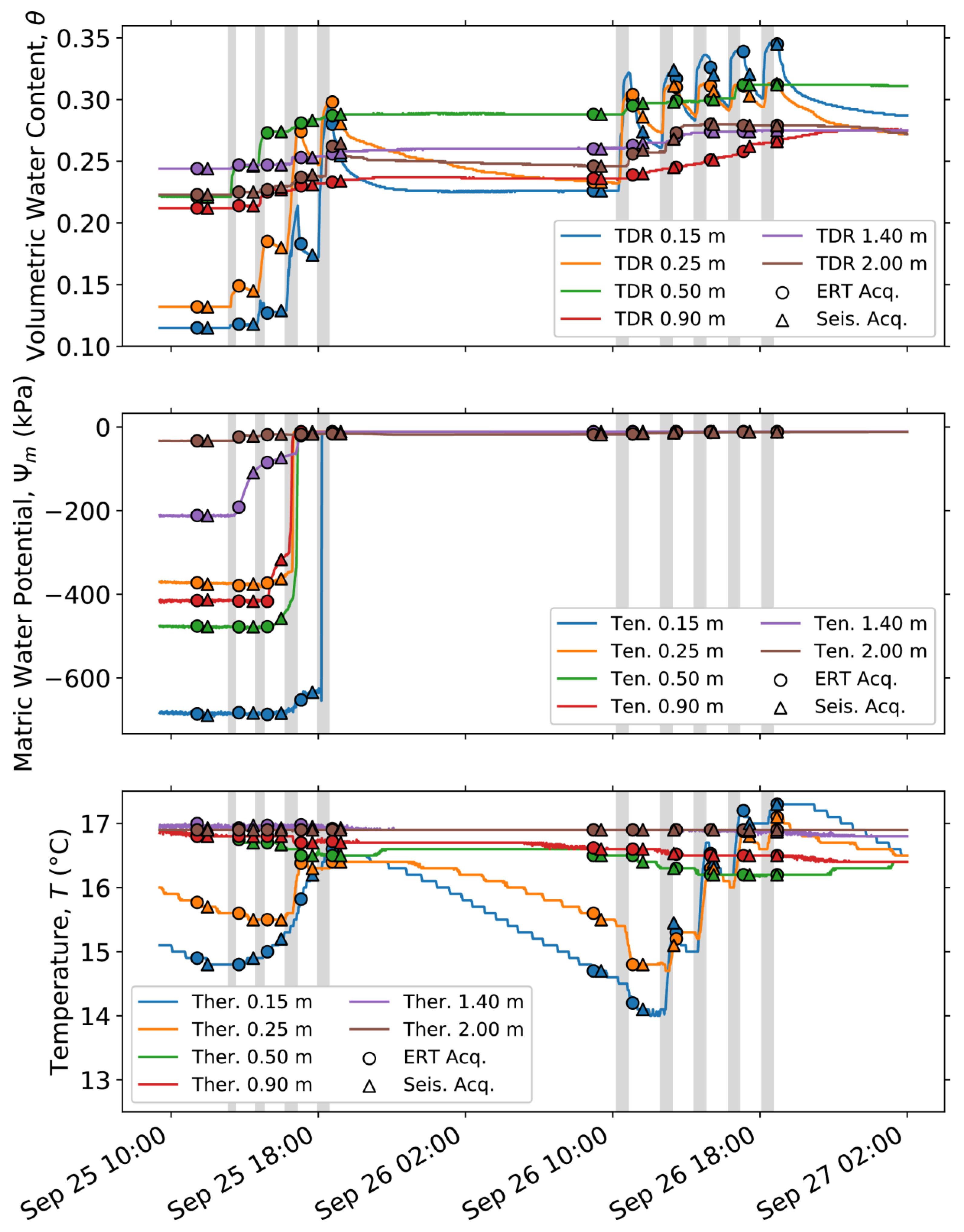
3. Results
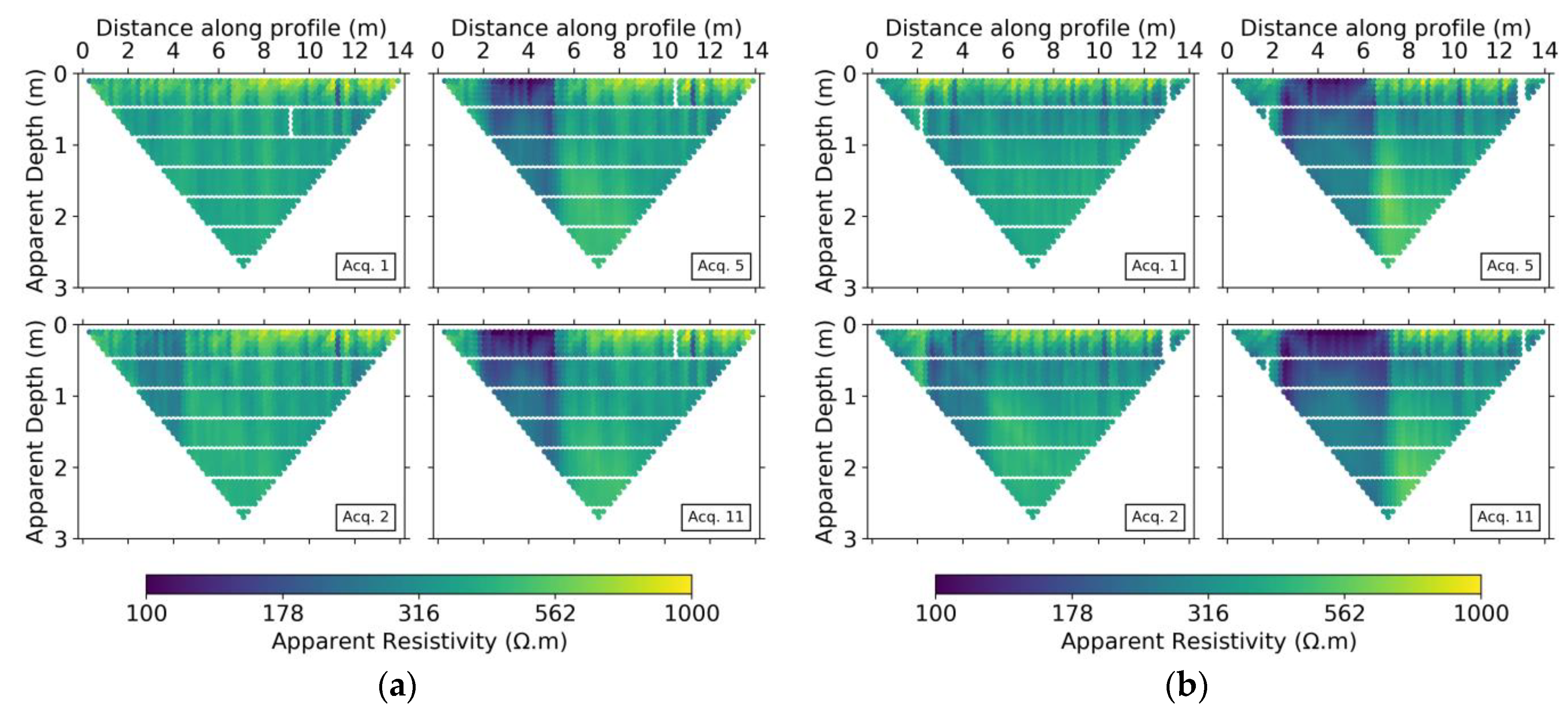
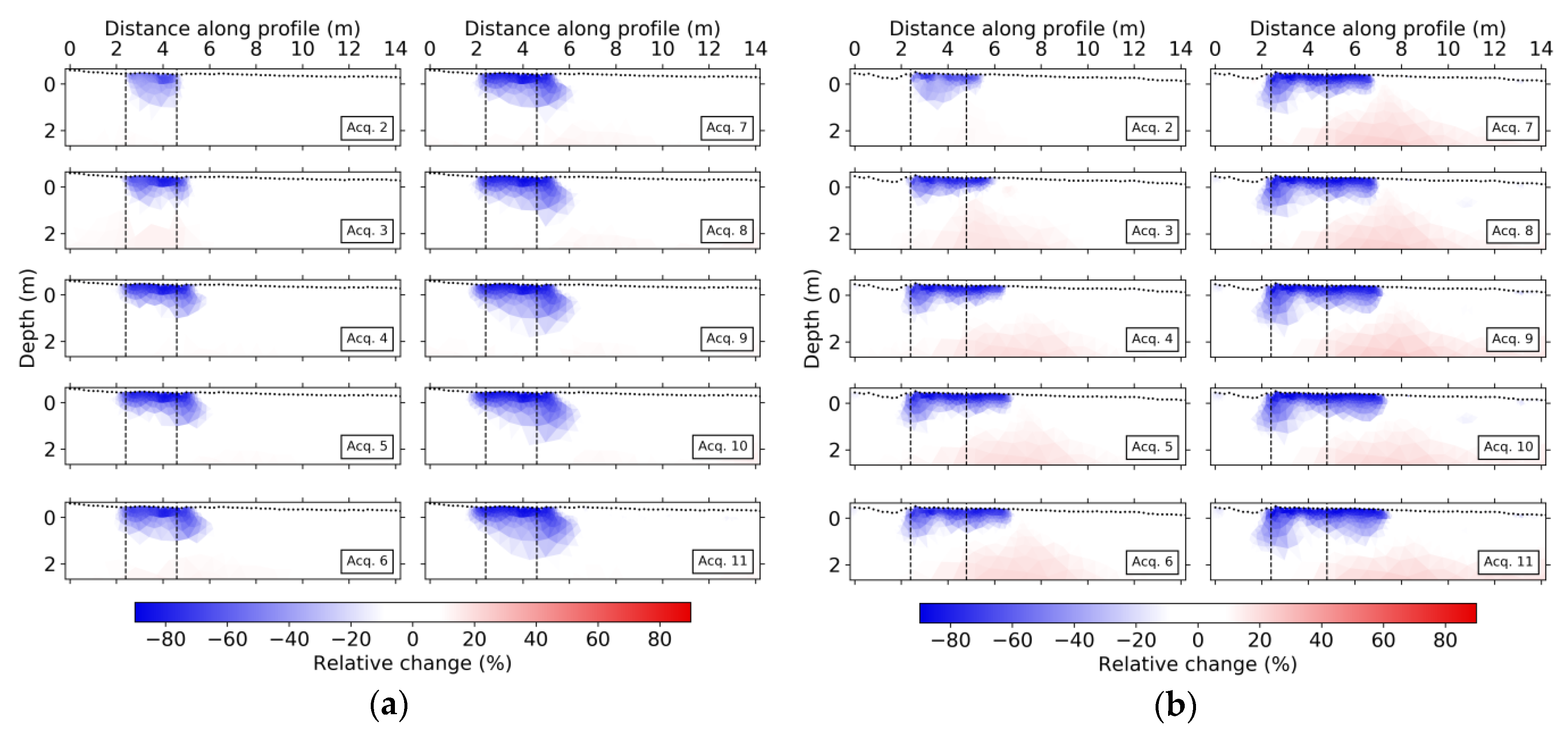
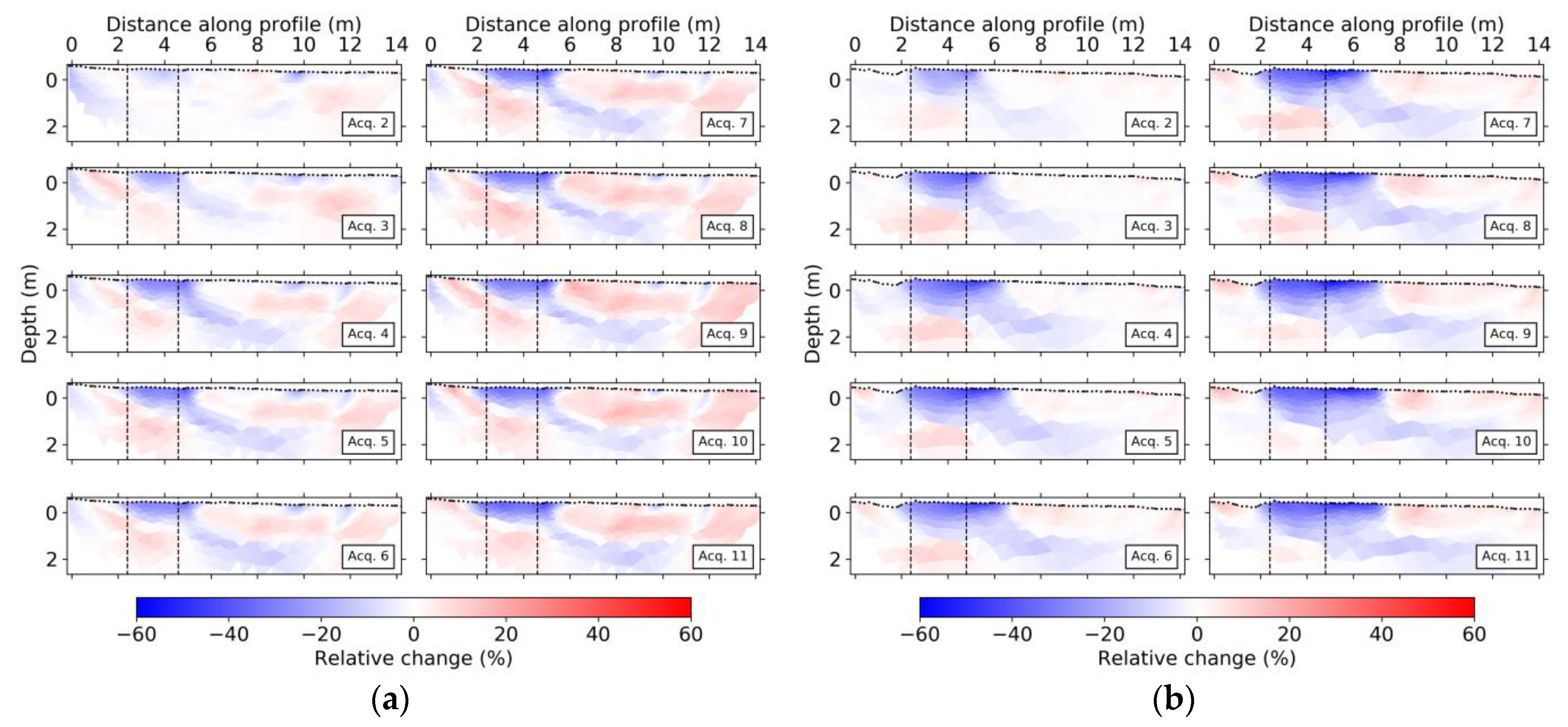
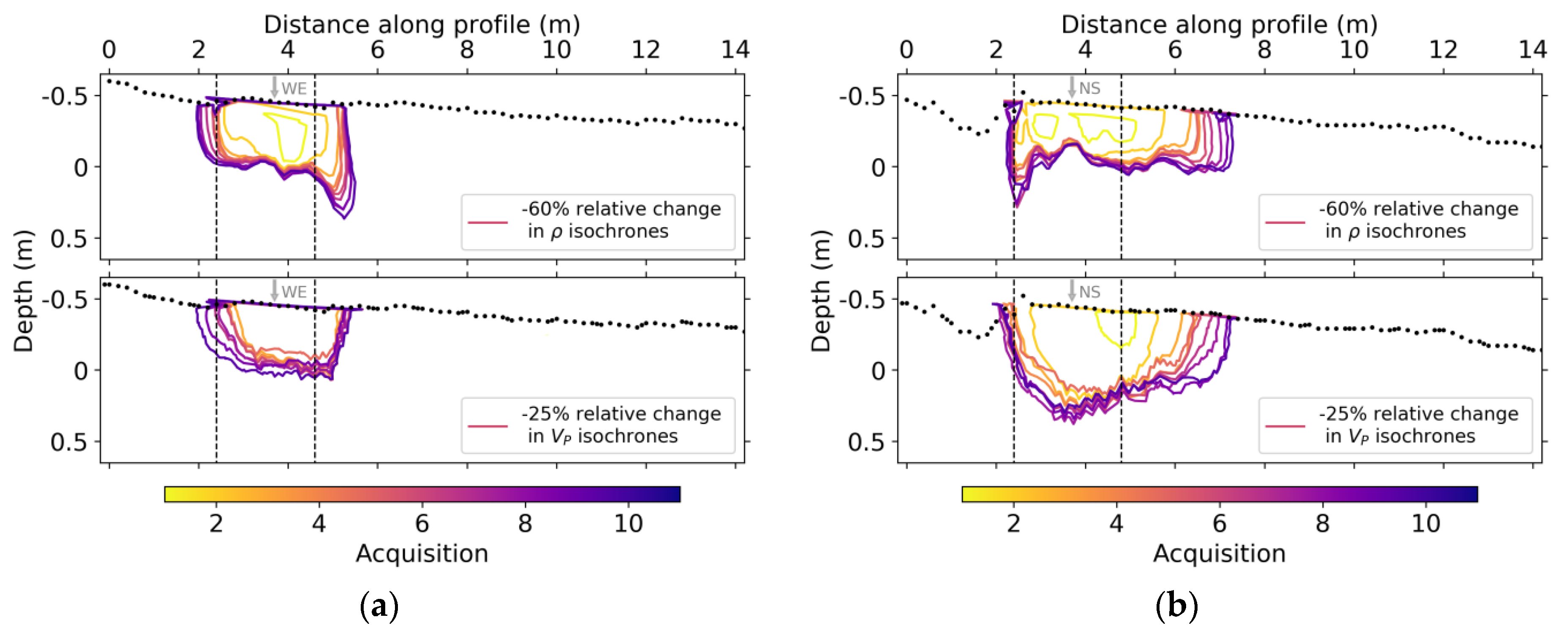
3.1. Electrical Resistivity Tomography
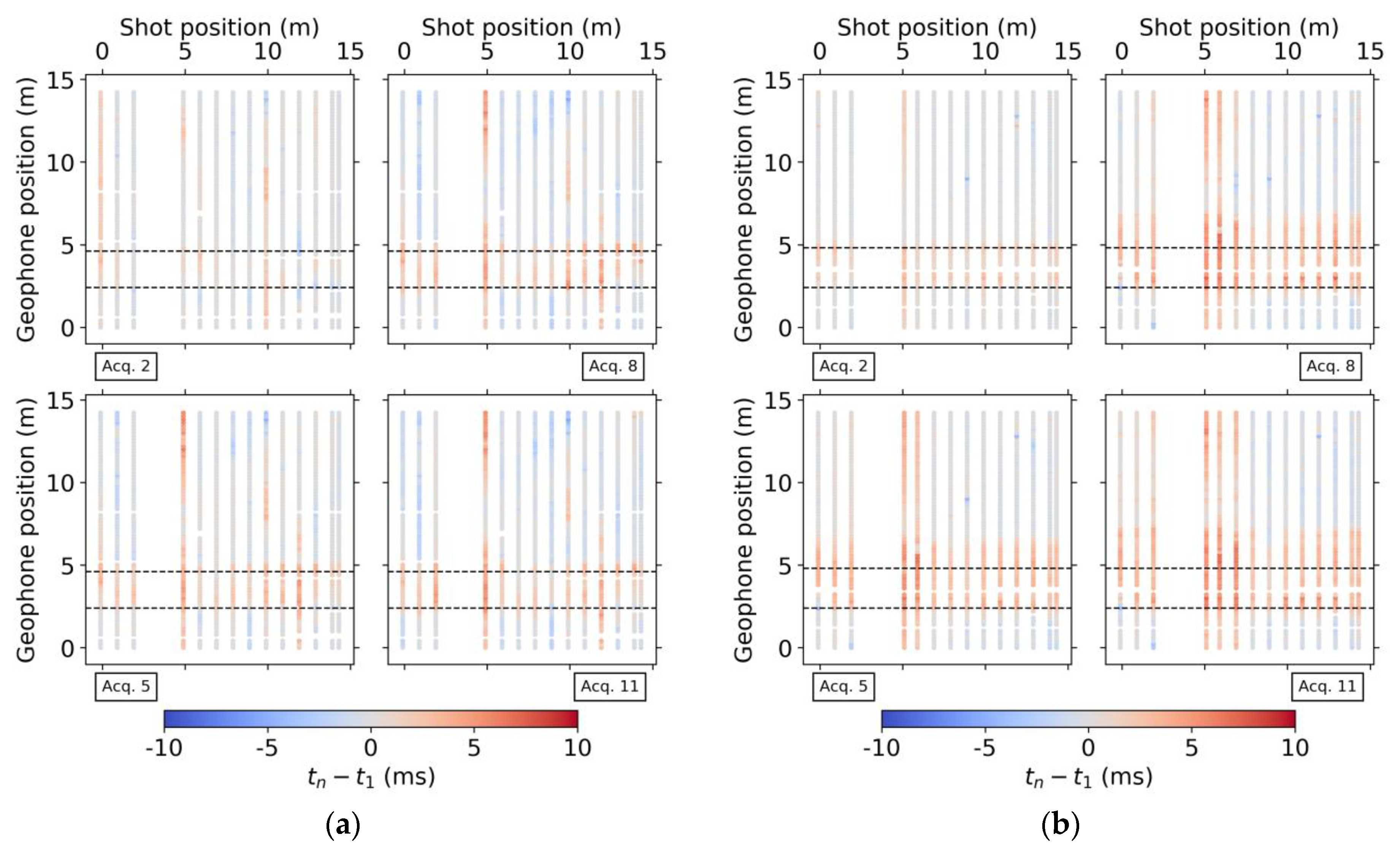
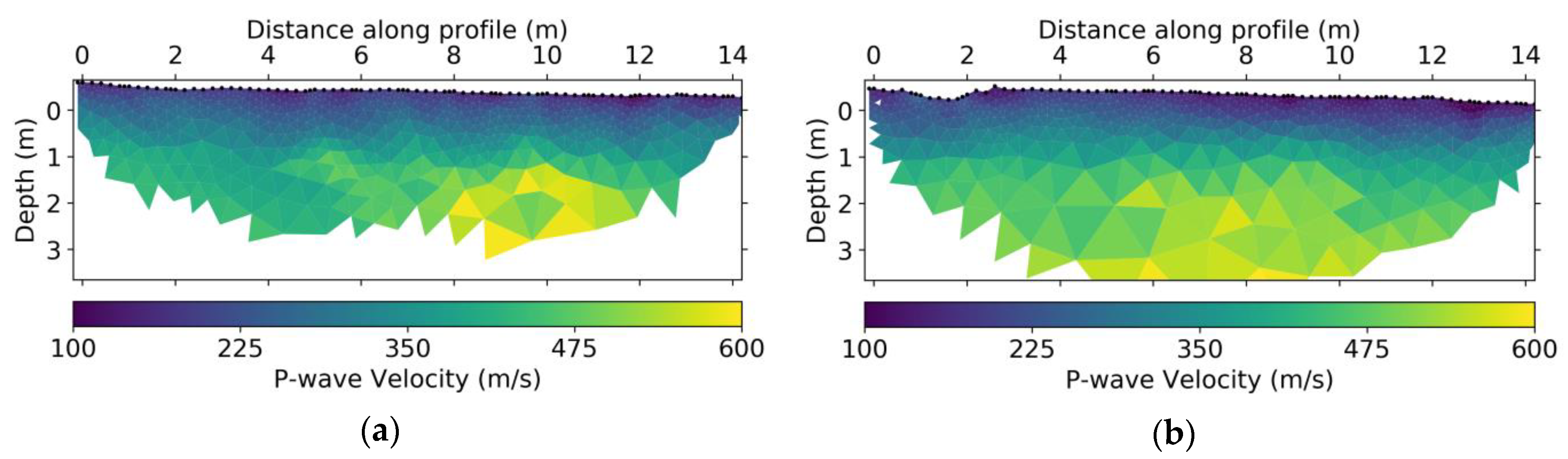
3.2. Seismic Refraction: Traveltimes and P-wave Velocity
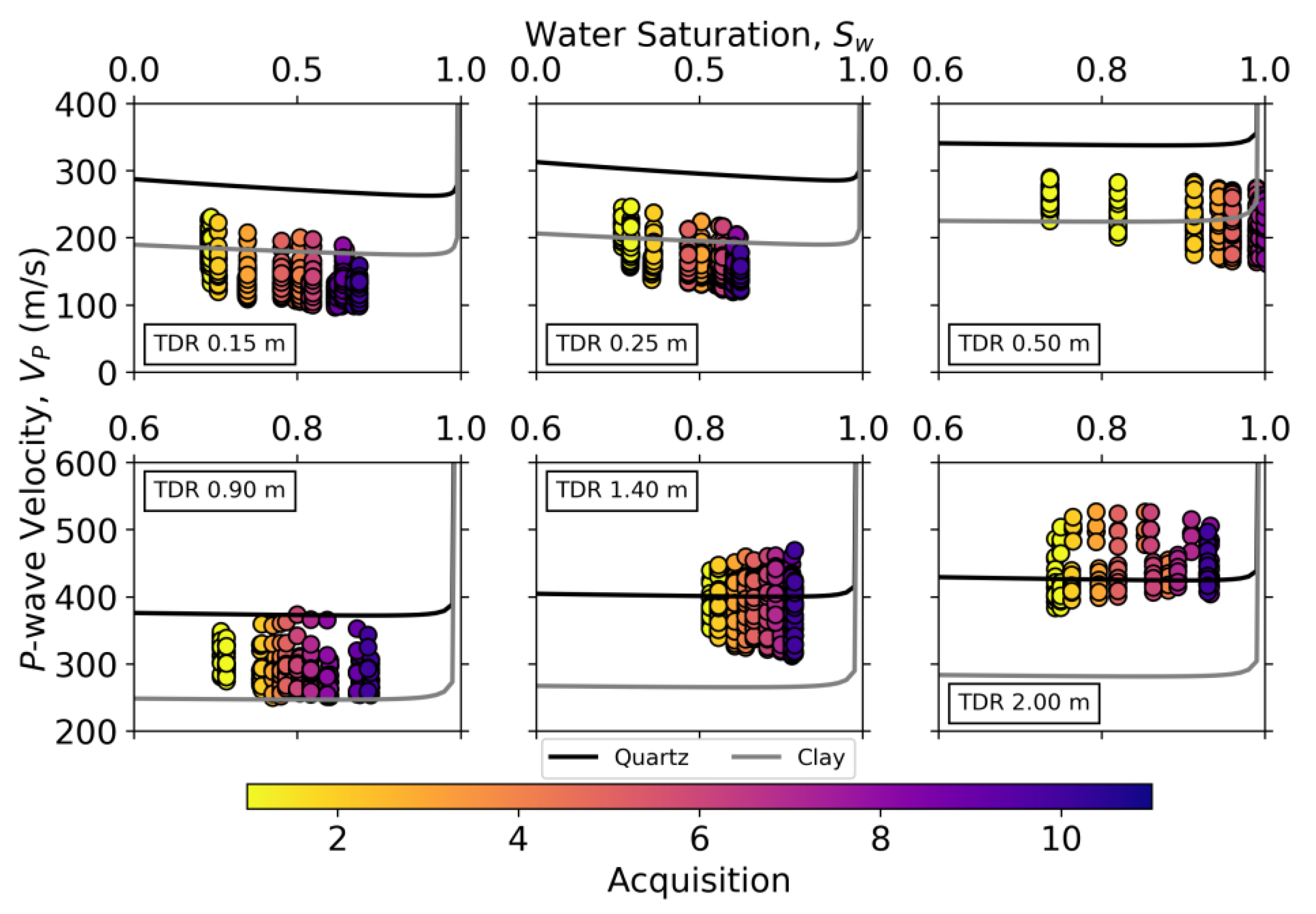
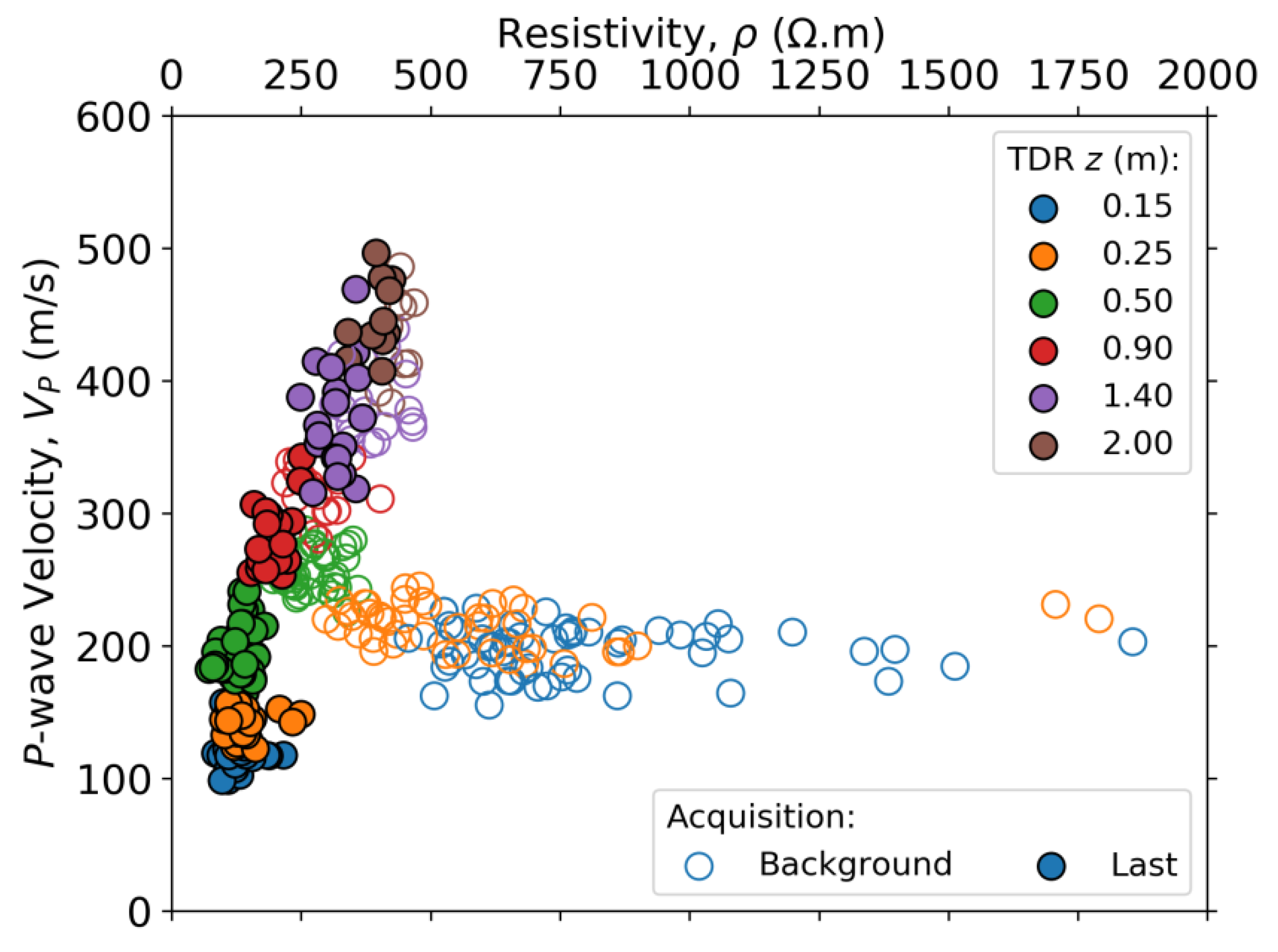
3.3. Petrophysical relationships
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Availability of Data and Materials
References
- Vereecken, H.; Huisman, J.A.; Bogena, H.; Vanderborght, J.; Vrugt, J.A.; Hopmans, J.W. On the value of soil moisture measurements in vadose zone hydrology: A review. Water Resour. Res. 2008, 44, W00D06. [Google Scholar] [CrossRef] [Green Version]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture-climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Vereecken, H.; Huisman, J.A.; Pachepsky, Y.; Montzka, C.; van der Kruk, J.; Bogena, H.; Weihermüller, L.; Herbst, M.; Martinez, G.; Vanderborght, J. On the spatio-temporal dynamics of soil moisture at the field scale. J. Hydrol. 2014, 516, 76–96. [Google Scholar] [CrossRef]
- Dobriyal, P.; Qureshi, A.; Badola, R.; Hussain, S.A. A review of the methods available for estimating soil moisture and its implications for water resource management. J. Hydrol. 2012, 458–459, 110–117. [Google Scholar] [CrossRef]
- Fan, Y.; Grant, G.; Anderson, S.P. Water within, moving through, and shaping the Earth’s surface: Introducing a special issue on water in the critical zone. Hydrol. Process. 2019, 33, 3146–3151. [Google Scholar] [CrossRef]
- Cassiani, G.; Binley, A.; Ferré, T.P.A. Unsaturated Zone Processes. In Applied Hydrogeophysics; Vereecken, H., Binley, A., Cassiani, G., Revil, A., Titov, K., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2007; pp. 75–116. [Google Scholar] [CrossRef]
- Susha Lekshmi, S.U.; Singh, D.N.; Shojaei Baghini, M. A critical review of soil moisture measurement. Measurement 2014, 54, 92–105. [Google Scholar] [CrossRef]
- Rubin, Y.; Hubbard, S.S.; Wilson, A.; Cushey, M.A. Aquifer Characterization. In Handbook of Groundwater Engineering; Delleur, J.W., Ed.; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Hubbard, S.S.; Linde, N. Hydrogeophysics. In Treatise on Water Science; Wilderer, P., Ed.; Elsevier Science: Amsterdam, The Netherlands, 2011; pp. 401–434. [Google Scholar] [CrossRef]
- Parsekian, A.D.; Singha, K.; Minsley, B.J.; Holbrook, W.S.; Slater, L. Multiscale geophysical imaging of the critical zone. Rev. Geophys. 2015, 53, 1–26. [Google Scholar] [CrossRef]
- Binley, A.; Hubbard, S.S.; Huisman, J.A.; Revil, A.; Robinson, D.A.; Singha, K.; Slater, L.D. The emergence of hydrogeophysics for improved understanding of subsurface processes over multiple scales. Water Resour. Res. 2015, 51, 3837–3866. [Google Scholar] [CrossRef] [Green Version]
- Casto, D.W.; Luke, B.; Calderón-Macías, C.; Kaufmann, R. Interpreting surface-wave data for a site with shallow bedrock. J. Environ. Eng. Geophys. 2009, 14, 115–127. [Google Scholar] [CrossRef] [Green Version]
- Parker, E.H.; Hawman, R.B. Multi-channel analysis of surface waves (MASW) in karst terrain, southwest georgia: Implications for detecting anomalous features and fracture zones. J. Environ. Eng. Geophys. 2011, 17, 149–160. [Google Scholar] [CrossRef]
- St Clair, J.; Moon, S.; Holbrook, W.S.; Perron, J.T.; Riebe, C.S.; Martel, S.J.; Carr, B.; Harman, C.; Singha, K.; deB Richter, D. Geophysical imaging reveals topographic stress control of bedrock weathering. Science 2015, 350, 534–538. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pride, S.R. Relationships between Seismic and Hydrological Properties. In Hydrogeophysics; Rubin, Y., Hubbard, S.S., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2005; pp. 253–290. [Google Scholar] [CrossRef]
- Haeni, F.P. Application of Seismic-Refraction Techniques to Hydrologic Studies; U. S. Geological Survey: Hartford, CT, USA, 1986. [CrossRef]
- Socco, L.V.; Foti, S.; Boiero, D. Surface-wave analysis for building near-surface velocity models—Established approaches and new perspectives. Geophysics 2010, 75, 75A83–75A102. [Google Scholar] [CrossRef]
- Turesson, A. A comparison of methods for the analysis of compressional, shear, and surface wave seismic data, and determination of the shear modulus. J. Appl. Geophys. 2007, 61, 83–91. [Google Scholar] [CrossRef]
- Grelle, G.; Guadagno, F.M. Seismic refraction methodology for groundwater level determination: “Water seismic index”. J. Appl. Geophys. 2009, 68, 301–320. [Google Scholar] [CrossRef]
- Cameron, A.; Knapp, C. A New Approach to Predict Hydrogeological Parameters Using Shear Waves from Multichannel Analysis of Surface Waves Method. In Proceedings of the Symposium on the Application of Geophysics to Engineering and Environmental Problems, Fort Worth, TX, USA, 29 March–2 April 2009; Environmental & Engineering Geophysical Society: Denver, CO, USA, 2009; p. 475. [Google Scholar] [CrossRef] [Green Version]
- Konstantaki, L.A.; Carpentier, S.; Garofalo, F.; Bergamo, P.; Socco, L.V. Determining hydrological and soil mechanical parameters from multichannel surface-wave analysis across the Alpine Fault at Inchbonnie, New Zealand. Near Surf. Geophys. 2013, 11, 435–448. [Google Scholar] [CrossRef]
- Pasquet, S.; Bodet, L.; Dhemaied, A.; Mouhri, A.; Vitale, Q.; Rejiba, F.; Flipo, N.; Guérin, R. Detecting different water table levels in a shallow aquifer with combined P-, surface and SH-wave surveys: Insights from VP/VS or Poisson’s ratios. J. Appl. Geophys. 2015, 113, 38–50. [Google Scholar] [CrossRef] [Green Version]
- Pasquet, S.; Bodet, L.; Longuevergne, L.; Dhemaied, A.; Camerlynck, C.; Rejiba, F.; Guérin, R. 2D characterization of near-surface VP/VS: Surface-wave dispersion inversion versus refraction tomography. Near Surf. Geophys. 2015, 13, 315–331. [Google Scholar] [CrossRef] [Green Version]
- Pasquet, S.; Holbrook, W.S.; Carr, B.J.; Sims, K.W.W. Geophysical imaging of shallow degassing in a Yellowstone hydrothermal system. Geophys. Res. Lett. 2016, 43, 12027–12035. [Google Scholar] [CrossRef]
- Pasquet, S.; Bodet, L. SWIP: An integrated workflow for surface-wave dispersion inversion and profiling. Geophysics 2017, 82, WB47–WB61. [Google Scholar] [CrossRef]
- Dangeard, M.; Bodet, L.; Pasquet, S.; Thiesson, J.; Guérin, R.; Jougnot, D.; Longuevergne, L. Estimating picking errors in near-surface seismic data to enable their time-lapse interpretation of hydrosystems. Near Surf. Geophys. 2018, 16, 613–625. [Google Scholar] [CrossRef]
- Bergamo, P.; Dashwood, B.; Uhlemann, S.; Swift, R.; Chambers, J.E.; Gunn, D.A.; Donohue, S. Time-lapse monitoring of climate effects on earthworks using surface waves. Geophysics 2016, 81, EN1–EN15. [Google Scholar] [CrossRef] [Green Version]
- Bergamo, P.; Dashwood, B.; Uhlemann, S.; Swift, R.; Chambers, J.E.; Gunn, D.A.; Donohue, S. Time-lapse monitoring of fluid-induced geophysical property variations within an unstable earthwork using P-wave refraction. Geophysics 2016, 81, EN17–EN27. [Google Scholar] [CrossRef] [Green Version]
- Pasquet, S.; Bodet, L.; Bergamo, P.; Guérin, R.; Martin, R.; Mourgues, R.; Tournat, V. Small-Scale Seismic Monitoring of Varying Water Levels in Granular Media. Vadose Zone J. 2016, 15, 1–14. [Google Scholar] [CrossRef]
- Bachrach, R.; Nur, A. High-resolution shallow-seismic experiments in sand, Part I: Water table, fluid flow, and saturation. Geophysics 1998, 63, 1225–1233. [Google Scholar] [CrossRef]
- Bachrach, R.; Dvorkin, J.; Nur, A. High-resolution shallow-seismic experiments in sand, Part II: Velocities in shallow unconsolidated sand. Geophysics 1998, 63, 1234–1240. [Google Scholar] [CrossRef]
- Bachrach, R.; Dvorkin, J.; Nur, A.M. Seismic velocities and Poisson’s ratio of shallow unconsolidated sands. Geophysics 2000, 65, 559–564. [Google Scholar] [CrossRef]
- West, M.; Menke, W. Fluid-Induced Changes in Shear Velocity from Surface Waves. In Proceedings of the Symposium on the Application of Geophysics to Engineering and Environmental Problems, Arlington, VA, USA, 20–24 February 2000; Environmental & Engineering Geophysical Society: Denver, CO, USA, 2000; pp. 21–28. [Google Scholar] [CrossRef]
- Shen, J.; Crane, J.M.; Lorenzo, J.M.; White, C.D. Seismic Velocity Prediction in Shallow (<30 m) Partially Saturated, Unconsolidated Sediments Using Effective Medium Theory. J. Environ. Eng. Geophys. 2016, 21, 67–78. [Google Scholar] [CrossRef] [Green Version]
- Holbrook, W.S.; Riebe, C.S.; Elwaseif, M.; Hayes, J.L.; Basler-Reeder, K.; Harry, D.L.; Malazian, A.; Dosseto, A.; Hartsough, P.C.; Hopmans, J.W. Geophysical constraints on deep weathering and water storage potential in the Southern Sierra Critical Zone Observatory. Earth Surf. Process. Landf. 2014, 39, 366–380. [Google Scholar] [CrossRef] [Green Version]
- Cho, G.-C.; Santamarina, J.C. Unsaturated Particulate Materials—Particle-Level Studies. J. Geotech. Geoenviron. Eng. 2001, 127, 84–96. [Google Scholar] [CrossRef]
- Sawangsuriya, A.; Edil, T.B.; Bosscher, P.J. Modulus-suction-moisture relationship for compacted soils in postcompaction state. J. Geotech. Geoenviron. Eng. 2009, 135, 1390–1403. [Google Scholar] [CrossRef]
- Taylor, O.-D.S.; Cunningham, A.L.; Walker, R.E.; Mckenna, M.H.; Martin, K.E.; Kinnebrew, P.G. The behaviour of near-surface soils through ultrasonic near-surface inundation testing. Near Surf. Geophys. 2019, 17, 331–344. [Google Scholar] [CrossRef] [Green Version]
- Gassmann, F. Elastic waves through a packing of spheres. Geophysics 1951, 16, 673–685. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. I. Low-Frequency Range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Makse, H.A.; Gland, N.; Johnson, D.L.; Schwartz, L. Granular packings: Nonlinear elasticity, sound propagation, and collective relaxation dynamics. Phys. Rev. E 2004, 70, 061302. [Google Scholar] [CrossRef] [Green Version]
- Linder, S.; Paasche, H.; Tronicke, J.; Niederleithinger, E.; Vienken, T. Zonal cooperative inversion of crosshole P-wave, S-wave, and georadar traveltime data sets. J. Appl. Geophys. 2010, 72, 254–262. [Google Scholar] [CrossRef]
- Meju, M.A.; Gallardo, L.A.; Mohamed, A.K. Evidence for correlation of electrical resistivity and seismic velocity in heterogeneous near-surface materials. Geophys. Res. Lett. 2003, 30, 1–26. [Google Scholar] [CrossRef]
- Doetsch, J.; Linde, N.; Coscia, I.; Greenhalgh, S.A.; Green, A.G. Zonation for 3D aquifer characterization based on joint inversions of multimethod crosshole geophysical data. Geophysics 2010, 75, G53–G64. [Google Scholar] [CrossRef]
- Hilbich, C. Time-lapse refraction seismic tomography for the detection of ground ice degradation. Cryosphere 2010, 4, 243–259. [Google Scholar] [CrossRef] [Green Version]
- Valois, R.; Galibert, P.Y.; Guerin, R.; Plagnes, V. Application of combined time-lapse seismic refraction and electrical resistivity tomography to the analysis of infiltration and dissolution processes in the epikarst of the Causse du Larzac (France). Near Surf. Geophys. 2016, 14, 13–22. [Google Scholar] [CrossRef]
- Ruelleu, S.; Moreau, F.; Bour, O.; Gapais, D.; Martelet, G. Impact of gently dipping discontinuities on basement aquifer recharge: An example from Ploemeur (Brittany, France). J. Appl. Geophys. 2010, 70, 161–168. [Google Scholar] [CrossRef]
- Touchard, F. Caracterisation Hydrogeologique d’un Aquifere en Socle Fracture—Site de Ploemeur (Morbihan). Ph.D. Thesis, Université de Rennes 1, Rennes, France, 1999. [Google Scholar]
- Le Borgne, T.; Bour, O.; Paillet, F.L.; Caudal, J.P. Assessment of preferential flow path connectivity and hydraulic properties at single-borehole and cross-borehole scales in a fractured aquifer. J. Hydrol. 2006, 328, 347–359. [Google Scholar] [CrossRef]
- Jiménez-Martínez, J.; Longuevergne, L.; Le Borgne, T.; Davy, P.; Russian, A.; Bour, O. Temporal and spatial scaling of hydraulic response to recharge in fractured aquifers: Insights from a frequency domain analysis. Water Resour. Res. 2013, 49, 3007–3023. [Google Scholar] [CrossRef] [Green Version]
- Coulon, E. Rapport de Stage. Master’s Thesis, Université de Rennes 1, Rennes, France, 2012. [Google Scholar]
- Rücker, C.; Günther, T.; Wagner, F.M. pyGIMLi: An open-source library for modelling and inversion in geophysics. Comput. Geosci. 2017, 109, 106–123. [Google Scholar] [CrossRef]
- Daily, W.; Ramirez, A.; LaBrecque, D.; Nitao, J. Electrical resistivity tomography of vadose water movement. Water Resour. Res. 1992, 28, 1429–1442. [Google Scholar] [CrossRef]
- Doetsch, J.; Linde, N.; Vogt, T.; Binley, A.; Green, A.G. Imaging and quantifying salt-tracer transport in a riparian groundwater system by means of 3D ERT monitoring. Geophysics 2012, 77, B207–B218. [Google Scholar] [CrossRef] [Green Version]
- Rosas Carbajal, M.; Linde, N.; Kalscheuer, T. Focused time-lapse inversion of radio and audio magnetotelluric data. J. Appl. Geophys. 2012, 84, 29–38. [Google Scholar] [CrossRef] [Green Version]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef] [Green Version]
- Linde, N.; Binley, A.; Tryggvason, A.; Pedersen, L.B.; Revil, A. Improved hydrogeophysical characterization using joint inversion of cross-hole electrical resistance and ground-penetrating radar traveltime data. Water Resour. Res. 2006, 42, W12404. [Google Scholar] [CrossRef] [Green Version]
- Archie, G.E. The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics. In Proceedings of the Transactions of the AIME, Dallas, TX, USA, October 1941; Society of Petroleum Engineers: Richardson, TX, USA, 1942; Volume 146, pp. 9–16. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media, 2nd ed.; Cambridge University Press: New York, NT, USA, 2009. [Google Scholar] [CrossRef]
- Looms, M.C.; Jensen, K.H.; Binley, A.; Nielsen, L. Monitoring Unsaturated Flow and Transport Using Cross-Borehole Geophysical Methods. Vadose Zone J. 2008, 7, 227–237. [Google Scholar] [CrossRef] [Green Version]
- Barrière, J.; Bordes, C.; Brito, D.; Sénéchal, P.; Perroud, H. Laboratory monitoring of P waves in partially saturated sand. Geophys. J. Int. 2012, 191, 1152–1170. [Google Scholar] [CrossRef] [Green Version]
- Fratta, D.; Alshibli, K.; Tanner, W.M.; Roussel, L. Combined TDR and P-wave velocity measurements for the determination of in situ soil density-experimental study. Geotech. Test. J. 2005, 28, 553–563. [Google Scholar] [CrossRef]
- Day-Lewis, F.D. Applying petrophysical models to radar travel time and electrical resistivity tomograms: Resolution-dependent limitations. J. Geophys. Res. 2005, 110, B08206. [Google Scholar] [CrossRef] [Green Version]
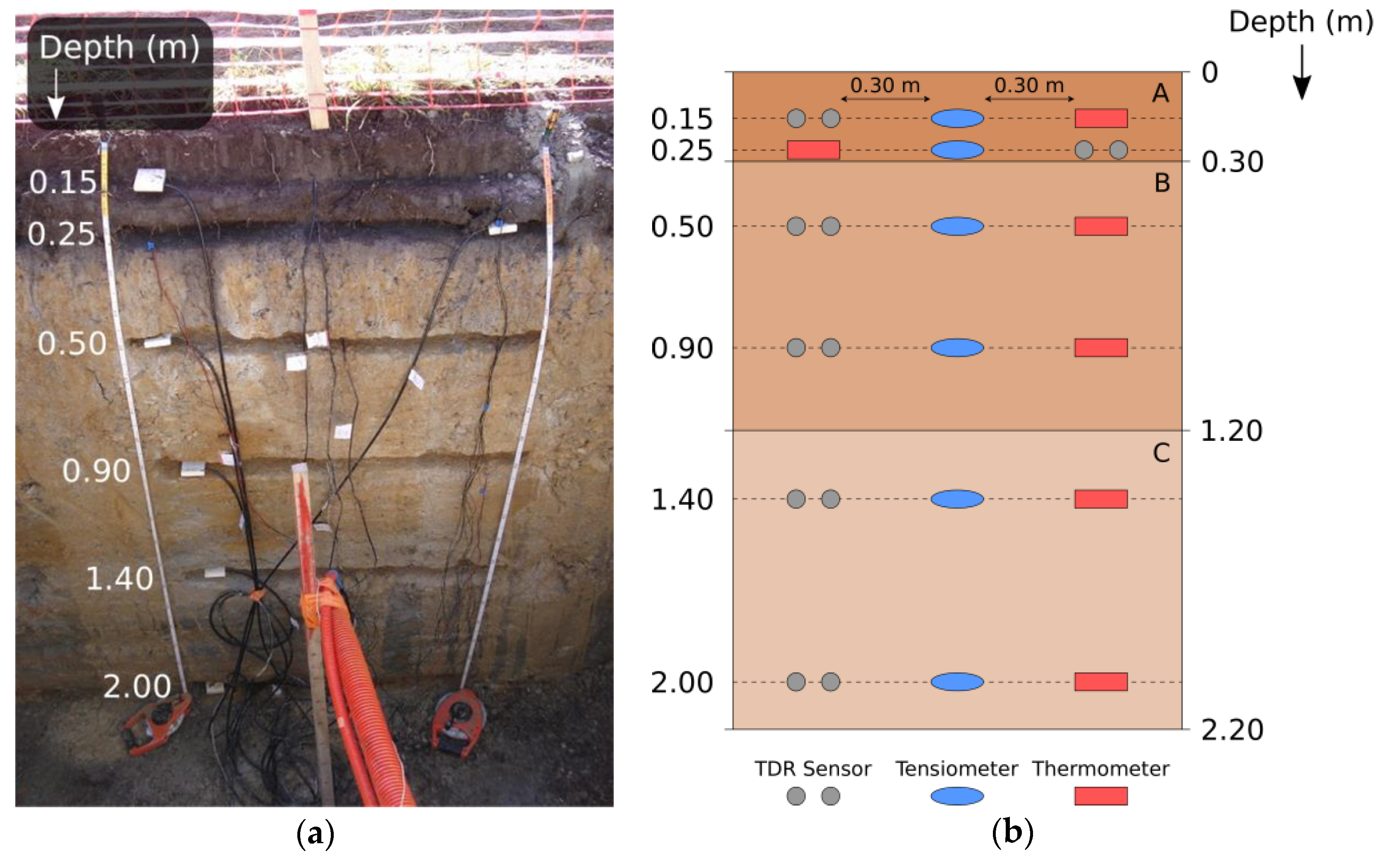



| Horizon | Horizon Limits (m) | Clay (%) | Silt (%) | Sand (%) | Soil Type | Sampling Depth (m) | ρb (g/cm3) | ϕ (%) |
|---|---|---|---|---|---|---|---|---|
| A | 0–0.3 | 7.50 | 85.14 | 7.36 | Silt | 0.15 0.25 | 1.04 ± 0.02 1.31 ± 0.05 | 50 50 |
| B | 0.3–1.2 | 2.76 | 68.39 | 28.85 | Silty loam | 0.50 0.90 | 1.79 ± 0.01 1.71 ± 0.02 | 30 30 |
| C | 1.2–2 | 2.38 | 62.43 | 32.81 | Silty loam | 1.40 2.00 | 1.86 ± 0.02 1.65 ± 0.05 | 30 30 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blazevic, L.A.; Bodet, L.; Pasquet, S.; Linde, N.; Jougnot, D.; Longuevergne, L. Time-Lapse Seismic and Electrical Monitoring of the Vadose Zone during a Controlled Infiltration Experiment at the Ploemeur Hydrological Observatory, France. Water 2020, 12, 1230. https://doi.org/10.3390/w12051230
Blazevic LA, Bodet L, Pasquet S, Linde N, Jougnot D, Longuevergne L. Time-Lapse Seismic and Electrical Monitoring of the Vadose Zone during a Controlled Infiltration Experiment at the Ploemeur Hydrological Observatory, France. Water. 2020; 12(5):1230. https://doi.org/10.3390/w12051230
Chicago/Turabian StyleBlazevic, Lara A., Ludovic Bodet, Sylvain Pasquet, Niklas Linde, Damien Jougnot, and Laurent Longuevergne. 2020. "Time-Lapse Seismic and Electrical Monitoring of the Vadose Zone during a Controlled Infiltration Experiment at the Ploemeur Hydrological Observatory, France" Water 12, no. 5: 1230. https://doi.org/10.3390/w12051230
APA StyleBlazevic, L. A., Bodet, L., Pasquet, S., Linde, N., Jougnot, D., & Longuevergne, L. (2020). Time-Lapse Seismic and Electrical Monitoring of the Vadose Zone during a Controlled Infiltration Experiment at the Ploemeur Hydrological Observatory, France. Water, 12(5), 1230. https://doi.org/10.3390/w12051230






