Effect of Rainfall, Runoff and Infiltration Processes on the Stability of Footslopes
Abstract
:1. Introduction
2. Method and Materials
2.1. Mathematical Basis
2.1.1. Hydrological Module
Kinematic Wave Equation
Infiltration Equation
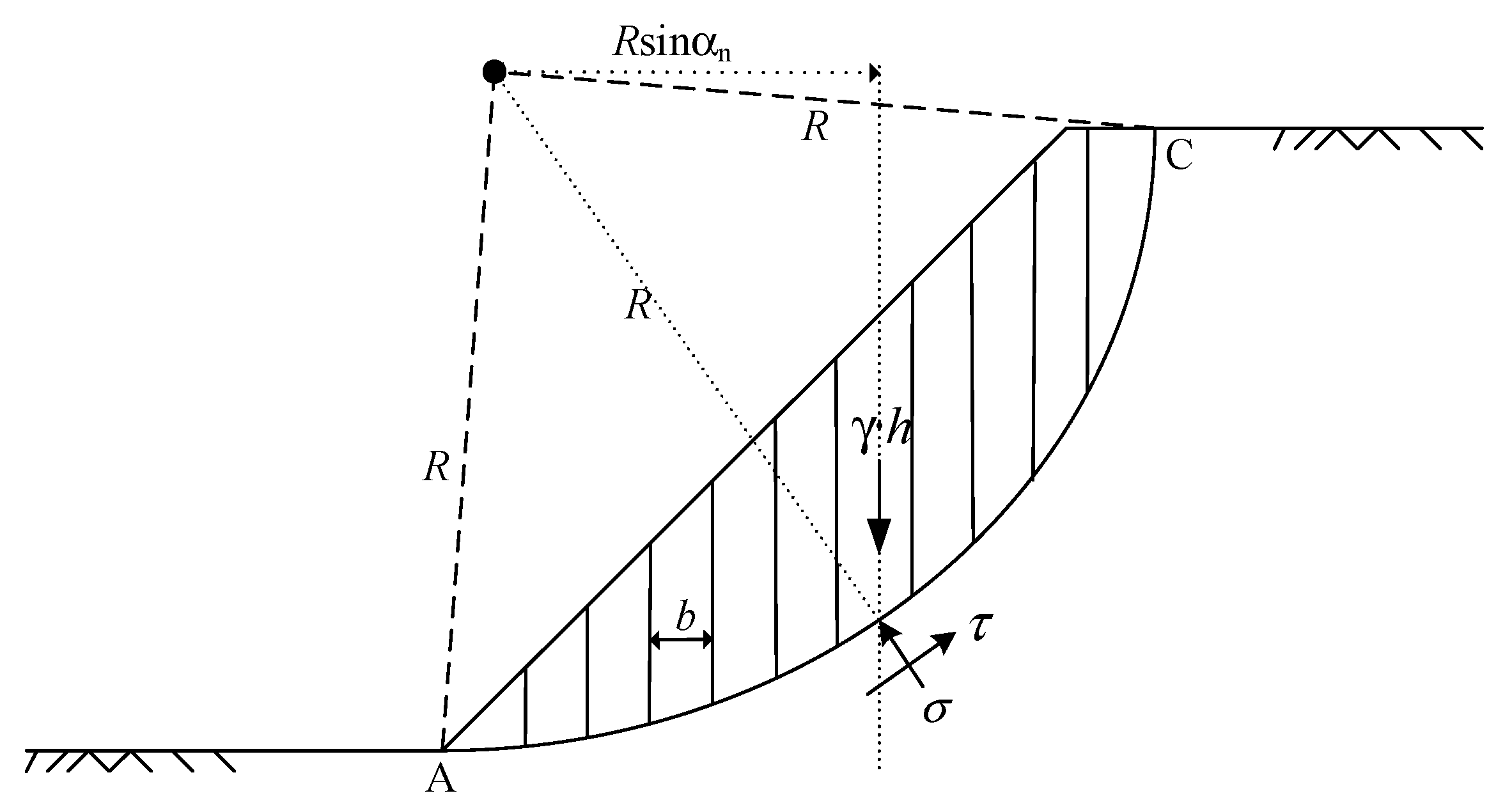
2.1.2. Soil Failure Module (Slope Stability Analysis)
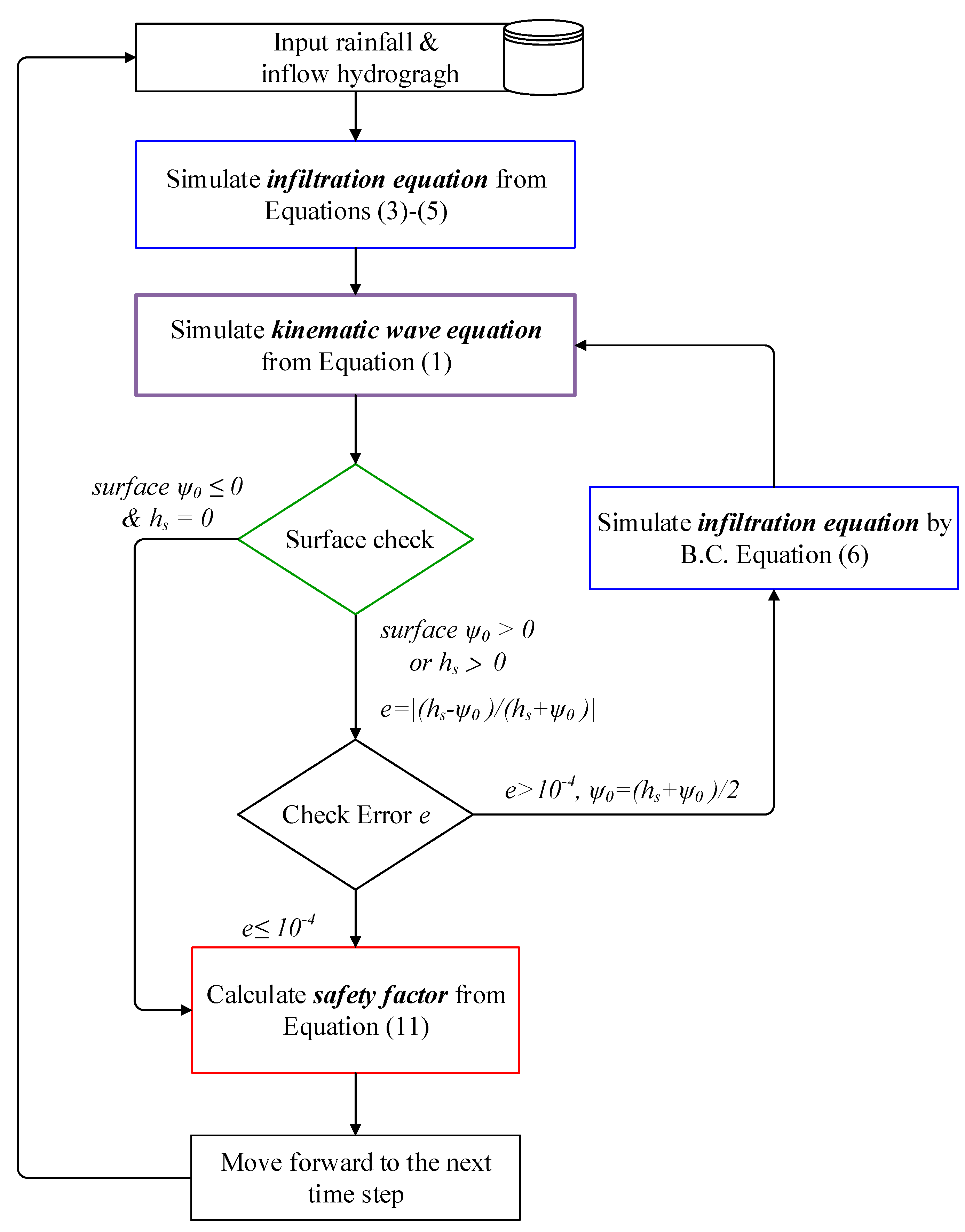
2.1.3. Computational Procedure
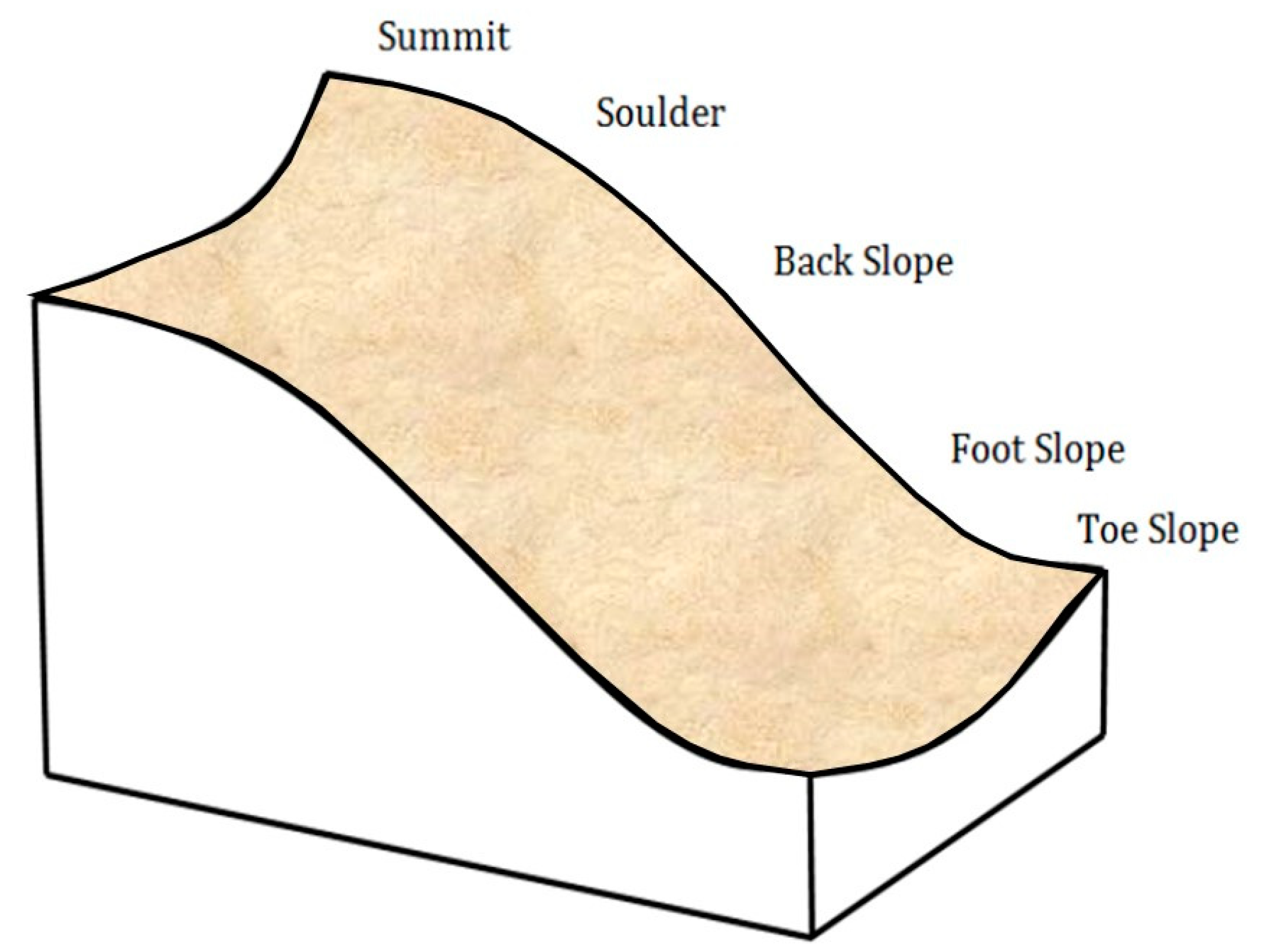
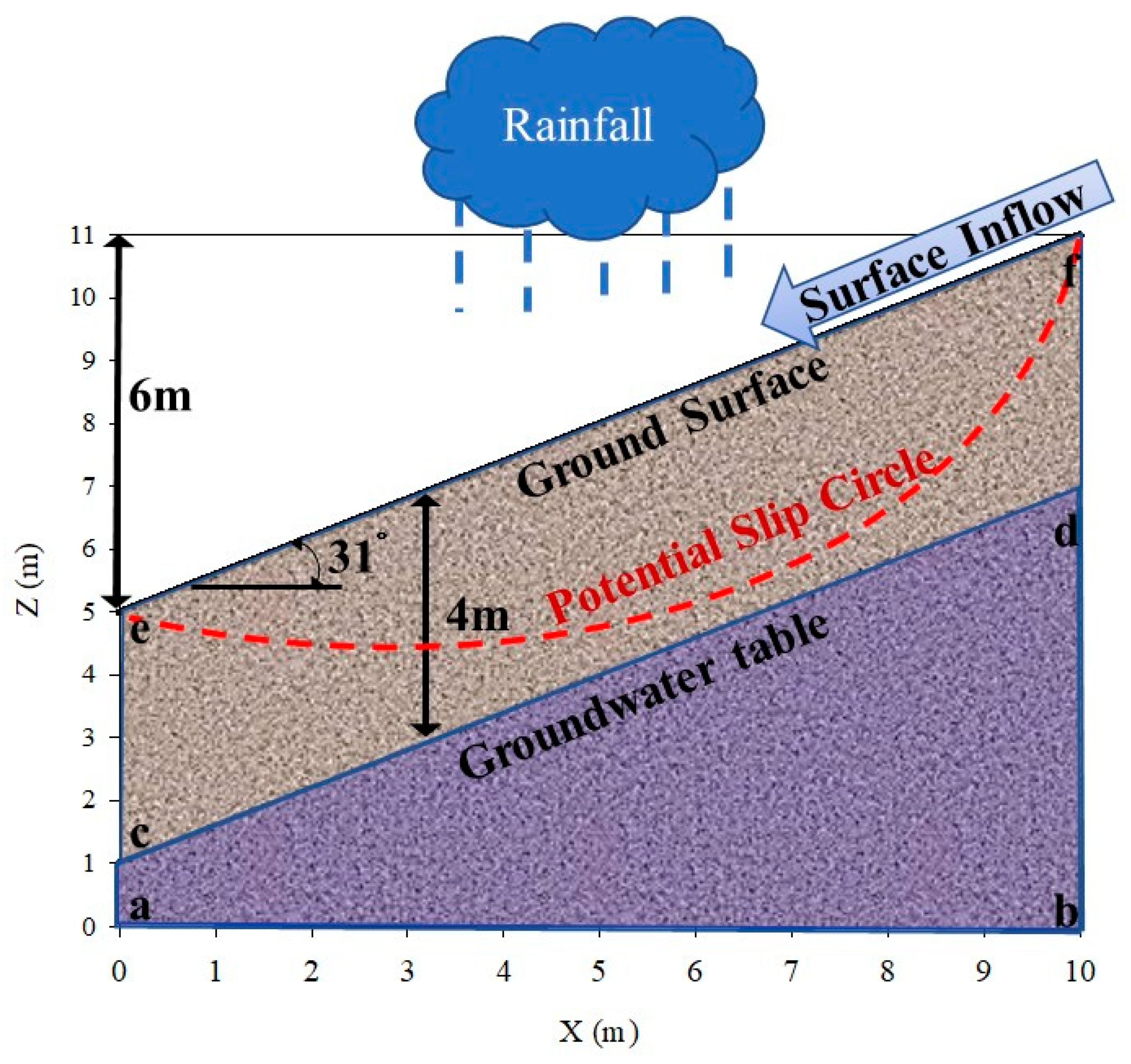
2.2. Description of the Study Case
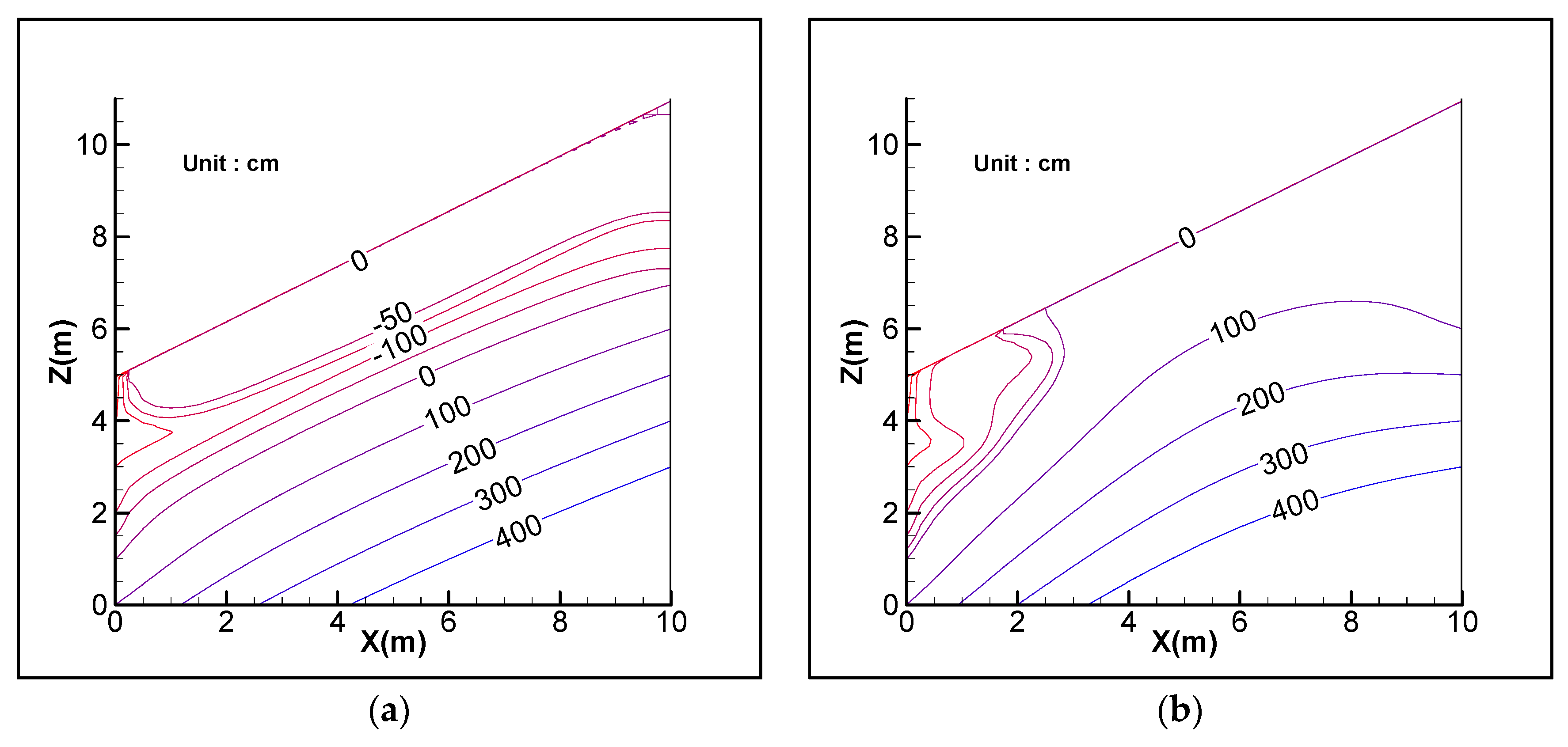
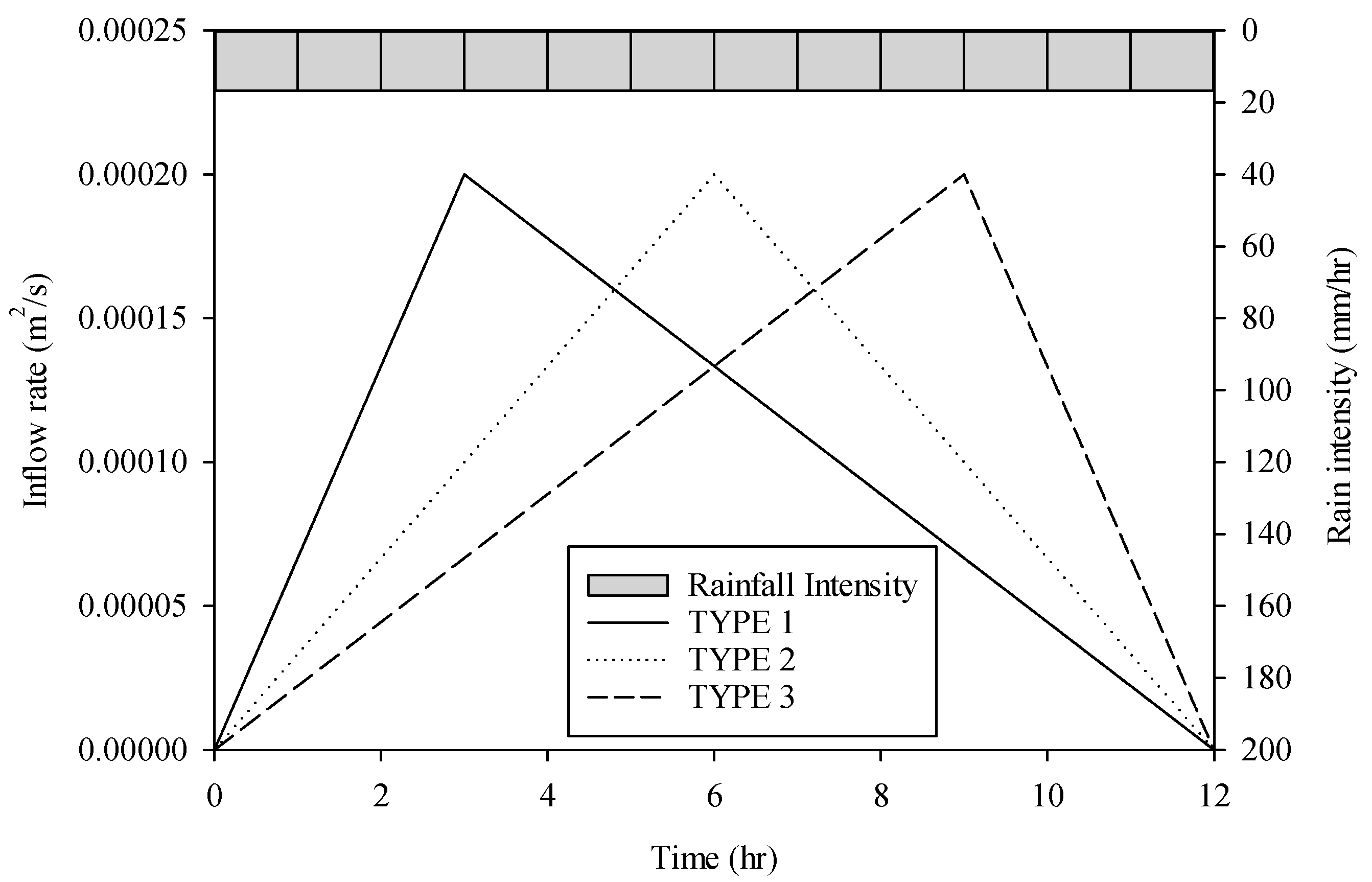
3. Results and Discussions
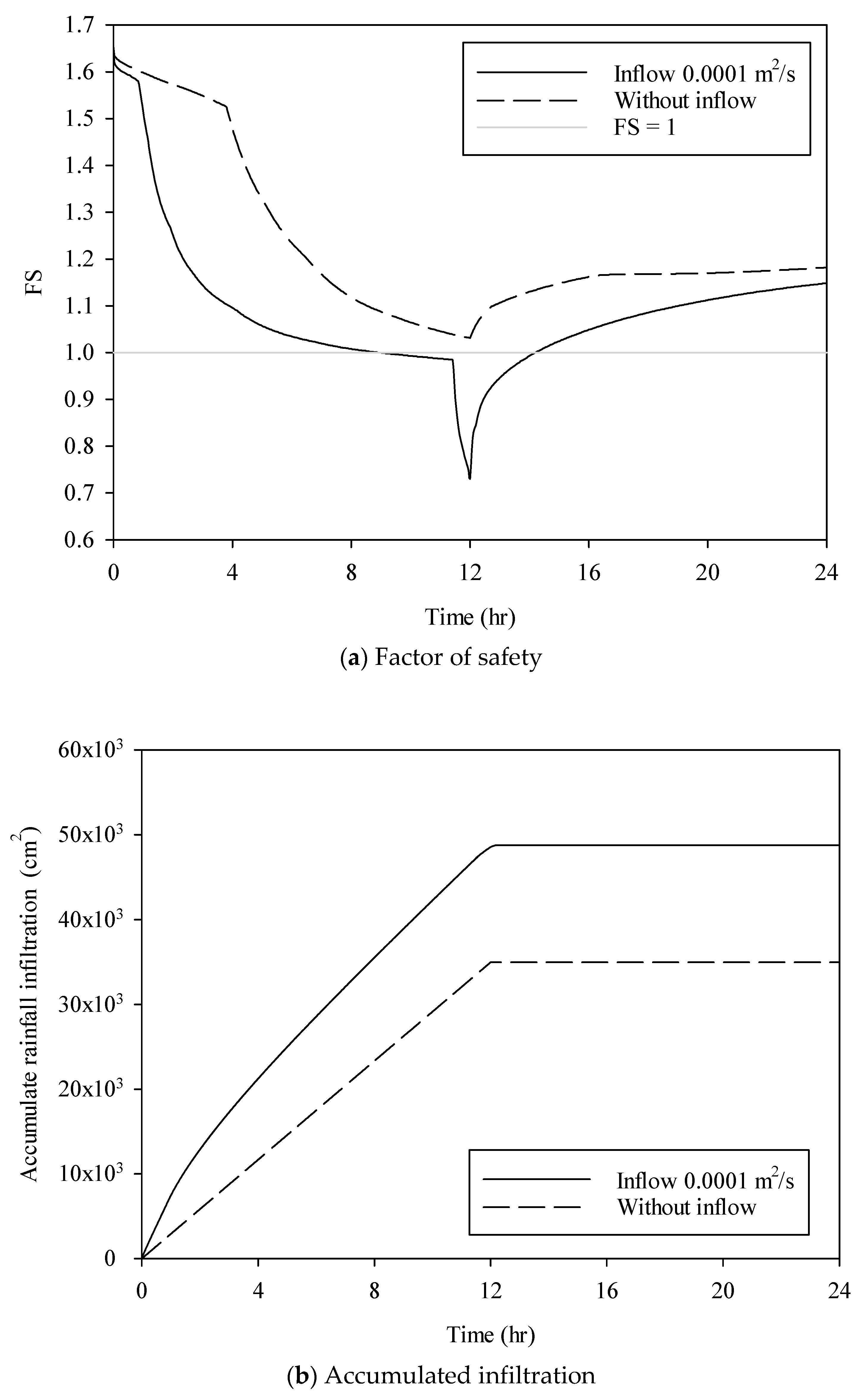
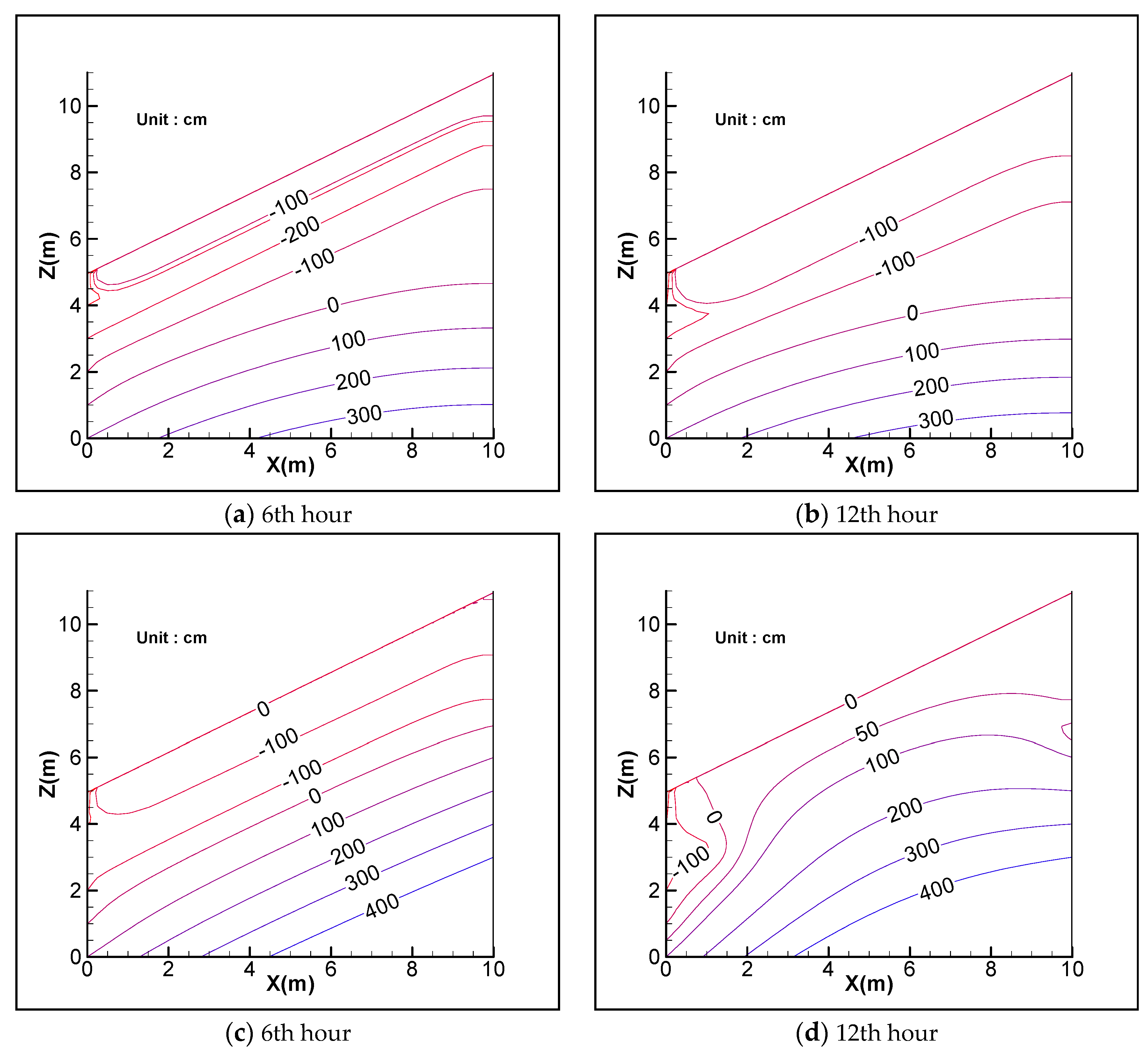
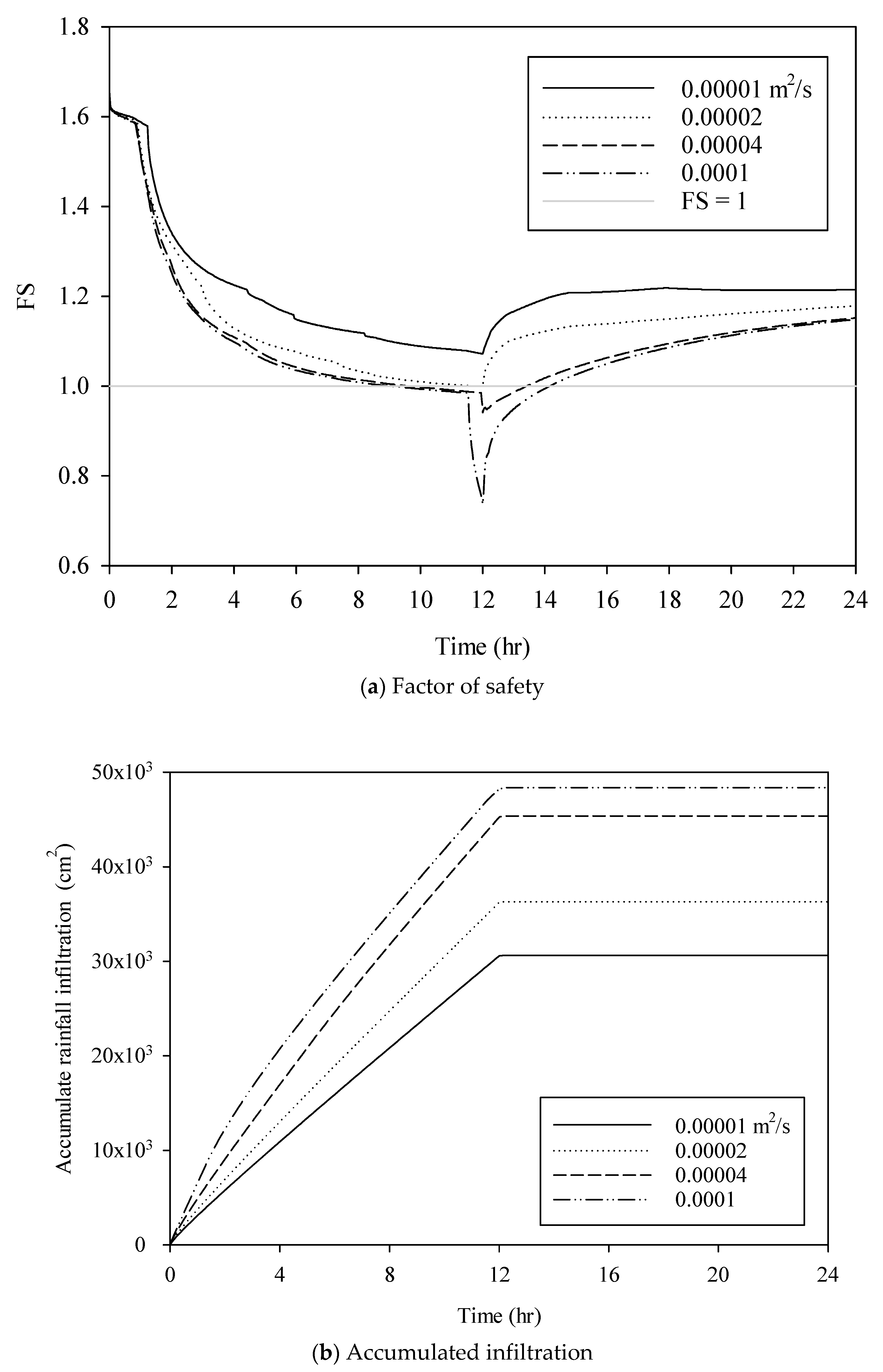
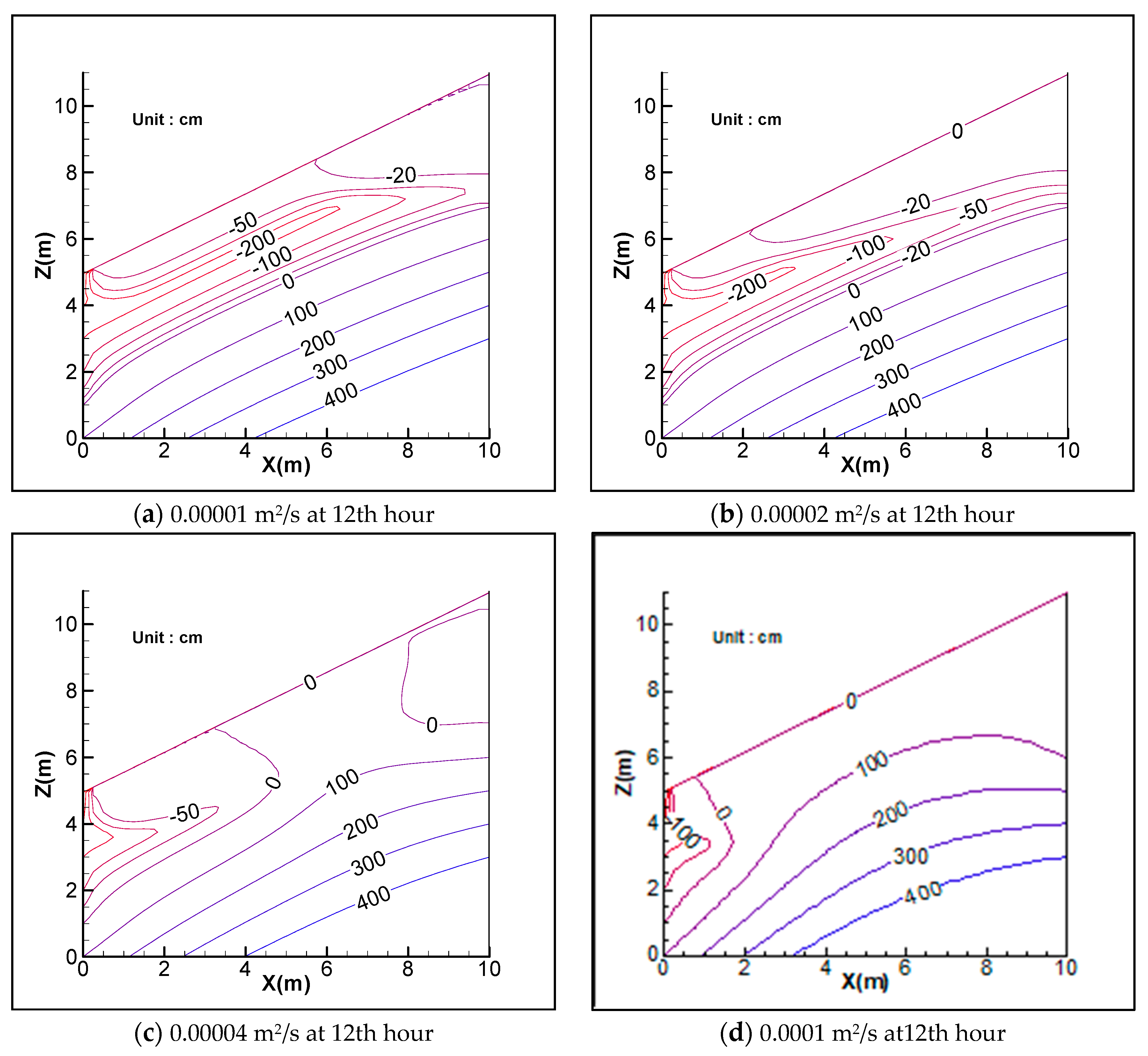
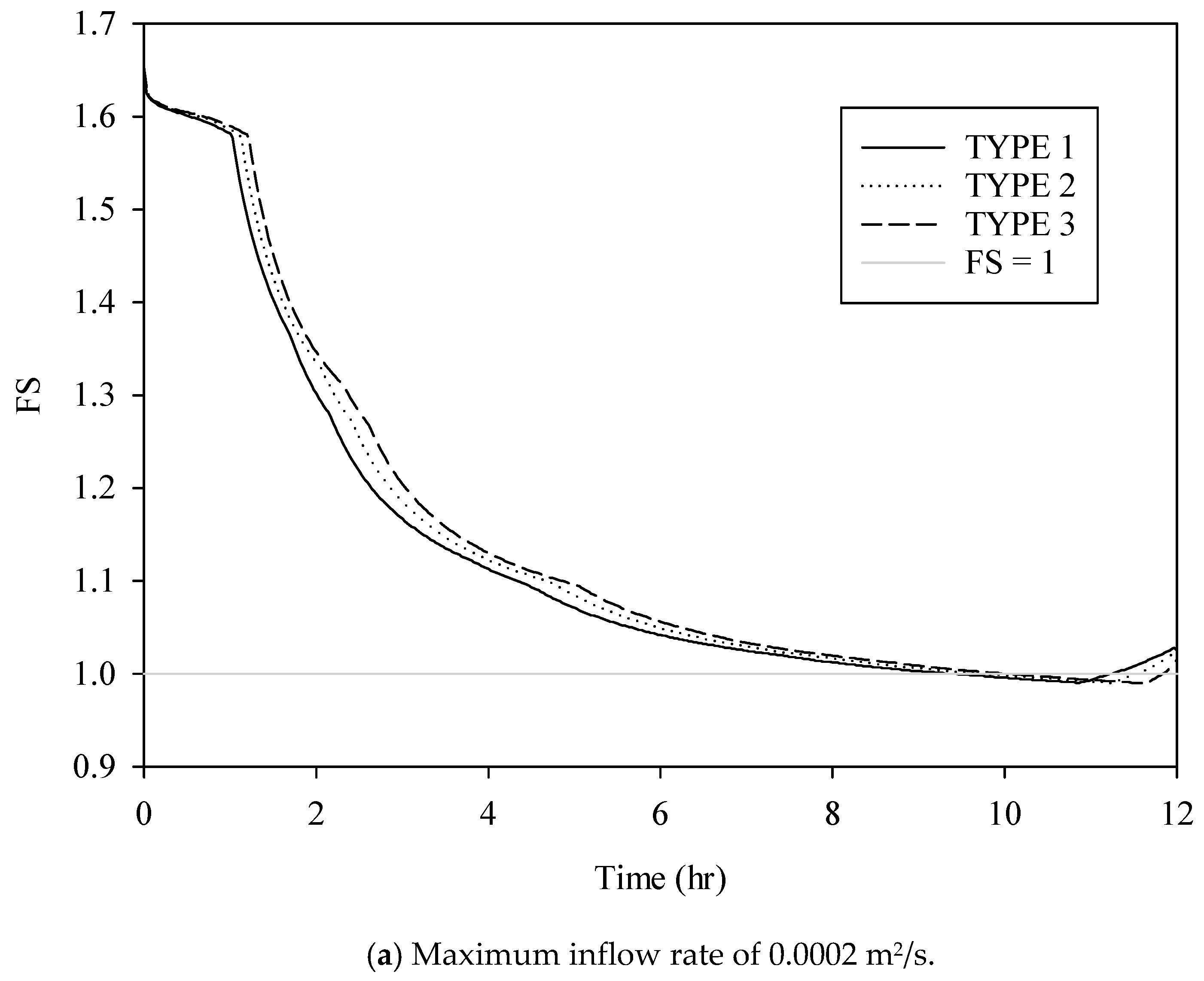
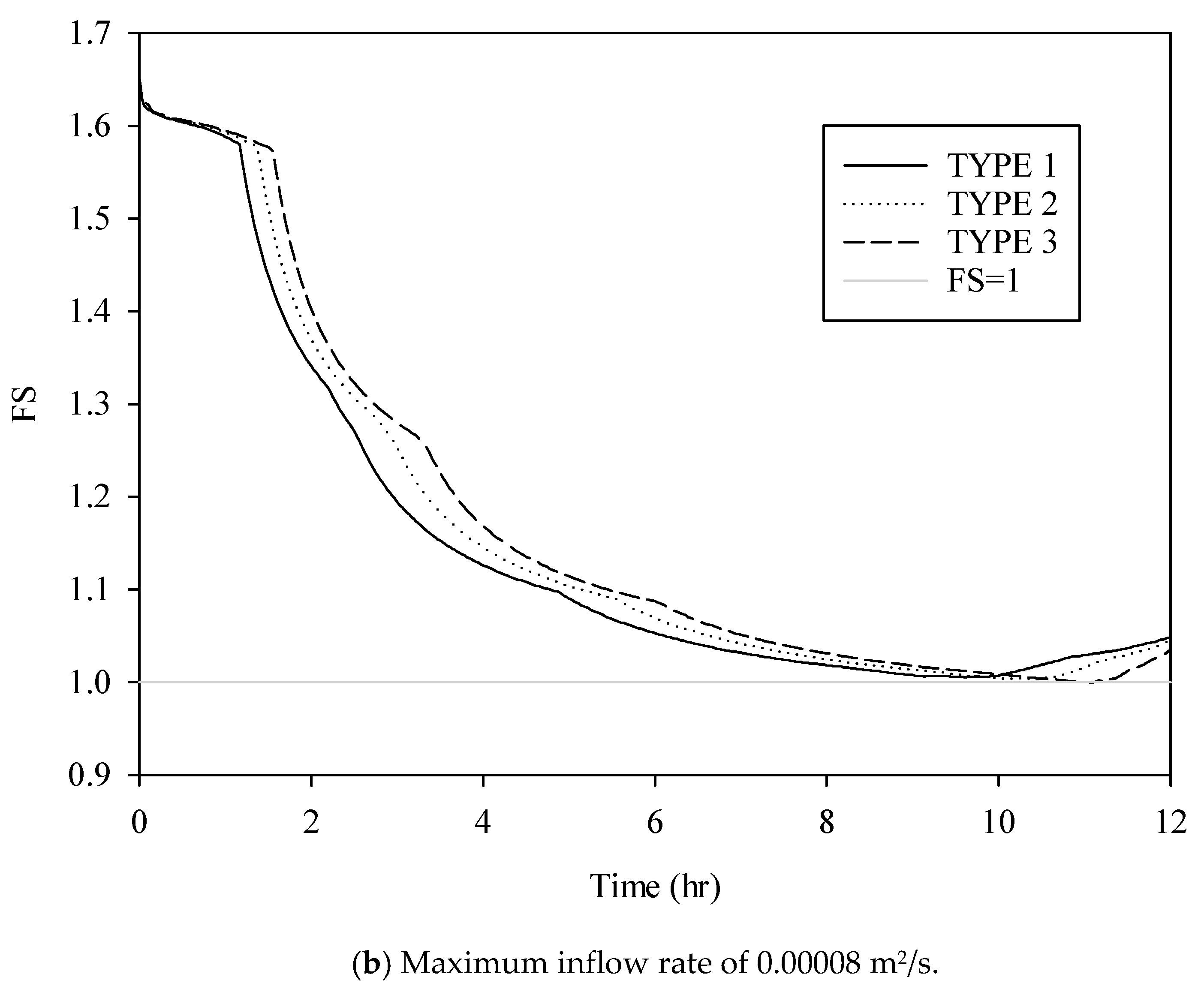
3.1. Magnitude of Surface Inflow
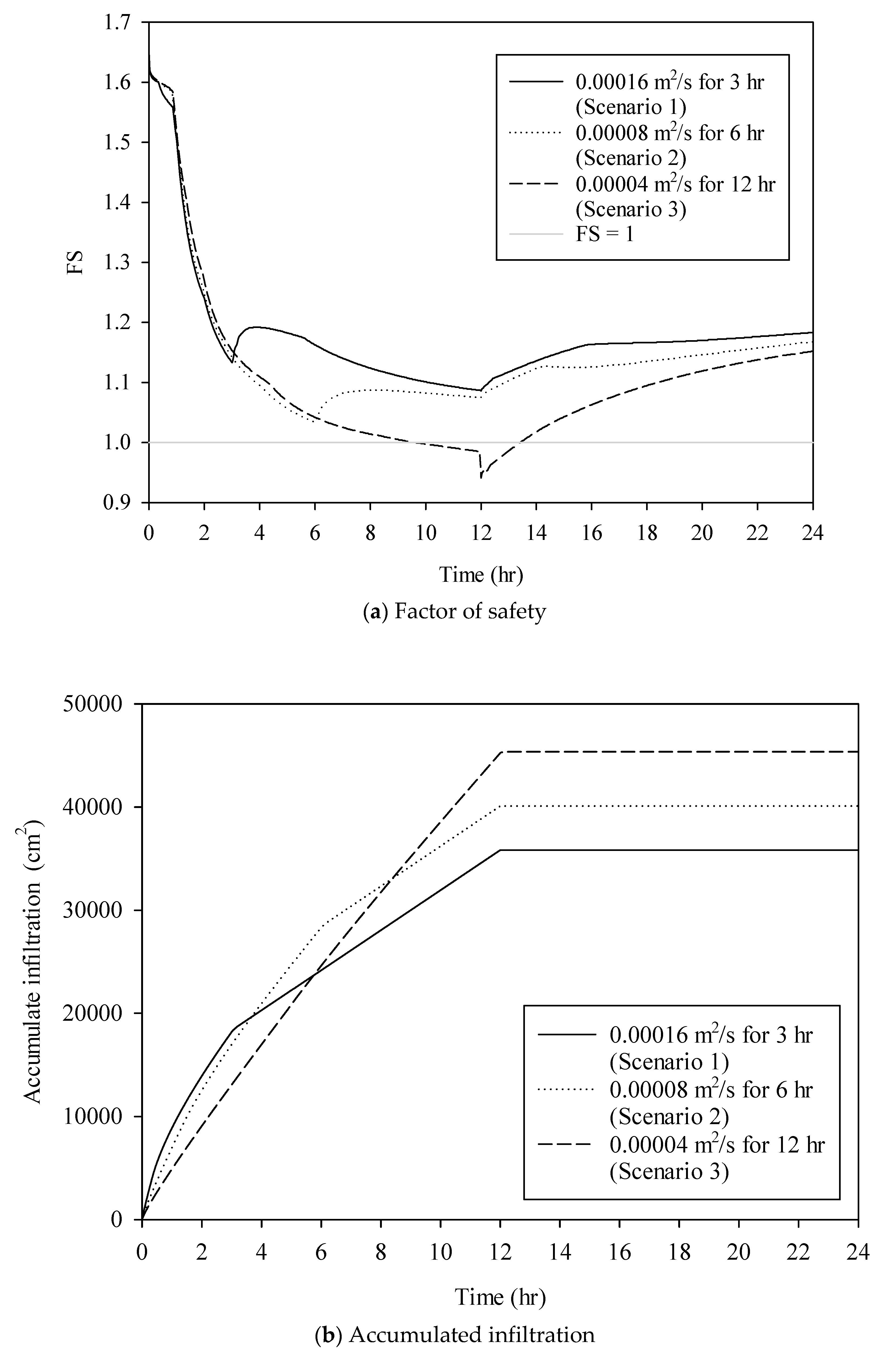
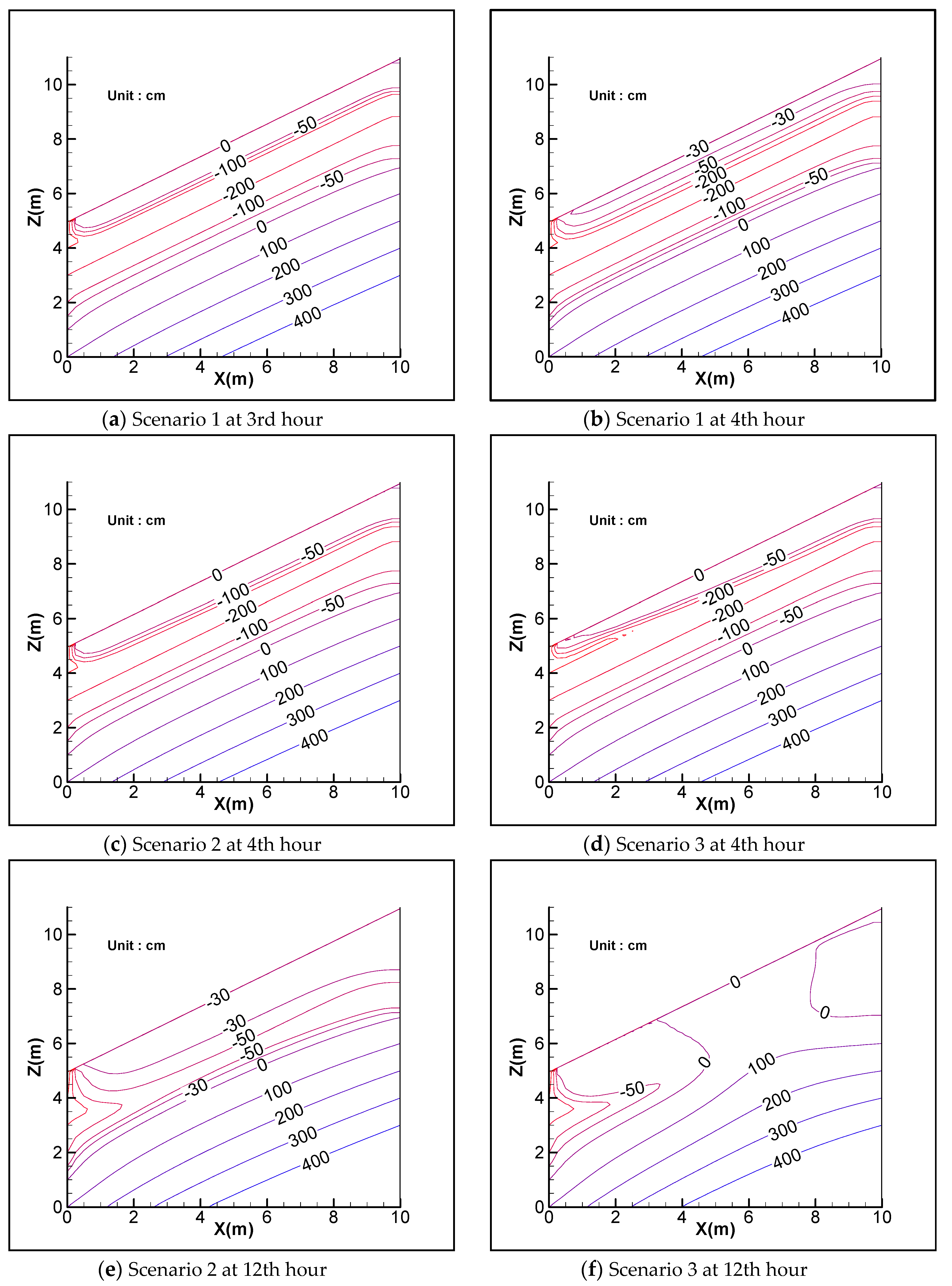
3.2. Duration
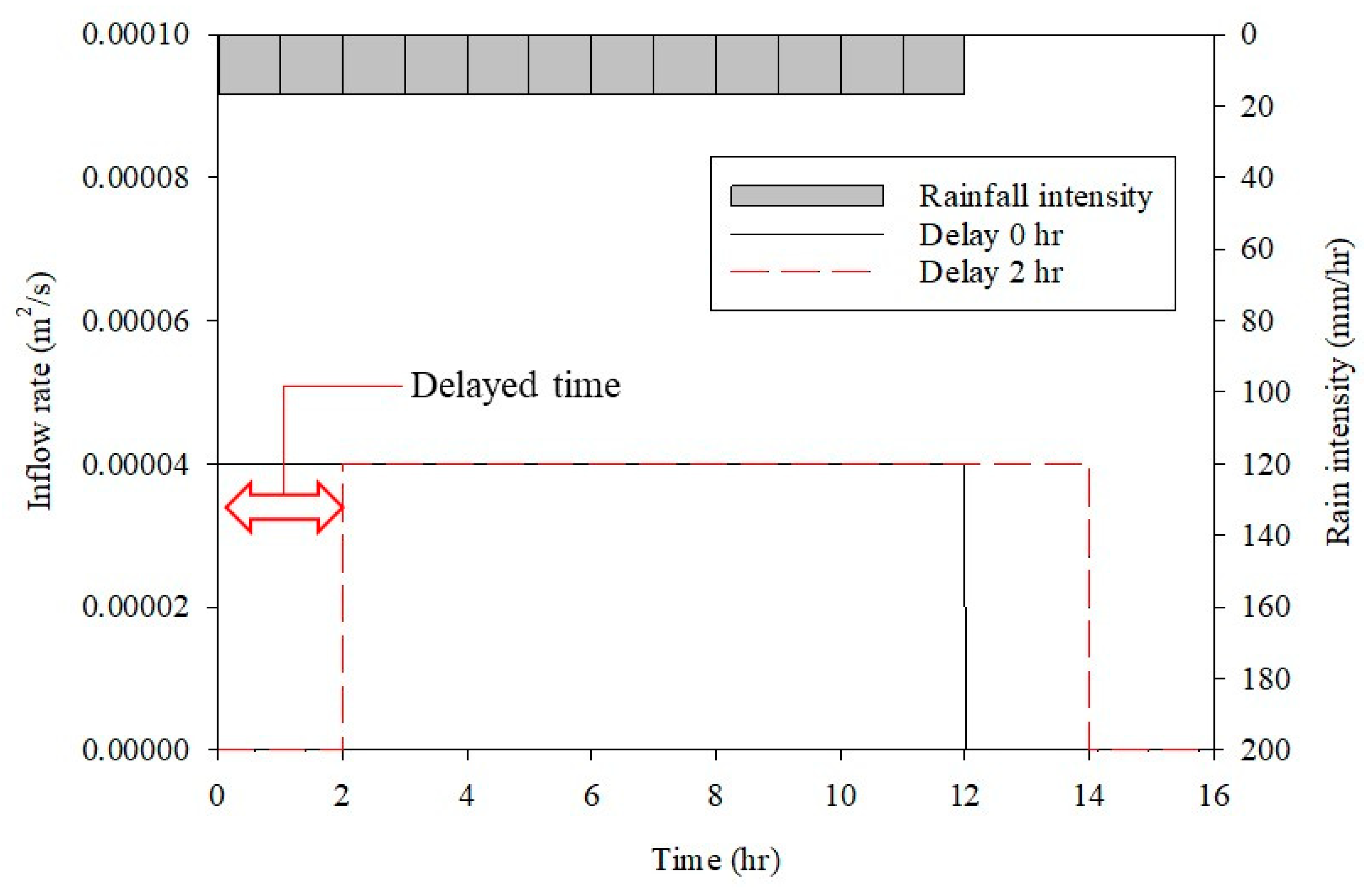
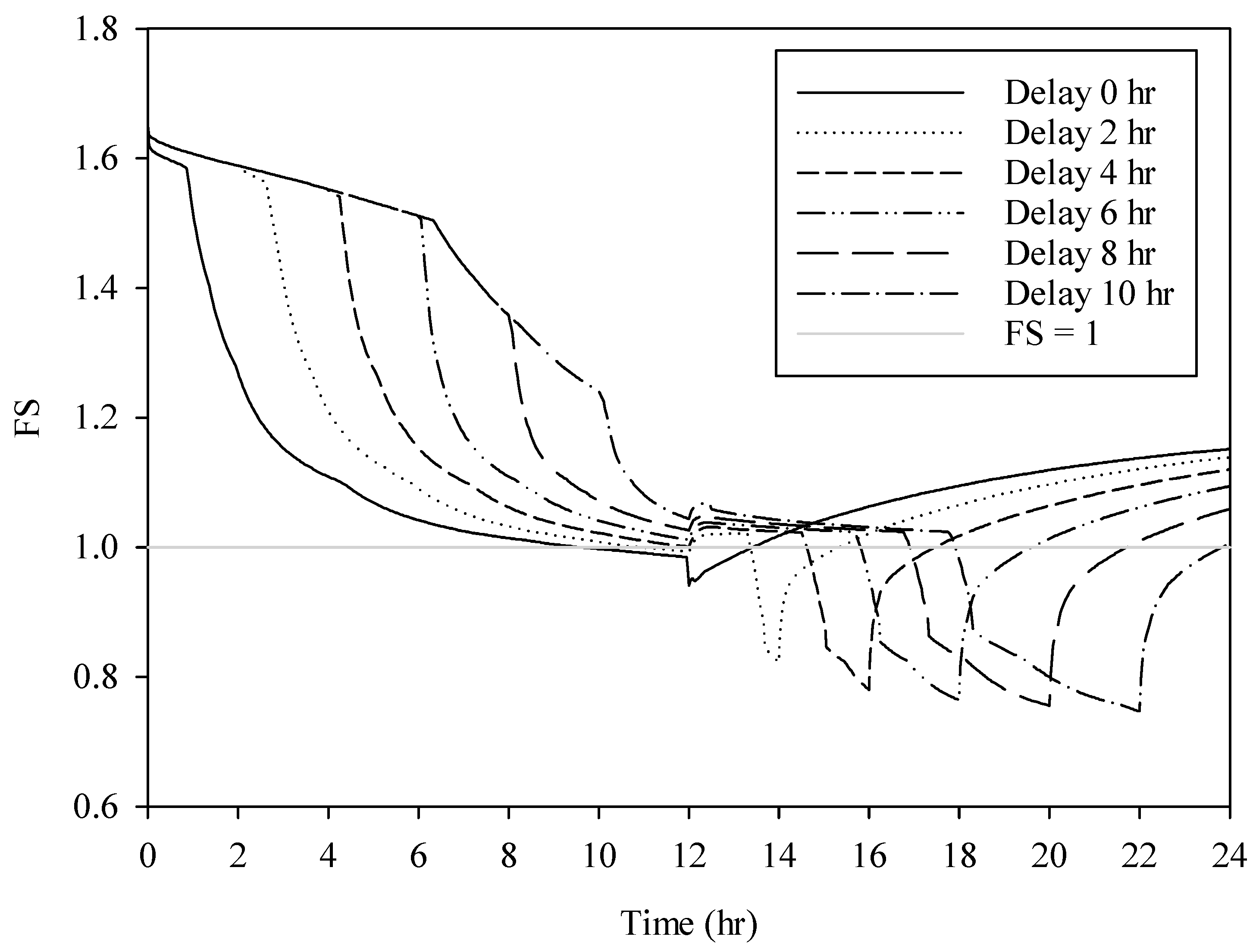
3.3. Delayed Surface Inflow
3.4. Shape of Inflow
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| List of Symbols | |
| b | Slice width |
| Effective cohesion | |
| Infiltrate rate | |
| Depth of slope surface flow | |
| Rainfall intensity | |
| n | Manning’s roughness coefficient. |
| Bed slope | |
| Time | |
| ua | Pore air pressure |
| uw | Pore water pressure |
| Hydraulic conductivities in the x-direction | |
| Hydraulic conductivities in the z-direction | |
| M | Fitting parameter |
| N | Fitting parameter |
| Degree of saturation | |
| Distance downslope | |
| Slope angle | |
| unit weight of soil | |
| unit weight of water | |
| Fitting parameter | |
| Normal effective stress | |
| Moisture content | |
| Residual moisture content | |
| Saturated moisture content | |
| Effective friction angle | |
| Friction angle with respect to the matric suction | |
| Pore water pressure head | |
| Positive pore water pressure head | |
| Negative pore water pressure head | |
References
- Sidle, C.R.; Greco, R.; Bogaard, T. Overview of Landslide Hydrology. Water 2019, 11, 148. [Google Scholar] [CrossRef] [Green Version]
- Bogaard, T.A.; Greco, R. Landslide Hydrology: From Hydrology to Pore Pressure. WIREs Water 2016, 3, 439–459. [Google Scholar] [CrossRef]
- Pujades, E.; DeSimone, S.; Carrera, J.; Vázquez-Suñé, E.; Jurado, A. Settlements around Pumping Wells: Analysis of Influential Factors and a Simple Calculation Procedure. J. Hydrol. 2017, 548, 225–236. [Google Scholar] [CrossRef]
- Pujades, E.; Jurado, A.; Carrera, J.; Vázquez-Suñé, E.; Dassargues, A. Hydrogeological Assessment of Non-Linear Underground Enclosures. Eng. Geol. 2016, 207, 91–102. [Google Scholar] [CrossRef]
- Wu, Y.-X.; Shen, S.-L.; Lyu, H.-M.; Zhou, A. Analyses of Leakage Effect of Waterproof Curtain during Excavation Dewatering. J. Hydrol. 2020, 583, 124582. [Google Scholar] [CrossRef]
- Wu, Y.-X.; Lyu, H.-M.; Shen, S.-L.; Zhou, A. A Three-Dimensional Fluid-Solid Coupled Numerical Modeling of the Barrier Leakage below the Excavation Surface Due to Dewatering. Hydrogeol. J. 2020. [Google Scholar] [CrossRef]
- Wu, H.-N.; Shen, S.-L.; Chen, R.-P.; Zhou, A. Three-Dimensional Numerical Modelling on Localised Leakage in Segmental Lining of Shield Tunnels. Comput. Geotech. 2020, 122, 103549. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef] [Green Version]
- Baum, R.L.; Savage, W.Z.; Godt, J.W. TRIGRS–A Fortran Program for Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Analysis, Version 2.0; US Geological Survey: Reston, VA, USA, 2008.
- Tsai, T.-L.; Yang, J.-C. Modeling of rainfall-triggered shallow landslide. Environ. Geol. 2006, 50, 525–534. [Google Scholar] [CrossRef]
- Tarantino, A.; Bosco, G. Role of soil suction in understanding the triggering mechanisms of flow slides associated with rainfall. In Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment, Proceedings of the Second International Conference on Debris-Flow Hazards Mitigation, Taipei, Taiwan, 16–18 August 2000; A.A. Balkema: Rotterdam, The Netherlands, 2000; pp. 81–88. [Google Scholar]
- Collins, B.D.; Znidarcic, D. Stability Analyses of Rainfall Induced Landslides. J. Geotech. Geoenviron. Eng. 2004, 130, 362–372. [Google Scholar] [CrossRef]
- Tsai, T.-L.; Chen, H.-E.; Yang, J.-C. Numerical modeling of rainstorm-induced shallow landslides in saturated and unsaturated soils. Environ. Geol. 2008, 55, 1269–1277. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Morgenstern, N.R.; Widger, R.A. The shear strength of unsaturated soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]
- Tsai, T.-L. The influence of rainstorm pattern on shallow landslide. Environ. Geol. 2008, 53, 1563–1569. [Google Scholar] [CrossRef]
- Tsai, T.-L.; Wang, J.-K. Examination of influences of rainfall patterns on shallow landslides due to dissipation of matric suction. Environ. Earth Sci. 2011, 63, 65–75. [Google Scholar] [CrossRef]
- Chen, H.-E.; Tsai, T.-L.; Yang, J.-C. Threshold of slope instability induced by rainfall and lateral flow. Water 2017, 9, 722. [Google Scholar] [CrossRef] [Green Version]
- Chan, H.-C.; Chen, P.-A.; Lee, J.-T. Rainfall-induced landslide susceptibility using a rainfall–runoff model and logistic regression. Water 2018, 10, 1354. [Google Scholar] [CrossRef] [Green Version]
- Chiu, Y.-Y.; Chen, H.-E.; Yeh, K.-C. Investigation of the influence of rainfall runoff on shallow landslides in unsaturated soil using a mathematical model. Water 2019, 11, 1178. [Google Scholar] [CrossRef] [Green Version]
- Wysocki, D.A.; Schoeneberger, P.J.; LaGarry, H.E. Geomorphology of soil landscapes. Handb. Soil Sci. 2000, 1, 315–321. [Google Scholar]
- Fazlollahi Mohammadi, M.; Jalali, S.G.H.; Kooch, Y.; Said-Pullicino, D. Slope Gradient and Shape Effects on Soil Profiles in the Northern Mountainous Forests of Iran. Eurasian Soil Sci. 2016, 49, 1366–1374. [Google Scholar] [CrossRef] [Green Version]
- Henderson, F.M. Open-Channel Flow; Macmillan: New York, NY, USA, 1966. [Google Scholar]
- Gunaratnam, D.J.; Perkins, F.E. Numerical Solution of Unsteady Flows in Open Channels; Report No. 127; Massachusetts Institute of Technology, Department of Civil Engineering, Hydrodynamics Laboratory: Cambridge, MA, USA, 1970; 216p. [Google Scholar]
- Miller, J.E. Basic Concepts of Kinematic-Wave Models (No. 1302); US Geological Survey: Reston, VA, USA, 1984.
- Nguyen, T.S.; Luong, T.A.; Luong, H.D.; Tran, H.T. A finite element one-dimensional kinematic wave rainfall-runoff model. Pac. Sci. Rev. A Nat. Sci. Eng. 2016, 18, 233–240. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Bishop, A.W. The use of pore-pressure coefficients in practice. Geotechnique 1954, 4, 148–152. [Google Scholar] [CrossRef]
- Preissmann, A. Propagation of translatory waves in channels and rivers. In Proceedings of the 1st Congress of French Association for Computation, Grenoble, France, 14–16 September 1961; pp. 433–442. [Google Scholar]
- Celia, M.A.; Bouloutas, E.T.; Zarba, R.L. A general mass conservative numerical solution for unsaturated flow equation. Water Resour. Res. 1990, 26, 14. [Google Scholar] [CrossRef]
- Subramanya, K. Engineering Hydrology, 4e; Tata McGraw-Hill Education: New York, NY, USA, 2013. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.-E.; Chiu, Y.-Y.; Tsai, T.-L.; Yang, J.-C. Effect of Rainfall, Runoff and Infiltration Processes on the Stability of Footslopes. Water 2020, 12, 1229. https://doi.org/10.3390/w12051229
Chen H-E, Chiu Y-Y, Tsai T-L, Yang J-C. Effect of Rainfall, Runoff and Infiltration Processes on the Stability of Footslopes. Water. 2020; 12(5):1229. https://doi.org/10.3390/w12051229
Chicago/Turabian StyleChen, Hung-En, Yen-Yu Chiu, Tung-Lin Tsai, and Jinn-Chuang Yang. 2020. "Effect of Rainfall, Runoff and Infiltration Processes on the Stability of Footslopes" Water 12, no. 5: 1229. https://doi.org/10.3390/w12051229
APA StyleChen, H.-E., Chiu, Y.-Y., Tsai, T.-L., & Yang, J.-C. (2020). Effect of Rainfall, Runoff and Infiltration Processes on the Stability of Footslopes. Water, 12(5), 1229. https://doi.org/10.3390/w12051229




