Flood Control Versus Water Conservation in Reservoirs: A New Policy to Allocate Available Storage
Abstract
:1. Introduction
- Stochastic assessment of hydrological dam and downstream river safety through return periods related to maximum reservoir levels and maximum outflows.
- Determination of MCLs that increase/maintain the water yield for a specific reliability while maintaining/improving hydrologic dam safety.
2. Materials and Methods
2.1. Study Set of Seasonal Maximum Conservation Levels
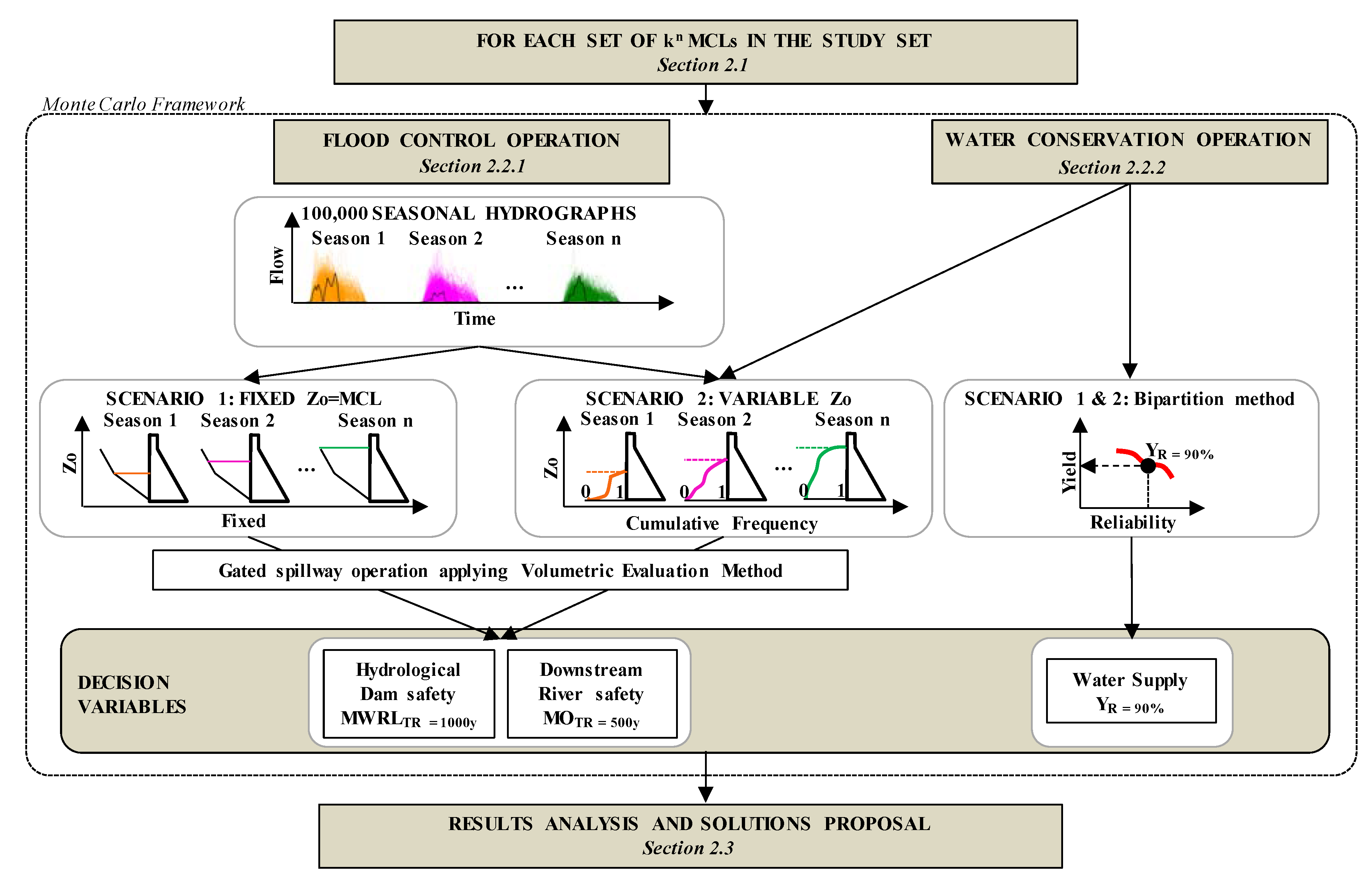
2.2. Reservoir Operation Simulations
2.2.1. Simulation of Flood Control Operation
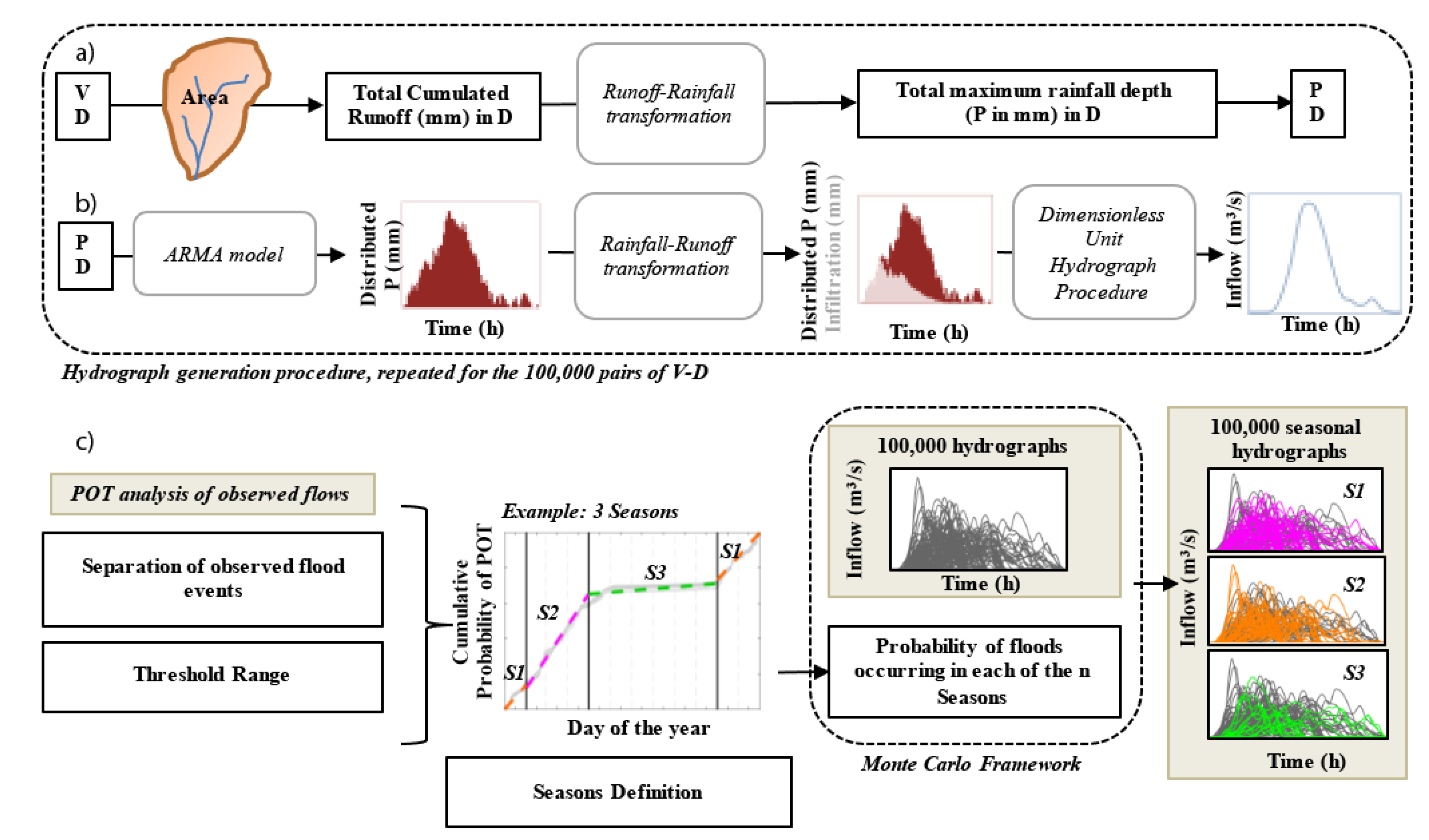
- Generation of 100,000 pairs of flood duration (D) with their associated maximum annual flood volume (V). Pairs of 100,000 flood event durations were generated following the empirical probability distribution of historical floods. For each element of the 100,000 generated durations, the corresponding hydrograph volume was obtained following the probability distribution of the associated duration within a Monte Carlo framework.
- Generation of 100,000 values of cumulated precipitation depth. The value of the cumulated net precipitation was obtained by dividing the volume of each hydrograph by the area of the study basin. By applying the curve number method inversely [15] to the cumulated net precipitation, the value of the cumulated precipitation depth was obtained (Figure 3a)
- Generation of 100,000 hourly-distributed hydrographs. By applying the curve number method [15] and the soil conservation service dimensionless unit hydrograph procedure [15], 100,000 hydrographs were generated, which followed the empirical probability distributions of volume and duration (Figure 3b).
- Scenario 1 (Sc.1): Zo is constant and corresponds to the seasonal MCL. The reservoir is assumed to be at its maximum operating level when the maximum annual flood occurs.
- Scenario 2 (Sc.2): Zo is variable, and the reservoir can be at any level when the maximum annual flood occurs. Zo is randomly sampled from the cumulative probability distribution of Zo associated to the season of occurrence of the maximum annual flood event. This distribution is obtained from the simulation of the water conservation operation of the reservoir (Section 2.2.2).
2.2.2. Simulation of Water Conservation Operation
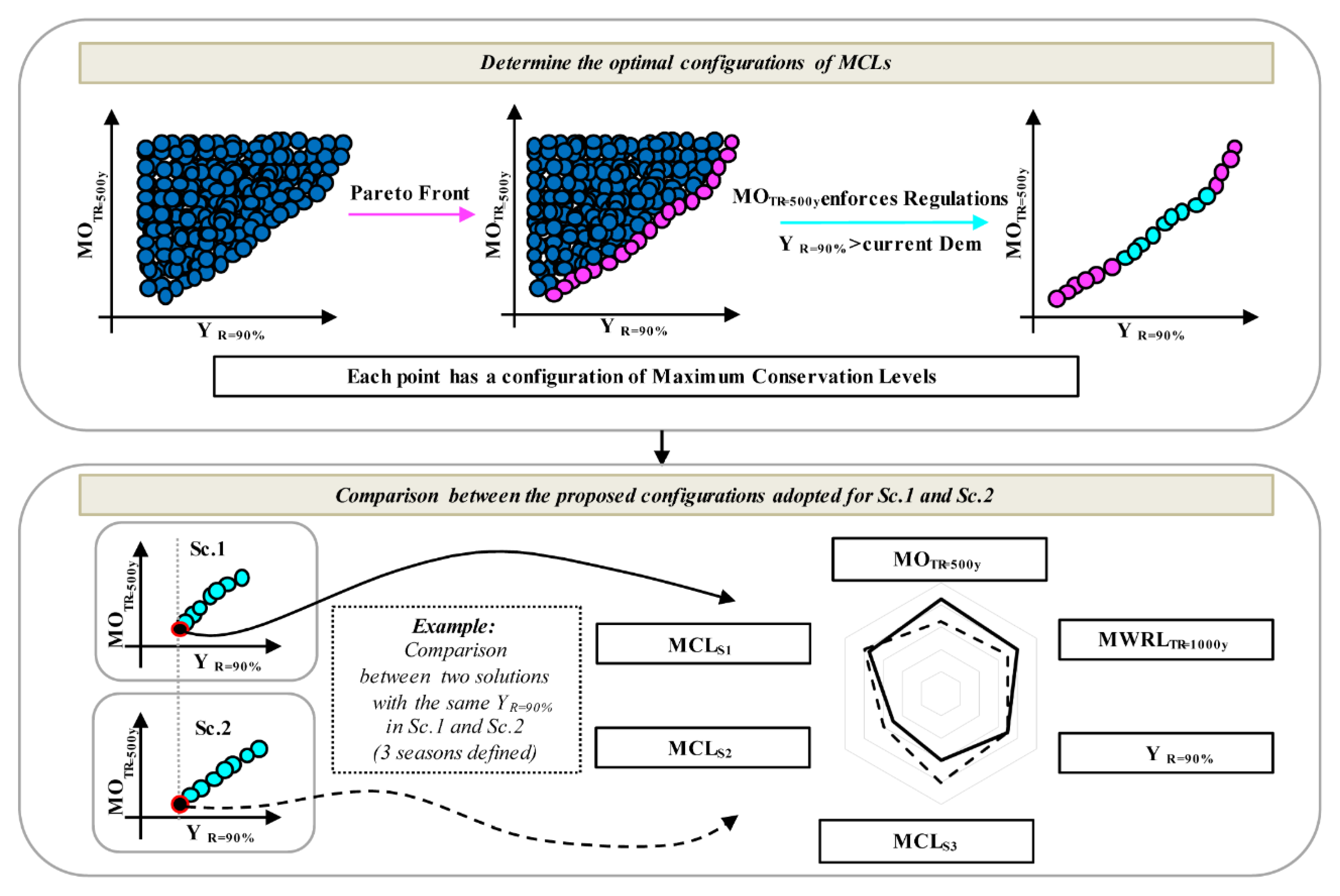
2.3. Results Analysis and Solutions Proposal
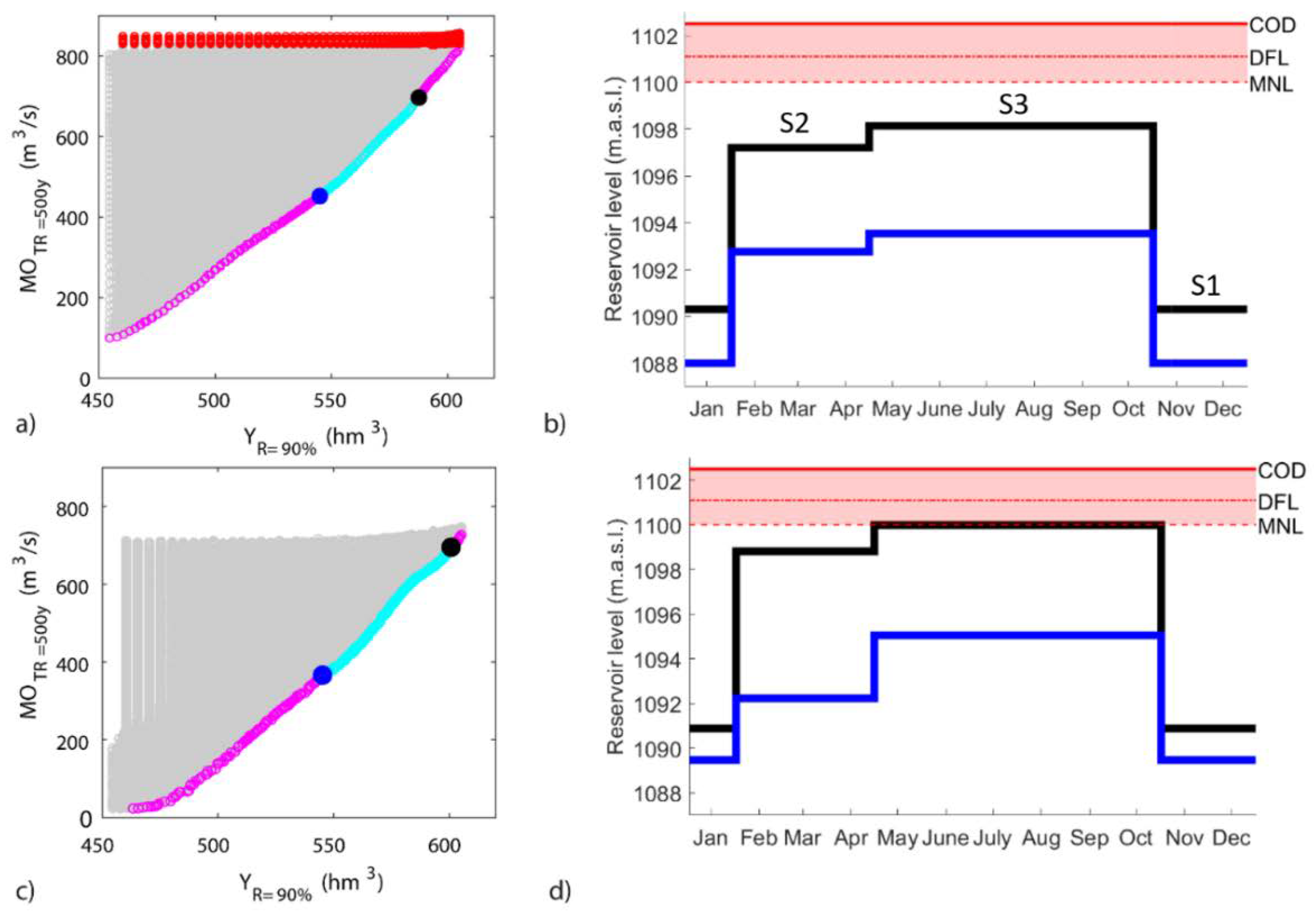
Determination of Possible MCLs by Applying a Pareto Analysis
2.4. Case Study
- Simulation of flood control operation. Besides the flood control structures and dam configuration shown, we used 30 years of unaltered daily flow series data from a gauge located right downstream the Riaño reservoir (from the years 1954 to 1984 and prior to the existence of the dam). With this time series, the 100,000 seasonal synthetic flood hydrographs were generated.
- Simulation of water conservation operation. We used a monthly time series of naturalized inflows from 1940 to 2013, environmental flow restrictions, evaporation rates, monthly demand distribution, storage–area–height reservoir curves and dead storage volume (all data obtained from the Duero River Basin Management Plan [27]) and the reservoir characteristics previously stated.
2.5. Limitations of the Methodology
3. Results and Discussion
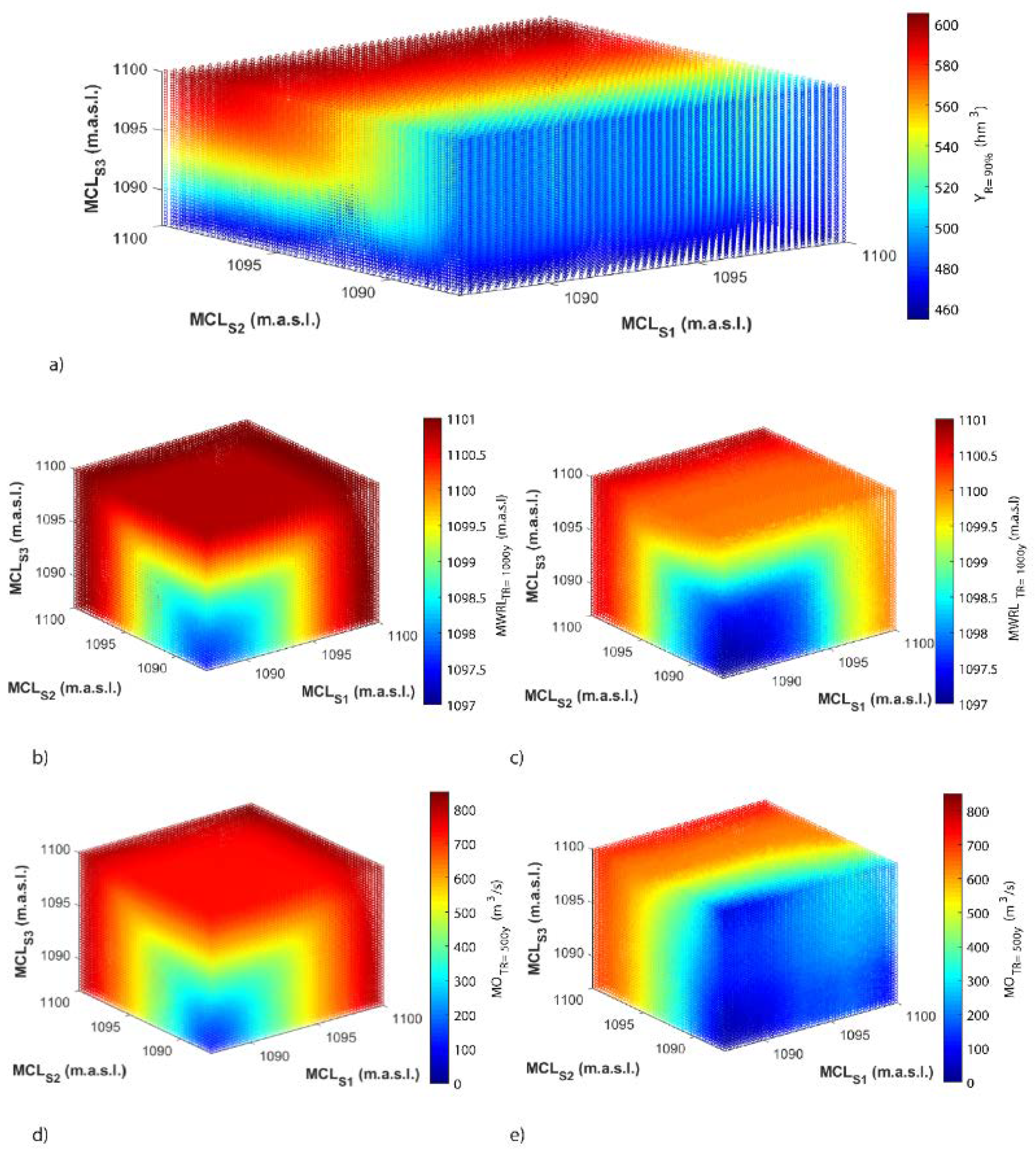
3.1. Determination of the Study Set of MCLs to be Analyzed
3.2. Simulation of the Water Conservation and Flood Operation of the Dam
3.3. Solutions Proposal
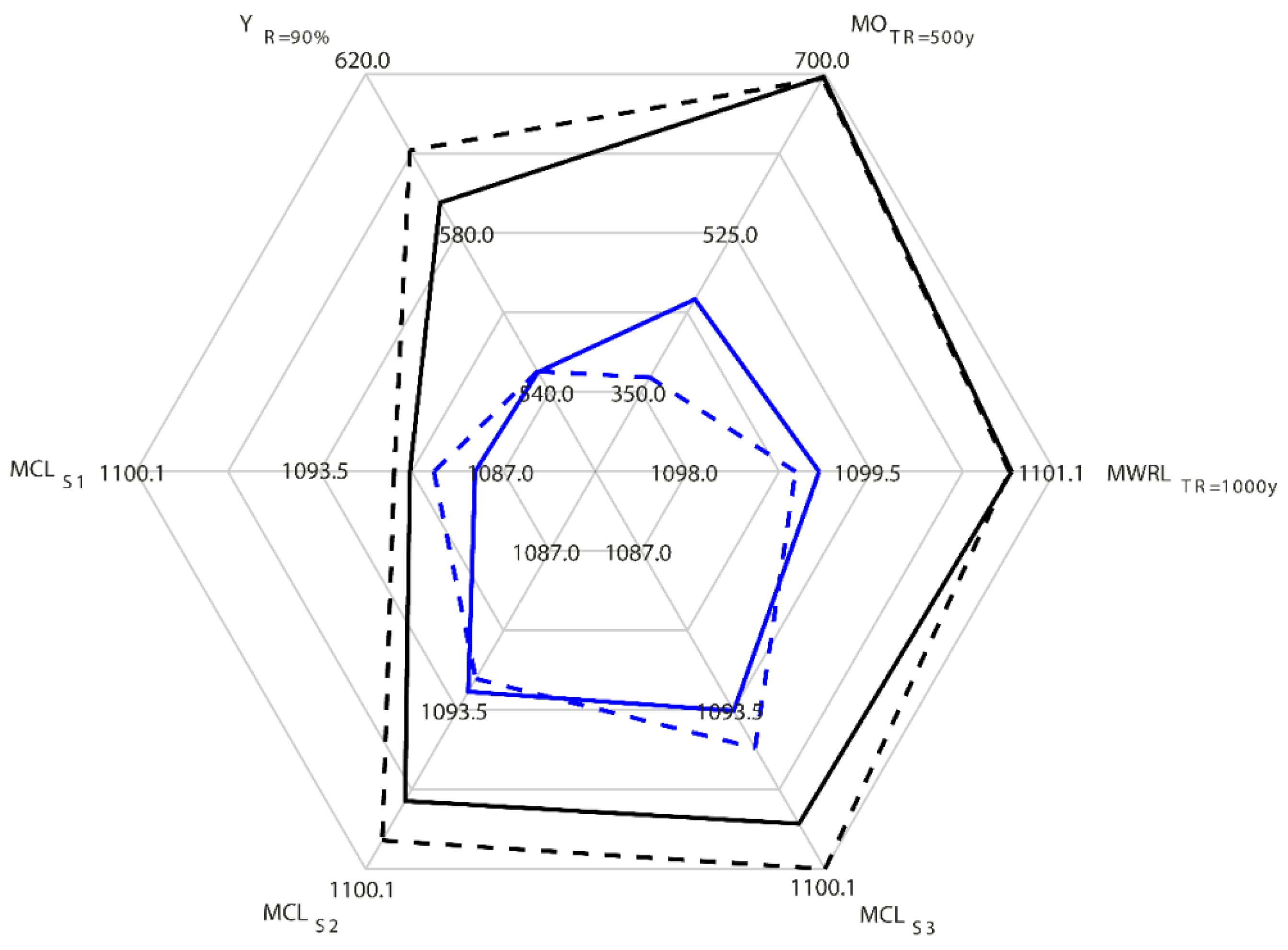
3.4. Comparison between the Proposed Configurations in the Two Scenarios
4. Conclusions
- The use of a stochastic methodology allowed us to assess hydrological dam safety and downstream safety by obtaining the frequency curves of outflow and maximum reservoir water levels, while accounting for the variability in hydrological loads with respect to deterministic procedures. As a drawback, it implied a more complex procedure and computational effort.
- We proposed a set of 98 non-inferior solutions while considering the initial reservoir level equal to the MCL for each season and 135 possible configurations while considering variable initial reservoir level. From the proposed configurations, dam stakeholders are able to decide which configuration to use depending on whether their preference is to increase dam and downstream hydrological safety or to increase water supply (with a specific reliability) in the water resources system. In the Riaño case study, the presented procedure showed improvements in the regular operation that satisfied an increase of up to 10.1% of the current annual demand of 545 hm3 (with a reliability of 90%) while maintaining the same level of hydrological dam safety.
- Accounting for initial reservoir variability resulted in the possibility of supplying an extra demand of 13 hm3 (2.4% of the current annual demand) compared to the optimal solution without accounting for initial reservoir level variability.
- The proposed stochastic procedure can improve the results obtained by deterministic procedures, increasing supply up to 26.8% of the current annual demand, from the worst regular operation configuration (not accounting for initial reservoir level variability) to the optimal configuration (accounting for initial reservoir level variability) of MCLs.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bocchiola, D.; Rosso, R. Safety of Italian dams in the face of flood hazard. Adv. Water Resour. 2014, 71, 23–31. [Google Scholar] [CrossRef]
- Li, X.; Guo, S.L.; Liu, P.; Chen, G.Y. Dynamic control of flood limited water level for reservoir operation by considering inflow uncertainty. J. Hydrol. 2010, 391, 124–132. [Google Scholar] [CrossRef]
- Xie, A.; Liu, P.; Guo, S.; Zhang, X.; Jiang, H.; Yang, G. Optimal Design of Seasonal Flood Limited Water Levels by Jointing Operation of the Reservoir and Floodplains. Water Resour. Manag. 2018, 32, 179–193. [Google Scholar] [CrossRef]
- Solera-Solera, A.; Morales-Torres, A.; Serrano-Lombillo, A. Cost estimation of freeboard requirements in water resources management. In Risk Analysis, Dam Safety, Dam Security and Critical Infrastructure Management; CRC Press: Boca Raton, FL, USA, 2012; pp. 9–14. [Google Scholar]
- Ouyang, S.; Zhou, J.; Li, C.; Liao, X.; Wang, H. Optimal design for flood limit water level of cascade reservoirs. Water Resour. Manag. 2015, 29, 445–457. [Google Scholar] [CrossRef]
- Moridi, A.; Yazdi, J. Optimal Allocation of Flood Control Capacity for Multi-Reservoir Systems Using Multi-Objective Optimization Approach. Water Resour. Manag. 2017, 31, 4521–4538. [Google Scholar] [CrossRef]
- Michailidi, E.M.; Bacchi, B. Dealing with uncertainty in the probability of overtopping of a flood mitigation dam. Hydrol. Earth System Sci. 2017, 21, 2497. [Google Scholar] [CrossRef] [Green Version]
- Micovic, Z.; Hartford, D.N.D.; Schaefer, M.G.; Barker, B.L. A non-traditional approach to the analysis of flood hazard for dams. Stoch. Environ. Res. Risk Assess. 2016, 30, 559–581. [Google Scholar] [CrossRef]
- USACE. Flood Control by Reservoirs. International Hydrological Decade; USACE: Washington, DC, USA, 1976; Volume 7. [Google Scholar]
- Sordo-Ward, A.; Garrote, L.; Martín-Carrasco, F.; Bejarano, M.D. Extreme flood abatement in large dams with fixed-crest spillways. J. Hydrol. 2012, 466-467, 60–72. [Google Scholar] [CrossRef] [Green Version]
- Sordo-Ward, A.; Garrote, L.; Bejarano, M.D.; Castillo, L.G. Extreme flood abatement in large dams with gate-controlled spillways. J. Hydrol. 2013, 498, 113–123. [Google Scholar] [CrossRef]
- Carvajal, C.; Peyras, L.; Arnaud, P.; Boissier, D.; Royet, P. Probabilistic Modeling of Floodwater Level for Dam Reservoirs. J. Hydrol. Eng. 2009, 14, 223–232. [Google Scholar] [CrossRef]
- Gabriel-Martin, I.; Sordo-Ward, A.; Garrote, L.; Castillo, L.G. Influence of initial reservoir level and gate failure in dam safety analysis. Stochastic approach. J. Hydrol. 2017, 550, 669–684. [Google Scholar] [CrossRef]
- Gabriel-Martin, I.; Sordo-Ward, A.; Garrote, L.; Granados, I. Hydrological Risk Analysis of Dams: The Influence of Initial Reservoir Level Conditions. Water 2019, 11, 461. [Google Scholar] [CrossRef] [Green Version]
- USDA Soil Conservation Service. National Engineering Handbook; Section 4; Hydrology. U.S. Department of Agriculture: Washington, DC, USA, 1972. [Google Scholar]
- Ouarda, T.B.M.J.; Ashkar, F.; Ejabi, N. Peaks over threshold model for seasonal flood variations. In Engineering hydrology (Proc. of the Symposium of San Francisco, California, 25–30 July); Kuo, C.Y., Ed.; ASCE Publication: San Francisco, CA, USA, 1993; pp. 341–346. [Google Scholar]
- Ouarda, T.B.M.J.; Cunderlik, J.M.; St-Hilaire, A.; Barbet, M.; Brunear, P.; Bobée, B. Data-based comparison of seasonality-based regional flood frequency methods. J. Hydrol. 2006, 330, 329–339. [Google Scholar] [CrossRef]
- Lang, M.; Ouarda, T.B.M.J.; Bobee, B. Towards operational guidelines for over-threshold modeling. J. Hydrol. 1999, 225, 103–117. [Google Scholar] [CrossRef]
- USWRC. Guidelines for Determining Flood Flow Frequency; United States Water Resources Council, Bulletin 17, of the Hydrology Subcommittee: Washington, DC, USA, 1976. [Google Scholar]
- Gabriel-Martin, I.; Sordo-Ward, A.; Garrote, L. Influence of initial reservoir level on the allocation of seasonal maximum conservation levels. Ingeniería del agua 2018, 22, 225–238. [Google Scholar] [CrossRef]
- Girón, F. The evacuation of Floods during the Operation of Reservoirs. In Transactions Sixteenth International Congress on Large Dams; Report 75; International Commission on Large Dams (ICOLD): San Francisco, CA, USA, 1988; Volume 4, pp. 1261–1283. [Google Scholar]
- Sordo-Ward, A.; Gabriel-Martin, I.; Bianucci, P.; Garrote, L. A Parametric Flood Control Method for Dams with Gate-Controlled Spillways. Water 2017, 9, 237. [Google Scholar] [CrossRef] [Green Version]
- Chavez-Jimenez, A.; Lama, B.; Garrote, L.; Martin-Carrasco, F.; Sordo-Ward, A.; Mediero, L. Characterisation of the sensitivity of water resources systems to climate change. Water Resour. Manag. 2013, 27, 4237–4258. [Google Scholar] [CrossRef]
- Sordo-Ward, A.; Bianucci, P.; Garrote, L.; Granados, A. The influence of the annual number of storms on the derivation of the flood frequency curve through event-based simulation. Water 2016, 8, 335. [Google Scholar] [CrossRef] [Green Version]
- Sordo-Ward, A.; Granados, A.; Iglesias, A.; Bejarano, M.D. Adaptation Effort and Performance of Water Management Strategies to Face Climate Change Impacts in Six Representative Basins of Southern Europe. Water 2019, 11, 1078. [Google Scholar] [CrossRef] [Green Version]
- Sordo-Ward, A.; Granados, I.; Iglesias, A.; Garrote, L. Blue Water in Europe: Estimates of Current and Future Availability and Analysis of Uncertainty. Water 2019, 11, 420. [Google Scholar] [CrossRef] [Green Version]
- CHD (Confederación Hidrográfica del Duero). Plan hidrológico de la parte española de la D.H.Duero (2015–2021); Official Report of the Ministry of Agriculture, Food and Environment of Spain: Valladolid, Spain, 2015. [Google Scholar]
- Garrote, L.; Iglesias, A.; Granados, A.; Mediero, L.; Martin-Carrasco, F. Quantitative assessment of climate change vulnerability of irrigation demands in Mediterranean Europe. Water Resour. Manag. 2015, 29, 325–338. [Google Scholar] [CrossRef]
- Chong, E.; Zak, S.H. An introduction to Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- International Commission on Large Dams (ICOLD). Technical Dictionary on Dams: A Glossary of Words and Phrases Related to Dams; ICOLD: Paris, France, 1994; p. 365. [Google Scholar]
- Andreu, J.; Capilla, J.; Sanchís, E. AQUATOOL, a generalized decision support system for water-resources planning and management. J. Hydrol. 1996, 177, 269–291. [Google Scholar] [CrossRef]
- Yates, D.; Sieber, J.; Purkey, D.; Huber-Lee, A. WEAP21–A Demand-, Priority-, and Preference-Driven Water Planning Model. Part 1: Model characteristics. Water Int. 2005, 30, 487. [Google Scholar] [CrossRef]
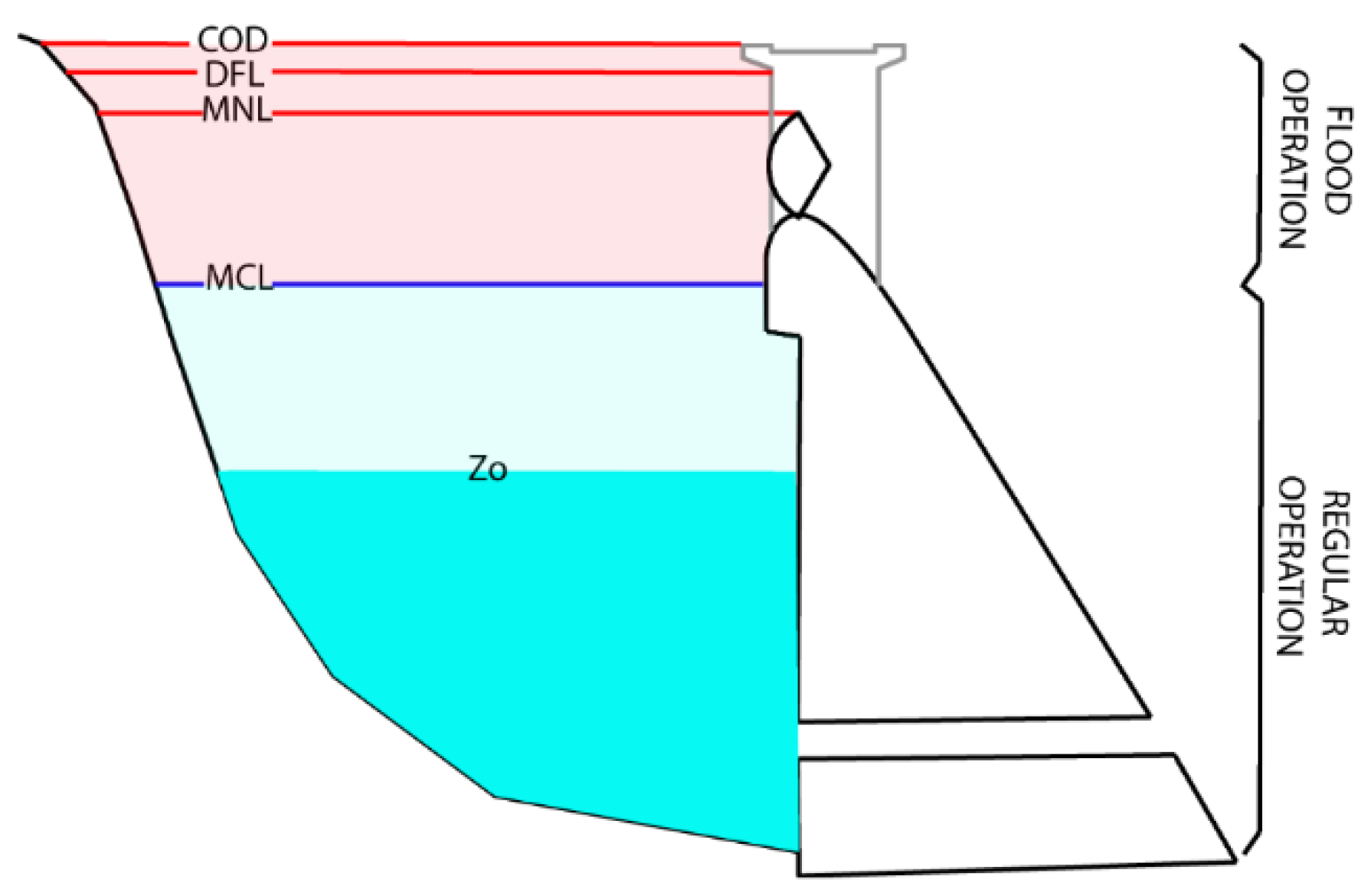
| Basin Features | Value | Dam Features | Value |
|---|---|---|---|
| Basin area | 582 km2 | Maximum normal level (MNL) | 1100.1 m |
| Concentration time | 11 h | Design flood level (DFL) | 1101.1 m |
| Mean annual Runoff | 680 hm3 | Crest of dam (COD) | 1102.5 m |
| Annual Current Demand (Da) | 545 hm3 | Gated spillway capacity at MNL | 621 m3/s |
| Emergency downstream flow (OEMER) | 700 m3/s | Auxiliary spillway capacity at DFL | 98.7 m3/s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabriel-Martin, I.; Sordo-Ward, A.; Santillán, D.; Garrote, L. Flood Control Versus Water Conservation in Reservoirs: A New Policy to Allocate Available Storage. Water 2020, 12, 994. https://doi.org/10.3390/w12040994
Gabriel-Martin I, Sordo-Ward A, Santillán D, Garrote L. Flood Control Versus Water Conservation in Reservoirs: A New Policy to Allocate Available Storage. Water. 2020; 12(4):994. https://doi.org/10.3390/w12040994
Chicago/Turabian StyleGabriel-Martin, Ivan, Alvaro Sordo-Ward, David Santillán, and Luis Garrote. 2020. "Flood Control Versus Water Conservation in Reservoirs: A New Policy to Allocate Available Storage" Water 12, no. 4: 994. https://doi.org/10.3390/w12040994
APA StyleGabriel-Martin, I., Sordo-Ward, A., Santillán, D., & Garrote, L. (2020). Flood Control Versus Water Conservation in Reservoirs: A New Policy to Allocate Available Storage. Water, 12(4), 994. https://doi.org/10.3390/w12040994







