1. Introduction
Riverbank erosion is considered one of the major issues in the deltaic regions of the world, especially in the Ganges–Brahmaputra–Meghna (GBM) delta region, from which more than sixty thousand people migrate each year due to riverbank erosion [
1,
2]. Among the deltaic rivers in the GBM region, the sand bed-braided Brahmaputra–Jamuna River erodes five hundred meters per year [
2]. The rapid change in braided channel geometry triggers variations in the flow boundary conditions and the hydraulic structures, and changes are considered the key management issues for dynamic alluvial rivers worldwide, particularly the Brahmaputra–Jamuna River [
3,
4]. Several countermeasures are generally used to protect the river banks, e.g., revetment with rip rap made of different materials and the establishment of hardpoints (heavy-duty embankments) and permeable and impermeable spurs [
4,
5]. Previous studies have shown that almost all types of structures are partly or totally damaged when exposed to the main channel [
6]. However, spur-type structures experienced frequent and severe damage compared to other high-cost river training structures, e.g., long embankments, due to the dynamic characteristics of the river and instability of the flows (governed by local scouring) induced by the structures [
6,
7]. Around the world, previous studies documented the use of spur dikes in rivers to provide adequate depth, mitigate bank erosion, and improve land reclamation and ecological richness by creating stagnant zones [
4,
6,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18]. However, field observations and multiple laboratory studies have revealed relatively large scour holes produced by impermeable spur dike fields. Angled flows, bedform movement, and rapid siltation or erosion downstream create favorable conditions for local scouring [
7,
8,
16,
17,
18,
19,
20,
21,
22,
23] Therefore, a detailed understanding of the flow around such structures is crucial for the optimum design of spur dikes to manage this type of dynamic river.
As an alternate solution, permeable spur dikes that produce less severe morphological consequences have become popular in India, Bangladesh, the United States of America (USA), and the Netherlands, among other countries [
10,
24,
25]. Although this type of spur dike is reported to work very well in some rivers, the performance is questionable in large rivers [
6].
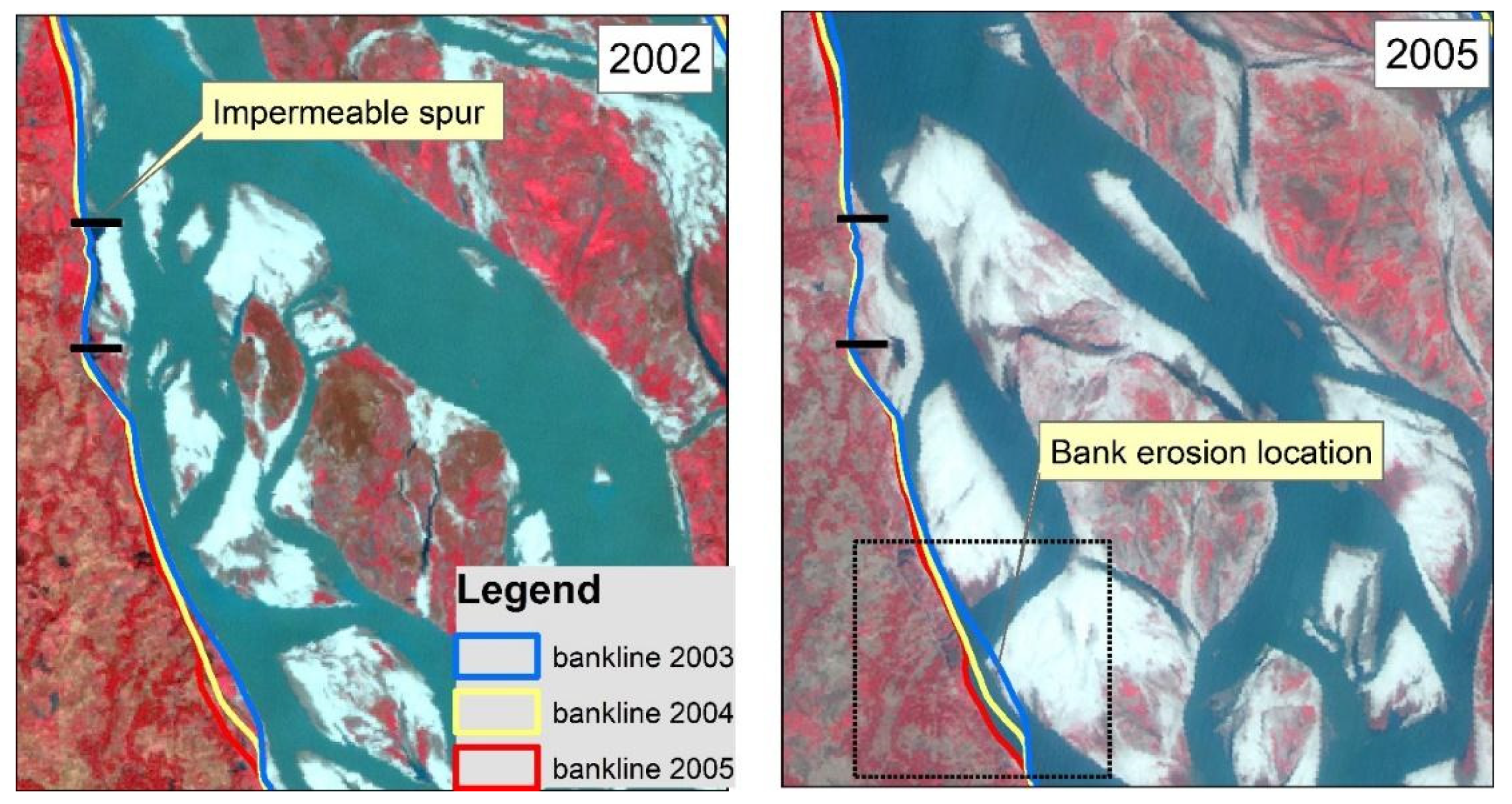
Figure 1a shows an example of a failed semipermeable spur dike in the Brahmaputra–Jamuna River in Bangladesh,
Figure 1b shows the initial spur constructed approximately 500 m from the main channel in 2013, and
Figure 1c illustrates the reinforced cement concrete (RCC) part of the dike, which is completely immersed when the river flows through the main channel at certain times.
Figure 1c also shows the flow pattern of the river. The authors surveyed the velocity of the river near the structure (500 m downstream) and upstream (12 km) of the structure (
Figure 1c shows the survey points), using an acoustic Doppler current profiler (ADCP) (
Figure 1d).
Figure 1d gives no indication of very high flow velocities near the structure, but the structure still failed. A previous study [
4] analyzed the failure cases of different types of structures in this river and found that the transverse flow generated due to spur-type structures has the potential to create local scouring, which is frequently ignored during dike design. The local vortex at the structure tip also plays a significant role in creating local scour. This type of failure indicates an improper understanding of the flow field around a spur dike. These circumstances are the motivation for this research.
We propose a highly permeable slit-type pile spur dike field (permeability > 70%; the width of the individual pile is small relative to the channel width, and the channel width/pile width ratio is 200) to overcome the aforementioned issues by decreasing the impact on the riverbed. As the first step in our research, we performed a laboratory experiment and numerical simulations to understand the three-dimensional flow properties around this type of structure. Then, a successful alignment was numerically tested for a reach of the Brahmaputra River.
Although many experimental and numerical studies have been conducted to examine the mean flow properties around impermeable spurs [
9,
10,
19,
26,
27,
28], relatively few studies have examined permeable cases [
11,
17,
18,
24,
29,
30,
31].
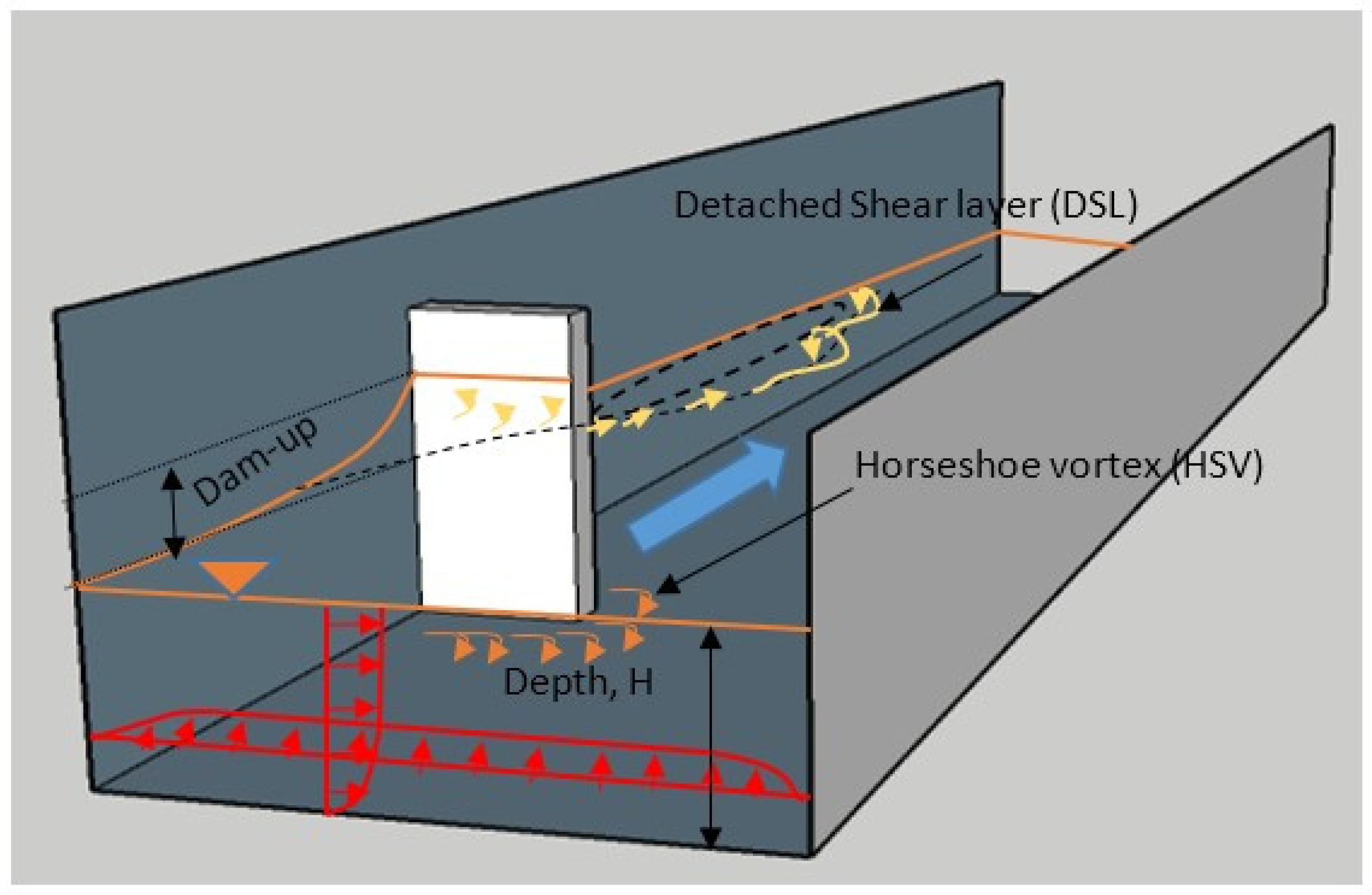
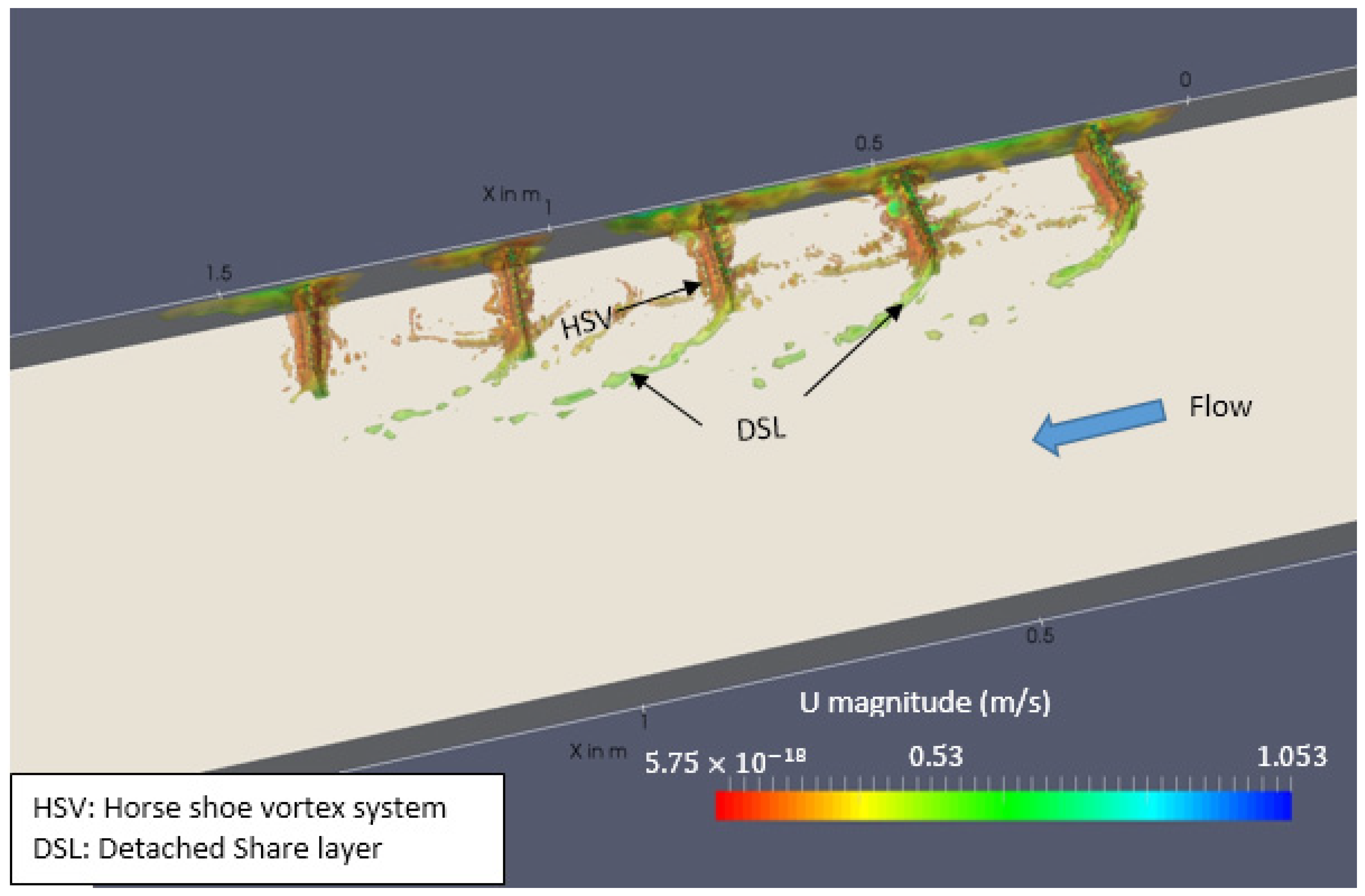
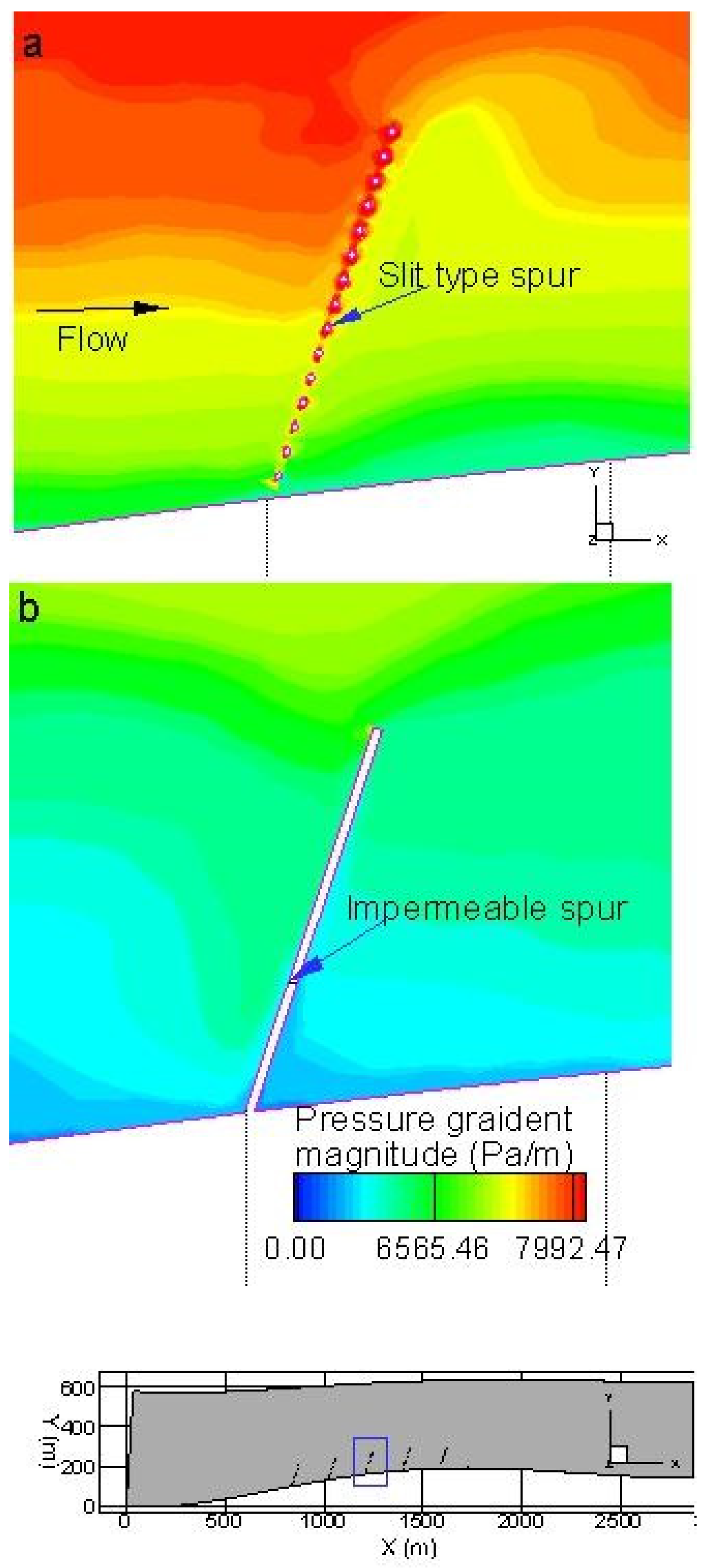
The flow around the spur dike (see
Figure 2) is relatively complex due to the adverse pressure gradient immediately upstream of the spur dike, a quasi-periodic recirculation zone, the formation of a horseshoe vortex (HSV) system at the base of the spur dike, the development of a wake zone, a fully turbulent and dynamic detached shear layer (DSL), and vortex shedding at the tip of the spur dike [
32,
33,
34]. These phenomena, particularly the HSV system, accelerated flow at the tip, and the DSL produce a large shear stress and turbulence at the spur tip, which may undermine a spur in an alluvial river by producing large scour holes [
35,
36,
37]. In a spur dike field, the eroded material deposited further downstream increases the channel roughness. To successfully design a spur dike field, knowledge of the combined effects of these phenomena is crucial. However, most of the previous work focused on the flow field, bed scouring, and three-dimensional turbulent features of impermeable spur dikes, and less is known about the flow features around permeable spur dikes.
Some researchers [
38] investigated a permeable pile groin in the Baltic Sea and reported its efficiency at reducing the turbulence intensity at the bed and improving large-scale recirculation. Others [
39] investigated a permeable groin by considering vegetation as a permeable groin and focused on determining the corresponding effects on flood control and the environment. Certain researchers [
40] examined permeable spurs as rubble-mound structures using laboratory experiments and a two-dimensional model focusing on the rubble geometry of a group of groins in terms of the flow structure and the flow force. A study [
41] examined the three-dimensional flow features around a porous spur dike by developing a three-dimensional analytical model using the k-ε model of turbulence and found some discrepancies downstream of the spur dike. Another study [
17] used a laboratory experiment to compare suspended sediment transport in permeable and impermeable spur dike fields and concluded that the suspended sediment concentration decreases in the downstream direction due to sedimentation in the transition zone for permeable spur dikes; they used a staggered group of poles as an individual spur dike. Researchers [
18] examined the effect of permeability on a single spur based on laboratory experimentation and recommended an appropriate permeability to reduce the velocity at the groin tip. In summary, the definition of a permeable spur dike differs throughout the literature, and there are few studies on pile spur dike fields.
Hence, the main objective of this research was to identify the three-dimensional flow behavior around a series of slit-type spur dike fields with different installation arrangements. The specific objective was to find the optimal solution for this type of spur dike in terms of the installation angle and spur position through experimentation and numerical simulations. In addition, we investigated the efficacy of this type of structure for riverbank protection. For this purpose, six experimental cases were investigated; these cases are described in later sections of the paper. The numerical simulation was performed by solving the three-dimensional Reynolds-averaged Navier–Stokes (RANS) equations, considering multiphase flow and using the SST model of turbulence. We hypothesized that a better understanding of the flow phenomena around this type of structure will be helpful for understanding the flow patterns of similar geometrical structures. Finally, the appropriate solutions were tested in a small river reach.
2. Laboratory Experiment
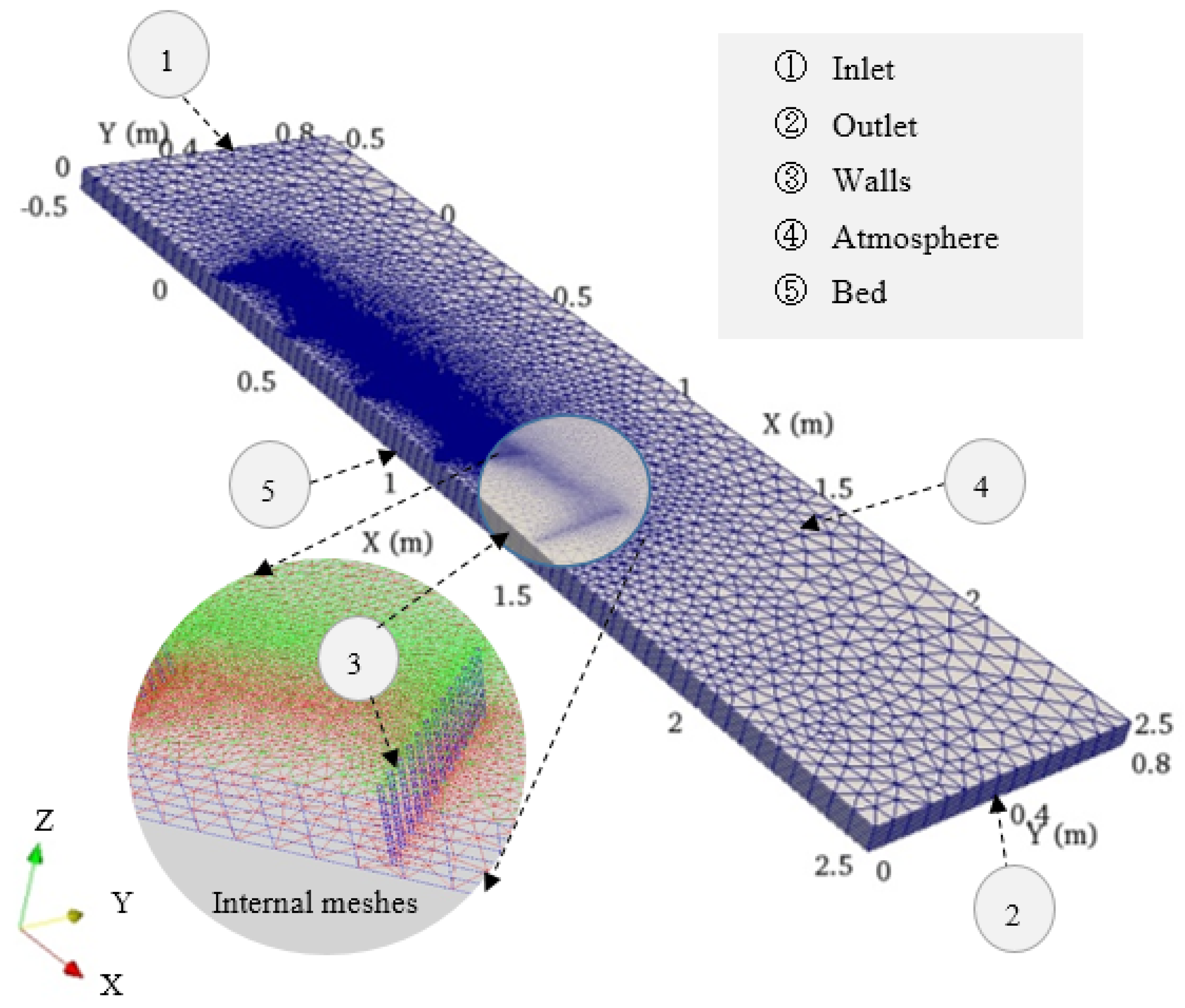
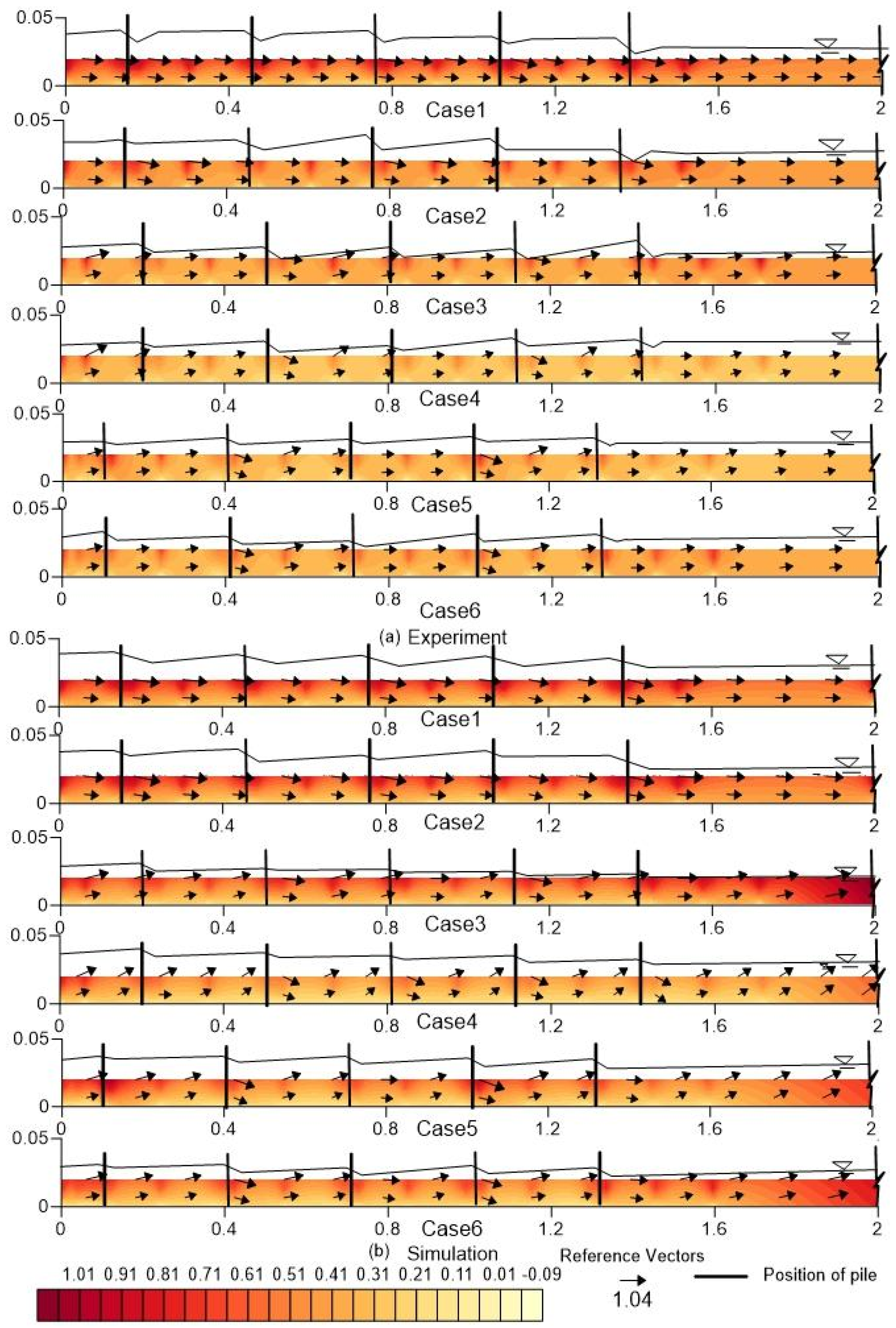
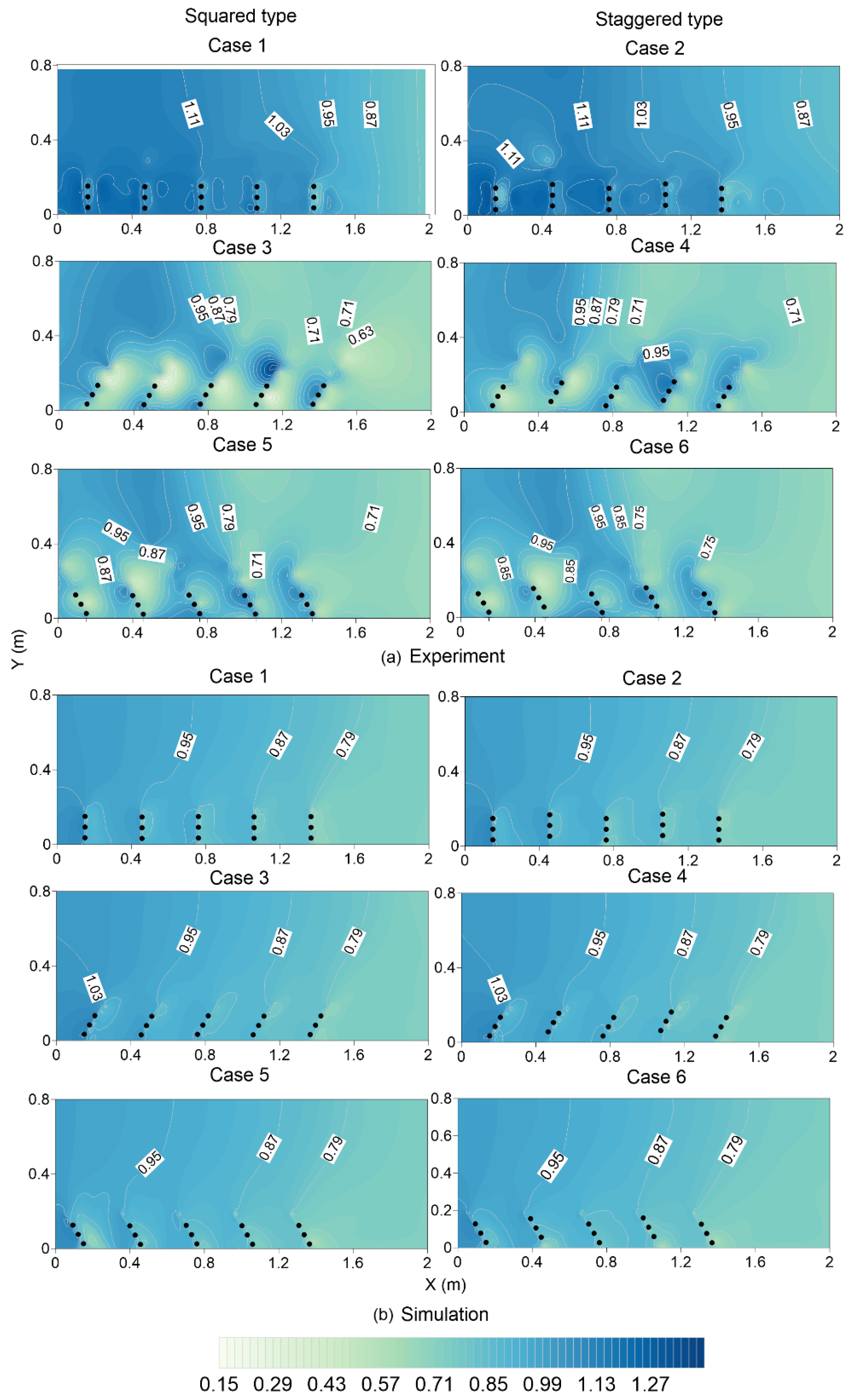
To understand the flow around a slit-type spur dike field, experiments were performed under fixed-bed conditions at Ujigawa Open Laboratory, Kyoto University. A movable bed may provide a better understanding of the scouring process near spur dikes, but the flow depth of movable beds can vary around spur dikes, and the appropriate procedures to accurately measure the adjusted flow dam-up are ambiguous. In contrast, with a fixed bed, it is straightforward to measure the flow depth or dam-up variation and the three-dimensional velocity at multiple depths. Therefore, as a first step, experiments were performed using a fixed-bed condition. The flume was 10 m long and 0.8 m wide with a longitudinal slope of 1/300. The details of the experimental configuration are shown in
Table 1 and
Figure 3.
Figure 3a–c describes the plan and sections of the flume.
Figure 3d shows a photograph of the flume for case 1. A continuous discharge of 0.01 m
3/s was supplied from the upstream region. The five spur dikes were installed 7 m from the upstream end of the right bank. Each spur dike consisted of cylindrical brass piles with diameters of 0.004 m. The spacing between two individual piles was 0.001 m, and the longitudinal interval of each was 0.30 m. A total of five spur dikes were installed, each with a permeability of 71%. Two types of installations were considered: a squared grid-type pile setting and a staggered grid-type pile setting (
Figure 3e). The approach flow depth was 0.032 m, and uniform flow was confirmed by adjusting the flume-end weir height. The details of the hydraulic conditions of the flume are described in
Table 2.
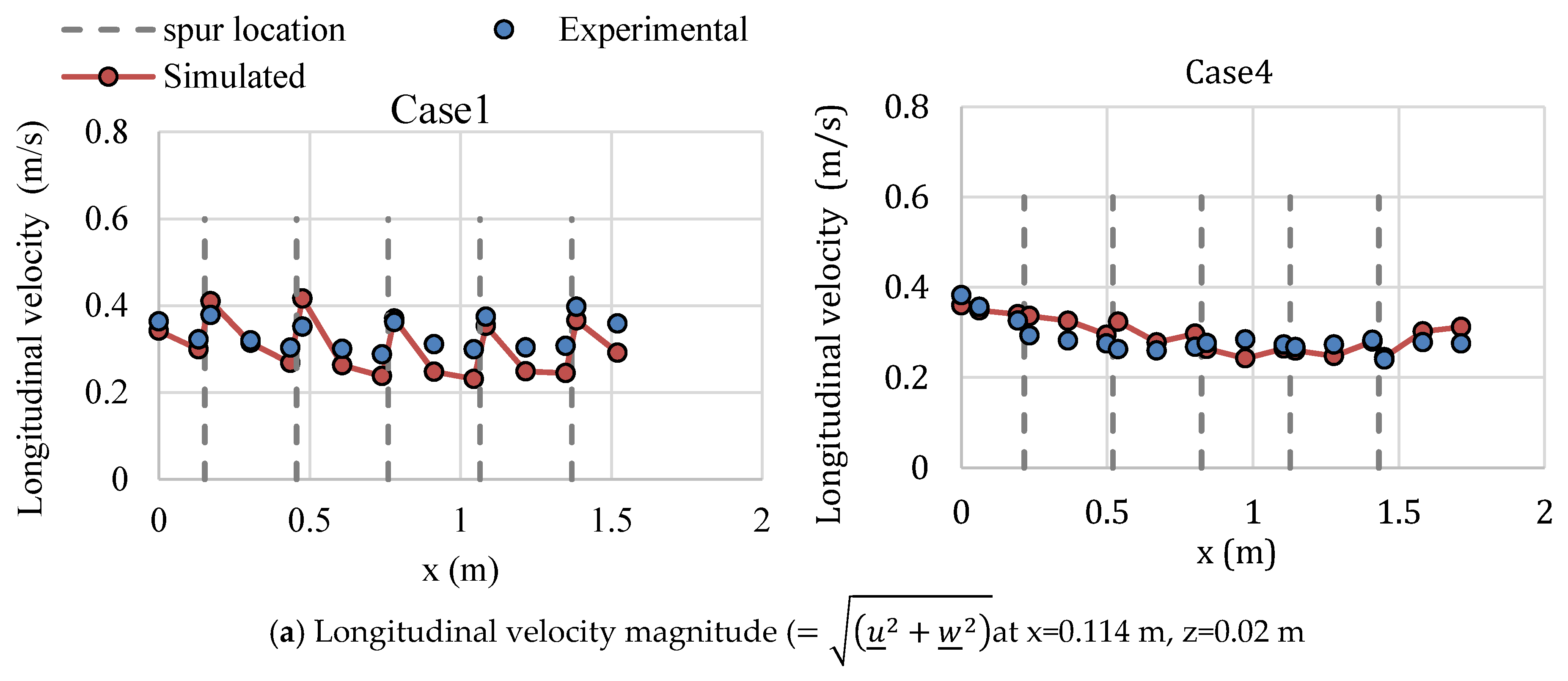
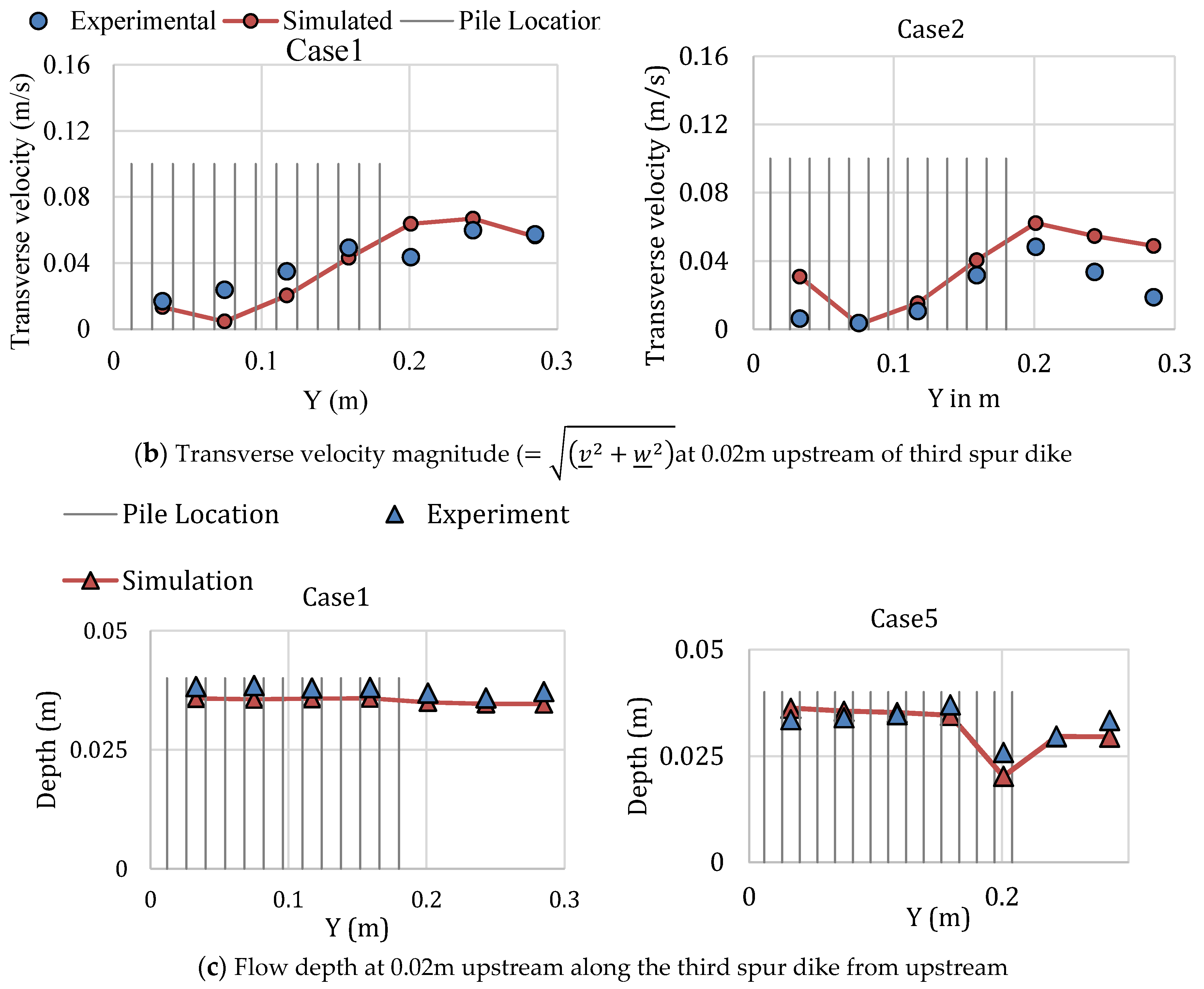
The water depth was measured using an OMRON ultrasonic water level sensor (accuracy ), and the particle image velocimetry (PIV) method was used to measure the surface flow velocity. Model ACM250-A, JFE Alec Co., Ltd.’s L-type electromagnetic velocity meter was used to measure the three-dimensional velocity () components (accuracy ). All types of velocity data were measured at depths of Z = 0.01 m and Z = 0.02 m from the bottom. Longitudinal velocity data were gathered 0.117 m from the right bank at a distance of 0.02 m from each individual spur and at the midpoint of two consecutive spurs (0.152 m away). The transverse velocity () and water depth were measured 0.02 m from each spur at the same projected perpendicular location from the right bank. In addition, the flow depth was measured at mid-channel (0.40 m from the right bank of channel).
5. Conclusions
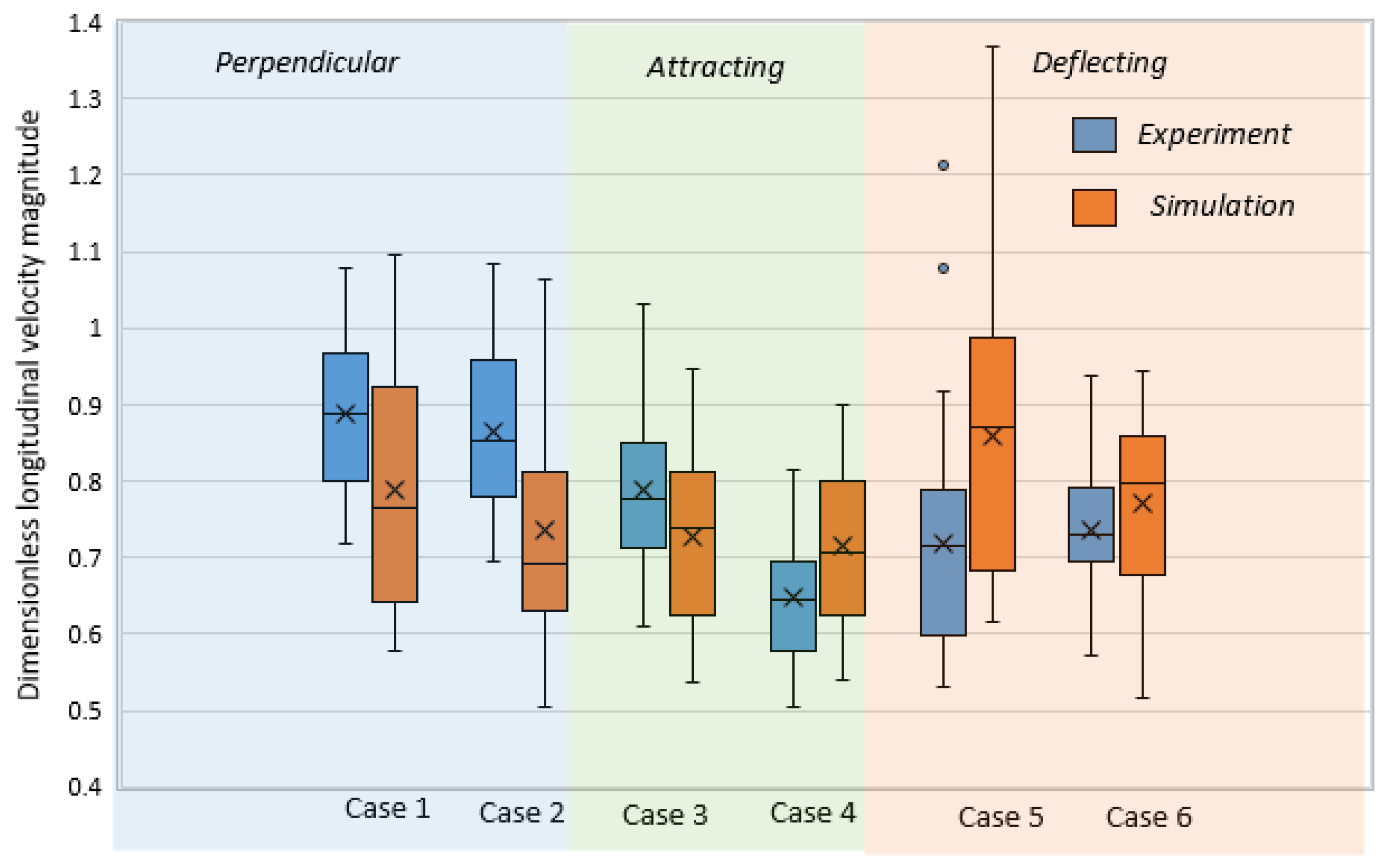
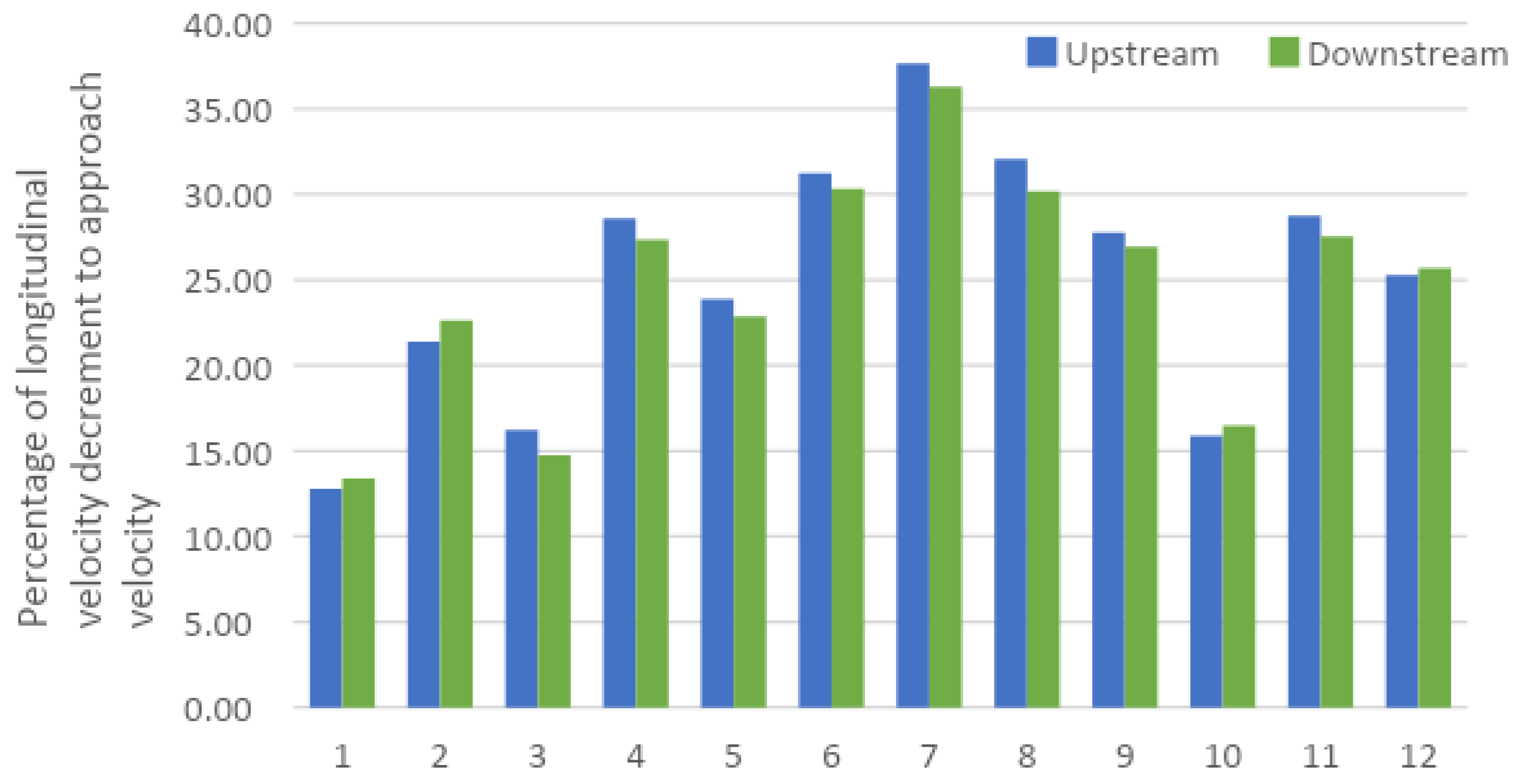
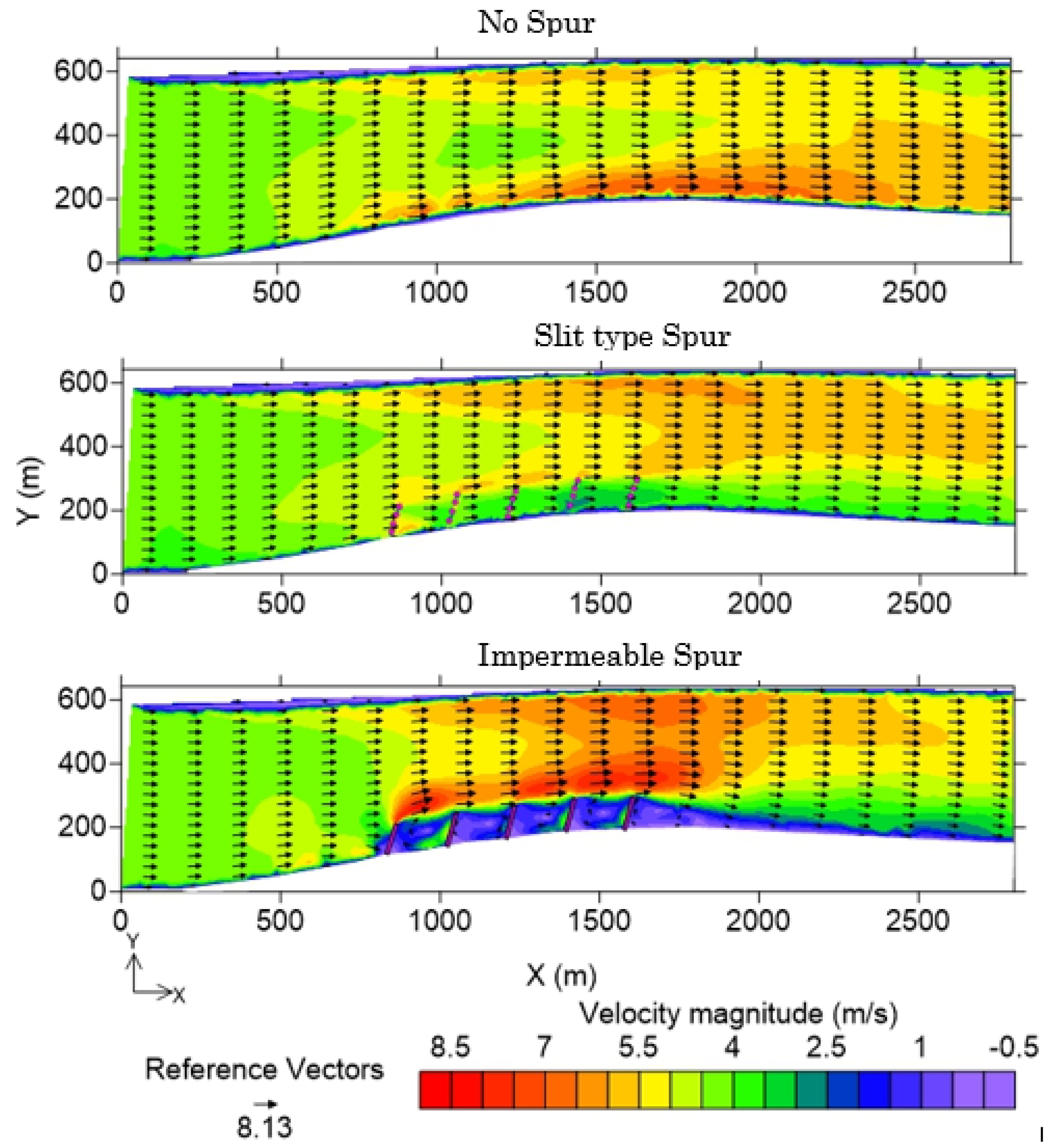
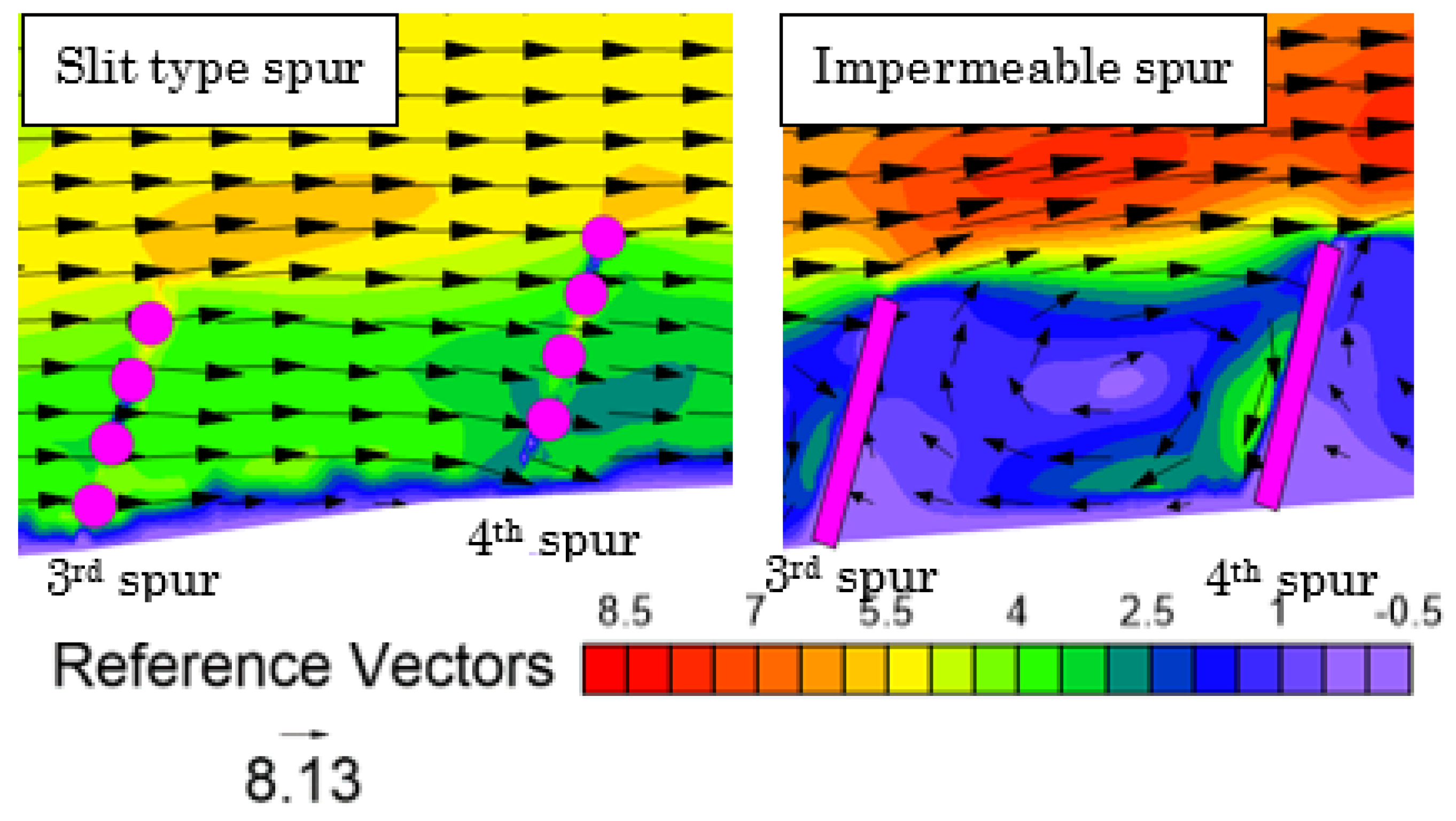
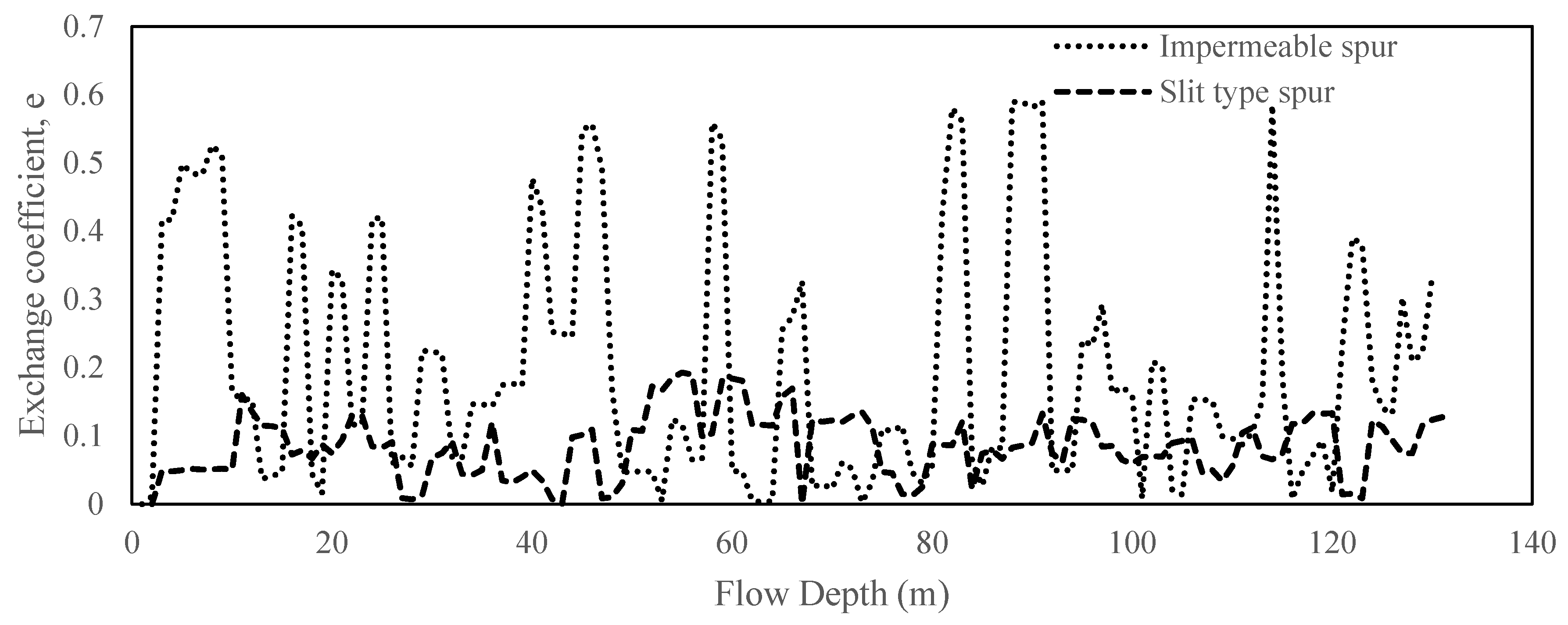
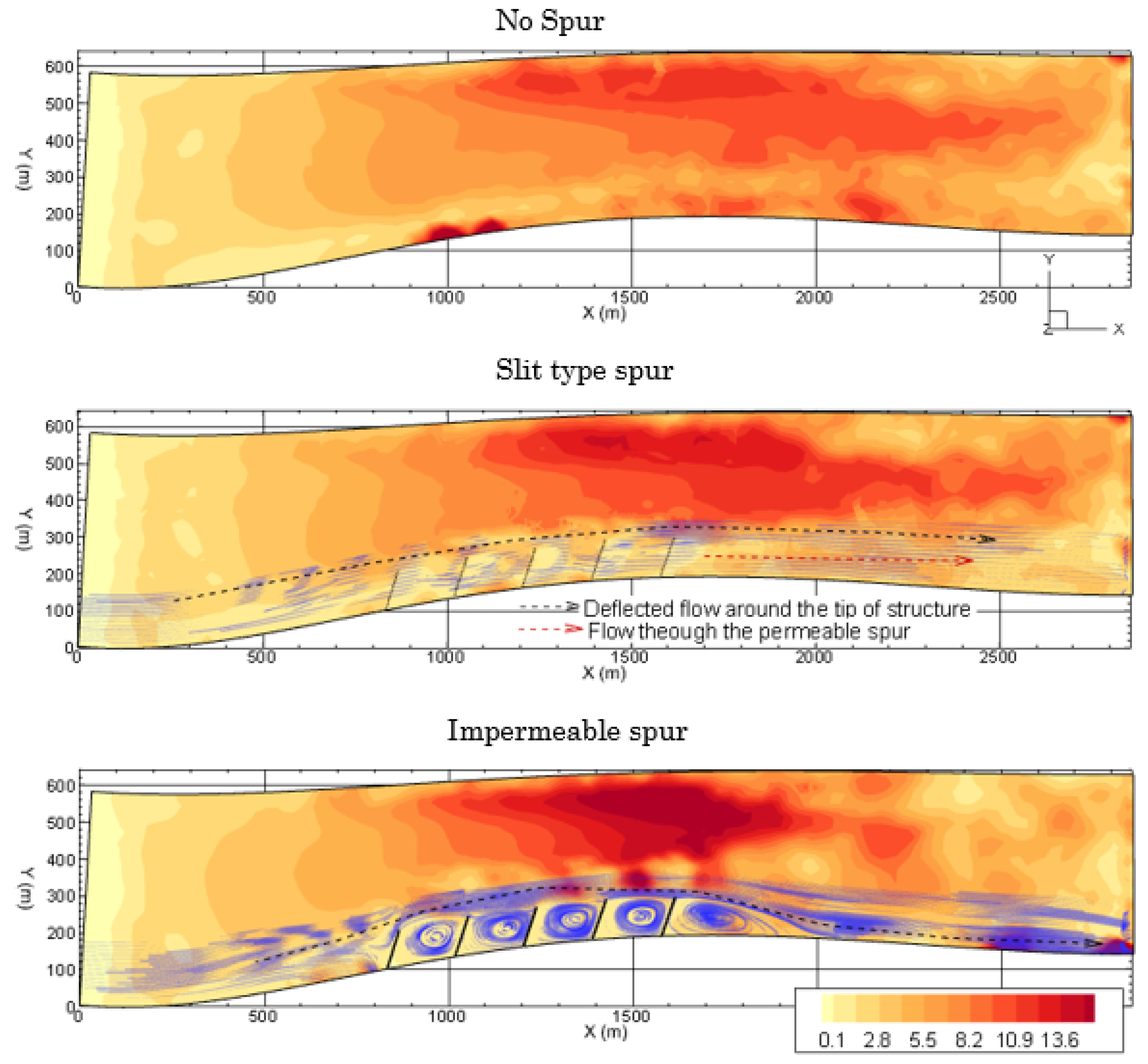
Through laboratory experiments and numerical simulations, this study investigated the flow structure around slit-type permeable spur dike fields, including several layout alternatives for practical use. The three-dimensional RANS equations were coupled with the k-ω SST turbulence model and the VOF method to capture the free water surface, and we found the hydrodynamic model results to be consistent with the experimental results for the flow structure around permeable pile spur dike fields and slit-type spur dike fields. This study revealed that by using a slit-type permeable spur dike, the approach velocity of flow can be reduced by a considerable amount within the spur dike zone. This type of spur dike is well suited for reducing the longitudinal velocity within the spur dike region. However, deflecting spurs were more successful at producing transverse flow to the opposite bank. This study also indicated that arranging the piles in a staggered grid in different spurs leads to better dike functionality in terms of reducing the bed shear stress and creating a quasi-uniform turbulence zone. However, high bed shear stress at the spur tip, especially for the initial spur, cannot be avoided in this type of spur dike field. Hence, for field applications of this type of structure, better protection measures should be taken for initial spurs.
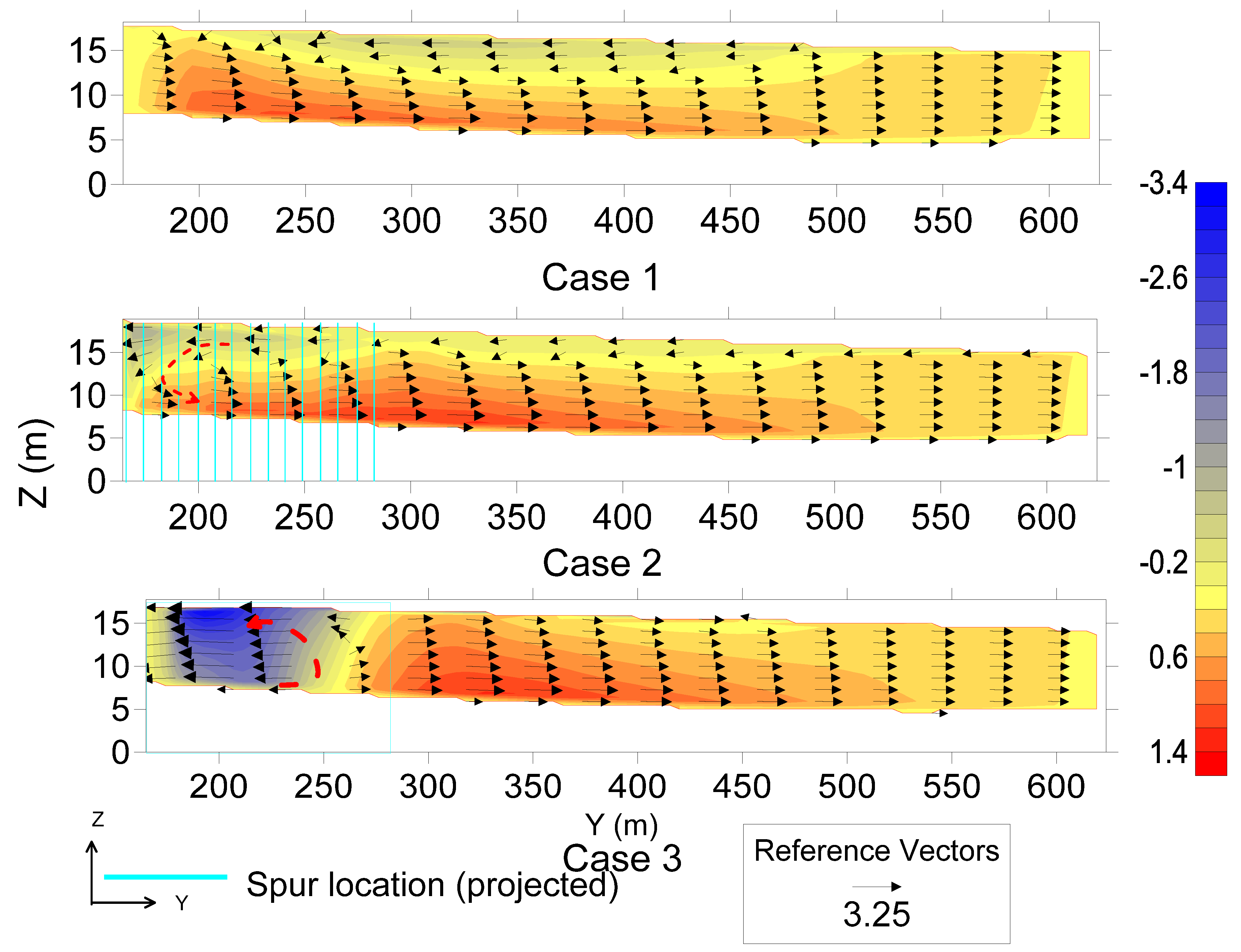
From the field numerical simulation, it can be concluded that using slit-type spurs in a staggered pile position provides the best solution, as the velocity near the bank can be reduced by a considerable amount compared to that obtained with conventional impermeable spurs in a braided channel. Although the study is conducted in a small river reach of a braided river, it can be replicated in other alluvial rivers with fine sediment. The impermeable spur dike field creates a relatively strong transverse velocity (greater than the sediment suspension velocity) in the recirculation zone, which may aggravate local scouring. However, the recirculation velocity is weaker for slit-type spurs than for other structures. As the spatial velocity is gradually reduced in the slit-type spur zone, attention should be given to field installation methods, e.g., this approach may not work well if installed very near an eroding bank. Inside the first embayment, a relatively high velocity is observed. The bed shear stress can be effectively reduced using both slit and impermeable spurs, but in the case of impermeable spurs, the deflected flow can be intensified near the bank further downstream due to riverbed variations. This type of intensification can be avoided by using a slit-type permeable spur.