Impact of Disdrometer Types on Rainfall Erosivity Estimation
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Sites and Devices
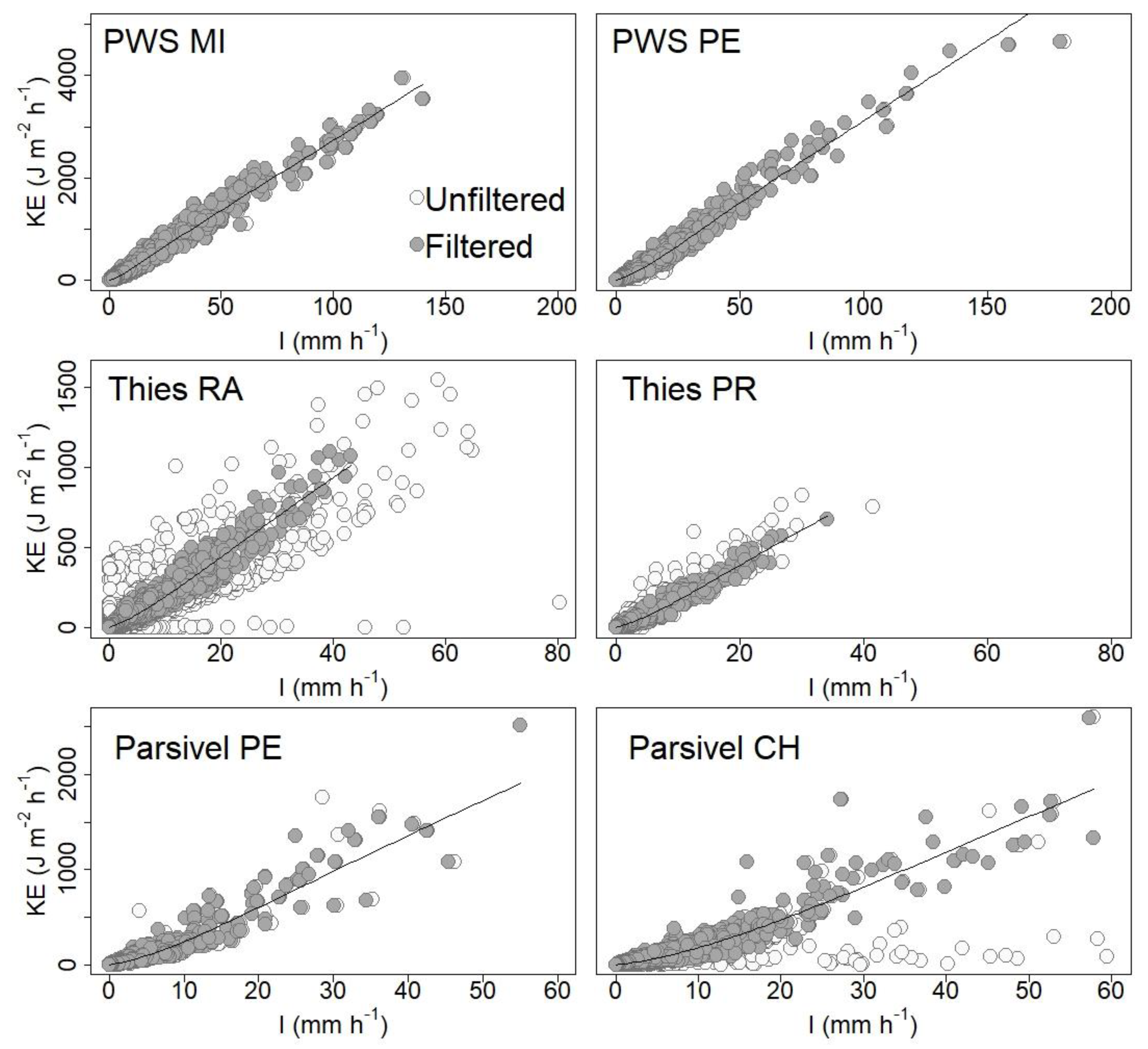
2.2. Filtering of Data
2.3. Development of Site-Specific Rainfall Kinetic Energy–Intensity Relationships
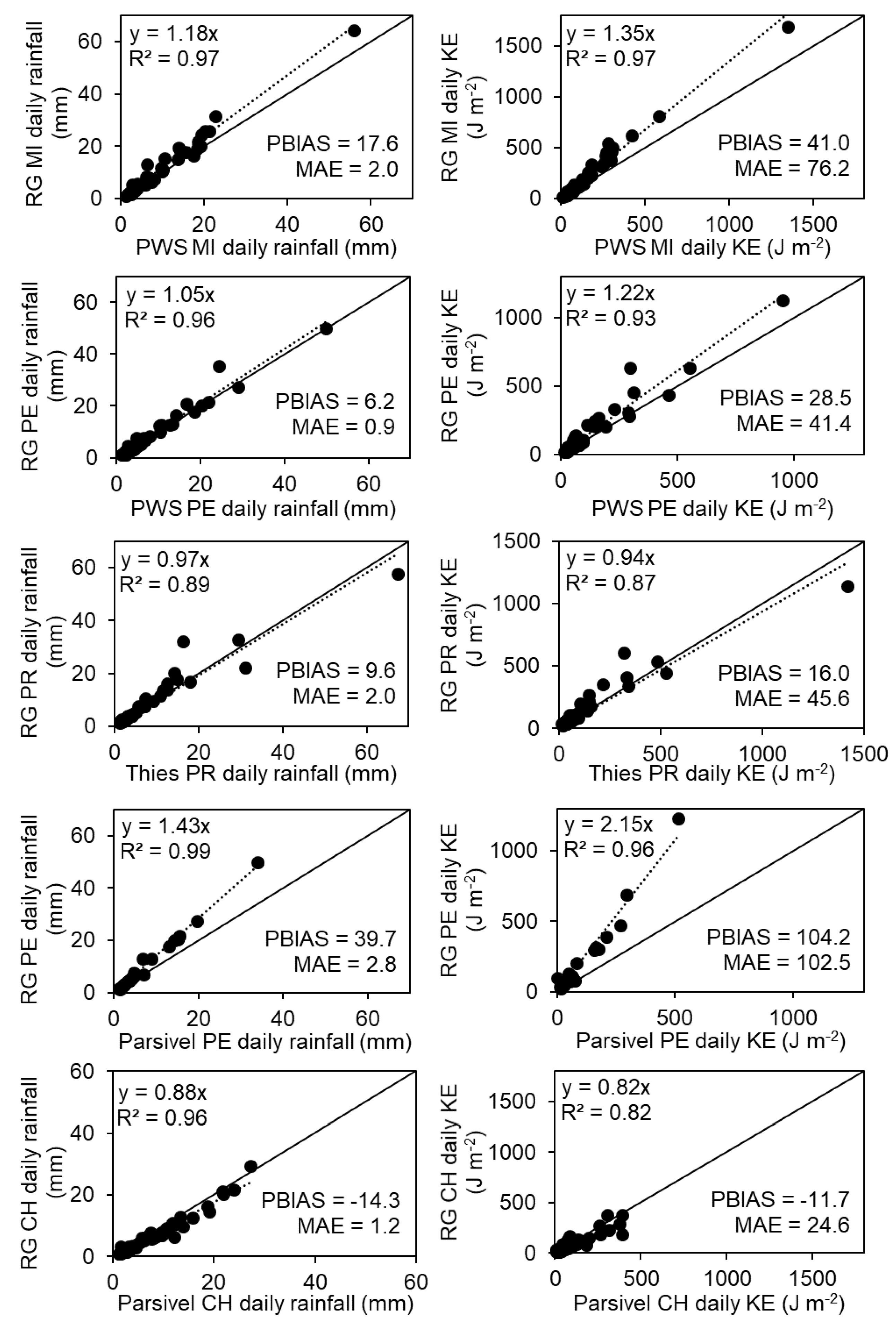
2.4. Validation of Site-Specific Rainfall Kinetic Energy–Intensity Relationships on Rain Gauge Data
3. Results and Discussion
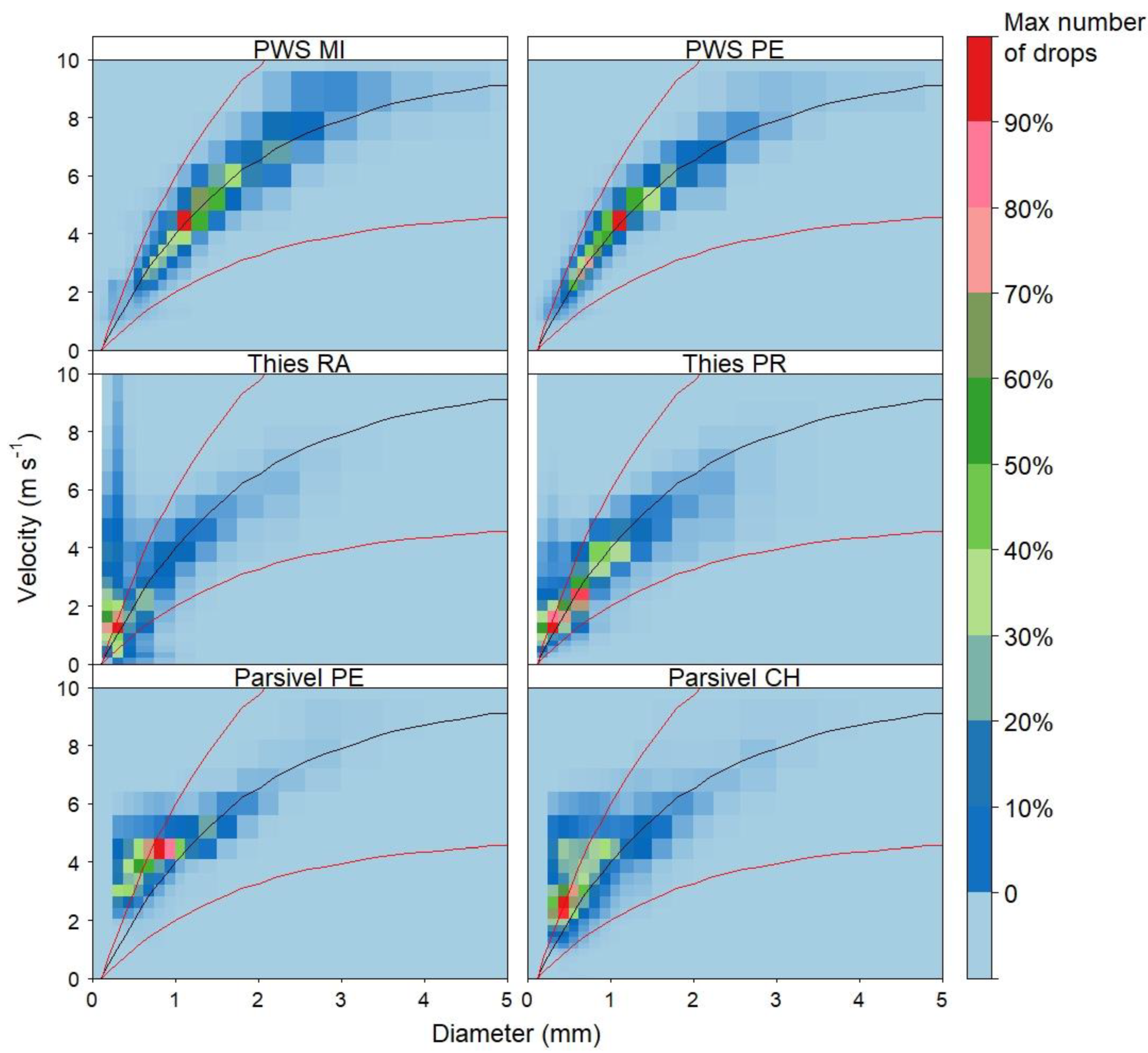
3.1. Drop Size and Velocity Distributions
3.2. Filtering of Drops
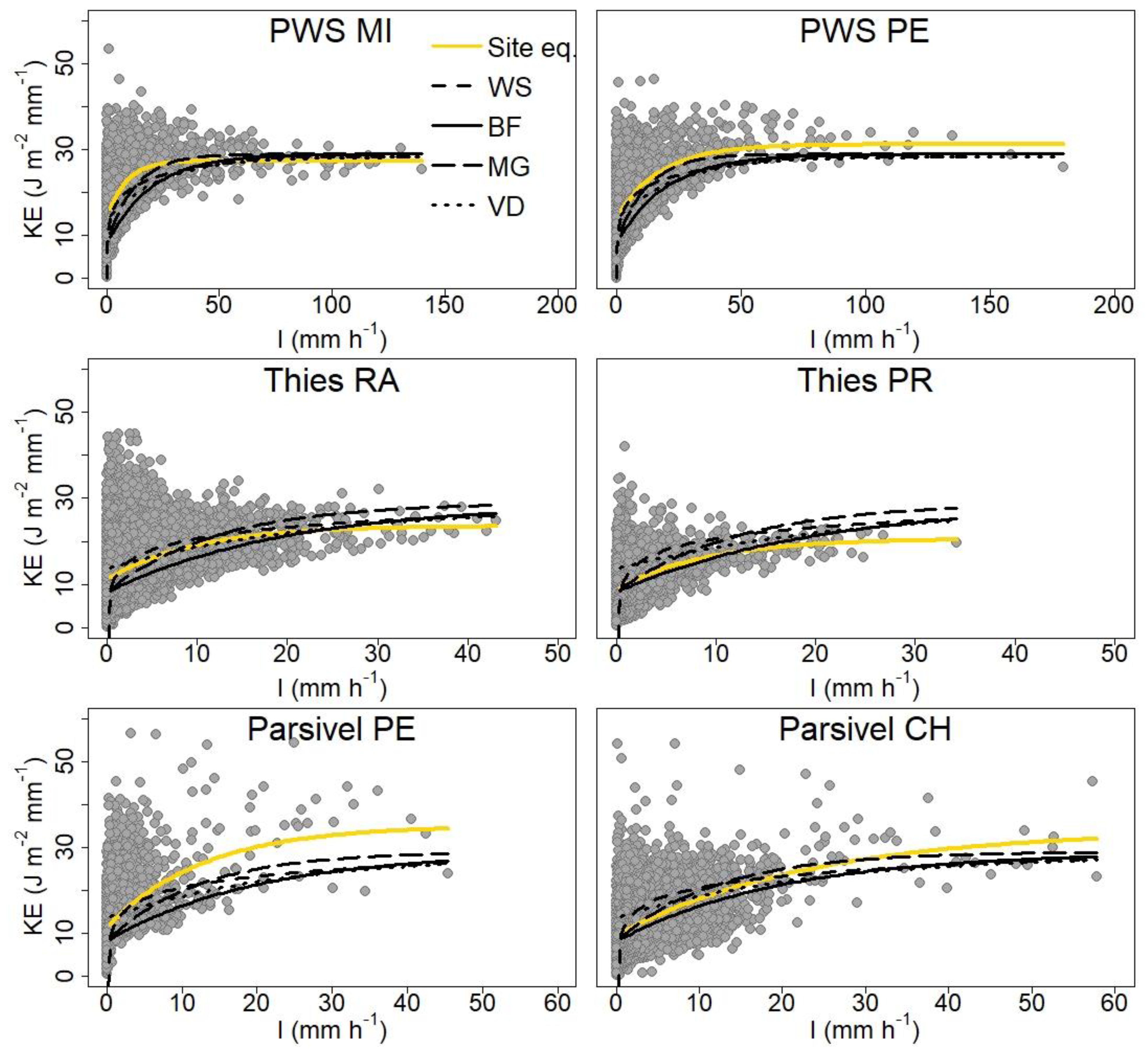
3.3. Development of New Rainfall Kinetic Energy–Intensity Relationships
3.4. Comparison with Rainfall Kinetic Energy–Intensity Relationships from the Literature
3.5. Validation of Site-Specific Rainfall Kinetic Energy–Intensity Relationships on Rain Gauge Data
3.6. Implications of Disdrometer Differences for the Estimation of Rainfall Erosivity
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Montanarella, L.; Pennock, D.J.; McKenzie, N.; Badraoui, M.; Chude, V.; Baptista, I.; Mamo, T.; Yemefack, M.; Aulakh, M.S.; Yagi, K.; et al. World’s soils are under threat. Soil 2016, 2, 79–82. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Rainfall energy and its relationship to soil loss. Trans. Am. Geophys. Union 1958, 39, 285–291. [Google Scholar] [CrossRef]
- Sempere Torres, D.; Salles, C.; Creutin, J.D.; Delrieu, G. Quantification of soil detachment by raindrop impact: performance of classical formulae of kinetic energy in Mediterranean storms. In Erosion and Sediment Transport Monitoring Programmes in River Basins; The International Association of Hydrological Sciences: Wallingford, UK, 1992; pp. 115–124. [Google Scholar]
- Usón, A.; Ramos, M.C. An improved rainfall erosivity index obtained from experimental interrill soil losses in soils with a mediterranean climate. Catena 2001, 43, 293–305. [Google Scholar] [CrossRef]
- Petan, S.; Rusjan, S.; Vidmar, A.; Mikoš, M. The rainfall kinetic energy–intensity relationship for rainfall erosivity estimation in the mediterranean part of Slovenia. J. Hydrol. 2010, 391, 314–321. [Google Scholar] [CrossRef]
- Fornis, R.L.; Vermeulen, H.R.; Nieuwenhuis, J.D. Kinetic energy-rainfall intensity relationship for Central Cebu, Philippines for soil erosion studies. J. Hydrol. 2005, 300, 20–32. [Google Scholar] [CrossRef]
- Rosewell, C.J. Rainfall Kinetic Energy in Eastern Australia. J. Clim. Appl. Meteorol. 1986, 25, 1695–1701. [Google Scholar] [CrossRef]
- Coutinho, M.A.; Tomás, P.P. Characterization of raindrop size distributions at the Vale Formoso Experimental Erosion Center. Catena 1995, 25, 187–197. [Google Scholar] [CrossRef]
- Brandt, C.J. Simulation of the size distribution and erosivity of raindrops and throughfall drops. Earth Surf. Process. Landf. 1990, 15, 687–698. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses—A Guide to Conservation Planning; U.S. Department of Agriculture: Washington, DC, USA, 1978.
- Shin, S.S.; Park, S.D.; Choi, B.K. Universal power law for relationship between rainfall kinetic energy and rainfall intensity. Adv. Meteorol. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Smith, J.A.; De Veaux, R.D. The temporal and spatial variability of rainfall power. Environmetrics 1992, 3, 29–53. [Google Scholar] [CrossRef]
- Sanchez-Moreno, J.F.; Mannaerts, C.M.; Jetten, V.; Löffler-Mang, M. Rainfall kinetic energy-intensity and rainfall momentum-intensity relationships for Cape Verde. J. Hydrol. 2012, 454–455, 131–140. [Google Scholar] [CrossRef]
- Lim, Y.S.; Kim, J.K.; Kim, J.W.; Park, B.I.; Kim, M.S. Analysis of the relationship between the kinetic energy and intensity of rainfall in Daejeon, Korea. Quat. Int. 2015, 384, 107–117. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M.; Bruijnzeel, L.A.; Rosewell, C.J. Rainfall intensity-kinetic energy relationships: A critical literature appraisal. J. Hydrol. 2002, 261, 1–23. [Google Scholar] [CrossRef]
- Brown, L.C.; Foster, G.R. Storm erosivity using idealized intensity distributions. Trans. ASAE 1987, 30, 379–386. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. Rainfall Intensity-Kinetic Energy Relationships for Soil Loss Prediction. Soil Sci. Soc. Am. J. 1981, 45, 153. [Google Scholar] [CrossRef]
- Nanko, K.; Moskalski, S.M.; Torres, R. Rainfall erosivity-intensity relationships for normal rainfall events and a tropical cyclone on the US southeast coast. J. Hydrol. 2016, 534, 440–450. [Google Scholar] [CrossRef]
- Angulo-Martínez, M.; Beguería, S.; Kyselý, J. Use of disdrometer data to evaluate the relationship of rainfall kinetic energy and intensity (KE-I). Sci. Total Environ. 2016, 568, 83–94. [Google Scholar] [CrossRef]
- Meshesha, D.T.; Tsunekawa, A.; Haregeweyn, N. Influence of raindrop size on rainfall intensity, kinetic energy, and erosivity in a sub-humid tropical area: A case study in the northern highlands of Ethiopia. Theor. Appl. Climatol. 2019, 136, 1221–1231. [Google Scholar] [CrossRef]
- McGregor, K.C.; Bingner, R.L.; Bowie, A.J.; Foster, G.R. Erosivity index values for northern Mississippi. Trans. ASAE (Am. Soc. Agric. Eng.) 1995, 38, 1039–1047. [Google Scholar] [CrossRef]
- Nearing, M.A.; Yin, S.Q.; Borrelli, P.; Polyakov, V.O. Rainfall erosivity: An historical review. Catena 2017, 157, 357–362. [Google Scholar] [CrossRef]
- Klik, A.; Haas, K.; Dvorackova, A.; Fuller, I.C. Spatial and temporal distribution of rainfall erosivity in New Zealand. Soil Res. 2015, 53, 815–825. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K.; Klik, A.; Rousseva, S.; Perčec Tadić, M.; Michaelides, S.; Hrabalíková, M.; Olsen, P.; et al. Rainfall erosivity in Europe. Sci. Total Environ. 2015, 511C, 801–814. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Yin, S.Q.; Liu, B.Y.; Nearing, M.A.; Zhao, Y. Models for estimating daily rainfall erosivity in China. J. Hydrol. 2016, 535, 547–558. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; Yu, B.; Klik, A.; Lim, K.J.; Yang, J.E.; Ni, J.; Miao, C.; Chattopadhyay, N.; et al. Global rainfall erosivity assessment based on high-temporal resolution rainfall records. Sci. Rep. 2017, 7, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Panagos, P.; Ballabio, C.; Meusburger, K.; Spinoni, J.; Alewell, C.; Borrelli, P. Towards estimates of future rainfall erosivity in Europe based on REDES and WorldClim datasets. J. Hydrol. 2017, 548, 251–262. [Google Scholar] [CrossRef]
- Wilken, F.; Baur, M.; Sommer, M.; Deumlich, D.; Bens, O.; Fiener, P. Uncertainties in rainfall kinetic energy-intensity relations for soil erosion modelling. Catena 2018, 171, 234–244. [Google Scholar] [CrossRef]
- Lobo, G.P.; Bonilla, C.A. Sensitivity analysis of kinetic energy-intensity relationships and maximum rainfall intensities on rainfall erosivity using a long-term precipitation dataset. J. Hydrol. 2015, 527, 788–793. [Google Scholar] [CrossRef]
- Cerro, C.; Bech, J.; Codina, B.; Lorente, J. Modeling Rain Erosivity Using Disdrometric Techniques. Soil Sci. Soc. Am. J. 1998, 62, 731–735. [Google Scholar] [CrossRef]
- Jayawardena, A.W.; Rezaur, R.B. Drop size distribution and kinetic energy load of rainstorms in Hong Kong. Hydrol. Process. 2000, 14, 1069–1082. [Google Scholar] [CrossRef]
- Angulo-Martínez, M.; Barros, A.P.P. Measurement uncertainty in rainfall kinetic energy and intensity relationships for soil erosion studies: An evaluation using PARSIVEL disdrometers in the Southern Appalachian Mountains. Geomorphology 2015, 228, 28–40. [Google Scholar] [CrossRef]
- Ramon, R.; Minella, J.P.G.; Merten, G.H.; de Barros, C.A.P.; Canale, T. Kinetic energy estimation by rainfall intensity and its usefulness in predicting hydrosedimentological variables in a small rural catchment in southern Brazil. Catena 2017, 148, 176–184. [Google Scholar] [CrossRef]
- Grossklaus, M.; Uhlig, K.; Hasse, L. An optical disdrometer for use in high wind speeds. J. Atmos. Ocean. Technol. 1998, 15, 1051–1059. [Google Scholar] [CrossRef]
- de Moraes Frasson, R.P.; da Cunha, L.K.; Krajewski, W.F. Assessment of the Thies optical disdrometer performance. Atmos. Res. 2011, 101, 237–255. [Google Scholar] [CrossRef]
- Battaglia, A.; Rustemeier, E.; Tokay, A.; Blahak, U.; Simmer, C. PARSIVEL Snow Observations: A Critical Assessment. J. Atmos. Ocean. Technol. 2010, 27, 333–344. [Google Scholar] [CrossRef]
- Fraile, R.; Castro, A.; Fernández-Raga, M.; Palencia, C.; Calvo, A.I. Error in the sampling area of an optical disdrometer: Consequences in computing rain variables. Sci. World J. 2013, 2013. [Google Scholar] [CrossRef]
- Angulo-Martínez, M.; Beguería, S.; Latorre, B.; Fernández-Raga, M. Comparison of precipitation measurements by OTT Parsivel2 and Thies LPM optical disdrometers. Hydrol. Earth Syst. Sci. 2018, 22, 2811–2837. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Kruger, A.; Caracciolo, C.; Golé, P.; Barthes, L.; Creutin, J.-D.; Delahaye, J.-Y.; Nikolopoulos, E.I.; Ogden, F.; Vinson, J.-P. DEVEX-disdrometer evaluation experiment: Basic results and implications for hydrologic studies. Adv. Water Resour. 2006, 29, 311–325. [Google Scholar] [CrossRef]
- Liu, X.C.; Gao, T.C.; Liu, L. A comparison of rainfall measurements from multiple instruments. Atmos. Meas. Tech. 2013, 6, 1585–1595. [Google Scholar] [CrossRef]
- Raupach, T.H.; Berne, A. Correction of raindrop size distributions measured by Parsivel disdrometers, using a two-dimensional video disdrometer as a reference. Atmos. Meas. Tech. 2015, 8, 343–365. [Google Scholar] [CrossRef]
- Tokay, A.; Petersen, W.A.; Gatlin, P.; Wingo, M. Comparison of Raindrop Size Distribution Measurements by Collocated Disdrometers. J. Atmos. Ocean. Technol. 2013, 30, 1672–1690. [Google Scholar] [CrossRef]
- Johannsen, L.L.; Zambon, N.; Strauss, P.; Dostal, T.; Neumann, M.; Zumr, D.; Cochrane, T.A.; Blöschl, G.; Klik, A. Comparison of three types of laser optical disdrometers under natural rainfall conditions. Hydrol. Sci. J. 2020, 65, 524–535. [Google Scholar] [CrossRef]
- Land Niederösterreich. Wasserstandsnachrichten und Hochwasserprognosen. Messstellendaten. Mistelbach. Available online: https://www.noe.gv.at/wasserstand/#/de/Messstellen/Details/99116541/Niederschlag/3Tage (accessed on 25 November 2019).
- Land Niederösterreich. Wasserstandsnachrichten und Hochwasserprognosen. Messstellendaten. Wieselburg. Available online: https://www.noe.gv.at/wasserstand/#/de/Messstellen/Details/107235/Niederschlag/3Tage (accessed on 25 November 2019).
- ZAMG. Klimadaten von Österreich 1971-2000: Schwechat. Available online: http://www.zamg.ac.at/fix/klima/oe71-00/klima2000/klimadaten_oesterreich_1971_frame1.htm (accessed on 25 November 2019).
- Czech Hydrometeorological Institute. Prague Clementinum: Basic data on Prague Clementinum Station. Available online: http://portal.chmi.cz/historicka-data/pocasi/praha-klementinum?l=en# (accessed on 25 November 2019).
- NIWA Climate Summaries. Available online: https://niwa.co.nz/education-and-training/schools/resources/climate/summary (accessed on 25 November 2019).
- World Meteorological Organization (WMO). Manual on Codes—International Codes, Volume I.1, Annex II to the WMO Technical Regulations: Part A—Alphanumeric Codes; World Meteorological Organization: Geneva, Switzerland, 2011. [Google Scholar]
- Atlas, D.; Srivastava, R.C.; Sekhon, R.S. Doppler Radar Characteristics of Precipitation at Vertical Incidence. Rev. Geophys. 1973, 11, 1–35. [Google Scholar] [CrossRef]
- Adirosi, E.; Roberto, N.; Montopoli, M.; Gorgucci, E.; Baldini, L. Influence of disdrometer type on weather radar algorithms from measured DSD: Application to Italian climatology. Atmosphere (Basel) 2018, 9, 360. [Google Scholar] [CrossRef]
- Jaffrain, J.; Berne, A. Experimental quantification of the sampling uncertainty associated with measurements from PARSIVEL disdrometers. J. Hydrometeorol. 2011, 12, 352–370. [Google Scholar] [CrossRef]
- Kruger, A.; Krajewski, W.F. Two-Dimensional Video Disdrometer: A Description. J. Atmos. Ocean. Technol. 2002, 19, 602–617. [Google Scholar] [CrossRef]
- Tokay, A.; Kruger, A.; Krajewski, W.F. Comparison of drop size distribution measurements by impact and optical disdrometers. J. Appl. Meteorol. 2001, 40, 2083–2097. [Google Scholar] [CrossRef]
- Hauser, D.; Amayenc, P.; Nutten, B.; Waldteufel, P. A New Optical Instrument for Simultaneous Measurement of Raindrop Diameter and Fall Speed Distributions. J. Atmos. Ocean. Technol. 1984, 1, 256. [Google Scholar] [CrossRef]
- Donnadieu, G. Comparison of results obtained with the VIDIAZ spectropluviometer and the Joss-Waldvogel rainfall disdrometer in a “rain of a thundery type”. J. Appl. Meteorol. 1980, 19, 593–597. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning With the Revised Universal Soil Loss Equation (RUSLE); U.S. Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1997.
- Bates, D.M.; Watts, D.G. Nonlinear Regression Analysis and Its Applications. In Wiley Series in Probability and Statistics, Bates, D.M., Watts, D.G., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1988. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Tokay, A.; Wolff, D.B.; Petersen, W.A. Evaluation of the New Version of the Laser-Optical Disdrometer, OTT Parsivel 2. J. Atmos. Ocean. Technol. 2014, 31, 1276–1288. [Google Scholar] [CrossRef]
- OTT. Operating Instructions. Present Weather Sensor Parsivel; OTT Messtechnik GmbH & Co. KG.: Kempten, Germany, 2005. [Google Scholar]
- Thies Clima. Instruction for Use. Laser Precipitation Monitor; Adolf Thies GmbH & Co. KG.: Göttingen, Germany, 2015. [Google Scholar]
- Campbell Scientific Inc. PWS100 Present Weather Sensor. Instruction manual. Revision 3/12; Campbell Scientific, Inc.: Logan, UT, USA, 2012. [Google Scholar]
- Montero-Martínez, G.; García-García, F. On the behaviour of raindrop fall speed due to wind. Q. J. R. Meteorol. Soc. 2016, 142, 2013–2020. [Google Scholar] [CrossRef]
- Salles, C.; Poesen, J.; Sempere-Torres, D. Kinetic energy of rain and its functional relationship with intensity. J. Hydrol. 2002, 257, 256–270. [Google Scholar] [CrossRef]
- Mineo, C.; Ridolfi, E.; Moccia, B.; Russo, F.; Napolitano, F. Assessment of Rainfall Kinetic-Energy–Intensity Relationships. Water 2019, 11, 1994. [Google Scholar] [CrossRef]
- Lanza, L.G.; Vuerich, E. The WMO Field Intercomparison of Rain Intensity Gauges. Atmos. Res. 2009, 94, 534–543. [Google Scholar] [CrossRef]
- Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J.E. Precipitation: Measurement, remote sensing, climatology and modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
- Fraile, R.; Palencia, C.; Castro, A.; Giaiotti, D.; Stel, F. Fitting an exponential distribution: Effect of discretization. Atmos. Res. 2009, 93, 636–640. [Google Scholar] [CrossRef]
- Marzuki, M.; Randeu, W.L.; Schönhuber, M.; Bringi, V.N.; Kozu, T.; Shimomai, T. Raindrop size distribution parameters of distrometer data with different bin sizes. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3075–3080. [Google Scholar] [CrossRef]
- Jaffrain, J.; Berne, A. Quantification of the small-scale spatial structure of the raindrop size distribution from a network of disdrometers. J. Appl. Meteorol. Climatol. 2012, 51, 941–953. [Google Scholar] [CrossRef]

| Reference | Equation | Abbreviation |
|---|---|---|
| Wischmeier and Smith [10] | , I ≤ 76 mm h−1 | WS |
| , I > 76 mm h−1 | ||
| Brown and Foster [16] | BF | |
| McGregor et al. [21] | MG | |
| van Dijk et al. [15] | VD |
| Measurement Site | Coordinates | Altitude | Mean Annual Precipitation | Mean Annual Temperature | Disdrometer Type |
|---|---|---|---|---|---|
| (m.a.s.l.) | (mm) | (°C) | |||
| Mistelbach | 48°34′59″ N, 16°35′14″ E | 245 | 537 | 9.8 | PWS100 |
| Petzenkirchen | 48°09′17″ N, 15°08′53″ E | 277 | 902 | 9.6 | PWS100 and Parsivel |
| Rauchenwarth | 48°05′ N, 16°32′ E | 210 | 533 | 9.8 | Thies |
| Prague | 50°06′16″ N, 14°23′14″ E | 230 | 459 | 10.8 | Thies |
| Christchurch | 43°31′18″ S, 172°34′59″ E | 24 | 648 | 12.1 | Parsivel |
| Before Filtering | After Filtering | |||
|---|---|---|---|---|
| Device and Site | Mean Size | Mean Velocity | Mean Size | Mean Velocity |
| (mm) | (m s−1) | (mm) | (m s−1) | |
| PWS MI | 1.2 (±0.3) | 4.3 (±2.7) | 1.2 (±0.3) | 4.3 (±2.5) |
| PWS PE | 0.9 (±0.2) | 3.7 (±1.9) | 1.0 (±0.2) | 3.7 (±1.9) |
| Thies RA | 0.4 (±0.1) | 2.0 (±2.4) | 0.6 (±0.1) | 2.0 (±1.6) |
| Thies PR | 0.6 (±0.1) | 2.3 (±1.5) | 0.7 (±0.2) | 2.4 (±1.5) |
| Parsivel PE | 0.7 (±0.1) | 4.0 (±0.7) | 0.9 (±0.1) | 4.2 (±0.8) |
| Parsivel CH | 0.6 (±0.1) | 3.2 (±1.3) | 0.8 (±0.1) | 3.1 (±1.3) |
| Disdrometer and Site | Rainfall Kinetic Energy–Intensity Relationship (J m−2 h−1) | R2 | Minutes Analyzed | Total Rain (mm) |
|---|---|---|---|---|
| PWS MI | 27.4·I·(1−0.49·e−0.121·I) | 0.98 | 18001 | 582 |
| PWS PE | 31.2·I·(1−0.55·e−0.057·I) | 0.97 | 85605 | 1255 |
| Thies RA | 23.6·I·(1−0.53·e−0.103·I) | 0.95 | 152284 | 1397 |
| Thies PR | 20.6·I·(1−0.57·e−0.111·I) | 0.96 | 15708 | 190 |
| Parsivel PE | 35.0·I·(1−0.68·e−0.079·I) | 0.91 | 19059 | 181 |
| Parsivel CH | 34.0·I·(1−0.72·e−0.043·I) | 0.90 | 47058 | 787 |
| Disdrometer and Measurement Site | Rainfall Kinetic Energy–Intensity Relationship | Sum KE (J m−2) | PBIAS (%) | RMSE (J m−2) | MAE (J m−2) |
|---|---|---|---|---|---|
| PWS MI | Measured | 12719 | |||
| Site-specific relationship | 12956 | 1.9 | 0.393 | 0.117 | |
| WS | 11657 | −8.3 | 0.482 | 0.150 | |
| BF | 10108 | −20.5 | 0.515 | 0.171 | |
| MG | 11293 | −11.2 | 0.427 | 0.134 | |
| VD | 11409 | −10.3 | 0.463 | 0.127 | |
| PWS PE | Measured | 22807 | |||
| Site-specific relationship | 23566 | 3.3 | 0.219 | 0.054 | |
| WS | 20614 | −9.5 | 0.295 | 0.070 | |
| BF | 16899 | −25.9 | 0.294 | 0.077 | |
| MG | 19004 | −16.7 | 0.246 | 0.064 | |
| VD | 21311 | −6.6 | 0.273 | 0.057 | |
| Thies RA | Measured | 19174 | |||
| Site-specific relationship | 20194 | 5.3 | 0.102 | 0.033 | |
| WS | 20244 | 5.8 | 0.135 | 0.049 | |
| BF | 15919 | −17.0 | 0.123 | 0.036 | |
| MG | 18020 | −6.0 | 0.116 | 0.032 | |
| VD | 21777 | 13.6 | 0.104 | 0.038 | |
| Thies PR | Measured | 2273 | |||
| Site-specific relationship | 2356 | 3.6 | 0.096 | 0.035 | |
| WS | 2819 | 24.2 | 0.175 | 0.065 | |
| BF | 2225 | −2.1 | 0.108 | 0.035 | |
| MG | 2524 | 11.0 | 0.153 | 0.040 | |
| VD | 2997 | 31.8 | 0.129 | 0.056 | |
| Parsivel PE | Measured | 2968 | |||
| Site-specific relationship | 2966 | −0.1 | 0.219 | 0.037 | |
| WS | 2526 | −14.6 | 0.305 | 0.053 | |
| BF | 2071 | −30.2 | 0.296 | 0.051 | |
| MG | 2313 | −22.1 | 0.254 | 0.043 | |
| VD | 2831 | −4.6 | 0.280 | 0.043 | |
| Parsivel CH | Measured | 10713 | |||
| Site-specific relationship | 10799 | 0.8 | 0.237 | 0.064 | |
| WS | 12408 | 16.0 | 0.300 | 0.094 | |
| BF | 9565 | −10.7 | 0.251 | 0.062 | |
| MG | 10954 | 2.3 | 0.243 | 0.064 | |
| VD | 12640 | 18.0 | 0.256 | 0.078 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johannsen, L.L.; Zambon, N.; Strauss, P.; Dostal, T.; Neumann, M.; Zumr, D.; Cochrane, T.A.; Klik, A. Impact of Disdrometer Types on Rainfall Erosivity Estimation. Water 2020, 12, 963. https://doi.org/10.3390/w12040963
Johannsen LL, Zambon N, Strauss P, Dostal T, Neumann M, Zumr D, Cochrane TA, Klik A. Impact of Disdrometer Types on Rainfall Erosivity Estimation. Water. 2020; 12(4):963. https://doi.org/10.3390/w12040963
Chicago/Turabian StyleJohannsen, Lisbeth Lolk, Nives Zambon, Peter Strauss, Tomas Dostal, Martin Neumann, David Zumr, Thomas A. Cochrane, and Andreas Klik. 2020. "Impact of Disdrometer Types on Rainfall Erosivity Estimation" Water 12, no. 4: 963. https://doi.org/10.3390/w12040963
APA StyleJohannsen, L. L., Zambon, N., Strauss, P., Dostal, T., Neumann, M., Zumr, D., Cochrane, T. A., & Klik, A. (2020). Impact of Disdrometer Types on Rainfall Erosivity Estimation. Water, 12(4), 963. https://doi.org/10.3390/w12040963









