A Generic Method for Predicting Environmental Concentrations of Hydraulic Fracturing Chemicals in Soil and Shallow Groundwater
Abstract
:1. Introduction
2. Materials and Methods
2.1. Leakage Pathways
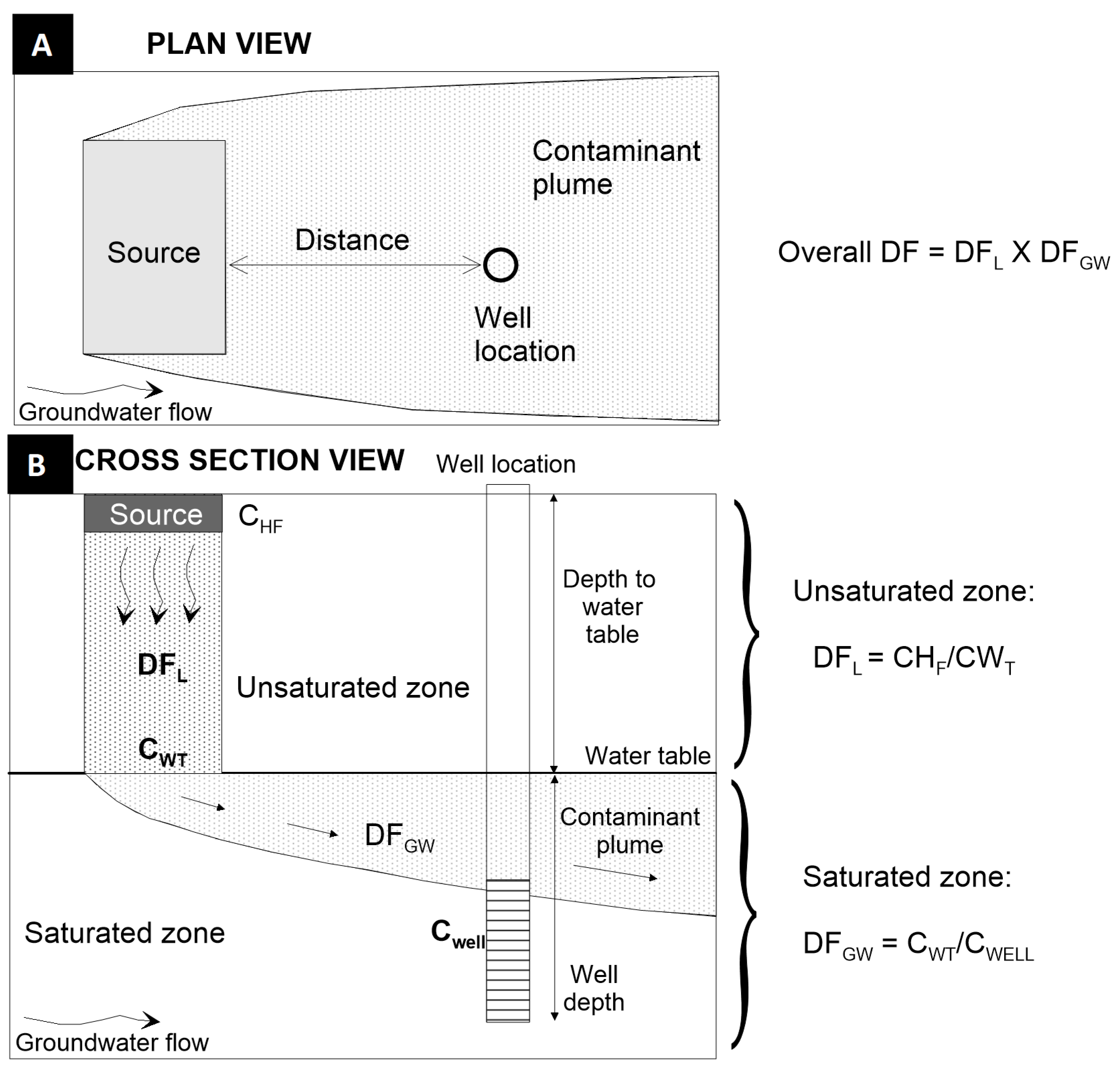
2.2. Soil-Groundwater Pathway Coupling
2.3. Soil Pathway
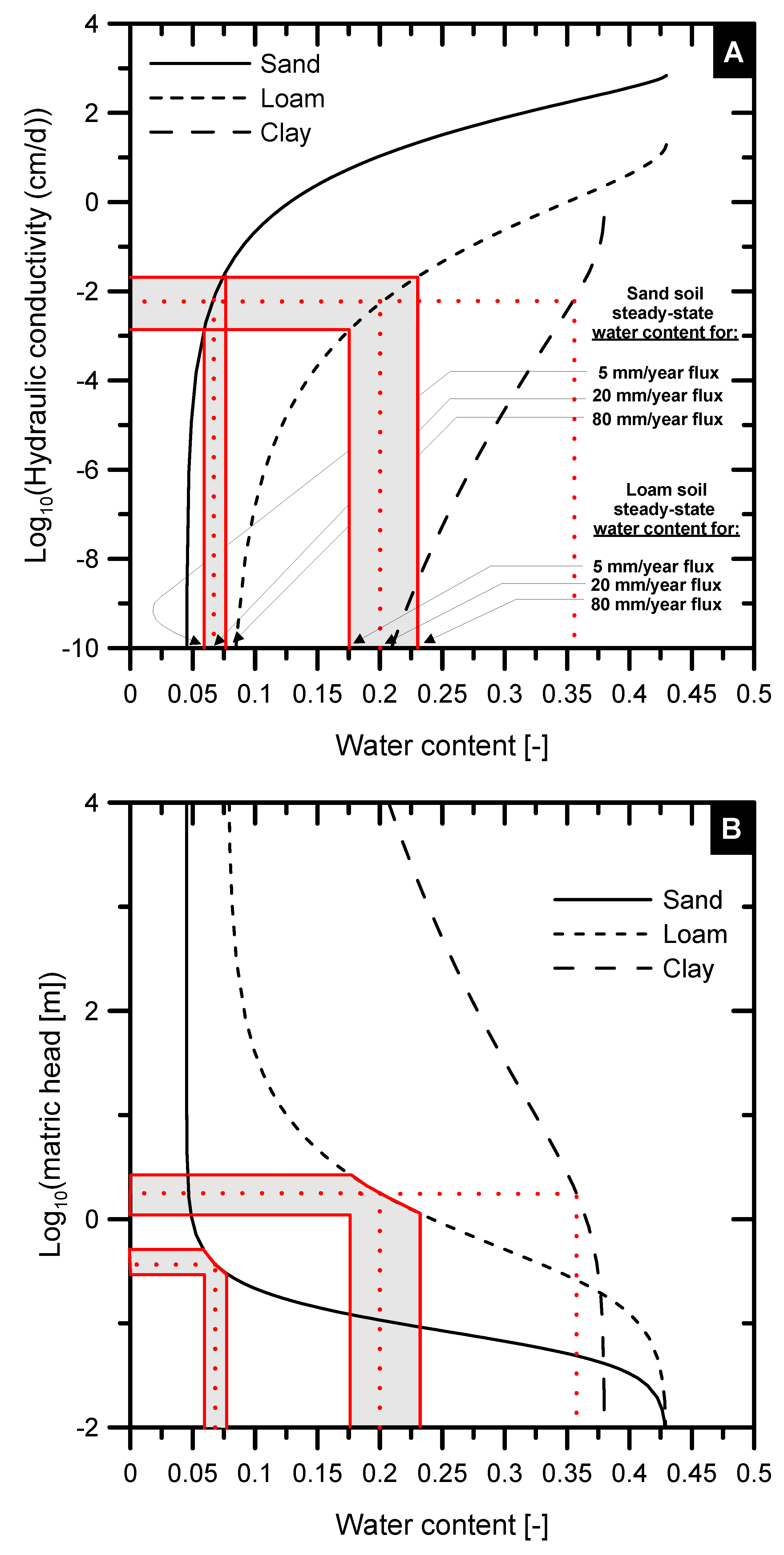
2.3.1. Soil Hydraulic Model
2.3.2. Solute Transport Model
2.3.3. Accounting for Variations in Depth to Groundwater
2.3.4. Boundary Conditions for Unsaturated Solute Transport
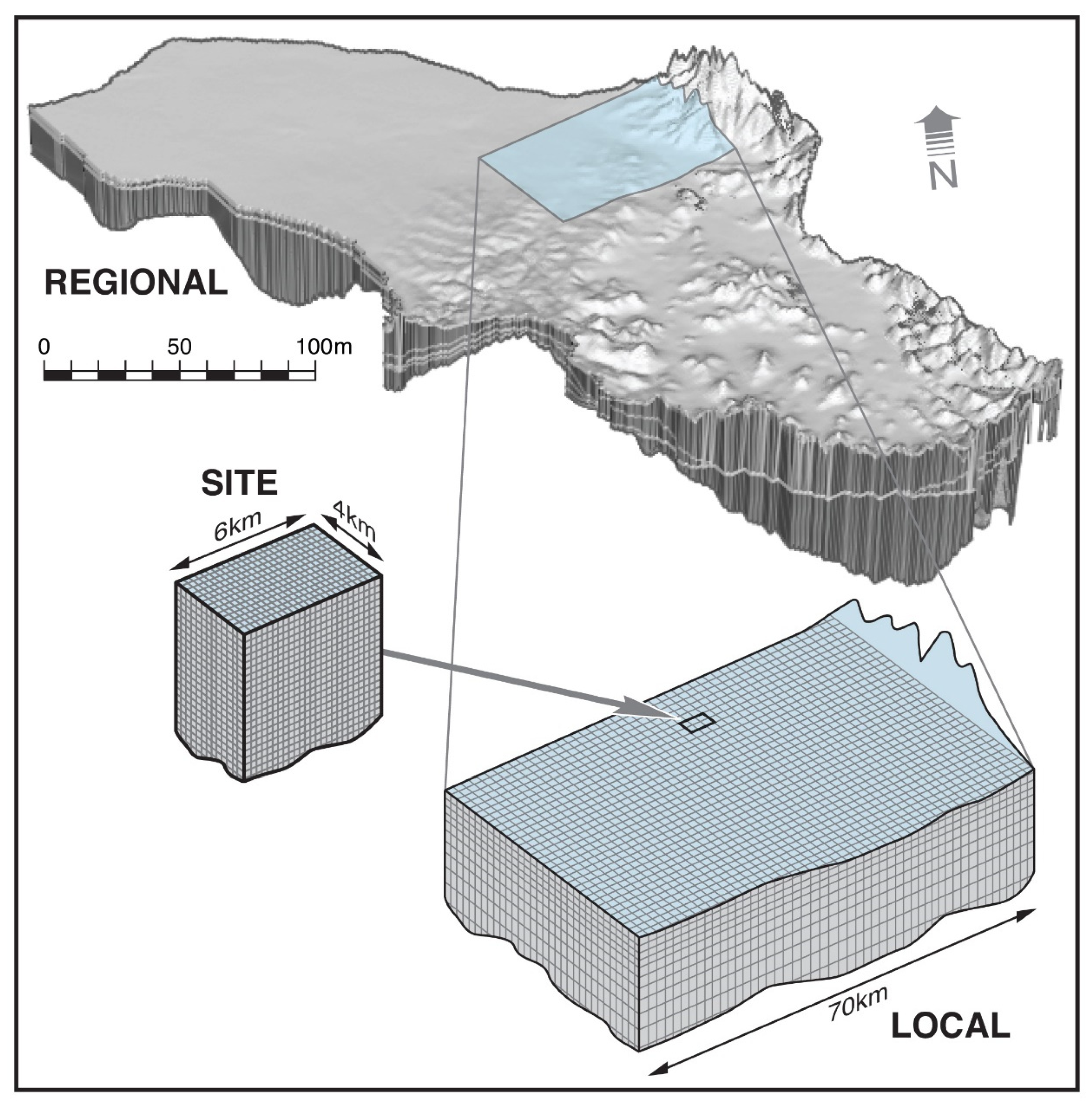
2.4. Groundwater Pathway
2.4.1. Groundwater Flow Model
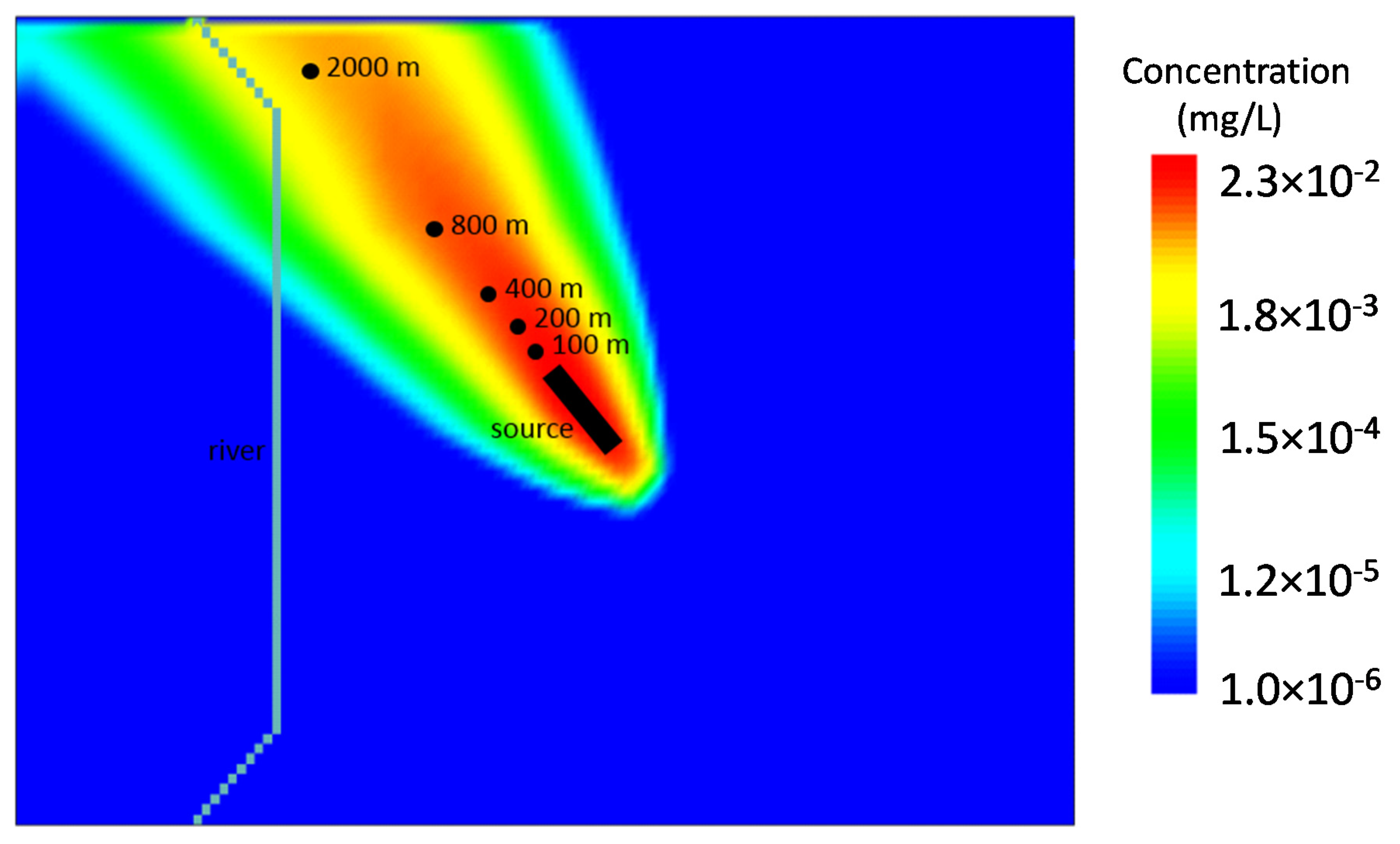
2.4.2. Solute Transport Modelling
2.5. Dilution Factors
3. Results
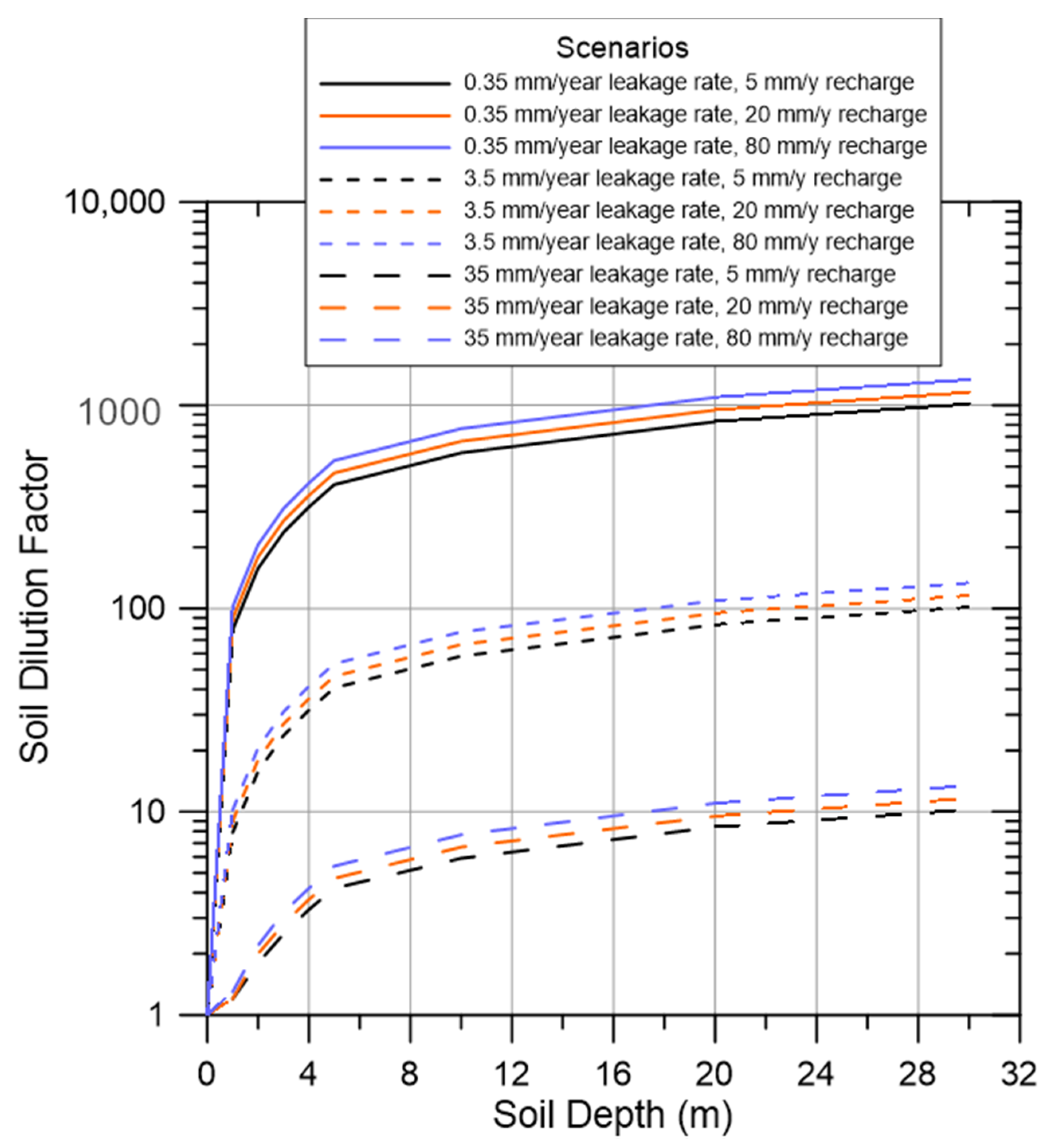
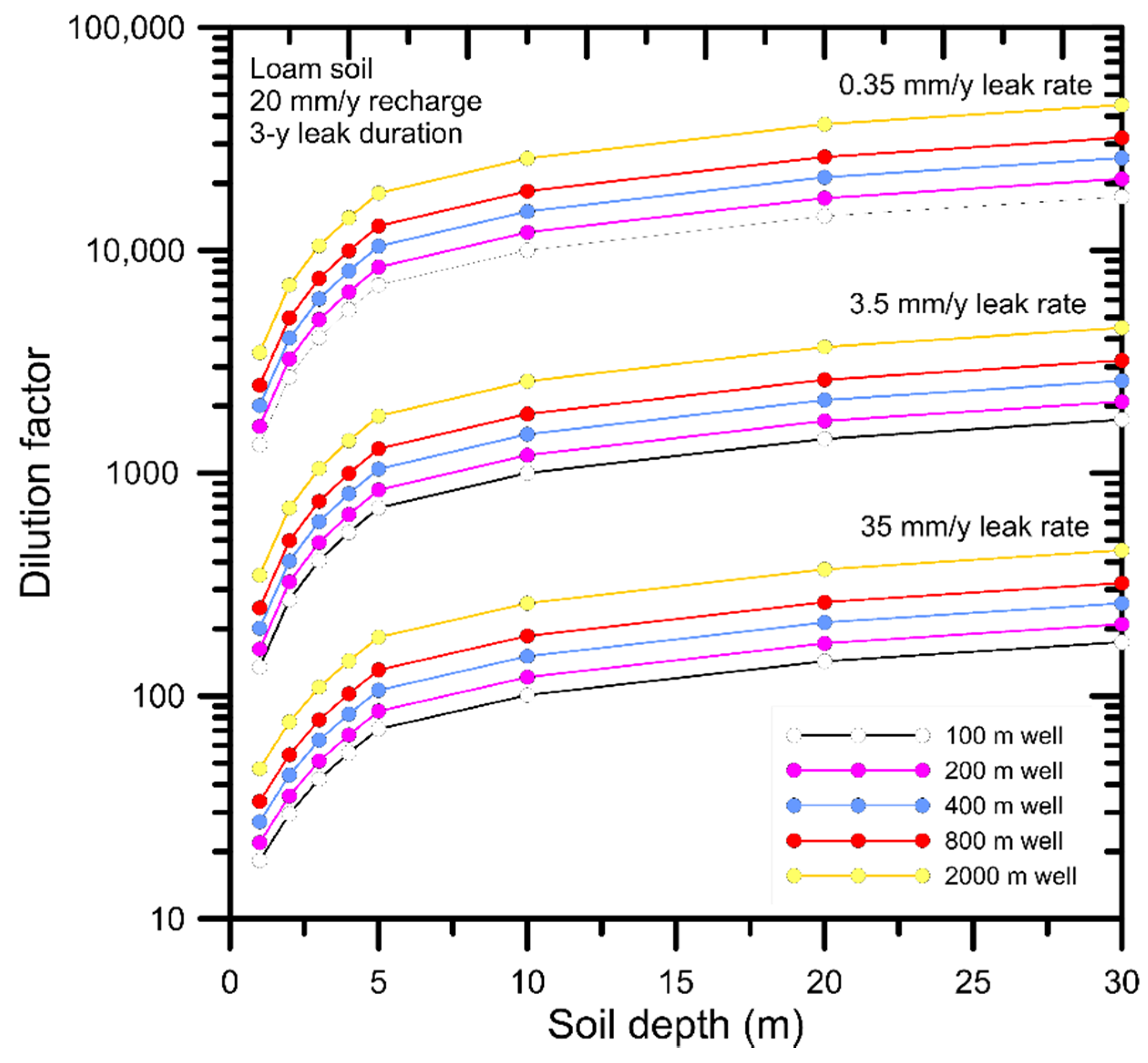
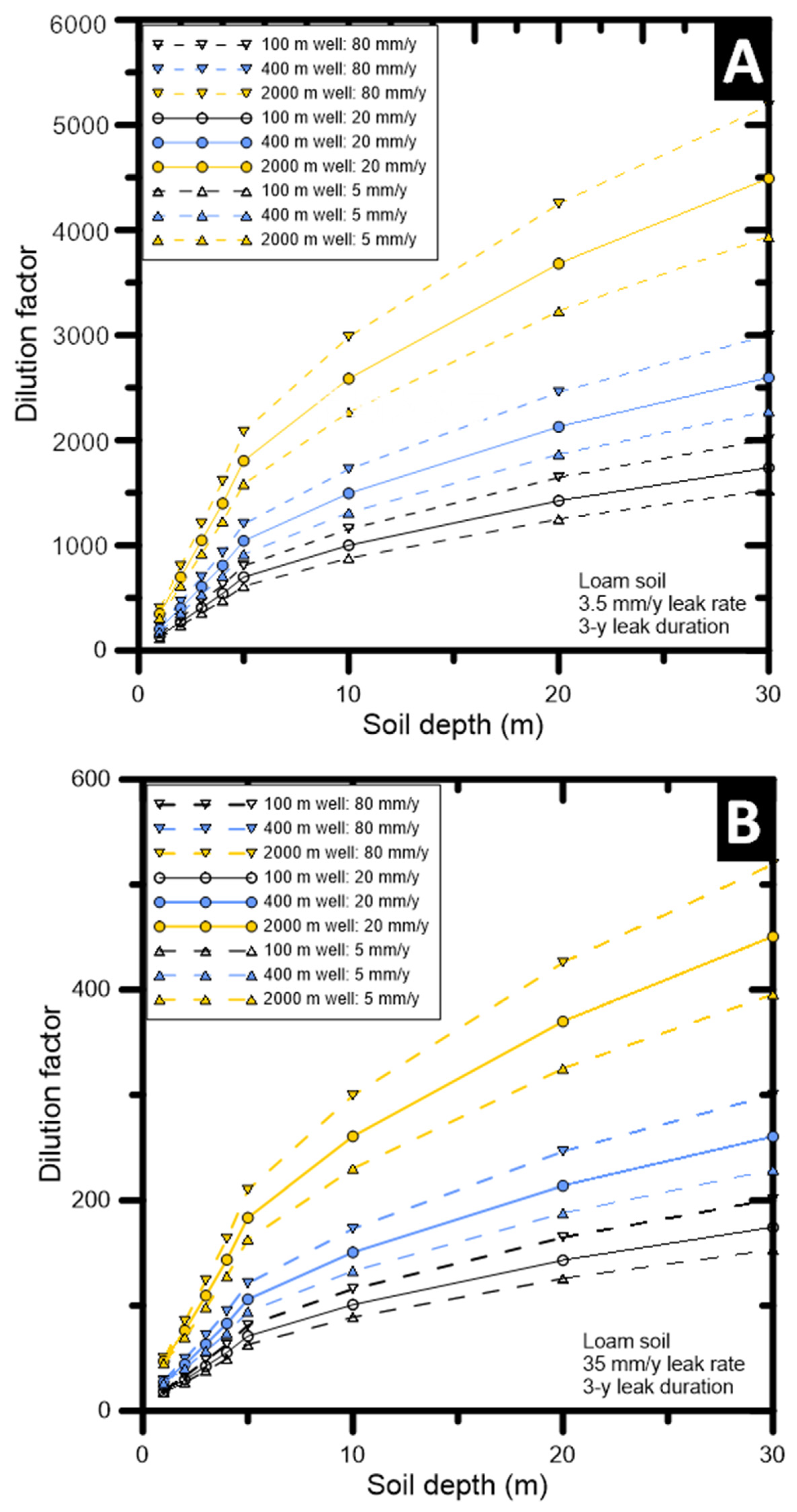
3.1. Soil Dilution Factors
3.2. Groundwater Dilution Factors
3.3. Combined Dilution Factors
3.4. Uncertainty Propagation
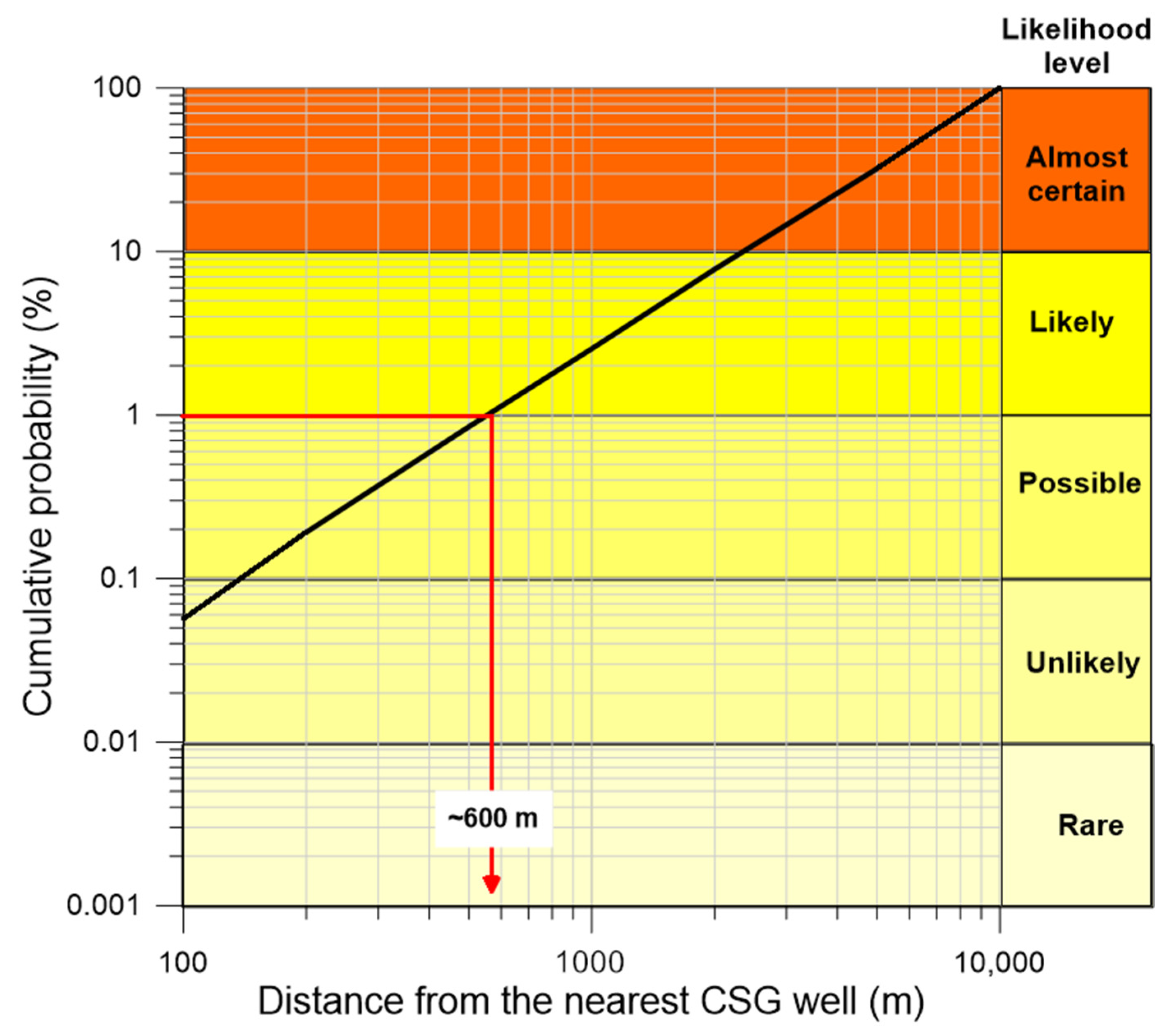
3.5. Likelihood of Dilution Factors
3.6. Predicted Environmental Concentrations for CSG Chemicals
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- DoEE. Environmental Risks Associated with Surface Handling of Chemicals Used in Coal Seam Gas Extraction, Project Report Prepared by the Chemicals and Biotechnology Assessments Section (Cbas) of the Department of the Environment and Energy (Doee) as Part of the National Assessment of Chemicals Associated with Coal Seam Gas Extraction in Australia; Commonwealth of Australia: Canberra, Australia, 2017.
- Balaba, R.S.; Smart, R.B. Total arsenic and selenium analysis in Marcellus shale, high-salinity water, and hydrofracture flowback wastewater. Chemosphere 2012, 89, 1437–1442. [Google Scholar] [CrossRef] [PubMed]
- Farag, A.M.; Harper, D.D. A review of environmental impacts of salts from produced waters on aquatic resources. Int. J. Coal Geol. 2014, 126, 157–161. [Google Scholar] [CrossRef] [Green Version]
- Mallants, D.; Simunek, J.; van Genuchten MTh Jacques, D. Using Hydrus and its Modules to Simulate the Fate and Transport of Coal Seam Gas Chemicals in Variably-Saturated Soils. Water 2017, 9, 385. [Google Scholar] [CrossRef] [Green Version]
- Skalak, K.J.; Engle, M.A.; Rowan, E.L.; Jolly, G.D.; Conko, K.M.; Benthem, A.J.; Kraemer, T.F. Surface disposal of produced waters in western and southwestern Pennsylvania: Potential for accumulation of alkali-earth elements in sediments. Int. J. Coal Geol. 2014, 126, 162–170. [Google Scholar] [CrossRef]
- Stearman, W.; Taulis, M.; Smith, J.; Corkeron, M. Assessment of Geogenic Contaminants in Water Co-Produced with Coal Seam Gas Extraction in Queensland, Australia: Implications for Human Health Risk. Geosciences 2014, 4, 219–239. [Google Scholar] [CrossRef] [Green Version]
- DiGiulio, D.C.; Jackson, R.B. Impact to Underground Sources of Drinking Water and Domestic Wells from Production Well Stimulation and Completion Practices in the Pavillion, Wyoming, Field. Environ. Sci. Technol. 2016, 50, 4524–4536. [Google Scholar] [CrossRef] [PubMed]
- Kahrilas, G.A.; Blotevogel, J.; Stewart, P.S.; Borch, T. Biocides in Hydraulic Fracturing Fluids: A Critical Review of Their Usage, Mobility, Degradation, and Toxicity. Environ. Sci. Technol. 2014, 49, 16–32. [Google Scholar] [CrossRef]
- Olsson, O.; Weichgrebe, D.; Rosenwinkel, K.H. Hydraulic fracturing wastewater in Germany: Composition, treatment, concerns. Environ. Earth Sci. 2013, 70, 3895–3906. [Google Scholar] [CrossRef]
- Orem, W.H.; Tatu, C.A.; Lerch, H.E.; Rice, C.A.; Bartos, T.T.; Bates, A.L.; Tewalt, S.; Corum, M.D. Organic compounds in produced waters rom coalbed natural gas wells in the Powder River Basin, Wyoming, USA. Appl. Geochem. 2007, 22, 2240–2256. [Google Scholar] [CrossRef]
- Rogers, J.D.; Burke, T.L.; Osborn, S.G.; Ryan, J.N. A Framework for Identifying Organic Compounds of Concern in Hydraulic Fracturing Fluids Based on Their Mobility and Persistence in Groundwater. Environ. Sci. Technol. Lett. 2015, 2, 158–164. [Google Scholar] [CrossRef] [Green Version]
- US EPA. Hydraulic Fracturing for Oil and Gas: Impacts from the Hydraulic Fracturing Watr Cycle on Drinking Water Resources in the United States; Office of Research and Development: Washington, DC, USA, 2016.
- Vengosh, A.; Jackson, R.B.; Warner, N.; Darrah, T.H.; Kondash, A. A Critical Review of the Risks to Water Resources from Unconventional Shale Gas Development and Hydraulic Fracturing in the United States. Environ. Sci. Technol. 2014, 48, 8334–8348. [Google Scholar] [CrossRef]
- Adgate, J.L.; Goldstein, B.D.; McKenzie, L.M. Potential public health hazards, exposures and health effects from unconventional gas development. Environ. Sci. Technol. 2014, 48, 8307–8320. [Google Scholar] [CrossRef]
- Groat, C.G.; Grimshaw, T.W. Fact-Based Regulation for Environmental Protection in Shale Gas Development; The Energy Institute, University of Texas at Austin: Austin, TX, USA, 2012. [Google Scholar]
- Flewelling, S.A.; Sharma, M. Constraints on Upward Migration of Hydraulic Fracturing Fluid and Brine. Groundwater 2014, 52, 9–19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jeffrey, R.; Wu, B.; Bunger, A.; Zhang, X.; Chen, Z.; Kear, J.; Kasperczyk, D. Literature Review: Hydraulic Fracture Growth and Well Integrity, Project Report Prepared by the Commonwealth Scientific and Industrial Research Organisation (CSIRO) as Part of the National Assessment of Chemicals Associated with Coal Seam Gas Extraction in Australia; Commonwealth of Australia: Canberra, Australia, 2017.
- Mallants, D.; Bekele, E.; Schmid, W.; Miotlinski, K.; Bristow, K. Literature Review: Identification of Potential Pahways to Shallow Groundwater of Fluids Associated with Hydraulic Fracturing, Project Report Prepared by the Commonwealth Scientific and Industrial Research Organisation (CSIRO) as Part of the National Assessment of Chemicals Associated with Coal Seam Gas Extraction in Australia; Commonwealth of Australia: Canberra, Australia, 2017.
- Myers, T. Potential contaminant pathways from hydraulically fractured shale to aquifers. Groundwater 2012, 50, 872–882. [Google Scholar] [CrossRef] [PubMed]
- Rozell, D.J.; Reaven, S.J. Water pollution risk associated with natural gas extraction from the Marcellus Shale. Risk Anal. 2012, 32, 1382–1393. [Google Scholar] [CrossRef] [PubMed]
- Rutovitz, J.; Harris, S.M.; Kuruppu, N.; Dunstan, C. Drilling down: Coal Seam Gas-a Background Paper, Institute for Sustainable Futures; University of Technology Sydney (UTS): Sydney, Australia, 2011; pp. 1–83. Available online: http://cfsites1.uts.edu.au/find/isf/publications/rutovitzetal2011sydneycoalseamgasbkgd.pdf (accessed on 12 October 2015).
- Stringfellow, W.T.; Domen, J.K.; Camarillo, M.K.; Sandelin, W.L.; Borglin, S. Physical, chemical, and biological characteristics of compounds used in hydraulic fracturing. J. Hazard. Mater. 2014, 275, 37–54. [Google Scholar] [CrossRef] [PubMed]
- The Royal Society and Royal Academy of Engineering. Shale Gas Extraction in the UK: A Review of Hydraulic Fracturing; The Royal Society and Royal Academy of Engineering: London, UK, 2012. [Google Scholar]
- Vidic, R.D.; Brantley, S.L.; Vandenbossche, J.M.; Yoxtheimer, D.; Abad, J.D. Impact of shale gas development on regional water quality. Science 2013, 340, 6134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dusseault, M.; Jackson, R. Seepage pathways assessment for natural gas to shallow groundwater during well stimulation, in production, and after abandonment. Environ. Geosci. 2014, 21, 107–126. [Google Scholar] [CrossRef]
- Engelder, T.; Cathless, L.M.; Bryndzia, L.T. The fate of residual treatment water in gas shale. J. Unconv. Oil Gas Resour. 2014, 7, 33–48. [Google Scholar] [CrossRef]
- Mallants, D.; Jeffrey, R.; Kear, J.; Chen, Z.; Wu, B.; Bekele, E.; Apte, S.; Gray, B. Review of migration pathways for hydraulic fracturing chemicals. Int. J. Coal Geol. 2018, 195, 280–303. [Google Scholar] [CrossRef]
- Lechtenböhmer, S.; Altmann, M.; Capito, S.; Matra, Z.; Weindorf, W.; Zittel, W. Impacts of Shale Gas and Shale Oil Extraction on the Environment and on Human Health, Wuppertal Institute for Climate, Environment and Energy and Ludwig-Bölkow-Systemtechnik GmbH, Study Requested by the European Parliament’s Committee on Environment; Public Health and Food Safety: Brussels, Belgium, 2011. [Google Scholar]
- Mastrandrea, M.D.; Field, C.B.; Stocker, T.F.; Edenhofer, O.; Ebi, K.L.; Frame, D.J.; Held, H.; Kriegler, E.; Mach, K.J.; Matschoss, P.R.; et al. Guidance Note for Lead Authors of the IPCC Fifth Assessment Report on Consistent Treatment of Uncertainties; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2011. [Google Scholar]
- DERM. CSG/LNG Compliance Plan 2011 Update: January 2011 to June 2011; Department of Environment and Resource Management: Brisbane, Australia, 2011. Available online: http://www.ehp.qld.gov.au/management/coal-seam-gas/pdf/csg-lng-compliance-update1.pdf (accessed on 12 October 2015).
- NICNAS. Identification of Chemicals Associated with Coal Seam Gas Extraction in Australia, Project Report Prepared by the National Industrial Chemicals Notification and Assessment Scheme (NICNAS) as Part of the National Assessment of Chemicals Associated with Coal Seam Gas Extraction in Australia; Commonwealth of Australia: Canberra, Australia, 2017.
- NICNAS. Human Health and Environmental Risks Associated with Surface Spills and Leaks of Chemicals, Project Report, Report Prepared by the National Industrial Chemicals Notification and Assessment Scheme (NICNAS) as Part of the National Assessment of Chemicals Associated with Coal Seam Gas Extraction in Australia; Commonwealth of Australia: Canberra, Australia, 2017.
- Chapuis, R.P. Full-scale hydraulic performance of soil–bentonite and compacted clay liners. Can. Geotech. J. 2002, 39, 417–439. [Google Scholar] [CrossRef]
- Council of Canadian Academies. Environmental Impacts of Shale Gas Extraction in Canada; Council of Canadian Academies: Ottawa, ON, Canada, 2014. [Google Scholar]
- Giroud, J.P.; Bonaparte, R. Leakage through liners constructed with geomembranes -1. Geomembrane liners. Geotext. Geomembr. 1989, 8, 27–67. [Google Scholar] [CrossRef]
- Rowe, R.K. Short- and long-term leakage through composite liners, the 7th Arthur Casagrande Lecture. Can. Geotech. J. 2012, 49, 141–169. [Google Scholar] [CrossRef] [Green Version]
- Benson, C.H. Waste containment: Strategies and Performance. Aust. Geomech. 2001, 36, 1–25. [Google Scholar]
- Folkes, D.J. Control of contaminant migration by the use of liners. Can. Geotech. J. 1982, 19, 320–344. [Google Scholar] [CrossRef]
- Rowe, R.K.; Quigley, R.M.; Brachman, R.W.I.; Booker, J.R. Barrier Systems for Waste Disposal Facilities; Taylor and Francis Books Ltd. (E and FN Spon): London, UK, 2004. [Google Scholar]
- Rowe, R.K.; Hosney, M.S. A systems engineering approach to minimizing leachate leakage from landfills. In Proceedings of the 9th International Conference on Geosynthetics, Guaruja, Brazil, 23–27 May 2010; pp. 501–510. [Google Scholar]
- Bonaparte, R.; Daniel, D.; Koerner, R.M. Assessment and Recommendations for Improving the Performance of Waste Containment Systems; EPA Report EPA/600/R-02/099; U.S. Environmental Protection Agency (US EPA): Washington, DC, USA, 2002.
- Beck, A.L. A Statistical Approach to Minimizing Landfill Leakage. In Proceedings of the Solid Waste Association of North America (SWANA) Wastecon, Washington, DC, USA, 14–16 August 2012. [Google Scholar]
- Mallants, D.; Bekele, E.; Schmid, W.; Miotlinski, K.; Taylor, A.; Gerke, K. Human and Environmental Exposure Assessment: Soil to Shallow Groundwater Pathways—A Study of Predicted Environmental Concentrations, Project Report Prepared by the Commonwealth Scientific and Industrial Research Organisation (CSIRO) as Part of the National Assessment of Chemicals Associated with Coal Seam Gas Extraction in Australia; Commonwealth of Australia: Canberra, Australia, 2017.
- Mallants, D.; Apte, S.; Kear, J.; Turnadge, C.; Janardhanan, S.; Gonzalez, D.; Williams, M.; Chen, Z.; Kookana, R.; Taylor, A.; et al. Deeper Groundwater Hazard Screening Research; The Commonwealth Scientific and Industrial Research Organisation (CSIRO): Canberra, Australia, 2017. [Google Scholar]
- USEPA. Soil Screening Guidance: Technical Background Document; EPA/540/R95/12.8; Office of Solid Waste and Emergency Response, US Environmental Protection Agency: Washington, DC, USA, 1996.
- Van Genuchten, M.T.H. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Mallants, D.; van Genuchten MTh Simunek, J.; Jacques, D.; Seetharam, S. Leaching of contaminants to groundwater—Chapter 18. In Dealing with Contaminated Sites. from Theory towards Practical Application; Swartjens, F., Ed.; Springer: Dordrecht, The Netherlands, 2011; pp. 787–850. ISBN 978-90-481-9756-9. [Google Scholar] [CrossRef]
- Šimůnek, J.; Sejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media, Version 4.08; HYDRUS Software Series 3; Department of Environmental Sciences, University of California Riverside: Riverside, CA, USA, 2009; p. 330. [Google Scholar]
- Rassam, D.; Šimůnek, J.; Mallants, D.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media: Tutorial, Version 1.00; CSIRO Land and Water: Canberra, Australia, 2018; p. 183. ISBN 978-1-4863-1001-2. [Google Scholar]
- Gerke, K.M.; Sidle, R.C.; Mallants, D. Preferential flow mechanisms identified from staining experiments in forested hillslopes. Hydrol. Process. 2015, 29, 4562–4578. [Google Scholar] [CrossRef]
- Vanderborght, J.; Vereecken, H. Review of dispersivities for solute transport modeling in soils. Vadose Zone J. 2007, 6, 29–52. [Google Scholar] [CrossRef]
- US EPA. Overview of the Ecological Risk Assessment Process in the Office of Pesticide Programs; Report Prepared by the Office of Prevention, Pesticides and Toxic Substances and Office of Pesticide Programs for the US Environmental Protection Agency (USEPA); US EPA: Washington, DC, USA, 2004.
- McNeilage, C. Upper Namoi Groundwater Flow Model, Model Development and Calibration; NSW Government Department of Natural Resources: Parramatta, Australia, 2006.
- Sun, H.; Cornish, P.S. A catchment-based approach to recharge estimation in the Liverpool Plains, NSW Australia. Aust. J. Agric. Res. 2006, 57, 309–320. Available online: http://www.publish.csiro.au/cp/AR04015 (accessed on 12 October 2015). [CrossRef]
- Zhang, L.; Stauffacher, M.; Walker, G.R.; Dyce, P. Recharge Estimation in the Liverpool Plains (Nsw) for Input to Groundwater Models; CSIRO Land and Water Technical Report 10/97; CSIRO: Canberra, Australia, 1997.
- Daniells, I.G.; Brown, R.; Deegan, L. (Eds.) Northern Wheat-belt SOILpak. NSW Agriculture: Tamworth, UK, 1994; p. 47. [Google Scholar]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef] [Green Version]
- Soil Survey Staff. Keys to Soil Taxonomy. United States Department of Agriculture-Natural Resources Conservation Service, 12th ed.; NRCS: Lincoln, NE, USA, 2014.
- Mallants, D.; Bekele, E.; Schmid, W.; Miotliński, K. Human and Environmental Exposure Conceptualisation: Soil to Shallow Groundwater Pathways, Project Report Prepared by the Commonwealth Scientific and Industrial Research Organisation (CSIRO) as Part of the National Assessment of Chemicals Associated with Coal Seam Gas Extraction in Australia; Commonwealth of Australia: Canberra, Australia, 2017.
- SWS. The Namoi Catchment Water Study Independent Expert Final Study Report, Prepared by Schlumberger Water Services for the Department of Trade and Investment; Regional Infrastructure and Services, NSW (DTIRIS NSW): Sydney, Australia, 2012.
- SWS. Namoi Catchment Water Study Independent Expert Phase 3 Report, Prepared by Schlumberger Water Services for the Department of Trade and Investment; Regional Infrastructure and Services, NSW (DTIRIS NSW): Sydney, Australia, 2012.
- Engesgaard, P.; Jensen, K.H.; Molson, J.; Frind, E.O.; Olsen, H. Large-scale dispersion in a sandy aquifer: Simulation of subsurface transport of environmental tritium. Water Resour. Res. 1996, 32, 3253–3266. [Google Scholar] [CrossRef]
- Mallants, D.; Espino, A.; Van Hoorick, M.; Ferson, S.; Feyen, J.; Vandenberghe, N.; Loy, W. Dispersivity estimates from a tracer test in a sandy aquifer. Groundwater 2000, 38, 304–310. [Google Scholar] [CrossRef]
- Sudicky, E.A.; Illman, W.A.; Goltz, I.K.; Adams, J.J.; McLaren, R.G. Heterogeneity in hydraulic conductivity and its role on the macroscale transport of a solute plume: From measurements to a practical application of stochastic flow and transport theory. Water Resour. Res. 2010, 46, W01508. [Google Scholar] [CrossRef]
- Gedeon, M.; Mallants, D. Description of the hydrogeology. In Project Near Surface Disposal of Category a Waste at Dessel; NIRAS/ONDRAF: Brussel, Belgium, 2009; p. 174. [Google Scholar]
- Mehl, S.; Hill, M.C. MODFLOW-2005, the U.S. geological survey modular ground-water model. In Documentation of Local Grid Refinement (LGR) and the Boundary Flow and Head (BFH) Package; US Geological Survey Techniques and Methods 6-A12; US Geological Survey: Denver, CO, USA, 2005; p. 68. [Google Scholar]
- Zheng, C.; Wang, P. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide; US Army Corps of Engineers: Washington, DC, USA, 1999.
- Gelhar, L.W.; Welty, C.; Rehfeldt, K.R. A critical overview of data on field-scale dispersion in aquifers. Water Resour. Res. 1992, 28, 1955–1974. [Google Scholar] [CrossRef]
- Anderson, M.P.; Cherry, J.A. Using models to simulate the movement of contaminants through groundwater flow systems. Crit. Rev. Environ. Sci. Technol. 1979, 9, 97–156. [Google Scholar] [CrossRef]
- Rumbaugh, J.; Rumbaugh, D. Groundwater Vistas, Tutorial Manual for Groundwater Vistas; Version 6; Environmental Simulations; Reinholds: Lancaster County, PA, USA, 2011. [Google Scholar]
- Barnett, B.; Townley, L.R.; Post, V.; Evans, R.E.; Hunt, R.J.; Peeters, L.; Richardson, S.; Werner, A.D.; Knapton ABoronkay, A. Australian Groundwater Modelling Guidelines; Waterlines Report Series No 82, June 2012; Sinclair Knight Merz and the National Centre for Groundwater Research and Training for the National Water Commission: Canberra, Australia, 2012. [Google Scholar]
- Flury, M.; Fluhler, H.; Jury, W.; Leuenberger, J. Susceptibility of soils to preferential flow of water: A field study. Water Resour. Res. 1994, 30, 1945–1954. [Google Scholar] [CrossRef]
- Hendrickx, J.M.H.; Flury, M. Uniform and preferential flow, mechanisms in the Vadose zone. In Conceptual Models of Flow and Transport in the Fractured Vadose Zone; National Research Council, National Academy: Washington, DC, USA, 2001; pp. 149–187. [Google Scholar]
- Mallants, D. Field-scale solute transport parameters derived from tracer tests in large undisturbed soil columns. Soil Res. 2014, 52, 13–26. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.H. Contaminant transport in the unsaturated zone: Theory and modeling, chapter 22. In The Handbook of Groundwater Engineering, 2nd ed.; Delleur, J., Ed.; CRC: Boca Raton, FL, USA, 2006; pp. 22.1–22.46. [Google Scholar]
- Palmer, C.D.; Johnson, R.L. Physical Processes Controlling the Transport of Contaminants in the Aqueous Phase: Transport and Fate of Contaminants in the Subsurface; U.S. Environmental Protection Agency, Center for Environmental Research Information: Cincinnati, OH, USA; Robert S. Kerr Environmental Research Laboratory: Ada, OK, USA, 1989.
- USEPA. Guidelines for Exposure Assessment; Federal Register 57:22888-22938. EPA/600/Z-92/001 May 1992; U.S. Environmental Protection Agency: Washington, DC, USA, 1992; p. 139. Available online: http://cfpub.epa.gov/ncea/cfm/recordisplay.cfm?deid=15263#Download (accessed on 12 October 2015).
- USEPA. Determination of Groundwater Dilution Attenuation Factors for Fixed Waste Site Areas Using EPACMTP-Appendix E; US Environmental Protection Agency Office of Solid Waste: Washington, DC, USA, 1994.
- NSW Government. Pinneena Database, New South Wales Government. 2014. Available online: waterinfo.nsw.gov.au/pinneena/ (accessed on 12 October 2015).
- NICNAS. Chemicals of Low Concern for Human Health, Project Report Prepared by the National Industrial Chemicals Notification and Assessment Scheme (NICNAS) as Part of the National Assessment of Chemicals Associated with Coal Seam Gas Extraction in Australia; Commonwealth of Australia: Canberra, Australia, 2017.
- Heys, K.A.; Shore, R.F.; Pereira, M.G.; Jones, K.C.; Martin, F.L. Risk assessment of environmental mixture effects. RSC Adv. 2016, 6, 47844–47857. [Google Scholar] [CrossRef] [Green Version]
- Gedeon, M.; Mallants, D. Sensitivity analysis of a combined groundwater flow and solute transport model using local-grid refinement: A case study. Math. Geosci. 2012, 44, 881–900. [Google Scholar] [CrossRef]


| Distance to Water Bore | Hydraulic Conductivity, K | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Low K | Reference K | High K | |||||||
| Riverbed Conductance | Riverbed Conductance | Riverbed Conductance | |||||||
| L | M | H | L | M | H | L | M | H | |
| 100 m | 3.0 | 2.9 | 9.6 | 15 | 15 | 20 | 59 | 60 | 66 |
| 200 m | 3.8 | 3.5 | 15 | 18 | 18 | 24 | 70 | 70 | 77 |
| 400 m | 4.9 | 4.4 | 37 | 24 | 23 | 31 | 84 | 85 | 93 |
| 800 m | 6.4 | 6.5 | 469 | 32 | 28 | 57 | 103 | 104 | 120 |
| 2000 m | 15 | 27 | Nc | 57 | 38 | nc | 142 | 142 | 212 |
| Bore Distance→ | 100 m | 200 m | 400 m | 800 m | 2000 m |
|---|---|---|---|---|---|
| Soil Depth↓ | |||||
| 1 m | 1340 | 1613 | 1999 | 2466 | 3450 |
| 2 m | 2700 | 3246 | 4025 | 4965 | 6968 |
| 3 m | 4050 | 4876 | 6055 | 7465 | 10,478 |
| 4 m | 5410 | 6516 | 8085 | 9965 | 13,988 |
| 5 m | 6980 | 8396 | 10,425 | 12,855 | 18,038 |
| 10 m | 9995 | 12,038 | 14,932 | 18,418 | 25,839 |
| 20 m | 14,245 | 17,138 | 21,272 | 26,238 | 36,799 |
| 30 m | 17,435 | 20,991 | 26,043 | 32,119 | 45,055 |
| CAS No. | CAS Chemical Name (Common Name/Formula) | Concentration after Final Dilution Prior to Injection (g/kg or g/L) | Groundwater PEC (mg/L) | PNEC (mg/L) |
|---|---|---|---|---|
| 10,043-35-3 | Boric acid (H3BO3) | 0.216 | 0.031 | 0.83@ |
| 107-21-1 | 1,2-Ethanediol (Ethylene glycol) | 0.496 | 0.071 | 10 |
| 111-76-2 | 2-Butoxyethanol (Butoxyethanol) | 0.04 | 0.0057 | 0.165 |
| 1310-73-2 | Sodium hydroxide (Na(OH)) | 0.1375 | 0.020 | 2.4 |
| 26,172-55-4 | 3(2H)-Isothiazolone, 5-chloro-2-methyl- (Methyl-chloroisothiazolinone) | 0.0037 | 0.00053 | 0.00062 |
| 2682-20-4 | 3(2H)-Isothiazolone, 2-methyl- (Methyliso-thiazolone) | 0.0011 | 0.00016 | 0.0007 |
| 497-19-8 | Carbonic acid sodium salt (1:2) (Soda ash) | 0.316 | 0.045 | 4.24 |
| 55,566-30-8 | Phosphonium, tetrakis(hydroxymethyl)-, sulfate (2:1) (salt) (THPS) | 0.04125 | 0.0059 | 0.94 |
| 64-19-7 | Acetic acid (Acetic acid) | 0.525 | 0.075 | 15 |
| 67-63-0 | 2-Propanol (Isopropanol) | 0.0134 | 0.0019 | 500 |
| 7447-40-7 | Potassium chloride (KCl) | 22.96 | 3.3 | 3.73 |
| 75-57-0 | Methanaminium, N,N,N-trimethyl-, chloride (1:1) (Tetramethylammonium chloride) | 1.273 | 0.18 | 4.62 |
| 7647-14-5# | Sodium chloride (Common salt) | 0.4 | 0.057 | 3.14 |
| 7647-01-0 | Hydrochloric acid (Hydrochloric acid) | 0.0525 | 0.0075 | 6.2 |
| 7681-52-9 | Hypochlorous acid, sodium salt (1:1) (Sodium hypochlorite) | 0.0578 | 0.0083 | 0.000023 |
| 7727-54-0 | Peroxydisulfuric acid ([(HO)S(O)2]2O2), ammonium salt (1:2) (Ammonium persulfate) | 0.4521 | 0.065 | 0.92 |
| 7786-30-3# | Magnesium chloride (MgCl2) | 0.0034 | 0.00049 | 2.12 |
| 77-92-9# | 1,2,3-Propanetricarboxylic acid, 2-hydroxy- (citric acid) | 1.765 | 0.25 | 15.3 |
| 9000-30-0# | Guar gum (Guar gum) | 2.6 | 0.37 | 0.22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallants, D.; Bekele, E.; Schmid, W.; Miotlinski, K.; Taylor, A.; Gerke, K.; Gray, B. A Generic Method for Predicting Environmental Concentrations of Hydraulic Fracturing Chemicals in Soil and Shallow Groundwater. Water 2020, 12, 941. https://doi.org/10.3390/w12040941
Mallants D, Bekele E, Schmid W, Miotlinski K, Taylor A, Gerke K, Gray B. A Generic Method for Predicting Environmental Concentrations of Hydraulic Fracturing Chemicals in Soil and Shallow Groundwater. Water. 2020; 12(4):941. https://doi.org/10.3390/w12040941
Chicago/Turabian StyleMallants, Dirk, Elise Bekele, Wolfgang Schmid, Konrad Miotlinski, Andrew Taylor, Kirill Gerke, and Bruce Gray. 2020. "A Generic Method for Predicting Environmental Concentrations of Hydraulic Fracturing Chemicals in Soil and Shallow Groundwater" Water 12, no. 4: 941. https://doi.org/10.3390/w12040941
APA StyleMallants, D., Bekele, E., Schmid, W., Miotlinski, K., Taylor, A., Gerke, K., & Gray, B. (2020). A Generic Method for Predicting Environmental Concentrations of Hydraulic Fracturing Chemicals in Soil and Shallow Groundwater. Water, 12(4), 941. https://doi.org/10.3390/w12040941






