A Landslide Probability Model Based on a Long-Term Landslide Inventory and Rainfall Factors
Abstract
:1. Introduction
2. Research Area and Materials
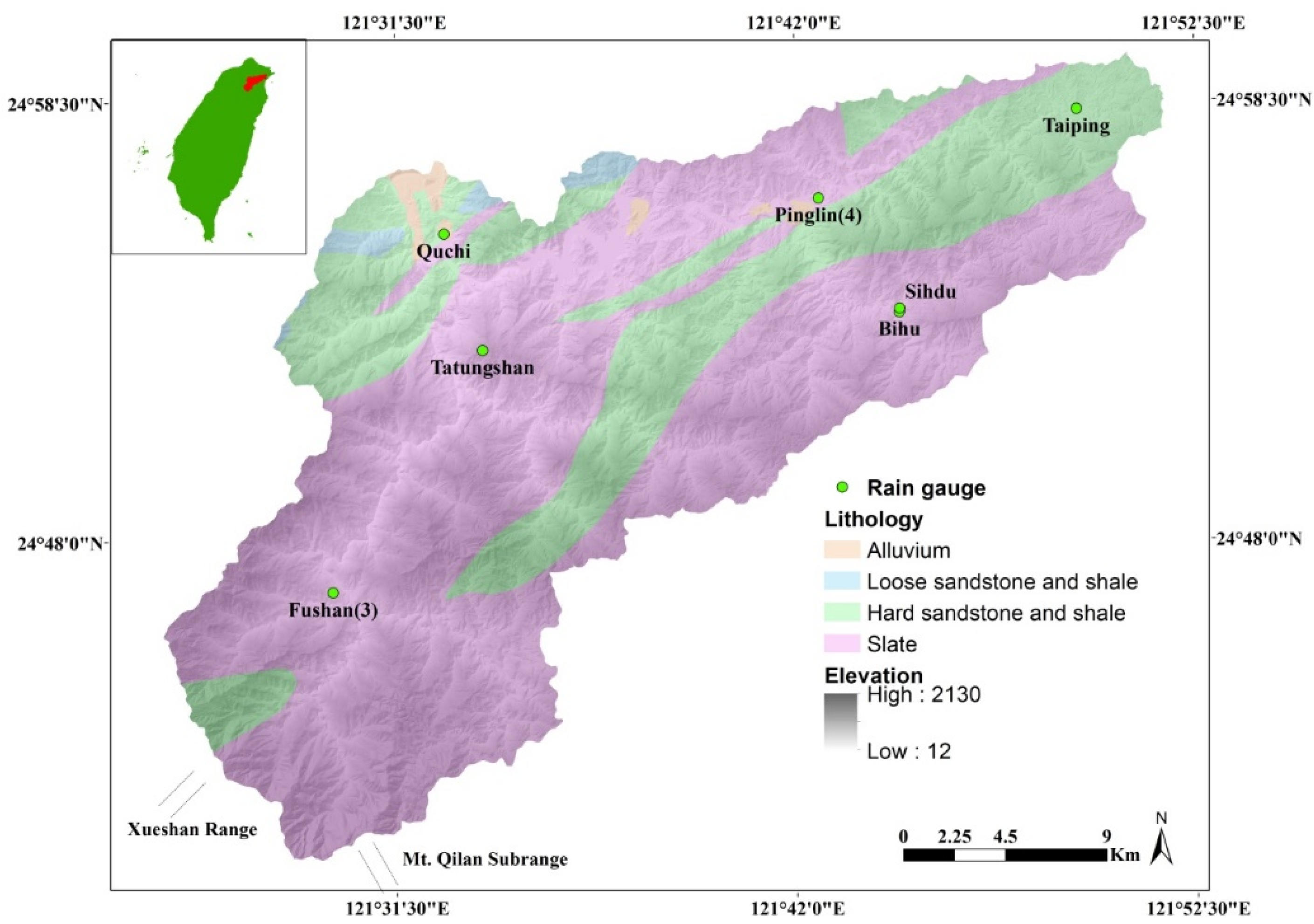
2.1. Environmental Setting of Taipei Water Source Domain
2.2. Rainfall Data
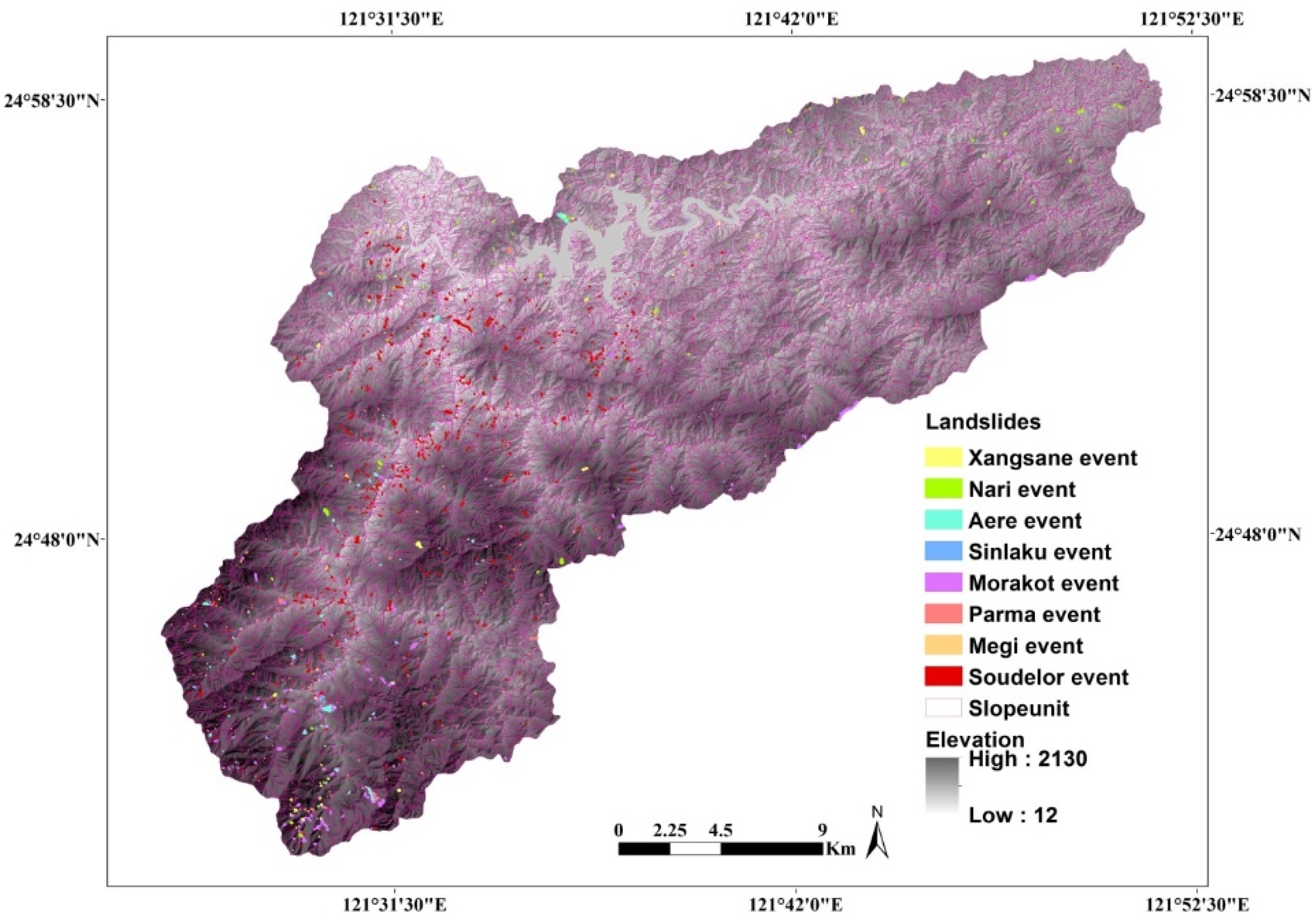
2.3. Landslide Inventory
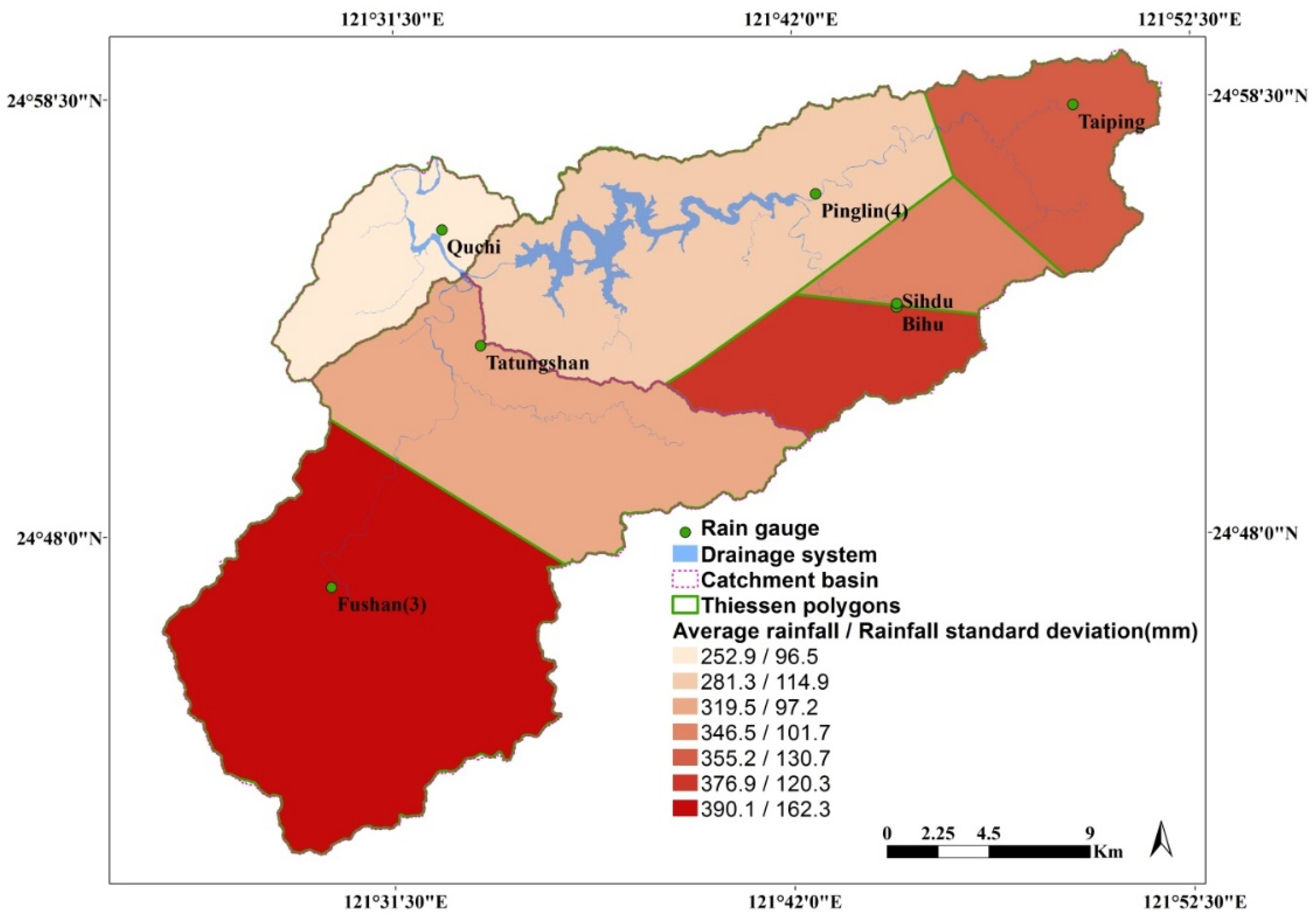
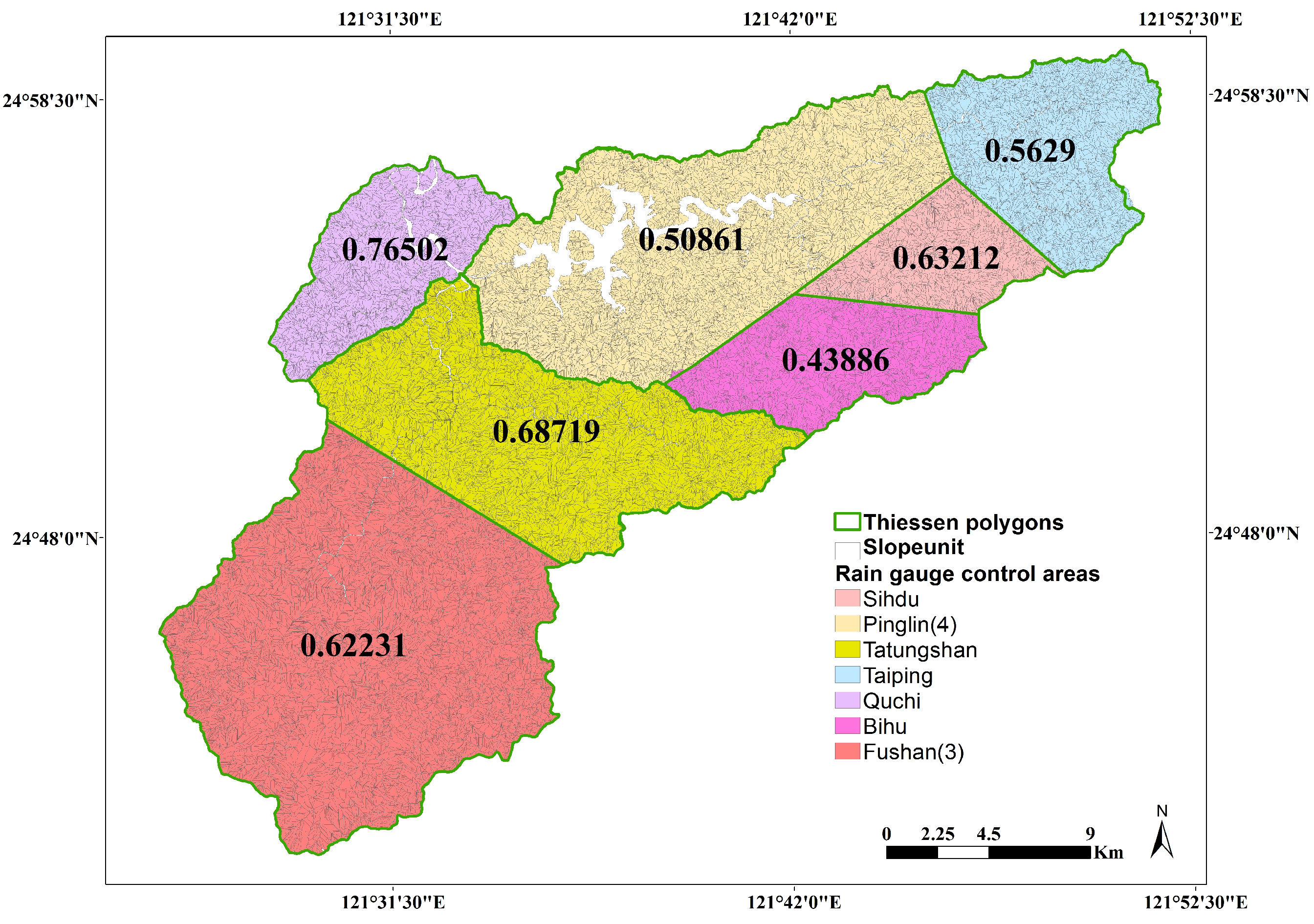
2.4. Analytical Units and Rain Gauge Control Areas
3. Methods
3.1. Analysis of Discrete Rainfall Groups
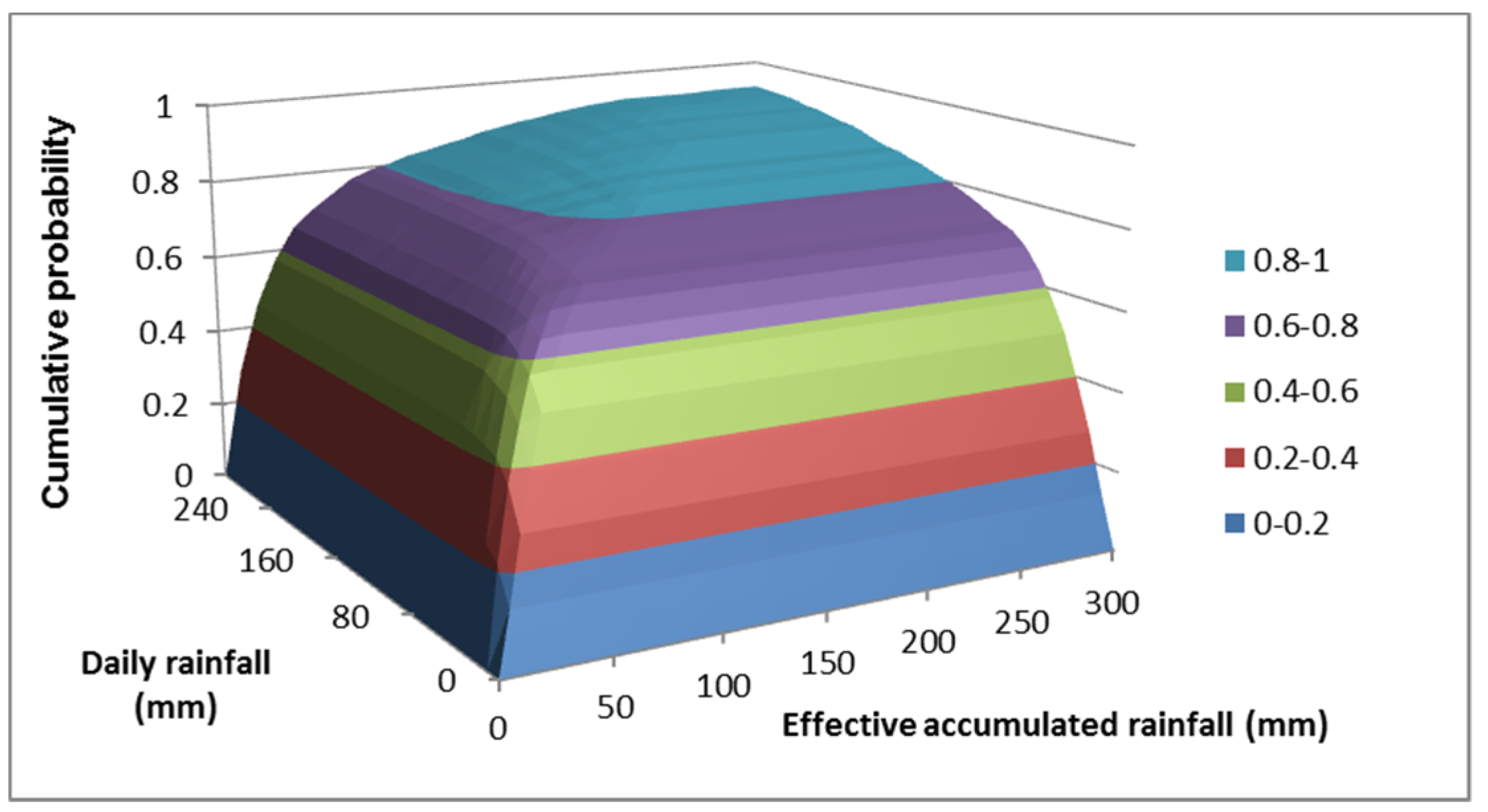
3.2. Joint Cumulative Distribution Function
3.3. Selection of a Rainfall Probability Threshold
3.4. Poisson Probability Model
3.5. Conditional Probability
4. Results and Discussion
4.1. Joint Cumulative Distribution Functions of the Rain Gauges
4.2. Selection of Rainfall Probability Thresholds of the Rain Gauges
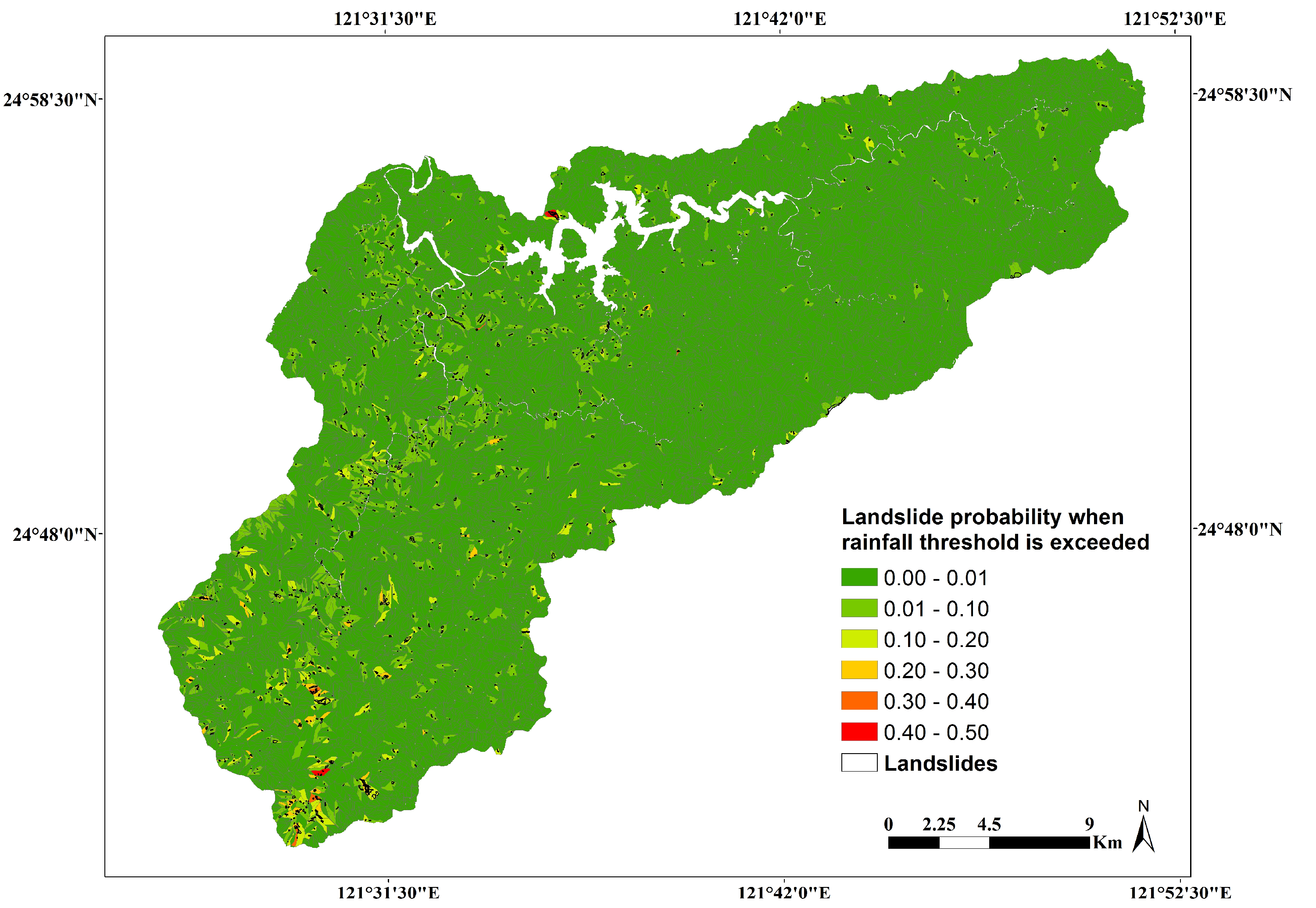
4.3. Landslide Probability Analysis Employing a Rainfall Probability Threshold and a Long-Term Landslide Inventory
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Varnes, D.J. IAEG Landslide Hazard Zonation: A Review of Principles and Practice (No.3); United Nations: New York, NY, USA, 1984. [Google Scholar]
- Carrara, A. Multivariate models for landslide hazard evaluation. J. Int. Assoc. Math. Geol. 1983, 15, 403–426. [Google Scholar] [CrossRef]
- Chung, C.J.F.; Fabbri, A.G. The representation of geoscience information for data integration. Nonrenew. Resour. 1993, 2, 122–139. [Google Scholar] [CrossRef]
- Baeza, C.; Corominas, J. Assessment of shallow landslide susceptibility by means of multivariate statistical techniques. Earth Surf. Process. Landf. 2001, 26, 1251–1263. [Google Scholar] [CrossRef]
- Guzzetti, F.; Galli, M.; Reichenbach, P.; Ardizzone, F.; Cardinali, M. Landslide hazard assessment in the Collazzone area, Umbria, Central Italy. Nat. Hazards Earth Syst. Sci. 2006, 6, 115–131. [Google Scholar] [CrossRef]
- Zêzere, J.L.; Oliveira, S.C.; Garcia, R.A.C.; Reis, E. Landslide risk analysis in the area North of Lisbon (Portugal): Evaluation of direct and indirect costs resulting from a motorway disruption by slope movements. Landslides 2007, 4, 123–136. [Google Scholar] [CrossRef]
- Carrara, A.; Crosta, G.; Frattini, P. Comparing models of debris-flow susceptibility in the alpine environment. Geomorphology 2008, 94, 353–378. [Google Scholar] [CrossRef]
- Lee, C.T.; Huang, C.C.; Lee, J.F.; Pan, K.L.; Lin, M.L.; Dong, J.J. Statistical approach to storm event-induced landslides susceptibility. Nat. Hazards Earth Syst. Sci. 2008, 8, 941–960. [Google Scholar] [CrossRef] [Green Version]
- Rossi, M.; Guzzetti, F.; Reichenbach, P.; Mondini, A.C.; Peruccacci, S. Optimal landslide susceptibility zonation based on multiple forecasts. Geomorphology 2010, 114, 129–142. [Google Scholar] [CrossRef]
- Nefeslioglu, H.A.; Gokceoglu, C. Probabilistic risk assessment in medium scale for rainfall-induced earthflows: Catakli catchment area (Cayeli, Rize, Turkey). Math. Probl. Eng. 2011, 2011, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Chan, H.C.; Chen, P.A.; Lee, J.T. Rainfall-induced landslide susceptibility using a rainfall–runoff model and logistic regression. Water 2018, 10, 1354. [Google Scholar] [CrossRef] [Green Version]
- Roccati, A.; Faccini, F.; Luino, F.; Ciampalini, A.; Turconi, L. Heavy rainfall triggering shallow landslides: A susceptibility assessment by a GIS-approach in a Ligurian Apennine catchment (Italy). Water 2019, 11, 605. [Google Scholar] [CrossRef] [Green Version]
- Corominas, J.; van Westen, C.; Frattini, P.; Cascini, L.; Malet, J.P.; Fotopoulou, S.; Catani, F.; Van Den Eeckhaut, M.; Mavrouli, O.; Agliardi, F.; et al. Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 2014, 73, 209–263. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Galli, M.; Ardizzone, F. Probabilistic landslide hazard assessment at the basin scale. Geomorphology 2005, 72, 272–299. [Google Scholar] [CrossRef]
- Jaiswal, P.; van Westen, C.J.; Jetten, V. Quantitative landslide hazard assessment along a transportation corridor in southern India. Eng. Geol. 2010, 116, 236–250. [Google Scholar] [CrossRef]
- Das, I.; Stein, A.; Kerle, N.; Dadhwal, V.K. Probabilistic landslide hazard assessment using homogeneous susceptible units (HSU) along a national highway corridor in the northern Himalayas, India. Landslides 2011, 8, 293–308. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; van Westen, C.J.; Carranza, E.J.M.; Jetten, V.G.; Cardinali, M.; Rossi, M.; Guzzetti, F. Generating event-based landslide maps in a data-scarce Himalayan environment for estimating temporal and magnitude probabilities. Eng. Geol. 2012, 128, 49–62. [Google Scholar] [CrossRef]
- Segoni, S.; Tofani, V.; Rosi, A.; Catani, F.; Casagli, N. Combination of Rainfall Thresholds and Susceptibility Maps for Dynamic Landslide Hazard Assessment at Regional Scale. Front. Earth Sci. 2018, 6, 85. [Google Scholar] [CrossRef] [Green Version]
- Salvatici, T.; Tofani, V.; Rossi, G.; D’Ambrosio, M.; Stefanelli, C.T.; Masi, E.B.; Rosi, A.; Pazzi, V.; Vannocci, P.; Petrolo, M.; et al. Application of a physically based model to forecast shallow landslides at a regional scale. Nat. Hazards Earth Syst. Sci. 2018, 18, 1919–1935. [Google Scholar] [CrossRef] [Green Version]
- Rosi, A.; Canavesi, V.; Segoni, S.; Nery, T.D.; Catani, F.; Casagli, N. Landslides in the Mountain Region of Rio de Janeiro: A Proposal for the Semi-Automated Definition of Multiple Rainfall Thresholds. Geosciences 2019, 9, 203. [Google Scholar] [CrossRef] [Green Version]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Vasu, N.N.; Lee, S.R.; Pradhan, A.M.S.; Kim, Y.T.; Kang, S.H.; Lee, D.H. A new approach to temporal modelling for landslide hazard assessment using an extreme rainfall induced-landslide index. Eng. Geol. 2016, 215, 36–49. [Google Scholar] [CrossRef]
- Lee, C.T. Multi-Stage Statistical Landslide Hazard Analysis: Earthquake-Induced Landslides. In Landslide Science for a Safer Geoenvironment, Proceedings of the International Consortium on Landslides (ICL) Third Landslide Forum, Beijing, China, 2–6 June 2014; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Lee, C.T.; Chung, C.C. Common Patterns Among Different Landslide Susceptibility Models of the Same Region. In Advancing Culture of Living with Landslides, Proceedings of the 4th World Landslide Forum, Ljubljana, Slovenia, 29 May–2 June 2017; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Önöz, B.; Bayazit, M. Effect of the occurrence process of the peaks over threshold on the flood estimates. J. Hydrol. 2001, 244, 86–96. [Google Scholar] [CrossRef]
- Jaiswal, P.; van Westen, C.J. Estimating temporal probability for landslide initiation along transportation routes based on rainfall thresholds. Geomorphology 2009, 112, 96–105. [Google Scholar] [CrossRef]
- Wu, C.Y.; Chen, S.C. Integrating spatial, temporal, and size probabilities for the annual landslide hazard maps in the Shihmen watershed, Taiwan. Nat. Hazards Earth Syst. Sci. 2013, 13, 2353–2367. [Google Scholar] [CrossRef] [Green Version]
- Althuwaynee, O.F.; Pradhan, B.; Ahmad, N. Estimation of rainfall threshold and its use in landslide hazard mapping of Kuala Lumpur metropolitan and surrounding areas. Landslides 2015, 12, 861–875. [Google Scholar] [CrossRef]
- Afungang, R.N.; Bateira, C.V. Temporal probability analysis of landslides triggered by intense rainfall in the Bamenda Mountain Region, Cameroon. Environ. Earth Sci. 2016, 75, 1032. [Google Scholar] [CrossRef]
- Sangelantoni, L.; Gioia, E.; Marincioni, F. Impact of climate change on landslides frequency: The Esino river basin case study (Central Italy). Nat. Hazards 2018, 93, 849–884. [Google Scholar] [CrossRef]
- Endo, T. Probable Distribution of the Amount of Rainfall Causing Landslides; Annual Report 1968; Hokkaido Branch: Sapporo, Japan, 1969; pp. 122–136. [Google Scholar]
- Onodera, T.; Yoshinaka, R.; Kazama, H. Slope failures caused by heavy rainfall in Japan. J. Jpn. Soc. Eng. Geol. 1974, 15, 191–200. [Google Scholar] [CrossRef]
- Campbell, R.H. Soil Slip, Debris Flows, and Rainstorms in the Santa Monica Mountains and Vicinity, Southern California; US Government Printing Office: Washington, DC, USA, 1975; Volume 851, p. 51.
- Aleotti, P. A warning system for rainfall-induced shallow failures. Eng. Geol. 2004, 73, 247–265. [Google Scholar] [CrossRef]
- Caine, N. The rainfall intensity-duration control of shallow landslides and debris flows. Geogr. Ann. Ser. A Phys. Geogr. 1980, 62, 23–27. [Google Scholar]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Cannon, S.H.; Gartner, J.E.; Wilson, R.C.; Bowers, J.C.; Laber, J.L. Storm rainfall conditions for floods and debris flows from recently burned areas in southwestern Colorado and southern California. Geomorphology 2008, 96, 250–269. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Peruccacci, S.; Rossi, M.; Luciani, S.; Valigi, D.; Guzzetti, F. Rainfall thresholds for the possible occurrence of landslides in Italy. Nat. Hazards Earth Syst. Sci. 2010, 10, 447–458. [Google Scholar] [CrossRef]
- Ciervo, F.; Rianna, G.; Mercogliano, P.; Papa, M.N. Effects of climate change on shallow landslides in a small coastal catchment in southern Italy. Landslides 2017, 14, 1043–1055. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, Ø.B. Regional prediction of landslide hazard using probability analysis of intense rainfall in the Hoa Binh province, Vietnam. Nat. Hazards 2013, 66, 707–730. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Luciani, S.; Vennari, C.; Guzzetti, F. Lithological and seasonal control on rainfall thresholds for the possible initiation of landslides in central Italy. Geomorphology 2012, 139, 79–90. [Google Scholar] [CrossRef]
- Crozier, M.J. Landslides: Causes, Consequences & Environment; Taylor & Francis: Oxfordshire, UK, 1986. [Google Scholar]
- Wieczorek, G.F. Landslides: Investigation and Mitigation. Chapter 4-Landslide Triggering Mechanisms; Special Report 247; Turner, A.K., Schuster, R.L., Eds.; Transportation Research Board: Washington, DC, USA, 1996. [Google Scholar]
- Lee, S.; Won, J.S.; Jeon, S.W.; Park, I.; Lee, M.J. Spatial landslide hazard prediction using rainfall probability and a logistic regression model. Math. Geosci. 2015, 47, 565–589. [Google Scholar] [CrossRef]
- Saadatkhah, N.; Kassim, A.; Lee, L.M. Hulu Kelang, Malaysia regional mapping of rainfall-induced landslides using TRIGRS model. Arab. J. Geosci. 2015, 8, 3183–3194. [Google Scholar] [CrossRef]
- Guzzetti, F. Landslide Hazard and Risk Assessment. Ph.D. Thesis, Universitäts und Landesbibliothek Bonn, Bonn, Germany, 2006. [Google Scholar]
- Van Den Eeckhaut, M.; Reichenbach, P.; Guzzetti, F.; Rossi, M.; Poesen, J. Combined landslide inventory and susceptibility assessment based on different mapping units: An example from the Flemish Ardennes, Belgium. Nat. Hazards Earth Syst. Sci. 2009, 9, 507–521. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.W.; Lin, M.L.; Chang, C.P.; Wu, M.C.; Wang, T.T.; Chen, T.C. Geohazards Susceptibility Analysis of Damaged Areas in Typhoon Morakot (1/3); Central Geological Survey MOEA: Taipei, Taiwan, 2010. (In Chinese)
- Wu, C.Y.; Tsai, C.W.; Chen, S.C. Topographic characteristic analysis of landslides in Kaoping River Watershed. J. Chin. Soil Water Conserv. 2016, 47, 156–164. (In Chinese) [Google Scholar]
- Liu, J.K.; Weng, T.C.; Hung, C.H.; Yang, M.T. Remote Sensing Analysis of Heavy Rainfall Induced Landslide. In Proceedings of the 21st Century Civil Engineering Technology and Management Conference, Hsinchu, Taiwan, 28 December 2001; Minghsin University of Science and Technology: Xinfeng Township, Taiwan, 2001; pp. C21–C31. (In Chinese). [Google Scholar]
- Xie, M.; Esaki, T.; Zhou, G. GIS-based probabilistic mapping of landslide hazard using a three-dimensional deterministic model. Nat. Hazards 2004, 33, 265–282. [Google Scholar] [CrossRef]
- Jan, C.D. Using Rainfall Factors to Determine Debris-Flow Warning Criteria; Soil and Water Conservation Bureau, Council of Agriculture, Executive Yuan: Tainan, Taiwan, 2003. (In Chinese)
- Tsai, M.C. Establishment of Critical Line for Early Warning of Debris Flow Based onTwo-Factors Survival Analysis—A Case Study in Sheng-Mu Area. Ph.D. Thesis, Feng Chia University, Taichung, Taiwan, 2 June 2016. (In Chinese). [Google Scholar]
- Song, W.M. Principle of Probability and Inferential Statistics; McGraw-Hill: Taipei, Taiwan, 2007. (In Chinese) [Google Scholar]
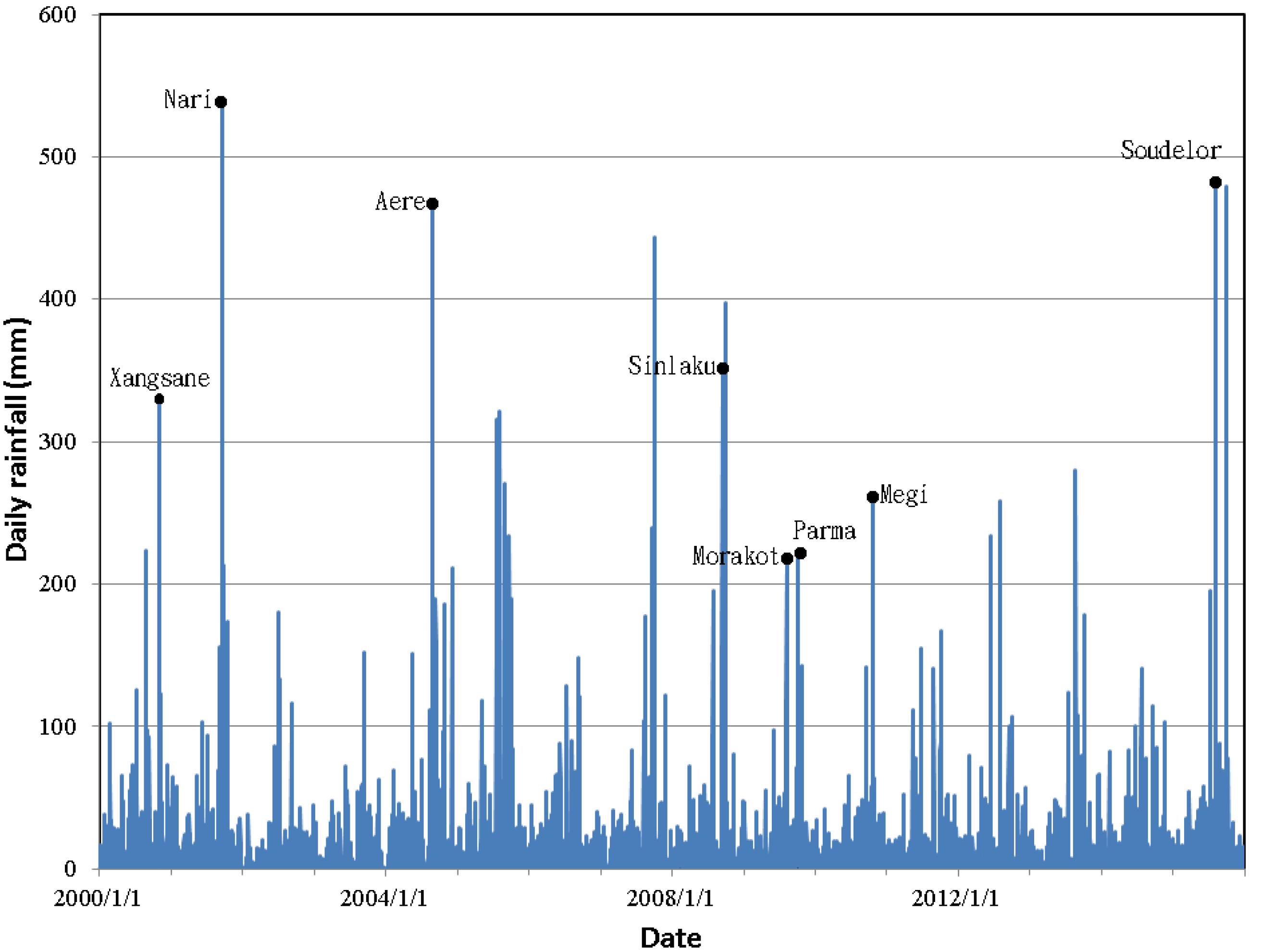



| Typhoon Event | Date (MM/DD/YYYY) | Average Rainfall at the Date (mm) | Number of New Landslide Sites | Smallest Landslide Area (m2) | Largest Landslide Area (m2) | Total Area of Landslides (m2) | Average Area of Landslides (m2) |
|---|---|---|---|---|---|---|---|
| Xangsane | 11/01/2000 | 326.67 | 42 | 326 | 19,619 | 131,148 | 3123 |
| Nari | 09/16/2001 | 538.05 | 92 | 107 | 68,032 | 261,650 | 2844 |
| Aere | 08/24/2004 | 465.57 | 97 | 140 | 27,270 | 239,856 | 2473 |
| Sinlaku | 09/13/2008 | 348.18 | 32 | 475 | 21,101 | 71,111 | 2222 |
| Morakot | 08/07/2009 | 219.83 | 173 | 16 | 118,108 | 1,016,448 | 5875 |
| Parma | 10/05/2009 | 221.79 | 302 | 47 | 49,369 | 484,785 | 1605 |
| Megi | 10/21/2010 | 262.35 | 47 | 407 | 27,318 | 118,874 | 2529 |
| Soudelor | 08/08/2015 | 478.99 | 589 | 257 | 48,041 | 1,075,263 | 1826 |
| Rainfall Probability Threshold | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 |
| Number of landslide events predicted correctly | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| Number of rainfall events triggering landslides actually | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| TPR | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% |
| Number of no landslide events predicted correctly | 0 | 0 | 92 | 92 | 173 | 237 | 237 | 292 | 332 | 361 |
| Number of rainfall events triggering no landslides actually | 608 | 608 | 608 | 608 | 608 | 608 | 608 | 608 | 608 | 608 |
| TNR | 0% | 0% | 15% | 15% | 28% | 39% | 39% | 48% | 55% | 59% |
| PPV | 1.3% | 1.3% | 1.5% | 1.5% | 1.8% | 2.1% | 2.1% | 2.5% | 2.8% | 3.1% |
| Youden’s index | 0% | 0% | 15% | 15% | 28% | 39% | 39% | 48% | 55% | 59% |
| Rainfall Probability Threshold | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | 1.00 |
| Number of landslide events predicted correctly | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 7 | 0 |
| Number of rainfall events triggering landslides actually | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| TPR | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 88% | 0% |
| Number of no landslide events predicted correctly | 407 | 431 | 469 | 494 | 526 | 549 | 575 | 588 | 602 | 608 |
| Number of rainfall events triggering no landslides actually | 608 | 608 | 608 | 608 | 608 | 608 | 608 | 608 | 608 | 608 |
| TNR | 67% | 71% | 77% | 81% | 87% | 90% | 95% | 97% | 99% | 100% |
| PPV | 3.8% | 4.3% | 5.4% | 6.6% | 8.9% | 11.9% | 19.5% | 28.6% | 53.8% | - |
| Youden’s index | 67% | 71% | 77% | 81% | 87% | 90% | 95% | 97% | 87% | 0% |
| Rainfall Gauge | Bihu | Fushan (3) | Tatungshan | Pinglin (4) | Sihdu | Taiping | Quchi |
|---|---|---|---|---|---|---|---|
| Number of landslide events predicted correctly | 7 | 4 | 8 | 5 | 8 | 7 | 7 |
| Number of rainfall events triggering landslides actually | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| TPR | 88% | 50% | 100% | 63% | 100% | 88% | 88% |
| Number of no landslide events predicted correctly | 602 | 586 | 652 | 598 | 563 | 549 | 610 |
| Number of rainfall events triggering no landslides actually | 608 | 599 | 662 | 605 | 583 | 565 | 629 |
| TNR | 99% | 98% | 98% | 99% | 97% | 97% | 97% |
| PPV | 53.8% | 23.5% | 44.4% | 41.7% | 28.6% | 30.4% | 26.9% |
| Youden’s index | 87% | 48% | 98% | 61% | 97% | 85% | 84% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.-Y.; Yeh, Y.-C. A Landslide Probability Model Based on a Long-Term Landslide Inventory and Rainfall Factors. Water 2020, 12, 937. https://doi.org/10.3390/w12040937
Wu C-Y, Yeh Y-C. A Landslide Probability Model Based on a Long-Term Landslide Inventory and Rainfall Factors. Water. 2020; 12(4):937. https://doi.org/10.3390/w12040937
Chicago/Turabian StyleWu, Chun-Yi, and Yen-Chu Yeh. 2020. "A Landslide Probability Model Based on a Long-Term Landslide Inventory and Rainfall Factors" Water 12, no. 4: 937. https://doi.org/10.3390/w12040937





