Probability Distribution and Characterization of Daily Precipitation Related to Tropical Cyclones over the Korean Peninsula
Abstract
:1. Introduction
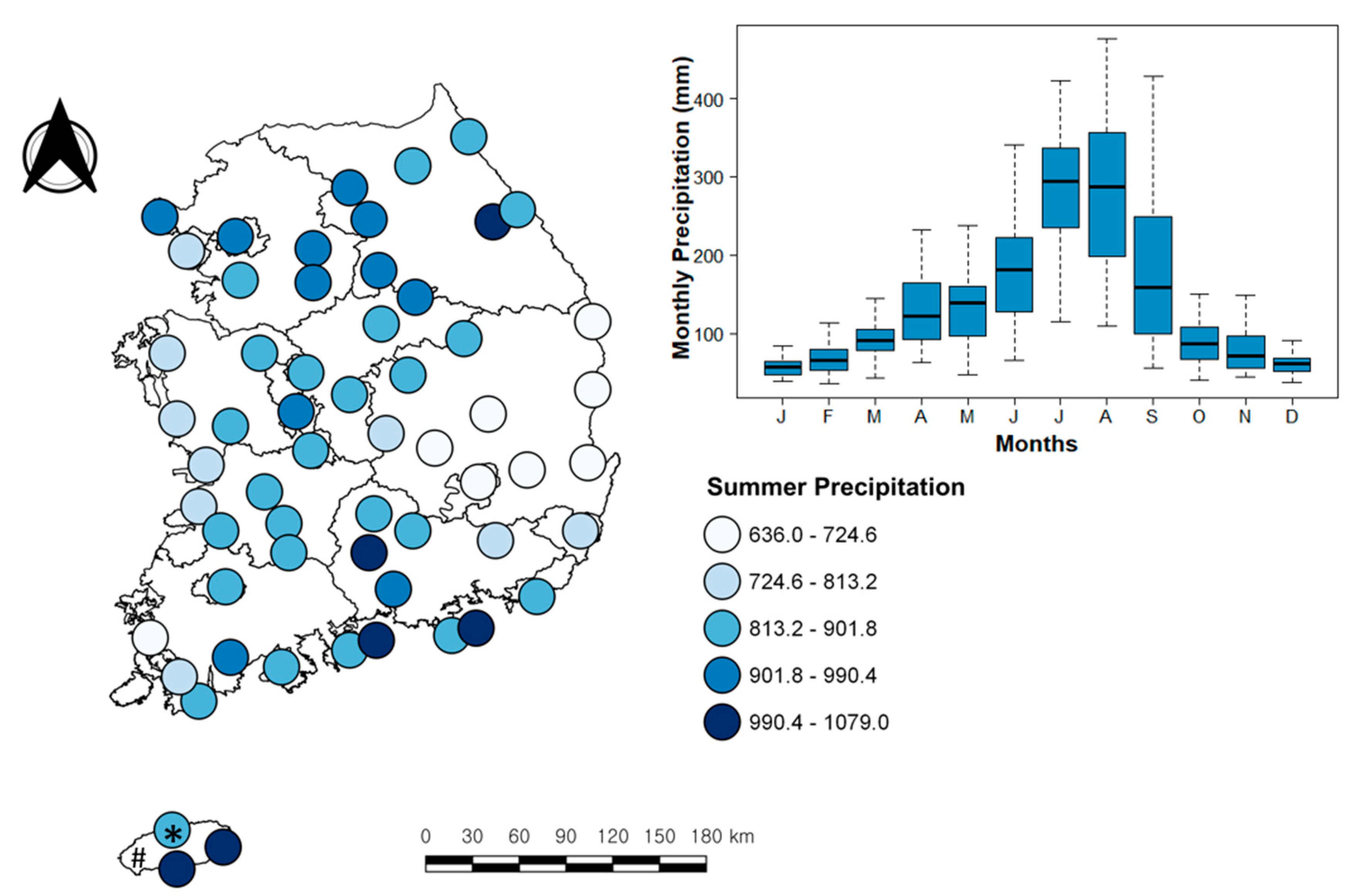
2. Study Area and Data
3. Methodologies
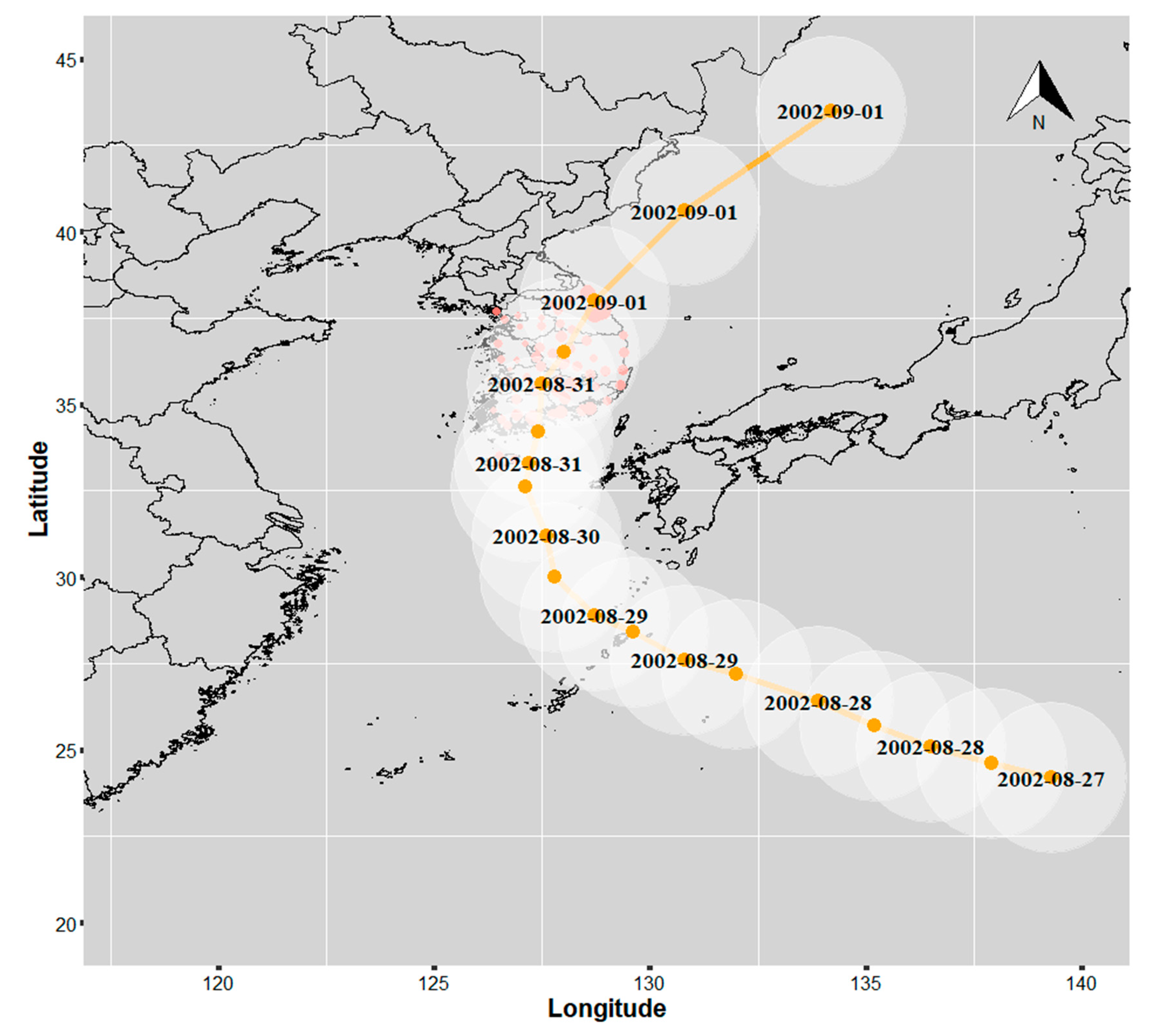
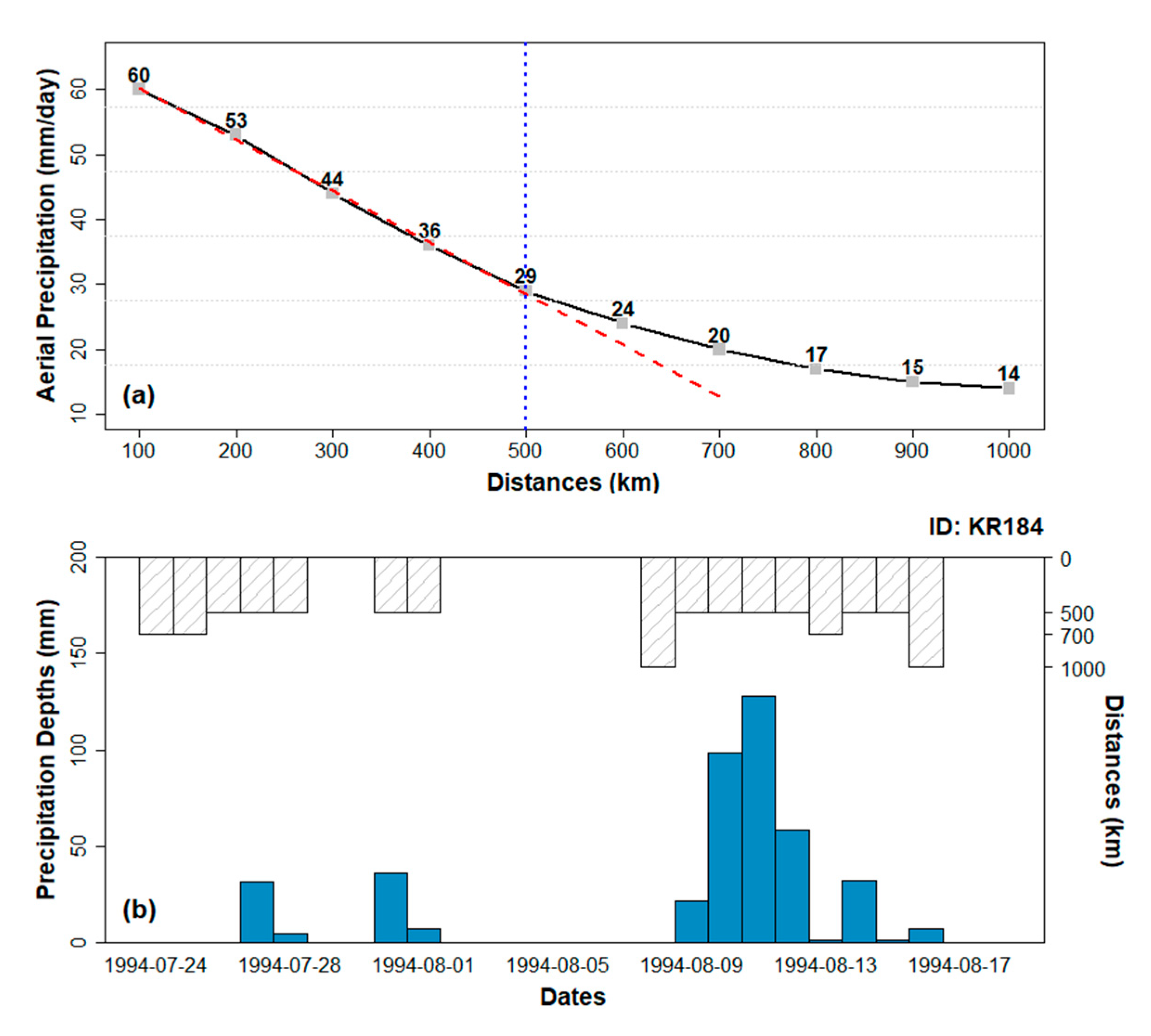
3.1. TC and Non-TC Rainfall Estimation
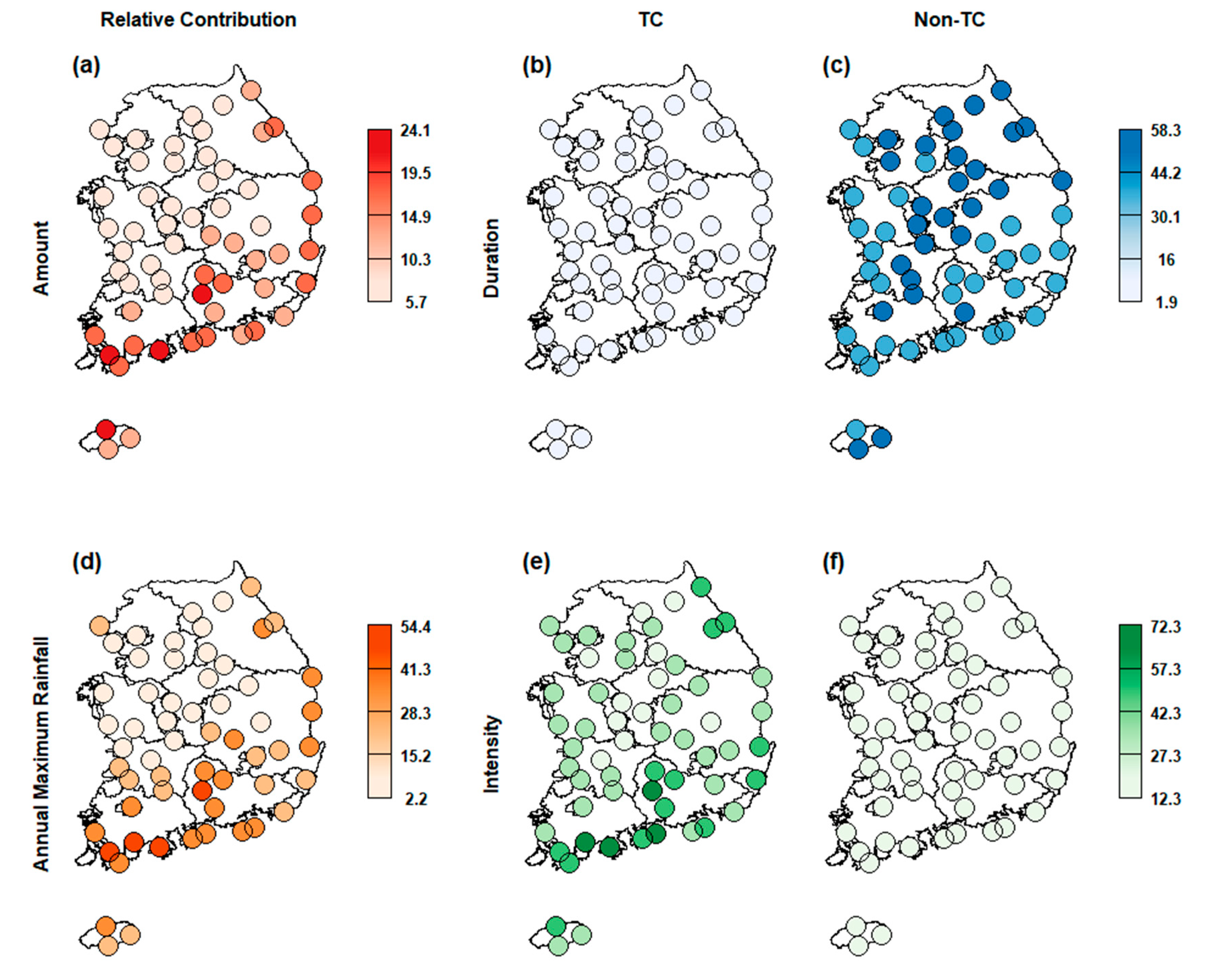
3.2. TC and Non-TC Rainfall Contributions
3.3. Optimal Distributions for TC and Non-TC Rainfall
4. Results
4.1. TC and Non-TC Rainfall Estimation
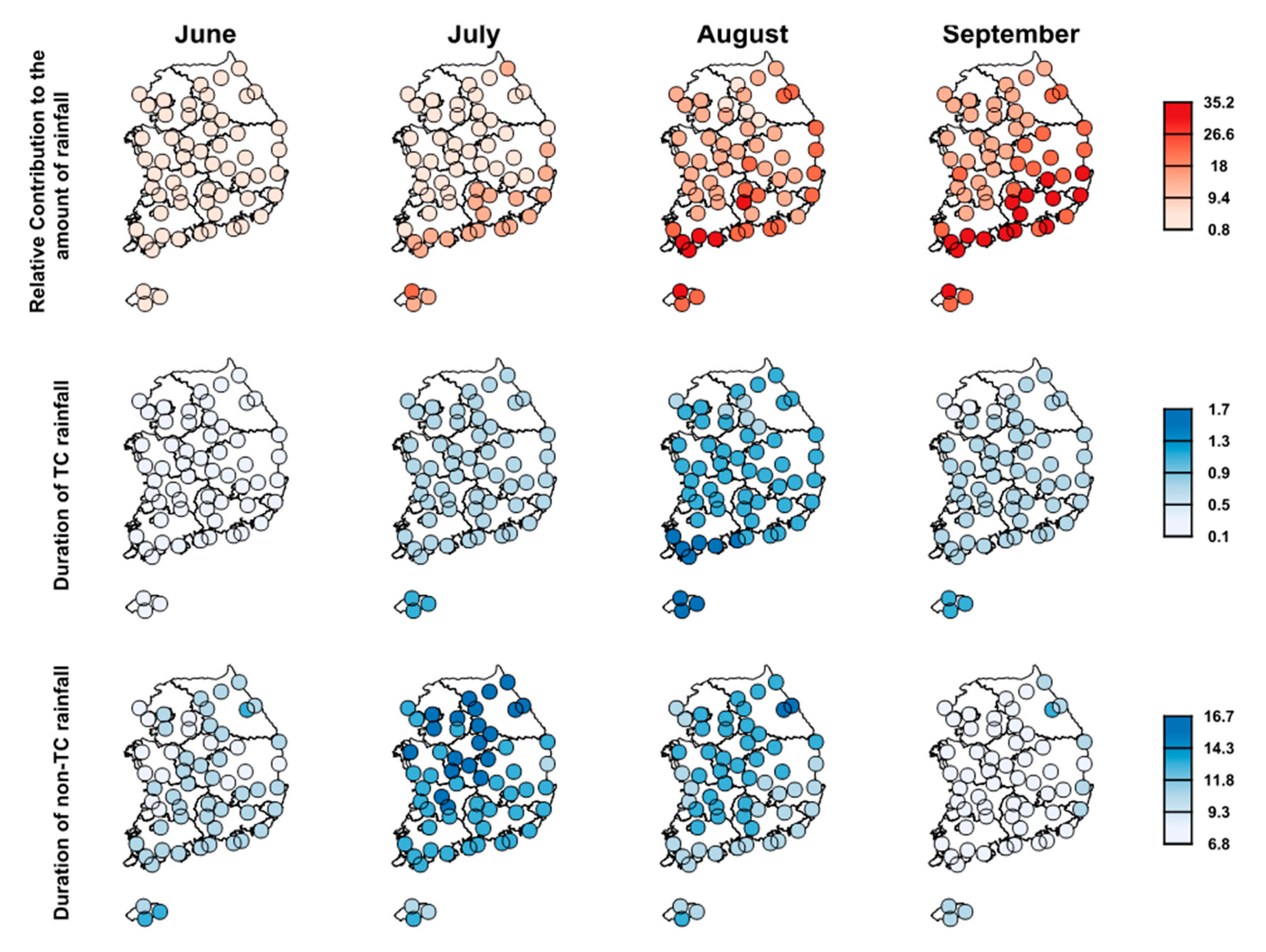
4.2. TC and Non-TC Rainfall Contributions
4.3. Optimal Distributions for TC and Non-TC Rainfall
5. Discussions and Conclusions
Author Contributions
Funding
Acknowledgements
Conflicts of Interest
References
- Harmel, R.; King, K.; Richardson, C.; Williams, J. Long–term precipitation analyses for the central Texas blackland prairie. Trans. ASAE 2003, 46, 1381. [Google Scholar] [CrossRef]
- Hundecha, Y.; Pahlow, M.; Schumann, A. Modeling of daily precipitation at multiple locations using a mixture of distributions to characterize the extremes. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef] [Green Version]
- De Michele, C.; Avanzi, F. Superstatistical distribution of daily precipitation extremes: A worldwide assessment. Sci. Rep. 2018, 8, 14204. [Google Scholar] [CrossRef]
- Ye, L.; Hanson, L.S.; Ding, P.; Wang, D.; Vogel, R.M. The probability distribution of daily precipitation at the point and catchment scales in the United States. Hydrol. Earth Syst. Sci. 2018, 22, 6519–6531. [Google Scholar] [CrossRef] [Green Version]
- Yue, S.; Hashino, M. Probability distribution of annual, seasonal and monthly precipitation in Japan. Hydrol. Sci. J. 2007, 52, 863–877. [Google Scholar] [CrossRef]
- Blöschl, G.; Gaál, L.; Hall, J.; Kiss, A.; Komma, J.; Nester, T.; Parajka, J.; Perdigão, R.A.; Plavcová, L.; Rogger, M.; et al. Increasing river floods: Fiction or reality? Wiley Interdiscip. Rev. Water 2015, 2, 329–344. [Google Scholar] [CrossRef]
- Merz, B.; Aerts, J.; Arnbjerg-Nielsen, K.; Baldi, M.; Becker, A.; Bichet, A.; Blöschl, G.; Bouwer, L.; Brauer, A.; Cioffi, F.; et al. Floods and climate: Emerging perspectives for flood risk assessment and management. Nat. Hazards Earth Syst. Sci. 2014, 14, 1921–1942. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.-S.; Vinayachandran, P.; Ha, K.-J.; Jhun, J.-G. Shift of peak in summer monsoon rainfall over Korea and its association with El Niño–Southern Oscillation. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Son, C.; Lee, T.; Kwon, H. Integrating nonstationary behaviors of typhoon and non-typhoon extreme rainfall events in East Asia. Sci. Rep. 2017, 7, 5097. [Google Scholar] [CrossRef] [Green Version]
- Chang, H.; Kwon, W.-T. Spatial variations of summer precipitation trends in South Korea, 1973–2005. Environ. Res. Lett. 2007, 2, 045012. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.-W.; Cha, Y.; Kim, H.-D. Interdecadal variation of precipitation days in August in the Korean Peninsula. Dyn. Atmos. Ocean. 2017, 77, 74–88. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Kwon, M.; Yun, K.-S.; Min, S.-K.; Park, I.-H.; Ham, Y.-G.; Jin, E.K.; Kim, J.-H.; Seo, K.-H.; Kim, W.; et al. The long-term variability of Changma in the East Asian summer monsoon system: A review and revisit. Asia Pac. J. Atmos. Sci. 2017, 53, 257–272. [Google Scholar] [CrossRef]
- Seo, E.-K.; Kim, K.-M. Precipitating cloud characteristics during Changma as seen in TRMM PR observations. Adv. Meteorol. 2017, 2017. [Google Scholar] [CrossRef] [Green Version]
- Mei, W.; Xie, S.-P.; Primeau, F.; McWilliams, J.C.; Pasquero, C. Northwestern Pacific typhoon intensity controlled by changes in ocean temperatures. Sci. Adv. 2015, 1, e1500014. [Google Scholar] [CrossRef] [Green Version]
- Ho, C.-H.; Lee, J.-Y.; Ahn, M.-H.; Lee, H.-S. A sudden change in summer rainfall characteristics in Korea during the late 1970s. Int. J. Climatol. A J. R. Meteorol. Soc. 2003, 23, 117–128. [Google Scholar] [CrossRef]
- Kim, J.-S.; Li, R.C.-Y.; Zhou, W. Effects of the Pacific-Japan teleconnection pattern on tropical cyclone activity and extreme precipitation events over the Korean peninsula. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Son, C.-Y.; Kim, J.-S.; Moon, Y.-I.; Lee, J.-H. Characteristics of tropical cyclone-induced precipitation over the Korean River basins according to three evolution patterns of the Central-Pacific El Nino. Stoch. Environ. Res. Risk Assess. 2014, 28, 1147–1156. [Google Scholar] [CrossRef]
- Knutson, T.; Mcbride, J.; Chan, J.; Emanuel, K.; Holland, G.; Landsea, C.; Held, I.; Kossin, J.; Srivastava, A.; Sugi, M. Tropical Cyclones and Climate Change. Nat. Geosci. 2010, 3. [Google Scholar] [CrossRef] [Green Version]
- Walsh, K.J.; McBride, J.L.; Klotzbach, P.J.; Balachandran, S.; Camargo, S.J.; Holland, G.; Knutson, T.R.; Kossin, J.P.; Lee, T.; Sobel, A.; et al. Tropical cyclones and climate change. Wiley Interdiscip. Rev. Clim. Chang. 2016, 7, 65–89. [Google Scholar] [CrossRef]
- Corbosiero, K.L.; Dickinson, M.J.; Bosart, L.F. The contribution of eastern North Pacific tropical cyclones to the rainfall climatology of the southwest United States. Mon. Weather Rev. 2009, 137, 2415–2435. [Google Scholar] [CrossRef]
- Farfán, L.M.; Fogel, I. Influence of tropical cyclones on humidity patterns over southern Baja California, Mexico. Mon. Weather Rev. 2007, 135, 1208–1224. [Google Scholar] [CrossRef]
- Ritchie, E.A.; Wood, K.M.; Gutzler, D.S.; White, S.R. The influence of eastern Pacific tropical cyclone remnants on the southwestern United States. Mon. Weather Rev. 2011, 139, 192–210. [Google Scholar] [CrossRef]
- Lu, R.; Ye, H.; Jhun, J.-G. Weakening of interannual variability in the summer East Asian upper-tropospheric westerly jet since the mid-1990s. Adv. Atmos. Sci. 2011, 28, 1246. [Google Scholar] [CrossRef]
- Sun, Y.; Ding, Y. A projection of future changes in summer precipitation and monsoon in East Asia. Sci. China Earth Sci. 2010, 53, 284–300. [Google Scholar] [CrossRef]
- Xiang, B.; Wang, B. Mechanisms for the advanced Asian summer monsoon onset since the mid-to-late 1990s. J. Clim. 2013, 26, 1993–2009. [Google Scholar] [CrossRef]
- Chang, W.; Stein, M.L.; Wang, J.; Kotamarthi, V.R.; Moyer, E.J. Changes in spatiotemporal precipitation patterns in changing climate conditions. J. Clim. 2016, 29, 8355–8376. [Google Scholar] [CrossRef]
- Prein, A.F.; Liu, C.; Ikeda, K.; Bullock, R.; Rasmussen, R.M.; Holland, G.J.; Clark, M. Simulating North American mesoscale convective systems with a convection-permitting climate model. Clim. Dyn. 2017, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Byun, K.-Y.; Lee, T.-Y. Remote effects of tropical cyclones on heavy rainfall over the Korean peninsula–statistical and composite analysis. Tellus A Dyn. Meteorol. Oceanogr. 2012, 64, 14983. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Tachikawa, Y.; Takara, K. Recent Flood Disasters and Progress of Disaster Management System in Korea. 2007. Available online: http://hdl.handle.net/2433/73352 (accessed on 23 April 2020).
- Kim, J.-S.; Jain, S. Precipitation trends over the Korean peninsula: Typhoon-induced changes and a typology for characterizing climate-related risk. Environ. Res. Lett. 2011, 6, 034033. [Google Scholar] [CrossRef]
- Yang, T.; Shao, Q.; Hao, Z.-C.; Chen, X.; Zhang, Z.; Xu, C.-Y.; Sun, L. Regional frequency analysis and spatio-temporal pattern characterization of rainfall extremes in the Pearl River Basin, China. J. Hydrol. 2010, 380, 386–405. [Google Scholar] [CrossRef]
- Yang, X.; Qian, J. Joint occurrence probability analysis of typhoon-induced storm surges and rainstorms using trivariate Archimedean copulas. Ocean Eng. 2019, 171, 533–539. [Google Scholar] [CrossRef]
- Yoon, P.; Kim, T.-W.; Yoo, C. Rainfall frequency analysis using a mixed GEV distribution: A case study for annual maximum rainfalls in South Korea. Stoch. Environ. Res. Risk Assess. 2013, 27, 1143–1153. [Google Scholar] [CrossRef]
- Bezak, N.; Brilly, M.; Šraj, M. Comparison between the peaks-over-threshold method and the annual maximum method for flood frequency analysis. Hydrol. Sci. J. 2014, 59, 959–977. [Google Scholar] [CrossRef] [Green Version]
- Papalexiou, S.M.; Koutsoyiannis, D. Entropy based derivation of probability distributions: A case study to daily rainfall. Adv. Water Resour. 2012, 45, 51–57. [Google Scholar] [CrossRef]
- Suhaila, J.; Jemain, A.A. Fitting daily rainfall amount in Peninsular Malaysia using several types of exponential distributions. J. Appl. Sci. Res. 2007, 3, 1027–1036. [Google Scholar]
- Klein Tank, A.; Wijngaard, J.; Können, G.; Böhm, R.; Demarée, G.; Gocheva, A.; Mileta, M.; Pashiardis, S.; Hejkrlik, L.; Kern-Hansen, C.; et al. Daily dataset of 20th-century surface air temperature and precipitation series for the European Climate Assessment. Int. J. Climatol. A J. R. Meteorol. Soc. 2002, 22, 1441–1453. [Google Scholar] [CrossRef]
- Jung, H.-S.; Choi, Y.; Oh, J.-H.; Lim, G.-H. Recent trends in temperature and precipitation over South Korea. Int. J. Climatol. A J. R. Meteorol. Soc. 2002, 22, 1327–1337. [Google Scholar] [CrossRef]
- Vieux, B.E.; Park, J.-H.; Kang, B. Distributed hydrologic prediction: Sensitivity to accuracy of initial soil moisture conditions and radar rainfall input. J. Hydrol. Eng. 2009, 14, 671–689. [Google Scholar] [CrossRef]
- Ryoo, S.-B.; Kwon, W.-T.; Jhun, J.-G. Characteristics of wintertime daily and extreme minimum temperature over South Korea. Int. J. Climatol. A J. R. Meteorol. Soc. 2004, 24, 145–160. [Google Scholar] [CrossRef]
- Ahn, K.-H.; Kim, Y.-O. Incorporating climate model similarities and hydrologic error models to quantify climate change impacts on future riverine flood risk. J. Hydrol. 2019, 570, 118–131. [Google Scholar] [CrossRef]
- Xiao, Q.; Kuo, Y.-H.; Sun, J.; Lee, W.-C.; Barker, D.M.; Lim, E. An approach of radar reflectivity data assimilation and its assessment with the inland QPF of Typhoon Rusa (2002) at landfall. J. Appl. Meteorol. Climatol. 2007, 46, 14–22. [Google Scholar] [CrossRef] [Green Version]
- Lee, I.; Ha, Y.; Kim, Y.; Kwon, Y. PTSD symptoms in elementary school children after Typhoon Rusa. J. Korean Acad. Nurs. 2004, 34, 636–645. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.W.; Woo, H.; Kim, W.; Lee, D.H.; Yoon, K.S. Re-channelization of stream channels affected by an extreme flood due to the 2002 Typhoon Rusa in Korea. In Critical Transitions in Water and Environmental Resources Management; American Society of Civil Engineers: New York, NY, USA, 2004; pp. 1–10. [Google Scholar] [CrossRef]
- Li, R.C.; Zhou, W.; Lee, T.C. Climatological characteristics and observed trends of tropical cyclone–induced rainfall and their influences on long-term rainfall variations in Hong Kong. Mon. Weather Rev. 2015, 143, 2192–2206. [Google Scholar] [CrossRef]
- Tennant, W.J.; Hewitson, B.C. Intra-seasonal rainfall characteristics and their importance to the seasonal prediction problem. Int. J. Climatol. A J. R. Meteorol. Soc. 2002, 22, 1033–1048. [Google Scholar] [CrossRef]
- Kumar, V. Others Statistical distribution of rainfall in Uttarakhand, India. Appl. Water Sci. 2017, 7, 4765–4776. [Google Scholar] [CrossRef]
- Waseem, M.; Mani, N.; Andiego, G.; Usman, M. A review of criteria of fit for hydrological models. Int. Res. J. Eng. Technol. 2017, 4, 1765–1772. [Google Scholar]
- Hosking, J.R. L-moments: Analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. Ser. B 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Filliben, J.J. The probability plot correlation coefficient test for normality. Technometrics 1975, 17, 111–117. [Google Scholar] [CrossRef]
- Akaike, H.; Petrov, B.N.; Csaki, F. Second International Symposium on Information Theory; Akadémiai Kiadó: Budapest, Hungary, 1973. [Google Scholar]
- Asquith, W.H. Distributional Analysis with L-Moment Statistics Using the R Environment for Statistical Computing; CreateSpace: Scotts Valley, CA, USA, 2011. [Google Scholar]
- Heo, J.-H.; Kho, Y.W.; Shin, H.; Kim, S.; Kim, T. Regression equations of probability plot correlation coefficient test statistics from several probability distributions. J. Hydrol. 2008, 355, 1–15. [Google Scholar] [CrossRef]
- Lenart, A.; Missov, T.I. Goodness-of-fit tests for the Gompertz distribution. Commun. Stat. Theory Methods 2016, 45, 2920–2937. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Kim, S.; Shin, H.; Heo, J.-H. Appropriate model selection methods for nonstationary generalized extreme value models. J. Hydrol. 2017, 547, 557–574. [Google Scholar] [CrossRef]
- Li, C.; Singh, V.P.; Mishra, A.K. A bivariate mixed distribution with a heavy-tailed component and its application to single-site daily rainfall simulation. Water Resour. Res. 2013, 49, 767–789. [Google Scholar] [CrossRef] [Green Version]
- Schoups, G.; Van de Giesen, N.; Savenije, H. Model complexity control for hydrologic prediction. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Wang, Y. A comparison of inner and outer spiral rainbands in a numerically simulated tropical cyclone. Mon. Weather Rev. 2012, 140, 2782–2805. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Q.; Singh, V.P.; Liu, L.; Shi, P. Spatiotemporal patterns of annual and seasonal precipitation extreme distributions across China and potential impact of tropical cyclones. Int. J. Climatol. 2017, 37, 3949–3962. [Google Scholar] [CrossRef]
- Zhang, Q.; Gu, X.; Li, J.; Shi, P.; Singh, V.P. The impact of tropical cyclones on extreme precipitation over coastal and inland areas of China and its association to ENSO. J. Clim. 2018, 31, 1865–1880. [Google Scholar] [CrossRef]
- Kim, J.-S.; Kang, H.; Son, C.-Y.; Moon, Y.-I. Spatial variations in typhoon activities and precipitation trends over the Korean Peninsula. J. Hydro Environ. Res. 2015, 13, 144–151. [Google Scholar] [CrossRef]
- Park, S.K.; Lee, E. Synoptic features of orographically enhanced heavy rainfall on the east coast of Korea associated with Typhoon Rusa (2002). Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
- IPCC. IPCC Fifth Assessment Synthesis Report. In Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014; Available online: https://www.ipcc.ch (accessed on 23 April 2020).
- Trenberth, K.E. Changes in precipitation with climate change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef] [Green Version]
- Kendall, M.G. Rank Correlation Method; Griffin: London, UK, 1975. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. Available online: https://www.jstor.org/stable/1907187 (accessed on 4 April 2020). [CrossRef]
- Wi, S.; Valdés, J.B.; Steinschneider, S.; Kim, T.-W. Non-stationary frequency analysis of extreme precipitation in South Korea using peaks-over-threshold and annual maxima. Stoch. Environ. Res. Risk Assess. 2016, 30, 583–606. [Google Scholar] [CrossRef]



| Distribution | Abbreviation | Probability Density Function (PDF) |
|---|---|---|
| Exponential | EXP | |
| Gamma | GAM | |
| Gumbel | GUM | |
| Lognormal | LN2 | |
| Uniform | UNI | |
| Normal | NOR | |
| Weibull | WEI2 | |
| Generalized extreme value type III | GEV | |
| Generalized Logistic | GLO | |
| Lognormal | LN3 | |
| Pearson Type III | PT3 | |
| Weibull | WEI3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alcantara, A.L.; Ahn, K.-H. Probability Distribution and Characterization of Daily Precipitation Related to Tropical Cyclones over the Korean Peninsula. Water 2020, 12, 1214. https://doi.org/10.3390/w12041214
Alcantara AL, Ahn K-H. Probability Distribution and Characterization of Daily Precipitation Related to Tropical Cyclones over the Korean Peninsula. Water. 2020; 12(4):1214. https://doi.org/10.3390/w12041214
Chicago/Turabian StyleAlcantara, Angelika L., and Kuk-Hyun Ahn. 2020. "Probability Distribution and Characterization of Daily Precipitation Related to Tropical Cyclones over the Korean Peninsula" Water 12, no. 4: 1214. https://doi.org/10.3390/w12041214
APA StyleAlcantara, A. L., & Ahn, K.-H. (2020). Probability Distribution and Characterization of Daily Precipitation Related to Tropical Cyclones over the Korean Peninsula. Water, 12(4), 1214. https://doi.org/10.3390/w12041214






