A Large-Scale 3D Study on Transport of Humic Acid-Coated Goethite Nanoparticles for Aquifer Remediation
Abstract
1. Introduction
2. Materials and Methods
2.1. Humic Acid-Coated Goethite Nanoparticles and Particle Suspension
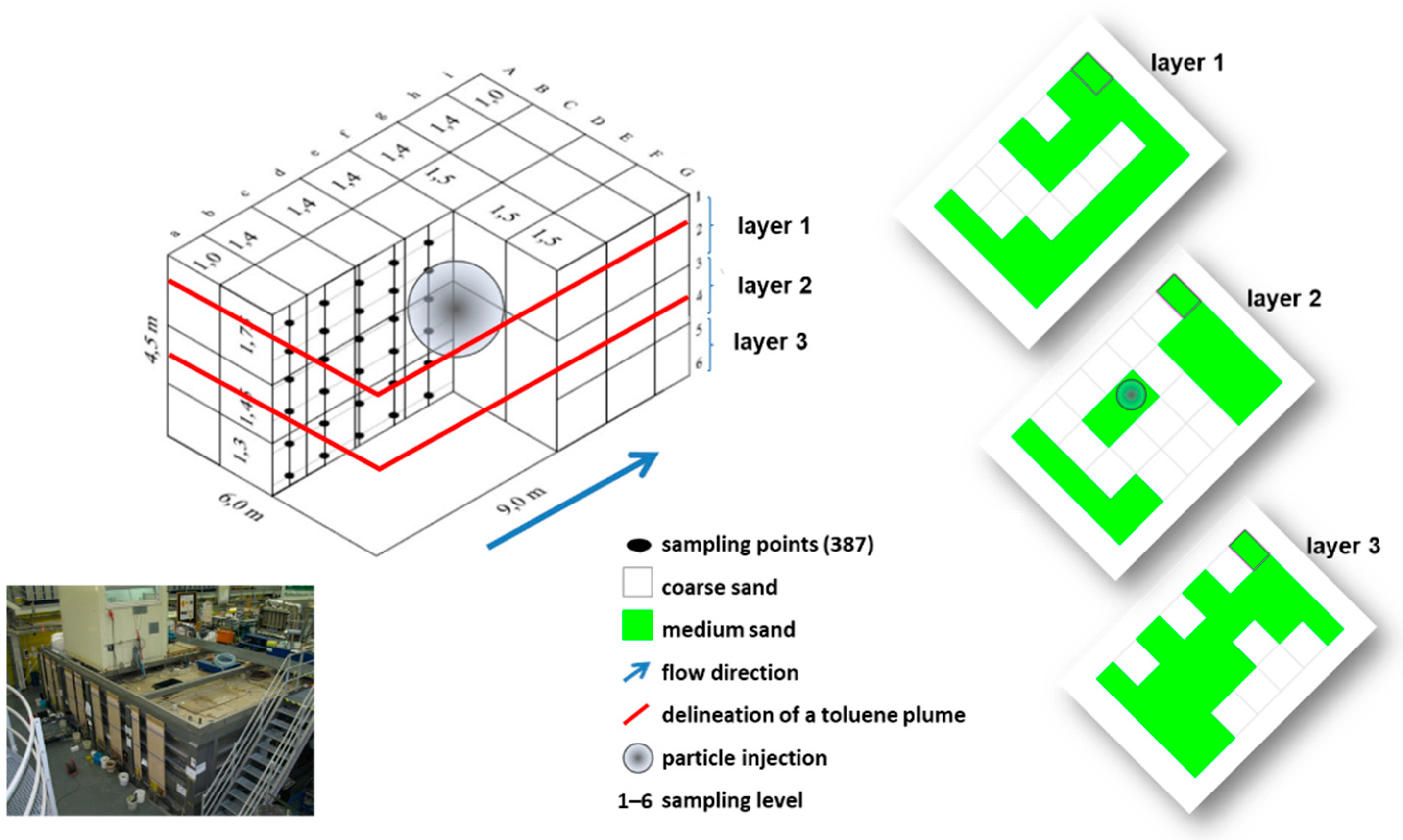
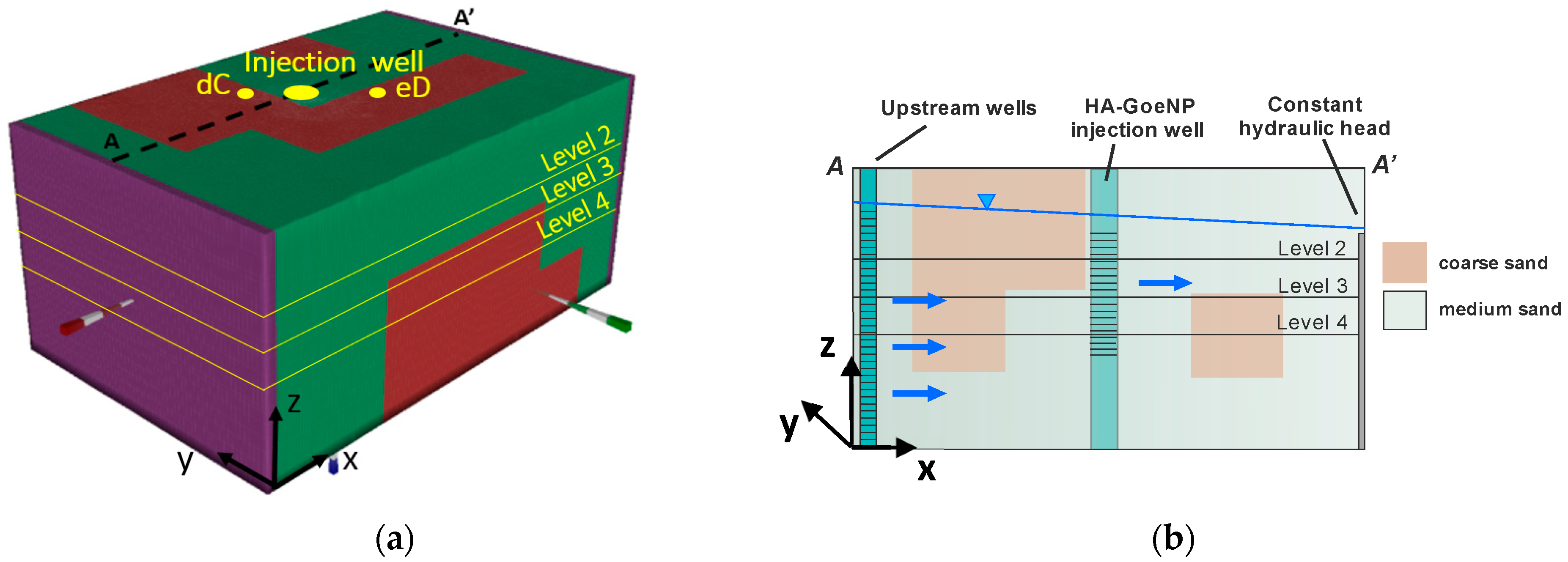
2.2. The Large-Scale Three-Dimensional (3D) Container
2.3. Transport Experiment
2.3.1. Injection of HA-GoeNPs
2.3.2. Monitoring Set Up
2.4. Modeling Approach for Assessing the Transport of HA-GoeNPs
- Column transport tests were run in the laboratory by injecting the HA-GoeNPs in saturated columns packed with a sand similar to the one present in the large tank container;
- Particle transport kinetic parameters (attachment/detachment coefficients, etc.) were obtained by fitting the results of the laboratory tests using MNMs 2018 (the procedure is further described in Section 2.4.1);
- A numerical model of the large-scale container was built in Visual Modflow.
- The HA-GoeNPs were injected into the large-scale container;
- The HA-GoeNP injection was simulated by using MNM3D, the particle transport parameters obtained from column tests, and numerical results compared with experimental ones.
2.4.1. Derivation of the Kinetic Parameters for the Simulation of HA-GoeNPs Transport in A Large-Scale 3D Container
- Two column tests were performed at two different Darcy velocities (v1 = 100 m/d, v2 = 10 m/d). Columns, having a diameter of 0.025 m and a length of 0.22 m, were wet-packed with the same sand used for the preparation of the container to mimic case-specific conditions. Nanoparticles were injected at a concentration C0 of 10 g/L;
- The physical–chemical nature of the particle–soil interactions was determined by a qualitative analysis of the breakthrough curves shape, which suggested the mechanical filtration to be the dominant process. As a consequence, the particle transport in the column was modeled using Equation (1) with h = 1 (one-dimensional domain), and the following formulation was adopted for the interaction with the solid phase (i.e., second equation in Equation (1)), corresponding to an irreversible linear deposition (A = 0, B = 1, kd = 0)
- A least-squares fitting of the column test results was conducted (Figure S7 in Supporting Information) to obtain the case-specific kinetic parameters. Modeled and experimental breakthrough curves are reported in the Supporting Information of Figure S8, where details of the numerical solution of Equations (1) and (2) are also provided. Two values of were found ( = 3.75 × 10−5 1/s, = 2.63 × 10−5 1/s), respectively, for the high- and low-velocity test. An average value of equal to 3.19 × 10−5 1/s was then considered and implemented in MNM3D;
- Particle transport in the large-scale container was simulated using MNM3D to numerically solve Equation (1) with a linear irreversible deposition kinetics (i.e., Equation (2) replaces the second term of the system of Equation (1)). The attachment coefficient in the 3D model was imposed equal to the value derived from column test modeling, i.e., = 3.19 × 10−5 1/s. A third type boundary condition was applied at the particle injection well, and a second type zero-gradient boundary condition was applied at the outlet of the domain.
2.4.2. The Simulation of Water Flow and HA-GoeNPs Transport in Large-Scale 3D Container
3. Results and Discussion
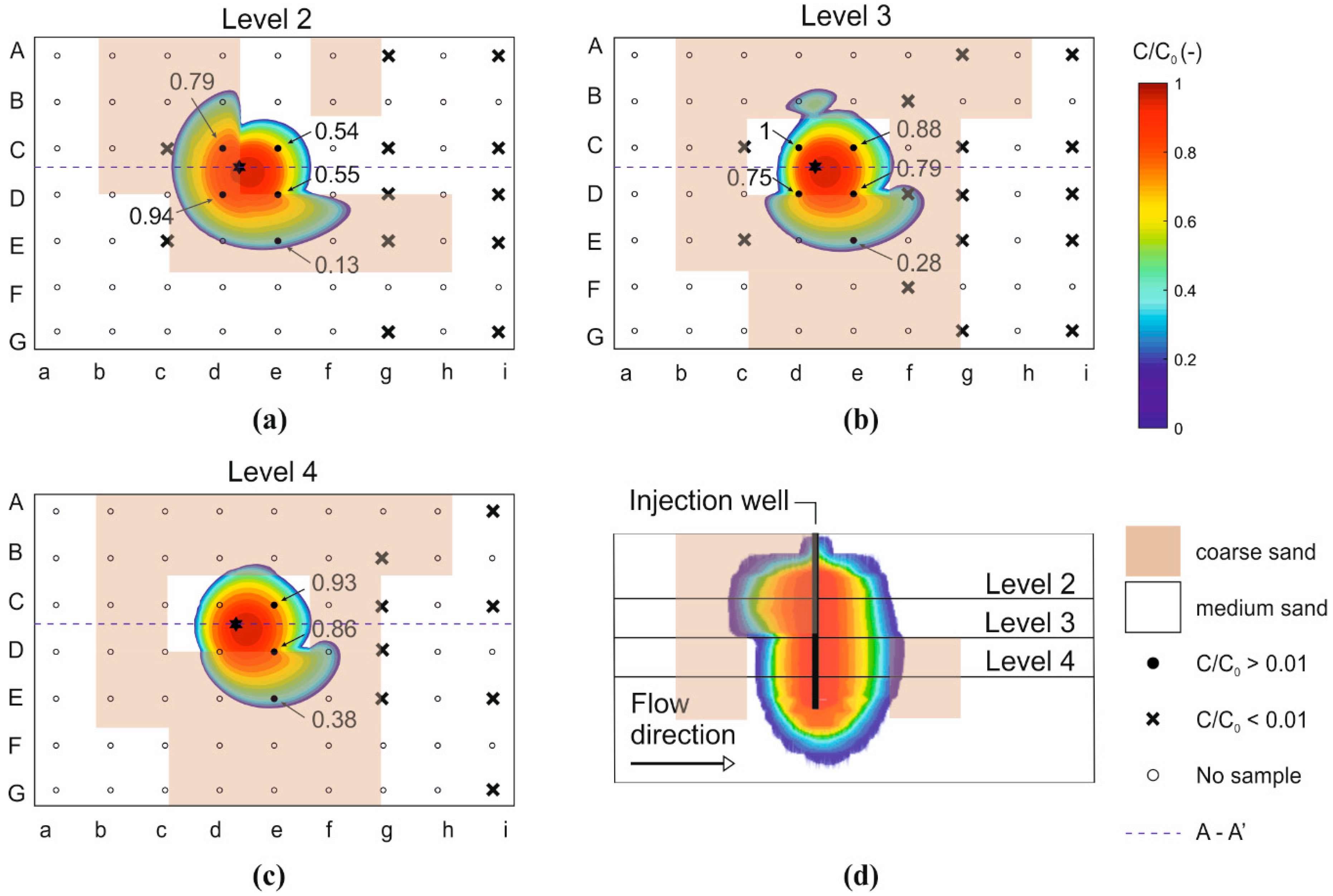
3.1. Transport of HA-GoeNPs in A Heterogenous Unconfined Aquifer–Experimental Concentration
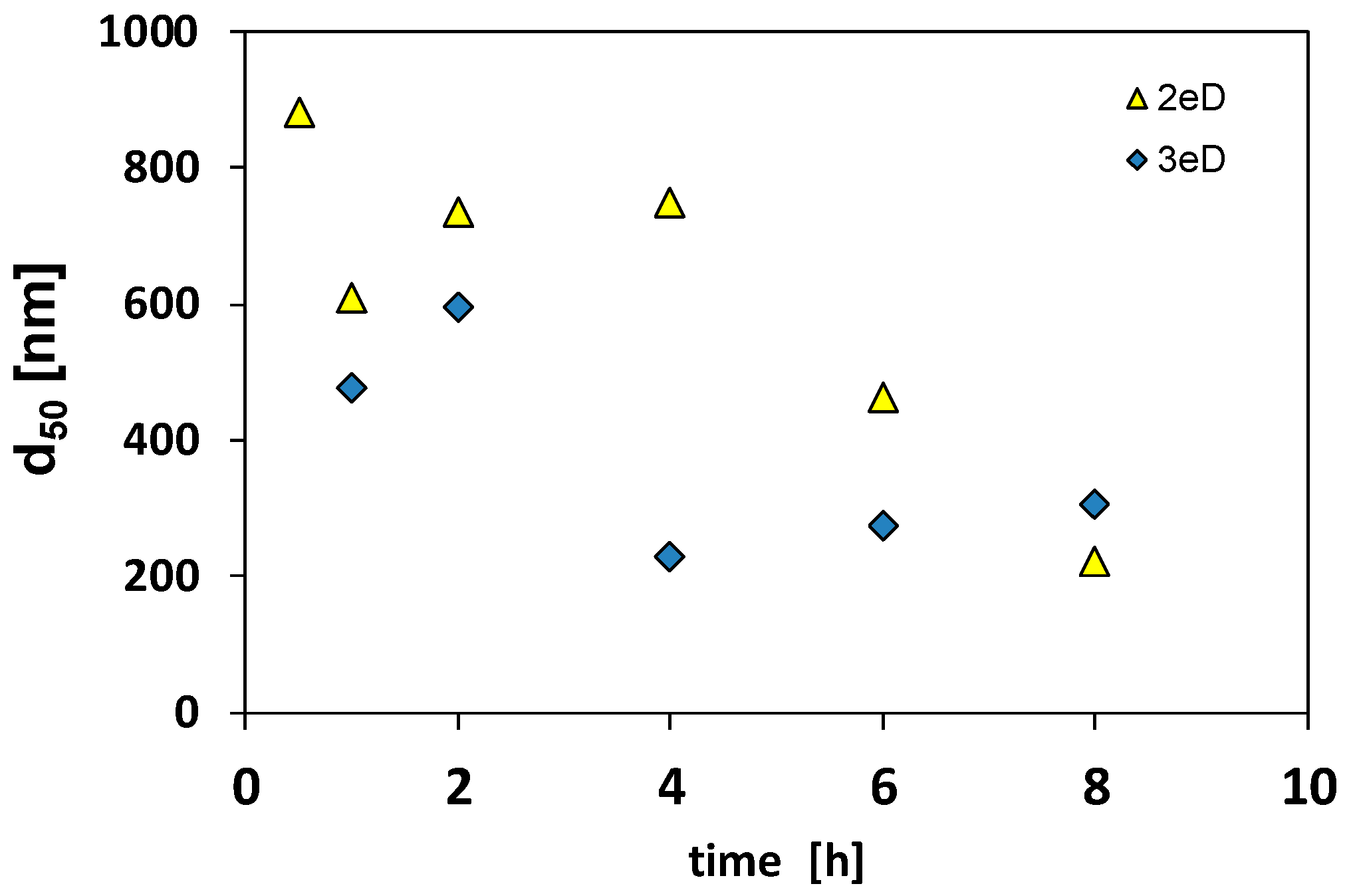
3.2. Change of HA-GoeNPs Size After Injection in A Heterogenous Unconfined Aquifer
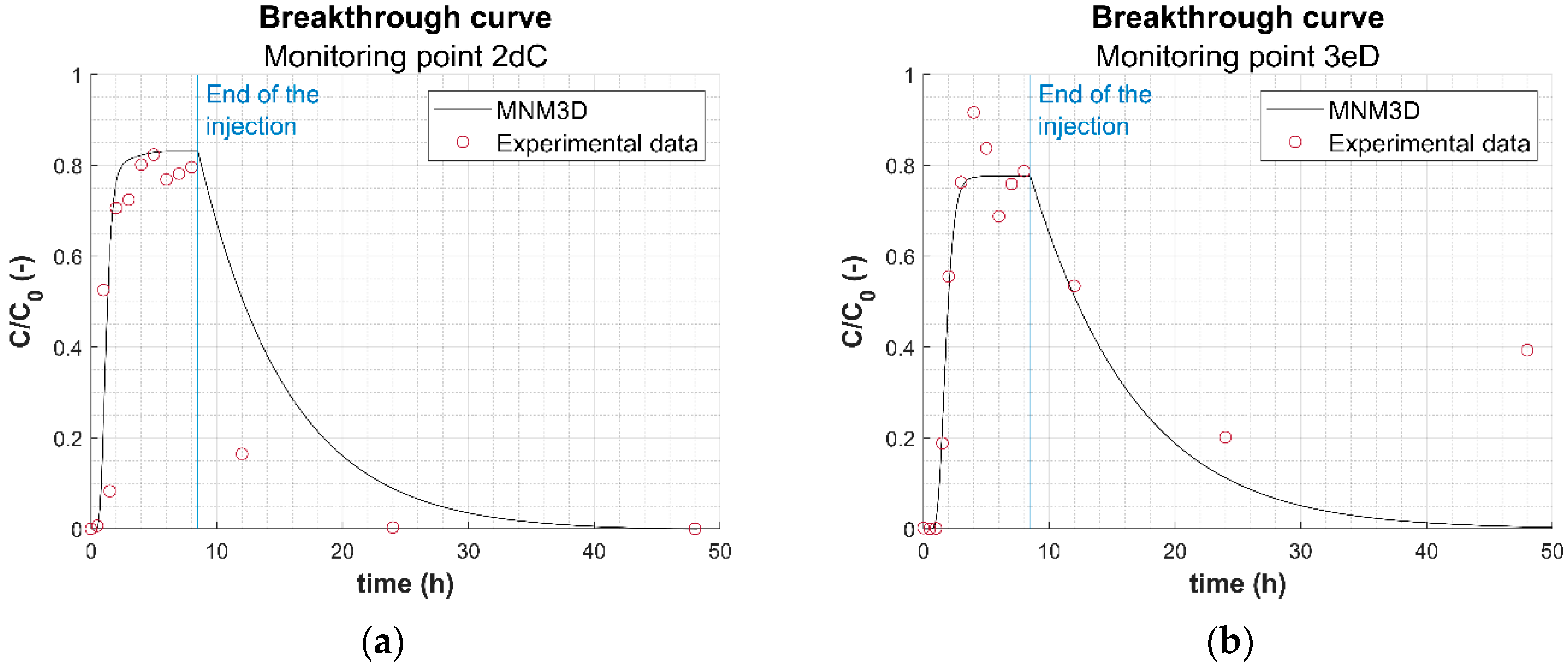
3.3. Use of Modeling Tools for Assessing the Transport of HA-GoeNPs
- A slight sinking of the particle suspension within the container was observed, especially for long times. Since the model equations do not take into account the gravitational effects induced by the slurry density and the nanoparticle sedimentation on the long term, the simulated concentration curves may overestimate the actual concentration of suspended particles, particularly in the upper sampling ports. This hypothesis is confirmed also by the less accurate agreement between modeled and experimental breakthrough curves observed in most sampling points after injection (i.e., time higher than 8.5 h), when the experimental concentrations decrease more sharply compared to the modeled curve (see, e.g., Figure 4a and the breakthrough curves reported in Figure S8);
- Changes over time in particle size were observed, as discussed in Section 3.2, which could play a role in particle transport, and are not included in the transport model MNM3D here used to simulate goethite injection;
- The blocks of different sand types in the experimental container may have not been perfectly regular or partial interpenetrations may have existed, and consequently the space-dependent distribution of hydrodynamic properties implemented in the numerical model may be partly inaccurate in some specific areas.
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karn, B.; Kuiken, T.; Otto, M. Nanotechnology and in situ remediation: A review of the benefits and potential risks. Environ. Health Perspect. 2009, 117, 1823–1831. [Google Scholar] [CrossRef] [PubMed]
- Crane, R.A.; Scott, T.B. Nanoscale zero-valent iron: Future prospects for an emerging water treatment technology. J. Hazard. Mater. 2012, 211–212, 112–125. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Lowry, G.V.; Capiro, N.L.; Chen, J.; Chen, W.; Chen, Y.; Dionysiou, D.D.; Elliott, D.W.; Ghoshal, S.; Hofmann, T.; et al. In situ remediation of subsurface contamination: Opportunities and challenges for nanotechnology and advanced materials. Environ. Sci. 2019, 6, 1283–1302. [Google Scholar] [CrossRef]
- Tosco, T.; Petrangeli Papini, M.; Cruz Viggi, C.; Sethi, R. Nanoscale zerovalent iron particles for groundwater remediation: A review. J. Clean. Prod. 2014, 77, 10–21. [Google Scholar] [CrossRef]
- O’Carroll, D.; Sleep, B.; Krol, M.; Boparai, H.; Kocur, C. Nanoscale zero valent iron and bimetallic particles for contaminated site remediation. Adv. Water Resour. 2013, 51, 104–122. [Google Scholar] [CrossRef]
- Gallo, A.; Bianco, C.; Tosco, T.; Tiraferri, A.; Sethi, R. Synthesis of eco-compatible bimetallic silver/iron nanoparticles for water remediation and reactivity assessment on bromophenol blue. J. Clean. Prod. 2019, 211, 1367–1374. [Google Scholar] [CrossRef]
- Sethi, R.; Di Molfetta, A. Groundwater Engineering: A Technical Approach to Hydrogeology, Contaminant Transport and Groundwater Remediation; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Mondino, F.; Piscitello, A.; Bianco, C.; Gallo, A.; de Folly D’Auris, A.; Tosco, T.; Tagliabue, M.; Sethi, R. Injection of zerovalent iron gels for aquifer nanoremediation: Lab experiments and modeling. Water 2020, 12, 826. [Google Scholar] [CrossRef]
- Bleyl, S.; Kopinke, F.D.; Mackenzie, K. Carbo-iron ®-synthesis and stabilization of fe(0)-doped colloidal activated carbon for in situ groundwater treatment. Chem. Eng. J. 2012, 191, 588–595. [Google Scholar] [CrossRef]
- Bosch, J.; Heister, K.; Hofmann, T.; Meckenstock, R.U. Nanosized iron oxide colloids strongly enhance microbial iron reduction. Appl. Environ. Microb. 2010, 76, 184–189. [Google Scholar] [CrossRef]
- Benjamin, M.M.; Sletten, R.S.; Bailey, R.P.; Bennett, T. Sorption and filtration of metals using iron-oxide-coated sand. Water Res. 1996, 30, 2609–2620. [Google Scholar] [CrossRef]
- Montalvo, D.; Vanderschueren, R.; Fritzsche, A.; Meckenstock, R.U.; Smolders, E. Efficient removal of arsenate from oxic contaminated water by colloidal humic acid-coated goethite: Batch and column experiments. J. Clean. Prod. 2018, 189, 510–518. [Google Scholar] [CrossRef]
- Tiraferri, A.; Saldarriaga Hernandez, L.A.; Bianco, C.; Tosco, T.; Sethi, R. Colloidal behavior of goethite nanoparticles modified with humic acid and implications for aquifer reclamation. J. Nanoparticle Res. 2017, 19, 107. [Google Scholar] [CrossRef]
- Bianco, C.; Patiño Higuita, J.E.; Tosco, T.; Tiraferri, A.; Sethi, R. Controlled deposition of particles in porous media for effective aquifer nanoremediation. Sci. Rep. 2017, 7, 12992. [Google Scholar] [CrossRef] [PubMed]
- Meckenstock, R.U.; Bosch, J. Method for the Degradation of Pollutants in Water and/or Soil. US Patent 8921091 B2, 30 December 2014. [Google Scholar]
- Tosco, T.; Bosch, J.; Meckenstock, R.U.; Sethi, R. Transport of ferrihydrite nanoparticles in saturated porous media: Role of ionic strength and flow rate. Environ. Sci. Technol. 2012, 46, 4008–4015. [Google Scholar] [CrossRef] [PubMed]
- Bianco, C.; Tosco, T.; Sethi, R. A 3-dimensional micro- and nanoparticle transport and filtration model (mnm3d) applied to the migration of carbon-based nanomaterials in porous media. J. Contam. Hydrol. 2016, 193, 10–20. [Google Scholar] [CrossRef] [PubMed]
- Tosco, T.; Tiraferri, A.; Sethi, R. Ionic strength dependent transport of microparticles in saturated porous media: Modeling mobilization and immobilization phenomena under transient chemical conditions. Environ. Sci. Technol. 2009, 43, 4425–4431. [Google Scholar] [CrossRef]
- Katzourakis, V.E.; Chrysikopoulos, C.V. Mathematical modeling of colloid and virus cotransport in porous media: Application to experimental data. Adv. Water Resour. 2014, 68, 62–73. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V.; Syngouna, V.I.; Vasiliadou, I.A.; Katzourakis, V.E. Transport of pseudomonas putida in a 3-d bench scale experimental aquifer. Transp. Porous. Media. 2012, 94, 617–642. [Google Scholar] [CrossRef]
- Tosco, T.; Sethi, R. Transport of non-newtonian suspensions of highly concentrated micro- and nanoscale iron particles in porous media: A modeling approach. Environ. Sci. Technol. 2010, 44, 9062–9068. [Google Scholar] [CrossRef]
- Ryan, J.N.; Elimelech, M. Colloid mobilization and transport in groundwater. Colloids Surf. A 1996, 107, 1–56. [Google Scholar] [CrossRef]
- Bedrikovetsky, P.; Siqueira, F.; Furtado, C.; Souza, A. Modified particle detachment model for colloidal transport in porous media. Transp. Porous. Media. 2011, 86, 353–383. [Google Scholar] [CrossRef]
- Bradford, S.A.; Torkzaban, S. Colloid transport and retention in unsaturated porous media: A review of interface-, collector-, and pore-scale processes and models. Vadose Zone J. 2008, 7, 667–681. [Google Scholar] [CrossRef]
- Beryani, A.; Alavi Moghaddam, M.R.; Tosco, T.; Bianco, C.; Hosseini, S.M.; Kowsari, E.; Sethi, R. Key factors affecting graphene oxide transport in saturated porous media. Sci. Total Environ. 2020, 698, 134224. [Google Scholar] [CrossRef] [PubMed]
- Tosco, T.; Sethi, R. Mnm1d: A numerical code for colloid transport in porous media: Implementation and validation. Am. J. Environ. Sci. 2009, 5, 517–525. [Google Scholar] [CrossRef]
- Tosco, T.; Gastone, F.; Sethi, R. Guar gum solutions for improved delivery of iron particles in porous media (part 2): Iron transport tests and modeling in radial geometry. J. Contam. Hydrol. 2014, 166, 34–51. [Google Scholar] [CrossRef]
- Clement, T.P. Rt3d—A Modular Computer Code for Simulating Reactive Multi-Species Tansport in 3-Dimensional Gundwater Aaquifers; Pacific Northwest National Laboratory: Richland, WA, USA, 1997; PNNL-11720. [Google Scholar]
| Medium Sand | Coarse Sand | |
|---|---|---|
| Grain size distribution (m) | 0–4 × 10−3 | 0.2–8 × 10−3 |
| Sand particle density (kg/m3) | 2.65 × 103 | 2.65 × 103 |
| Bulk density (kg/m3) | 1.72 × 103 | 1.59 × 103 |
| Hydraulic conductivity (m/s) | 4 × 10−4 | 3.5 × 10−3 |
| Porosity | 0.35 | 0.4 |
| Longitudinal dispersivity (m) | 0.02 | 0.04 |
| Flow Simulation | Transport Simulation | |
|---|---|---|
| Solver type | MODFLOW 2005 (WHS method) | MNM3D (GCG method) |
| Numerical discretization | Central finite difference | Central finite difference |
| State | Steady | Transient |
| Time-step | - | Automatic control (Multiplayer 1.02) |
| Error tolerance | Residual criterion (10−5) | Relative convergence criterion (10−4) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velimirovic, M.; Bianco, C.; Ferrantello, N.; Tosco, T.; Casasso, A.; Sethi, R.; Schmid, D.; Wagner, S.; Miyajima, K.; Klaas, N.; et al. A Large-Scale 3D Study on Transport of Humic Acid-Coated Goethite Nanoparticles for Aquifer Remediation. Water 2020, 12, 1207. https://doi.org/10.3390/w12041207
Velimirovic M, Bianco C, Ferrantello N, Tosco T, Casasso A, Sethi R, Schmid D, Wagner S, Miyajima K, Klaas N, et al. A Large-Scale 3D Study on Transport of Humic Acid-Coated Goethite Nanoparticles for Aquifer Remediation. Water. 2020; 12(4):1207. https://doi.org/10.3390/w12041207
Chicago/Turabian StyleVelimirovic, Milica, Carlo Bianco, Natalia Ferrantello, Tiziana Tosco, Alessandro Casasso, Rajandrea Sethi, Doris Schmid, Stephan Wagner, Kumiko Miyajima, Norbert Klaas, and et al. 2020. "A Large-Scale 3D Study on Transport of Humic Acid-Coated Goethite Nanoparticles for Aquifer Remediation" Water 12, no. 4: 1207. https://doi.org/10.3390/w12041207
APA StyleVelimirovic, M., Bianco, C., Ferrantello, N., Tosco, T., Casasso, A., Sethi, R., Schmid, D., Wagner, S., Miyajima, K., Klaas, N., Meckenstock, R. U., von der Kammer, F., & Hofmann, T. (2020). A Large-Scale 3D Study on Transport of Humic Acid-Coated Goethite Nanoparticles for Aquifer Remediation. Water, 12(4), 1207. https://doi.org/10.3390/w12041207









