An Index-Flood Statistical Model for Hydrological Drought Assessment
Abstract
1. Introduction
2. Study Area—Czech Republic
3. Data and Methods
3.1. Data
Drought Definition
- event severity (deficit volume), D [mm or m3];
- event length, L [months];
- event intensity, [mm/month or m3/month];
- relative severity (i.e., deficit volume to monthly runoff ratio), [-];
- relative event intensity, [t−1].
3.2. Statistical Model
3.3. Model Assessment
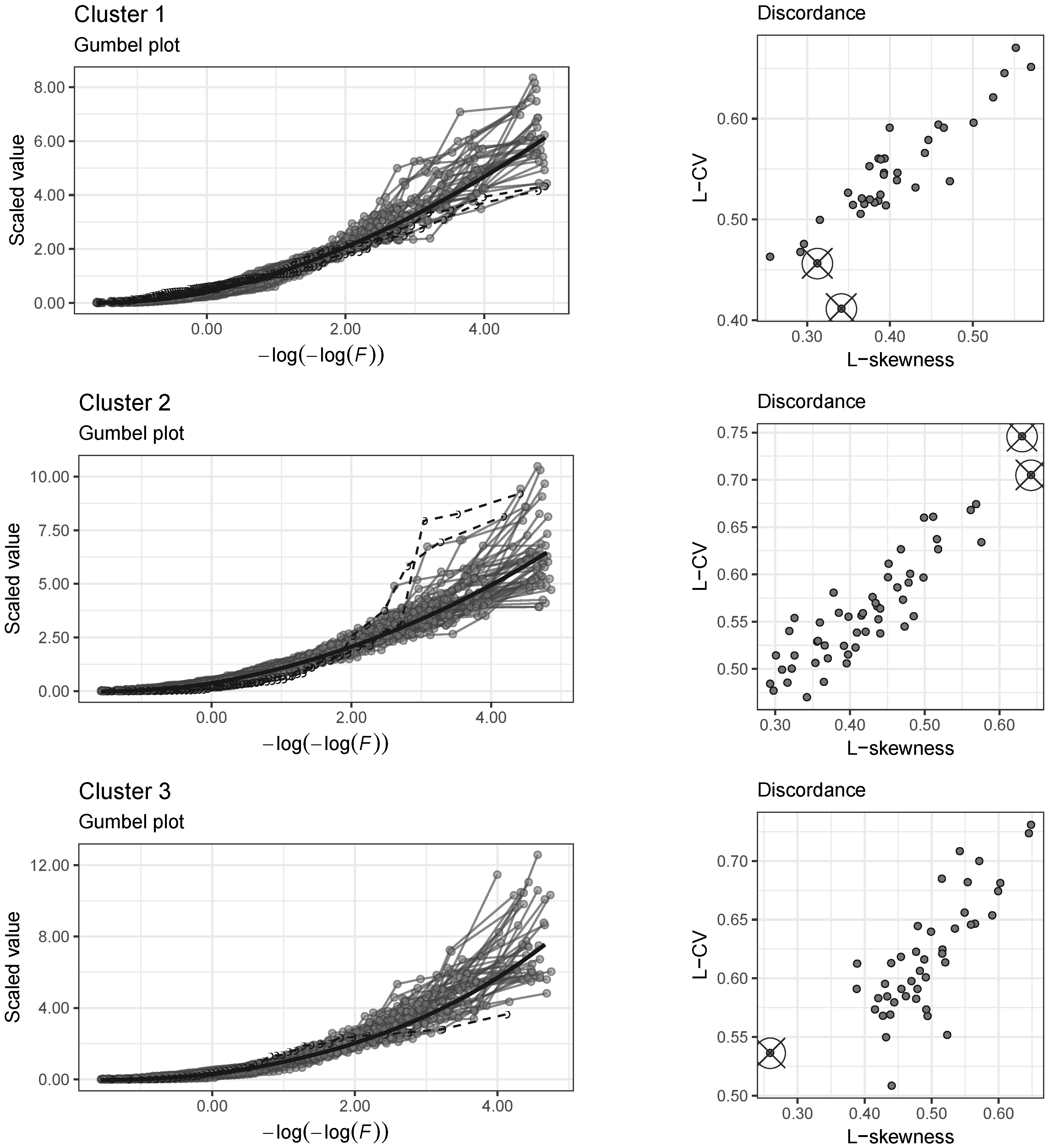
3.3.1. Ratio Diagrams and Gumbel Plot
3.3.2. Discordance
3.3.3. Anderson–Darling Test
- Fit the statistical model to the original sample.
- Calculate standard normal residuals with the parameter estimates from step using quantile mapping.
- Calculate the average correlation of the standard normal residuals.
- Generate a sample of S equicorrelated standard normal variables with correlation .
- Transform the sample from step 4 back to the original scale using the parameter estimates from step 1.
- Fit the statistical model again.
- Calculate the A2 statistics.
- Repeat steps 4–7 until the desired number of bootstrap samples is obtained.
4. Results and Discussion
4.1. Spatial Pooling
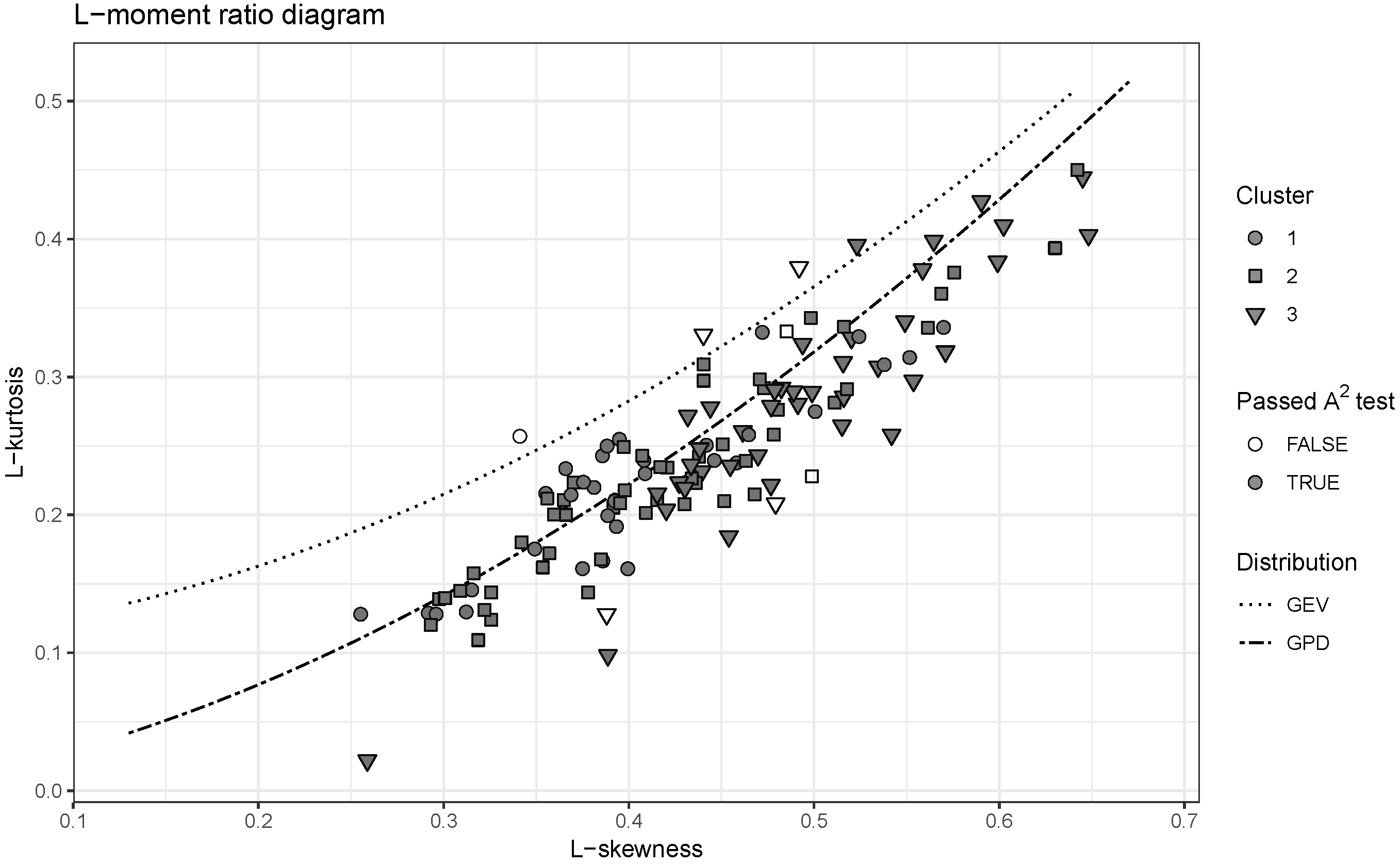
4.2. Choice of the At-Site Distribution
4.3. Drought Definition
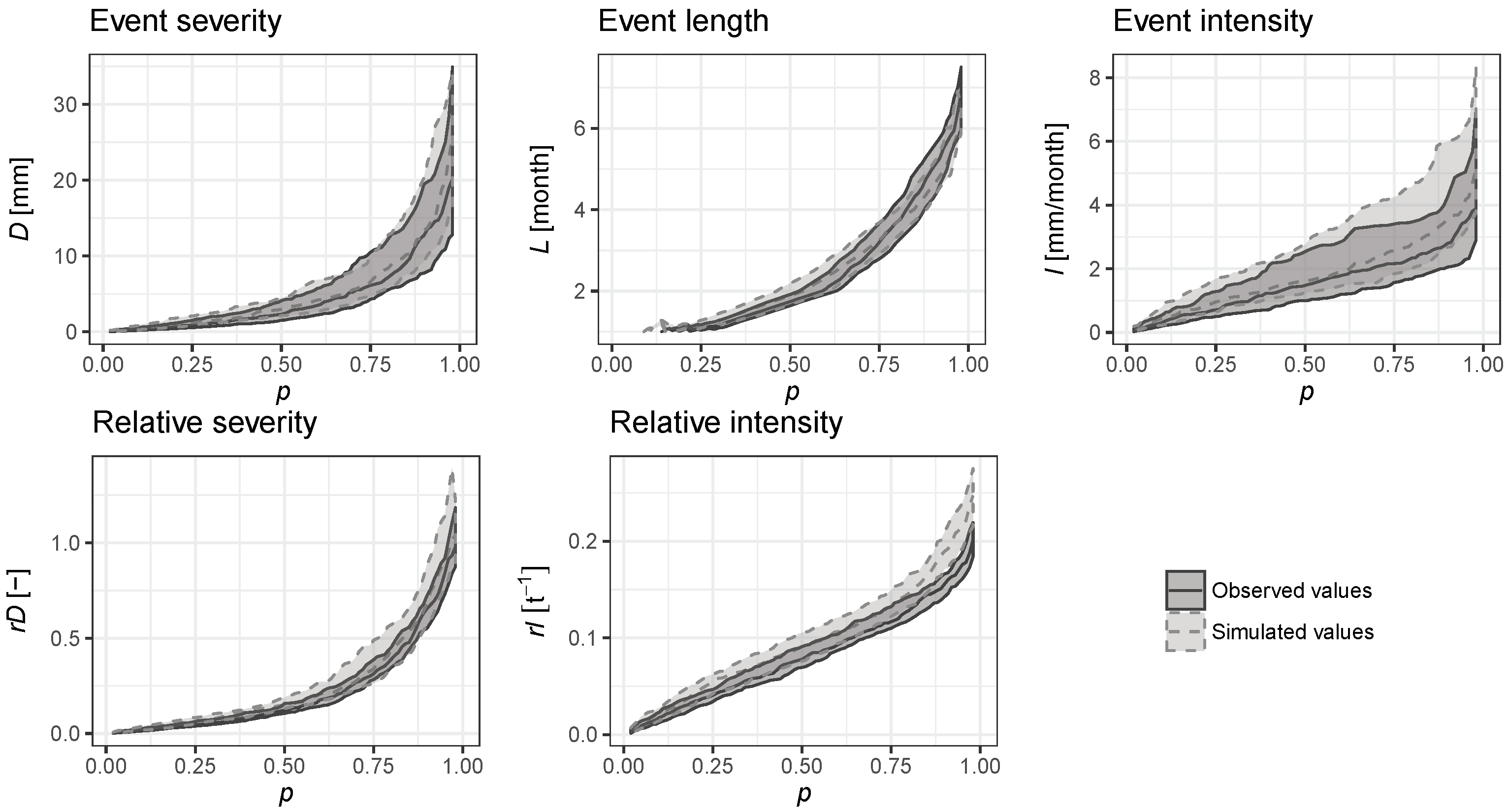
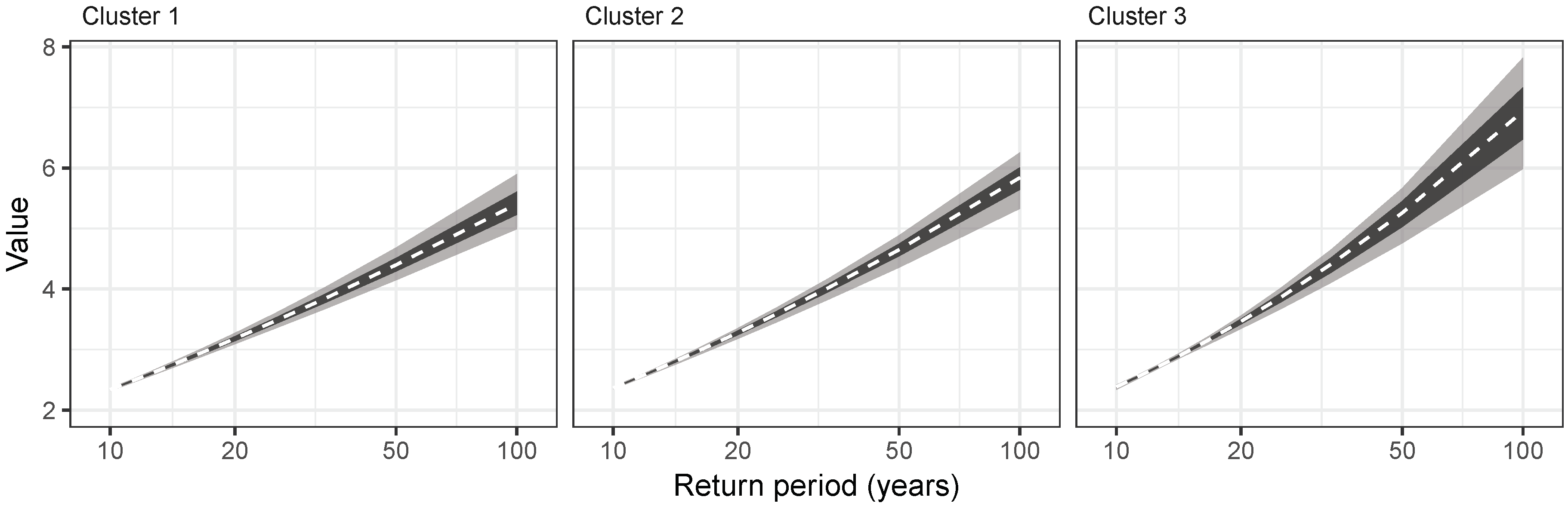
4.4. Reduction of Uncertainty
4.5. Identification of Homogeneous Regions
5. Summary and Concluding Remarks
- Regional frequency analysis reduces uncertainty of estimated drought characteristics and parameters of its distribution.
- Use of Generalized Pareto Distribution is appropriate to describe the deficit volumes on majority of catchments, which is not the case for Generalized Extreme Value distribution. However, it is not clear to what extent this result depends on characteristics of the area under study and other parameters of the analysis like the threshold defining drought.
- The most subjective part of the regional frequency analysis is the definition of homogeneous regions—methods such as region of influence or Self Organizing maps could be considered to minimize the subjective decisions within the regional frequency analysis.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fink, A.H.; Brücher, T.; Krüger, A.; Leckebusch, G.C.; Pinto, J.G.; Ulbrich, U. The 2003 European summer heatwaves and drought–synoptic diagnosis and impacts. Weather 2004, 59, 209–216. [Google Scholar] [CrossRef]
- Laaha, G.; Gauster, T.; Tallaksen, L.; Vidal, J.P.; Stahl, K.; Prudhomme, C.; Heudorfer, B.; Vlnas, R.; Ionita, M.; Van Lanen, H.A.; et al. The European 2015 drought from a hydrological perspective. Hydrol. Earth Syst. Sci. 2016, 21, 3001–3024. [Google Scholar] [CrossRef]
- Ionita, M.; Tallaksen, L.; Kingston, D.; Stagge, J.; Laaha, G.; Van Lanen, H.; Scholz, P.; Chelcea, S.; Haslinger, K. The European 2015 drought from a climatological perspective. Hydrol. Earth Syst. Sci. 2017, 21, 1397–1419. [Google Scholar] [CrossRef]
- Dalrymple, T. Flood-Frequency Analyses, Manual Of Hydrology: Part 3; Technical Report; USGPO: Washington, DC, USA, 1960. [Google Scholar]
- Burn, D.H. Evaluation of regional flood frequency analysis with a region of influence approach. Water Resour. Res. 1990, 26, 2257–2265. [Google Scholar] [CrossRef]
- Blazkov, S.; Beven, K. Flood frequency prediction for data limited catchments in the Czech Republic using a stochastic rainfall model and TOPMODEL. J. Hydrol. 1997, 195, 256–278. [Google Scholar] [CrossRef]
- Iacobellis, V.; Fiorentino, M.; Gioia, A.; Manfreda, S. Best fit and selection of theoretical flood frequency distributions based on different runoff generation mechanisms. Water 2010, 2, 239–256. [Google Scholar] [CrossRef]
- Wayne, C.P. Meteorological Drought; US Weather Bureau Research Paper; US Weather Bureau: Silver Spring, MD, USA, 1965. [Google Scholar]
- Alley, W.M. The Palmer drought severity index: Limitations and assumptions. J. Clim. Appl. Meteorol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Tsakiris, G.; Vangelis, H. Establishing a drought index incorporating evapotranspiration. Eur. Water 2005, 9, 3–11. [Google Scholar]
- Myronidis, D.; Fotakis, D.; Ioannou, K.; Sgouropoulou, K. Comparison of ten notable meteorological drought indices on tracking the effect of drought on streamflow. Hydrol. Sci. J. 2018, 63, 2005–2019. [Google Scholar] [CrossRef]
- Beran, M.A.; Rodier, J.A. Hydrological Aspects of Drought: A Contribution to the International Hydrological Programme; Unesco: Paris, France, 1985; Volume 39. [Google Scholar]
- Nalbantis, I.; Tsakiris, G. Assessment of hydrological drought revisited. Water Resour. Manag. 2009, 23, 881–897. [Google Scholar] [CrossRef]
- Zelenhasić, E.; Salvai, A. A method of streamflow drought analysis. Water Resour. Res. 1987, 23, 156–168. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Myronidis, D.; Ioannou, K.; Fotakis, D.; Dörflinger, G. Streamflow and hydrological drought trend analysis and forecasting in Cyprus. Water Resour. Manag. 2018, 32, 1759–1776. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Hisdal, H. Regional analysis of extreme streamflow drought duration and deficit volume. IAHS Publ. 1997, 246, 141–150. [Google Scholar]
- Fekete, B.; Vörösmarty, C.; Grabs, W. Global Composite Runoff Data Set (v1. 0); Complex Systems Research Center, University of New Hampshire: Durham, NH, USA, 2000. [Google Scholar]
- Hosking, J.; Wallis, J. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Clausen, B.; Pearson, C. Regional frequency analysis of annual maximum streamflow drought. J. Hydrol. 1995, 173, 111–130. [Google Scholar] [CrossRef]
- Noto, L.V.; La Loggia, G. Use of L-moments approach for regional flood frequency analysis in Sicily, Italy. Water Resour. Manag. 2009, 23, 2207–2229. [Google Scholar] [CrossRef]
- Fowler, H.; Kilsby, C. A regional frequency analysis of United Kingdom extreme rainfall from 1961 to 2000. Int. J. Climatol. 2003, 23, 1313–1334. [Google Scholar] [CrossRef]
- Modarres, R. Regional dry spells frequency analysis by L-moment and multivariate analysis. Water Resour. Manag. 2010, 24, 2365–2380. [Google Scholar] [CrossRef]
- Santos, J.F.; Portela, M.M.; Pulido-Calvo, I. Regional frequency analysis of droughts in Portugal. Water Resour. Manag. 2011, 25, 3537. [Google Scholar] [CrossRef]
- Brown, B.G.; Katz, R.W. Regional analysis of temperature extremes: Spatial analog for climate change? J. Clim. 1995, 8, 108–119. [Google Scholar] [CrossRef][Green Version]
- Madsen, H.; Rosbjerg, D. A regional Bayesian method for estimation of extreme streamflow droughts. In Statistical and Bayesian Methods in Hydrological Sciences; UNESCO: Paris, France, 1998; pp. 327–340. [Google Scholar]
- Chen, Y.D.; Huang, G.; Shao, Q.; Xu, C.Y. Regional analysis of low flow using L-moments for Dongjiang basin, South China. Hydrol. Sci. J. 2006, 51, 1051–1064. [Google Scholar] [CrossRef]
- Núnez, J.H.; Verbist, K.; Wallis, J.R.; Schaefer, M.G.; Morales, L.; Cornelis, W. Regional frequency analysis for mapping drought events in north-central Chile. J. Hydrol. 2011, 405, 352–366. [Google Scholar] [CrossRef]
- Abdi, A.; Hassanzadeh, Y.; Talatahari, S.; Fakheri-Fard, A.; Mirabbasi, R. Regional drought frequency analysis using L-moments and adjusted charged system search. J. Hydroinform. 2017, 19, 426–442. [Google Scholar] [CrossRef]
- Zítek, J. Hydrologické Poměry ČSSR; Hydrometeorologický ústav: Praha, ČSSR, 1965. [Google Scholar]
- Tallaksen, L.M.; Van Lanen, H.A. Hydrological Drought: Processes and Estimation Methods for Streamflow and Groundwater; Elsevier: Amsterdam, The Netherlands, 2004; Volume 48. [Google Scholar]
- Horáček, S.; Rakovec, O.; Kašpárek, L.; Vizina, A. Development of the hydrological balance model BILAN. Water Manag. Tech. Econ. Inf. J. 2009, 51, 2–5. [Google Scholar]
- Vizina, A.; Horáček, S.; Hanel, M. Recent developments of the BILAN model. Water Manag. Tech. Econ. Inf. J. 2015, 57, 7–10. [Google Scholar]
- Kašpárek, L.; Hanel, M.; Horáček, S.; Máca, P.; Vizina, A. Bilan Water Balance Model, R package version 2016-10-20. 2016.
- Horáček, S.; Kašpárek, L.; Novický, O. Estimation of Climate Change Impact on Water Resources by Using Bilan Water Balance Model; IOP conference series: Earth and environmental science; IOP Publishing: Bristol, UK, 2008; Volume 4, p. 012023. [Google Scholar]
- Hanel, M.; Mrkvičková, M.; Máca, P.; Vizina, A.; Pech, P. Evaluation of simple statistical downscaling methods for monthly regional climate model simulations with respect to the estimated changes in runoff in the Czech Republic. Water Resour. Manag. 2013, 27, 5261–5279. [Google Scholar] [CrossRef]
- Beran, A.; Hanel, M. Identification of regions vulnerable to deficits in water resources in the Czech Republic. Water Manag. Tech. Econ. Inf. J. 2015, 57, 23–26. [Google Scholar]
- Beran, A.; Hanel, M.; Nesládková, M. Changes in the hydrological balance caused by climate change impacts in the Karlovy Vary district. Water Manag. Tech. Econ. Inf. J. 2016, 58, 20–25. [Google Scholar]
- Harris, I.; Jones, P.; Osborn, T.; Lister, D. Updated high-resolution grids of monthly climatic observations–the CRU TS3. 10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Štěpánek, P.; Zahradníček, P.; Huth, R. Interpolation techniques used for data quality control and calculation of technical series: An example of a Central European daily time series. Idojaras 2011, 115, 87–98. [Google Scholar]
- Tolasz, R.; Brázdil, R.; Bulíř, O.; Dobrovolnỳ, P.; Dubrovskỳ, M.; Hájková, L.; Halásková, O.; Hostỳnek, J.; Janouch, M.; Kohut, M.; et al. Atlas podnebí Česka. 1. vydání; Českỳ hydrometeorologickỳ ústav: Praha, Czech Republic; Universita Palackého: Olomouc, Czech Republic, 2007. [Google Scholar]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall–runoff model?: Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall–runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Tallaksen, L.M. Streamflow drought frequency analysis. In Drought and Drought Mitigation in Europe; Springer: Berlin/Heidelberg, Germany, 2000; pp. 103–117. [Google Scholar]
- Van Loon, A.F. Hydrological drought explained. Wiley Interdiscip. Rev. Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Luo, L.; Apps, D.; Arcand, S.; Xu, H.; Pan, M.; Hoerling, M. Contribution of temperature and precipitation anomalies to the California drought during 2012–2015. Geophys. Res. Lett. 2017, 44, 3184–3192. [Google Scholar] [CrossRef]
- Rice, S.O. Mathematical analysis of random noise. Bell Syst. Tech. J. 1945, 24, 46–156. [Google Scholar] [CrossRef]
- Cramér, H.; Leadbetter, M.R. Stationary and Related Stochastic Processes; John Wiley & Sons: Hoboken, NJ, USA, 1967. [Google Scholar]
- Yevjevich, V.M. An objective approach to definitions and investigations of continental hydrologic droughts. In Hydrology Papers; Colorado State University: Fort Collins, CO, USA, 1967. [Google Scholar]
- Hisdal, H.; Tallaksen, L.; Peters, E.; Stahl, K.; Zaidman, M. Drought event definition. ARIDE Tech. Rep. 2000, 6, 15. [Google Scholar]
- Fleig, A.K.; Tallaksen, L.M.; Hisdal, H.; Demuth, S. A global evaluation of streamflow drought characteristics. Hydrol. Earth Syst. Sci. Discuss. 2006, 10, 535–552. [Google Scholar] [CrossRef]
- Hosking, J.; Wallis, J. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Hosking, J.; Wallis, J. Some statistics useful in regional frequency analysis. Water Resour. Res. 1993, 29, 271–281. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M.; Wagener, T.; Savenije, H.; Viglione, A. Runoff Prediction in Ungauged Basins: Synthesis across Processes, Places and Scales; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. A global survey on the seasonal variation of the marginal distribution of daily precipitation. Adv. Water Resour. 2016, 94, 131–145. [Google Scholar] [CrossRef]
- Hosking, J. L-Moments, R Package, Version 2.8; 2019. Available online: https://CRAN.R-project.org/package=lmom (accessed on 24 April 2020).
- Papalexiou, S.; Koutsoyiannis, D.; Makropoulos, C. How extreme is extreme? An assessment of daily rainfall distribution tails. Hydrol. Earth Syst. Sci. 2013, 17, 851–862. [Google Scholar] [CrossRef]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; Volume 208. [Google Scholar]
- Hosking, J.; Wallis, J. Parameter and quantile estimation for the generalized Pareto distribution. Technometrics 1987, 29, 339–349. [Google Scholar] [CrossRef]
- Grover, P.L.; Burn, D.H.; Cunderlik, J.M. A comparison of index flood estimation procedures for ungauged catchments. Can. J. Civ. Eng. 2002, 29, 734–741. [Google Scholar] [CrossRef]
- Bocchiola, D.; De Michele, C.; Rosso, R. Review of recent advances in index flood estimation. Hydrol. Earth Syst. Sci. Discuss. 2003, 7, 283–296. [Google Scholar] [CrossRef]
- Engeland, K.; Hisdal, H.; Frigessi, A. Practical extreme value modelling of hydrological floods and droughts: A case study. Extremes 2004, 7, 5–30. [Google Scholar] [CrossRef]
- Viglione, A.; Laio, F.; Claps, P. A comparison of homogeneity tests for regional frequency analysis. Water Resour. Res. 2007, 43, W03428. [Google Scholar] [CrossRef]
- Cramér, H. On the composition of elementary errors: First paper: Mathematical deductions. Scand. Actuar. J. 1928, 1928, 13–74. [Google Scholar] [CrossRef]
- Von Mises, R. Vorlesungen aus dem Gebiete der Angewandten Mathematik: Wahrscheinlichkeitsrechnung und ihre Anwendung in der Statistik und Theoretischen Physik; F. Deuticke: Vienna, Austria, 1931. [Google Scholar]
- Smirnov, N.V. Sur la distribution de w2. Comp. Rend. Acad. Sci. 1936, 202, 449–452. [Google Scholar]
- Farrell, P.J.; Rogers-Stewart, K. Comprehensive study of tests for normality and symmetry: Extending the Spiegelhalter test. J. Stat. Comput. Simul. 2006, 76, 803–816. [Google Scholar] [CrossRef]
- Masqat, O. Anderson Darling and modified Anderson Darling tests for generalized Pareto distribution. Pak. J. Appl. Sci. 2003, 3, 85–88. [Google Scholar]
- Anderson, T.W.; Darling, D.A. A test of goodness of fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge university press: Cambridge, UK, 1997; Volume 1. [Google Scholar]
- Hanel, M.; Buishand, T.A.; Ferro, C.A. A nonstationary index flood model for precipitation extremes in transient regional climate model simulations. J. Geophys. Res. Atmos. (1984–2012) 2009, 114, D15107. [Google Scholar] [CrossRef]
- Faulkner, D.; Jones, D. The FORGEX method of rainfall growth estimation III: Examples and confidence intervals. Hydrol. Earth Syst. Sci. Discuss. 1999, 3, 205–212. [Google Scholar] [CrossRef][Green Version]
- Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Hegerl, G.C. Changes in temperature and precipitation extremes in the IPCC ensemble of global coupled model simulations. J. Clim. 2007, 20, 1419–1444. [Google Scholar] [CrossRef]
- Blinka, P. Climatological evaluation of drought and dry periods on the territory of Czech Republic in the years 1876-2002. Meteorol. Bull. 2005, 58, 10–18. [Google Scholar]
- Treml, P. The largest droughts in the Czech Republic in the period 1875–2010. Meteorol. Bull. 2011, 64, 168–176. [Google Scholar]
- Spinoni, J.; Naumann, G.; Vogt, J.V.; Barbosa, P. The biggest drought events in Europe from 1950 to 2012. J. Hydrol. Reg. Stud. 2015, 3, 509–524. [Google Scholar] [CrossRef]
- Brázdil, R.; Trnka, M.; Zahradníček, P.; Dobrovolný, P.; Řezníčková, L.; Treml, P.; Stachoň, Z. The Central European drought of 1947: Causes and consequences, with particular reference to the Czech Lands. Clim. Res. 2016, 70, 161–178. [Google Scholar] [CrossRef]
- Hanel, M.; Rakovec, O.; Markonis, Y.; Máca, P.; Samaniego, L.; Kyselý, J.; Kumar, R. Revisiting the recent European droughts from a long-term perspective. Sci. Rep. 2018, 8, 9499. [Google Scholar] [CrossRef] [PubMed]
- Markonis, Y.; Hanel, M.; Máca, P.; Kyselý, J.; Cook, E. Persistent multi-scale fluctuations shift European hydroclimate to its millennial boundaries. Nat. Commun. 2018, 9, 1767. [Google Scholar] [CrossRef] [PubMed]
- Trnka, M.; Brázdil, R.; Možný, M.; Štěpánek, P.; Dobrovolný, P.; Zahradníček, P.; Balek, J.; Semerádová, D.; Dubrovský, M.; Hlavinka, P.; et al. Soil moisture trends in the Czech Republic between 1961 and 2012. Int. J. Climatol. 2015, 35, 3733–3747. [Google Scholar] [CrossRef]
- Potopova, V.; Boroneanţ, C.; Možný, M.; Štěpánek, P.; Skalák, P. Observed spatiotemporal characteristics of drought on various time scales over the Czech Republic. Theor. Appl. Climatol. 2014, 115, 563–581. [Google Scholar] [CrossRef]
- Phillips, I.D.; McGregor, G.R. The utility of a drought index for assessing the drought hazard in Devon and Cornwall, South West England. Meteorol. Appl. 1998, 5, 359–372. [Google Scholar] [CrossRef]
- Dobrovolný, P.; Brázdil, R.; Trnka, M.; Kotyza, O.; Valášek, H. Precipitation reconstruction for the Czech Lands, AD 1501-2010. Int. J. Climatol. 2015, 35, 1–14. [Google Scholar] [CrossRef]
- Yan, M.; Ye, K. Determining the number of clusters using the weighted gap statistic. Biometrics 2007, 63, 1031–1037. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B Stat. Methodol. 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Neurocomputing 1998, 21, 1–6. [Google Scholar] [CrossRef]
- Lin, G.F.; Chen, L.H. Identification of homogeneous regions for regional frequency analysis using the self-organizing map. J. Hydrol. 2006, 324, 1–9. [Google Scholar] [CrossRef]
- Kraemer, G.; Reichstein, M.; Mahecha, M.D. dimRed and coRanking—unifying dimensionality reduction in R. R J. 2018, 10, 342–358. [Google Scholar] [CrossRef]
- Acreman, M.; Wiltshire, S. Identification of regions for regional flood frequency analysis. Eos 1987, 68, 1262. [Google Scholar]
- Acreman, M. Regional Flood Frequency Analysis in the UK: Recent Research-New Ideas; Institute of Hydrology: Wallingford, UK, 1987. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]

| Period | D | I | L | rD | rI |
|---|---|---|---|---|---|
| 1901–1930 | 4.46 | 1.70 | 2.34 | 0.24 | 0.09 |
| 1931–1960 | 6.01 | 1.97 | 2.76 | 0.36 | 0.11 |
| 1961–1990 | 6.68 | 2.19 | 2.95 | 0.44 | 0.12 |
| 1991–2015 | 4.74 | 1.79 | 2.38 | 0.29 | 0.10 |
| D | I | L | rD | rI | |
|---|---|---|---|---|---|
| Observed runoff | 5.25 | 1.94 | 2.29 | 0.24 | 0.09 |
| Simulated runoff | 6.15 | 2.35 | 2.36 | 0.28 | 0.10 |
| P [mm] | DV [mm] | p0 | |
|---|---|---|---|
| Cluster 1 | 993.87 | 21.65 | 0.30 |
| Cluster 2 | 699.80 | 10.73 | 0.36 |
| Cluster 3 | 574.50 | 6.43 | 0.49 |
| ξ | α | κ | A2 Critical Value | |
|---|---|---|---|---|
| Cluster 1 | −0.01 | 0.86 | −0.15 | 2.42 |
| Cluster 2 | −0.02 | 0.83 | −0.19 | 2.64 |
| Cluster 3 | −0.04 | 0.71 | −0.32 | 2.79 |
| α | κ | 2yr | 50yr | |
|---|---|---|---|---|
| Cluster 1 | 99.86 | 69.97 | 67.99 | 66.44 |
| Cluster 2 | 99.84 | 75.03 | 74.95 | 72.82 |
| Cluster 3 | 99.40 | 55.94 | 56.28 | 52.04 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strnad, F.; Moravec, V.; Markonis, Y.; Máca, P.; Masner, J.; Stočes, M.; Hanel, M. An Index-Flood Statistical Model for Hydrological Drought Assessment. Water 2020, 12, 1213. https://doi.org/10.3390/w12041213
Strnad F, Moravec V, Markonis Y, Máca P, Masner J, Stočes M, Hanel M. An Index-Flood Statistical Model for Hydrological Drought Assessment. Water. 2020; 12(4):1213. https://doi.org/10.3390/w12041213
Chicago/Turabian StyleStrnad, Filip, Vojtěch Moravec, Yannis Markonis, Petr Máca, Jan Masner, Michal Stočes, and Martin Hanel. 2020. "An Index-Flood Statistical Model for Hydrological Drought Assessment" Water 12, no. 4: 1213. https://doi.org/10.3390/w12041213
APA StyleStrnad, F., Moravec, V., Markonis, Y., Máca, P., Masner, J., Stočes, M., & Hanel, M. (2020). An Index-Flood Statistical Model for Hydrological Drought Assessment. Water, 12(4), 1213. https://doi.org/10.3390/w12041213





