Landsat Hourly Evapotranspiration Flux Assessment using Lysimeters for the Texas High Plains
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description
2.2. Weather Parameter Measurements
2.3. Landsat Imagery
2.4. Image Analysis
2.5. Statistical Analysis
3. Results
Lysimeter Comparison
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sentelhas, P.C.; Gillespie, T.J.; Santos, E.A. Evaluation of FAO Penman-Monteith and alternative methods for estimating reference evapotranspiration with missing data in Southern Ontario, Canada. Agric. Water Manag. 2010, 97, 635–644. [Google Scholar] [CrossRef]
- Gavilán, V.; Lillo-Saavedra, M.; Holzapfel, E.; Rivera, D.; García-Pedrero, A. Seasonal Crop Water Balance Using Harmonized Landsat-8 and Sentinel-2 Time Series Data. Water 2019, 11, 2236. [Google Scholar] [CrossRef] [Green Version]
- Qualls, R.J.; Brutsaert, W. Effect of Vegetation Density on the Parameterization of Scalar Roughness to Estimate Spatially Distributed Sensible Heat Fluxes. Water Resour. Res. 1996, 32, 645–652. [Google Scholar] [CrossRef]
- Ayyad, S.; Al Zayed, I.S.; Ha, V.T.T.; Ribbe, L. The Performance of Satellite-Based Actual Evapotranspiration Products and the Assessment of Irrigation Efficiency in Egypt. Water 2019, 11, 1913. [Google Scholar] [CrossRef] [Green Version]
- PÔças, I.; Paço, T.A.; Cunha, M.; Andrade, J.A.; Silvestre, J.; Sousa, A.; Santos, F.L.; Pereira, L.S.; Allen, R.G. Satellite-based evapotranspiration of a super-intensive olive orchard: Application of METRIC algorithms. Biosyst. Eng. 2014, 128, 69–81. [Google Scholar] [CrossRef] [Green Version]
- Torres-Rua, A.; Ticlavilca, A.; Bachour, R.; McKee, M. Estimation of Surface Soil Moisture in Irrigated Lands by Assimilation of Landsat Vegetation Indices, Surface Energy Balance Products, and Relevance Vector Machines. Water 2016, 8, 167. [Google Scholar] [CrossRef] [Green Version]
- Idso, S.B.; Jackson, R.D.; Reginato, R.J. Estimating evaporation: A technique adaptable to remote sensing. Science 1975, 189, 991–992. [Google Scholar] [CrossRef]
- Evett, S.; Schwartz, R.; Howell, T.A.; Baumhardt, R.L.; Copeland, K.S. Can weighing lysimeter ET represent surrounding field ET well enough to test flux station measurements of daily and sub-daily ET? Adv. Water Resour. 2012, 50, 79–90. [Google Scholar] [CrossRef]
- Howell, T.A.; Schneider, A.D.; Jensen, M.E. History of lysimeter design and use for evaportanspiration measurements. In Proceedings of the International Symposium on Lysimetry, Honolulu, HI, USA, 23–25 July 1991. [Google Scholar]
- Allen, R.; Fisher, D.K. Direct load cell-based weighing lysimeter system. In Proceedings of the International Symposium on Lysimetry, Honolulu, HI, USA, 23–25 July 1991. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Gowda, P.H.; Chavez, J.L.; Colaizzi, P.D.; Evett, S.R.; Howell, T.A.; Tolk, J.A. ET mapping for agricultural water management: Present status and challenges. Irrig. Sci. 2008, 26, 223–237. [Google Scholar] [CrossRef] [Green Version]
- Senay, G.B.; Schauer, M.; Velpuri, N.M.; Singh, R.K.; Kagone, S.; Friedrichs, M.; Litvak, M.E.; Douglas-Mankin, K.R. Long-Term (1986–2015) Crop Water Use Characterization over the Upper Rio Grande Basin of United States and Mexico Using Landsat-Based Evapotranspiration. Remote Sens. 2019, 11, 1587. [Google Scholar] [CrossRef] [Green Version]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational Evapotranspiration Mapping Using Remote Sensing and Weather Datasets: A New Parameterization for the SSEB Approach. JAWRA J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: II. Recommended documentation. Agric. Water Manag. 2011, 98, 921–929. [Google Scholar] [CrossRef]
- Allen, R.G.; Burnett, B.; Kramber, W.; Huntington, J.; Kjaersgaard, J.; Kilic, A.; Kelly, C.; Trezza, R. Automated Calibration of the METRIC-Landsat Evapotranspiration Process. J. Am. Water Resour. Assoc. 2013, 49, 563–576. [Google Scholar] [CrossRef]
- Unger, P.W.; Pringle, F.B. Pullman Soils: Distribution Importance, Variability, and Management; Texas Agricultural Experiment Station: College Station, TX, USA, 1981.
- Moorhead, J.E.; Marek, G.W.; Gowda, P.H.; Lin, X.; Colaizzi, P.D.; Evett, S.R.; Kutikoff, S. Evaluation of Evapotranspiration from Eddy Covariance Using Large Weighing Lysimeters. Agronomy 2019, 9, 99. [Google Scholar] [CrossRef] [Green Version]
- Evett, S.R.; Marek, G.W.; Copeland, K.S.; Colaizzi, P.D. Quality Management for Research Weather Data: USDA-ARS, Bushland, TX. Agrosyst. Geosci. Environ. 2018, 1. [Google Scholar] [CrossRef] [Green Version]
- Colaizzi, P.D.; Evett, S.R.; Agam, N.; Schwartz, R.C.; Kustas, W.P.; Cosh, M.H.; McKee, L. Soil heat flux calculation for sunlit and shaded surfaces under row crops: 2. Model test. Agric. For. Meteorol. 2016, 216, 115–128. [Google Scholar] [CrossRef] [Green Version]
- Senay, G.B.; Friedrichs, M.; Singh, R.K.; Velpuri, N.M. Evaluating Landsat 8 evapotranspiration for water use mapping in the Colorado River Basin. Remote Sens. Environ. 2016, 185, 171–185. [Google Scholar] [CrossRef] [Green Version]
- Evett, S.R.; Kustas, W.P.; Gowda, P.H.; Anderson, C.A.; Prueger, J.H.; Howell, T.A. Overview of the Bushland Evapotranspiration and Agricultural Remote sensing EXperiment 2008 (BEAREX08): A field experiment evaluating methods for quantifying ET at multiple scales. Elsevier 2012, 50, 4–19. [Google Scholar] [CrossRef]
- Allen, R.; Morse, A.; Tasumi, M.; Trezza, R.; Bastiaanssen, W.; Wright, J.L.; Kramber, W. Evapotranspiration from a satellite-based surface energy balance for the Snake Plain Aquifer in Idaho. In Proceedings of the USCID Conference, San Luis Obispo, CA, USA, 9–12 July 2002. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Trezza, R.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Tasumi, M.; Trezza, R.; Allen, R.G.R.; Wright, J.L.J. Operational aspects of satellite-based energy balance models for irrigated crops in the semi-arid U.S. Irrig. Drain. Syst. 2005, 19, 355–376. [Google Scholar] [CrossRef]
- Hashem, A.A. Irrigation Water Management Using Remote Sensing and Hydrologic Modeling. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2018. [Google Scholar]
- Gowda, P.H.; Terry, A.H.; Jose, L.C.; George, P.; Moorhead, J.E.; Daniel, H.; Marek, T.H.; Porter, D.O.; Marek, G.H.; Colaizzi, P.D.; et al. A Decade of Remote Sensing and Evapotranspiration Research at USDA-ARS Conservation and Production Research Laboratory; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2015; pp. 1–14. [Google Scholar]
- Santos, C.; Lorite, I.J.; Allen, R.G.; Tasumi, M. Aerodynamic Parameterization of the Satellite-Based Energy Balance (METRIC) Model for ET Estimation in Rainfed Olive Orchards of Andalusia, Spain. Water Resour. Manag. 2012, 26, 3267–3283. [Google Scholar] [CrossRef]
- Numata, I.; Khand, K.; Kjaersgaard, J.; Cochrane, M.; Silva, S. Evaluation of Landsat-Based METRIC Modeling to Provide High-Spatial Resolution Evapotranspiration Estimates for Amazonian Forests. Remote Sens. 2017, 9, 46. [Google Scholar] [CrossRef] [Green Version]
- Madugundu, R.; Al-Gaadi, K.A.; Tola, E.; Hassaballa, A.A.; Patil, V.C. Performance of the METRIC model in estimating evapotranspiration fluxes over an irrigated field in Saudi Arabia using Landsat-8 images. Hydrol. Earth Syst. Sci. 2017, 21, 6135–6151. [Google Scholar]
- El Ghandour, F.-E.; Alfieri, S.M.; Houali, Y.; Habib, A.; Akdim, N.; Labbassi, K.; Menenti, M. Detecting the Response of Irrigation Water Management to Climate by Remote Sensing Monitoring of Evapotranspiration. Water 2019, 11, 2045. [Google Scholar] [CrossRef] [Green Version]
- Morton, C.G.; Huntington, J.L.; Pohll, G.M.; Allen, R.G.; McGwire, K.C.; Bassett, S.D. Assessing Calibration Uncertainty and Automation for Estimating Evapotranspiration from Agricultural Areas Using METRIC. J. Am. Water Resour. Assoc. 2013, 49, 549–562. [Google Scholar] [CrossRef]
- Tasumi, M.; Allen, R.G.; Trezza, R.; Wright, J.L. Satellite-Based Energy Balance to Assess Within-Population Variance of Crop Coefficient Curves. J. Irrig. Drain. Eng. 2005, 131, 94–109. [Google Scholar] [CrossRef]
- Markham, L.B. Landsat MSS and TM post-calibration dynamic ranges, exoatmospheric reflectances and at-satellite temperatures. Landsat Tech. Notes 1986, 1, 3–8. [Google Scholar]
- Wukelic, G.E.G.E.; Gibbons, D.E.; Martucci, L.M.M.; Foote, H.P.P. Radiometric calibration of Landsat Thematic Mapper thermal band. Remote Sens. Environ. 1989, 28, 339–347. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Molden, D.J.; Makin, I.W. Remote sensing for irrigated agriculture: Examples from research and possible applications. Agric. Water Manag. 2000, 46, 137–155. [Google Scholar] [CrossRef]
- Tasumi, M. Progress in Operational Estimation of Regional Evapotranspiration Using Satellite Imagery. Ph.D. Thesis, University of Idaho, Moscow, ID, USA, 2003. [Google Scholar]
- Wright, J.L. New evapotranspiration crop coefficients. Proc. Am. Soc. Civ. 1982, 108, 57–74. [Google Scholar]
- Kustas, W.P.; Moran, M.S.; Humes, K.S.; Stannard, D.I.; Pinter, J.; Hipps, L.E.; Swiatek, E.; Goodrich, D.C. Surface energy balance estimates at local and regional scales using optical remote sensing from an aircraft platform and atmospheric data collected over semiarid rangelands. Water Resour. Res. 1994, 30, 1241–1259. [Google Scholar] [CrossRef]
- Norman, J.; Kustas, W.; Humes, K. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1996, 77, 263–293. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M. Regionalization of surface flux densities and moisture indicators in composite terrain: A Remote Sensing Approach under Clear Sskies in Mediterranean Climates. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, 1995. [Google Scholar]
- Gowda, P.; Howell, T.; Paul, G.; Colaizzi, P.D.; Marek, T.H.; Su, B.; Copeland, K.S. Deriving hourly evapotranspiration rates with SEBS: A lysimetric evaluation. Vadose Zo. J. 2013, 12, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Hashem, A.A.; Engel, B.A.; Bralts, V.F.; Radwan, S.; Rashad, M. Performance evaluation and development of daily reference evapotranspiration model. Irrig. Drain. Syst. Eng. 2016, 5, 1–6. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I - A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation Of The SWAT Model On A Large Rwer Basin With Point And Nonpoint Sources. J. Am. Water Resour. Assoc. 2001, 37, 1169–1188. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Torn, R.D.; Kustas, W.P.; Basara, J.B.; Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Torn, R.D.; et al. A Multiscale Remote Sensing Model for Disaggregating Regional Fluxes to Micrometeorological Scales. J. Hydrometeorol. 2004, 5, 343–363. [Google Scholar] [CrossRef]
- Chávez, J.L.; Gowda, P.H.; Howell, T.A.; Copeland, K.S. Radiometric surface temperature calibration effects on satellite based evapotranspiration estimation. Int. J. Remote Sens. 2009, 30, 2337–2354. [Google Scholar] [CrossRef]
- Elhaddad, A.; Garcia, L.A.; Chávez, J.L. Using a Surface Energy Balance Model to Calculate Spatially Distributed Actual Evapotranspiration. J. Irrig. Drain. Eng. 2011, 137, 17–26. [Google Scholar] [CrossRef]
- Hashem, A.A.; Engel, B.A.; Rashad, M.; Ramadan, M.H.; Radwan, S.M. Development and validation of mathematical model for calculating daily reference evapotranspiration. In Proceedings of the American Society of Agricultural and Biological Engineers, Evapotranspiration: Challenges in Measurement & Modeling from Leaf to the Landscape Scale & Beyond, Raleigh, NC, USA, 7–10 April 2014. [Google Scholar]
- Key, J.R.; Schweiger, A.J.; Stone, R.S. Expected uncertainty in satellite-derived estimates of the surface radiation budget at high latitudes. J. Geophys. Res. C Ocean. 1997, 102, 15837–15847. [Google Scholar] [CrossRef]
- Chávez, J.L.; Howell, T.A.; Copeland, K.S. Evaluating eddy covariance cotton ET measurements in an advective environment with large weighing lysimeters. Irrig. Sci. 2009, 28, 35–50. [Google Scholar] [CrossRef]
- Mkhwanazi, M.; Chávez, J.L.; Rambikur, E.H. Comparison of Large Aperture Scintillometer and Satellite-based Energy Balance Models in Sensible Heat Flux and Crop Evapotranspiration Determination. Int. J. Remote Sens. Appl. 2012, 2, 24. [Google Scholar]
- Mkhwanazi, M.M.; Chávez, J.L. Mapping evapotranspiration with the remote sensing ET algorithms METRIC and SEBAL under advective and non-advective conditions: Accuracy determination with weighing lysimeters. Hydrol. Days 2013, 1, 68–72. [Google Scholar]
- French, A.N.; Hunsaker, D.J.; Thorp, K.R. Remote sensing of evapotranspiration over cotton using the TSEB and METRIC energy balance models. Remote Sens. Environ. 2015, 158, 281–294. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P. Assessing the impact of end-member selection on the accuracy of satellite-based spatial variability models for actual evapotranspiration estimation. Water Resour. Res. 2013, 49, 2601–2618. [Google Scholar] [CrossRef]


| Parameter | Condition | Constraint | Outcome | |
|---|---|---|---|---|
| Ts | NDVI | |||
| Lowest ET | Bare agricultural soil | High | Hot pixel location (x,y) | |
| Highest ET | Cultivated agricultural soil | Low | Cold pixel location (x,y) | |
| Mean | Regression | ||||||
|---|---|---|---|---|---|---|---|
| Estimated Parameter | Observed | Estimated | RMSE | MBE | NSE | R2 | Slope |
| T (°C) | 33.8 | 33.0 | 2.3 | 0.8 | 0.65 | 0.76 | 0.70 |
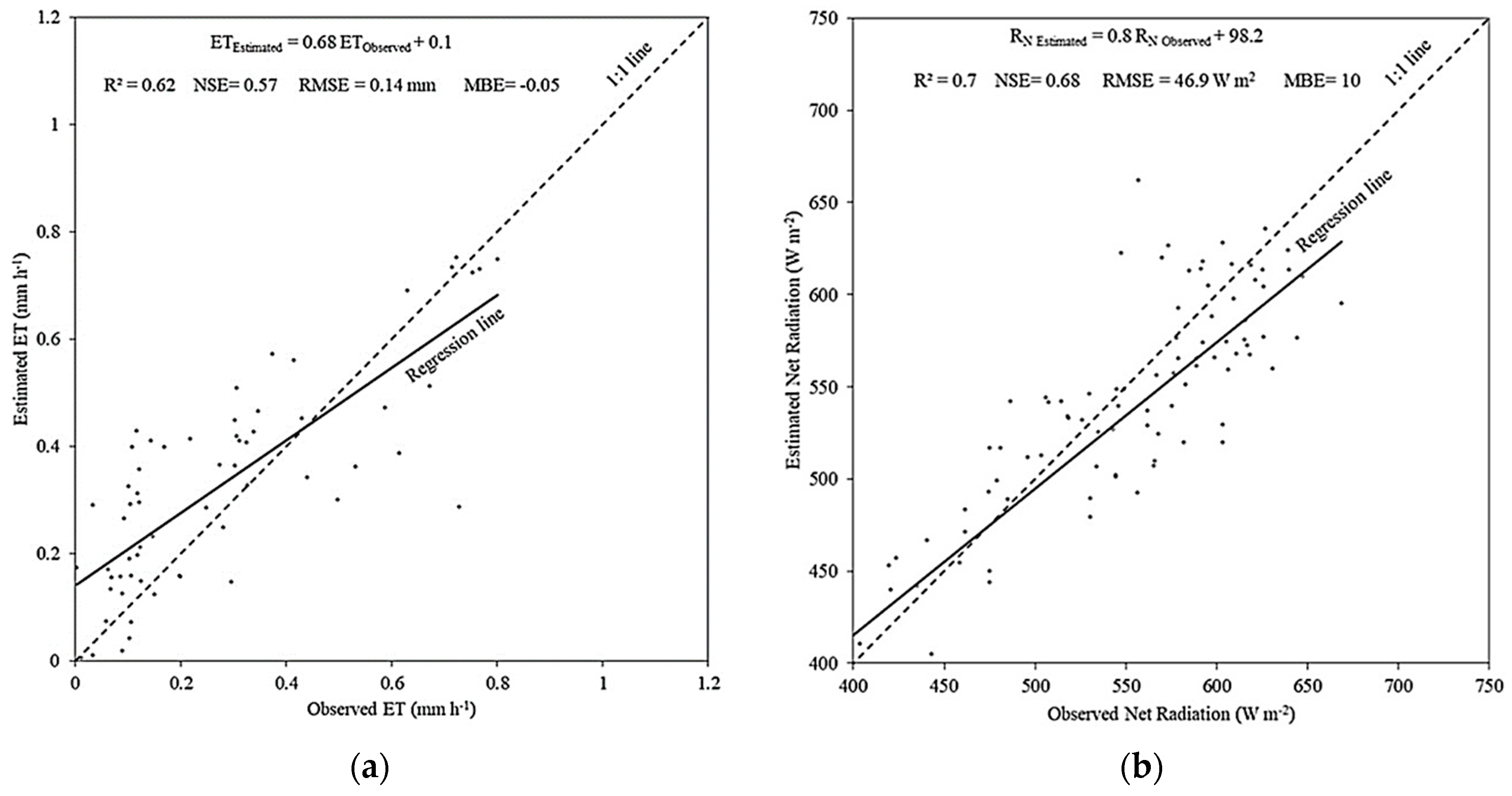
| Rn (W m−2) | 533.5 | 521.5 | 46.9 | 10.0 | 0.68 | 0.71 | 0.80 |
| Go (W m−2) | 38.6 | 34.5 | 21.2 | 4.2 | 0.17 | 0.20 | 0.20 |
| ET (mm h−1) | 0.28 | 0.33 | 0.14 | −0.05 | 0.57 | 0.62 | 0.68 |
| Mean | Regression | ||||||
|---|---|---|---|---|---|---|---|
| Estimated Parameter | Observed | Estimated | RMSE | MBE | NSE | R2 | Slope |
| T (°C) | 31.5 | 31.2 | 4.6 | 0.55 | 0.76 | 0.80 | 0.63 |
| Rn (W m−2) | 542.3 | 551.3 | 84.8 | −9.0 | 0.17 | 0.22 | 0.29 |
| Go (W m−2) | 36.4 | 35.6 | 32.6 | 0.8 | −0.47 | 0.08 | 0.30 |
| ET (mm h−1) | 0.43 | 0.47 | 0.16 | −0.04 | 0.63 | 0.65 | 0.64 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hashem, A.A.; Engel, B.A.; Bralts, V.F.; Marek, G.W.; Moorhead, J.E.; Rashad, M.; Radwan, S.; Gowda, P.H. Landsat Hourly Evapotranspiration Flux Assessment using Lysimeters for the Texas High Plains. Water 2020, 12, 1192. https://doi.org/10.3390/w12041192
Hashem AA, Engel BA, Bralts VF, Marek GW, Moorhead JE, Rashad M, Radwan S, Gowda PH. Landsat Hourly Evapotranspiration Flux Assessment using Lysimeters for the Texas High Plains. Water. 2020; 12(4):1192. https://doi.org/10.3390/w12041192
Chicago/Turabian StyleHashem, Ahmed A., Bernard A. Engel, Vincent F. Bralts, Gary W. Marek, Jerry E. Moorhead, Mohamed Rashad, Sherif Radwan, and Prasanna H. Gowda. 2020. "Landsat Hourly Evapotranspiration Flux Assessment using Lysimeters for the Texas High Plains" Water 12, no. 4: 1192. https://doi.org/10.3390/w12041192
APA StyleHashem, A. A., Engel, B. A., Bralts, V. F., Marek, G. W., Moorhead, J. E., Rashad, M., Radwan, S., & Gowda, P. H. (2020). Landsat Hourly Evapotranspiration Flux Assessment using Lysimeters for the Texas High Plains. Water, 12(4), 1192. https://doi.org/10.3390/w12041192





