2.1.1. Statistical Models
Three statistical models, including Linear Regression, Poisson Regression, and EPR are used to estimate the number of expected failures in pipe groups. These models are selected because they produce explicit polynomial expressions, which provide a high level of correlation between input variables and the dependent variable [
11,
14]. Linear Regression is an extension of regression analysis that includes independent variables as explanatory in a predictive equation. In the linear regression model, the value of the dependent variable ranges at a constant rate as the value of the independent variable increases or decreases. Thus, the equation of a straight line exhibits the relationship between the true value of Y and X
i, as shown in Equation (1) [
24].
where
is the dependent variable,
are the independent variables,
are the coefficients to be estimated, and
is the error term that represents the deviation of the conditional mean to the observation.
Poisson Regression is a count data model which describes the number of failures for a given time and can consider the non-negativity integer nature of the dependent variable [
25]. It is assumed that the failures at a year (t) for a pipe i follow a Poisson distribution with mean intensity
. The probability of having
failures can be estimated as follows [
26].
where
,
are the independent variables,
are the coefficients to be estimated, and
is the number of failure events.
EPR is a hybrid regression method that combines conventional regression techniques and genetic programming, producing a range of equations in trade-off between the number of polynomial terms and accuracy [
14]. EPR consists of two main stages: (1) the exploration of the best model structure using a multiobjective genetic algorithm and (2) the estimation for parameters for an assumed model structure using the least-squares method [
5]. The general form of the ERP model is expressed in Equation (3) [
27].
where
is the dependent variable,
are the independent variables,
are the parameters to be estimated,
is an optional bias, F is the function constructed by the EPR model,
f is the function selected by the user, and
m is the maximum number of polynomial terms.
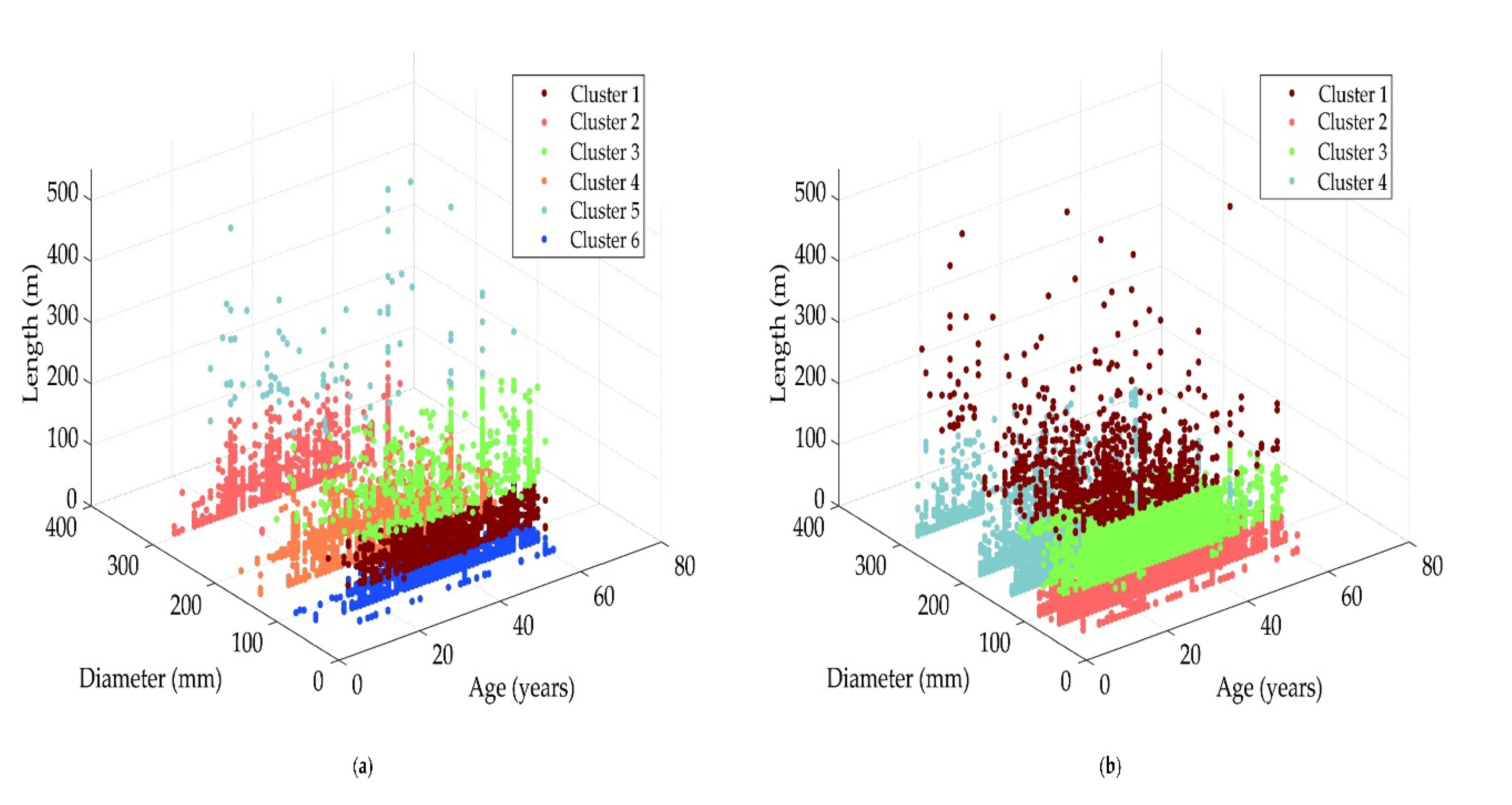
The pipes’ data is processed by removing attributes considered irrelevant to the prediction task (e.g., pipe ID) and those with missing values (e.g., pipe depth). The K-means clustering approach is applied to create pipe groups with similar characteristics. Following this approach, K clusters are created assigning
n data samples to them. The required inputs are the data samples, the number of
k clusters, and the stopping condition. The formulation of the clusters is based on the principle of maximizing intracluster similarity and minimizing intercluster similarity [
14]. Therefore, the algorithm starts from an initial distribution of clusters’ centroids, such that they are as distant as possible from each other, and determines which centroid is closest to each data point. All data points are assigned to its nearest cluster. Then, the clusters’ centroids are recalculated as the arithmetic mean of all its assigned data points. This process is replicated either until no data points can be assigned to a closer cluster or until the stopping condition is achieved [
28].
The Euclidean distance is selected as the objective function of the dissimilarity measure. This function, based on the Euclidean distance between a vector
in a group
, and the corresponding cluster center
, is defined in Equation (4) [
29]. Further, the optimal center that minimizes Equation (4) is expressed in Equation (5).
where
is the objective function within group
and
is the size of
.
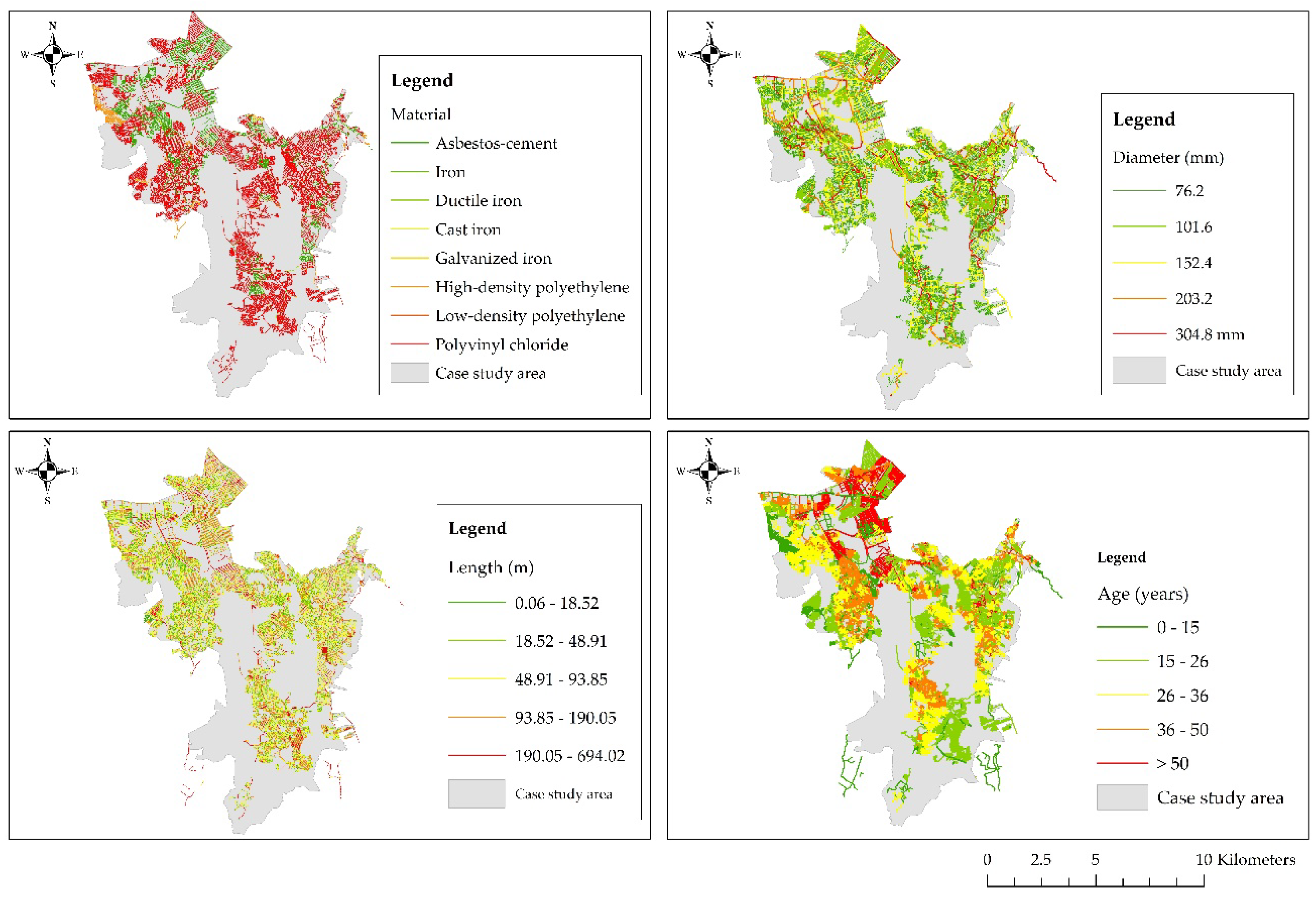
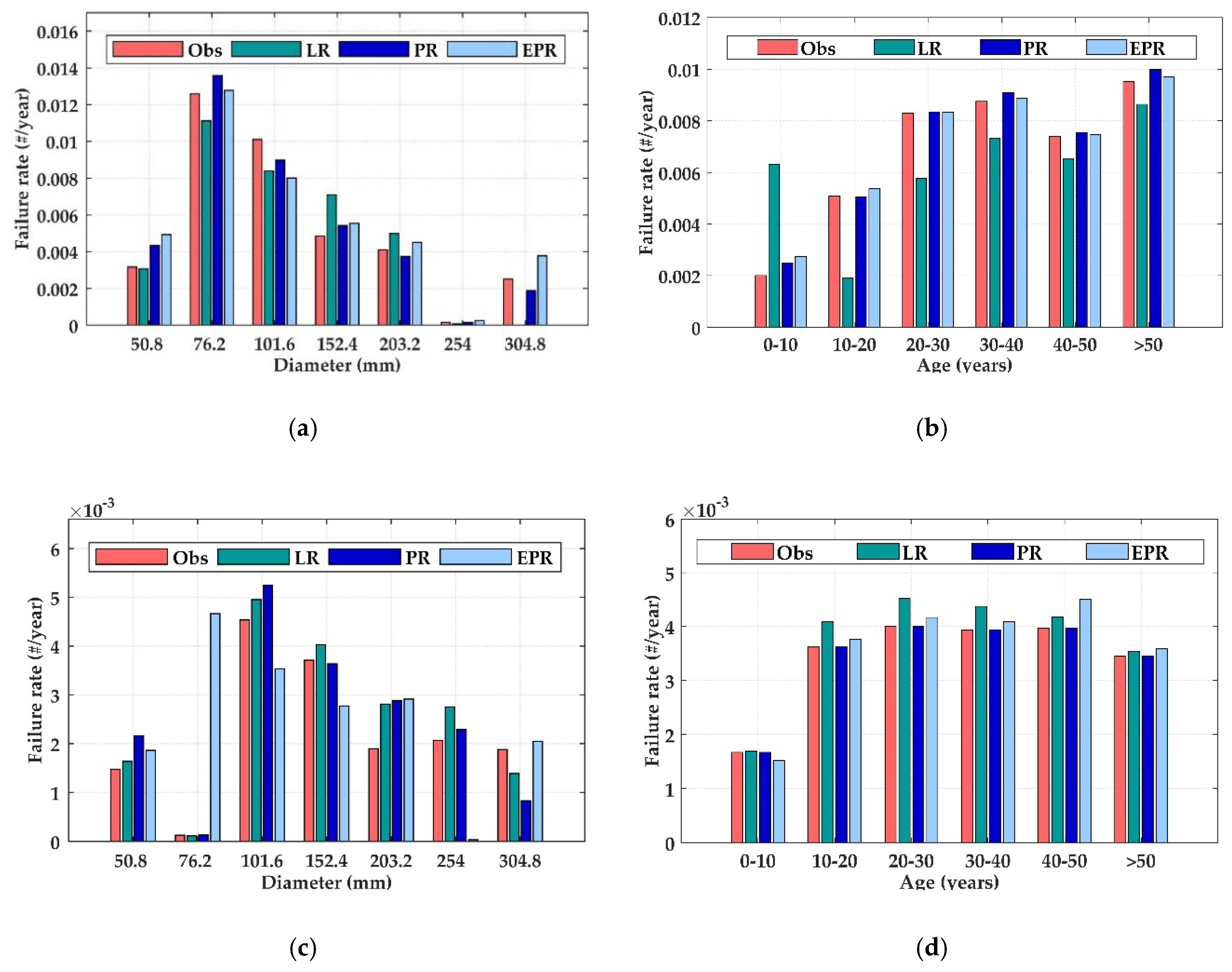
Data are grouped using pipe diameter, age, and length based on the premise that pipes with similar characteristics are expected to have the same breakage pattern [
13]. Consequently, each pipe takes a number of failures and a length equal to the total lengths and the total number of failures for the individual pipes of the same group. The Davies–Bouldin criterion is used to select the optimal number of clusters (K). This criterion is based on the ratio between the distances within-clusters and between-clusters. The Davies–Bouldin Index (DBI) is a measure that evaluates the separation between the ith and the jth cluster. The DBI has proven a suitable measure to evaluate the clustering performance [
30,
31]. It can be calculated by means of Equation (6) [
32]. According to the Davies–Bouldin criterion, the best clustering partition is the one that minimizes the DBI.
where K is the number of clusters,
is the average distance between each data point of the ith cluster and the centroid of the respective cluster (similarly to
), and
is the Euclidean distance between the centroids of the clusters i and j.
Training and test datasets are built randomly. The models are trained on 70% of the available data and tested on the remaining 30%. The K-fold cross-validation technique is used to minimize the risk of overfitting [
14]. This technique divides the dataset randomly into
k-partitions and, at each step, it uses one partition for testing and the rest for training [
33]. The explanatory variables of the models are pipe diameter (in mm), total length (in m), and pipe age (in years), while the dependent variable is the total number of failures (FR). The performance of each model is compared using the coefficient of determination (R
2) and the root mean square error (RMSE), defined as follows.
where
prediction value for the sample i,
mean value of measurements,
measurement value for the sample i,
mean value of predictions, and
number of data samples.
2.1.2. Machine Learning Models
ML approaches, namely GBT, Bayes, SVMs, and ANNs, are compared in predicting individual pipe condition. ML techniques are classified into two main categories: supervised learning and nonsupervised learning. The selected models are categorized as supervised learning. Within such learning, the ML algorithm receives the inputs and intends to converge to the best classifier. These methods can learn the patterns of the underlying process from past data and generalize the relationships between input and output data to predict or estimate an output given a new set of input variables [
34]. Inputs capture the application of concepts, instances, and variables. An instance then is an independent example of the concept, and comprises a set of variables.
GBT is a forward-learning ensemble method that obtains predictive results through gradually improved estimations, which combines the performance of many weak classifiers from previous iterations to produce a powerful one [
35]. After each boosting iteration, misclassified data have their weights increased and, for correctly classified data, their weights decreased. The output of the GBT model can be written as shown below [
36].
where j is the size of the tree,
is the region associated with the jth leaf after space partition imposed by the tree,
is the label associated with
,
is the characteristic function, and
, consisting of (
), are the estimated parameters during training.
Bayes is a graphic approach that represents a probabilistic relationship between a set of variables utilized to forecast the behavior of a system based on an observed process [
37,
38]. This model is composed of (a) a set of variables and links between the variables, (b) a set of states for each variable, and (c) an assigned conditional probability for each variable. This model has the advantage of demanding less estimated parameters. Given a scenario comprising A
i (i = 1, 2, …, n) independent variables and an observed data Y, the Bayes formula can be written as shown in Equation (10) [
38].
where
is the posterior occurrence of the probability of A given the condition that Y occurs,
is the prior occurrence of the probability
, and
the conditional occurrence probability of Y given that A occurs.
In addition, SVM is a supervised learning technique based on the principle of optimal separation classes. The SVM method builds a linear model called maximum margin hyperplane, which provides the greatest separation between instances with different values of the dependent variable [
39]. Datasets containing instances that cannot be separated with a straight line are projected into a higher-dimensional space through a kernel function. Common kernels are the polynomial, hyperbolic tangent, and radial basis functions. The SVM model is presented in Equations (11)–(13) [
22].
where
is the kernel used to transform the data from the input to the high-dimensional space,
is a regularization parameter, w is the weight vector to the hyperplane, and b is the hyperplane offset parameter.
represents the slack variables measuring the degree of misclassification, and x and y are the data points of the dataset with N points.
ANNs are parametric regression estimators that use an iterative process to adjust weights and biases within their layers to recognize patterns between inputs and outputs [
1]. Particularly, Multilayer Perceptron Networks (MLP) are fully connected networks comprised of several nodes or neurons organized in input and output layers, as well as hidden layers. The principle of MLP is based on summarizing input signals with a suitable weight, considering that each neuron is activated by a function. Common activation functions are the sigmoid logistic, tangent sigmoid, and linear functions. The signals are transferring from node i to node j and the output signal (e.g., pipe condition or failure rate) is described by the relation shown below [
40].
where
are the input signals or the explanatory variables,
are the synaptic weights, and
f is the neuron activation function that simulates the information transmission.
The pipes’ data is processed as described above.
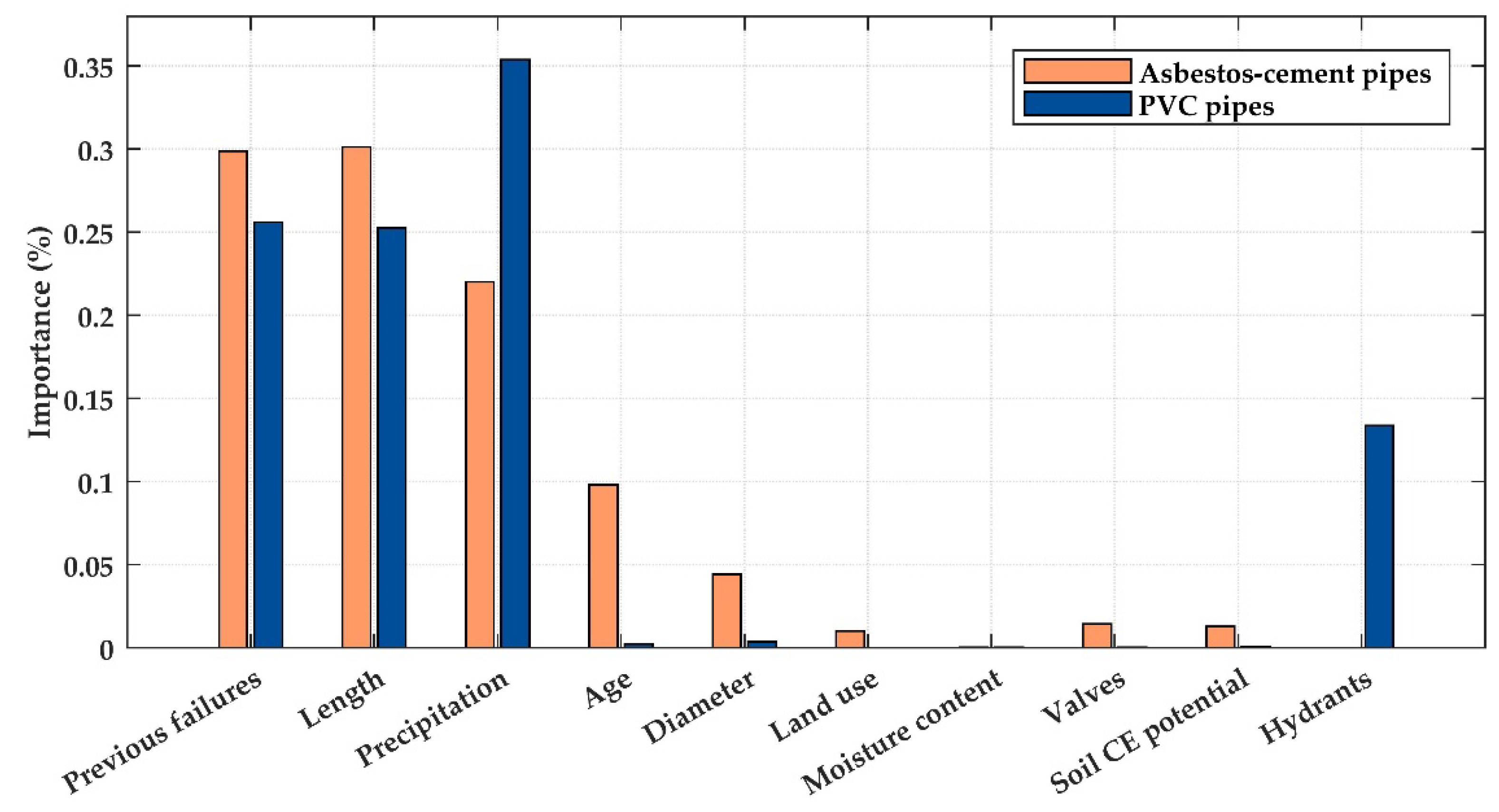
Table 1 provides an overview of the explanatory variables adopted for the models’ training. The selected variables are separated into nominal and numerical, and the nominal are changed to a numeric type. In the process, the nominal variables become into real-valued attributes. For example, land use can be classified as (a) residential, (b) commercial, (c) industrial, and (d) institutional. The four categories of the variable are converted into one variable coded as (a) 0 for residential use, (b) 1 for commercial use, (c) 2 for industrial use, and (d) 3 for institutional use. Then, land use is converted to a variable with numeric integer values from 0 to 3. The dataset is divided randomly into training and test datasets, as is described previously. K-fold cross-validation technique is also applied to decrease the risk of overfitting.
The models are used to establish the predictions of pipe condition (i.e., failure or nonfailure). For the GBT model, the parameters that must be established are the number of boosting iterations (M), the size of each tree (J), and the learning rate (λ). Experiences suggest that values of J ranging between 4 and 8 work properly in the context of boosting, with results being insensitive to particular choices in this range [
41]. In addition, the learning rate varies between 0 and 1. Empirically, it has been found that smaller values of λ (lead to larger values of M) can decrease the test error. An automated trial and error approach is adopted to select the best tree configuration [
35]. To select the parameters, a 10-fold cross-validation is carried out varying J between 4 and 8, and the learning rate between 0.1 and 0.5.
Concerning the SVMs, the parameters that must be defined are the capacity (C), gamma (γ), and epsilon (ε). The capacity (C) is a coefficient that regulates the trade-off between the training errors and the prediction risk minimization. Higher values of C lead to higher weights assigned to misclassifications [
34]. The γ parameter is a coefficient that controls the complexity of the solution and ε is the loss function that describes the regression vector without all the input data [
42]. Thus, an automated trial and error approach is adopted for testing polynomial, radial, and neural kernel functions. A 10-fold cross-validation is carried out varying the capacity from 0.1 to 50, and γ between 0.1 and 20. The radial kernel is implemented as the kernel function, and the combination of parameters that produce the best classification is selected.
Regarding the ANNs, the parameters that must be defined are the number of input layers, the number of hidden layers, the neurons in the hidden layers, the training cycles, the learning rate, and the activation function. Thus, the number of input layer is defined as the number of explanatory variables. The number of hidden layers is selected on the basis that additional layers produce additional errors. The literature suggests using one or two hidden layers [
43,
44]. The typical sizes of the learning rate range between 0.01 and 0.6 and the most common activation functions are logistic and sigmoid [
44]. Furthermore, the number of neurons can be calculated using the following equation.
where HL is the number of hidden layers, N
i is the number of input variables, and N
c is the number of classes. An automated approach is adopted to choose the best ANN configuration considering one or two hidden layers with eight neurons. Several activation functions are tested (i.e., exponential, logistic, sigmoid, and hyperbolic tangent). For each model, the selected values of the parameters are presented in
Appendix A.
The performance of the ML methods is evaluated using accuracy, confusion matrices, and receiver operating characteristic (ROC) curves. Accuracy is estimated as the fraction of correct predictions to the total predictions [
9], as shown in Equation (16). The confusion matrix, presented in
Table 2, provides more information on model performance because it categorizes the results according to predictions and observations. Pipes that are correctly classified as fail are represented by true positive (TP) and pipes correctly classified as not fail, by true negative (TN). Incorrect classifications are described by false negative (FN), which occurs when the model predicts that the pipe does not fail, but is broken, and false positive (FP), when a pipe does not fail, but is predicted to fail.
A set of alternative metrics, particularly true positive rate (TPR), true negative rate (TNR), false positive rate (FPR), false negative rate (FNR), and the F-measure, can be used for assessing the predictive capability of the models. The TPR, or recall, measures the percentage of right predictions made from the class of interest (i.e., the failed pipes). The TNR gives the percentage of correct classification of the other class (i.e., the pipes that do not fail). Similarly, the FPR represents the proportion of all negatives incorrectly classified as positive, and the FNR evaluates the positives incorrectly classified as negatives. The rates presented are related to each other thought the equations FNR + TPR = 1 and FPR + TNR = 1 [
45]. Finally, the F-measure compares the models’ performance in terms of recall and precision (i.e., a measure of exactness) using a factor that controls their relative importance. The F-measure, precision, and recall tend to 1 as the models’ performance increases [
46]. The metrics are defined below.
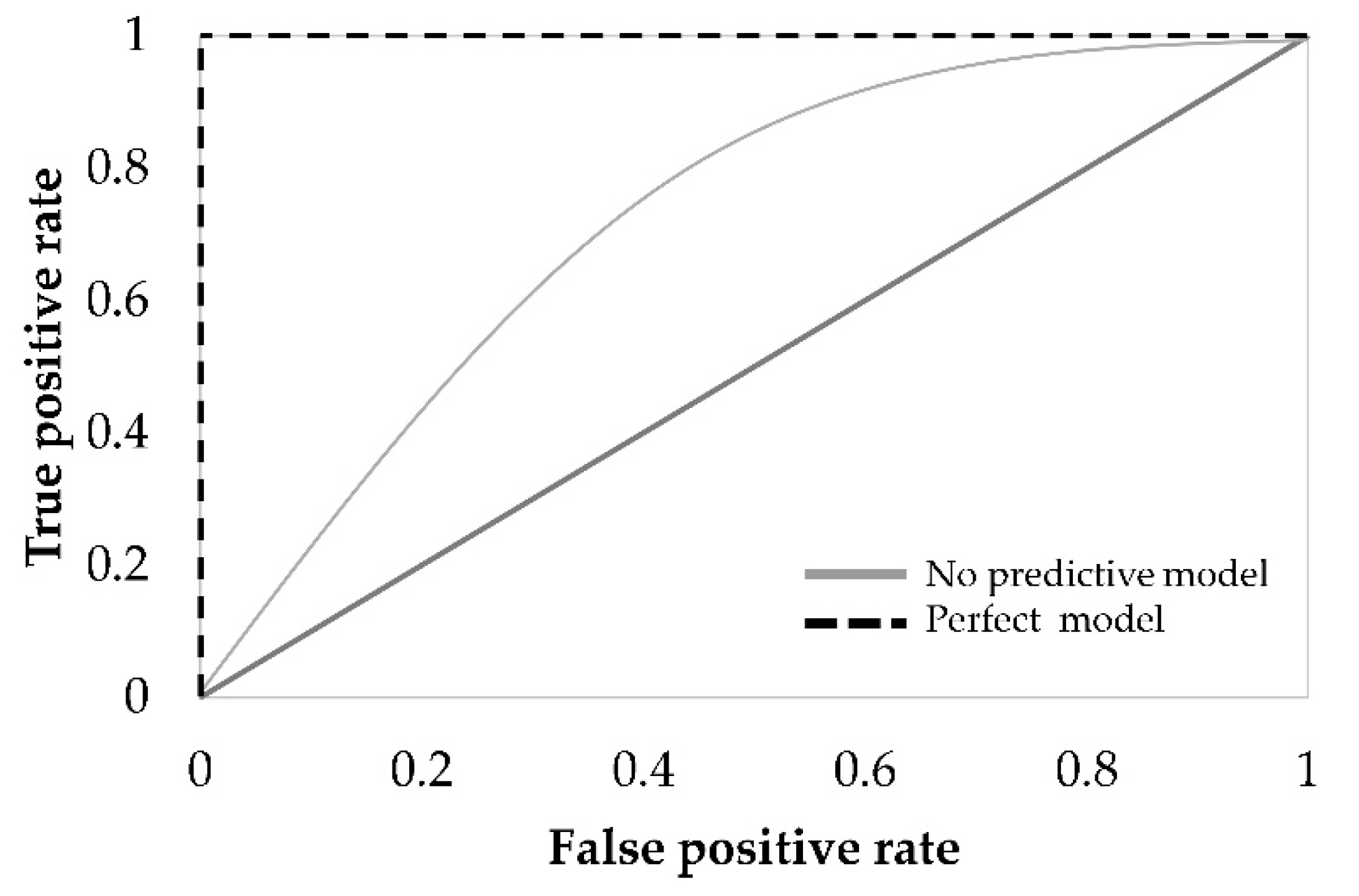
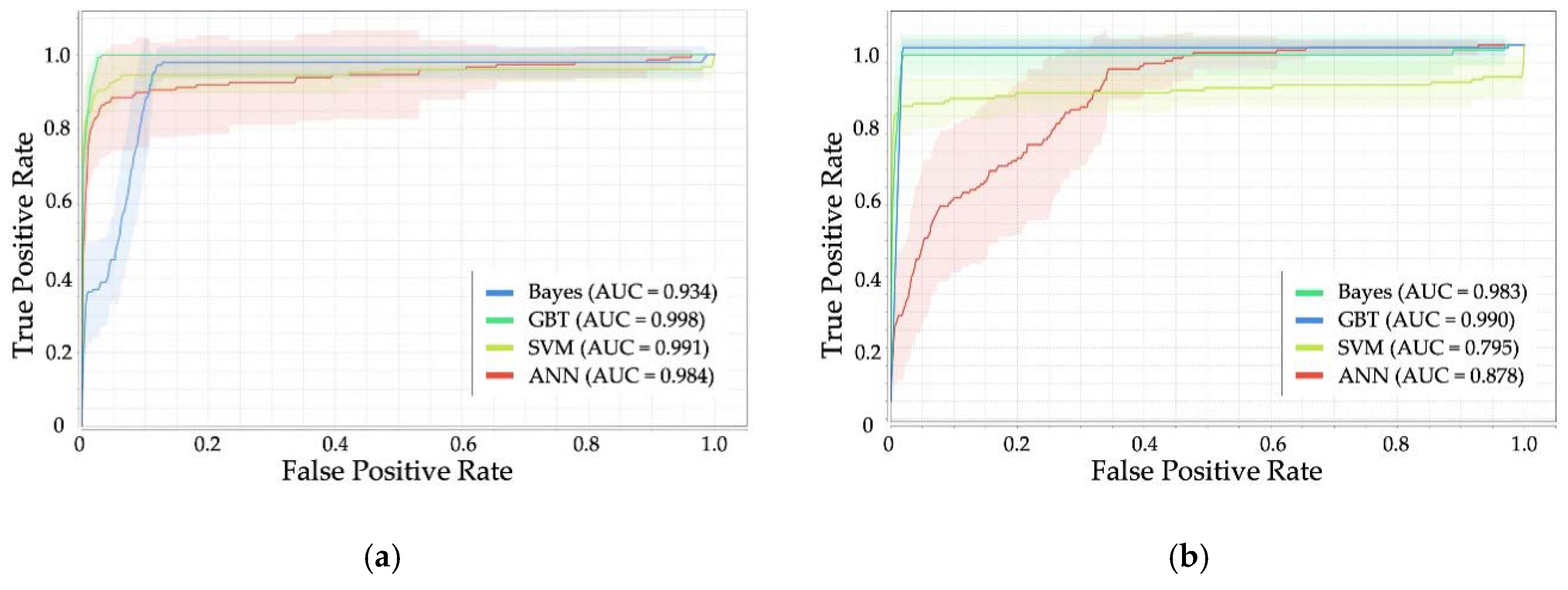
The ROC curve is a helpful technique for visualizing and selecting the most suitable model based on performance [
47]. This curve is obtained by plotting the TPR as a function of the FPR (
Figure 1), considering different probability thresholds to make class predictions [
39]. The ROC curve is considered reliable when the curve is over the 45° line. Perfect classification is graphically defined by the union of two lines, corresponding to FPR equal to 1 and TPR equal to 1 [
9].
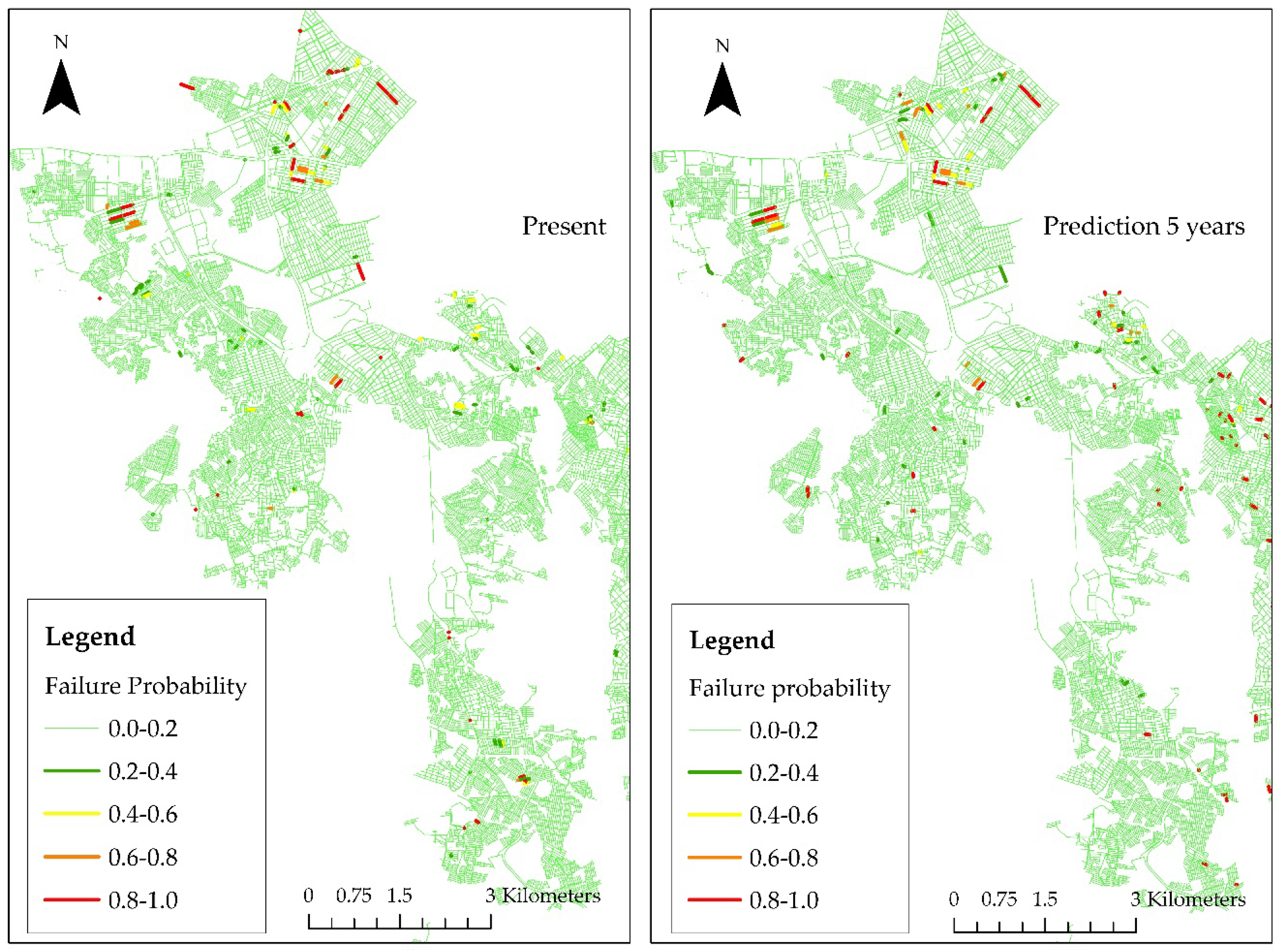
Generally, a baseline probability threshold, where any pipe with a predicted probability of failure greater than 50% will be assigned as failed, is used to train the models. A new threshold can be determined using Youden’s J index.
This index allows a new threshold that is closest to the optimal model. Youden’s J index does not modify the trained model as the same parameters are being used, and it is only employed to increase the sensitivity of the model to the minority class of interest [
48].