Smoothed Particle Hydrodynamics Modeling with Advanced Boundary Conditions for Two-Dimensional Dam-Break Floods
Abstract
:1. Introduction
2. The Numerical Model
2.1. SPH “Semi-Analytic Approach” of SPHERA for the Boundary Condition Scheme
2.2. The SPHERA Scheme for the Transport of Solid Bodies as a Boundary Treatment Scheme
2.3. Time Integration Scheme
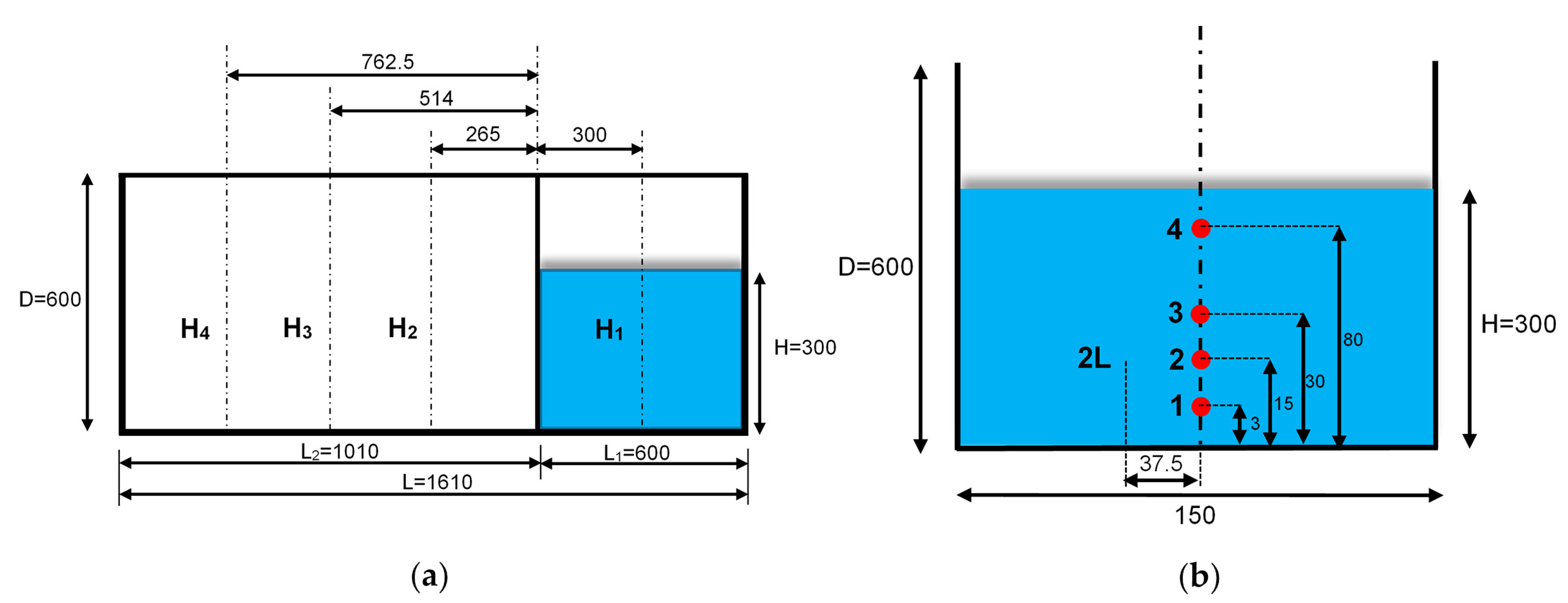
3. Case Study
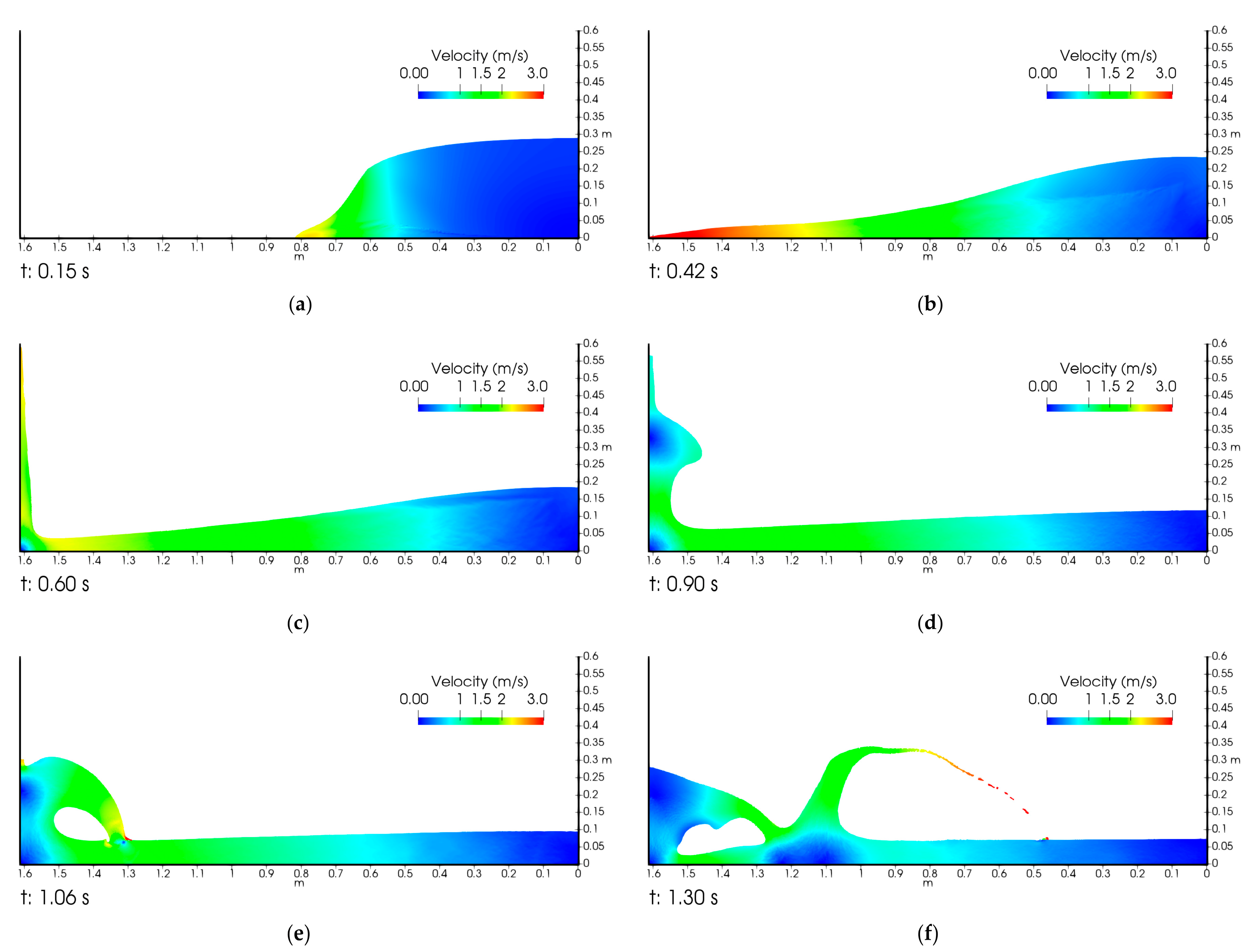
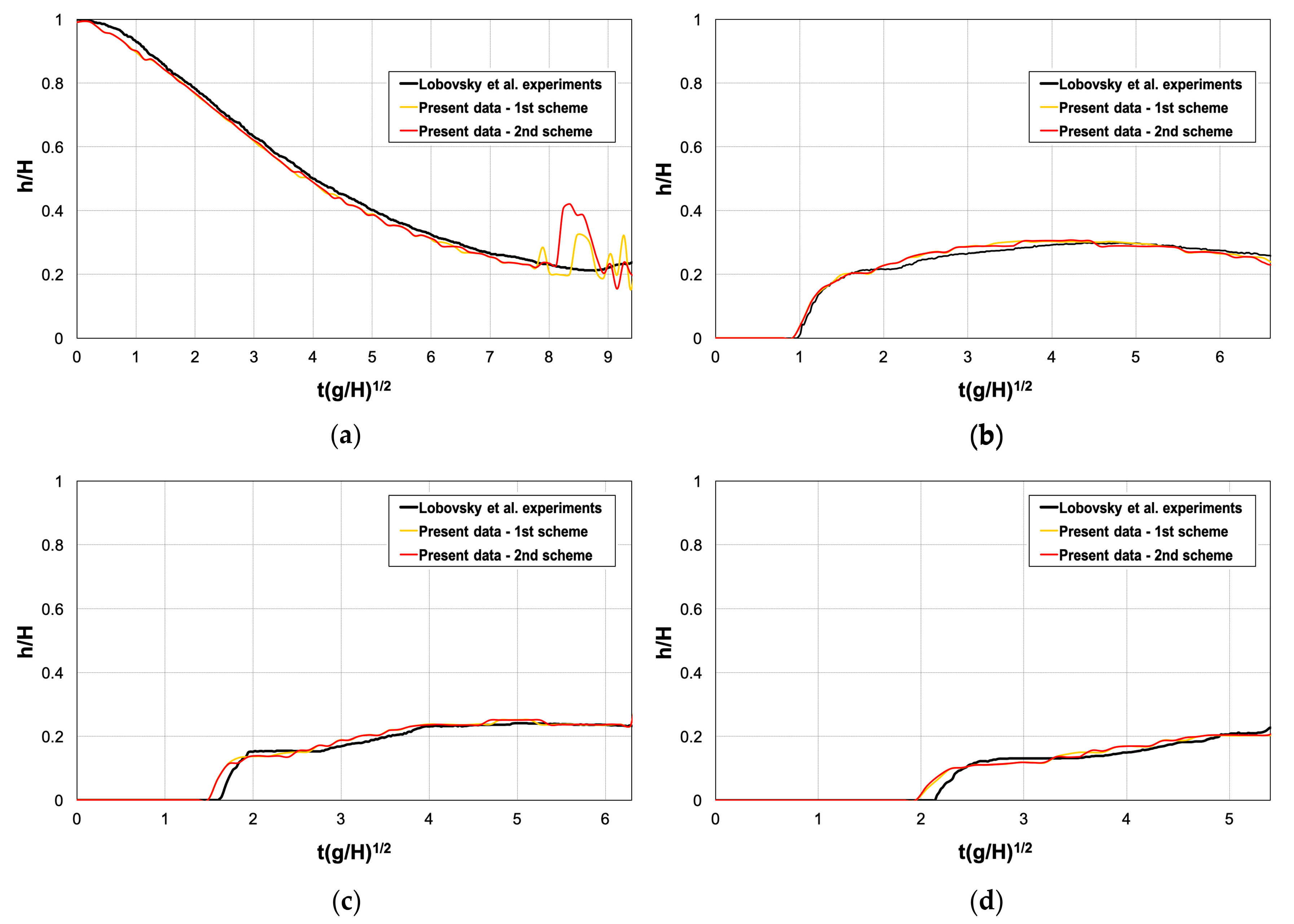
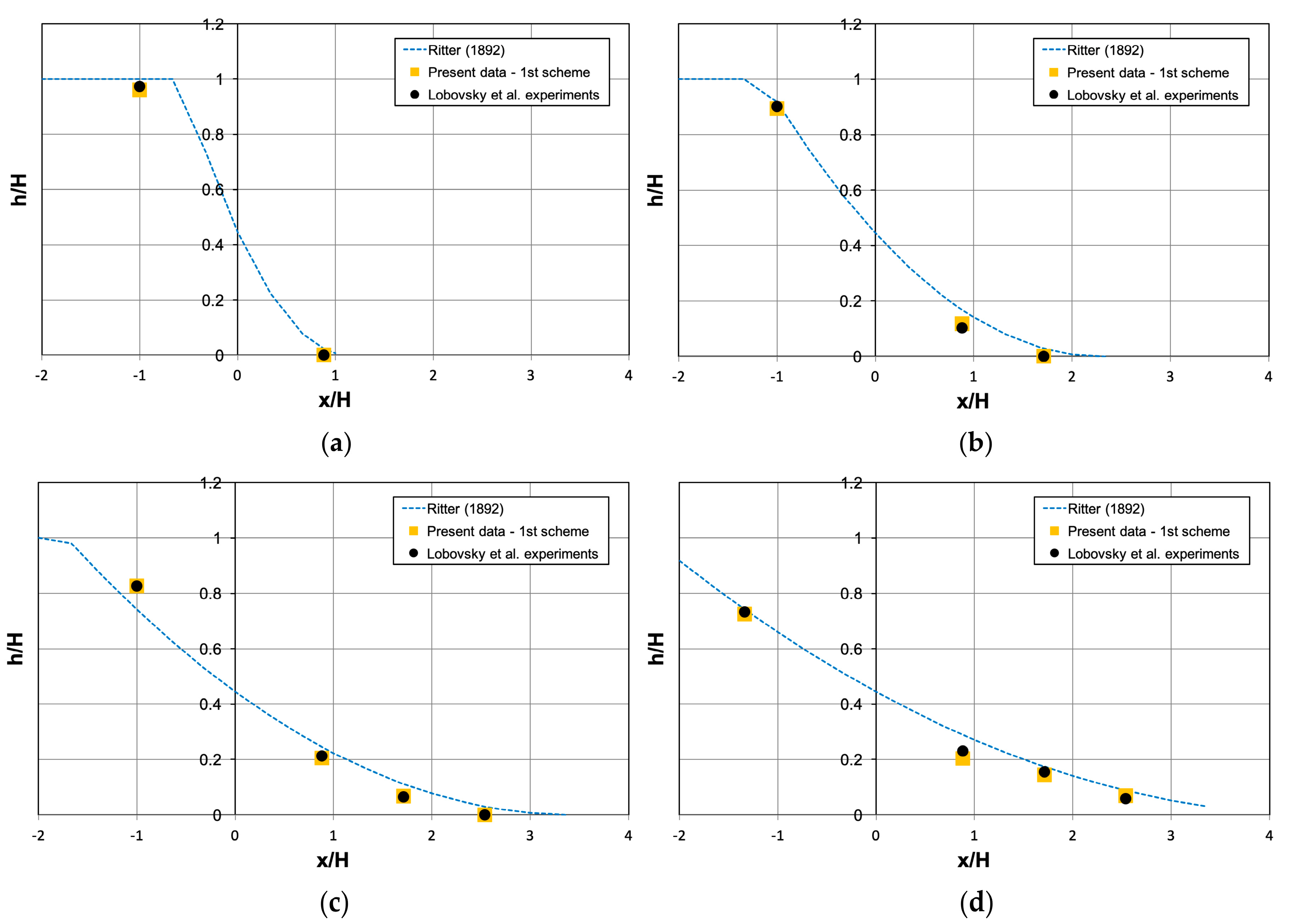
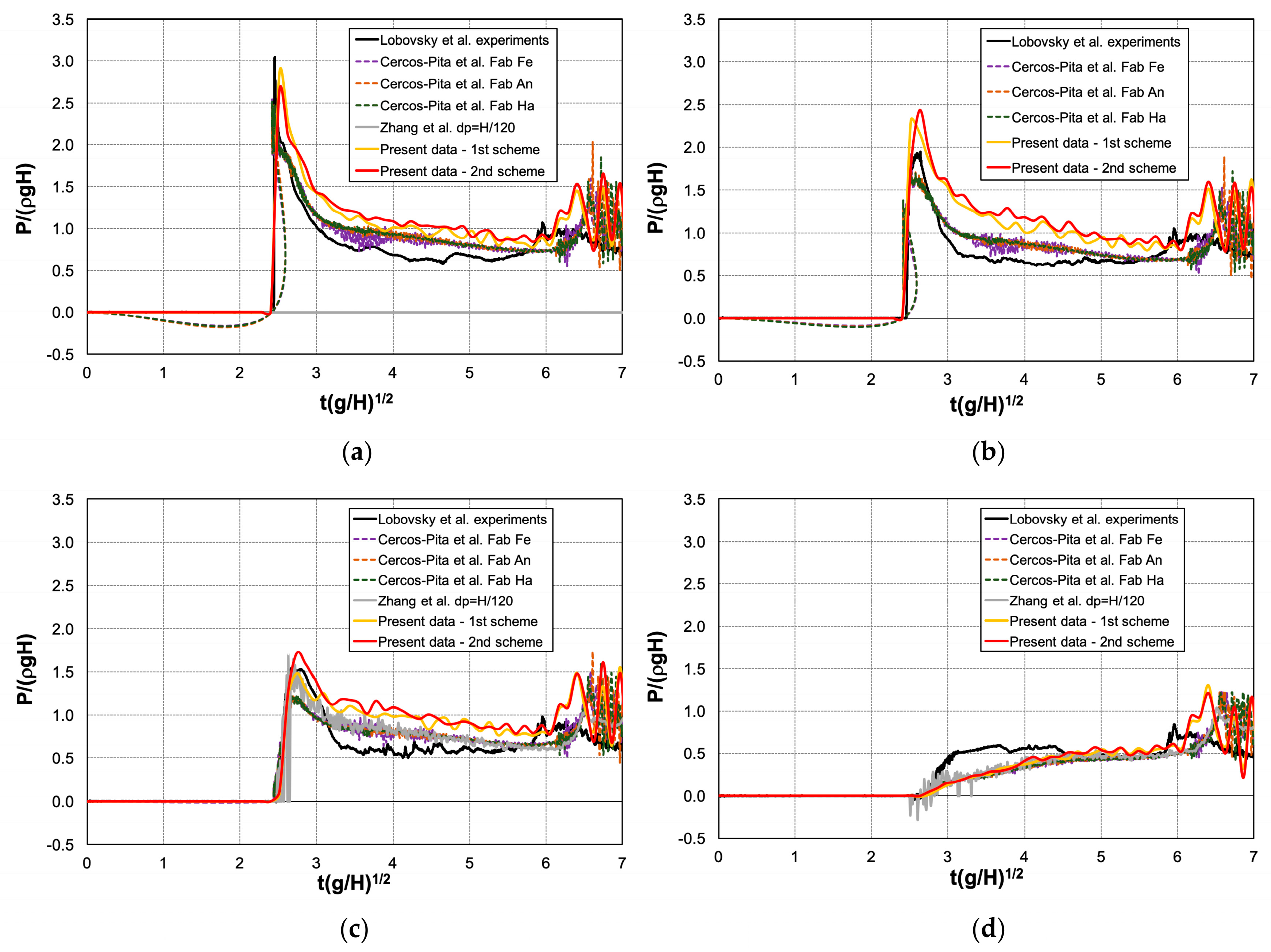
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Albano, R.; Mancusi, L.; Adamowski, J.; Cantisani, A.; Sole, A. A GIS Tool for Mapping Dam-Break Flood Hazards in Italy. ISPRS Int. J. Geo Inf. 2019, 8, 250. [Google Scholar] [CrossRef] [Green Version]
- Scarpino, S.; Albano, R.; Cantisani, A.; Mancusi, L.; Sole, A.; Milillo, G. Multitemporal SAR Data and 2D Hydrodynamic Model Flood Scenario Dynamics Assessment. ISPRS Int. J. Geo Inf. 2018, 7, 105. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, A.; Fraccarollo, L.; Dumbser, M.; Toro, E.F.; Armanini, A. Three-dimensional flow evolution after a dam-break. J. Fluid Mech. 2010, 663, 456–477. [Google Scholar] [CrossRef]
- Liang, D. Evaluating shallow water assumptions in dam-break flows. Proc. Inst. Civ. Eng. Water Manag. 2010, 163, 227–237. [Google Scholar] [CrossRef]
- Manenti, S.; Wang, D.; Domínguez, J.M.; Li, S.; Amicarelli, A.; Albano, R. SPH Modeling of Water-Related Natural Hazards. Water 2019, 11, 1875. [Google Scholar] [CrossRef] [Green Version]
- Albano, R.; Manenti, S.; Domínguez, J.M.; Li, S.; Wang, D. Computational Methods and Applications to Simulate Water-Related Natural Hazards. Math. Probl. Eng. 2020, 4363095. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Smoothed Particle Hydrodynamics (SPH): An Overview and Recent Developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef] [Green Version]
- Amicarelli, A.; Kocak, B.; Sibilla, S.; Grabe, J. A 3D Smoothed Particle Hydrodynamics model for erosional dam-break floods. Int. J. Comput. Fluid D. 2017, 31, 413–434. [Google Scholar] [CrossRef]
- Vacondio, R.; Rogers, B.D.; Stansby, P.; Mignosa, P. SPH Modeling of Shallow Flow with Open Boundaries for Practical Flood Simulation. J. Hydraul. Eng. 2012, 138, 530–541. [Google Scholar] [CrossRef]
- Amicarelli, A.; Leuzzi, G.; Monti, P.; Alessandrini, S.; Ferrero, E. A stochastic Lagrangian micromixing model for the dispersion of reactive scalars in turbulent flows: Role of concentration fluctuations and improvements to the conserved scalar theory under non-homogeneous conditions. Environ. Fluid Mech. 2017, 17, 715–753. [Google Scholar] [CrossRef]
- He, J.; Tofighi, N.; Yildiz, M.; Lei, J.; Suleman, A. A Coupled WC-TL SPH Method for Simulation of Hydroelastic Problems. Int. J. Comput. Fluid D. 2017, 31, 174–187. [Google Scholar] [CrossRef]
- Colagrossi, A.; Souto-Iglesias, A.; Antuono, M.; Marrone, S. Smoothed-Particle-Hydrodynamics Modeling of Dissipation Mechanisms in Gravity Waves. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2013, 87, 023302. [Google Scholar] [CrossRef] [PubMed]
- Espa, P.; Sibilla, S.; Gallati, M. SPH Simulations of a Vertical 2-D Liquid Jet Introduced from the Bottom of a Free-Surface Rectangular Tank. Adv. Appl. Fluid Mech. 2008, 3, 105–140. [Google Scholar]
- Price, D.J. Smoothed Particle Hydrodynamics and Magneto hydrodynamics. J. Comput. Phys. 2012, 231, 759–794. [Google Scholar] [CrossRef] [Green Version]
- Amicarelli, A.; Albano, R.; Mirauda, D.; Agate, G.; Sole, A.; Guandalini, R. A Smoothed Particle Hydrodynamics Model for 3D Solid Body Transport in Free Surface Flows. Comput. Fluids 2015, 116, 205–228. [Google Scholar] [CrossRef]
- Manenti, S.; Sibilla, S.; Gallati, M.; Agate, G.; Guandalini, R. SPH Simulation of Sediment Flushing Induced by a Rapid Water Flow. J. Hydraul. Eng. 2012, 138, 227–311. [Google Scholar] [CrossRef]
- Abdelrazek, A.M.; Kimura, I.; Shimizu, Y. Simulation of Three-Dimensional Rapid Free-Surface Granular Flow Past Different Types of Obstructions Using the SPH Method. J. Glaciol. 2016, 62, 335–347. [Google Scholar] [CrossRef] [Green Version]
- Danis, M.E.; Orhan, M.; Ecder, A. ISPH Modelling of Transient Natural Convection. Int. J. Comput. Fluid D. 2013, 27, 15–31. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical Simulation of Interfacial Flows by Smoothed Particle Hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Antoci, C.; Gallati, M.; Sibilla, S. Numerical Simulation of Fluid-Structure Interaction by SPH. Comput. Struct. 2007, 85, 879–890. [Google Scholar] [CrossRef]
- Crespo, A.J.; Gómez-Gesteira, M.; Dalrymple, R.A. Modeling Dam-break Behavior over a Wet Bed by a SPH Technique. J. Waterw. Port. Coast. Ocean. Eng. 2008, 134, 313–320. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. On Particle-Based Simulation of a Dam-break over a Wet bed. J. Hydraul. Res. 2010, 48, 238–249. [Google Scholar] [CrossRef]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; Le Touzé, D.; Graziani, G. ?-SPH Model for Simulating Violent Impact Flows. Comput. Methods Appl. Mech. Eng. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Chang, T.J.; Kao, H.M.; Chang, K.H.; Hsu, M.H. Numerical simulation of shallow-water dam-break flows in open channels using smoothed particle hydrodynamics. J. Hydrol. 2011, 408, 78–90. [Google Scholar] [CrossRef]
- Kao, H.M.; Chang, T.J. Numerical modeling of dambreak-induced flood and inundation using smoothed particle hydrodynamics. J. Hydrol. 2012, 448–449, 232–244. [Google Scholar] [CrossRef]
- Pu, J.H.; Shao, S.; Huang, Y.; Hussain, K. Evaluations of SWEs and SPH Numerical Modelling Techniques for Dam-break Flows. Eng. Appl. Comput. Fluid Mech. 2013, 7, 544–563. [Google Scholar]
- Wu, J.; Zhang, H.; Dalrymple, R.A.; Hérault, A. Numerical modeling of Dam-Break Flood in City Layouts Including Underground Spaces Using GPU-Based SPH Method. J. Hydrodynam. 2013, 25, 818–828. [Google Scholar] [CrossRef]
- St-Germain, P.; Nistor, I.; Townsend, R.; Shibayama, T. Smoothed-Particle Hydrodynamics Numerical Modeling of Structures Impacted by Tsunami Bores. J. Waterway Port. Coastal Ocean. Eng. 2014, 140, 66–81. [Google Scholar] [CrossRef]
- Nishiura, D.; Wüthrich, D.; Furuichi, M.; Nomura, S.; Pfister, M.; De Cesare, G. Numerical Approach in the Study of Tsunami-like Waves and Comparison with Experimental Data. In Proceedings of the Twenty-ninth International Ocean and Polar Engineering Conference, Honolulu, HI, USA, 16–21 June 2019; pp. 3166–3173. [Google Scholar]
- Wüthrich, D.; Nishiura, D.; Furuichi, M.; Nomura, S.; Pfister, M.; De Cesare, G. Experimental and numerical study on wave-impact on buildings. In Proceedings of the 38th IAHR World Congress, Panama City, Panama, 1–6 September 2019; pp. 6047–6056. [Google Scholar] [CrossRef]
- Jian, W.; Liang, D.; Shao, S.; Chen, R.; Liu, X. SPH study of the evolution of water-water interfaces in dam-break flows. Nat. Hazards 2015, 78, 531–553. [Google Scholar] [CrossRef] [Green Version]
- Cercos-Pita, J.L.; Dalrymple, R.A.; Herault, A. Diffusive terms for the conservation of mass equation in SPH. Appl. Math. Model. 2016, 40, 8722–8736. [Google Scholar] [CrossRef]
- Gu, S.; Zheng, X.; Ren, L.; Xie, H.; Huang, Y.; Wei, J.; Shao, S. SWE-SPHysics Simulation of Dam-break Flows at South-Gate Gorges Reservoir. Water 2017, 9, 387. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Hu, X.Y.; Adams, N.A. A weakly compressible SPH method based on a low-dissipation Riemann solver. J. Comput. Phys. 2017, 335, 605–620. [Google Scholar] [CrossRef]
- Albano, R.; Sole, A.; Mirauda, D.; Adamowski, J. Modelling large floating bodies in urban area flash-floods via a Smoothed Particle Hydrodynamics model. J. Hydrol. 2016, 541, 344–358. [Google Scholar] [CrossRef]
- Amicarelli, A.; Agate, G.; Guandalini, R. A 3D Fully Lagrangian Smoothed Particle Hydrodynamics model with both volume and surface discrete elements. Int. J. Numer. Meth. Eng. 2013, 95, 419–450. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Koss, A. Solitary waves on a Cretan beach. J. Waterw. Port. Coast. Ocean. Eng. 2002, 125, 145–155. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Lobovský, L.; Groenenboomb, P.H.L. Smoothed particle hydrodynamics modelling in continuum mechanics: Fluid-structure interaction. ACM 2009, 3, 101–110. [Google Scholar]
- Yildiz, M.; Rook, R.A.; Suleman, A. SPH with the boundary tangent method. Int. J. Numer. Meth. Eng. 2009, 77, 1416–1438. [Google Scholar] [CrossRef] [Green Version]
- Fourtakas, G.; Vacondio, R.; Rogers, B.D. On the approximate zeroth and first-order consistency in the presence of 2-D irregular boundaries in SPH obtained by the virtual boundary particle methods. Int. J. Num. Meth. Fl. 2015, 78, 475–501. [Google Scholar] [CrossRef]
- Adami, S.; Hu, X.Y.; Adams, N.A. A generalized wall boundary condition for smoothed particle hydrodynamics. J. Comput. Phys. 2012, 231, 7057–7075. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Gómez-Gesteira, M.; Dalrymple, R.A. Boundary conditions generated by dynamic particles in SPH methods. CMC Comput. Mater. Contin. 2007, 5, 173–184. [Google Scholar]
- Gómez-Gesteira, M.; Rogers, B.D.; Crespo, A.J.C.; Dalrymple, R.A.; Narayanaswamy, M.; Dominguez, J.M. SPHysics-development of a free surface fluid solver-part 1: Theory and formulations. Comput. Geosci. 2012, 48, 289–299. [Google Scholar] [CrossRef]
- Fraga Filho, C.A.D.; Chacaltana, J.T.A. Boundary treatment techniques in smoothed particle hydrodynamics: Implementations in fluid and thermal sciences and results analysis. In Proceedings of the XXXVII Iberian Latin American Congress on Computational Methods in Engineering (CILAMCE 2016), Brasília, DF, Brazil, 6–9 November 2016. [Google Scholar]
- House, D.H.; Keyser, J.C. Foundations of Physically Based Modeling & Animation, 1st ed.; CRC Press—Taylor & Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- Fraga Filho, C.A.D. An algorithmic implementation of physical reflective boundary conditions in particle methods: Collision detection and response. Phys. Fluids 2017, 29, 113602. [Google Scholar] [CrossRef]
- Kulasegaram, S.; Bonet, J.; Lewis, R.W.; Profit, M. A variational formulation based contact algorithm for rigid boundaries in two-dimensional SPH applications. Comput. Mech. 2004, 33, 316–325. [Google Scholar] [CrossRef]
- Ferrand, M.; Laurence, D.R.; Rogers, B.D.; Violeau, D.; Kassiotis, C. Unified semi-analytical wall boundary conditions for inviscid, laminar or turbulent flows in the meshless SPH method. Int. J. Num. Meth. Fl. 2013, 71, 446–472. [Google Scholar] [CrossRef] [Green Version]
- Leroy, A.; Violeau, D.; Ferrand, M.; Kassiotis, C. Unified semi-analytical wall boundary conditions applied to 2-D incompressible SPH. J. Comput. Phys. 2014, 261, 106–129. [Google Scholar] [CrossRef] [Green Version]
- Mayrhofer, A.; Ferrand, M.; Kassiotis, C.; Violeau, D.; Morel, F. Unified semi-analytical wall boundary conditions in SPH: Analytical extension to 3-D. Numer. Algor. 2015, 68, 15–34. [Google Scholar] [CrossRef]
- Macià, F.; Gonzales, L.M.; Cercos-Pita, J.L.; Souto-Iglesias, A.A. Boundary Integral SPH Formulation—Consistency and Applications to ISPH and WCSPH. Prog. Theor. Phys. 2012, 128, 439–462. [Google Scholar] [CrossRef] [Green Version]
- Chiron, L.; De Leffe, M.; Oger, G.; Le Touzé, D. Fast and accurate SPH modelling of 3D complex wall boundaries in viscous and non viscous flows. Comput. Phys. Commun. 2019, 234, 93–111. [Google Scholar] [CrossRef]
- Amicarelli, A.; Manenti, S.; Albano, R.; Agate, G.; Paggi, M.; Longoni, L.; Mirauda, D.; Ziane, L.; Viccione, G.; Todeschini, S.; et al. SPHERA v.9.0.0: A Computational Fluid Dynamics research code, based on the Smoothed Particle Hydrodynamics mesh-less method. Comput. Phys. Commun. 2020, 250, 107157. [Google Scholar] [CrossRef]
- Lobovský, L.; Botia-Vera, E.; Castellana, F.; Mas-Soler, J.; Souto-Iglesias, A. Experimental investigation of dynamic pressure loads during dam-break. J. Fluids Struct. 2014, 48, 407–434. [Google Scholar] [CrossRef] [Green Version]
- Lee, T.; Zhou, Z.; Cao, Y. Numerical simulations of hydraulic jumps in water sloshing and water impacting. J. Fluids Eng. 2002, 124, 215–226. [Google Scholar] [CrossRef]
- Di Monaco, A.; Manenti, S.; Gallati, M.; Sibilla, S.; Agate, G.; Guandalini, R. SPH modeling of solid boundaries through a semi-analytic approach. Eng. Appl. Comput. Fluid Mech. 2011, 5, 1–15. [Google Scholar] [CrossRef]
- Vila, J.P. On particle weighted methods and Smooth Particle Hydrodynamics. Math. Models Methods Appl. Sci. 1999, 9, 161–209. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- Ritter, A. Die Fortpflanzung de Wasserwellen. Z. Ver. Deutscher Ingenieure Ger. 1892, 36, 947–954. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirauda, D.; Albano, R.; Sole, A.; Adamowski, J. Smoothed Particle Hydrodynamics Modeling with Advanced Boundary Conditions for Two-Dimensional Dam-Break Floods. Water 2020, 12, 1142. https://doi.org/10.3390/w12041142
Mirauda D, Albano R, Sole A, Adamowski J. Smoothed Particle Hydrodynamics Modeling with Advanced Boundary Conditions for Two-Dimensional Dam-Break Floods. Water. 2020; 12(4):1142. https://doi.org/10.3390/w12041142
Chicago/Turabian StyleMirauda, Domenica, Raffaele Albano, Aurelia Sole, and Jan Adamowski. 2020. "Smoothed Particle Hydrodynamics Modeling with Advanced Boundary Conditions for Two-Dimensional Dam-Break Floods" Water 12, no. 4: 1142. https://doi.org/10.3390/w12041142
APA StyleMirauda, D., Albano, R., Sole, A., & Adamowski, J. (2020). Smoothed Particle Hydrodynamics Modeling with Advanced Boundary Conditions for Two-Dimensional Dam-Break Floods. Water, 12(4), 1142. https://doi.org/10.3390/w12041142







