Source Water Apportionment of a River Network: Comparing Field Isotopes to Hydrodynamically Modeled Tracers
Abstract
:1. Introduction
2. Methods
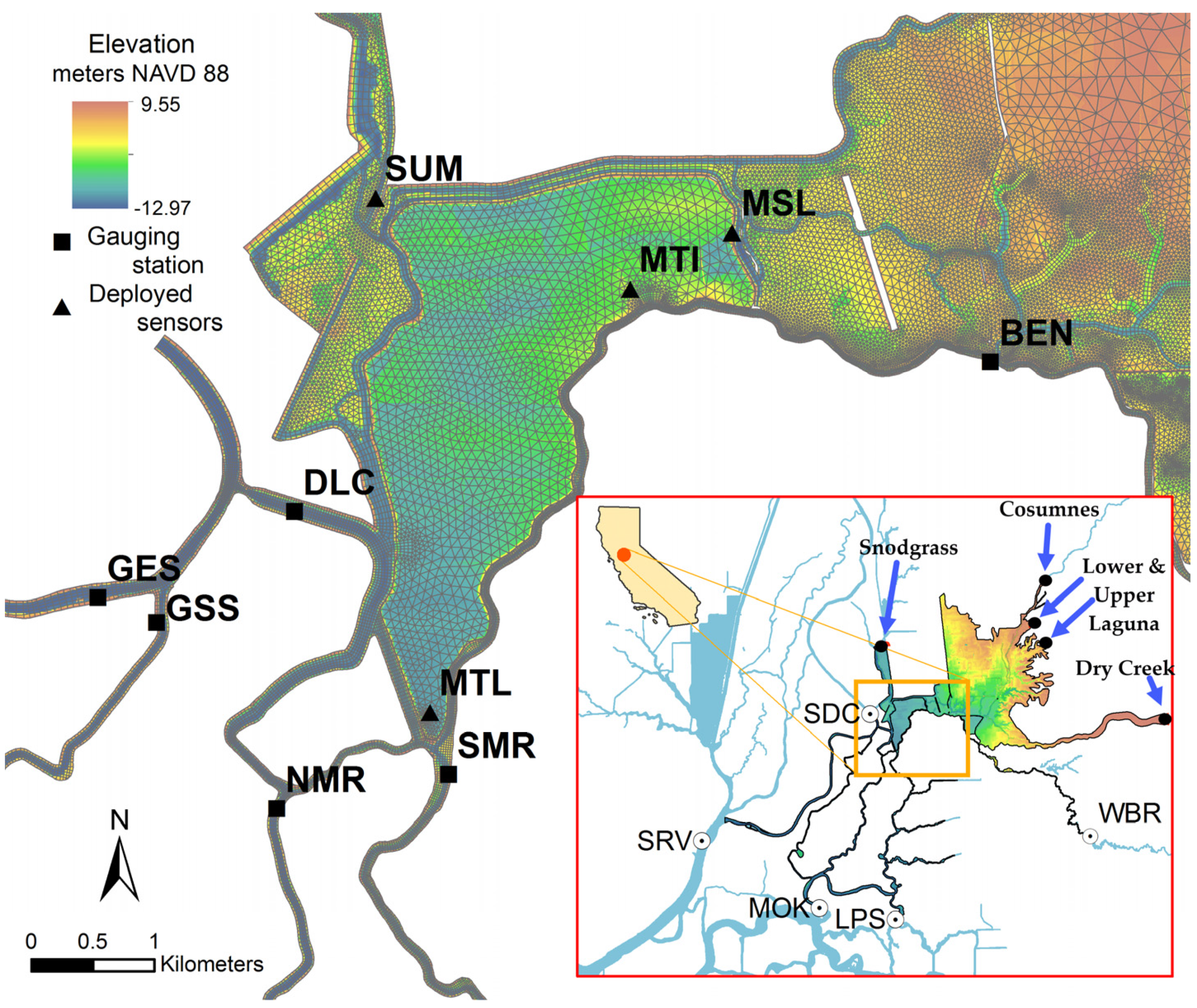
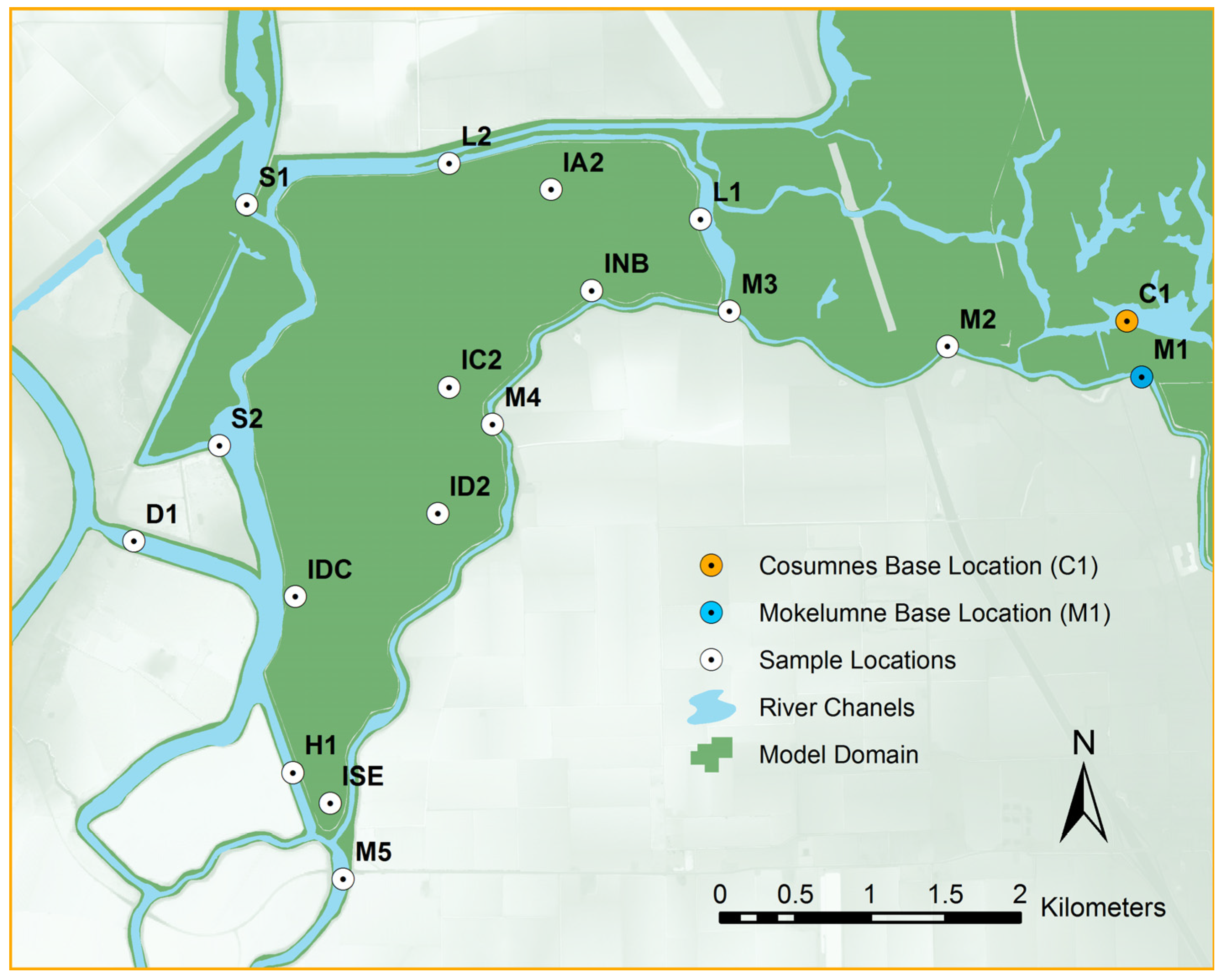
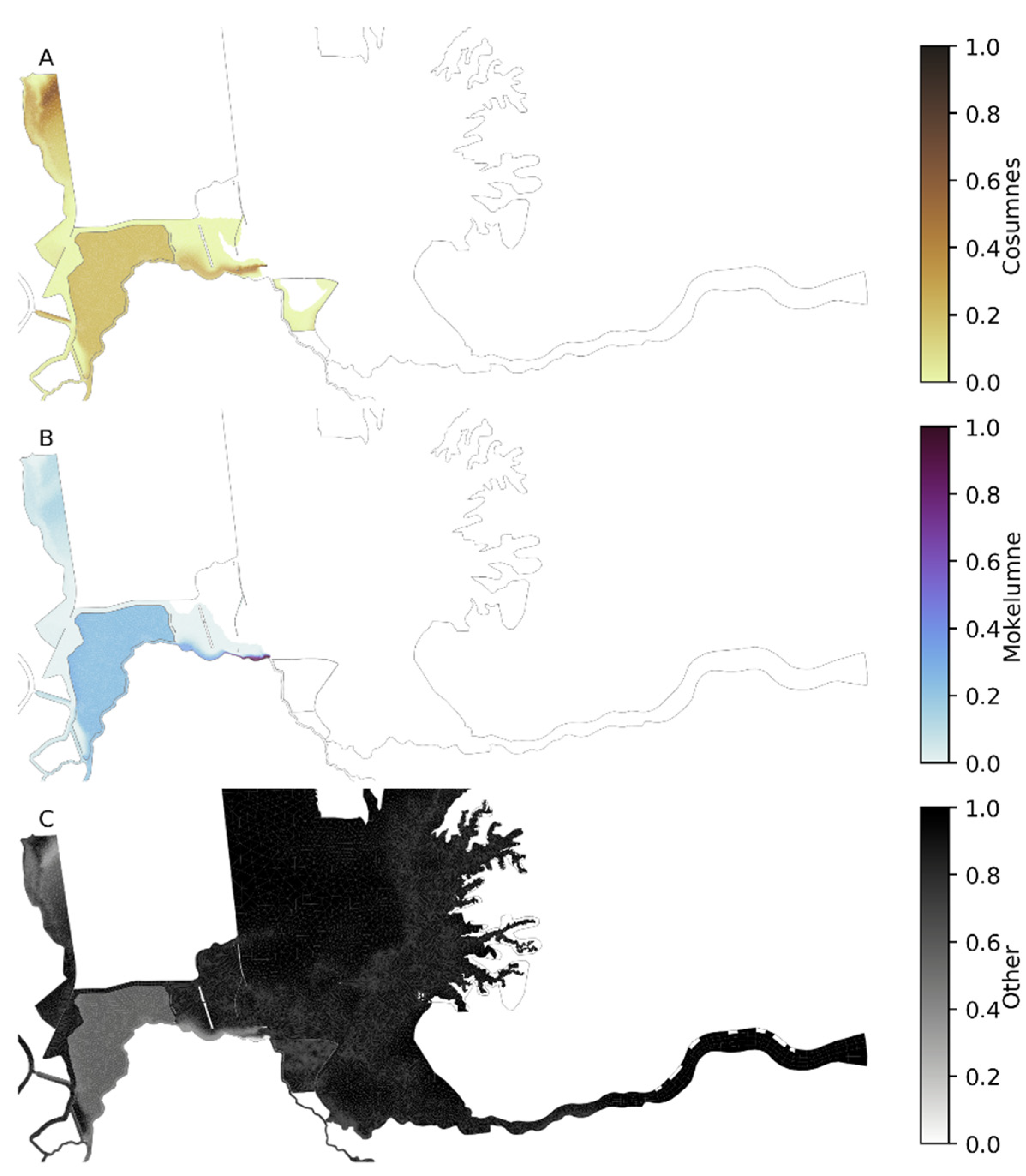
2.1. Study Area
2.2. SWF Method I: Isotope Mixing Model
2.2.1. Mixing Model Theory
2.2.2. Field Data—Collecting Isotope Samples
2.2.3. Isotope Processing
2.2.4. Application of Mixing Model
2.3. SWF Method II: Hydrodynamic Model
2.3.1. Hydrodynamic Model Development
2.3.2. Boundary Condition Development
2.3.3. Model Calibration
2.3.4. Model Tracers
3. Results
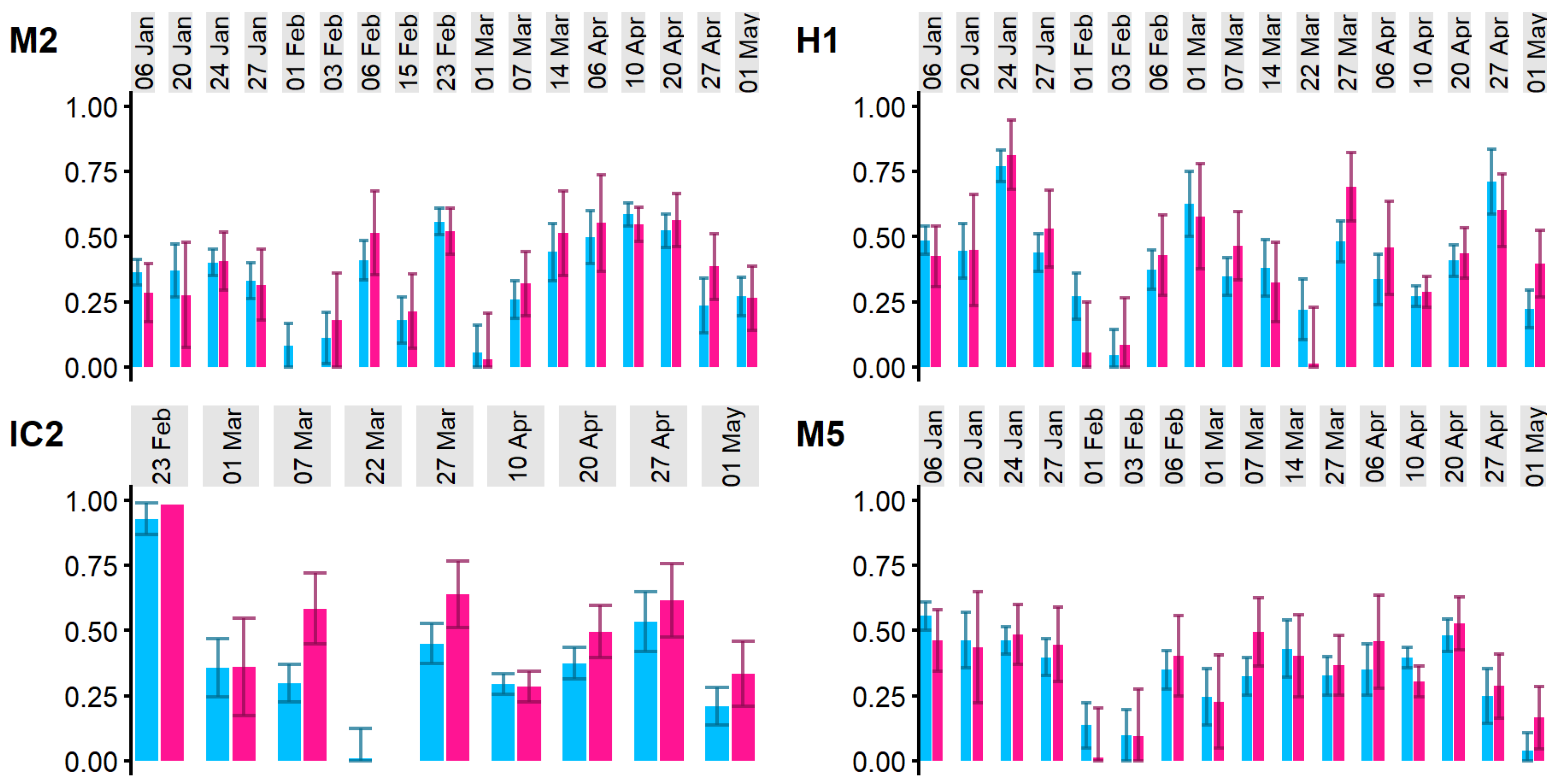
3.1. Isotope Mixing Model Results
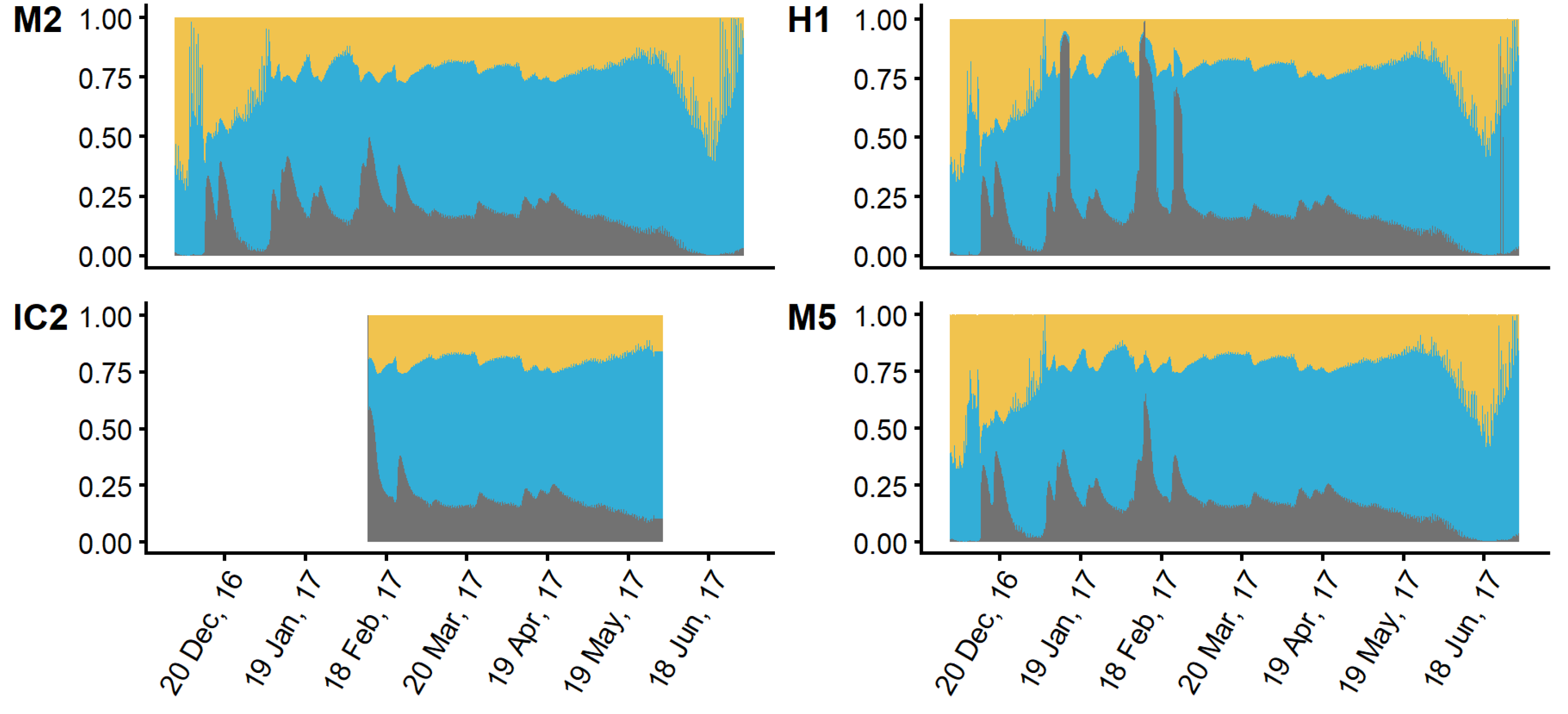
3.2. Hydrodynamic Tracer Results
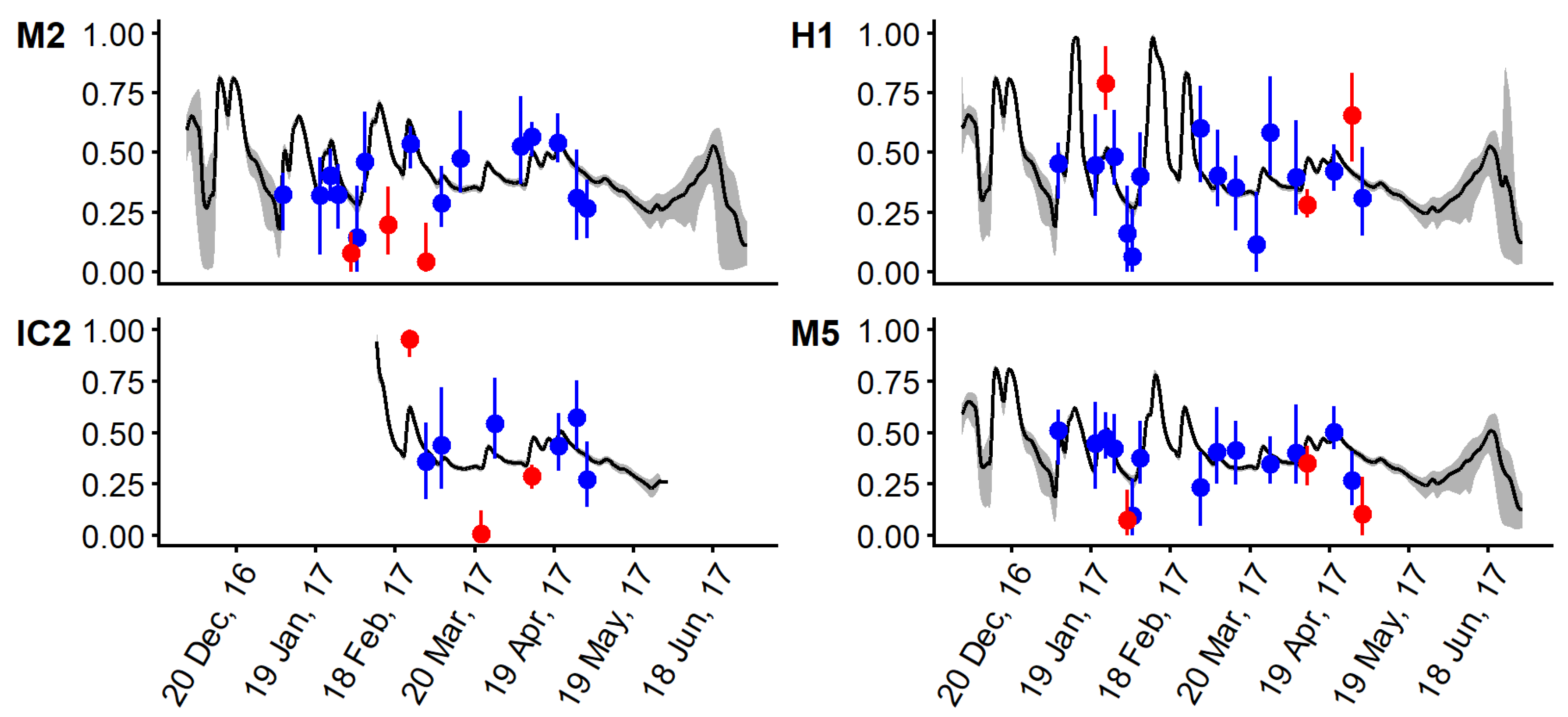
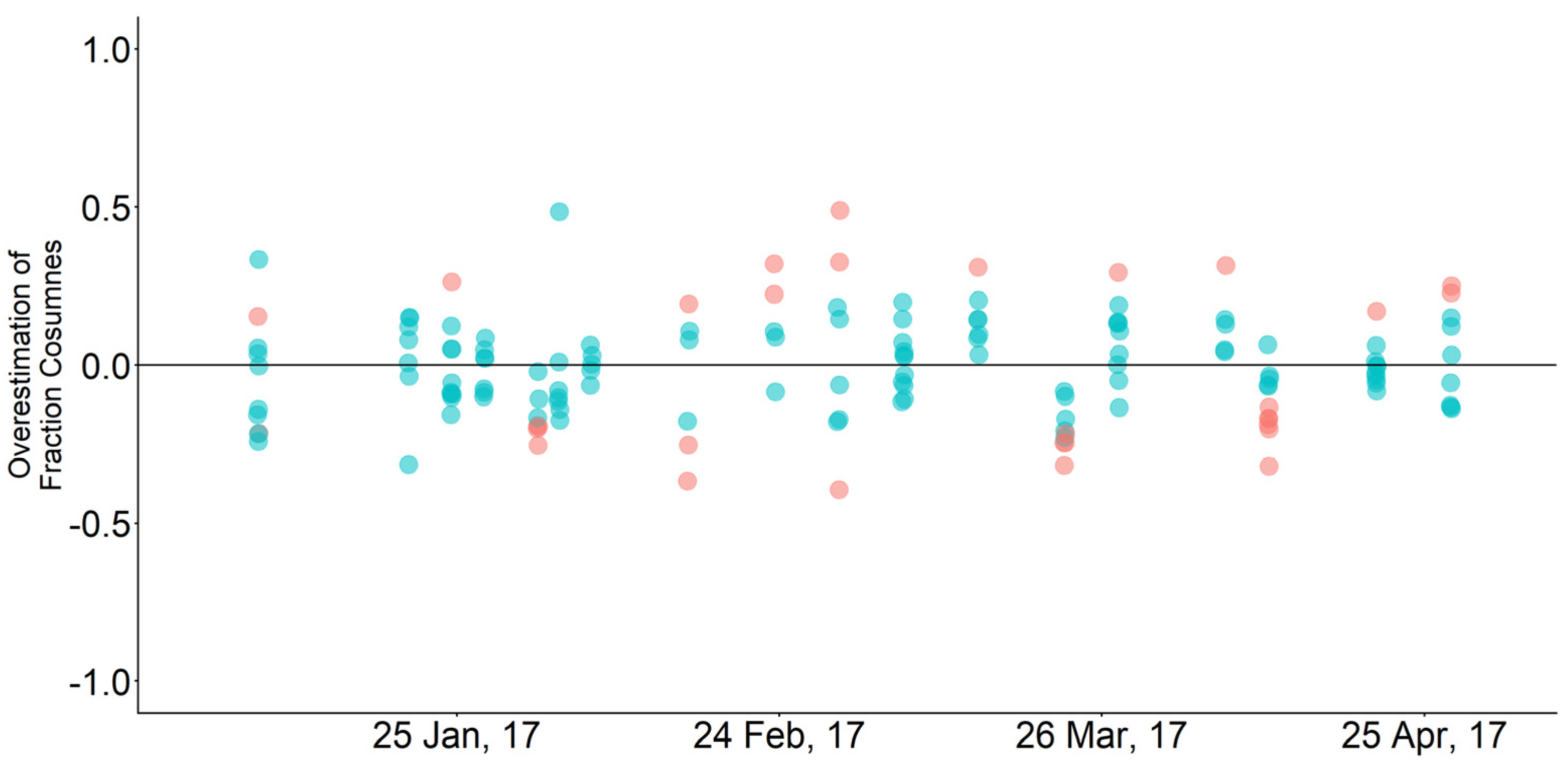
3.3. Mixing Model and Hydrodynamic Model Comparison
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Day, J.W.; Hall, C.A.S.; Kemp, W.M.; Yanez-Arancibia, A. Estuarine Ecology, 2nd ed.; Day, J.W.J., Crump, B.C., Kemp, W.M., Yanez-Arancibia, A., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1988. [Google Scholar] [CrossRef]
- Ruiz, G.M.; Carlton, J.T.; Grosholz, E.D.; Hines, A.H. Global invasions of marine and estuarine habitats by non-indigenous species: Mechanisms, extent, and consequences. Am. Zool. 1997, 37, 621–632. [Google Scholar] [CrossRef]
- Worm, B.; Barbier, E.B.; Beaumont, N.; Duffy, J.E.; Folke, C.; Halpern, B.S.; Jackson, J.B.C.; Lotze, H.K.; Micheli, F.; Palumbi, S.R.; et al. Impacts of Biodiversity Loss on Ocean Ecosystem Services. Science 2006, 314, 787–790. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lotze, H.K.; Lenihan, H.S.; Bourque, B.J.; Bradbury, R.H.; Cooke, R.G.; Kay, M.C.; Kidwell, S.M.; Kirby, M.X.; Peterson, C.H.; Jackson, J.B.C. Depletion, degradation, and recovery potential of estuaries and coastal seas. Science 2006, 312, 1806–1809. [Google Scholar] [CrossRef] [PubMed]
- Bowen, J.L.; Valiela, I. The ecological effects of urbanization of coastal watersheds: Historical increases in nitrogen loads and eutrophication of Waquoit Bay estuaries. Can. J. Fish. Aquat. Sci. 2001, 58, 1489–1500. [Google Scholar] [CrossRef]
- Kuivila, K.; Hladik, M.L. Understanding the occurrence and transport of current-use pesticides in the San Francisco estuary watershed. San Fr. Estuary Watershed Sci. 2008, 6. [Google Scholar] [CrossRef] [Green Version]
- Hong, B.; Shen, J. Responses of estuarine salinity and transport processes to potential future sea-level rise in the Chesapeake Bay. Estuar. Coast. Shelf Sci. 2012, 104–105, 33–45. [Google Scholar] [CrossRef]
- Nilsson, C.; Reidy, C.A.; Dynesius, M.; Revenga, C. Fragmentation and flow regulation of the world’s large river systems. Science 2005, 308, 405–408. [Google Scholar] [CrossRef] [Green Version]
- Drinkwater, K.F. On the Role of Freshwater Outflow on Coastal Marine Ecosystems—A Workshop Summary. In The Role of Freshwater Outflow in Coastal Marine Ecosystems; Skreslet, S., Ed.; Springer: Berlin/Heidelberg, Germany, 1986; pp. 429–438. [Google Scholar]
- Whipple, A.A.; Grossinger, R.M.; Rankin, D.; Stanford, B.; Askevold, R.A. Sacramento-San Joaquin Delta Historical Ecology Investigation: Exploring Pattern and Process; SFEI Contribution No. 672; San Francisco Estuary Institute-Aquatic Science Center: Richmond, CA, USA, 2012. [Google Scholar]
- Dahl, T.E.; Allord, G.J. Technical Aspects of Wetlands: History of Wetlands in the Conterminous United States; United States Geological Survey Water Supply Paper 2425; US Geological Survey: Reston, VA, USA, 1996.
- Ahearn, D.S.; Viers, J.H.; Mount, J.F.; Dahlgren, R.A. Priming the productivity pump: Flood pulse driven trends in suspended algal biomass distribution across a restored floodplain. Freshw. Biol. 2006, 51, 1417–1433. [Google Scholar] [CrossRef]
- Fischer, H.B.; List, E.J.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press: San Diego, CA, USA, 1979. [Google Scholar]
- Gibson, J.J.; Reid, R. Water balance along a chain of tundra lakes: A 20-year isotopic perspective. J. Hydrol. 2014, 519, 2148–2164. [Google Scholar] [CrossRef]
- Sherman, L.S.; Blum, J.D.; Dvonch, J.T.; Gratz, L.E.; Landis, M.S. The use of Pb, Sr, and Hg isotopes in great lakes precipitation as a tool for pollution source attribution. Sci. Total Environ. 2015, 502, 362–374. [Google Scholar] [CrossRef]
- Krabbenhoft, D.P.; Bowser, C.J.; Kendall, C.; Gat, J.R. Use of oxygen-18 and deuterium to assess the hydrology of groundwater-lake systems. Environ. Chem. Lakes Reserv. 1994, 90. [Google Scholar] [CrossRef]
- Vitvar, T.; Burns, D.A.; Lawrence, G.B.; Mcdonnell, J.J.; Wolock, D.M. Estimation of baseflow residence times in watersheds from the runoff hydrograph recession: Method and application in the Neversink Watershed, Catskill Mountains, New York. Hydrol. Process. 2002, 16, 1871–1877. [Google Scholar] [CrossRef]
- Marchina, C.; Bianchini, G.; Natali, C.; Pennisi, M.; Colombani, N.; Tassinari, R.; Knoeller, K. The Po river water from the Alps to the Adriatic Sea (Italy): New insights from geochemical and isotopic (Δ18O-ΔD) data. Environ. Sci. Pollut. Res. 2015, 22, 5184–5203. [Google Scholar] [CrossRef] [PubMed]
- Penna, D.; Zuecco, G.; Crema, S.; Trevisani, S.; Cavalli, M.; Pianezzola, L.; Marchi, L.; Borga, M. Response time and water origin in a steep nested catchment in the Italian dolomites. Hydrol. Process. 2017, 31, 768–782. [Google Scholar] [CrossRef]
- Marchina, C.; Lencioni, V.; Paoli, F.; Rizzo, M.; Bianchini, G. Headwaters’ isotopic signature as a tracer of stream origins and climatic anomalies: Evidence from the Italian Alps in summer 2018. Water 2020, 12, 309. [Google Scholar] [CrossRef] [Green Version]
- Halder, J.; Decrouy, L.; Vennemann, T.W. Mixing of Rhône River water in Lake Geneva (Switzerland–France) inferred from stable hydrogen and oxygen isotope profiles. J. Hydrol. 2013, 477, 152–164. [Google Scholar] [CrossRef]
- Peter, K.T.; Wu, C.; Tian, Z.; Kolodziej, E.P. Application of nontarget high resolution mass spectrometry data to quantitative source apportionment. Environ. Sci. Technol. 2019, 53, 12257–12268. [Google Scholar] [CrossRef]
- Sridharan, V.K.; Monismith, S.G.; Fong, D.A.; Hench, J.L. One-dimensional particle tracking with streamline preserving junctions for flows in channel networks. J. Hydraul. Eng. 2018, 144, 1–10. [Google Scholar] [CrossRef]
- Bai, H.; Chen, Y.; Wang, D.; Zou, R.; Zhang, H.; Ye, R.; Ma, W.; Sun, Y. Developing an EFDC and numerical source-apportionment model for nitrogen and phosphorus contribution analysis in a lake basin. Water 2018, 10, 1315. [Google Scholar] [CrossRef] [Green Version]
- Lund, J.R. Envisioning Futures for the Sacramento-San Joaquin Delta; Public Policy Institute of California: San Francisco, CA, USA, 2007. [Google Scholar]
- Mount, J.; Bennett, W.; Durand, J.; Fleenor, W.; Hanak, E.; Lund, J.; Moyle, P. Aquatic Ecosystem Stressors in the Sacramento–San Joaquin Delta; The Public Policy Institute of California (PPIC): San Francisco, CA, USA, 2012. [Google Scholar]
- Gross, E.S.; Hutton, P.H.; Draper, A.J. A comparison of outflow and salt intrusion in the pre-development and contemporary San Francisco Estuary. San Fr. Estuary Watershed Sci. 2018, 16. [Google Scholar] [CrossRef] [Green Version]
- Lund, J.; Hanak, E.; Fleenor, W.; Bennett, W.; Howitt, R.; Mount, J.; Moyle, P. Comparing Futures for the Sacramento-San Joaquin Delta; University of California Press: Berkely, CA, USA, 2010. [Google Scholar]
- Moyle, P.B.; Crain, P.K.; Whitener, K. Patterns in the use of a restored california floodplain by native and alien fishes. San Fr. Estuary Watershed Sci. 2007, 5, 1–29. [Google Scholar] [CrossRef]
- Brown, K.J.; Pasternack, G.B. The geomorphic dynamics and environmental history of an upper deltaic floodplain tract in the Sacramento-San Joaquin Delta, California, USA. Earth Surf. Process. Landforms 2004, 29, 1235–1258. [Google Scholar] [CrossRef]
- Whipple, A.A.; Viers, J.H.; Dahlke, H.E. Flood regime typology for floodplain ecosystem management as applied to the unregulated Cosumnes River of California, United States. Ecohydrology 2017, 10, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Jeffres, C.A.; Opperman, J.J.; Moyle, P.B. Ephemeral floodplain habitats provide best growth conditions for juvenile Chinook salmon in a California River. Environ. Biol. Fishes 2008, 83, 449–458. [Google Scholar] [CrossRef]
- Gat, J.R. Oxygen and hydrogen isotopes in the hydrologic cycle. Annu. Rev. Earth Planet. Sci. 1996, 24, 225–262. [Google Scholar] [CrossRef] [Green Version]
- Casulli, V.; Walters, R.A. An unstructured grid, three-dimensional model based on the shallow water equations. Int. J. Numer. Methods Fluids 2000, 32, 331–348. [Google Scholar] [CrossRef]
- Walters, R.A.; Casulli, V. A robust, finite element model for hydrostatic surface water flows. Commun. Numer. Methods Eng. 1998, 14, 931–940. [Google Scholar] [CrossRef]
- David Ford Consulting Engineers. Cosumnes and Mokelumne River Watersheds—Design Storm Runoff Analysis; David Ford Consulting Engineers: Sacramento, CA, USA, 2004. [Google Scholar]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Casulli, V.; Zanolli, P. Semi-implicit numerical modeling of nonhydrostatic free-surface flows for environmental problems. Math. Comput. Model. 2002, 36, 1131–1149. [Google Scholar] [CrossRef]
- Pasternack, G.B.; Wang, C.L.; Merz, J.E. Application of a 2D hydrodynamic model to design of reach-scale spawning gravel replenishment on the Mokelumne River, California. River Res. Appl. 2004, 20, 205–225. [Google Scholar] [CrossRef]
- Whipple, A.A. Managing Flow Regimes and Landscapes Together: Hydrospatial Analysis for Evaluating Spatiotemporal Floodplain Inundation Patterns with Restoration and Climate Change Implications. Ph.D. Thesis, University of California, Davis, CA, USA, June 2018. [Google Scholar]
- Kondolf, G.M.; Angermeier, P.L.; Cummins, K.; Dunne, T.; Healey, M.; Kimmerer, W.; Moyle, P.B.; Murphy, D.; Patten, D.; Railsback, S.; et al. Projecting cumulative benefits of multiple river restoration projects: An example from the Sacramento-San Joaquin River System in California. Environ. Manag. 2008, 42, 933–945. [Google Scholar] [CrossRef] [PubMed]
- Parker, S.S.; Remson, E.J.; Verdone, L.N. Restoring conservation nodes to enhance biodiversity and ecosystem function along the Santa Clara River. Ecol. Restor. 2014, 32, 6–8. [Google Scholar] [CrossRef]
- Hassett, B.; Palmer, M.; Bernhardt, E.; Smith, S.; Carr, J.; Hart, D. Restoring watersheds project by project: Trends in Chesapeake Bay tributary restoration. Front. Ecol. Environ. 2005, 3, 259–267. [Google Scholar] [CrossRef]
- Vannote, R.L.; Minshall, G.W.; Cummins, K.W.; Sedell, J.R.; Cushing, C.E. The river continuum concept. Can. J. Fish. Aquat. Sci. 1980, 37, 130–137. [Google Scholar] [CrossRef]
- Palmer, M.A.; Bernhardt, E.S.; Allan, J.D.; Lake, P.S.; Alexander, G.; Brooks, S.; Carr, J.; Clayton, S.; Dahm, C.N.; Follstad Shah, J.; et al. Standards for ecologically successful river restoration. J. Appl. Ecol. 2005, 42, 208–217. [Google Scholar] [CrossRef]
- Swenson, R.O.; Whitener, K.; Eaton, M. Restoring floods on floodplains: Riparian and floodplain restoration at the Cosumnes River Preserve. In California Riparian Systems: Processes and Floodplain Management, Ecology and Restoration; Riparian Habitat Joint Venture: Sacramento, CA, USA, 2003; pp. 224–229. [Google Scholar]
- Opperman, J.J.; Luster, R.; McKenney, B.A.; Roberts, M.; Meadows, A.W. Ecologically functional floodplains: Connectivity, flow regime, and scale. J. Am. Water Resour. Assoc. 2010, 46, 211–226. [Google Scholar] [CrossRef]
- California Natural Resources Agency; California Department of Food and Agriculture; California Environmental Protection Agency. California Water Action Plan: 2016 Update; California Natural Resources Agency: Sacramento, CA, USA; California Department of Food and Agriculture: Sacramento, CA, USA; California Environmental Protection Agency: Sacramento, CA, USA, 2016.
- Farly, L.; Hudon, C.; Cattaneo, A.; Cabana, G. Seasonality of a floodplain subsidy to the fish community of a large temperate river. Ecosystems 2019, 22, 1823–1837. [Google Scholar] [CrossRef]

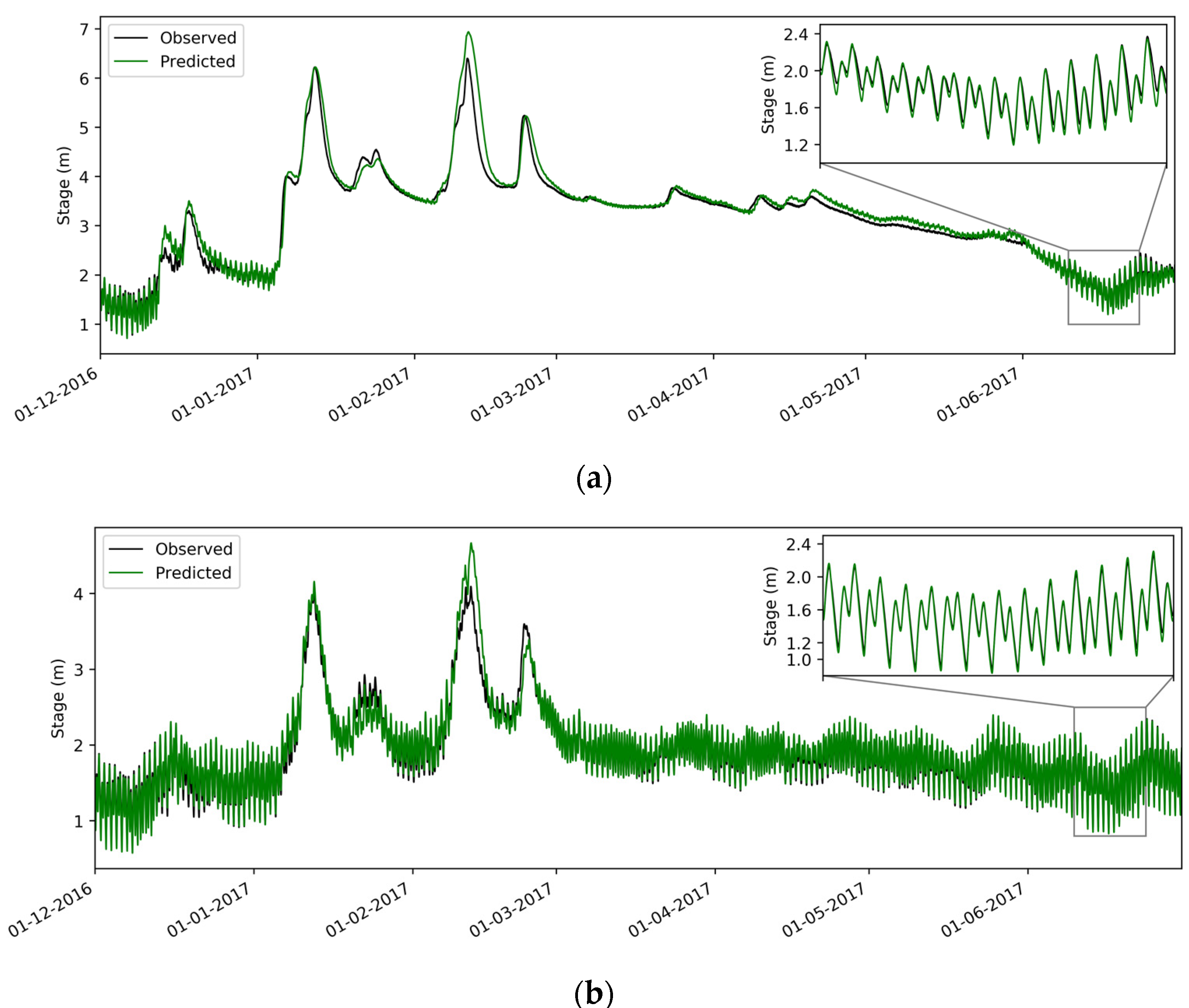
| Gage Name | Gage ID * | R2 | Skill | Date Range | |
|---|---|---|---|---|---|
| Stage | Mokelumne R @ Benson’s Ferry NR Thornton | BEN C | 0.976 | 0.991 | 1 December 2016–1 July 2017 |
| Delta Cross Channel BTW Sac R & Snodgrass | DLC U | 0.963 | 0.989 | 1 December 2016–1 July 2017 | |
| Sacramento River Below Georgiana Slough | GES U | 0.977 | 0.99 | 1 December 2016–1 July 2017 | |
| Georgiana Slough at Sacramento River | GSS U | 0.976 | 0.989 | 1 December 2016–1 July 2017 | |
| Middle Slough | MSL L | 0.959 | 0.986 | 20 January 2017–1 July 2017 | |
| McCormack-Williamson Tract – Inlet | MTI L | 0.932 | 0.974 | 16 February 2017–31 May 2017 | |
| McCormack-Williamson Tract – Lower | MTL L | 0.914 | 0.976 | 16 February 2017–31 May 2017 | |
| North Mokelumne R at W Walnut Grove Rd | NMR U | 0.985 | 0.996 | 1 December 2016–1/11/2017 | |
| South Mokelumne R at W Walnut Grove Rd | SMR U | 0.969 | 0.99 | 1 December 2016–1 July 2017 | |
| Snodgrass Slough Upstream of Meadow | SUM L | 0.922 | 0.979 | 1 January 2017–1 July 2017 | |
| Flow | Sacramento River Below Georgiana Slough | GES U | 0.993 | 0.997 | 1 December 2016–1 July 2017 |
| Georgiana Slough at Sacramento River | GSS U | 0.974 | 0.973 | 1 December 2016–1 July 2017 | |
| South Mokelumne R at W Walnut Grove Rd | SMR U | 0.914 | 0.965 | 1 December 2016–1 July 2017 | |
| North Mokelumne R at W Walnut Grove Rd | NMR U | 0.958 | 0.98 | 1 December 2016–11 January 2017 |
| Site | Total Samples | Overlapping Samples | Percentage Overlapping Samples |
|---|---|---|---|
| D1 | 5 | 8 | 82.4% |
| H1 | 14 | 17 | 62.5% |
| IA2 | 9 | 11 | 82.4% |
| IC2 | 6 | 9 | 81.8% |
| ID2 | 1 | 1 | 66.7% |
| IDC | 8 | 11 | 100.0% |
| INB | 1 | 2 | 72.7% |
| ISE | 4 | 10 | 50.0% |
| L1 | 10 | 11 | 40.0% |
| L2 | 8 | 9 | 90.9% |
| M2 | 14 | 17 | 75.0% |
| M3 | 16 | 17 | 88.9% |
| M4 | 6 | 8 | 94.1% |
| M5 | 13 | 16 | 83.3% |
| S1 | 5 | 6 | 100.0% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomkovic, L.A.; Gross, E.S.; Nakamoto, B.; Fogel, M.L.; Jeffres, C. Source Water Apportionment of a River Network: Comparing Field Isotopes to Hydrodynamically Modeled Tracers. Water 2020, 12, 1128. https://doi.org/10.3390/w12041128
Tomkovic LA, Gross ES, Nakamoto B, Fogel ML, Jeffres C. Source Water Apportionment of a River Network: Comparing Field Isotopes to Hydrodynamically Modeled Tracers. Water. 2020; 12(4):1128. https://doi.org/10.3390/w12041128
Chicago/Turabian StyleTomkovic, Lily A., Edward S. Gross, Bobby Nakamoto, Marilyn L. Fogel, and Carson Jeffres. 2020. "Source Water Apportionment of a River Network: Comparing Field Isotopes to Hydrodynamically Modeled Tracers" Water 12, no. 4: 1128. https://doi.org/10.3390/w12041128





