Spatial Variability of Preferential Flow and Infiltration Redistribution along a Rocky-Mountain Hillslope, Northern China
Abstract
:1. Introduction
2. Materials and Methods
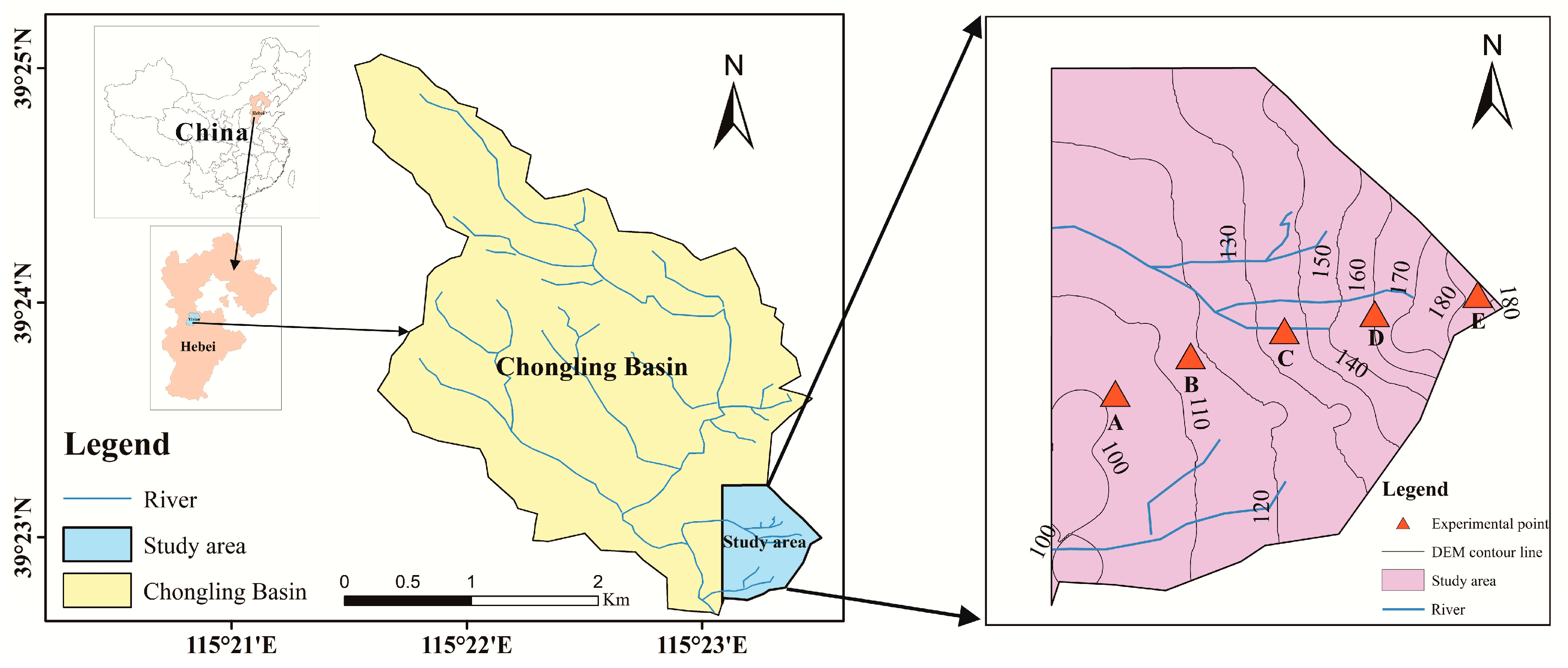
2.1. Study Area
2.2. Experimental Procedure
2.3. Image Analysis Techniques
2.4. Preferential Flow Indices
2.5. Evaluation of Infiltration Spatial Redistribution
2.5.1. Non–Uniformity Analysis of Infiltration Depth
2.5.2. Fractal Dimension of the Preferential Flow Wetting Front
2.6. Correlation and Error Analysis
3. Results and Discussion
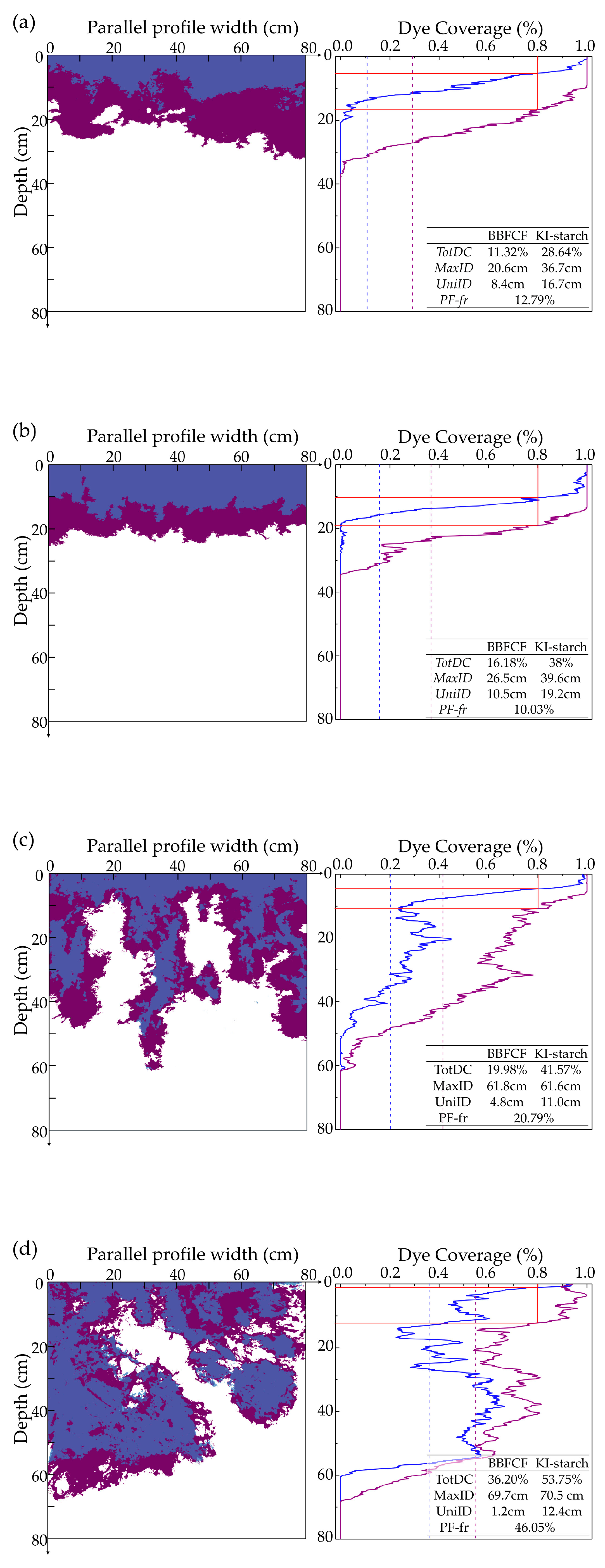
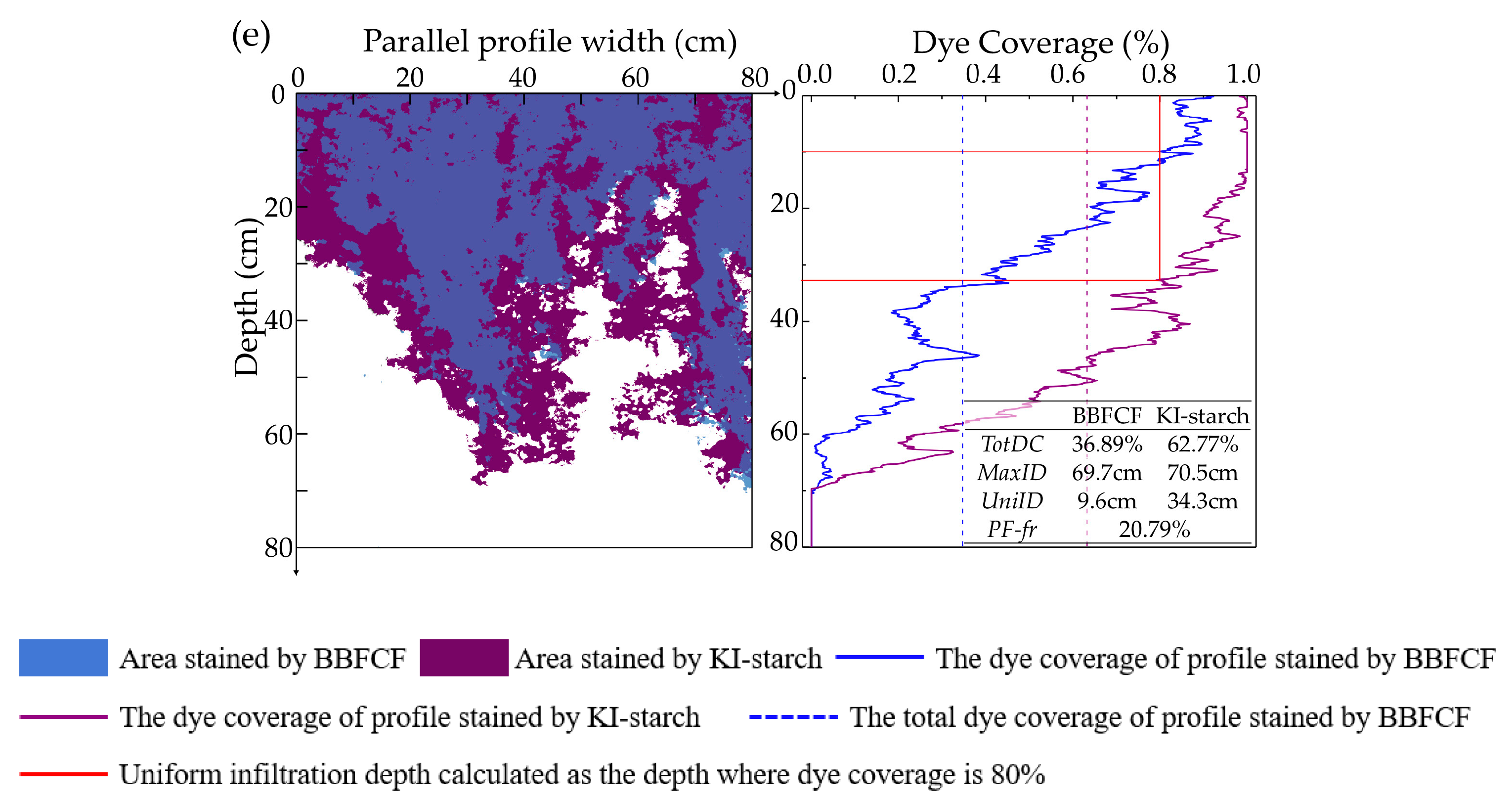
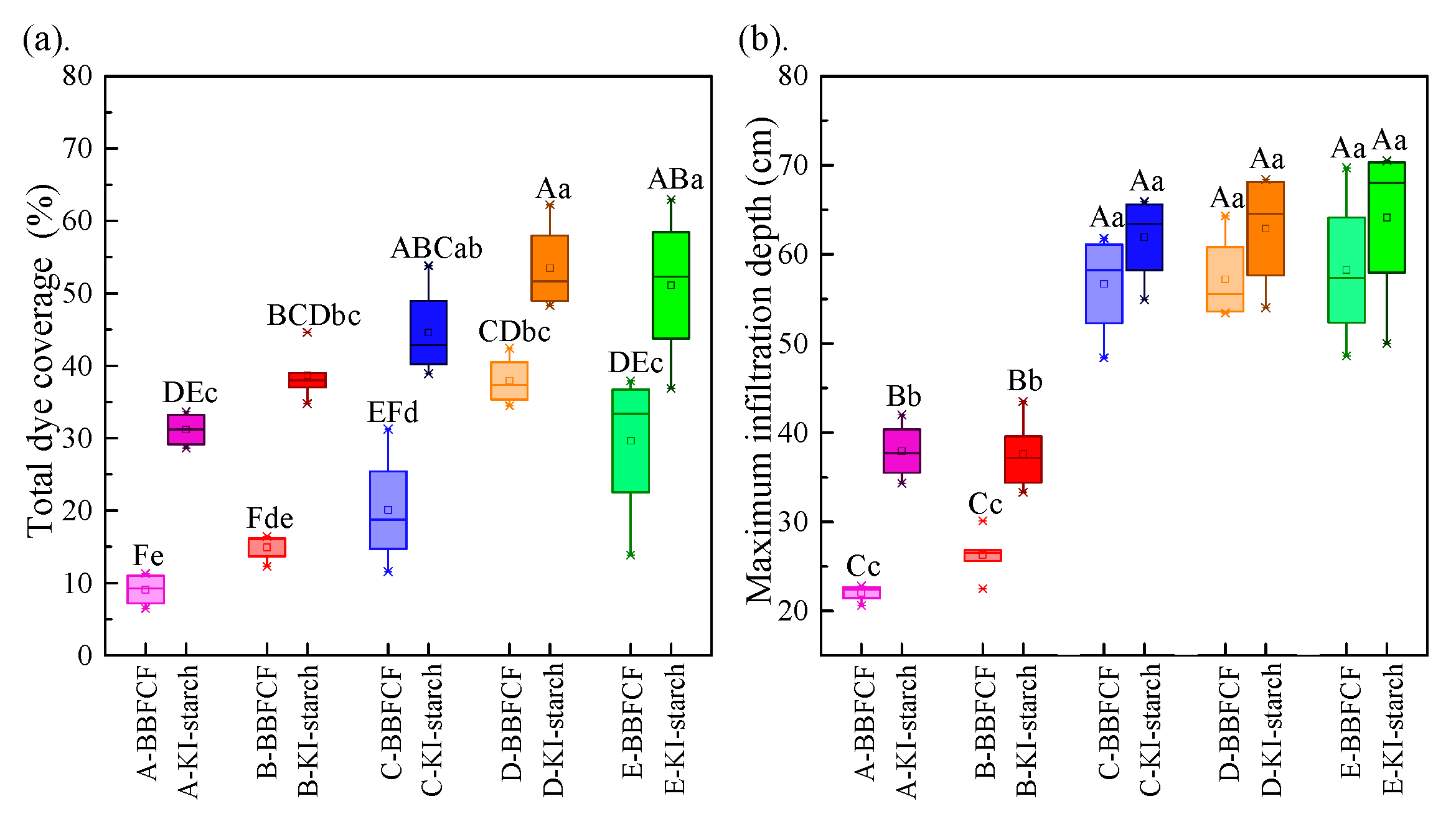
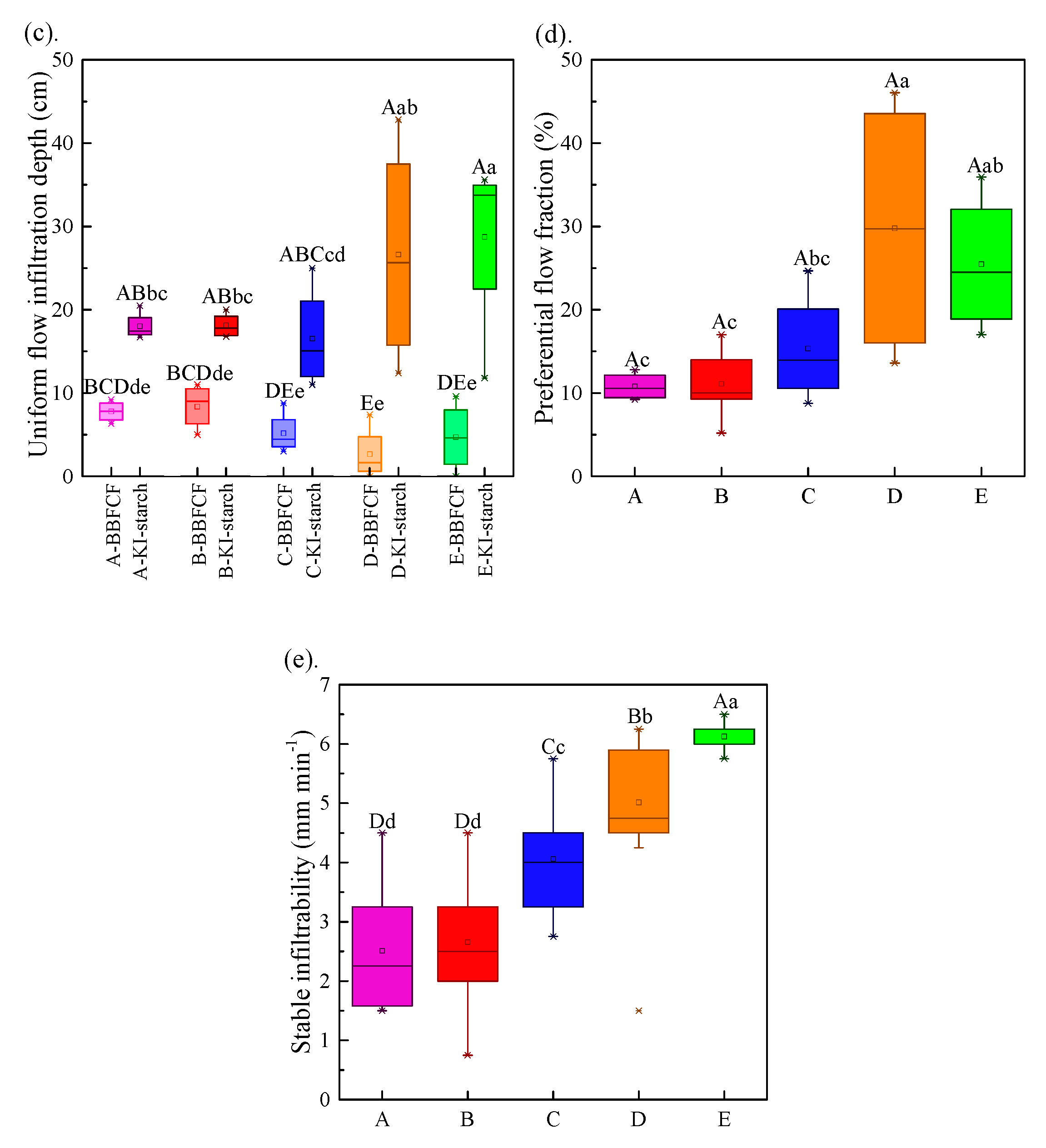
3.1. Degree of Preferential Flow
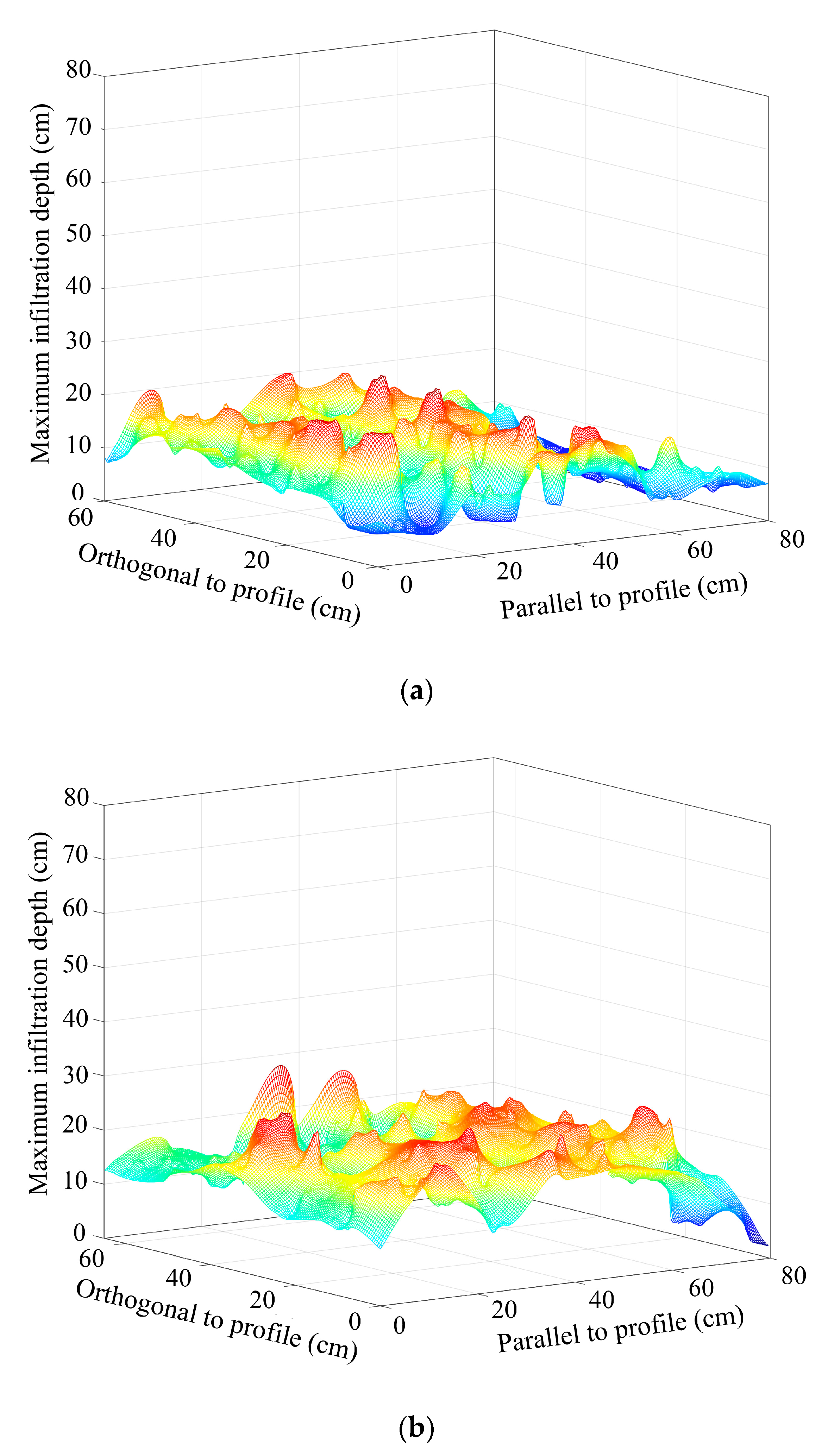
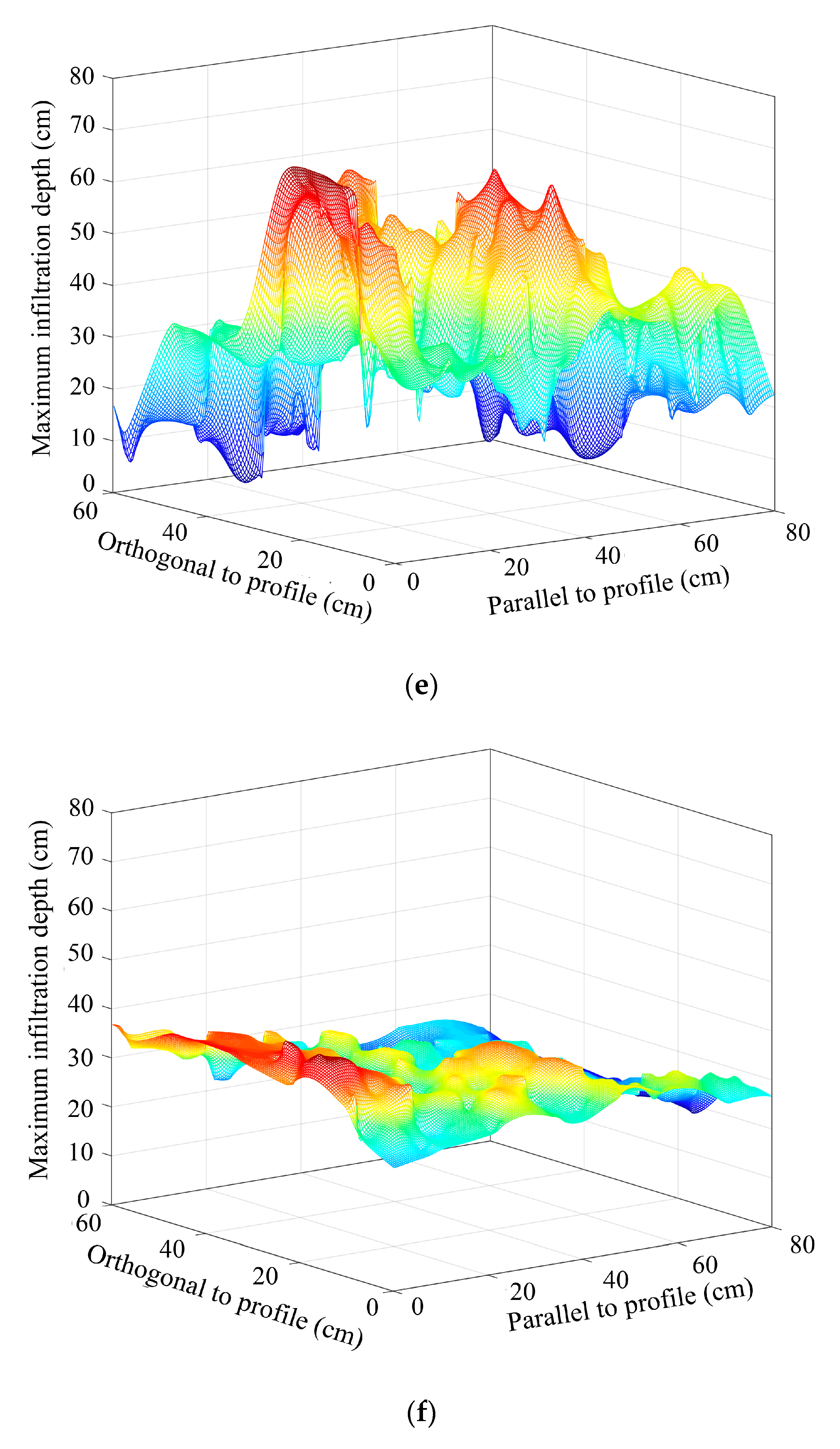
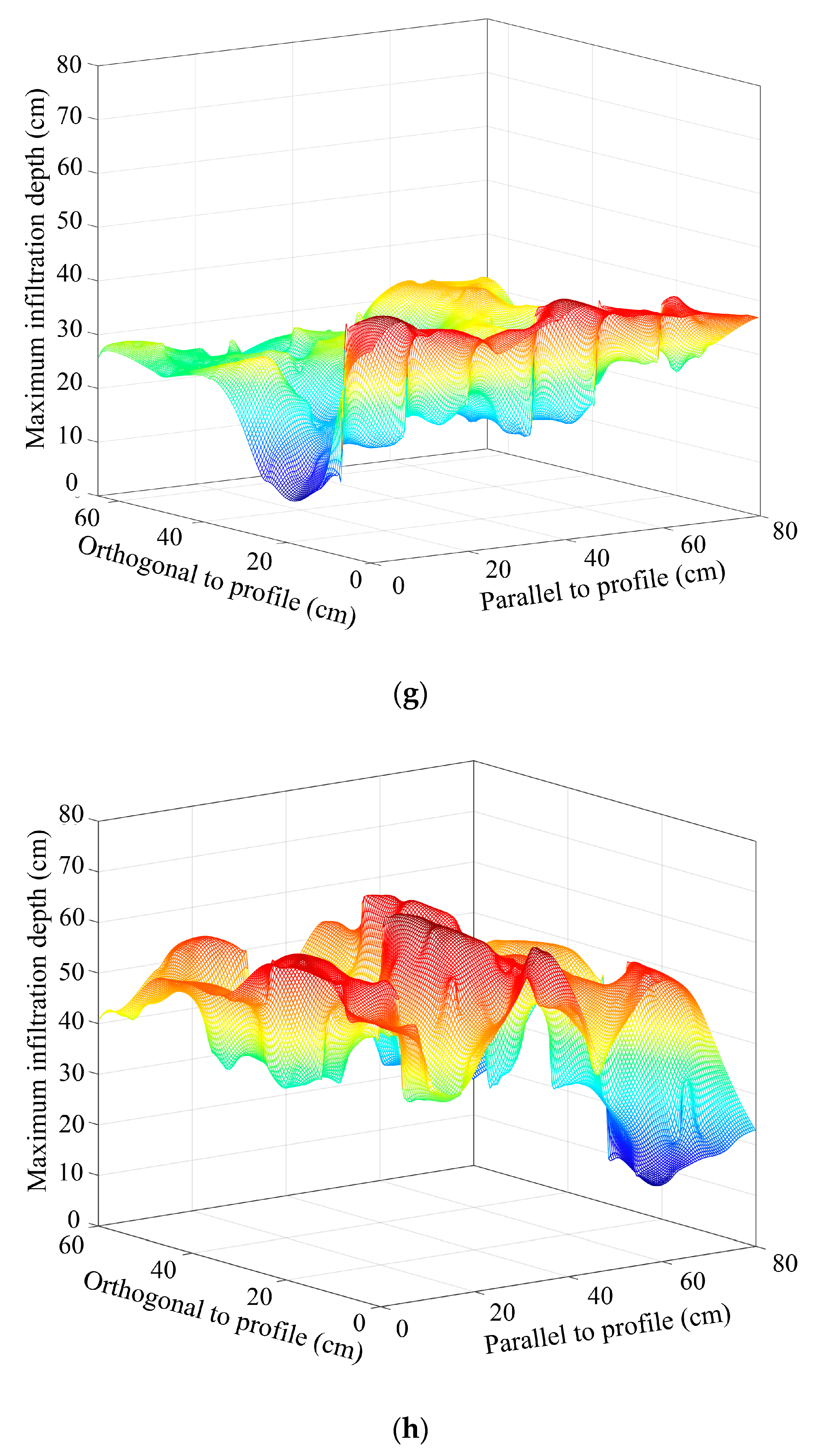
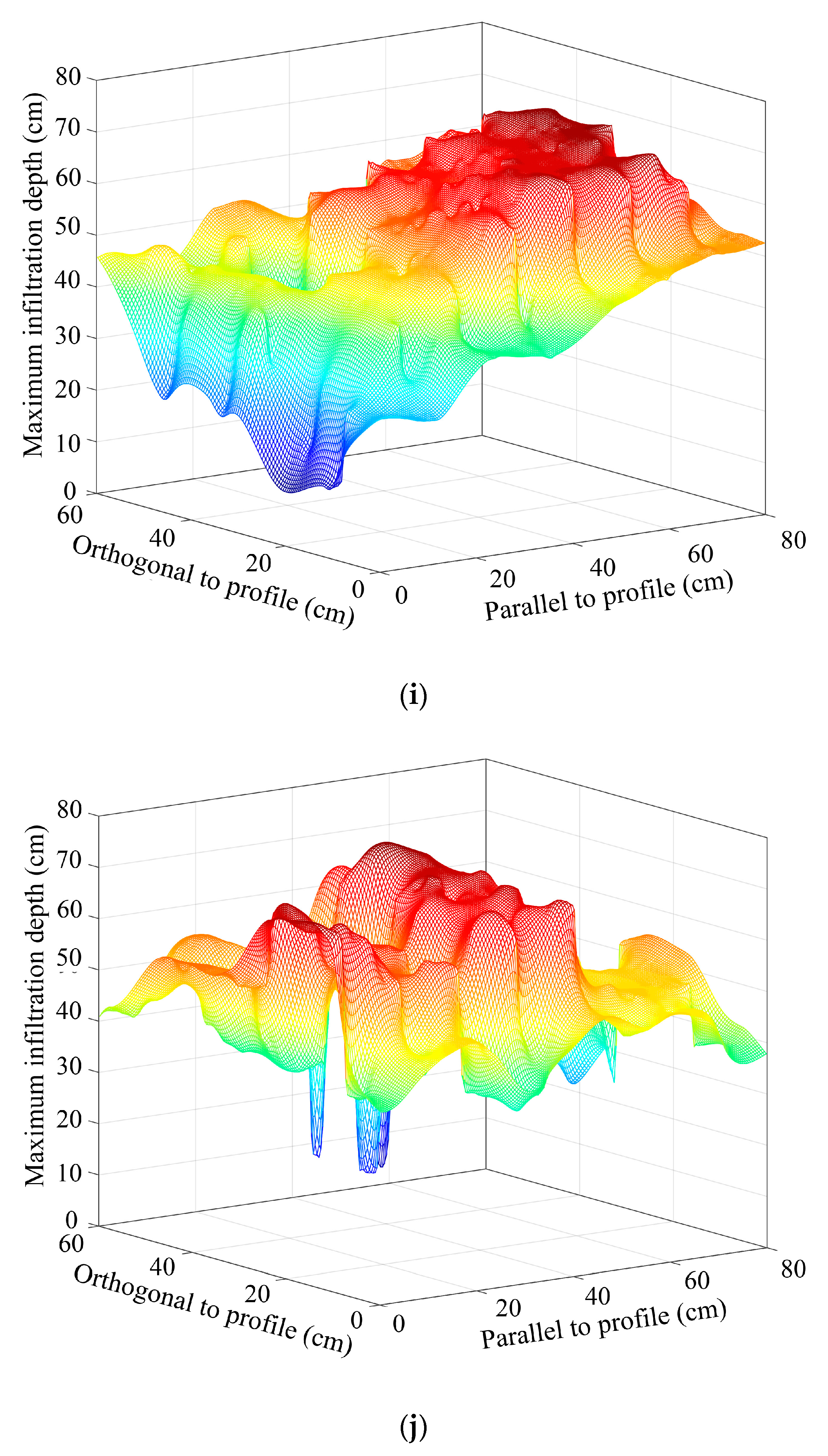
3.2. Spatial Redistribution of Infiltration
3.3. Factors Impacting Preferential Flow and Infiltration Redistribution
4. Conclusions
- (1)
- With increasing hillslope position, the total dye coverage, maximum infiltration depth, and saturation steady infiltration rate all showed obvious increasing trends; the contribution of preferential flow to the actual water infiltration gradually increased with plot elevation, whereby the value of the mean preferential flow fraction (PF-fr) was 0.10, 0.11, 0.15, 0.29, and 0.26 for the bottom–, lower–, mid–, upper–, and top–slope positions, respectively.
- (2)
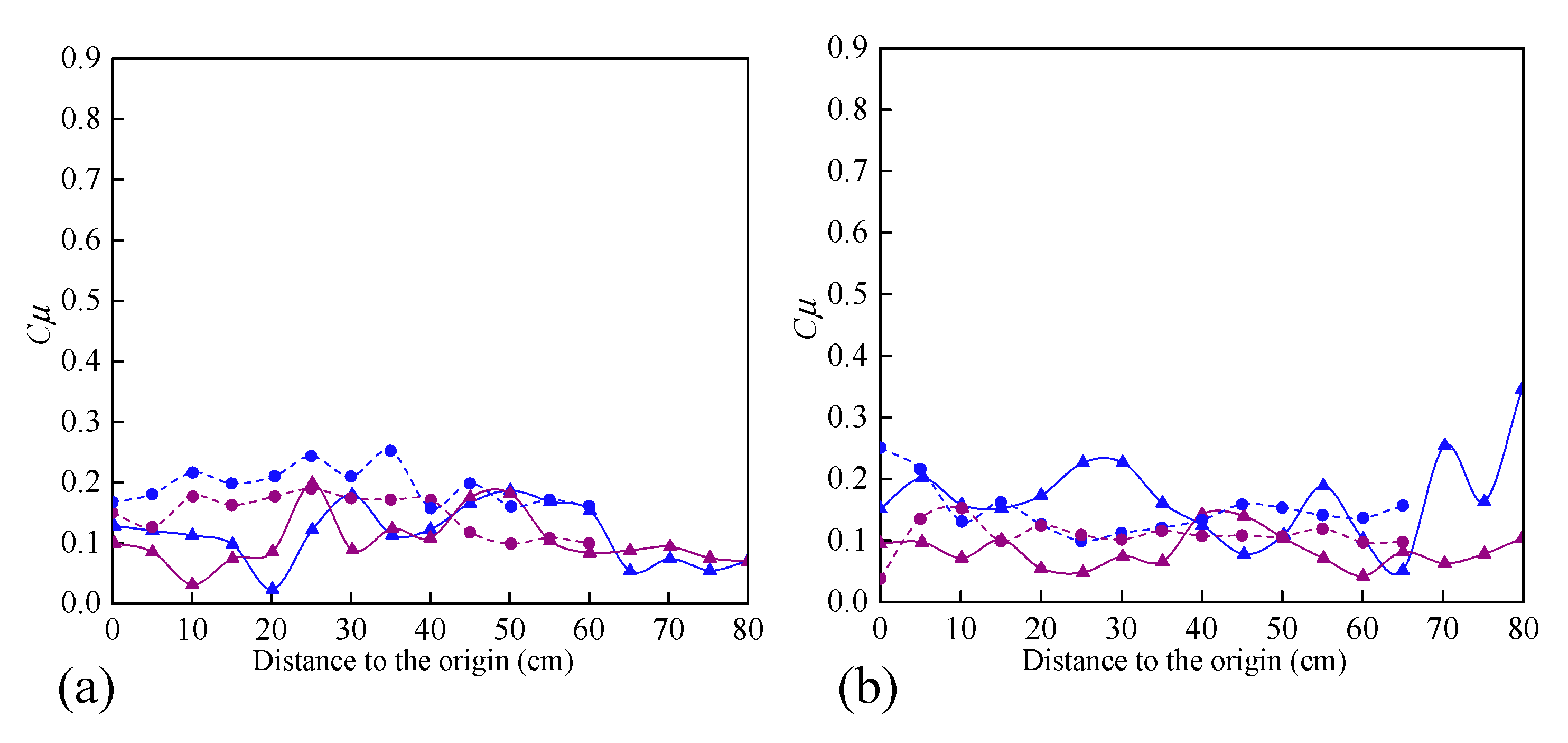
- The non–uniformity of the spatial redistribution of the soil water infiltration gradually increased with the rise in hillslope position. The mean non-uniformity coefficient (Cμ) of the actual water infiltration maximum depth at the bottom–, lower–, mid–, upper–, and top–slope positions was 0.12, 0.12, 0.14, 0.16, and 0.24 in orthogonal direction to the stained section, and 0.10, 0.08, 0.17, 0.15, and 0.19 in the parallel section direction, respectively. The dimension fraction (Df) value of the actual water infiltration wet front curve for five hillslope positions was 1.2015, 1.2561, 1.3257, 1.3525, and 1.4055 for the bottom–, lower–, mid–, upper–, and top–slope positions, respectively. Additionally, the degree of non–uniformity of the spatial redistribution for macropore flow revealed by the BBFCF dying pattern was larger than that of the actual water flow revealed by the KI–starch dying pattern.
- (3)
- The GMR, θsat, altitude, Ks, Φroot-stained were found to be the main positive factors impacting the degree of preferential flow and spatial non–uniformity of the infiltration redistribution. A lower BD and lower clay content could effectively promote preferential flow and the spatial distribution of heterogeneity.
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, N.; Yu, F.; Li, C.; Wang, H.; Liu, J.; Mu, W. Investigation of rainfall–runoff processes and soil moisture dynamics in grassland plots under simulated rainfall conditions. Water 2014, 6, 2671–2689. [Google Scholar] [CrossRef] [Green Version]
- Mu, W.; Yu, F.; Li, C.; Xie, Y.; Tian, J.; Liu, J.; Zhao, N. Effects of rainfall intensity and slope gradient on runoff and soil moisture content on different growing stages of spring maize. Water 2015, 7, 2990–3008. [Google Scholar] [CrossRef] [Green Version]
- Allaire, S.E.; Roulier, S.; Cessna, A.J. Quantifying preferential flow in soils: A review of different techniques. J. Hydrol. 2009, 378, 179–204. [Google Scholar] [CrossRef]
- Beven, K.; Germann, P. Macropores and water flow in soils. Water Resour. Res. 1982, 18, 1311–1325. [Google Scholar] [CrossRef] [Green Version]
- Capuliak, J.; Pichler, V.; Flühler, H.; Pichlerová, M.; Homolák, M. Beech forest density control on the dominant water flow types in andic soils. Vadose Zone J. 2010, 9, 747–756. [Google Scholar] [CrossRef]
- Alaoui, A.; Caduff, U.; Gerke, H.H.; Weingartner, R. Preferential flow effects on infiltration and runoff in grassland and forest soils. Vadose Zone J. 2011, 10, 367–377. [Google Scholar] [CrossRef]
- Peters, D.L.; Buttle, J.M.; Taylor, C.H.; LaZerte, B.D. Runoff production in a forested shallow soil, Canadian Shield basin. Water Resour. Res. 1995, 31, 1291–1304. [Google Scholar] [CrossRef]
- Van der Heijden, G.; Legout, A.; Pollier, B.; Bréchet, C.; Ranger, J.; Dambrine, E. Tracing and modeling preferential flow in a forest soil—Potential impact on nutrient leaching. Geoderma 2013, 195–196, 12–22. [Google Scholar] [CrossRef]
- Jarvis, N.; Etana, A.; Stagnitti, F. Water repellency, near–saturated infiltration and preferential solute transport in a macroporous clay soil. Geoderma 2008, 143, 223–230. [Google Scholar] [CrossRef]
- Jomaa, S.; Barry, D.A.; Heng, B.C.P.; Brovelli, A.; Sander, G.C.; Parlange, J.Y. Effect of antecedent conditions and fixed rock fragment coverage on soil erosion dynamics through multiple rainfall events. J. Hydrol. 2013, 484, 115–127. [Google Scholar] [CrossRef]
- Zhang, J.; Lei, T.; Qu, L.; Chen, P.; Gao, X.; Chen, C.; Yuan, L.; Zhang, M.; Su, G. Method to measure soil matrix infiltration in forest soil. J. Hydrol. 2017, 552, 241–248. [Google Scholar] [CrossRef]
- Bouma, J.; Belmans, C.F.M.; Dekker, L.W. Water infiltration and redistribution in a silt loam subsoil with vertical worm channels1. Soil Sci. Soc. Am. J. 1982, 46, 917–921. [Google Scholar] [CrossRef]
- Ritsema, C.J.; Dekker, L.; Hendrickx, J.M.H.; Hamminga, W. Preferential flow mechanism in a water repellent sandy soil. Water Resour. Res. 1993, 29, 2183–2194. [Google Scholar] [CrossRef]
- Gerke, H.H. Preferential flow descriptions for structured soils. J. Plant Nutri. Soil Sci. 2006, 169, 382–400. [Google Scholar] [CrossRef]
- Weiler, M.; Flühler, H. Inferring flow types from dye patterns in macroporous soils. Geoderma 2004, 120, 137–153. [Google Scholar] [CrossRef]
- Hagedorn, F.; Bundt, M. The age of preferential flow paths. Geoderma 2002, 108, 119–132. [Google Scholar] [CrossRef]
- Sheng, F.; Wang, K.; Zhang, R.; Liu, H. Characterizing soil preferential flow using iodine—Starch staining experiments and the active region model. J. Hydrol. 2009, 367, 115–124. [Google Scholar] [CrossRef] [Green Version]
- Weiler, M.; Naef, F. Simulating surface and subsurface initiation of macropore flow. J. Hydrol. 2003, 273, 139–154. [Google Scholar] [CrossRef]
- Alaoui, A.; Helbling, A. Evaluation of soil compaction using hydrodynamic water content variation: Comparison between compacted and non–compacted soil. Geoderma 2006, 134, 97–108. [Google Scholar] [CrossRef]
- Kan, X.; Cheng, J.; Hu, X.; Zhu, F.; Li, M. Effects of grass and forests and the infiltration amount on preferential flow in karst regions of China. Water 2019, 11, 1634. [Google Scholar] [CrossRef] [Green Version]
- Mei, X.; Zhu, Q.; Ma, L.; Zhang, D.; Wang, Y.; Hao, W. Effect of stand origin and slope position on infiltration pattern and preferential flow on a Loess hillslope. Land Degrad. Dev. 2018, 29, 1353–1365. [Google Scholar] [CrossRef]
- Dadkhah, M.; Gifford, G.F. Influence of vegetation, rock cover, and trampling on infiltration rates and sediment production. J. Am. Water Resour. Assoc. 1980, 16, 979–986. [Google Scholar] [CrossRef]
- Liu, C.; Cheng, S.; Yu, W.; Chen, S. Water infiltration rate in cracked paddy soil. Geoderma 2003, 117, 169–181. [Google Scholar] [CrossRef]
- Navar, J.; Mendez, J.; Bryan, R.B.; Kuhn, N.J. The contribution of shrinkage cracks to bypass flow during simulated and natural rainfall experiments in northeastern Mexico. Can. J. Soil Sci. 2002, 82, 65–74. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Shao, M.A.; Jia, Y. Effects of activities of ants (Camponotus japonicus) on soil moisture cannot be neglected in the northern Loess Plateau. Agric. Eco. Environ. 2017, 239, 182–187. [Google Scholar] [CrossRef]
- Bargués Tobella, A.; Reese, H.; Almaw, A.; Bayala, J.; Malmer, A.; Laudon, H.; Ilstedt, U. The effect of trees on preferential flow and soil infiltrability in an agroforestry parkland in semiarid Burkina Faso. Water Resour. Res. 2014, 50, 3342–3354. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, B.B.; Shao, M.A.; Wang, Q.J.; Yang, T. Effects of different rock fragment contents and sizes on solute transport in soil columns. Vadose Zone J. 2011, 10, 386–393. [Google Scholar] [CrossRef]
- Oshun, J.; Dietrich, W.E.; Dawson, T.E.; Fung, I. Dynamic, structured heterogeneity of water isotopes inside hillslopes. Water Resour. Res. 2016, 52, 164–189. [Google Scholar] [CrossRef] [Green Version]
- Mol, L.; Viles, H.A. Geoelectric investigations into sandstone moisture regimes: Implications for rock weathering and the deterioration of San Rock Art in the Golden Gate Reserve, South Africa. Geomorphology 2010, 118, 280–287. [Google Scholar] [CrossRef]
- Katra, I.; Lavee, H.; Sarah, P. The effect of rock fragment size and position on topsoil moisture on arid and semi–arid hillslopes. Catena 2008, 72, 49–55. [Google Scholar] [CrossRef]
- Oostwoud Wijdenes, D.J.; Poesen, J. The effect of soil moisture on the vertical movement of rock fragments by tillage. Soil Tillage Res. 1999, 49, 301–312. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, M.; Niu, J.; Li, H.; Xiao, R.; Zheng, H.; Bech, J. Rock fragments and soil hydrological processes: Significance and progress. Catena 2016, 147, 153–166. [Google Scholar] [CrossRef]
- Sepaskhah, A.R.; Tafteh, A. Pedotransfer function for estimation of soil–specific surface area using soil fractal dimension of improved particle–size distribution. Arch. Agron. Soil Sci. 2013, 59, 93–103. [Google Scholar] [CrossRef]
- Hlaváčiková, H.; Holko, L.; Danko, M.; Novák, V. Estimation of macropore flow characteristics in stony soils of a small mountain catchment. J. Hydrol. 2019, 574, 1176–1187. [Google Scholar] [CrossRef]
- Nimmo, J.R.; Creasey, K.M.; Perkins, K.S.; Mirus, B.B. Preferential flow, diffuse flow, and perching in an interbedded fractured–rock unsaturated zone. Hydrogeol. J. 2017, 25, 421–444. [Google Scholar] [CrossRef]
- Fu, Z.Y.; Chen, H.S.; Zhang, W.; Xu, Q.X.; Wang, S.; Wang, K.L. Subsurface flow in a soil–mantled subtropical dolomite karst slope: A field rainfall simulation study. Geomorphology 2015, 250, 1–14. [Google Scholar] [CrossRef]
- Corwin, D.L.; David, A.; Goldberg, S. Mobility of arsenic in soil from the Rocky Mountain Arsenal area. J. Contam. Hydrol. 1999, 39, 35–58. [Google Scholar] [CrossRef]
- Han, S.; Yang, Y.; Fan, T.; Xiao, D.; Moiwo, J.P. Precipitation–runoff processes in Shimen hillslope micro–catchment of Taihang Mountain, north China. Hydrol. Process. 2012, 26, 1332–1341. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, X.; Jia, G.; Jia, J.; Lou, Y.; Lu, W. Contrasting water sources of evergreen and deciduous tree species in rocky mountain area of Beijing, China. Catena 2017, 150, 108–115. [Google Scholar] [CrossRef]
- Du, J.; Jia, Y.; Hao, C.; Qiu, Y.; Niu, C.; Liu, H. Temporal and spatial changes of blue water and green water in the Taihang Mountain Region, China, in the past 60 years. Hydrol. Sci. J. 2019, 64, 2040–2056. [Google Scholar] [CrossRef]
- Xu, F.; Jia, Y.; Peng, H.; Niu, C.; Liu, J.; Hao, C.; Huang, G. Vertical zonality of the water cycle and the impact of land–use change on runoff in the Qingshui River Basin of Wutai Mountain, China. Hydrol. Sci. J. 2019, 64, 2080–2092. [Google Scholar] [CrossRef]
- Li, F.; Song, X.; Tang, C.; Liu, C.; Yu, J.; Zhang, W. Tracing infiltration and recharge using stable isotope in Taihang Mt., North China. Environ. Geol. 2007, 53, 687–696. [Google Scholar] [CrossRef]
- Song, X.; Wang, P.; Yu, J.; Liu, X.; Liu, J.; Yuan, R. Relationships between precipitation, soil water and groundwater at Chongling catchment with the typical vegetation cover in the Taihang mountainous region, China. Environ. Earth Sci. 2011, 62, 787–796. [Google Scholar] [CrossRef]
- Yu, J.; Yang, C.; Liu, C.; Song, X.; Hu, S.; Li, F.; Tang, C. Slope runoff study in situ using rainfall simulator in mountainous area of North China. J. Geogr. Sci. 2009, 19, 461–470. [Google Scholar] [CrossRef]
- Flury, M.; Flühler, H.; Jury, W.A.; Leuenberger, J. Susceptibility of soils to preferential flow of water—A field study. Water Resour. Res. 1994, 30, 1945–1954. [Google Scholar] [CrossRef]
- Sheng, F.; Liu, H.; Zhang, R.; Wang, K. Determining the active region model parameter from dye staining experiments for characterizing the preferential flow heterogeneity in unsaturated soils. Environ. Earth Sci. 2012, 65, 1977–1985. [Google Scholar] [CrossRef]
- Bamutaze, Y.; Tenywa, M.M.; Majaliwa, M.J.G.; Vanacker, V.; Bagoora, F.; Magunda, M.; Obando, J.; Wasige, J.E. Infiltration characteristics of volcanic sloping soils on Mt. Elgon, Eastern Uganda. Catena 2010, 80, 122–130. [Google Scholar] [CrossRef]
- Van Schaik, N.L.M.B. Spatial variability of infiltration patterns related to site characteristics in a semi–arid watershed. Catena 2009, 78, 36–47. [Google Scholar] [CrossRef]
- Gerke, K.M.; Sidle, R.C.; Mallants, D. Preferential flow mechanisms identified from staining experiments in forested hillslopes. Hydrol. Process. 2015, 29, 4562–4578. [Google Scholar] [CrossRef]
- Mandelbrot, B. How long is the coast of Britain? Statistical self–similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [Green Version]
- Tyler, S.W.; Wheatcraft, S.W. Fractal scaling of soil particle–size distributions: Analysis and limitations. Soil Sci. Soc. Am. J. 1992, 56, 362–369. [Google Scholar] [CrossRef]
- Falconer, K. Fractal Geometry—Mathematical Foundations and Applications, 4th ed.; Northeastern University Press: Shenyang, China, 1996; pp. 56–77. [Google Scholar]
- Flury, M. Dyes as tracers for vadose zone hydrology. Rev. Geophys. 2003, 41, 2. [Google Scholar] [CrossRef]
- Germán–Heins, J.; Flury, M. Sorption of Brilliant Blue FCF in soils as affected by pH and ionic strength. Geoderma 2000, 97, 87–101. [Google Scholar] [CrossRef]
- Jiang, X.; Liu, X.; Wang, E.; Li, X.G.; Sun, R.; Shi, W. Effects of tillage pan on soil water distribution in alfalfa–corn crop rotation systems using a dye tracer and geostatistical methods. Soil Tillage Res. 2015, 150, 68–77. [Google Scholar] [CrossRef]
- Liu, C.L.; Wu, Y.Z.; Liu, Q.J. Effects of land use on spatial patterns of soil properties in a rocky mountain area of Northern China. Arab. J. Geosci. 2015, 8, 1181–1194. [Google Scholar] [CrossRef]
- Öhrström, P.; Persson, M.; Albergel, J.; Zante, P.; Nasri, S.; Berndtsson, R.; Olsson, J. Field–scale variation of preferential flow as indicated from dye coverage. J. Hydrol. 2002, 257, 164–173. [Google Scholar] [CrossRef]
- Laine-Kaulio, H.; Backnäs, S.; Koivusalo, H.; Laurén, A. Dye tracer visualization of flow patterns and pathways in glacial sandy till at a boreal forest hillslope. Geoderma 2015, 259–260, 23–34. [Google Scholar]
- Yunusa, I.A.M.; Mele, P.M.; Rab, M.A.; Schefe, C.R.; Beverly, C.R. Priming of soil structural and hydrological properties by native woody species, annual crops, and a permanent pasture. Aust. J. Soil. Res 2002, 40, 207–219. [Google Scholar] [CrossRef]





| Plot | Altitude (m) | Hillslope Position | Hillslope Aspect | Hillslope Gradient (°) | Main Plant Type | Φroot (‰) | Φroot-stained (‰) | Droot (cm) | Land Coverage (%) |
|---|---|---|---|---|---|---|---|---|---|
| A | 101 | Bottom | SW | 5 | DT: Platycladus orientalis CT: Robinia pseudoacacia Linn. S: Ziziphus jujuba Mill | 11.09 ± 1.11 | 2.07 ± 0.73 | 55 | 85 |
| B | 126 | Lower | SW | 17 | DT: Platycladus orientalis CT: Robinia pseudoacacia Linn. S: Ziziphus jujuba Mill | 8.87 ± 1.45 | 1.88 ± 0.55 | 48 | 80 |
| C | 163 | Middle | SW | 29 | DT: Platycladus orientalis S: Ziziphus jujuba Mill, Vitex negundo L. | 3.59 ± 0.71 | 2.97 ± 0.43 | 35 | 80 |
| D | 184 | Upper | SW | 25 | DT: Platycladus orientalis S: Ziziphus jujuba Mill, Vitex negundo L. | 9.26 ± 1.22 | 8.40 ± 1.49 | 39 | 75 |
| E | 203 | Top | SW | 21 | DT: Platycladus orientalis S: Ziziphus jujuba Mill, Vitex negundo L. | 8.39 ± 1.61 | 7.87 ± 0.79 | 50 | 70 |
| Plot | ST (cm) | BD (g/cm3) | GMR (%) | Ks (mm/min) | FC (%) | θint (%) | θsat (%) | Particle Size | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Clay < 0.002 mm (%) | Silt 0.002–0.02 mm (%) | Sand 0.002–2 mm (%) | ||||||||
| A | 95 | 1.72 ± 0.09 a | 4.36 ± 0.16 a | 0.47 ± 0.05 a | 19.85 ± 1.28 a | 13.08 ± 1.75 a | 25.08 ± 3.77 a | 22.38 ± 1.18 a | 47.87 ± 1.28 a | 29.58 ± 2.42 a |
| B | 43 | 1.73 ± 0.02 a | 31.88 ± 11.05 b | 0.54 ± 0.07 a,b | 21.54 ± 4.21 a | 11.89 ± 0.73 a | 24.62 ± 3.73 a | 29.73 ± 1.14 a,b | 44.61 ± 1.81 a | 23.10 ± 2.89 b |
| C | 38 | 1.6 ± 0.09 a | 74.18 ± 6.64 c | 0.72 ± 0.69 a,b | 18.69 ± 2.08 a | 14.49 ± 2.25 a | 26.72 ± 2.82 a | 13.85 ± 1.98 b | 32.53 ± 3.45 a | 46.83 ± 1.21 c |
| D | 25 | 1.54 ± 0.19 a | 83.73 ± 9.33 c | 0.81 ± 0.26 a,b | 21.48 ± 0.86 a | 12.74 ± 4.41 a | 29.80 ± 3.56 a | 10.76 ± 2.11 c | 27.56 ± 2.77 b | 46.66 ± 4.21 c |
| E | 16.5 | 1.53 ± 0.19 a | 77.49 ± 8.03 c | 1.24 ± 0.80 b | 19.78 ± 1.76 a | 13.62 ± 2.77 a | 30.39 ± 8.85 a | 14.43 ± 2.51 d | 29.96 ± 4.10 b | 45.51 ± 2.18 c |
| BBFCF | KI–Starch | ||||||
|---|---|---|---|---|---|---|---|
| Plot | Ave. Cμ | Ran. Cμ | Std. Cμ | Ave. Cμ | Ran. Cμ | Std. Cμ | |
| InOrD | A | 0.22 | 0.11 | 0.03 | 0.12 | 0.10 | 0.07 |
| B | 0.17 | 0.17 | 0.04 | 0.12 | 0.13 | 0.03 | |
| C | 0.32 | 0.27 | 0.08 | 0.14 | 0.13 | 0.03 | |
| D | 0.35 | 0.44 | 0.14 | 0.16 | 0.23 | 0.06 | |
| E | 0.41 | 0.42 | 0.13 | 0.24 | 0.25 | 0.07 | |
| InPaD | A | 0.11 | 0.16 | 0.05 | 0.10 | 0.17 | 0.04 |
| B | 0.19 | 0.294 | 0.07 | 0.08 | 0.12 | 0.03 | |
| C | 0.23 | 0.44 | 0.12 | 0.17 | 0.19 | 0.07 | |
| D | 0.32 | 0.79 | 0.14 | 0.15 | 0.36 | 0.06 | |
| E | 0.38 | 0.83 | 0.21 | 0.19 | 0.48 | 0.11 | |
| BBFCF | KI–Starch | |||
|---|---|---|---|---|
| Plot | Df | R2 | Df | R2 |
| A | 1.21 ± 0.03 | 0.9952 | 1.20 ± 0.06 | 0.9941 |
| B | 1.27 ± 0.02 | 0.9946 | 1.26 ± 0.04 | 0.9959 |
| C | 1.39 ± 0.03 | 0.9904 | 1.33 ± 0.04 | 0.9940 |
| D | 1.43 ± 0.03 | 0.9892 | 1.35 ± 0.05 | 0.9924 |
| E | 1.45 ± 0.05 | 0.9868 | 1.41 ± 0.06 | 0.9938 |
| Altitude (m) | Slope Gradient (°) | ST (cm) | BD (g·cm−3) | GMR (%) | Ks (mm·min−1) | FC (%) | θint (%) | θsat (%) | Clay (%) | Silt (%) | Sand (%) | Φroot (‰) | Φroot-stained (‰) | Droot (cm) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BBFCF | TotDC | 0.753 | 0.413 | −0.558 | −0.839 | 0.706 | 0.619 | 0.239 | 0.095 | 0.906 * | −0.809 | −0.809 | 0.729 | 0.130 | 0.956 * | −0.305 |
| MaxID | 0.941 * | 0.858 | −0.814 | −0.962 ** | 0.974 ** | 0.782 | −0.270 | 0.593 | 0.855 | −0.982 ** | −0.891 * | 0.954 * | −0.574 | 0.764 | −0.680 | |
| UniID | −0.930 * | −0.655 | 0.734 | 0.987 ** | −0.897 * | −0.808 | 0.069 | −0.410 | −0.972 ** | 0.961 ** | 0.921 * | −0.917 * | 0.228 | −0.938 * | 0.473 | |
| Ave.Cμ in PaD | 0.924 * | 0.585 | −0.680 | −0.974 ** | 0.839 | 0.902 * | −0.310 | 0.587 | 0.950 * | −0.893 * | −0.901 * | 0.923 * | −0.296 | 0.861 | −0.346 | |
| Ave.Cμ in OrD | 0.984 ** | 0.631 | −0.866 | −0.952 * | 0.880 * | 0.949 * | −0.005 | 0.297 | 0.966 ** | −0.733 | −0.908 * | 0.782 | −0.207 | 0.924 * | −0.315 | |
| Std.Cμ in PaD | 0.949 * | 0.669 | −0.814 | −0.968 ** | 0.908 * | 0.819 | 0.086 | 0.262 | 0.974 ** | −0.840 | −0.957 * | 0.843 | −0.176 | 0.964 ** | −0.456 | |
| Std.Cμ in OrD | 0.967 ** | 0.600 | −0.813 | −0.941 * | 0.845 | 0.984 ** | −0.188 | 0.442 | 0.936 * | −0.734 | −0.872 | 0.803 | −0.281 | 0.855 | −0.268 | |
| Df | 0.990 ** | 0.746 | −0.895 * | −0.976 ** | 0.979 ** | 0.861 | −0.114 | 0.441 | 0.913 * | −0.984 ** | −0.824 | 0.888 * | −0.452 | 0.846 | −0.579 | |
| KI–starch | TotDC | 0.964 ** | 0.796 | −0.919 * | −0.936 * | 0.961 ** | 0.793 | 0.129 | 0.222 | 0.908 * | −0.967 ** | −0.761 | 0.800 | −0.313 | 0.894 * | −0.571 |
| MaxID | 0.932 * | 0.810 | −0.767 | −0.973 ** | 0.973 ** | 0.792 | −0.305 | 0.625 | 0.875 | −0.975 ** | −0.891 * | 0.954 * | −0.533 | 0.781 | −0.638 | |
| UniID | 0.790 | 0.245 | −0.636 | −0.781 | 0.603 | 0.833 | 0.276 | −0.034 | 0.918 * | −0.685 | −0.564 | 0.536 | 0.275 | 0.954 * | 0.053 | |
| Ave.Cμ in PaD | 0.820 | 0.289 | −0.637 | −0.780 | 0.598 | 0.977 ** | −0.171 | 0.324 | 0.849 | −0.532 | −0.644 | 0.590 | −0.027 | 0.777 | 0.096 | |
| Ave.Cμ in OrD | 0.397 | 0.035 | −0.560 | −0.214 | 0.211 | 0.494 | 0.654 | −0.590 | 0.379 | 0.192 | −0.182 | −0.153 | 0.383 | 0.471 | 0.301 | |
| Std.Cμ in PaD | 0.907 * | 0.442 | −0.724 | −0.918 * | 0.766 | 0.903 * | 0.081 | 0.203 | 0.989 ** | −0.740 | −0.838 | 0.736 | 0.032 | 0.981 ** | −0.156 | |
| Std.Cμ in OrD | 0.625 | 0.052 | −0.570 | −0.514 | 0.358 | 0.827 | 0.212 | −0.128 | 0.668 | −0.160 | −0.385 | 0.205 | 0.285 | 0.673 | 0.360 | |
| Df | 0.997 ** | 0.746 | −0.895 * | −0.962 ** | 0.935 * | 0.934 * | −0.136 | 0.429 | 0.922 * | −0.940 * | 0.762 | 0.839 | −0.398 | 0.847 | −0.447 | |
| PF–fr | 0.877 | 0.541 | −0.728 | −0.912 * | 0.818 | 0.754 | 0.216 | 0.127 | 0.962 ** | −0.890 * | 0.799 | 0.765 | 0.007 | 0.989 ** | −0.353 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.-y.; Jia, Y.-w.; Gong, J.-g.; Niu, C.-w.; Su, H.-d.; Gan, Y.-d.; Liu, H. Spatial Variability of Preferential Flow and Infiltration Redistribution along a Rocky-Mountain Hillslope, Northern China. Water 2020, 12, 1102. https://doi.org/10.3390/w12041102
Zhao S-y, Jia Y-w, Gong J-g, Niu C-w, Su H-d, Gan Y-d, Liu H. Spatial Variability of Preferential Flow and Infiltration Redistribution along a Rocky-Mountain Hillslope, Northern China. Water. 2020; 12(4):1102. https://doi.org/10.3390/w12041102
Chicago/Turabian StyleZhao, Si-yuan, Yang-wen Jia, Jia-guo Gong, Cun-wen Niu, Hui-dong Su, Yong-de Gan, and Huan Liu. 2020. "Spatial Variability of Preferential Flow and Infiltration Redistribution along a Rocky-Mountain Hillslope, Northern China" Water 12, no. 4: 1102. https://doi.org/10.3390/w12041102





