1. Introduction
Heavy rainfall, waves, storm surges, and high tides during cyclone (typhoon or hurricane) periods cause hazards, such as flooding/inundation and shoreline erosion in coastal areas. A full understanding of the behavior of water bodies and their movement in estuarine areas during cyclone periods is essential for flood control, disaster mitigation, coastal erosion protection, and coastal structure preservation. Integrated coastal and estuarine process models (ICEPM) can simulate multiple physical processes, such as tides, waves, surges, river flows, wind, sediment transport, and morphological changes, e.g., [
1,
2,
3,
4,
5]. They are applicable to study hydrodynamic and morphodynamic processes in response to what-if scenarios of coastal protection practices, and, therefore, facilitate safety assessment of estuarine areas and the determination of coastal management measures to prevent or reduce disasters and to stabilize shorelines.
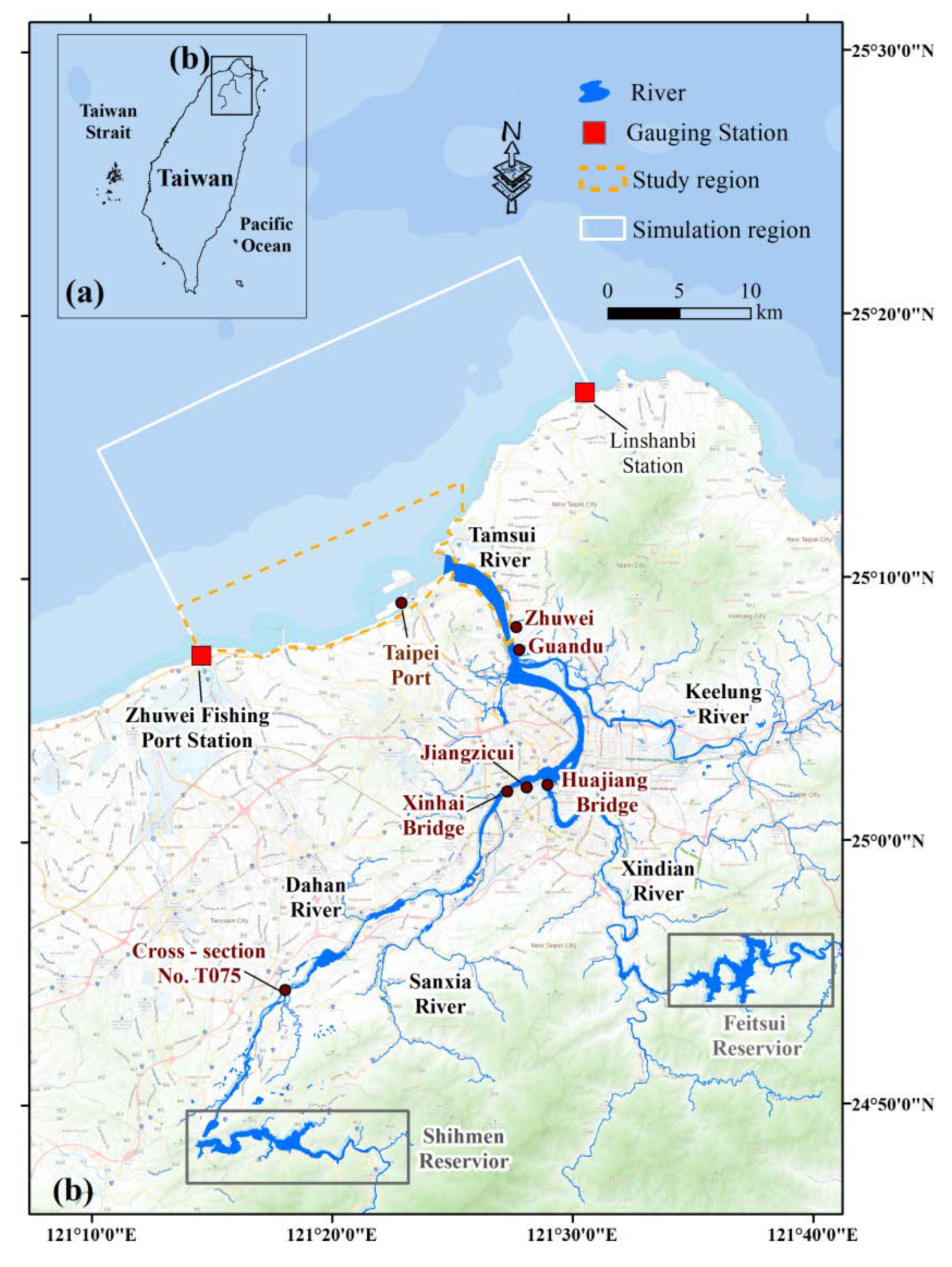
Surrounded by seas on all sides, Taiwan is subjected to 3–4 typhoons on average per year. The Tamsui River is the largest river in northern Taiwan, and variations of erosion and deposition on the river bed are closely related to flows and sediment transport in the adjacent marine waters (
Figure 1). In recent years, owing to the construction of the Taipei Port, the littoral drift in the estuary and adjacent coastal areas has been gradually changed, which affects the adjacent coastal terrain and landscape [
6]. In addition, serious siltation occurs in the Shihmen Reservoir upstream of the Tamsui River, with the total siltation in the Shihmen Reservoir reaching 1.86 million m
3 by the beginning of 2017—a volume accounting for 32.6% of the designed water-storage capacity of the reservoir [
7]. To alleviate the reservoir siltation problem, meet the industrial water demand, and extend the reservoir life, the Water Resources Agency of the Ministry of Economic Affairs plans to add a desilting tunnel under the water storage limit of the Shihmen Reservoir at the Amuping and Dawanping areas [
8]. The Amuping desilting tunnel is expected to be completed by 2022, and it will lead to changes in the amount of sediment transport in the Tamsui River and indirectly affect the sediment transport equilibrium between the river and the sea.
For assessing the impact of sediment management plans, such as reservoir sediment flushing, on the sediment transport and morphological changes in the Tamsui River Estuary and its adjacent coasts, it is necessary to apply numerical models to predict the spatiotemporal redistribution of sediments from the reservoir into the areas downstream. For this impact assessment of sediment flushing, it is important to apply a validated numerical model, which can demonstrate its capability to reproduce flows, waves, sediment transport, and morphological changes in the estuary. This requires integrated coastal and estuarine processes modeling by taking into account all the hydrological forces, such as river flows, tides, waves, storm surges, and wind-induced currents, along with the movement of sediment in the river and that flushed from the reservoir.
In the shallow coastal zone, the flow near the bottom, which drives sediment transport and causes bed changes, is composed mainly of wave motion and mean currents. The mean current in coasts and estuaries may be a combination of tidal flows, river flows, wave-phase-averaged currents, etc. Interaction of wave and current is a highly nonlinear process, particularly in coastal and estuarine areas. Since the 1970s, many studies have been conducted by experimental methods to explain the wave–current boundary layer interaction ([
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23]) on the theoretical side. Wave–current interaction can be simulated by using the so-called wave-phase-resolving numerical models [
24,
25], which are usually computationally costly. For long-term and large-scale simulations, the phase-averaged models [
26,
27] are often used to provide engineering answers to coastal problems, such as dredging, erosion, flooding/inundation, etc.
It is important to simulate sediment transport and morphological changes by taking into account the combination of wave and current. The high shear velocity within the bottom boundary layer produces strong turbulence and large bed shear stresses impacting on the current, bringing increased bottom resistance in the presence of combined flow [
28]. Hence, the combined wave-current flow is the basic element on sediment transport, mixing processes, diffusion, and other important coastal phenomena. Therefore, some researchers determine physical mechanisms by analyzing the combined flow over smooth or rough beds, both experimentally and numerically [
29,
30].
By developing the numerical models and experiments, researchers have analyzed that the sandpit morphodynamics might be caused by wave transformation, refraction, and diffraction induced by the pit itself. Van Rijn [
31] developed a mathematical model to predict the sedimentation of dredged channels by waves and currents. Roos et al. [
32] developed an idealized process-based morphodynamic model for the evolution of large-scale sandpits in a tide-dominated offshore environment. Benedet and List [
33] use a numerical model to evaluate the effects of bathymetric features, such as dredged borrow areas, on the formation of erosion hot spots. Faraci et al. [
34] conducted experimental to explain the possibility of exploiting sandpits at intermediate and shallow water depths.
Most of the existing storm-surge models can be used to simulate the storm surge-induced coastal flooding, such as the POM (Princeton Ocean Model) [
35], SLOSH (Sea, Lake and Overland Surges from Hurricanes) [
36,
37], and SHORECIRC (Quasi-3D NearSHORE CIRCulation Model) [
38,
39] models, but they are unable to consider sediment transport processes and bed variations when simulating coastal hydrodynamics. Since 1996, scholars have developed the ICEPM to simulate dynamic changes in coastal morphology, including shoreline changes, erosion, barrier breaching, and dam break [
1,
40,
41,
42,
43]. This model is an integrated product of the wave spectrum, tidal current with wave effects (considering the radiation stress effect), sediment transport, and bed variation models with the computing process. By introducing an empirical sediment transport formula, the ICEPM allows calculating long-term morphological changes [
2,
3], whereas the computational period and relevant parameters need to be verified using actual data of morphological changes. Some researchers also estimate long-term changes in estuaries and lagoons using empirical semi-numerical approaches, such as tidal averaging and rapid morphologic assessment [
4]. However, such types of tidal-averaging models mostly adopt the tidal phase averaging for computing, and thus, are unable to effectively simulate the maximum waves and surges caused by a typhoon and the resulting flooding event. Moreover, the abundant rainfall brought by a typhoon will lead to an increase in the upstream flood volume, which in turn will transport more sediment to the estuary, thereby making the estuarine flow field more complicated. To find maximum sedimentation and erosion is one of the important tasks in the impact assessment of hazardous typhoons and sediment flushing operations upstream the estuary. For the purpose, it is necessary to simulate all the hydrodynamic and morphodynamic processes in the estuary, including wave dynamics, river hydrology, oceanography, and sediment transport mechanics.
CCHE2D-Coast [
5,
44] is an integrated ICEPM model, capable of simulating these multiple coastal and estuarine processes. By using empirical sediment transport formulas, this model can simulate sediment transport driven by waves and currents in coasts and estuaries, and, therefore, enable the simulation of morphological changes in a wide region from the river upstream to the river mouth, and coasts. Through many years of development, validation, and improvement, this model demonstrated its applicability to help engineering planning and design of coastal flood and erosion protection by considering complex hydrological and morphological conditions in estuaries [
3,
5,
45]. The wave model of CCHE2D-Coast has the following major features: (1) It simulates deformation and transformation of irregular waves in coastal and estuarine conditions, including wave breaking, refraction, diffraction, and interaction of wave and current at river mouth [
27]; (2) it considers the effect of wave roller due to breaking to compute more accurate radiation stresses to include the effect of varying vertical mean current structure in the surf zone. The sediment transport model takes into account the effect of combined waves and currents in an estuary [
5]. This model has been successfully applied to study the sediment transport and flood flows in the Touchien River Estuary, Hsinchu, Taiwan, and it has provided numerical results of flow and morphological changes under the conditions of various planning scenarios [
5,
45]. Therefore, this model was selected to simulate sediment transport and morphological changes in a river estuary such as Tamsui River Estuary, which are mainly driven by coastal waves, tidal currents, and river inflows.
Since the construction of the Taipei Port in 1993, the Tamsui River estuary has undergone changes in the type of sediment movement. According to the statistics of Shihmen Reservoir’s discharge and sediment delivery ratio during 2006–2017, the sediment delivery ratio has been tending to increase since the desilting tunnel of Shihmen Reservoir was put into use for the first time in 2013 [
8]. The Amuping desilting tunnel of Shihmen Reservoir is expected to be completed in 2022, and it will further change the conditions of the water-sediment at the Tamsui River estuary. Therefore, this study used CCHE2D-Coast to explore the changes in the scouring and aggradation of the Tamsui River estuary after the opening of the Amuping desilting tunnel.
The rest of the paper is organized as follows:
Section 2 provides a brief introduction of the integrated coastal and estuarine processes model, CCHE2D-Coast.
Section 3 gives more information on the model for the study area, the Tamsui River estuary.
Section 4 is for model validation and model skill assessment results by simulating hydrodynamic and morphological changes through the 2008 typhoon season.
Section 5 provides simulation results and discussions for sediment flushing from the Shihmen reservoir. Finally,
Section 6 concludes the paper and gives some preliminary suggestions on the management of flood and sediment in the estuary.
2. Brief Description of the Integrated Coastal and Estuarine Model
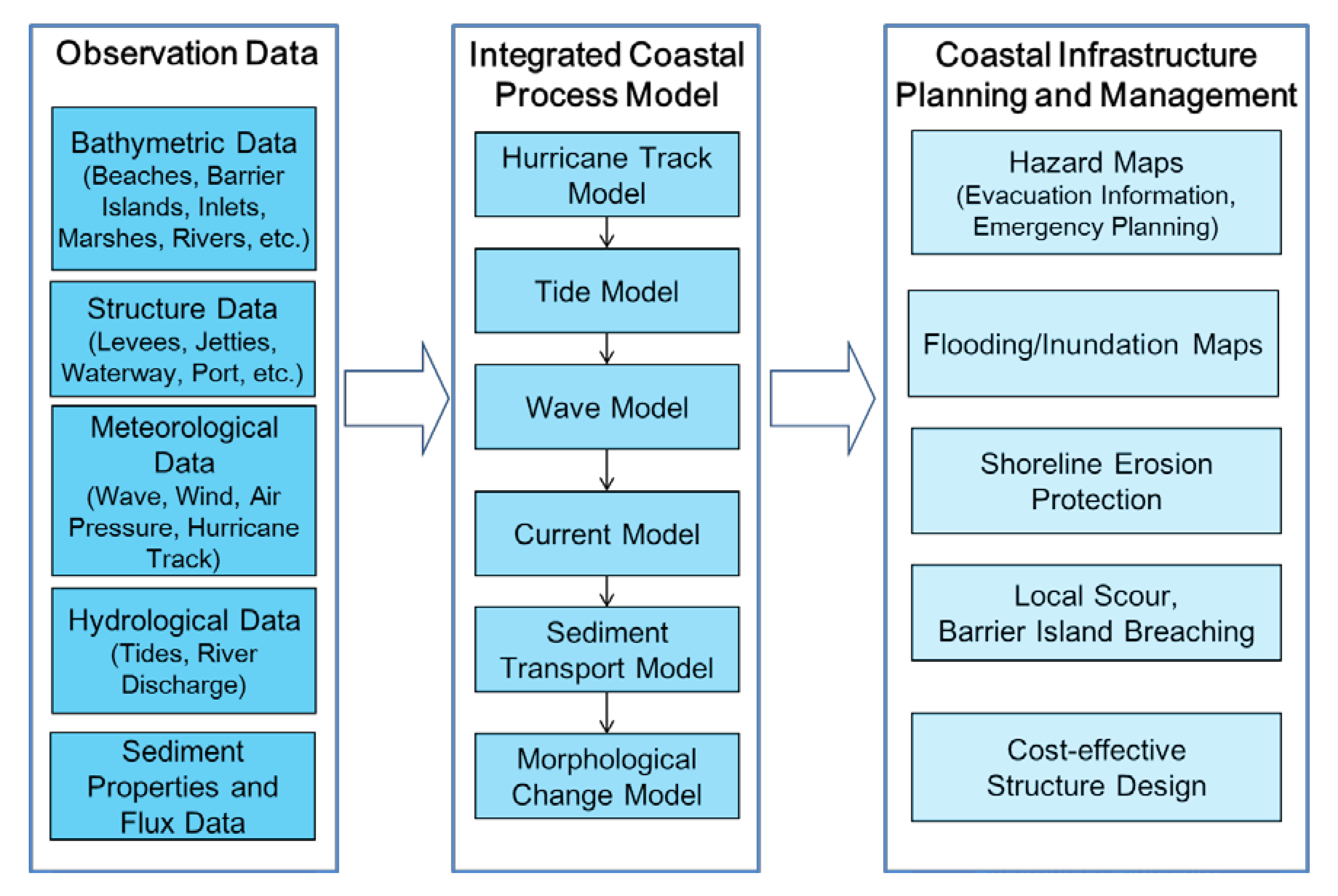
An integrated river/coastal/estuarine process modeling system, CCHE2D-Coast [
5,
44], was used to simulate the coupled hydrodynamic and morphodynamic processes driven by waves, tides, storm surges, and sediment transport for assessment of flooding and sedimentation in the Tamsui River Estuary (
Figure 2). CCHE2D-Coast contains a number of submodels for simulating the deformations and transformations of irregular/multidirectional waves, tropical cyclonic barometric pressure, and wind fields along storm tracks, tidal, and wave-induced currents, and morphological changes. For computing irregular waves, a multi-directional spectral wave action equation was adopted in the wave spectral module. It is capable of modeling wave deformation/transformation processes from deepwater to shallow water for nonbreaking and breaking waves, including wind-generated waves and whitecapping effects. For coastal structures, the wave model can take into account the transmission effect of wave energy through a permeable structure (e.g., a rubble mount breakwater). The flow model was used to simulate multi-scale hydrodynamic processes of free-surface water flows, such as river flows, tidal currents, nearshore currents, and storm surges. A non-orthogonal structured grid was used for all simulation models of waves, currents, sediment transport, and morphological changes.
In the current module, the two-dimensional (2-D) depth˗ and shortwave˗averaged shallow water equations with wave forcing were employed to simulate the flows driven by wave radiation stresses, tides, storm surges, river inflows, the Coriolis force, and turbulence in surf zones. This hydrodynamic model provides users with two options to calculate the wave radiation stresses: one is the traditional wave stress formulations by means of the sinusoidal wave assumption of the linear small-amplitude wave theory; another is the improved radiation stresses formulae derived from the non-sinusoidal wave assumption, which enables the three-dimensional (3-D) features of vertical current structures (e.g., surface rollers or undertow currents) in the surf zone to be taken into account [
44].
In the sediment transport submodel, empirical sediment transport models were used to calculate the sediment transport rates of bed materials and the suspended sediment under the conditions of combined waves and currents. A unified sediment transport model [
3] was used to calculate the sediment flux from upstream rivers to estuaries and coasts to consider the sediment transport seamlessly from the non-wave environment at a river to the wave–current interaction area at an estuary and a wave-dominant coastal zone. The local sediment transport rate vector
can be written as follows:
where
and
are the local sediment transport rates due to current and wave, respectively.
is the maximum bottom shear stress which has been modified to consider the difference of the stress in river flows and nearshore currents,
is the critical shear stress for moving bed materials,
is the water density, g is the gravitational acceleration,
is the velocity vector of mean current,
is the wave orbital velocity at the bottom,
and
are the empirical coefficient for sediment transport driven by mean currents and waves, respectively,
is a direction function (= −1 for offshore, +1 for onshore). By using computed mean velocity and wave orbital velocity, the maximum bottom stress is calculated as follows:
where
is the bottom friction coefficient due to current and wave [
44]. For detailed information on the sediment transport model, one may further refer to Ding and Wang (2007) [
3] and Ding et al. (2016) [
44].
Morphological changes were computed based on the mass balance of sediments, in which the diffusive transport for the anisotropic downslope gravitational effect was also included [
41]. The wetting and drying process was properly modeled to handle water level variations and bed changes.
This integrated processes model (CCHE2D-Coast) provides a variety of boundary conditions for computing wave actions, currents, sediment transport, and morphological changes. On the offshore boundary, wave spectral energy density was given by using the parametric wave spectrum defined by observed wave parameters in offshore buoys. Tidal levels were also specified on the offshore by using observed water level data or astronomical tidal level predictions. For river inflows upstream, hydrographs (time histories of discharge) can be given by observation data at hydrological stations or other model estimations. On the boundaries upstream for inputting river inflows, one may also give sediment transport fluxes based on measured (or planned) sediment release/flushing rates from hydraulic structures upstream, such as dams and reservoirs. The sediment transport fluxes can also be calculated by using a sediment transport formulation, such as Equation (1), by assuming the state of sediment transport through the boundaries is close to equilibrium. In general, it is assumed that no bed changes along the offshore boundaries occur through the computational period. More specific information on the boundary conditions for the present study in the Tamsui River Estuary is provided in the following sections.
The simulations performed with this integrated model are also supported by a user-friendly interface (CCHE2D-GUI) [
46], which assists users to generate computational grids, specify boundary conditions and model parameters, and monitor and visualize the simulation results. All the submodels work with the same computational grid. Thus, the wave and flow models run on the same computational cores, passing information between submodels through the local memory/cache. It does not need to switch any additional executable codes during computations. All simulations are performed efficiently on a PC.
CCHE2D-Coast has been validated by simulating waves and storm surges induced by hurricanes in the Gulf of Mexico and investigating the impact of sea-level rise on morphological changes in the Touchien River estuary, Hsinchu, Taiwan [
5]. The validated CCHE2D-Coast model was applied to the feasibility studies of coastal protection plans, such as those for river channel dredging and layout of new coastal structures in the Touchien River Estuary [
45].
4. Numerical Model Validation and Statistic Error Analysis
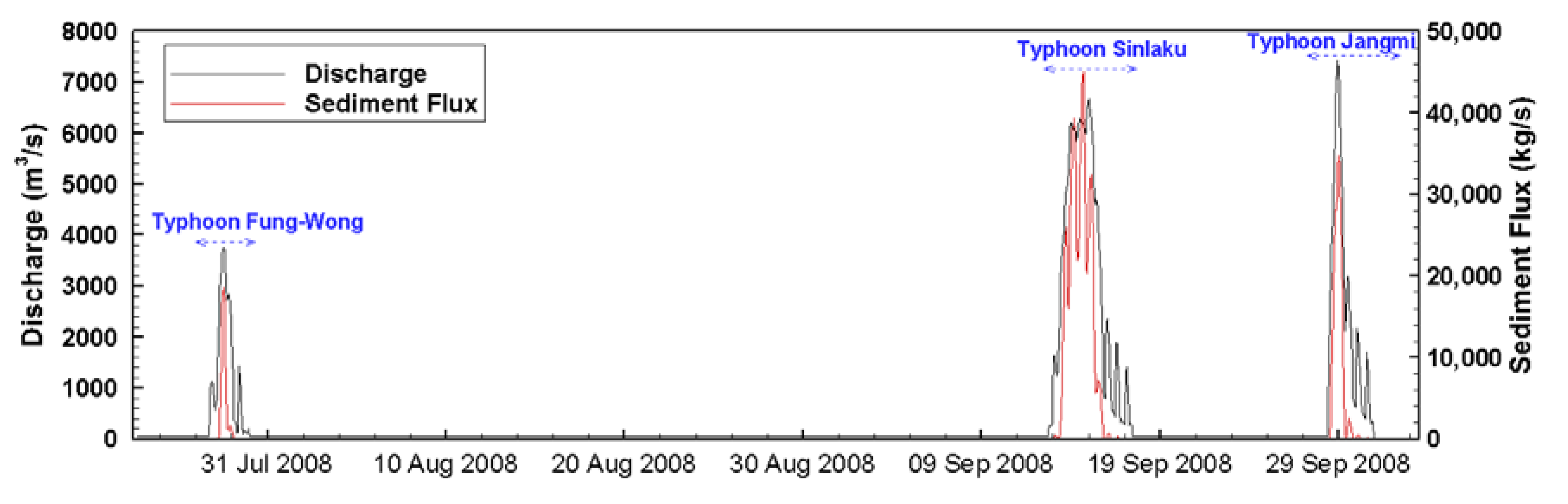
This study used the 2008 events of Typhoon Fung-Wong, Typhoon Sinlaku, and Typhoon Jangmi to carry out the model validation. The starting and ending times of each typhoon event are listed in
Table 1. The topo-bathymetric data used in the model were measured using single-beam echosounders in May 2008. The tidal levels at the west and east boundaries were given by measured tidal gauge data at the Linshanbi and Zhuwei Fishing Port stations. The wind data measured at the Taipei Harbor meteorological station were used to generate time-dependent and spatially-uniform wind fields. The peak flows in the three typhoon-induced flood events were 3798, 6476, and 7332 m
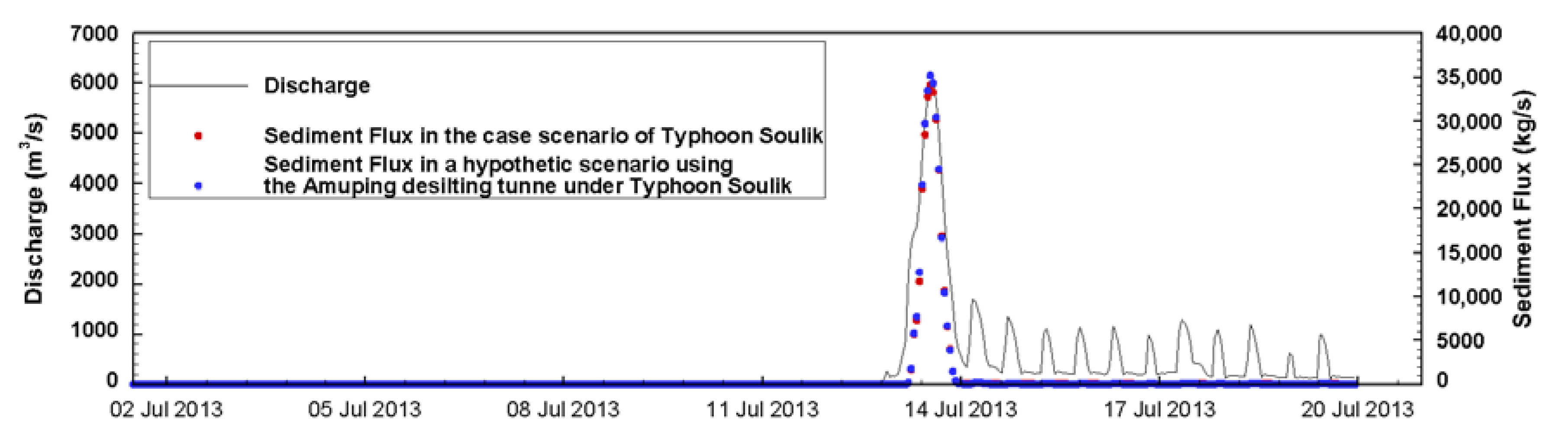
3/s, respectively, whereas the sediment concentration was controlled by the sediment discharge operation of the stream Shihmen Reservoir, with the maximum concentration of 45,042 kg/s occurring during the period of Typhoon Sinlaku (
Figure 4). It was assumed that the flow at the Guandu Bridge was 50 m
3/s, and the sediment concentration was 0 kg/s in the absence of flood drainage at the reservoir. The simulation period ranged from 17:00 on 23 July 2008 to 00:00 on 1 October 2008, totaling 1675 hours. The model was spun up by computing the tide flows from 17:00 on 23 July 2008 before introducing Typhoon Fung-Wong, in which the time step was set to 30 s. After the spin-up, the wave–current interaction for modeling morphological changes was conducted for 66 days until the end of Typhoon Jangmi at 00:00 on 1 October 2008. Then, the time step for computing flows was changed to 10 s; the time step for updating bed elevations was 100 s. The wave field was recomputed every one hour based on the latest flow field.
To quantify the difference between the calculated results and the observed values, this study employed the four parameters, such as the root-mean-square error (
RMSE), the Pearson correlation coefficient (
r), the scatter index (
SI), and the normalized bias (
NB). The calculation results of these parameters at three stations (the locations are marked in
Figure 3) are listed in
Table 2. The
RMSE was used to quantify the deviation between the simulated and observed values;
r was used to evaluate the correlation between the simulated and observed values;
SI was the ratio of the standard deviation between the simulated and observed values to the mean of the observed values; the indicator
NB evaluated the extent to which the calculated results were overestimated or underestimated relative to the true values.
RMSE,
r,
SI, and
NB can be calculated using the following expressions:
where
is the error between the simulated value
and observed value
in the simulation time series, i.e.,
;
is the total number of the observations;
is the average error of the simulated value expressed as
;
is the average observed value expressed as
;
is the average simulated value expressed as
.
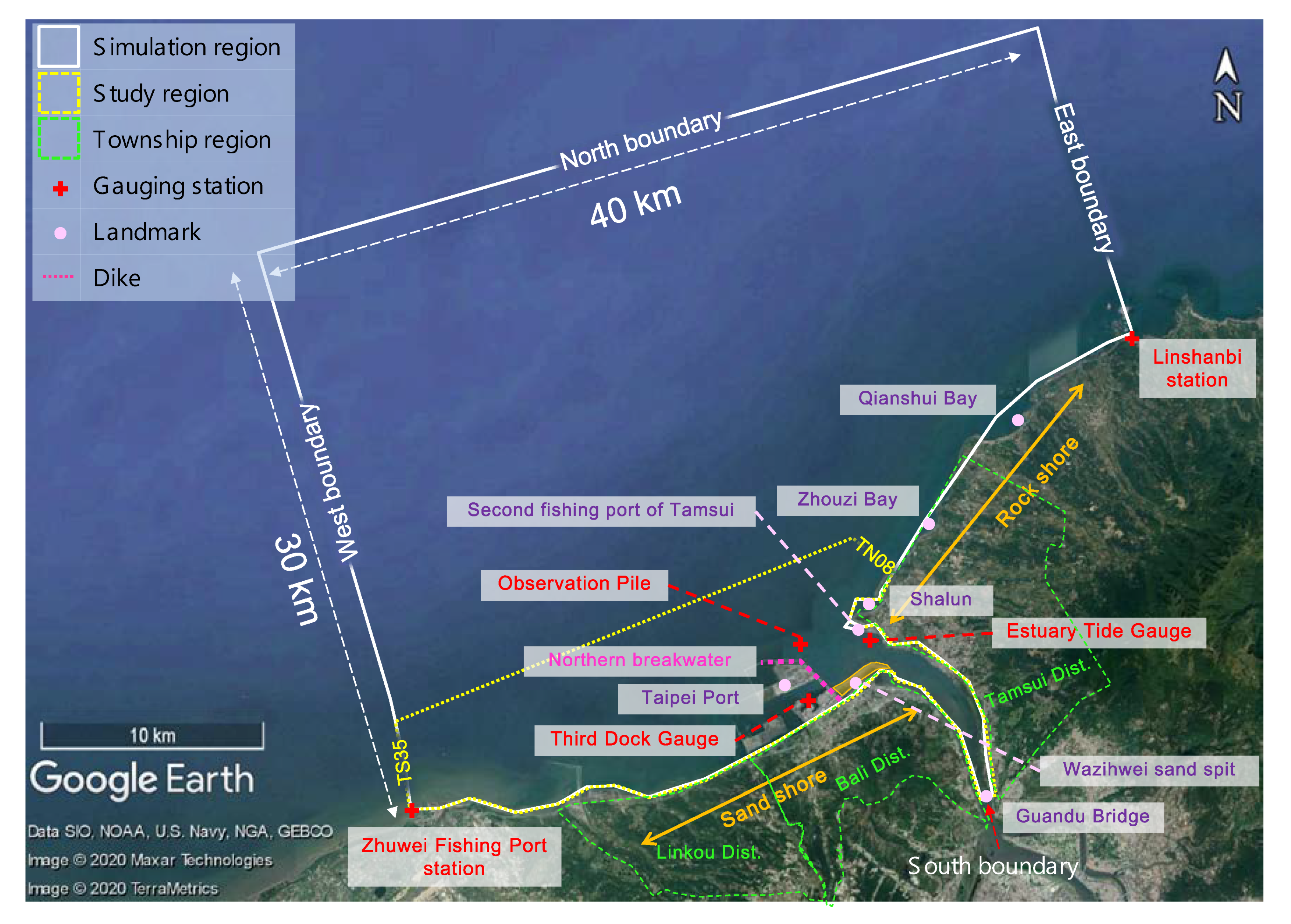
In the simulation range, tidal level gauges were installed in the Tamsui River estuary, the third dock in the Taipei Port, and the observation pile outside the Taipei Port, as shown in
Figure 3. Only at the observation pile outside the harbor at the estuary, were waves measured. In the Typhoon Fung-Wong event, the Shihmen Reservoir was operated for flood drainage and sediment discharge from 18:00 on 27 July 2008 to 23:00 on 29 July 2008, which resulted in a rapid increase in the water flow and sediment transport in the river channel.
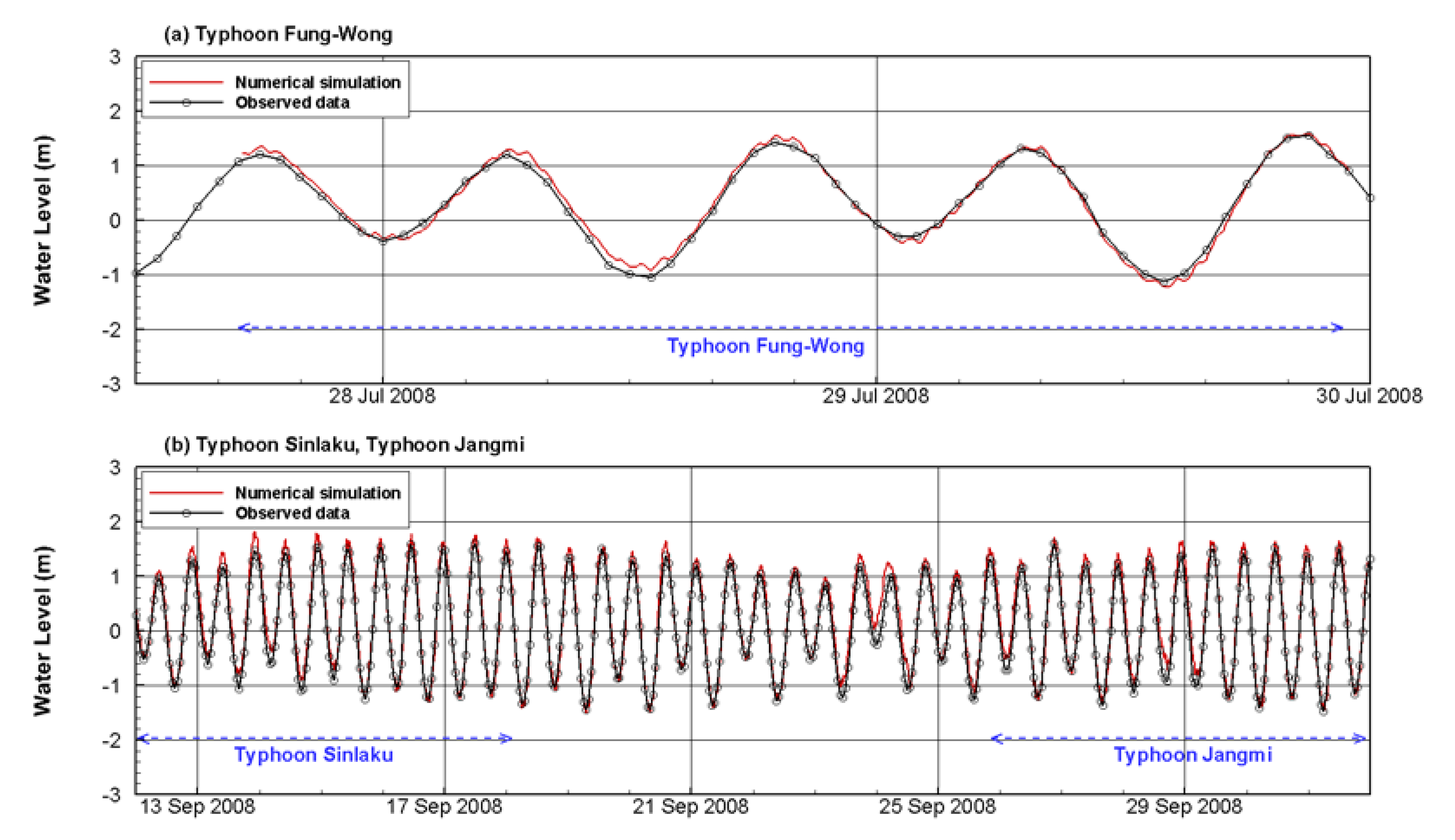
The overall r values shown in
Table 2 indicate a very strong correlation in tidal levels and wave parameters (wave heights and periods) between the observations and simulations at the four measurement stations. The simulation results in
Figure 5a show that the simulated water levels at the estuary tide gauge were quite close to the measured values (
RMSE = 0.10 m;
NB = 0.04).
Figure 5b presents the simulated and measured water levels at the same location from September 13 to October 1—covering the period of Typhoon Sinlaku and the period of Typhoon Jangmi (
RMSE = 0.16 m;
NB = 0.13). Although the
RMSE values were small relative to the tidal range in the area (2.0–3.0 m), the differences in the water levels were due to the effect of river inflows.
The simulated water levels at the other two gauges were also close to the measured data. The maximum RMSE was 0.35 m at the third dock gauge inside the harbor, calculated during the period of Typhoons Sinlaku and Jangmi. The values of NB varied from −0.34 at the third dock gauge inside the harbor to +0.46 at the observation pile outside the harbor. It means that the model underestimated the water levels inside the harbor but overestimated outside. The reason for the errors could be because two gauges are too close to breakwaters of the harbor. So the measurements of the water levels may contain the effect of reflections of the structures.
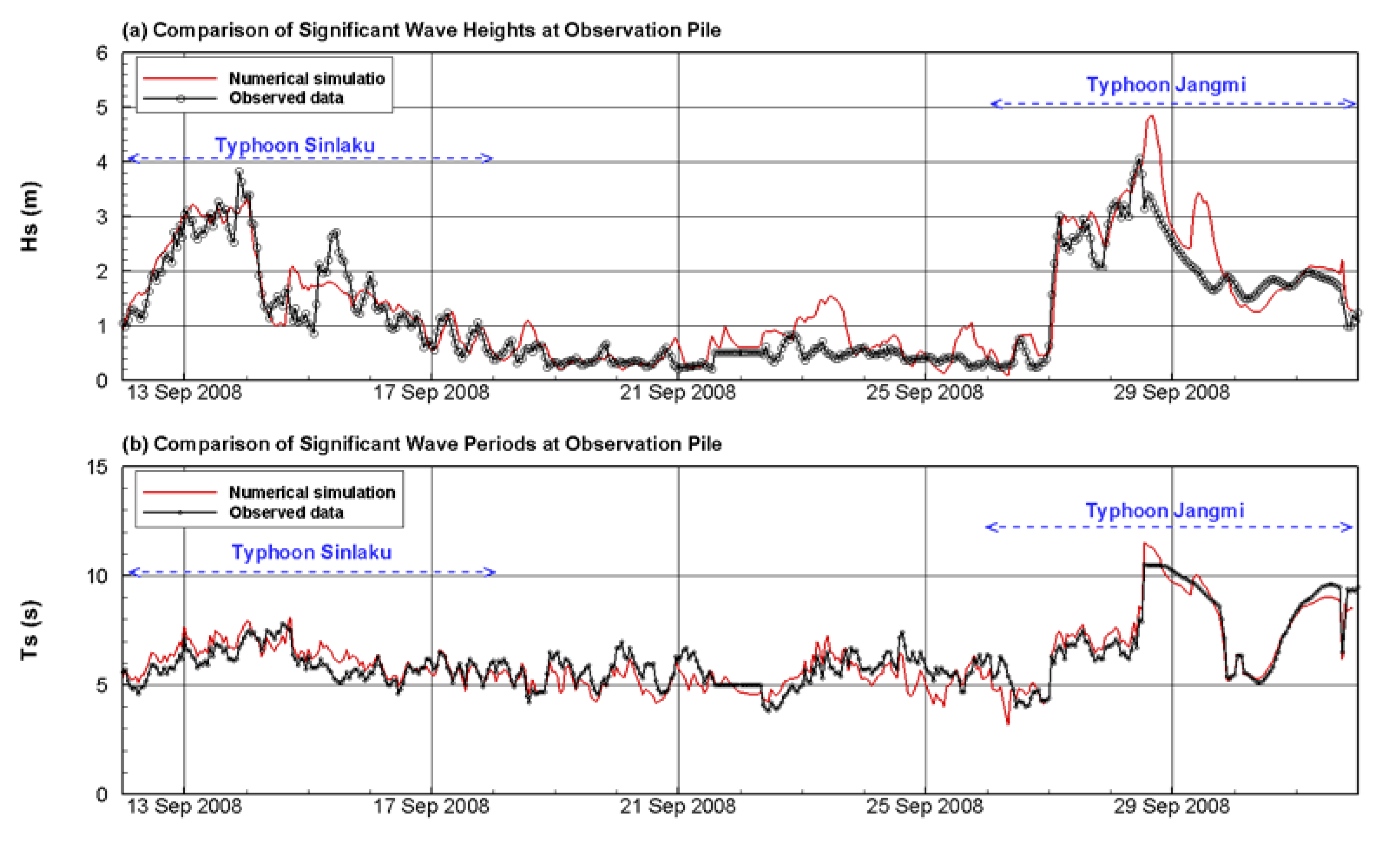
In the simulation range, only one buoy was installed near the Taipei Port at a site with water bottom elevation of approximately −10 m (
Figure 3) for wave parameter measurement.
Figure 6 presents the simulated and actual results of wave height and wave period during the periods of Typhoon Sinlaku, and Typhoon Jangmi. The results show that the wave height reached 4 m during the period of Typhoon Jangmi but varied between 0.4 and 0.6 m in the non-typhoon period. However, during the transition period from Typhoon Sinlaku to Typhoon Jangmi (
Figure 6), the
RMSE between the simulated and observed values of the significant wave height was only 0.42 m, the
r value was 0.93, and the
SI value was 0.33, with the simulated values tending to be slightly overestimated (
NB = 0.13); the
RMSE,
r,
SI, and
NB between the simulated and observed values of the significant wave period were 0.58 m, 0.92, 0.12, and −0.01, respectively, with the simulated values slightly lower than the observed ones. As expressed by the above quantitative indicators, CCHE2D-Coast could effectively reproduce the changes in water level, wave height, and wave period during typhoon-induced flooding periods and non-typhoon periods.
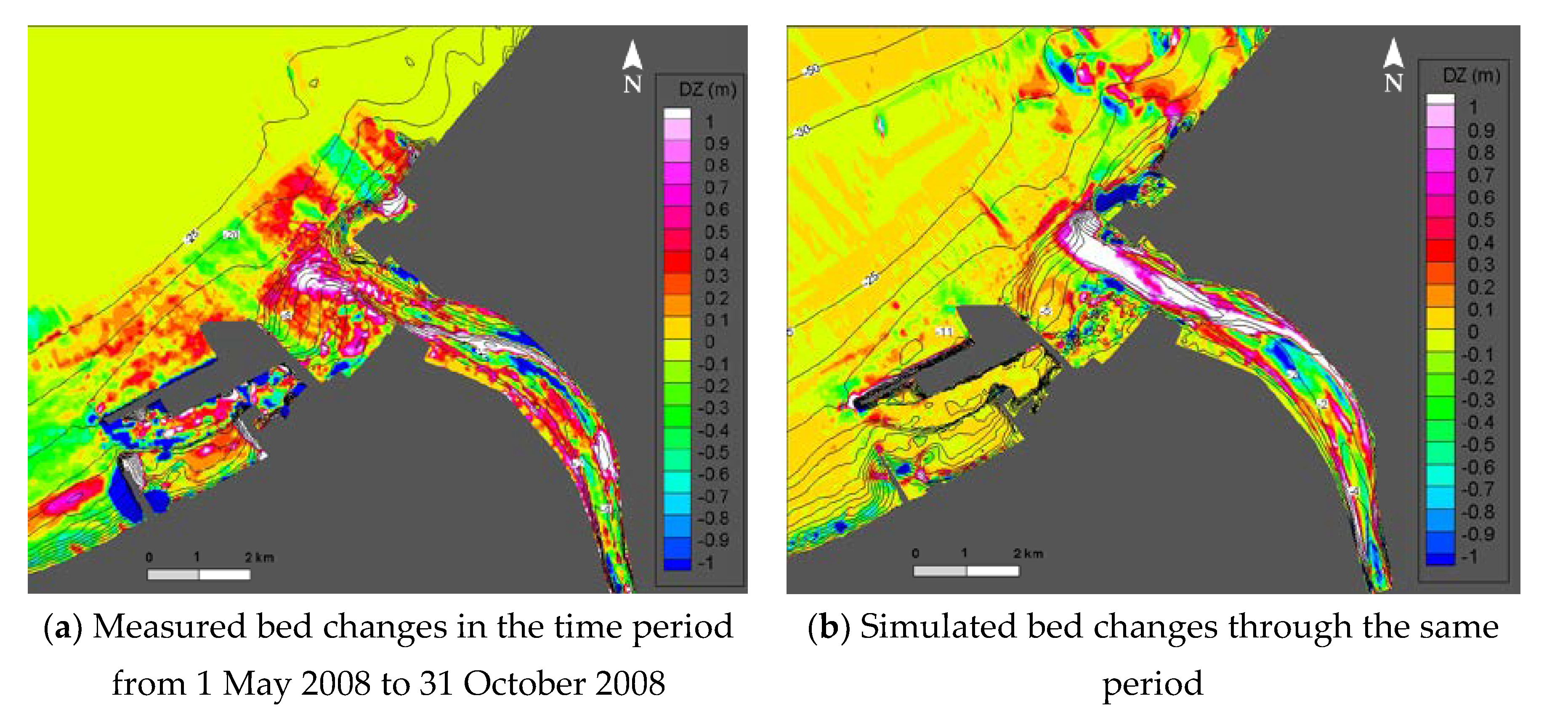
The topo-bathymetric data used in the analysis were measured by using the single-beam echosounders in 1 May 2008 and 31 October 2008. It may accurately reflect the morphological changes caused by Typhoon Fung-Wong, Typhoon Sinlaku, and Typhoon Jangmi. The total discharge of the Shihman Reservoir in three typhoon-induced flood events, respectively, were 142.83, 622.24, and 237.36 million m
3 with the total sediment discharge of 3.45 million tons.
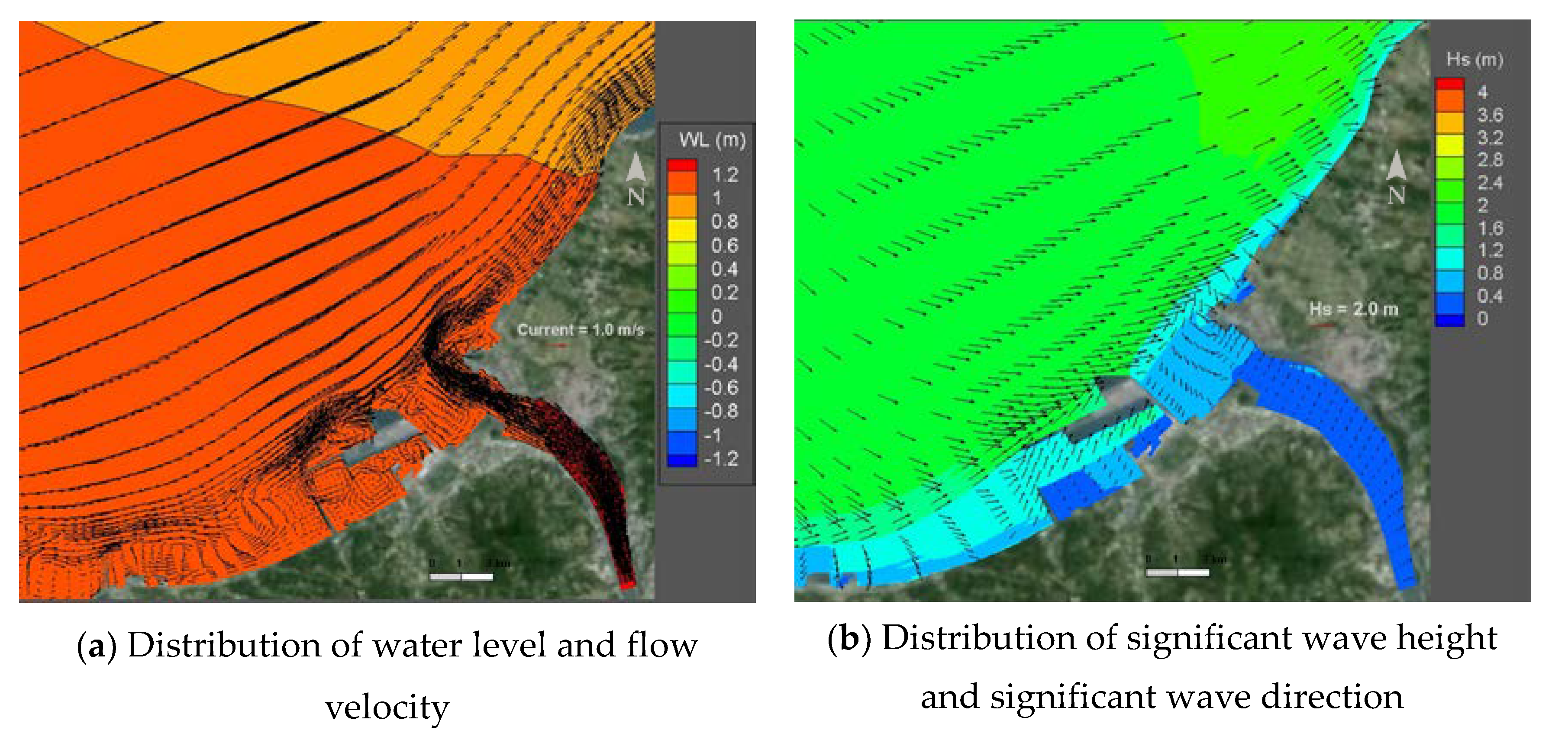
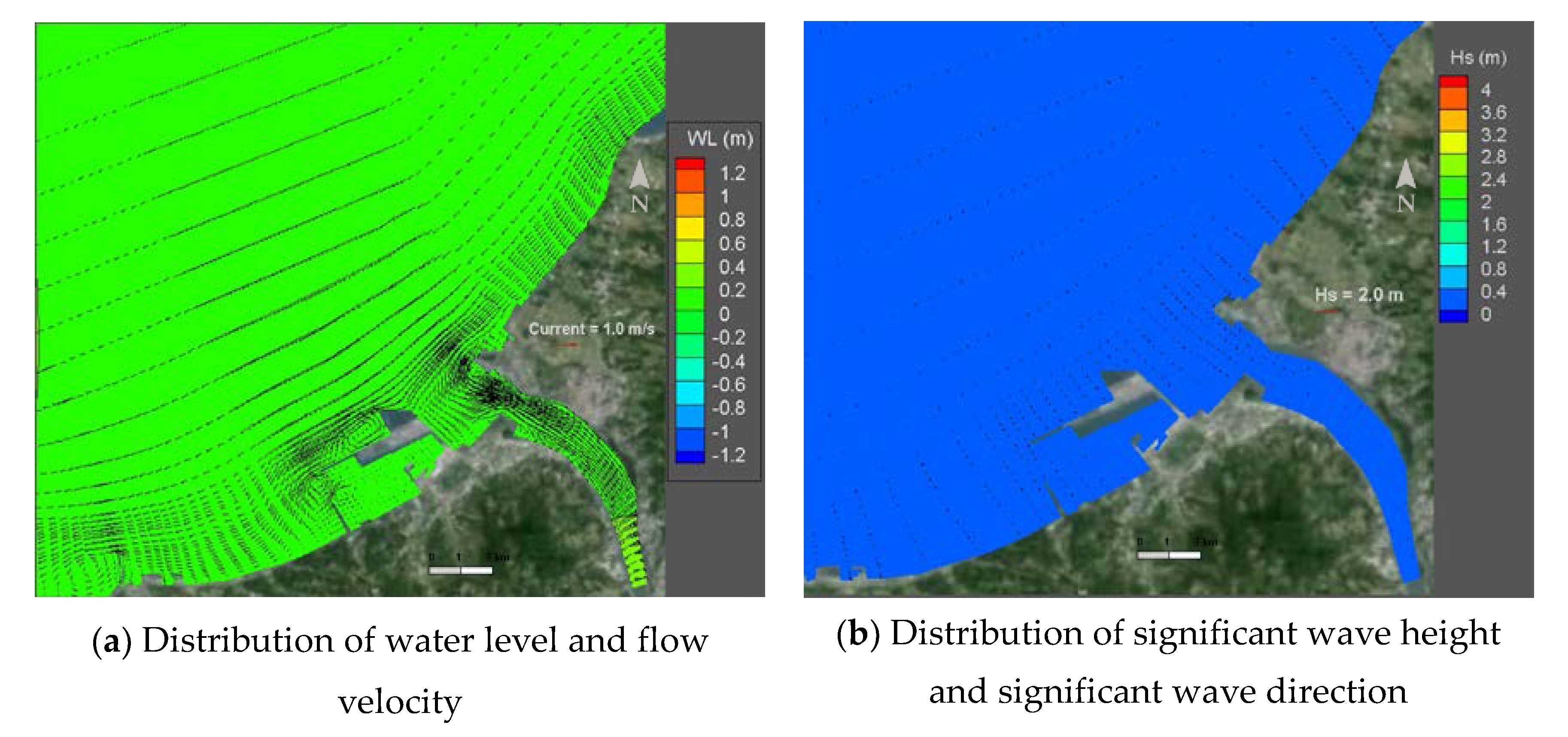
Figure 7a shows that the changes in the nearshore seabed did not comply with the sediment transport mechanism due to the anthropogenic disturbance. However, the morphological changes in the river estuary were from reasonable patterns of deposition and erosion. As indicated in
Figure 4, the sediment was transported in a large quantity to the estuary and channel bed, where it was deposited due to the large river flow during the typhoon periods. The farthest deposition site had the water bottom elevation of −10 m; meanwhile, the significant morphological variation occurred within water bottom elevation of −5 m.
Figure 7b indicates the bed changes simulated by the CCHE2D-Coast model through the same period from May to October of 2008. Comparing it with the observations in
Figure 7a, the simulated bed changes have a good agreement with the observed one. The morphological changes in the tidal river reach from the river upstream of the Guandu Bridge to the river mouth have consistent variations with the field measurement. The similar depositions which occurred in the river bend were close to the concave bank and a large area of the river mouth. Although the model captures the features of the scouring and erosion close to the center of the bend, the simulated deposition at the river mouth was overestimated; the field observation showed more settling of river sediments at the south side. The simulated results also showed the less sedimentation inside the Taipei harbor. The dredging may be conducted near the breakwater in this period; however, the proposed model did not incorporate the effect of the anthropogenic activities. Moreover, the obvious difference in the bed change at the north shore of the river mouth could be found. The simulated erosion was driven by the simulated tidal currents and nearshore currents due to waves, while the sea bed was assumed as erodible due to lacking data. Overall, the numerical model produced reasonable results on the morphological changes in a wide range of the Tamsui River estuary. The current developed numerical models for simulating the sediment transport and morphodynamic processes are still challenging, a few factors, e.g., using spatially-varying bed materials, inclusion of dredging, sand mining activities, and fractional sediment transport load, would be further considered in the future work.
6. Conclusions
To evaluate the trend of riverbed change by numerical modeling, the relevant model parameters were first validated using the 2008 events of Typhoons Fung-Wong, Sinlaku, and Jangmi, allowing the CCHE2D-Coast model to effectively reproduce the complex flow fields and sediment transport processes at the Tamsui River estuary, such as flooding, erosion, and aggradation along the coast, along with scouring of the estuarine sandbar. Next, this model was used to explore the effects that the operation of the Amuping desilting tunnel of Shihmen Reservoir would have on the downstream river channel, and to compare the sediment transport characteristics in the Tamsui River estuary during typhoon-induced flood and a period with the monsoon.
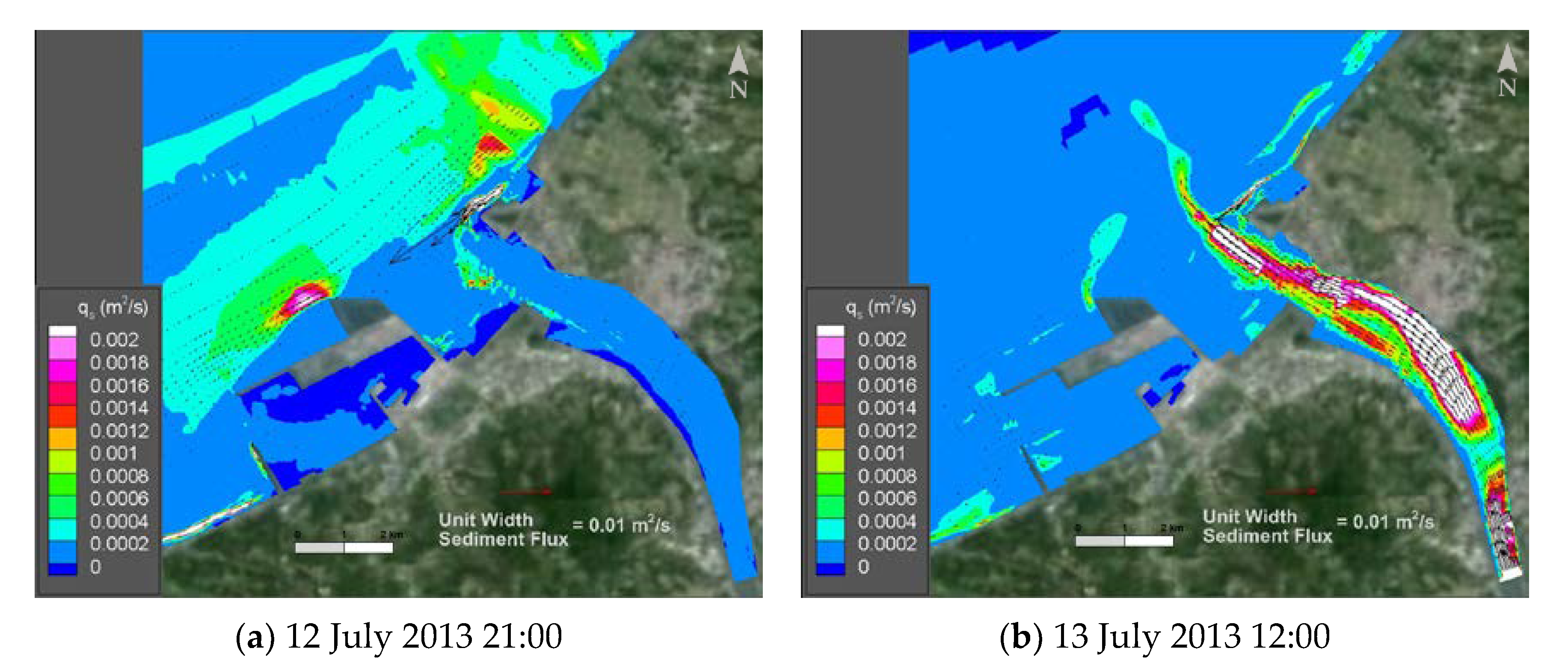
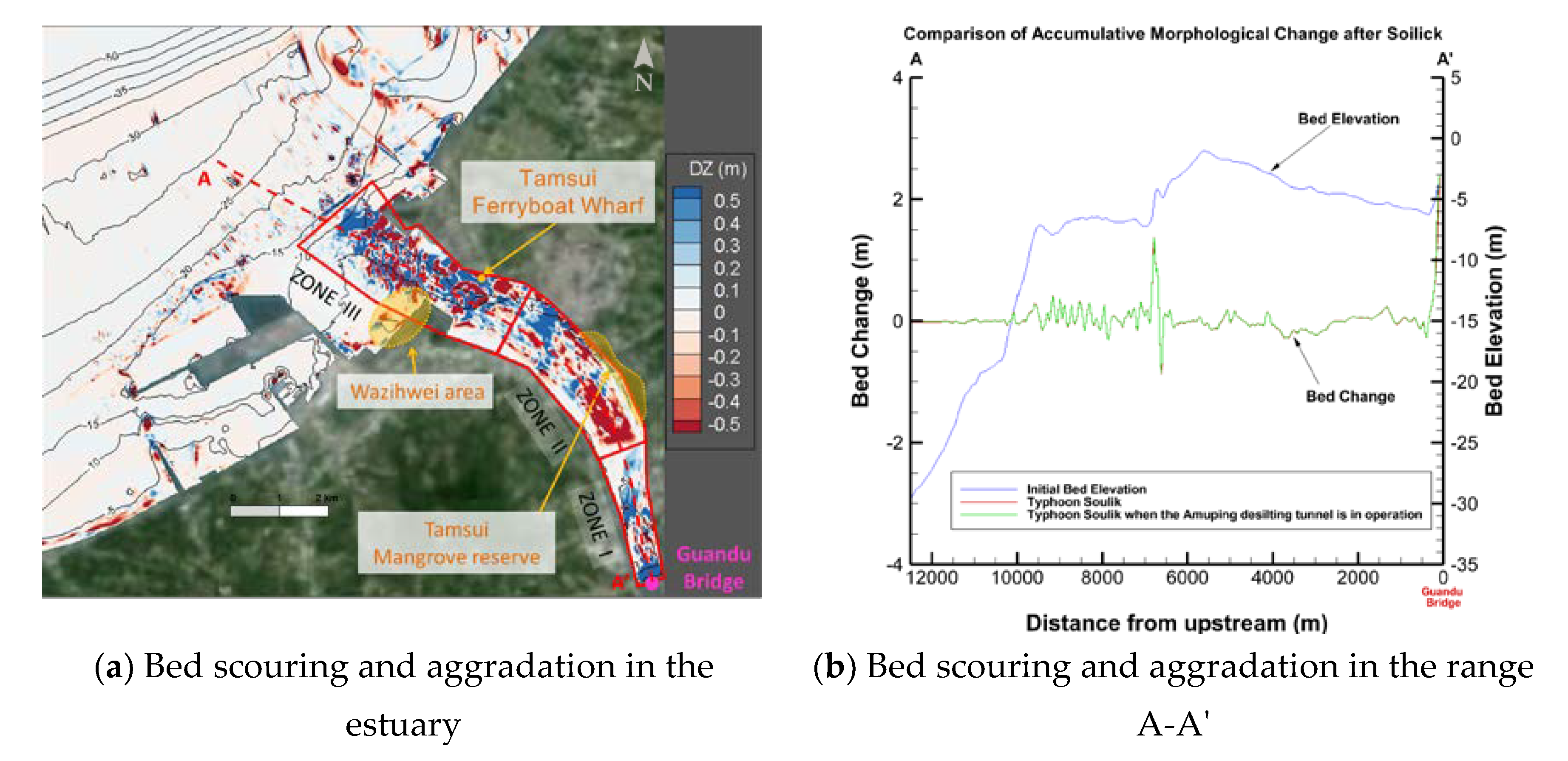
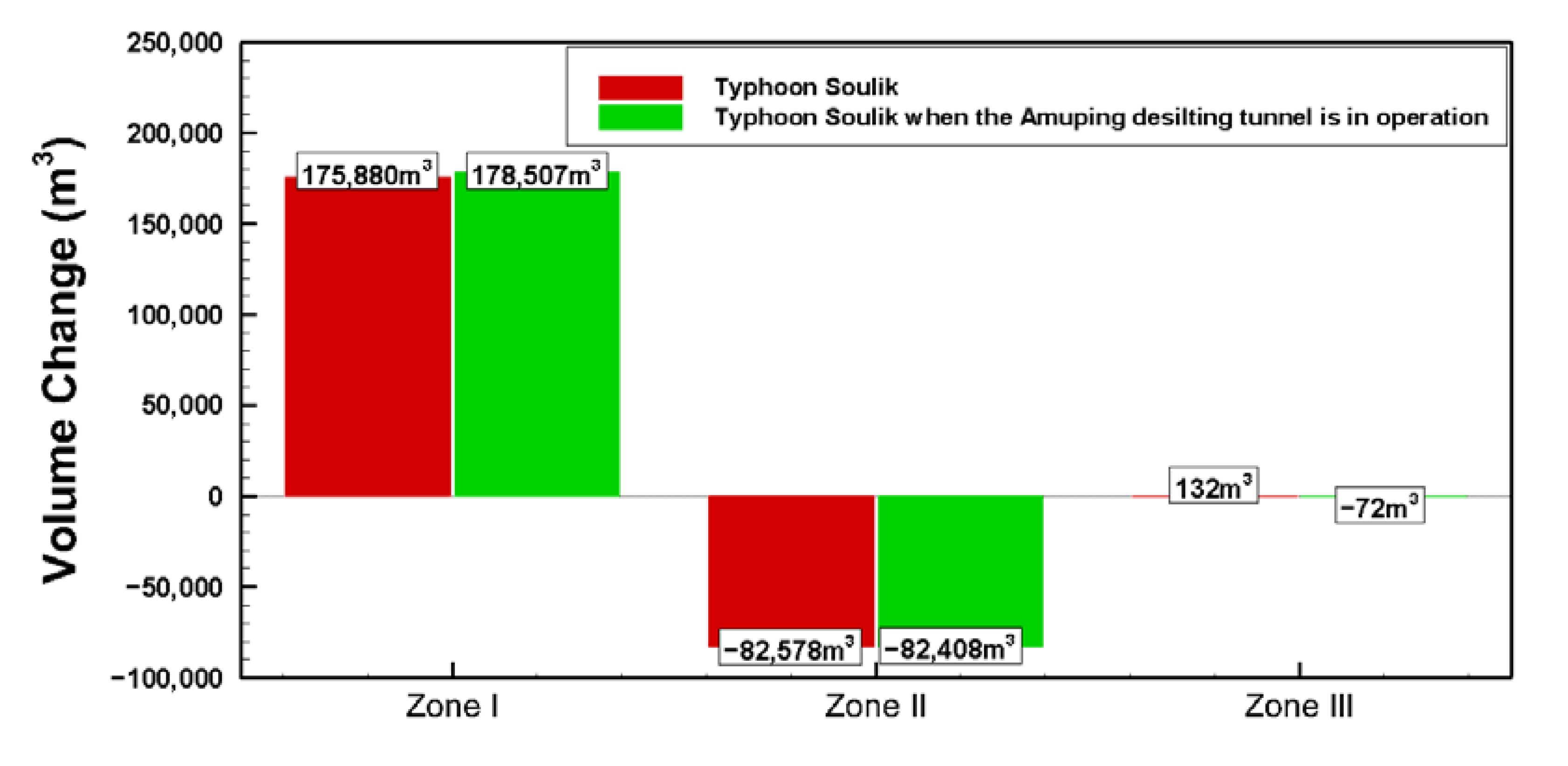
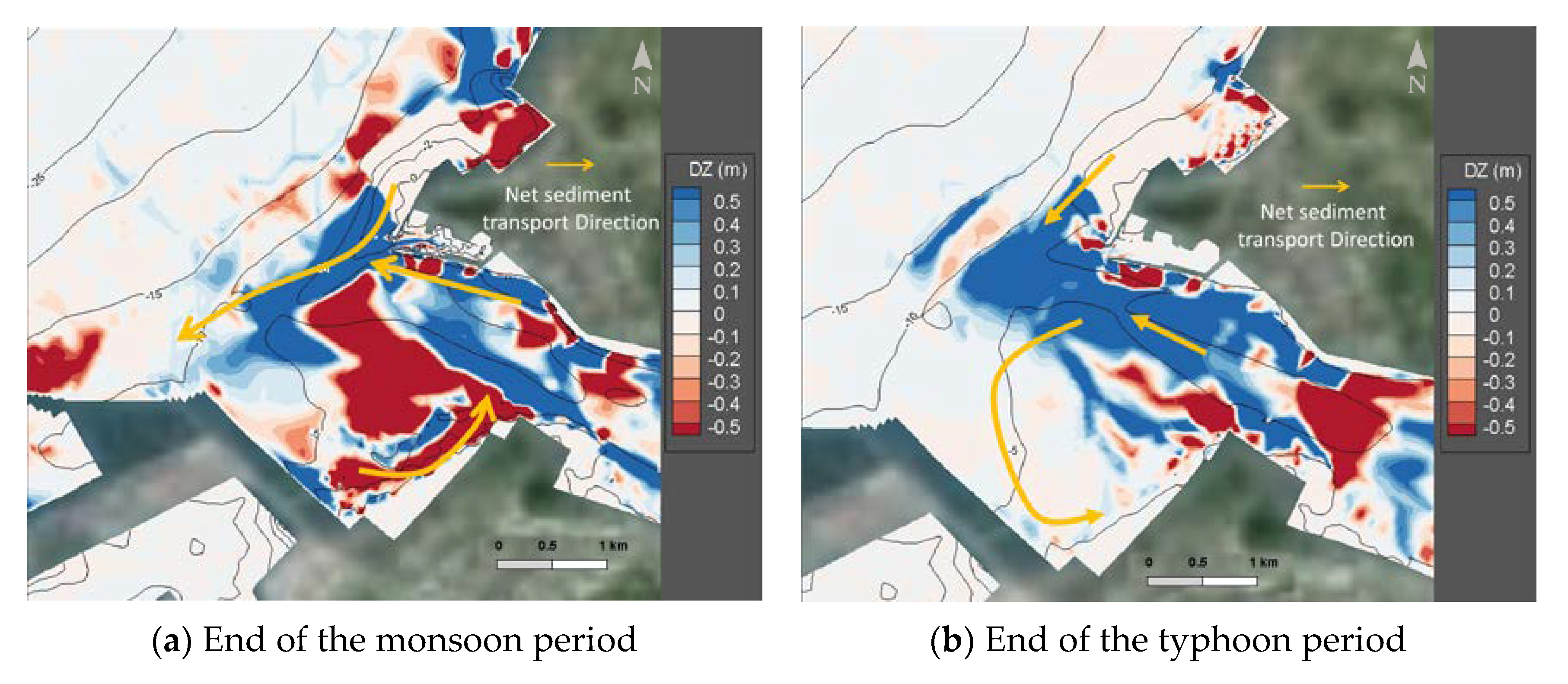
The results showed that for sediment transport during the typhoon-induced flood period, the upstream flood transported a large amount of sediment to be deposited in the estuary, and parts of sediment were transported by currents to the Wazihwei sand spit where they were deposited. Under the condition that the flow is kept unchanged and the sediment concentration is increased (after the construction of the Amuping desilting tunnel), the sediment transport capacity of the river water will be reduced, which in turn would increase the degree of aggradation in the river channel while slowing down of aggradation in the estuary. During the monsoon period, sedimentation was mainly determined by ocean currents, and the transport was also subject to coastal topo-bathymetry, coastal structures, and tidal currents. The sediment is deposited in the outside area of the second fishing port of Tamsui, the north breakwater of the Taipei Port, and in the estuarine areas. The Wazihwei sand spit would be subject to aggradation due to backflow. As to whether these processes would further lead to long-term morphological changes in the Wazihwei sand spit, it is necessary to address the issue by incorporating numerical modeling with topo-bathymetric data and satellite imagery in the future. Meanwhile, the Wazihwei area is in a nature reserve, and the effectiveness of conducting sediment management to maintain the sandbar area also can be evaluated by numerical modeling.
This numerical simulation study reproduced the changes in hydrodynamics and morphodyanmics of the Tamsui River estuary and will facilitate the management of sediment transport in the Tamsui River Estuary driven by multiple coastal and estuarine processes, such as waves, tidal currents, and river flows.